1 Introduction

During the past decades, the use of robotic fabrication practices has increased in many fields, especially in architecture. Robotic fabrication shows potential for improving processes across a variety of application, from improving the sustainability of additive manufacturing (Ford and Despeisse 2016), such as reduction in waster and energy saving (Faludi et al. 2015), to its use for the execution of both standardized and customized construction assembly tasks (Keating and Oxman 2013). Robotic fabrication shows its potential benefits for complex structures in concrete (Agustí-Juan et al. 2017), lightweight timber plates through robotic milling combined with manual assembly work (Krieg et al. 2015), and brick laying using mobile robots (Helm et al. 2012).Compared to CNC technologies, which are used in timber prefabrication predominantly to manufacture standard components like beams and plates (Popovic et al. 2016; Eversmann et al. 2017), robotic fabrication shows its strength in mass customization of movements to make more complicated timber joints due to the potential for complex manipulator trajectories (Jeffers 2016). However, the complexity of the design makes the trajectory more intricate which often increases process time. Robotic chainsaw cutting has a range of applications in timber fabrication industries, however, to achieve an efficient process there are specific aspects of the task which must be taken into consideration. The surfaces in the cutting task are in different surfaces and the cutting order passing through these surfaces has significant impact on working efficiency. When dealing with complex joints, path planning for robotic chainsaw cutting can be time-consuming and manual creation of paths can not guarantee the most efficient solution.

To generate an efficient trajectory requires the satisfaction of specific objectives like time reduction and minimizing of the quick short movements of the robot manipulator. These quick short movements create sudden jerks to the end effector and can reduce the quality of the cut of damage the chainsaw. There are diverse researches on robotic automation construction (Labonnote et al. 2016) and various trajectory optimization techniques (Ata 2007; Jeevamalar and Ramabalan 2012; Ratiu and Prichici 2017), however research on specific trajectory planning optimization methodology applied on a full-scale architecture joint fabrication is rare. Therefore, this study takes the following case as an example to test the feasibility of the trajectory optimization techniques in real practice.

1.1 Case study

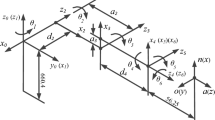
In this case, tree trunks are chosen to be the material which would be firstly scanned and then cut by a robot arm equipped with a chainsaw. This case study illustrates the problems within trajectory planning of complicated timber joints in order to test optimization methods for increasing process efficiency. The complicated timber joint was designed and fabricated in a workshop at the international conference: ROB|ARCH 2018. The timber joints are designed in Rhino, and the simulation of cutting process using a KUKA robot equipped with a planar cutting tool (chainsaw) uses KUKA|prc. The details of the robotic chainsaw cutting task including the design of the timber joints and the setting work space are shown in Fig. 1.

Fig. 1
figure 1

Diagram of chainsaw cutting

Full size image

The first parameter of the process is the shape of the cutting faces as the input surfaces. The cutting tool is always at the backside of the input surface, which could be achieved by reversing the normal direction of the input surfaces. This is to align the normal direction of the tool with the normal direction of input surfaces to be in the right offset side. The cutting direction and the cutting order of the four points within one cutting surface is consistent with the drawing order 1, 2, 3, 4, shown in Fig. 2. In this case, the surfaces that have similar orientation are grouped to reduce the amount of re-orientations to save time and avoid collisions.

Fig. 2
figure 2

Movement of chainsaw within one cutting surface

Full size image
Fig. 3
figure 3

On-site fabrication

Full size image

When planning multiple cuts, the main difficulty is to designate the cutting order of different cutting surfaces to avoid kinematic singularities and at the same time to avoid collisions. The timber joint in this case has been divided into four cutting parts, and every part has more than 10 cutting surfaces; each surface has four cutting points. The cutting order combinations could be \(n!\times C_{4}^{3}\), where n is the number of cutting surfaces, which means it is impractical to figure out every rational combination. Two parts of the timber joint have been fabricated in the work space (Fig. 3) and the results are shown in Fig. 4a, the same as the initial design in Rhino. During the workshop, the cutting order was set manually. The whole process took considerable time and decreased the degree of automation of robotic fabrication. This also added uncertainty as to whether the manually designed path was the shortest travel distance or not. To tackle the difficulty found during the workshop, one part of the joint (Fig. 4b) is selected to as an example to be optimized.

Fig. 4
figure 4

Timber joint fabrication

Full size image

This study took 13 cutting surfaces of the first part as the example for addressing complicated robotic timber joints within trajectory planning and utilizes a multi-objective technique to obtain trajectory planning optimization of robot manipulators corresponding to the specific example in this study, to put forward a feasible solution to find the best cutting order automatically to achieve the shortest distance and time.

1.2 Trajectory planning in robotics

The trajectory planning problem in robotics is to find a motion along the given geometric path, taking into account process constraints, to generate inputs for the control system of the manipulator, which ensures the implementation of the planned movement (Gasparetto and Zanotto 2010; Gasparetto et al. 2012). Trajectory planning in robotics is generally carried out in the operating space (Luh and Lin 1981) or joint space (Craig 2009). The trajectory described in the joint space returns the position for each joint of the manipulator, corresponding to the points set by the user.

Though in the operating space, the trajectory of the end-effector can be described directly, it is very difficult to solve the problem analytically due to the highly coupled and highly sub-linear characteristics of robot dynamics equations. In most cases, the trajectory planning is solved in joint space to avoid kinematic singularities or manipulator redundancy (Gasparetto et al. 2015). The most common method is to transform the trajectory function from operating space into joint space, and then to control the manipulator in the joint space.

The trajectories defined in the joint space are constructed by means of interpolation functions such as polynomial, spline, Bezier, and NURBS, etc., which are restricted to kinematic constraints. Conventional polynomial interpolation has developed 343,445 and novel 5455 methods based on different orders polynomial functions (Cook and Ho 1984; Petrinec and Kovacic 2007; Boscariol et al. 2012). Trajectories interpolated by spline functions shows good performance ensuring the continuity of the acceleration or jerk (derivative of the acceleration), cubic B-spline, quantic B-spline as 7th-order B-spline have been tested to obtain trajectory smoothness (Ramabalan et al. 2009; Gasparetto and Zanotto 2008; Zhu et al. 2010).

Numerous techniques for optimal offline trajectory planning have been developed in the last decades by different researchers in the field. The trajectory planning algorithm takes the geometric path, kinematic and dynamic constraints as inputs and generates the trajectory of the joints, or of the end-effector by means of position, velocity and acceleration expressed in time sequence (Siciliano et al. 2010). The aim of the trajectory planning optimization is to improve the manufacturing productivity and the movement stability, which means the short execution time or smooth path (Huang et al. 2018). Most of the trajectory planning algorithm optimizations are based on an objective function of some parameters to improve: (1) minimum execution time, (2) minimum energy, and (3) minimum jerk, or a combination of these (Gasparetto et al. 2012).

1.3 Optimal techniques

The most common used trajectory planning optimization techniques are minimum-time algorithms, due to the need for increasing productivity in the industrial sector (Gasparetto and Zanotto 2010; Piazzi and Visioli 1998). A convex optimization for time trajectory planning was put forward by converting time-optimal problem into convex optimal control problem, neglecting the viscous friction (Verscheure et al. 2009). When robot moved at high speed, time-optimal optimization could be non-convex taking the viscous friction of robots into consideration (Shen et al. 2019). To solve this inaccuracy, a new genetic algorithm for time-optimal and collision-free trajectory in complex environments was developed (Abu-Dakka et al. 2015). Also, these algorithms meet torque and acceleration discontinuity required by assuming that robot was a rigid body. To overcome these drawbacks, the actuator jerks were introduced as an additional metric for optimization (Constantinescu and Croft 2000).

Besides time optimization, jerk minimization results in better performance in tracking capacity (Gasparetto et al. 2015; Kyriakopoulos and Saridis 1988), being able to achieve smaller excitation of resonance frequencies (Gasparetto et al. 2015). Squared jerk has also been set as the optimization object using spline interpolation (Gasparetto and Zanotto 2007; Simon 1993; Zanotto et al. 2011).

Minimizing the energy consumption is another alternative optimization objectives, which leads to the smoothness of the trajectory with smaller stresses on the robot manipulator (Field and Stepanenko 1996). Cubic B-spline functions, fifth order B-spline and Lagrange interpolation have been applied to construction trajectories within energy minimization objective (Gasparetto and Zanotto 2007; Sato et al. 2007; Luo et al. 2015).

In addition, hybrid optimizations have also been proposed instead of a single optimization objective function. Time-energy optimal trajectories planning is composed by two terms, the first related to the travel time and the second to energy. The optimal objective is to reduce the stresses of the actuators and to promote the most efficient trajectory tracking (Balkan 1998; Shiller 1996). Similar to time-energy, time-jerk optimal trajectory planning also consists of two parts, time and jerk (third derivative of position) (Gasparetto and Zanotto 2007, 2008; Zanotto et al. 2011). The simulation and experiment results validated the effectiveness of the methods. However, the trade-off between the two criteria is controlled by two weights of the objective function which still requires artificial adjustment. To solve the multi-objective problems, there is an emerging alternative which is to employ evolutionary algorithms such as particle swarm optimization (PSO) and adaptive genetic algorithm (AGA) to solve the above-mentioned drawbacks (Ata and Myo 2005; Saravanan et al. 2008).

PSO was devised in 1995 inspired by the flock of birds’ behaviour and has been applied to many fields of optimization problems (Eberhart and Kennedy 1995). As a random-search algorithm, studies have verified the convergence speed of particle swarms by offering the initial behaviour of a population (Reyes-Sierra and Coello 2006; Helwig and Wanka 2008; Trelea 2003). In addition to the performance of PSO on continuous optimization problems, many studies have tested the application of PSO on discrete problems (Kennedy and Eberhart 1997; Wang et al. 2003; Shi et al. 2007), including the optimization of path planning (Hoffmann et al. 2011). PSO shows its potential in finding the shortest collision-free path for mobile robots effectively (Zhao and Yan 2005). More simulation results shows the competence of PSO in path planning in static or dynamic environments (Xu et al. 2008; Hao et al. 2007). PSO could also tackle multi-objective robot path planning with uncertainty in planar surface (Zhang et al. 2013). Apart from travel distance, a multi-objective particle swarm optimization algorithm is applied to minimize the travel time, energy and the distance of the end-effector (Xu et al. 2015).

Genetic algorithm (GA), inspired by natural genetic systems and natural selection (Davis 1991), is viewed as another advantageous evolutionary process to optimize nonlinear and complex problems which traditional method could not solve (Davis 1987). The AGA varied the probability of crossover and mutation probability depending on the fitness value of the objective function (Srinivas and Patnaik 1994). The AGA method significantly optimizes the time-intervals between each section of the trajectory so as to raise the efficiency of the robot (Liao et al. 2010). Combing the quintic polynomial function to interpolate the trajectory, time-optimal trajectory planning could be realized by AGA to reduce running time (Zhang et al. 2018). When tackling the same trajectory time-optimal problem, the simulation results show that AGA converge better than GA and reduce the probability of local best solutions to achieve better stability of robot (Fu and Ju 2011).

This study reports two optimal objectives (travel distance and execution time) to obtain smooth and short trajectories of robot manipulators. With respect to most path and time optimal algorithm techniques in scientific literature so far, the PSO along with AGA are selected to deal with the two optimization objectives, respectively.

This paper is organized as follows. In Sect. 2, the trajectory optimization problem is formulated and kinematic singularities are defined; fifth-order polynomial function is chosen to construct the joint trajectory, and Modified Denavit–Hartenberg is chosen to build the robot model. In Sect. 3, the robot arm model is built in MATLAB and the data of the model in Rhino is converted to interpolate the position, velocity and acceleration of the six joints according to the setting points. Section 4, describes the whole algorithms in detail and describes the execution. Section 5 shows the results of the simulation.

2 Methodology

2.1 Formulation of the optimization objectives

The KUKA robot with six degrees of freedom is considered in this study. The trajectory planning methodology described in this paper assumes that the geometric path is converted from the specific geometry vertices. The path is given as a sequence of points in the operating space, which represent the positions and orientations of the end-effector. The points would be transformed to consecutive points in the joint space through inverse kinematics. Based on the points in the joint space, a trajectory would be constructed and then optimized for the minimization objectives. Obstacle avoidance and collision problems are assumed solved and will not be in the scope of this study.

Considering the uniqueness of this case study, the proposed technique does not set the geometric path as a variable, which is different from the current trajectory planning. The minimization of the travel distance of the end-effector has direct effect on the time minimization. In this study, two objective functions are formulated: the travel distance and the execution time.

The two optimization problems are mathematically defined as follows and the meaning of the symbols are listed in Table 1 and Table 2: Minimize:

$$\begin{aligned} D = \sum _{i=1}^{N}L_i+\sum _{i=1}^{N-3}\sum _{j=1}^{M}L_{i,j} \end{aligned}$$
(1)

Subject to:

$$\begin{aligned} \left\{ \begin{array}{c} p_{k}(t) \in U_{j}, k=1,2, \ldots , n \\ x_{e}(t) \in U_{x} \\ y_{e}(t) \in U_{y} \\ z_{e}(t) \in U_{z} \\ |J| q \Vert \ne 0. \end{array}\right. \end{aligned}$$
(2)
Table 1 Meanings of symbols appearing in Eqs. (1) and (2)
Full size table
Table 2 Meanings of symbols appearing in Eqs. (3) and (4)
Full size table

Minimize:

$$\begin{aligned} T=\sum _{i=1}^{n-1} h_{i}=\sum _{i=1}^{n-1}\left( t_{i+1}-t_{i}\right) \end{aligned}$$
(3)

Subject to:

$$\begin{aligned} \left\{ \begin{array}{c} \left| {\dot{p}}_{i}(t)\right| \le V C_{i}, i=1,2, \ldots , N \\ \left| \ddot{p}_{i}(t)\right| \le W C_{i}, i=1,2, \ldots , N \\ \left| \ddot{p}_{i}(t)\right| \le J C_{i}, i=1,2, \ldots , N. \end{array}\right. \end{aligned}$$
(4)

The two objective functions are related. Objectives one would be optimized first to work out the fittest travel path and based on the optimal path travel time would be optimized to get the smooth trajectory. Also, the kinematic constraints for velocity, acceleration and jerk as well as the interpolation conditions for all via-points (vertices of the cutting surfaces) must be met.

2.2 Definition of the trajectory by means of fifth-order polynomial function

To solve the optimization problems above, fifth-order polynomial function is selected to construct the trajectory in joint space. \(\theta _{i}(t)\) denotes the position of six joints in angle. According to the definition of the quantic polynomial function (Thomas et al. 2010), the trajectories of six joints are expressed mathematically as follows, i means the number of joints:

$$\begin{aligned} \begin{aligned} \theta _{i}(t)&=a_{i0}+a_{i1} t+a_{i2} t^{2}+a_{i3} t^{3}+a_{i4} t^{4}+a_{i5} t^{5}\\&\qquad i = 1,2,\ldots ,6. \end{aligned} \end{aligned}$$
(5)

For one of the trajectories, the start time is set to be \(t_0\) and end time to be \(t_f\); the start point and end point of position, velocity and acceleration constraints are expressed as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \theta _{i}(0)=\theta _{i0} \\ \theta _{i}\left( t_{f}\right) =\theta _{if} \end{array}\right. \end{aligned}$$
(6)
$$\begin{aligned} \left\{ \begin{array}{l} {\dot{\theta }}_{i}(0)={\dot{\theta }}_{i0} \\ {\dot{\theta }}_{i}\left( t_{f}\right) ={\dot{\theta }}_{if} \end{array}\right. \end{aligned}$$
(7)
$$\begin{aligned} \left\{ \begin{array}{l} \ddot{\theta }_{i}(0)=\ddot{\theta }_{i0} \\ \ddot{\theta }_{i}\left( t_{f}\right) =\ddot{\theta }_{if} \end{array}\right. \end{aligned}$$
(8)
$$\begin{aligned} \left\{ \begin{array}{l} \dddot{\theta }_{i}(0)=\dddot{\theta }_{i0} \\ \dddot{\theta }_{i}\left( t_{f}\right) =\dddot{\theta }_{if}. \end{array}\right. \end{aligned}$$
(9)

Supposing the initial and ending positions of the 6-DOF robot are known, position constraints, velocity constraints, acceleration constraints of the initial and end points are also included. The 6 parameters of the fifth-degree polynomial uniquely determine a trajectory to meet the constraints. Deriving Eq. (5), the velocity expression \({\dot{\theta }}_{i}(t)\) of the trajectory is obtained as

$$\begin{aligned} \begin{aligned} {\dot{\theta }}_{i}(t)&=a_{i1}+2 a_{i2} t+3 a_{i3} t^{2}+4 a_{i4} t^{3}+5 a_{i5} t^{4}\\&\qquad i = 1,2,\ldots ,6. \end{aligned} \end{aligned}$$
(10)

Similarly, the acceleration function \(\ddot{\theta }_{i}(t)\) and jerk function \(\dddot{\theta }_{i}(t)\) are expressed as below as the second and third derivative of Eq. (5):

$$\begin{aligned} \begin{aligned} \ddot{\theta }_{i}(t)&=2 a_{i2}+6 a_{i3} t+12 a_{i4} t^{2}+20 a_{i5} t^{3}\\&\qquad i = 1,2,\ldots ,6. \end{aligned} \end{aligned}$$
(11)

According to the coefficients, the equation of jerk (third derivative of position) could be formed to get the constrains of the \(JC_i\).

$$\begin{aligned} \begin{aligned} \dddot{\theta }_{i}(t)&=6 a_{i3}+24 a_{i4} t+60 a_{i5} t^{2}\\&\qquad i = 1,2,\ldots ,6. \end{aligned} \end{aligned}$$
(12)

According to Eqs. (6)–(9), the constants of \(a_{ij}\) could be conducted, means the jth constant of the ith joint, \(i = 1,2,\ldots 6\), means the number of joint and \(j = 0,1,\ldots 5\), means the index of the constants a:

$$\begin{aligned} \left\{ \begin{aligned} \quad a_{i0}&=\theta _{i0} \\ a_{i1}&={\dot{\theta }}_{i0} \\ a_{i2}&=\frac{\ddot{\theta }_{i0}}{2} \\ a_{i3}&=\frac{\!20\theta _{if}-20 \theta _{i0}-\left( \!8 {\dot{\theta }}_{if}+12 {\dot{\theta }}_{i0}\right) t_{f}-\left( 3 \ddot{\theta }_{i0}-\ddot{\theta }_{if}\right) t_{f}^{2}}{2 t_{f}^{3}} \\ a_{i4}&=\frac{30 \theta _{i0}-30 \theta _{if}+\left( 14 {\dot{\theta }}_{if}+16 {\dot{\theta }}_{i0}\right) t_{f}+\left( 3 \ddot{\theta }_{i0}-2 \mathbf {\theta }_{if}\right) t_{f}^{2}}{2 t_{f}^{4}} \\ a_{i5}&=\frac{12 \theta _{if}-12 \theta _{i0}-\left( 6 {\dot{\theta }}_{if}+6 {\dot{\theta }}_{i0}\right) t_{f}-\left( \ddot{\theta }_{i0}-\ddot{\theta }_{if}\right) t_{f}^{2}}{2 t_{f}^{5}}. \end{aligned}\right. \end{aligned}$$
(13)

2.3 Modified Denavit–Hartenberg parameters

In 1955, Denavit and Hartenberg proposed a method for systematically describing multi-axis robots, which are now widely used in robotics research and are known as DH parameters (Denavit et al. 1955). The specific definition model of DH parameters is shown in Fig. 5. \(Z_{i-1}\)-axis means the rotation axis of the ith joint, and \(X_{i-1}\)-axis means the common perpendicular between the joint i and joint \(i+1\) . \(Y_{i-1}\) is determined by the right-hand rule following \(Z_i{-1}\)-axis and \(X_{i-1}\)-axis.

Besides the DH parameters, there is another definition used widely, which is called modified DH parameters, showing in Fig. 6 (Craig 2009). The difference between these two methods is that the coordinate system is based on the previous joint rather than the next one in standard DH, which means that the frame \(O_{i-1}\) is put on joint \(i-1\) not joint i.

Fig. 5
figure 5

Standard DH parameters

Full size image
Fig. 6
figure 6

Modified DH parameters

Full size image

2.4 Singularities identification

To identify the singularities, In Robotics, Jacobian matrix is a map that reflects the relationship between joint speed and end-effector speed, shown as Eq. (13):

$$\begin{aligned} V_{e}=J[q] \cdot {\dot{q}} \end{aligned}$$
(14)

\(V_e\) is the velocity of the end-effector, J[q] is the Jacobian matrix, and \({\dot{q}}\) is the velocity of the joints. To be more specific, \(V_e\) includes the linear velocity \(p_e\) and angular velocity \(W_e\), the same as J[q]:

$$\begin{aligned} V_{e}=\left[ \begin{array}{l} p_{e} \\ w_{e} \end{array}\right] =\left[ \begin{array}{l} \int _{p}[q] \\ J_{o}[q] \end{array}\right] \cdot {\dot{q}}. \end{aligned}$$
(15)

The number of rows in the matrix is the freedom of robot manipulator in operating space, and the number of columns equals the number of joints, so the Jacobian matrix could be divided as

$$\begin{aligned} \left[ \begin{array}{l} p_{e} \\ w_{e} \end{array}\right] =\left[ \begin{array}{lll} J_{P 1} J_{P 2} J_{P 3} J_{P 4} J_{P 5} J_{P 6} &{} \\ J_{W 1} J_{W 2} J_{W 3} J_{W 4} J_{W 5} J_{W 6} \end{array}\right] \cdot \left[ {\dot{q}}_{1} {\dot{q}}_{2} {\dot{q}}_{3} {\dot{q}}_{4} {\dot{q}}_{5} {\dot{q}}_{6}\right] ^{{\mathrm{T}}}. \end{aligned}$$
(16)

From above, the \(p_e\) and \(W_e\) could be mapped from the linear velocity of the joints.

$$\begin{aligned} \begin{array}{c} p_{e}=J_{P 1} \cdot {\dot{q}}_{1}+J_{P 2} \cdot {\dot{q}}_{2}+\cdots +J_{P 6} \cdot {\dot{q}}_{6} \\ W_{e}=J_{W 1} \cdot {\dot{q}}_{1}+J_{W 2} \cdot {\dot{q}}_{2}+\cdots +J_{W 6} \cdot {\dot{q}}_{6}. \end{array} \end{aligned}$$
(17)

When the end-effector approaches the kinematic singularities area, the rank of the matrix would decrease, which could conclude that \(det(j[q])=0\). From Eq. (18), when |J[q]| approaches 0, q could be so large to damage the robot.

$$\begin{aligned} \mathrm {q}=J[q]^{-1} \cdot V_{e}=\frac{(J[q]) *}{[J[q] |} \cdot V_{e}. \end{aligned}$$
(18)

So \(|J[q]|=0\) is the analyzing condition of the singularity zone of the robot manipulator.

3 Experiment setup

3.1 Robot model

The robot manipulator used in the case study is KUKA KR90. The DH parameters of the robot are shown in Table 3. Based on the DH parameter in Table 3, the robot link model could be built in MATLAB2018a using Robotics Toolbox 10.2, shown in Fig. 7.

Fig. 7
figure 7

KUKA-KR90 link model

Full size image
Table 3 DH parameters of the robot
Full size table

3.2 Data conversion

In this study, one custom wood joint (Fig. 4b) is selected as the research object, with 13 cutting surfaces. The coordinates of 52 vertices of these 13 cutting surfaces are converted from Rhino (Fig. 8) to Matlab (Fig. 9) to construct the via-points of the geometric path, based on which the trajectory would be interpolated using the fifth-order polynomial function. According to the motion control law of the chainsaw, the end-effector cuts the timber along the cutting surfaces. A total of 66 cutting trajectories are formed: (1) trajectories within the 13 cutting surfaces; (2) trajectories from nth surface to \((n+1)\)th surface; (3) two additional trajectories adding the start and end points.

Fig. 8
figure 8

Trajectory in Rhino

Full size image
Fig. 9
figure 9

Trajectory in Matlab

Full size image

3.3 Kinematics constraints

The vertices in form of o-xyz coordinate would be transformed into the points in joint space from operating space using inverse kinematics. The results of the 6 joints in form of angular position, velocity and acceleration are shown in Fig. 10.

Fig. 10
figure 10

Full trajectory

Full size image

In Fig. 10, there are 66 curves representing each of the six joints constructed by 66 fifth-order polynomial functions. The coefficients of the functions could be calculated according to Eq. (18) and the constraints for each joint along every trajectory would be obtained. The overall velocity, acceleration and jerk constraints for the objective function T in Eq. (4) can be obtained by setting as:

$$\begin{aligned} \left\{ \begin{aligned} \text {VC}_{i}|&=\max \left\{ \max \left\{ p_{i j}\right\} \right\} \\ \text {WC}_{i}&=\max \left\{ \max \left\{ p_{i j}\right\} \right\} \\ \text {JC}_{i}&=\max \left\{ \max \left\{ {\dot{p}}_{i j}\right\} \right\} \\ i&=\text {number of joint} \\ j&=\text {number of trajectory}. \end{aligned}\right. \end{aligned}$$
(19)

3.4 Working space

The work-space of a robot manipulator represents a set of positions that the end-effector could approach, showing the working range of its accessibility. The working space of the manipulator could be expressed as

$$\begin{aligned} W= \left\{ \begin{array}{l} p_{x}=p_{x}\left( \theta _{i}\right) \\ p_{y}=p_{y}\left( \theta _{i}\right) , \quad \theta _{i \min } \le \theta _{i} \le \theta _{i \max } \\ p_{z}=p_{z}\left( \theta _{i}\right) . \end{array}\right. \end{aligned}$$
(20)

Monte Carlo method is one discretization method widely used to compute the work space for complex robots (Rastegar and Fardanesh 1990; Cao et al. 2011). Monte Carlo method gets the approximate work-space by setting the random joint angle of every joints to get the random positions of the end-effector. The angle range of every joint is shown in Table 4.

Table 4 Angle range of every joint
Full size table

4 Running the optimization

4.1 Particle swarm optimization for path minimization

Particle swarm optimization is one typical algorithm in swarm intelligence. Eberhard and Kennedy proposed this optimization technique by observing the social behavior of bird flocking (Kennedy and Eberhart 1995). Research has shown the effectiveness of particle swarm optimization in path planning to achieve collision-free trajectories (Hereford 2006; Doctor et al. 2004). Specifically, a group of random particles (random solution) are initialized and the best solution are found through iteration. Within each iteration, the particles update itself by tracking two values: personal best and global best. After finding these two optimal values, the particles update their velocity and position using the following equations.

$$\begin{aligned} v_{i}= & {} \omega \times v_{i}+c_{1} \times {\text {rand}}() \times \left( p {\text {Best}}_{t i}-x_{i}\right) \nonumber \\&+c_{2} \times {\text {rand}}() \times \left( g {\text {Best}}_{t i}-x_{i}\right) \end{aligned}$$
(21)
$$\begin{aligned} x_{i}= & {} x_{i}+v_{i} \end{aligned}$$
(22)

where \(v_i\) is the velocity of the ith particle; \(\text {rand}()\) is the random number between 0 and 1; \(x_i\) is the current position of the particle; \(c_1\) and \(c_2\) are the learning factors, usually equal 2; \(\omega\) is the inertia weight, which is a positive number, the larger of the number, the better global searching ability and weaker local searching ability. The common method is to use the linearly decreasing weight strategy to get the dynamic \(\omega\) .

$$\begin{aligned} w^{(t)}=\frac{\left( \omega _{{\mathrm{ini}}}-\omega _{{\mathrm{end}}}\right) \left( G_{k}-g\right) }{G_{k}+\omega _{{\mathrm{end}}}} \end{aligned}$$
(23)

where \(\omega _{{\mathrm{ini}}}\) is the initial inertia weight; \(\omega _{{\mathrm{end}}}\) is the inertia weight of maximum iteration; \(G_k\) is the maximum number of iterations. In this study, \(\omega _{{\mathrm{ini}}}=1\), \(\omega _{{\mathrm{end}}}=4e^{(-5)}\). The detailed flow chart is shown as below in Figs. 11 and 12

Fig. 11
figure 11

Flow chart of PSO

Full size image
Fig. 12
figure 12

Flow chart of robot time optimization using AGA

Full size image

To combine the algorithm with the parameters in this case, a population of \(m\times 13\) particles are created: \(swarm = \{x_{1}^{k},x_{2}^{k},...,x_{m}^{k}\}\), k means the kth iteration. Within the kth iteration, the ith particle is expressed in a 13-dimension vector: \(x_i^k=[(x_{i1}^k),(x_{i2}^k),(x_{i3}^k),...,(x_{i13}^k)]\), \(i=1,2,..,m\). Every element of the vector stands for the index of the cutting surface and the index of the vertices within every surface, the jth element of the ith particle is: \(x_{ij}^{k}=(s_{in}^k,{ver}_{ip}^k), j=1,2,...,13,n=1,2,...,13,p=1,2,3,4\). Figure 13 explains the detailed layer information, from every particle to the swarm within every step of iteration.

Fig. 13
figure 13

Layers of iterations PSO

Full size image

4.2 Adaptive genetic algorithm for travel time minimization

To validate the adaptive genetic algorithm in this study, one closed surface was chosen as an example to optimize the travel time along four edges, which means four time-intervals. The time optimization of the manipulator could be concluded as the joint optimization. The objective functions of jth join is:

$$\begin{aligned} f(t)=\min \left( t_{j 1}+t_{j 2}+t_{j 3}+t_{j 4}\right) . \end{aligned}$$
(24)

According to Eq. (10), the trajectories of the manipulator are constructed by the fifth-order polynomial, the general formula for the trajectories could be expressed as:

$$\begin{aligned} \left\{ \begin{array}{l} h_{i j}(t)=a_{i j 5} t_{i}^{5}+a_{i j 4} t_{i}^{4}+a_{i j 3} t_{i}^{3}+a_{i j 2} t_{i}^{2}+a_{i j 1} t_{i}+a_{i j 0} \\ i=1,2, \ldots , N \\ j=1,2, \ldots , n \end{array}\right. \end{aligned}$$
(25)

\(h_{ij}(t)\) is the fifth-order polynomial function of the ith trajectory of the jth joint. In one specific surface optimization, \(N=4.\) The four positions of the six joints are known concluded from the inverse kinematics, expressed as \(X_{j1},X_{j2},X_{j3},X_{j4},X_{j5}\), and \(A_{j1},A_{j5},V_{j1},V_{j5}\) are also known as 0. Based on the known conditions, the relationship between the unknown \(a_{ij}\) and the known \(X_{ji}\) could be derived from \(A_j\) (a \(24\times 24\) matrix) and \(b_j\) (vector constructed from \(X_{ij}\)).

$$\begin{aligned} b_{j}= & {} \left[ \begin{array}{llllllllllllllllll} 0&0&0&0&0&0&0&0&0&X_{j 5}&0&0&X_{j 1}&0&0&X_{j 2}&X_{j 3}&X_{j 4} \end{array}\right] ^{{\mathrm{T}}}\end{aligned}$$
(26)
$$\begin{aligned} a_{j}= & {} {\text {in}} V(A) \times b_{j} \end{aligned}$$
(27)
$$\begin{aligned} a_{j}= & {} \left[ a_{i j 5} a_{i j 4} a_{i j 3} a_{i j 2} a_{i j 1} a_{i j 0}\right] ^{{\mathrm{T}}}. \end{aligned}$$
(28)

After integrating the John Holland genetic algorithm, the improvement of the process has developed a lot (Whitley 1994). Adaptive genetic algorithm is one method that adjusts the probability of crossover \(p_c\) and probability of mutation \(p_m\) dynamically according to the fitness value. The adjustment of the two operators are shown in Eqs. (29) and (30):

$$\begin{aligned} p_{c}= & {} \left\{ \begin{array}{ll} p_{c 1}-\frac{\left( p_{c 1}-p_{c 2}\right) \left( f^{\prime }-f_{{\mathrm{avg}}}\right) }{f_{\max }-f_{{\mathrm{avg}}}}, &{}\quad f^{\prime } \ge f_{{\mathrm{avg}}} \\ p_{c 1}, &{} \quad f^{\prime }<f_{{\mathrm{avg}}} \end{array}\right. \end{aligned}$$
(29)
$$\begin{aligned} p_{m}= & {} \left\{ \begin{array}{ll} p_{m 1}-\frac{\left( p_{m 1}-p_{m 2}\right) \left( f^{\prime }-f_{a v g}\right) }{f_{\max }-f_{{\mathrm{avg}}}}, &{} \quad f \ge f_{{\mathrm{avg}}} \\ p_{m 1}, &{}\quad f<f_{{\mathrm{avg}}} \end{array}\right. \end{aligned}$$
(30)

where f is the fitness value of the solution; \(f^{\prime }\) is the larger fitness values of the two solutions to cross; \(f_{\max }\) is the maximum fitness value of the population; \(f_{{\mathrm{avg}}}\) is the average fitness value of the population (Srinivas and Patnaik 1994). The parameters of the algorithm are selected as follows: population size \(M = 100\); \(P_{c1}=0.9, P_{c2}=0.4, P_{m1}=0.1, P_{m2}=0.01\). The \(M\times 6\) group of initial combinations of \([t_{1}\ t_{2}\ t_{3}\ t_{4}]\) as the evolution population would be taken to the algorithm as the independent variables and \(a_j\) would be the dependent variables to validate the constraints. After all the optimization for all the joints, the optimized time interval should equal the maximum one within one trajectory to satisfy the kinematics constraints, that is:

$$\begin{aligned} \left\{ \begin{aligned} t_{i}&=\max \left\{ t_{j i}\right\} \\ i&=1,2, \ldots n \\ j&=1,2, \ldots , N. \end{aligned}\right. \end{aligned}$$
(31)

5 Results and analysis

5.1 Distance-optimal simulation

After 300 PSO algorithm iterations, the travel distance decreases from 16.1373 to 15.2010 m. The travel distance within every cutting surface remain the same, the reduction is diminished by the distance between two cutting surfaces. The trajectories from the start point of nth cutting surface to next start point of \((n+1)\)th cutting surface are compared in Figs. 14 and 15. The effectiveness of the algorithm in decreasing the distance, from 16.1373 to 15.2010 m (Fig. 16), without singularities in new cutting order, is also validated in KUKA|prc.

Fig. 14
figure 14

Initial surface-to-surface trajectory

Full size image
Fig. 15
figure 15

Optimized the surface to surface trajectory

Full size image
Fig. 16
figure 16

Convergence of the distance optimization

Full size image

This optimization process provides a new method in fabricating complicated components, enhancing the degree in automation in robotic fabrication tool path generation instead of setting the cutting order manually. In addition, the shorter distance could save time and energy.

5.2 Time-optimal simulation

As for the decreased in travel distance, the time optimization is operated within the cutting surface. In the optimization process, the trajectories of the six joints are composed of four fifth polynomial curves, and precision is 0.0001. The results of the first cutting surface are shown in Table 5. From the optimal results, the travel time along the four edges, four points is reduced under the kinematics constraints of joint velocity, and acceleration.

Table 5 The optimized time
Full size table

For all the six joints, the initial total time is 54s, the time is shortened at least 33.3% to 36 s. As shown in Fig. 17a–f, the operating time for each joint would converge to the optimized time, and the optimized operating times are stable. Figure 18 shows after the optimization, the curves of the position, velocity and acceleration are smoother compared to the initial ones, which means the smooth transition after every trajectory ends. Furthermore, this leads to energy saving and deviation reduction in motion control.

6 Conclusion

Based on this research’s typical timber joint, this study briefly takes the 6 DOF KUKA-KR90 robot as an example, to convert the geometric information from Rhino into the position information in working space. To implement the objectives functions, the modified DH parameter is chosen to build the link model and the trajectories of the joints are interpolated by fifth-order polynomial functions in joint space. Particle swarm optimization and adaptive genetic algorithm are applied to optimize the path distance and travel time interval respectively.

The two optimization methods achieved the optimal objectives, satisfying the kinematics constraints, and showed effectiveness in decreasing the distance and travel time in the complicated trajectories in this case study. PSO technique improves the automation of robotic trajectory planning in complicated joint fabrication through generating a rational cutting order without singularities. At the same time the trajectory optimized by PSO is also shortened compared to the initial one. The trajectories within one cutting surface optimized by AGA results in time saving and smoother robotic paths, improves the working efficiency and stability by reducing the stress on the actuators in real practice. In real on-site fabrication, this control method could increase working efficiency and improve fabrication accuracy.

Future work would focus on different combinations of trajectories technique (like fifth-order B-spline, 3-5-3 polynomial interpolation, etc.) and optimal algorithms like grey wolf optimization (GWO), ant colony optimization (ACO) to choose the best combination to optimize the distance and time. Validation would also be tested on industrial timber which have similar properties to validate the algorithm.

Fig. 17
figure 17

Convergence of AGA

Full size image
Fig. 18
figure 18

Comparison of the initial trajectory and AGA time-optimal trajectory

Full size image