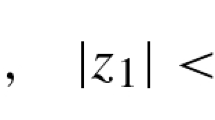Further regularity results in $P-$extremal setting

Abstract

In our paper, Pluripotential theory and convex bodies: a Siciak-Zaharjuta theorem (Computational Methods and Function Theory (2020), 20(3-4), 571-590) by Bayraktar et al., we proved a regularity result of $P-$extremal function. In this paper, we prove some other stronger regularity results analogue to those in the standard setting. Specifically we focus on proving the following proposition: Proposition: Let $K={\bar{D}}\subset {\mathbb {C}}^d$ be the closure of a bounded domain D with $\partial D$ of class $C^{1,1}$. Then, for any $Q\in {\mathcal {C}}_\alpha (K)$, where ${\mathcal {C}}_\alpha (K)$ is the Hölder class $\alpha$ on K, we have $V_{P,K,Q}\in {\mathcal {C}}_\alpha ({\mathbb {C}}^d) \text { for a convex body } P\subset (\mathbb {R^+})^d.$

1 Introduction

Standard pluripotential theory in the several complex variables space ${\mathbb {C}}^d$ deals with plurisubharmonic (PSH) functions and pluricomplex Green’s functions ([5]).

We deal with PSH functions with logarithmic growth to define the multi-dimensional classical Green’s function. We define Lelong classes as follows:

$$\begin{aligned}{} & {} L({\mathbb {C}}^d):=\{u\in PSH({\mathbb {C}}^d): u(z)-\log |z|=O(1), |z|\rightarrow \infty \}, \\{} & {} L^+({\mathbb {C}}^d):=\{u\in L({\mathbb {C}}^d): u(z)-\log ^+|z|\ge C_u, z\in {\mathbb C}^d\}. \end{aligned}$$

A set $K\subset {\mathbb C}^d$ is said to be globally pluripolar, or, simply, pluripolar, if there is a function $u\in PSH({\mathbb C}^d)$ such that $u|_K\equiv -\infty$. If $K\subset {\mathbb {C}}^d$ is non-pluripolar, the pluricomplex Green’s function of K is a PSH function in ${\mathbb {C}}^d$ that has logarithmic growth at infinity, which satisfies the homogeneous Monge-Ampère equation outside K. This function is often called the extremal function (denoted by $V_K^*$), and is defined as follows:

$$\begin{aligned} V_K^*(z):=\limsup _{\zeta \rightarrow z} V_K(\zeta ), \end{aligned}$$

(1.1)

where

$$\begin{aligned}\ V_K(z):=\sup \{u(z):u\in L({\mathbb {C}}^d), u\le 0 \;\text {on}\; K\}\qquad \text { for } z\in {\mathbb {C}}^d.\end{aligned}$$

Pluripotential theory associated with a convex body P was developed recently. We use the general set-up in [1] and refer to [2, 3, 6], and [7] for further results. A convex body $P\subset ({\mathbb {R}}^+)^d$ is a compact, convex set in $({\mathbb {R}}^+)^d$ with a non-empty interior. A standard example is the portion of an $l^p$ ball in $({\mathbb {R}}^+)^d$ with $1\le p\le \infty$, i.e., $P_p:=\{(x_1,\ldots ,x_d)\in ({\mathbb {R}}^+)^d: (x_1^p+\cdots +x_d^p)^{1/p}\le 1\}$. In particular, when $p=1$ we have $P_1=\Sigma$, where $\Sigma := \{(x_1,\ldots ,x_d)\in ({\mathbb {R}}^+)^d: x_1+\ldots +x_d\le 1\}$. In some instances of this paper, the convex bodies $P\subset ({\mathbb {R}}^+)^d$ with the following property will be considered:

$$\begin{aligned} \Sigma \subset kP \; \text {for some} \; k\in {\mathbb {Z}}^+. \end{aligned}$$

(1.2)

The indicator function of a convex body P is

$$\begin{aligned}\ \phi _P(x_1,\ldots ,x_d):=\sup _{(y_1,\ldots ,y_d)\in P} (x_1y_1+\ldots +x_dy_d)\qquad \text { for } (x_1,\ldots ,x_d)\in {\mathbb {R}}^d. \end{aligned}$$

For the P we consider, $\phi _P\ge 0$ on $({\mathbb {R}}^+)^d$ with $\phi _P(0)=0$. Define the logarithmic indicator function

$$\begin{aligned} \ H_P(z):= \sup _{J\in P} \log |z^J|:=\phi _P(\log |z_1|,\ldots ,\log |z_d|)\qquad \text { for } z=(z_1,\ldots ,z_d)\in {\mathbb {C}}^d. \end{aligned}$$

Here $|z^J|:=|z_1|^{j_1}\ldots |z_d|^{j_d}$ for $J=(j_1,\ldots ,j_d)\in P.$ The definition of $H_P$ will be used to define the analogue of the Lelong classes. Define

$$\begin{aligned}{} & {} L_P=L_P({\mathbb {C}}^d):=\{ u\in PSH({\mathbb {C}}^d):u(z)-H_P(z)=O(1),|z|\rightarrow \infty \},\\{} & {} L_P^+=L_P^+({\mathbb {C}}^d):=\{ u\in L_P({\mathbb {C}}^d):u(z)\ge H_P(z)+C_u \}.\end{aligned}$$

Given $E\subset {\mathbb {C}}^d$, the $P-$extremal function of E is defined by

$$\begin{aligned}\ V_{P,E}^*(z):=\limsup _{\zeta \rightarrow z} V_{P,E}(\zeta ),\end{aligned}$$

where

$$\begin{aligned}\ V_{P,E}(z):=\sup \{u(z):u\in L_P({\mathbb {C}}^d), u\le 0 \;\text {on}\; E\}\qquad \text { for } z\in {\mathbb {C}}^d.\end{aligned}$$

In the $P-$setting, we introduce another generalized notion of extremal functions, namely, the weighted $P-$ extremal function, as follows:

Let $K\subset {\mathbb {C}}^d$ be closed and let $w:K\rightarrow {\mathbb {R}}^+$ be an admissible weight function on K, i.e., w is non-negative, upper semicontinuous, and $\{z\in K: w(z)>0\}$ is non-pluripolar. Now let $Q:=-\log w$. In case K is unbounded, we need $\liminf _{\left| z\right| \rightarrow \infty , z\in K}[Q(z)-H_P(z)]=+\infty$. Then, the weighted $P-$extremal function is defined as

$$\begin{aligned} V^*_{P,K,Q}(z):=\limsup _{\zeta \rightarrow z} V_{P,K,Q}(\zeta ),\end{aligned}$$

where $V_{P,K,Q}(z):=\sup \{u(z):u\in L_P({\mathbb {C}}^d);u\le Q$ on $K\}.$

1.1 Regularity in standard pluripotential theory and $P-$pluripotential theory

In the standard setting, we define regularity as follows:

Definition 1.1

Let $K\subset {\mathbb {C}}^d$ be compact.

• 1. We say K is $L-$regular, if $V_{K}$ is continuous on K.

• 2. We say K is locally $L-$regular at a point $a\in K,$ if for every $r>0$ the function $V_{K\cap {\bar{B}}(a,r)}$ is continuous at a. We say K is locally $L-$regular, if K is locally $L-$regular at every point $a\in K$.

For a convex body $P \subset ({\mathbb {R}}^+)^d$ we define the analogous notions of $PL-$regularity and local $PL-$regularity by replacing $V_K$ by $V_{P,K}$.

Remark 1.2

For any convex body $P \subset ({\mathbb {R}}^+)^d$, there exists $A > 0$ with $P \subset A \Sigma$; hence $V_{P,K} (z) \le A \cdot V_K (z)$ and $V_{P,K \cap {\bar{B}}(a,r)}(z) \le A \cdot V_{K\cap {\bar{B}}(a,r )}(z)$ (see [3]). So, if K is $L-$regular (resp., locally $L-$regular), then K is $PL-$regular (resp., locally $PL-$regular). Note that for P satisfying (1.2) there exist $0< a< b < \infty$ with $a \Sigma \subset P \subset b \Sigma$ so that K is locally $PL-$regular if and only if K is locally $L-$regular.

1.2 Regularity results in $P-$pluripotential theory

In [2, Corollary 4.10], we proved the following regularity result for $P-$extremal function as a corollary to the main result.

Corollary 1.3

For K compact and locally $L-$regular, and Q continuous on K, the weighted $P-$extremal function $V_{P,K,Q}$ is continuous.

2 Further regularity results in $P-$pluripotential theory

In this paper, some other stronger regularity results analogue to those in the standard setting will be proved. First, we will state and prove some generalities.

2.1 Generalities

Recall that the set of all Hölder continuous functions on K with the Hölder exponent $\alpha$ is said to be the Hölder class $\alpha$ on K, and is denoted by ${\mathcal {C}}_\alpha (K)$.

Lemma 2.1

(cf. [10, Proposition 3.5]) Let P be a convex body and $K\subset {\mathbb {C}}^d$ be compact. If $V_{P,K}$ is Hölder continuous on K in the sense that for some $\delta >0$,

$$\begin{aligned}\ V_{P,K}(z)\le C \text {dist}(z,K)^{\alpha } \text { if dist } (z,K)\le \delta \end{aligned}$$

holds for a positive constant C and an $\alpha$ such that $0<\alpha \le 1$, then $V_{P,K}\in {\mathcal {C}}_\alpha (K)$.

Proof

For simplicity, take $C=1$. Thus, if dist$(z,K)\le \delta$, then $V_{P,K}(z)\le \delta ^{\alpha }$. Consider the set $L_{\alpha }:=\{z\in {\mathbb {C}}^d: V_{P,K}(z)\le \delta ^{\alpha }\}.$ Then $V_{P,K}(z)-\delta ^{\alpha }\le V_{P,L_{\alpha }}(z)$.

Let $K^{\delta }:=\{z\in {\mathbb {C}}^d: \text {dist}(z,K)\le \delta \}$. Then clearly $K^{\delta }\subset L_{\alpha }$. Thus, $V_{P,K}(z)-\delta ^{\alpha }\le V_{P,L_{\alpha }}(z)\le V_{P, K^{\delta }}(z)$. Now if $\left| h\right| \le \delta$, then $K-h:=\{z\in {\mathbb {C}}^d: z=w-h, w\in K\}\subset K^{\delta }.$ Therefore, $V_{P,K}(z+h)=V_{P,K-h}(z)\ge V_{P,K^{\delta }}(z)\ge V_{P,K}(z)-\delta ^\alpha$. This gives us $V_{P,K}(z)-V_{P,K}(z+h)\le \delta ^\alpha$ if $\left| h\right| \le \delta$. Replacing z by $z-h$ and h by $-h$ gives $\left| V_{P,K}(z)-V_{P,K}(z+h)\right| \le \delta ^\alpha$ if $\left| h\right| \le \delta$. $\square$

Remark 2.2

[1, Remark 2.2] If $u\in L^+_P$, then $\int _{{\mathbb {C}}^d}(dd^c u)^d=\int _{{\mathbb {C}}^d}(dd^c H_P)^d=d! Vol(P)$.

Proposition 2.3

Let $P\subset (\mathbb {R^+})^d$ be a convex body satisfying (1.2). If $u\in L^+_P({\mathbb {C}}^d)$ with $(dd^c u)^d$ having compact support K and if $u|_K$ is continuous, then $u\in C({\mathbb {C}}^d).$

Proof

Since $u\in L^+_P({\mathbb {C}}^d)$, we have $\int _{{\mathbb {C}}^d}(dd^c u)^d=d! Vol(P)$. Since $(dd^c u)^d$ puts no mass on pluripolar sets, K cannot be pluripolar.

Let $Q:=u|_K$. Then clearly u is a candidate of the family we consider for $V_{P,K,Q}$. Thus, $u\le V_{P,K,Q}\le V^*_{P,K,Q}$ on ${\mathbb C}^d$. On the other hand, $V^*_{P,K,Q}\in L_P$, $u\in L^+_P$, and $V^*_{P,K,Q}\le Q=u$ on $K=$ supp$(dd^cu)^d$. Therefore, by the $P-$extremal version of the Global Domination Principle (GDP) in [6, Proposition 2.2], $V^*_{P,K,Q}\le u$ on ${\mathbb {C}}^d$. This implies that $u=V_{P,K,Q}=V^*_{P,K,Q}$ on ${\mathbb {C}}^d$. Hence, u is continuous on ${\mathbb C}^d.$ $\square$

2.2 H$\ddot{\text {o}}$lder Regularity of Weighted $P-$Extremal Functions

In this section, H$\ddot{\text {o}}$lder regularity of weighted $P-$extremal functions will be discussed. These are also analogous results of the standard extremal setting. Our goal is to prove the proposition from the abstract, which is an analogue of [4, Proposition 2.2]. First a global version will be proved as a lemma as follows.

Lemma 2.4

Let $P\subset ({\mathbb {R}}^+)^d$ be a convex body. Let $Q\in {\mathcal {C}}_\alpha ({\mathbb {C}}^d)$ with $Q(z)\ge (1+\epsilon )H_P(z)$ as $\left| z\right| \rightarrow \infty$ for some $\epsilon >0.$ Then $V_{P,{\mathbb {C}}^d,Q}\in {\mathcal {C}}_\alpha ({\mathbb {C}}^d).$

Proof

For R sufficiently large and $\left| z\right| \ge R$,

$$\begin{aligned} \ V_{P,{\mathbb {C}}^d,Q}(z+h)\le H_P(z+h)+C \text { for } h(\ne -z)\in {\mathbb {C}}^d. \end{aligned}$$

First, for simplicity let us take $d=2$. The general case follows the same lines. Then, let us consider the three cases given below. Let ${\bar{x}}=\max \{x_i:(x_1,x_2)\in P\}.$

Case 1: When $\left| z|=|(z_1,z_2)\right| \ge R$ with $\left| z_1\right| <1$ and $\left| z_2\right| \ge 1$.

$$\begin{aligned}&\begin{aligned} V_{P,{\mathbb {C}}^d,Q}(z+h)&\quad \le H_P(z+h)+C\\&\quad = \sup _{(x_1,x_2)\in P}\{x_1 \log \left| z_1+h_1\right| +x_2 \log \left| z_2+h_2\right| \}+C\\&\quad \le \overbrace{\sup _{(x_1,x_2)\in P}x_2 \log \left| z_2\right| }^{=H_P(z)}+\sup _{(x_1,x_2)\in P}\bigg \{x_1 \log \left| z_1+h_1\right| +x_2 \log \left| 1+\frac{h_2}{z_2}\right| \bigg \}+C\\&\quad \le H_P(z)+{\bar{x}}\left\{ \log ^+\left| z_1+h_1\right| + \log \left| 1+\frac{h_2}{z_2}\right| \right\} +C\\&\quad \le H_P(z)+{\bar{x}}\left| z_1+h_1\right| +{\bar{x}}\frac{\left| h_2\right| }{\left| z_2\right| }+C\\&\quad \le H_P(z)+{\bar{x}}(1+\left| h_1\right| )+{\bar{x}}\left| h_2\right| +C\\&\quad \le H_P(z)+{\bar{x}}(\left| h_1\right| +\left| h_2\right| )+\overbrace{C+{\bar{x}}}^{:=C_1}\\&\quad \le H_P(z)+2{\bar{x}}\left| h\right| +C_1. \end{aligned} \end{aligned}$$

Case 2: When $\left| z|=|(z_1,z_2)\right| \ge R$ with $\left| z_1\right| \ge 1$ and $\left| z_2\right| <1$. By the argument used in Case 1, we have $V_{P,{\mathbb {C}}^d,Q}(z+h)\le H_P(z)+2{\bar{x}}\left| h\right| +C_1$ in this case too.

Case 3: When $\left| z|=|(z_1,z_2)\right| \ge R$ with $\left| z_1\right| >1$ and $\left| z_2\right| >1$.

$$\begin{aligned} \begin{aligned} V_{P,{\mathbb {C}}^d,Q}(z+h)&\le H_P(z+h)+C\\&=\sup _{(x_1,x_2)\in P}\{x_1 \log \left| z_1+h_1\right| +x_2 \log \left| z_2+h_2\right| \}+C\\&\le \sup _{(x_1,x_2)\in P}\left\{ x_1 \log \left| z_1\right| +x_2 \log \left| z_2\right| \right\} +\\ {}&\sup _{(x_1,x_2)\in P}\left\{ x_1 \log \left| 1+\frac{h_1}{z_1}\right| +x_2 \log \left| 1+\frac{h_2}{z_2}\right| \right\} +C\\&\le H_P(z)+{\bar{x}}\left( \frac{\left| h_1\right| }{\left| z_1\right| }+\frac{\left| h_2\right| }{\left| z_2\right| }\right) +C\\&\le H_P(z)+{\bar{x}}(\left| h_1\right| +\left| h_2\right| )+C\\&\le H_P(z)+2{\bar{x}}\left| h\right| +C. \end{aligned} \end{aligned}$$

So, in any case we have $V_{P,{\mathbb {C}}^d,Q}(z+h)\le H_P(z)+2{\bar{x}}\left| h\right| +C_1$ for $\left| z\right| \ge R$. Now it is obvious that we can generalize the same argument to any d. Note that $2{\bar{x}}|h|$ in the above inequality would be replaced by $d{\bar{x}}|h|$ for a general d.

By the hypothesis on Q, for $\left| z\right| \ge R$,

$$\begin{aligned} \ V_{P,{\mathbb {C}}^d,Q}(z+h)\le H_P(z)+2{\bar{x}}\left| h\right| +C_1\le (1+\epsilon )H_P(z)+\underbrace{2{\bar{x}}}_{:=k}\left| h\right| \le Q(z)+k\left| h\right| . \end{aligned}$$

We can assume that $Q(z)\ge 0$ for $\left| z\right| \le R.$ Let $C_R:=\max \bigg \{\displaystyle \frac{\left| Q(z)-Q(w)\right| }{\left| z-w\right| ^\alpha }: \left| z\right| ,\left| w\right| \le R, z\ne w \bigg \}$. Then for $\left| z\right| \le R$, $V_{P,{\mathbb {C}}^d,Q}(z+h)\le Q(z+h)\le Q(z)+C_R\left| h\right| ^\alpha$. It follows that for all $z\in {\mathbb {C}}^d$,

$$\begin{aligned} \ V_{P,{\mathbb {C}}^d,Q}(z+h)\le Q(z)+\max \{k\left| h\right| ,C_R\left| h\right| ^\alpha \}. \end{aligned}$$

Thus, $V_{P,{\mathbb {C}}^d,Q}(z+h)-\max \{k\left| h\right| ,C_R\left| h\right| ^\alpha \}\le V_{P,{\mathbb {C}}^d,Q}(z)$. Applying this inequality by replacing h by $-h$ and then z by $z+h$ gives, for $\left| h\right| \le 1,$

$$\begin{aligned} \begin{aligned} \left| V_{P,{\mathbb {C}}^d,Q}(z+h)-V_{P,{\mathbb {C}}^d,Q}(z)\right|&\le \max \{k\left| h\right| ,C_R\left| h\right| ^\alpha \}\\&\le \max \{k\left| h\right| ^\alpha ,C_R\left| h\right| ^\alpha \}\\&\le \max \{k,C_R\}\cdot \left| h\right| ^\alpha . \end{aligned} \end{aligned}$$

$\square$

We also need the following lemmas. Note that Lemma 2.5 is a univariate result.

Lemma 2.5

(cf. [4, Lemma 2.9]) Fix $0<\alpha <1$. Let u be bounded and subharmonic in a neighborhood of ${\bar{\Delta }}(0,2\delta )=\{z\in {\mathbb C}:|z|\le 2\delta \}.$ Suppose that for some constant $C>0,$ $u(z)\le C|z|^\alpha$ for all $z\in {\bar{\Delta }}(\delta , \delta )=\{z\in {\mathbb C}:|z-\delta |\le \delta \}$. Then, there exits $c=c(\alpha )>0$ such that $u(t)\le c C|t|^\alpha$ for $t\in [-\delta ,0].$

Lemma 2.6

For $K\subset {\mathbb {C}}^d$ compact and $Q\in \mathcal {C}_\alpha (K)$, there exists ${\tilde{Q}}\in \mathcal {C}_\alpha ({\mathbb {C}}^d)$ with ${\tilde{Q}}|_K=Q$.

Proof

We may assume that $Q\ge 0$ on K. Let

$$\begin{aligned} C:=\max _{z,w\in K, z\ne w} \frac{\left| Q(z)-Q(w)\right| }{\left| z-w\right| ^\alpha } \end{aligned}$$

and take $A\gg C$. Define

$$\begin{aligned} {\tilde{Q}}(z):=\min _{w\in K}\big (Q(w)+A\left| z-w\right| ^\alpha \big ) \qquad \text { for } z\in {\mathbb {C}}^d. \end{aligned}$$

It immediately follows from $Q\in {\mathcal {C}}_{\alpha }(K)$ and $A \gg C$ that ${{\tilde{Q}}} = Q$ on K. To see that ${{\tilde{Q}}}\in {\mathcal {C}}_{\alpha }({\mathbb {C}}^d)$, given $z\in {\mathbb {C}}^d$ take $w_0\in K$ with ${{\tilde{Q}}}(z)=Q(w_0)+A|z-w_0|^{\alpha }$. Then, for $z'\in {\mathbb {C}}^d$ we have

$$\begin{aligned} {{\tilde{Q}}}(z')-{{\tilde{Q}}}(z)\le (Q(w_0)+A|z'-w_0|^{\alpha })-(Q(w_0)+A|z-w_0|^{\alpha })\le A|z-z'|^{\alpha }. \end{aligned}$$

$\square$

Now we are ready to prove the proposition stated in the abstract. Let us recall it here.

Proposition

Let $K={\bar{D}}\subset {\mathbb {C}}^d$ be the closure of a bounded domain D with $\partial D$ of class $C^{1,1}$. Then, for any $Q\in {\mathcal {C}}_\alpha (K)$, where ${\mathcal {C}}_\alpha (K)$ is the Hölder class $\alpha$ on K, we have $V_{P,K,Q}\in {\mathcal {C}}_\alpha ({\mathbb {C}}^d) \text { for a convex body } P\subset (\mathbb {R^+})^d.$

Proof

Since we have Lemma 2.6, it suffices to show

$$\begin{aligned} V_{P,K,Q}\le {{\tilde{Q}}} \ \hbox {on} \ {\mathbb {C}}^d \end{aligned}$$

(2.1)

to complete the proof. For, given (2.1), we have, on the one hand, that $V_{P,K,Q}\le V_{P,{\mathbb {C}}^d,{{\tilde{Q}}}}$; on the other hand, since ${{\tilde{Q}}}|_K = Q$ we have $V_{P,{\mathbb {C}}^d,{{\tilde{Q}}}}\le V_{P,K,Q}$ and equality holds. The conclusion follows from Lemma 2.4, since clearly ${{\tilde{Q}}}(z) \ge (1+\epsilon )H_P(z)$ as $|z|\rightarrow \infty$ for some $\epsilon >0$.

We will soon see that it suffices to verify $V_{P,K,Q}\le {{\tilde{Q}}}$ at points near K. Here we will use the regularity of $\partial D$ where $K={{\bar{D}}}$. Fix z near K and, as in the proof of Lemma 2.6, let $w_0\in K$ with ${{\tilde{Q}}}(z)=Q(w_0)+A|z-w_0|^{\alpha }$. Finally, take $z_0\in K$ with $r:=|z-z_0|=\inf _{z' \in K}|z-z'|$.

Claim: We have $|z_0-w_0|\lesssim r$, i.e., there is a constant $C'>0$ such that $|z_0-w_0|\le C'r$, and there exists $A'$ large with ${{\tilde{Q}}}(z)\ge Q(z_0)+A'r^{\alpha }$ (here, $A'\rightarrow \infty$ as $A\rightarrow \infty$).

Proof of the Claim: If the estimate $|z_0-w_0|\lesssim r$ were false, then $|z-z_0|\ll |z-w_0|\approx |z_0-w_0|.$ Moreover, we have

$$\begin{aligned} {{\tilde{Q}}}(z)=Q(w_0)+A|z-w_0|^{\alpha }\le Q(z_0)+A|z-z_0|^{\alpha }. \end{aligned}$$

Thus,

$$\begin{aligned} Q(z_0)-Q(w_0) \ge A(|z-w_0|^{\alpha }- |z-z_0|^{\alpha }) \approx A |z_0-w_0|^{\alpha }\gg C|z_0-w_0|^{\alpha }, \end{aligned}$$

contradicting the definition of C. Finally,

$$\begin{aligned} {{\tilde{Q}}}(z)-Q(z_0)=Q(w_0)-Q(z_0)+A|z-w_0|^{\alpha } \ge Q(w_0)-Q(z_0)+A|z-z_0|^{\alpha } \gg r^{\alpha }. \end{aligned}$$

This proves the claim.

Since $\partial D$ is of class $C^{1,1}$, there is a $\delta =\delta (K) >0$ such that for each $w\in \partial D$, there is an internally tangent ball $B=B_w\subset K$ of radius $\delta$ with $w\in \partial B$ (thanks to [9]). We consider points $z\in {\mathbb {C}}^d{\setminus } K$ with $r=|z-z_0|=\inf _{z' \in K}|z-z'|\le \delta /2$. From the claim, to verify (2.1) for all points in $K^{\delta /2}:=\{s\in {\mathbb {C}}^d: \hbox {dist}(s,K)\le \delta /2\},$ it remains to show for such z that

$$\begin{aligned} V_{P,K,Q}(z)\le Q(z_0)+A'r^{\alpha }. \end{aligned}$$

(2.2)

Using a unitary change of coordinates, we can assume that $z_0=(0,\ldots ,0)$; $z=(-r,0,\ldots ,0)$; and the ball $B_{z_0}$ is the ball of radius $\delta$ centered at $(\delta ,0,\ldots ,0)$. In the complex line $\Lambda :=\{z=(z_1,\ldots ,z_d)\in {\mathbb {C}}^d: z_2=\cdots =z_d=0\},$ the function $u(z_1):= V_{P,K,Q}(z_1,0,\ldots ,0)-Q(0,\ldots ,0)$ is subharmonic and, on the disk $\Delta _{z_0}:=B_{z_0}\cap \Lambda$, we have $u(z_1)\le C|z_1|^{\alpha }$ (since $V_{P,K,Q}\le Q$ on $B_{z_0}$). By Lemma 2.5, there exists $c=c(\alpha )>0$ with $u(-r)\le cCr^{\alpha }$. Since cC is finite and A has been chosen so that $A\gg C,$ we can assume that $A'>cC$. This proves (2.2) and gives $V_{P,K,Q}\le {{\tilde{Q}}}$ for all points on $K^{\delta /2}$.

But since for each $w\in \partial K^{\delta /2}$ there is an internally tangent ball $B=B_w\subset K^{\delta /2}$ of radius $\delta /2$ with $w\in \partial B$, we may repeat the argument with K replaced by $K^{\delta /2}$ to get $V_{P,K,Q}\le {{\tilde{Q}}}$ for all points on $K^{\delta /2+\delta /4}$. Continuing this procedure countably many times gives $V_{P,K,Q}\le {{\tilde{Q}}}$ for all points in $K^{\delta }=K^{\delta /2 +\delta /4 +\ldots }$.

Now for each $w\in \partial K^{\delta }$, there is an internally tangent ball $B=B_w\subset K^{\delta }$ of radius $\delta$ with $w\in \partial B$, so we may repeat the procedure with $K^{\delta }$ to extend the inequality $V_{P,K,Q}\le {{\tilde{Q}}}$ to all points on $K^{\delta +\delta /2}$ and, after countably continuing, to $K^{2\delta }=K^{\delta +\delta /2 +\delta /4 +\ldots }$. Continuing in this fashion, we arrive at (2.1). $\square$