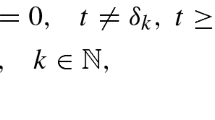Abstract
In this paper, we consider a new class of boundary value problem associated with fractional Emden–Fowler type neutral partial differential equations of the form
\(\int \nolimits _{t_0}^{\infty }\dfrac{dt}{r(t)}<\infty \). We will establish the sufficient conditions for the oscillation of given system by using the generalized Riccati technique and integral averaging method.
Similar content being viewed by others
References
Das, S. 2008. Functional fractional calculus for system identification and controls. Newyork: Springer.
Kilbas, A.A., H.M. Srivastava, and J.J. Trujillo. 2006. Theory and applications of fractional differential equations, vol. 204. Amsterdam: Elsevier Science B.V.
Samko, S.G., A.A. Kilbas, and O.I. Marichev. 1993. Fractional integrals and derivatives: theory and applications. Amsterdam: Elsevier.
Vasily, E. 2010. Fractional dynamics. Beijing: Higher eduction press,
Zhou, Y. 2014. Basic theory of fractional differential equations. Singapore: World Scientific.
Bagley, R.L., and P.J. Torvik. 1983. A theoritical basis for the application of fractional calculus to viscoelasticity. Journal of Rheology 27: 201–210.
Baillie, R.T. 1996. Long memory processes and fractional integration in econometrics. Journal of Econometrics 73: 5–59.
Denton, Z., and A.S. Vatsala. 2010. Fractional integral inequalities and applications. Computers and Mathematics with Applications 59: 1087–1094.
Diethelm, K., and N.J. Ford. 2002. Analysis of fractional differential equations. Journal of Mathematical Analysis and Applications 265: 229–248.
Mainardi, F. 1997. Fractional calculus some basic problems in continuum and statistical mechanics. In Fractals and fractional calculus in continuum mechanics, vol. 265, ed. A. Carpinteri, and F. Mainardi, 291–348. Newyork: Springer.
Magin, R.L. 2004. Fractional calculus in bioengineering. Critical ReviewsTM, Biomedical Engineering 32: 1–377.
Mandelbrot, B. 1967. Some noises with \(\frac{1}{f}\) spectrum, a brige between direct current and white noise. IEEE Transactions and Information Theory 13: 289–298.
Rossikhin, Y.A., and M.V. Shitikova. 1997. Applications to fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Applied Mechanics Reviews 50: 15–67.
Baleanu, D., O.G. Mustafa, and D. O’Regan. 2015. A Kamenev oscillation result for a linear \((1+\alpha )\)-order fractional differential equations. Applied Mathematics and Computation 259: 374–378.
Chen, D.X. 2013. Oscillatory behavior of a class of fractional differential equations with damping. UPB Scientific Bulletin Series A 75: 107–118.
Wang, Y., Z. Han, and S. Sun. 2014. Comment on ’On the Oscillation of Fractional-order Delay Differential Equations with Constant Coefficients’. Communication in Nonlinear Science 19 (11): 3988–3993.
Wang, Yi-Zhou, Zhen-Lai Han, Ping Zhao, and Shu-Rong Sun. 2015. Oscillation theorems for fractional neutral differential equations. Hacettepe Journal of Mathematics and Statistics 44: 1477–1488.
Yang, J., A. Li, and T. Liu. 2015. Forced oscillation of nonlinear fractional differential equations with damping term. Advances in Difference Equations 1: 1–7.
Prakash, P., S. Harikrishnan, and M. Benchohra. 2015. Oscillation of certain nonlinear fractional partial differentialequation with damping term. Applied Mathematics Letters 43: 72–79.
Sadhasivam, V., and J. Kavitha. 2015. Forced oscillation of solutions of a fractional neutral partial functional differential equation. Applied Mathematics, Scientific Research publishing 6: 1302–1317.
Sadhasivam, V., and J. Kavitha. 2016. Forced oscillation of fractional order partial differential equations with damping and functional arguments. International Journal of Pure and Applied Mathematics 106: 89–107.
Wei Nian Li. 2016. Oscillation of solutions for certain fractional partial differential equations. Advances in Difference Equations 16: 1–8.
Driver, D.R. 1984. A mixed neutral systems. Nonlinear Analysis 8: 155–158.
Hale, J.K. 1977. Theory of functional differential equations. Newyork: Springer.
Saker, S.H., and J.V. Manojlovic. 2004. Oscillation criteria for second superlinear neutral delay differential equations. Electronic Journal of Qualitative Theory of Differential Equation 10: 1–22.
Han, Z., T. Li, S. Sun, and Y. Sun. 2010. Remarks on the paper. Applied Mathematics and Computation 215: 3998–4007.
Li, T., Z. Han, C. Zhang, and S. Sun. 2011. On the oscillation of second-order emden-fowler neutral differential equations. Journal of Applied Mathematics and Computation 37: 601–610.
Agarwal, R.P., M. Bohner, T. Li, and C. Zhang. 2014. Oscillation of second order emden-fowler neutral delay differential equations. Annaali di Mathematica 193: 1861–1875.
Acknowledgements
The authors sincerely thank the referees for their valuable suggestions for the improvement of the paper. The authors also thank Prof.E. Thandapani for his support to complete the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sadhasivam, V., Kavitha, J. On the oscillation of fractional Emden–Fowler type neutral partial differential equations. J Anal 27, 741–759 (2019). https://doi.org/10.1007/s41478-018-0124-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41478-018-0124-3
Keywords
- Oscillation
- Riccati transformation
- Emden-Fowler neutral differential equation
- Fractional partial differential equation
- Forcing term