Divide and Invest: Bargaining in a Dynamic Framework

Abstract

Many negotiations (for instance, among political parties or partners in a business) are characterized by dynamic bargaining: current agreements affect future bargaining possibilities. We study such situations using bargaining games á la Rubinstein (Econometrica 50:97–109, 1982), with the novelty that players can decide how much to invest, as well as how to share the residual surplus for their own consumption. Their investment decisions affect the size of the next surplus. In line with the existing literature, we focus on Markov Perfect Equilibria, where consumption and investment are linear time-invariant functions of capital and show that standard results in bargaining theory can be overturned. For instance, a more patient proposer may consume less than his opponent. The intuition is that when capital is productive, both parties have incentives to invest, however, the most patient party wishes to invest significantly more than his opponent. Then, to prioritize investment—which affects future bargaining possibilities—the former must make larger concessions and let the latter consume more. Another interesting result is that if a player becomes more patient, both parties may reduce their investment. The key underlying driver of this result is that when counteroffers become cheaper for an impatient party, he is able to reduce his investment and consume more. This forces his opponent to make larger concessions (and reduce his investment plan). Moreover, extreme demands (where a player consumes all the residual surplus) are possible in equilibrium, under fairly modest assumptions. Finally, only when bargaining is frictionless, is the equilibrium efficient.

1 Introduction

Several bargaining situations, in the most diverse contexts, are dynamic, in that current agreement may affect future bargaining possibilities. For instance, partners in a business need to negotiate not only over how to split profits among themselves, but also over how much profit should be re-invested for the following production period, knowing that their level of investment today affects the size of production/profit tomorrow. Countries may attempt to find agreements over environmental issues by taking into account the fact that current decisions can affect the state of the environment and therefore future bargaining possibilities. The focus of the paper is on long-run negotiations in which parties can take actions today to affect the size of future potential benefits they could gain from the bargaining relationship.

To address this, we combine bargaining games with dynamic accumulation problems, that is, players do not simply split a surplus for their own consumption, but can also invest part of it and the invested surplus, in turn, affects the size of future surpluses. We modify the classic Rubinstein (1982) game by allowing two (risk-averse) players to consume and invest. The problem is complex, since not only do parties need to solve a (potentially protracted) bargaining stage, but also a dynamic accumulation problem since the agreement they reach at a specific stage affects future bargaining possibilities. Bargaining games which allow parties to make jointly both investment and consumption decisions in a dynamic context are almost unexplored (a discussion of the related literature is contained in the next section).

With a focus on (stationary) Markov Perfect Equilibria (MPE)—here consumption and investment are linear time-invariant functions of the state—we will show that the equilibrium is characterized by immediate agreement and is generally unique, but different types of equilibria may arise depending on the value of the parameters. Haggling cannot be an equilibrium phenomenon in our framework because delays are not strategically desirable. A delay in reaching a current agreement implies a delay in realizing not only current mutually beneficial gains but also all future gains. Therefore, even if the current cost of a one-period delay is very small, the total cost of a rejection can be very high for both parties. Also, a player can always avoid a rejection by investing sufficiently.¹ Although the equilibrium is generally unique, there are three types of outcome that can arise, depending on players’ characteristics, the rate of return and the depreciation rate. First, when there are some frictions in the bargaining process (i.e., both players are sufficiently impatient) and the rate of return is sufficiently high (and/or the depreciation rate is sufficiently low), then both parties extract all the residual surplus (we call this the polar consumption MPE). Second, under certain conditions, there is an (interior) MPE in which both parties leave a positive share of the residual surplus to the opponent. Third, when parties are sufficiently asymmetric, there is an hybrid version of the polar consumption MPE where only one party (the most patient) extracts all the surplus not invested (while the other makes concessions).

In standard bargaining games (without investment), extreme demands are not typical, unless the bargaining procedure and/or players’ impatience are also extreme (for instance, in ultimatum games and/or when players value any agreement reached in the future as little as the disagreement outcome). In our model, extreme demands are possible (even in the most interesting case in which a bargaining round is shorter than a production stage) as long as responders can be compensated for accepting them. In other words, the proposer can invest sufficiently and since a larger investment implies a larger surplus in the future, he can then extract the entire current residual surplus without facing a rejection. We will show that equilibria with polar consumption are possible if, first, there are some (not necessarily extreme) frictions in the bargaining process and, second, the rate of return is sufficiently high (and/or the depreciation rate is sufficiently low).

In our model, a key role is played by an enriched discounting structure. We not only assume that players’ have (potentially) different rates of time preference but also that in the game there are (potentially) different time intervals across bargaining and production stages. The differential in time preferences has been known to lead to significantly different results from the case in which players are homogeneous (see, for instance, see Lehrer and Pauzner (1999) in the context of repeated games). The assumption of (potentially) different time intervals captures the feature that typically the production stage, in which the surplus is generated, is longer than a bargaining round, that is the time to make a counteroffer.² Hence, one of the aims of the paper is to investigate the resulting (complex) interplay of incentives in the game. We find that while in standard bargaining theory a more patient proposer can extract a larger surplus, in our model this may not hold. The patient party may be forced to demand little to prioritize his investment plan and avoid (costly) rejections. Moreover, when a party becomes more patient, we may have expected that he would invest more, instead the MPE investment rates may decrease for both players (when there are asymmetries). This is because once counteroffers become cheaper for a fairly impatient party, he is able to consume more: investing less and demanding a larger share of the residual surplus. This, in turn, forces his (more patient) opponent to make larger concessions and invest less. Finally, if a party becomes more patient, this may make a rival better off.³ Investment plans can be high enough that the rival can effectively exploit the prospect of a higher future consumption levels and extract a larger share of the current surplus. As a result, he will be better off.

1.1 Related literature

Muthoo (1999, Chapter 10) is the first contribution with a focus on a repeated (non-cooperative) bargaining game with investment decisions in addition to the standard consumption decisions. Muthoo (1999)’s focus (and that of related contributions, e.g., Zapal 2018) is on steady-state stationary subgame perfect equilibria (while ours is on MPE). As a result, the investment decisions are simplified since parties need to invest as much as necessary to have surpluses of the same size. Indeed, Muthoo’s aim is to apply Muthoo (1995), which is a bargaining model without investment (where parties share an infinite number of surpluses with the same size) to the accumulation problem. In this sense, the problem of how much parties invest in a strategic framework remains open.⁴

Subsequently, Flamini (2012) develops an algorithm to identify the (symmetric) subgame perfect equilibrium in a dynamic bargaining model significantly simpler than in this model (e.g. the number of bargaining stages is finite). In contrast, the current paper focuses on a general model of dynamic bargaining with potentially an infinite number of bargaining stages and possible asymmetries between players (hence, one obvious complication is that it is not possible to apply backward induction and the asymmetry significantly enriches the interplay of forces within the game).

There are also two other literatures, namely, on the hold-up problem and on the tragedy of the commons, which are related to the problem considered in this paper. However, there are fundamental differences between these problems and our dynamic bargaining game with investment. In the hold-up problem, parties have the ability to make sunk investments that affect the size of a surplus, before bargaining over the division of such a surplus. Since the investor, who bears all the costs of the investment, cannot appropriate all the benefits, the resulting investment is lower than the efficient level. Typically, only one party is involved in the investment problem, moreover, the investment is once and for all (see, for instance, Gibbons 1992; Muthoo 1998; Gul 2001). An exception is in Che and Sákovics (2004), where parties keep investing until an agreement has been reached, however, once this is struck, the game ends. Differently, the focus of this paper is on parties who jointly and repeatedly need to agree on how much to invest and consume.

The second literature, on the tragedy of the commons, considers different parties who can extract part of a surplus for their own consumption and the remaining surplus will affect the size of surplus available in the next period (see, for instance, Levhari and Mirman 1980; Dutta and Sandaram 1993). The tragedy of the commons rests in the fact that parties consume more than the efficient level and therefore the surplus extinguishes quickly (over-exploitation of natural resources is a classic example). Although the typical framework analyzing the problem of the tragedy of the commons is a dynamic accumulation game, it does not include any negotiation (everyone can consume as much as he wishes, given the stock available). Two notable exceptions, which have introduced bargaining in these dynamic accumulation games are Houba et al. (2000) and Sorger (2006). In Houba et al. (2000) parties can potentially bargain forever (á la Rubinstein), but differently from our framework, they need only agree once, since this agreement will be ever-lasting. In contrast, Sorger (2006) is closer to our paper, since in each period parties can reach an agreement over the levels of consumption (Sorger 2006, also allows for endogenous threat points), however, the bargaining process is not formalized, in that it is given by the maximization of Nash products.⁵ We consider a fully non-cooperative bargaining approach and characterize (analytically for some cases) the strategic behavior that arises in equilibrium and the incentives that players need to take into account when forming their strategies. We show that the interplay of forces in our framework can be significantly different from Sorger (2006) and asymmetries can have important consequences in the solution of the problem.

The paper is also linked to the large literature on public good provision. A recent, very interesting example is Bowen et al. (2014) which investigate two parties who have to decide over public spending under a simple bargaining procedure (take-it-or-leave-it) with the crucial feature that in disagreement they spend nothing (under discretionary spending) or must implement the previous policy (under mandatory spending). Hence, the status quo is endogenous in the latter. Differently from our case, the size of the surplus is the same in every bargaining stage. Instead, we are interested in long-run relationships in which current decision can determine the size of future surpluses and the bargaining procedure is substantially richer than an ultimatum (players can make counteroffers).

The paper is organized as follows. In the next section, we present the model. In Sect. 3, we analyze the MPE; first, in a simple case, in which the elasticity of substitution is equal to 2 (in Sect. 3.1.1) then more generally with a focus on interior solutions in Sect. 3.1.2. The cases in which at least a player consumes all the residual surplus is in Sect. 3.2. Some final remarks are made in Sect. 4. Most of the proofs are contained in the Appendix.

2 The Model

We consider a two-player bargaining game in which bargaining and production stages alternate (and each stage can start only after the other has taken place). Time is discrete and the horizon is potentially infinite, $t\,\,=\,\,0,1, \ldots$ At the production stage, a surplus is generated according to the production function $F(k_{t})\,\,=\,\,Gk_{t},$ where G is the constant gross rate of return and $k_{t}$ is the capital stock at period t,  with $t\,\,=\,\,1,2 \ldots$. Production takes place in an interval of time $\tau$. Once the surplus, $F(k_{t})$, is generated, the bargaining stage begins and players attempt to divide this surplus. At the beginning of the game, $t\,\,=\,\,0$, both the capital stock, $k_{0},$ and the first surplus, $F(k_{0})\,\,=\,\,Gk_{0}$, are given, hence players start the game negotiating. The bargaining stage is a classic infinitely-repeated alternating-offer bargaining game (Rubinstein 1982) with the novelty that a proposal includes an investment plan. That is, a proposal by player i, with $i\,\,=\,\,1,2,$ is a pair $(x_{i},\varphi _{i})$ , where $\varphi _{i}$ is the investment share, with $\varphi _{i}\in [-(1-\lambda ),G]$—parties can disinvest their capital if they wish ($\varphi _{i}<0$) and, at most, they can invest the entire surplus⁶—and $x_{i}\in [0,1]$ is the share demanded by i over the remaining surplus. Player j can either accept or reject the proposal $(x_{i},\varphi _{i}),$ with $i,j\,\,=\,\,1,2$ and $i\ne j.$

If the proposal is accepted, the level of investment is $I_{it}\equiv I_{i}(\varphi _{i},k_{t})\,\,=\,\,\varphi _{i}k_{t}$ and the consumption levels are

$$\begin{aligned} c_{it}\equiv & {} c_{i}(x_{i},\varphi _{i},k_{t})\,\,=\,\,x_{i}(G-\varphi _{i})k_{t} \end{aligned}$$

(1)

$$\begin{aligned} c_{jt}\equiv & {} c_{j}(x_{i},\varphi _{i},k_{t})\,\,=\,\,(1-x_{i})(G-\varphi _{i})k_{t} \end{aligned}$$

(2)

for the proposer, i, and the responder, j, respectively, with $i,j\,\,=\,\,1,2$ and $i\ne j$. Both consumption and investment ($c_{it}$ and $I_{it}$, for player i) are linear time-invariant functions of the state variable, $k_{t}$, the capital stock.⁷ In each bargaining round, players’ utility function has a CES form⁸

$$\begin{aligned} u_{i}(c_{it})\,\,=\,\,\frac{c_{it}^{1-\eta }}{1-\eta }\text { for }\eta \in (0,1) \end{aligned}$$

(3)

with $i\,\,=\,\,1,2.$ Also after an acceptance, the bargaining stage ends and a production stage takes place. The output available at beginning of the next bargaining stage (at $t+1$) is $F(k_{t+1})$, with capital stock $k_{t+1}$ given by the investment level $I_{it}$ and the capital remaining after depreciation (during production)

$$\begin{aligned} k_{t+1}\,\,=\,\,I_{it}+(1-\lambda )k_{t} \end{aligned}$$

where $\lambda$ is the depreciation rate ($0<\lambda \le 1$).⁹ The player to make the first offer at the ($n+1$)th bargaining stage, say j, is the player who accepted player i’s division at the nth bargaining stage, with $i,j\,\,=\,\,1,2,$ $i\ne j$ and $n\,\,=\,\,1,2, \ldots$. At $t\,\,=\,\,0,$ player 1 is assumed to make the first offer.

If the proposal by player i, $(x_{i},\varphi _{i}),$ is rejected, player j can make a counteroffer after an interval of time $\Delta$ . In a one-period disagreement, d, parties receive $u_{i}(d)\,\,=\,\,0$. We assume that the capital stock remains unchanged, $k_{t}$.¹⁰ Players must agree on the division of the current surplus, $F(k_{t})$, before proceeding to a new production stage.¹¹

Player i’s time preference is represented by his discount rate $h_{i}$ (with $i\,\,=\,\,1,2).$ Since intervals of time may have different lengths ($\Delta$ for a bargaining round and $\tau$ for a production stage), there are two (potentially) distinct discount factors in our model: the between-cake discount factor, $\alpha _{i}\,\,=\,\,exp(-h_{i}\tau ),$ which captures the friction between bargaining stages (that is, the production time $\tau )$ and the within-cake discount factor, $\delta _{i}\,\,=\,\,exp(-h_{i}\Delta ),$ that takes into account the friction within the bargaining stage (that is, the interval of time between a rejection and a new proposal, $\Delta )$.

The payoff to players depends on how many surpluses they agree to split, N . If, for example, $N\,\,=\,\,0,$ they perpetually disagree and each player’s utility is 0. If, instead, they always agree at the first round in each bargaining stage, then the sum of discounted payoffs are

$$\begin{aligned} \underset{t\,\,=\,\,0}{\overset{\infty }{\sum }}\alpha _{i}^{t}u_{i}(c_{it}) \end{aligned}$$

We will show that this is what will happen in equilibrium. If, in a final example, at the first bargaining stage, a proposal is accepted after n rejections and, at the second bargaining stage, players immediately agree to disinvest their capital. Then, the game ends after two bargaining stages and the sum of discounted payoffs is

$$\begin{aligned} \delta _{i}^{n}[u_{i}(c_{i0})+\alpha _{i}u_{i}(c_{i1})] \end{aligned}$$

with $i\,\,=\,\,1,2.$ Table 1 summarizes the actions and per-period payoffs while time and state evolve. The capital stock $k_{t}$ does not simply evolve with time, since it is affected only by production stages (given the depreciation rate $\lambda >0$) and the agreed investment level ($k_{1}\,\,=\,\,(1-\lambda +{\small \varphi }_{2})k_{0}$, in Table 1).

These examples can then be generalized to capture any pattern of offers and responses in the bargaining stages.

Table 1 Actions, per-period payoffs and the evolution of the state variable in a game where a proposal is accepted, after n rejections, in the first stage and players immediately agree to disinvest, in the second bargaining stage

The focus is on (stationary) MPE, where the Markov strategies specify players’ actions, for each time period t,  as a function of the state of the system at the beginning of that period, $k_{t}$. Moreover, the aim of our analysis is to derive (time-invariant) rules describing the investment and consumption paths as linear functions of the state $k_{t}$. Often the linearity of investment and consumption plans is assumed for tractability, or it can be justified by players’ inability to elaborate more complex rules (see e.g., Houba et al. 2000 and Sorger 2006). In addition, Muthoo (1999) and Flamini (2012) show that in their simplified dynamic bargaining games, the subgame perfect equilibrium strategies are linear. Hence, the linear strategies are a natural candidate for our game (although more complex strategies cannot be excluded).

3 Characterization of the MPE Strategies

Let $V_{i}(k_{t})$ (respectively, $W_{i}(k_{t}))$ be the sum of discounted payoffs to player i, as a proposer (responder) in an arbitrary MPE. Then, the problem can be written in the following recursive form,

$$\begin{aligned} V_{i}(k_{t})\,\,=\,\, & {} \max \{V_{i}^{\prime }(k_{t}),\delta _{i}W_{i}(k_{t})\} \end{aligned}$$

(4)

$$\begin{aligned} W_{j}(k_{t})\,\,=\,\, & {} \max \{W_{j}^{\prime }(k_{t}),\delta _{j}V_{j}(k_{t})\} \end{aligned}$$

(5)

where $V_{i}^{\prime }(k_{t})$ and $W_{j}^{\prime }(k_{t})$ are the sums of discounted payoffs in case of an acceptance, that is,

$$\begin{aligned}&V_{i}^{\prime }(k_{t})\,\,=\,\,\underset{\varphi _{i}\in [-(1-\lambda ),G]}{ \underset{x_{i}\in [0,1]}{max}}u_{i}(x_{i},\varphi _{i},k_{t})+\alpha _{i}W_{i}(k_{t+1}) \end{aligned}$$

(6)

$$\begin{aligned}&\text {s.t. }W_{j}^{\prime }(k_{t})\ge \delta _{j}V_{j}(k_{t}) \end{aligned}$$

(7)

$$\begin{aligned}&\quad W_{j}^{\prime }(k_{t})\,\,=\,\,u_{j}(x_{i},\varphi _{i},k_{t})+\alpha _{j}V_{j}(k_{t+1}) \end{aligned}$$

(8)

with per-period utility as in (3) and consumption levels as in (1) and (2), while, in case of a rejection, the sum of discounted payoffs in (4) and (5) become

$$\begin{aligned} V_{i}(k_{t})\,\,=\,\,\delta _{i}W_{i}(k_{t})\text { and }W_{j}(k_{t})\,\,=\,\,\delta _{j}V_{j}(k_{t}) \end{aligned}$$

(9)

with the equation of motion given by

$$\begin{aligned} k_{t+1}\,\,=\,\,\left\{ \begin{array}{l} r_{i}k_{t}\quad \text { if there is an acceptance} \\ k_{t} \quad \quad \text { otherwise} \end{array} \right. \end{aligned}$$

(10)

where $r_{i}\,\,=\,\,\varphi _{i}+1-\lambda ,$ for $i,j\,\,=\,\,1,2$ and $i\ne j$. The rate $r_{i}$ indicates the gross rate of growth in the capital stock ($k_{t+1}/k_{t}$) once i’s proposal is implemented. Hence, it is given by the investment rate, $\varphi _{i}$, plus the non-depreciation rate, $1-\lambda$. As a result, when net investment, $\varphi _{i}-\lambda$ , is zero, then $r_{i}\,\,=\,\,1,$ while for a positive (negative) net investment, $r_{i}>1$ ($r_{i}<1$). Also, $r_{i}\in [0,l]$, where $l\,\,=\,\,G+1-\lambda .$ In the rest of the paper, to simply the notation, we often refer to MPE investment strategies in terms of the gross rate of growth $r_{i}$, rather than the investment rate $\varphi _{i}$ (which, obviously, coincide in the case of maximum depreciation, $\lambda \,\,=\,\,1$).

Problem (4)–(10) is a recursive constrained problem with a complex structure, since not only does (6) have a recursive form, but the constraint in (7) embodies another recursive problem (via the value functions $W_{j}^{\prime }(k_{t})$ and $V_{j}(k_{t})$). Although, generally such problems cannot be solved (see Stokey and Lucas 1989 and Ljungqvist and Sargent 2000), we can characterize the properties of the equilibrium outcomes and we can also obtain an analytical solution under certain conditions.

In the next lemma, we show that in a stationary MPE, delays cannot be sustained. The intuition is that not only is haggling never strategically profitable for a proposer, but he can always invest an appropriate amount of surplus so that a rejection is unprofitable for the responder.

Lemma 1

Assume that $\alpha _{i}l^{1-\eta }<1$, for $i\,\,=\,\,1,2$. Delays cannot be sustained in equilibrium.

Proof

In Appendix. $\square$

The condition $\alpha _{i}l^{1-\eta }<1$ is necessary for the existence of an equilibrium (as shown the proof of Lemma 1) and will be assumed henceforth (recall $l\,\,=\,\,G+1-\lambda$). Following Lemma 1, (4) and (5) become $V_{i}(k_{t})\,\,=\,\,V_{i}^{\prime }(k_{t})$ and $W_{j}(k_{t})\,\,=\,\,W_{j}^{ \prime }(k_{t})$ and the Lagrangian for the optimization problem in (6)–(8) and (10) is

$$\begin{aligned} L _{ i }(k_{ t })\,\,=\,\,V_{i}(k_{t})-m_{i}(\delta _{j}V_{j}(k_{t})-W_{j}(k_{t})) \end{aligned}$$

(11)

where $V_{i}(k_{t})$ and $W_{j}(k_{t})$ are in (6) and (8), $m_{i}$ is the (non-negative) Kuhn–Tucker multiplier (equal to zero when the constraint is slack) and $x_{i}$ (and $\varphi _{i}$) are the share consumed (and invested, respectively), with $i,j\,\,=\,\,1,2$ and $i\ne j$.

Given the linearity of the equilibrium consumption and investment plans, the value functions have the same functional form as the per-period utility function. Therefore, we write the value functions in such a form with coefficients which are left to be determined, we then solve the optimization problem and derive the correct values of such coefficients. Hence, let $\phi _{i}$ (and $\mu _{i}$) be the undetermined coefficients in player i’s value functions when he proposes (responds, respectively), that is

$$\begin{aligned} V_{i}(k_{t})\equiv \phi _{i}\frac{k_{t}^{1-\eta }}{1-\eta }\text { and } W_{i}(k_{t})\equiv \mu _{i}\frac{k_{t}^{1-\eta }}{1-\eta } \end{aligned}$$

Then, the optimization problem in (6)–(8) and (10) becomes

$$\begin{aligned} \phi _{i}\frac{k_{t}^{1-\eta }}{1-\eta }&\,\,=\,\,\underset{\varphi _{i}\in [-(1-\lambda ),G]}{\underset{x_{i}\in [0,1]}{max}}u_{i}(x_{i},\varphi _{i},k_{t})+\alpha _{i}\mu _{i}\frac{k_{t+1}^{1-\eta }}{1-\eta } \end{aligned}$$

(12)

$$\begin{aligned} \text {s.t. }\mu _{j}&\geqslant \delta _{j}\phi _{j}\text { with} \end{aligned}$$

(13)

$$\begin{aligned} \mu _{j}\frac{k_{t}^{1-\eta }}{1-\eta }&\,\,=\,\,u_{j}(x_{i},\varphi _{i},k_{t})+\alpha _{j}\phi _{j}\frac{k_{t+1}^{1-\eta }}{1-\eta } \end{aligned}$$

(14)

$$\begin{aligned} k_{t+1}&\,\,=\,\,r_{i}k_{t} \end{aligned}$$

(15)

with $r_{i}\,\,=\,\,\varphi _{i}+1-\lambda ,$ $i,j\,\,=\,\,1,2$ and $i\ne j.$ Hence, when optimizing, player i will take into account that his strategy $(x_{i},\varphi _{i})$ will have an impact on $\mu _{j}$ via (14), while will take $\phi _{j}$ as given.

Intuitively, the problem can be described as follows. On the one hand, player i has to decide how much to consume in the current period and how much to invest (which generates a larger surplus and therefore affects future consumption levels). On the other, he has to consider how to make his proposal acceptable to the opponent (13). For the latter, there are two possible channels: either keeping enough “money on the table” (that is, allowing the opponent to consume a sufficiently high share, $x_{i}<1$) or increasing investment (this gives the opponent a chance to propose with a relatively larger surplus next period, given the equation of motion (15)). We will show that, differently from the existing literature (e.g., Houba et al. 2000 and Sorger 2006), if the investment plan is large enough, a player can consume all the residual surplus ($x_{i}\,\,=\,\,1$) without facing a rejection. Moreover, this equilibrium can be sustained under realistic parameter constellations. In the rest of the paper, we formalize under which conditions the solution can be interior (in the next section) or not (in Sect. 3.2).

3.1 Interior MPE

To solve the optimization problem (12)–(15), first, we express the controls and subsequently the payoff coefficients only in terms of auxiliary variables¹²$\psi _{i}$ and Kuhn–Tucker multipliers $m_{i}$, with $i\,\,=\,\,1,2$ (aside from the parameters of the model, $\alpha _{i}$, $\delta _{i}$ and l). Then, we derive the equilibrium conditions to solve for $\psi _{i}$ and $m_{i}$, using a fixed point argument. Let¹³

$$\begin{aligned} M\,\,=\,\, & {} \bigg \{ (m_{i},\psi _{i})|m_{i},\psi _{i}>0,0<\left[ l\left( 1-\frac{ (1+m_{i}^{1/\eta })}{\psi _{i}}\right) \right] ^{1-\eta }\\&<\min \left( \frac{ \delta _{j}}{\alpha _{j}},\frac{1}{\alpha _{i}}\right) \text {for }i,j\,\,=\,\,1,2,i\ne j \bigg \} \end{aligned}$$

The first order conditions of (11) with respect of $x_{i}$ and $\varphi _{i}$ are as follows (see derivation in the Appendix),

$$\begin{aligned}&x_{i} \,\,=\,\,\frac{1}{1+m_{i}^{1/\eta }} \end{aligned}$$

(16)

$$\begin{aligned}&\varphi _{i}\,\,=\,\,\frac{(\alpha _{i}\mu _{i}+m_{i}\alpha _{j}\phi _{j})^{1/\eta }G-(1+m_{i}^{1/\eta })(1-\lambda )}{(\alpha _{i}\mu _{i}+m_{i}\alpha _{j}\phi _{j})^{1/\eta }+1+m_{i}^{1/\eta }} \end{aligned}$$

(17)

$$\begin{aligned}&\mu _{j}-\delta _{j}\phi _{j}\geqslant 0, m_{i}(\mu _{j}-\delta _{j}\phi _{j})\,\,=\,\,0 \end{aligned}$$

(18)

If there is an interior solution, $x_{i}<1$ in (16), it must be that $m_{i}>0$ and the constraint (18) holds as an equality (the indifference conditions), $\mu _{j}\,\,=\,\,\delta _{j}\phi _{j},$ for any $i,j\,\,=\,\,1,2$ and $i\ne j.$ By the complementary slackness condition, if the constraint (18) is not binding, the multiplier $m_{i}$ is zero. The cases implied by $m_{i}\,\,=\,\,0$ (with $i\,\,=\,\,1$ or 2 or both) hold under certain conditions and are considered in Sect. 3.2.

Using (16) and (17), the Bellman equation (12) can be re-written as

$$\begin{aligned} \phi _{i}\,\,=\,\,l^{1-\eta }\frac{1+\alpha _{i}\mu _{i}g_{i}^{(1-\eta )/\eta }}{ \psi _{i}^{1-\eta }} \end{aligned}$$

(19)

where

$$\begin{aligned} g_{i}\,\,=\,\, & {} \alpha _{i}\mu _{i}+m_{i}\alpha _{j}\phi _{j} \end{aligned}$$

(20)

$$\begin{aligned} \psi _{i}\,\,=\,\, & {} g_{i}^{1/\eta }+1+m_{i}^{1/\eta } \end{aligned}$$

(21)

while Eq. (14) becomes

$$\begin{aligned} \mu _{j}\,\,=\,\,l^{1-\eta }\frac{m_{i}^{\frac{^{1-\eta }}{\eta }}+\alpha _{j}\phi _{j}g_{i}^{(1-\eta )/\eta }}{\psi _{i}^{1-\eta }} \end{aligned}$$

Using the indifference conditions [constraints (13) as equality], then

$$\begin{aligned} \phi _{i}\,\,=\,\,\frac{l^{1-\eta }}{\psi _{i}^{1-\eta }-\alpha _{i}\delta _{i}l^{1-\eta }g_{i}^{\frac{1-\eta }{\eta }}}\text { and }\mu _{i}\,\,=\,\,\frac{ l^{1-\eta }\delta _{i}m_{j}^{\frac{1-\eta }{\eta }}}{\psi _{j}^{1-\eta }\delta _{i}-\alpha _{i}l^{1-\eta }g_{j}^{\frac{1-\eta }{\eta }}} \end{aligned}$$

(22)

with $i,j\,\,=\,\,1,2$ with $i\ne j.$ This implies that, the indifference conditions, can be written as in (25) below, while from the definition of the auxiliary variable $\psi _{i}$ in (21), or

$$\begin{aligned} \psi _{i}\,\,=\,\,(\alpha _{i}\mu _{i}+m_{i}\alpha _{j}\phi _{j})^{1/\eta }+1+m_{i}^{1/\eta } \end{aligned}$$

(23)

and using (20) and (22), we obtain

$$\begin{aligned}&g_{i}\,\,=\,\,l^{1-\eta }\left( \frac{\alpha _{i}\delta _{i}m_{j}^{\frac{1-\eta }{ \eta }}}{\psi _{j}^{1-\eta }\delta _{i}-\alpha _{i}l^{1-\eta }g_{j}^{\frac{ 1-\eta }{\eta }}}+\frac{\alpha _{j}m_{i}}{\psi _{j}^{1-\eta }-\alpha _{j}\delta _{j}l^{1-\eta }g_{j}^{\frac{1-\eta }{\eta }}}\right) \end{aligned}$$

(24)

$$\begin{aligned}&\frac{m_{j}^{\frac{1-\eta }{\eta }}}{\psi _{j}^{1-\eta }\delta _{i}-\alpha _{i}l^{1-\eta }g_{j}^{\frac{1-\eta }{\eta }}}\,\,=\,\,\frac{1}{\psi _{i}^{1-\eta }-\alpha _{i}\delta _{i}l^{1-\eta }g_{i}^{\frac{1-\eta }{\eta }}} \end{aligned}$$

(25)

where $g_{i}\,\,=\,\,\left( \psi _{i}-(1+m_{i}^{1/\eta })\right) ^{\eta }.$ The system in (24) and (25) characterizes the equilibrium: if there is a solution $(\psi _{i},m_{i})\in M$ to (24) and (25), this defines the value function coefficients, $\mu _{i}$ and $\phi _{i}$ in (22), and the MPE shares consumed, $x_{i}$ in (16), and invested, $r_{i}$ as given by

$$\begin{aligned} r_{i}\,\,=\,\,l\left( 1-\frac{(1+m_{i}^{1/\eta })}{\psi _{i}}\right) \end{aligned}$$

(26)

3.1.1 An Example (Symmetry and $\eta \,\,=\,\,1/2)$

In this section, we assume that players are symmetric and the intertemporal elasticity of substitution is equal to 2 (i.e., $\eta \,\,=\,\,1/2$, see Thimme (2017) for a justification for this value). In this case, the game can be solved analytically, as shown in the following proposition.

Proposition 1

For $\eta \,\,=\,\,1/2,$ $h_{i}\,\,=\,\,h$ (i.e., $\delta _{i}\,\,=\,\,\delta$, $\alpha _{i}\,\,=\,\,\alpha$ for $i\,\,=\,\,1,2$), if $\alpha ^{2}l<1,$ there is a unique symmetric linear MPE in which each player successfully proposes the following consumption and investment plans

$$\begin{aligned} x\,\,=\,\, & {} \frac{1}{1+m^{2}} \end{aligned}$$

(27)

$$\begin{aligned} r\,\,=\,\, & {} \frac{(\delta -m)^{2}}{\alpha ^{2}(\delta m-1)^{2}} \end{aligned}$$

(28)

where

$$\begin{aligned} m\,\,=\,\,\frac{-(1-\delta ^{2})(1+\alpha ^{2}l)+\Gamma ^{\frac{1}{2}}}{2\delta (1-\alpha ^{2}l)} \end{aligned}$$

(29)

with

$$\begin{aligned} \Gamma \,\,=\,\,\left[ (1+\delta ^{2})(1+\alpha ^{2}l)\right] ^{2}-2^{4}\alpha ^{2}l\delta ^{2} \end{aligned}$$

Hence, the MPE payoff coefficients are

$$\begin{aligned} \phi\,\,=\,\, & {} \frac{l^{1/2}}{\psi ^{1/2}-\alpha \delta l^{1/2}\left( \psi -(1+m^{2})\right) ^{1/2}} \end{aligned}$$

(30)

$$\begin{aligned} \mu\,\,=\,\, & {} \frac{l^{1/2}\delta m}{\psi ^{1/2}\delta -\alpha l^{1/2}\left( \psi -(1+m^{2})\right) ^{1/2}} \end{aligned}$$

(31)

where

$$\begin{aligned} \psi \,\,=\,\,\frac{(1+m^{2})(1-\delta m)^{2}\alpha ^{2}l}{\alpha ^{2}l(1-\delta m)^{2}-(m-\delta )^{2}} \end{aligned}$$

(32)

Proof

In Appendix. $\square$

It can be shown that a proposer consumes more than a responder in a given round ($x>1/2$ for $\delta \in [0,1)$). Typically, the investment level is inefficient, unless bargaining is frictionless, as shown below.

Corollary 1

For $h_{1}\,\,=\,\,h_{2},$ at the limit for $\Delta$ that tends to 0, the stationary MPE is socially optimal

$$\begin{aligned} \underset{\Delta \rightarrow 0}{\lim }x\,\,=\,\, & {} \frac{1}{2} \end{aligned}$$

(33)

$$\begin{aligned} \underset{\Delta \rightarrow 0}{\lim }r\,\,=\,\, & {} (\alpha l)^{2} \end{aligned}$$

(34)

For $\Delta >0$, bargaining leads to underinvestment.

Proof

At the limit for $\Delta$ that tends to 0, the multiplier m in (29) tends to 1, and therefore the consumption share x in (27) tends to 1/2. Moreover, given that $\psi$ tends to $2(1-\alpha ^{2}l)^{-1},$ then, r in (28) goes to ($\alpha l)^{2}$, hence (34). It can be shown that when players are symmetric, a (utilitarian) social planner, maximizing the sum of players’ discounted payoffs, would invest a share $r\,\,=\,\,(\alpha l)^{1/\eta }$ (this is in line with the efficient consumption path derived in (40)) and would split the remaining surplus equally among the two parties (hence x and r,  as in (33) and (34), are socially optimal). For $\Delta >0$, r in (28) is lower than (34). Hence, there is underinvestment. $\square$

In frictionless bargaining, players with the same rate of time preference consume half of the residual surplus and invest a non-negative amount of surplus if sufficiently patient (i.e., if $\alpha \ge (1-\lambda )^{1/2}/l$ ), otherwise parties disinvest as a social planner would efficiently choose to do. This result can be generalized for other values of $\eta$.¹⁴$^{,}$¹⁵ Instead, bargaining with frictions is inefficient, due to the same incentives as in the hold-up problem. Although in our framework a proposer can use a higher investment rate to facilitate an acceptance, he would tend to over-consume.

Differently from Muthoo (1995, (1999), where the polar consumption equilibrium ($x\,\,=\,\,1$) is sustainable for $\alpha \geqslant \delta$, in our dynamic model there will be always an interior solution for any $\alpha ,\delta ,$ with $\alpha ,\delta \in [0,1]$ and $\alpha ^{2}l<1.$ Indeed, it is straightforward to see that the equilibrium demands (27) and (28) are always interior for any value of discount factor $\alpha ,\delta \in (0,1)$.¹⁶ This result holds not only for $\eta \,\,=\,\,1/2,$ but can be generalized for other values of $\eta$ (as shown in the next section and 3.2).

In the rest of this section we highlight the effect of patience on the MPE division.

Corollary 2

The MPE consumption demand x, in (27), is decreasing with $\delta$, the within-cake discount factor and increasing with $\alpha$, the between-cake discount factor. The impact of patience on x can be either positive or negative. Instead, the MPE investment r, in (28), is increasing with both $\delta$ and $\alpha$.

Proof

In Appendix$\square$

In the case of symmetry, the impact of patience on the investment shares is unambiguous: more patient players invest more. Instead, the impact of patience on the consumption share x can be more complex. Corollary 2 shows that the two discount factors have conflicting effects on the share demanded x. As in the standard Rubinsteinian game, an increase in the within-cake discount factor, $\delta ,$ reduces the share demanded x, since counteroffers can be made more quickly. However, in dynamic bargaining, the between-cake discount factor, $\alpha ,$ increases the share demanded (ceteris paribus). Since production is quicker, a proposer can exploit the trade-off between current and future consumption successfully (this is the dominant effect when $\alpha$ increases, differently from the case in which $\delta$ increases).

As a result, the overall impact of patience (h decreases, hence both $\delta$ and $\alpha$ increase) on the share demanded can be either positive (the $\alpha$-effect dominates) or negative (the $\delta$-effect dominates) depending on the rate of return, depreciation rate (via $l\,\,=\,\,G+1-\lambda$) and the length of the production stage (see proof of Corollary 2). For instance, at the limit for l that tends to 0 (or for $\tau$ that tends to $\infty$) the impact of patience on x is negative (the $\delta$-effect). Instead when capital is sufficiently productive and production is short (with $\alpha ^{2}l<1)$, the impact of patience on the share consumed x is positive (the $\alpha$-effect dominates). The simple case of symmetry (and $\eta \,\,=\,\,1/2$) has highlighted a rich interplay of forces in our model. We next investigate this further in the more complex environment of (potentially) asymmetric players (and different values of $\eta$).

3.1.2 The General Case

We have solved system (24) and (25) for different values of the parameters. A selection of the numerical results is presented in the following figures and tables, while the properties of the equilibrium are highlighted in the following remarks.¹⁷ The aim of the section is to highlight the effects of the complex interplay of the discounting structure, the rate of return G and the depreciation rate $\lambda$ (via l) on the MPE. Typical results which hold in bargaining theory can be overturned, as shown next. In the first remark, the focus is on the share consumed ($x_{i}$ for $i\,\,=\,\,1,2$).

Fig. 1

MPE demands for $\eta \,\,=\,\,1/2$, $(\alpha _{i},\delta _{i})\,\,=\,\,(0.5,0.9)$ and $(\alpha _{j},\delta _{j})\,\,=\,\,(0.7,0.95)$

Remark 1

The more patient party, say j, demands to consume a larger share than his opponent $(x_{j}>x_{i})$, unless l is sufficiently large and the production stage is sufficiently longer than a bargaining round.

Table 2 and Fig. 1 are used to illustrate the remark. Table 2 presents an overview of the MPE demands for a range of discount factors¹⁸. In the case of symmetric players, we find the symmetric MPE demands, (x, r), in the diagonal. The table entries for the asymmetric cases include player i’s demands $(x_{i},r_{i})$, in the first line, followed by player j’s ($x_{j},r_{j})$, in the second line, with $i,j\,\,=\,\,1,2$ and $i\ne j$.

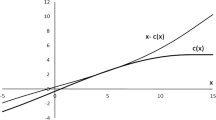
Table 2 shows the first part of Remark 1, the more patient proposer is able to consume a larger share (that is, in the first column within each non-diagonal table cell, the first value, $x_{i}$ is lower than the second $x_{j})$. This result is in line with standard bargaining theory (without investment). However, we show next that the possibility of investing overturns this result, when l is sufficiently large and the production stage is relatively long (see Fig. 1).

Figure 1 shows the MPE demands as the rate l increases, for relatively long production stages.¹⁹ When l is sufficiently large (i.e., $l\geqslant 1.7)$, the most patient proposer (j) demands a share smaller than his rival’s ($x_{j}<x_{i}$). The intuition is that for high rates of return G and/or low depreciation rates $\lambda$, both parties have incentives to invest more, however, the most patient party wishes to invest more and the gap between players’ investment plans, $r_{j}$ and $r_{i}$, increases with l. Then, to prioritize investment—which affects future bargaining possibilities—the most patient party must make larger concessions, while the impatient party can increase his demand (Fig. 1 shows that $x_{j}$ decreases with l,  while $x_{i}$ increases with l).

A crucial factor, aside from a large value of l,  is the difference in players’ discount factors ($\delta _{i}-\alpha _{i}$).²⁰ For large values of l, the most patient player must make larger concessions since counteroffers can be made fairly quickly ($\Delta$ is significantly smaller than $\tau$). It can be shown that with shorter production stages and/or smaller l there would be no crossing between $x_{j}$ and $x_{i}$ ($x_{j}>$ $x_{i}$), while l increases.

Table 2 Player i’s (j’s) MPE demands ($x_{i},r_{i}$) in the first (second) line (for asymmetic cases), for $\eta \,\,=\,\,1/2$ and $l\,\,=\,\,0.7$

Next, the focus is on the MPE investment plans. We will show that the within-cake discount factors ($\alpha _{i}$ with $i\,\,=\,\,1,2)$ and the difference between players in this dimension play an important role in defining the optimal investment plans.

Remark 2

The more patient party invests more than his opponent, unless $\alpha _{i}\,\,=\,\,\alpha _{j}$ (with $i,j\,\,=\,\,1,2,$ and $i\ne j$); in this case, they generally have the same investment plan.

In Remark 2, we are considering the scenario in which players have the same between-cake discount factors, but different within-cake discount factors. This can be contemplated in our model (apart from comparative statics) only if the common parameter $\alpha$ is re-interpreted as a probability of game continuation after an acceptance (while production is instantaneous and bargaining rounds still take time). We would expect that since the most patient party is the most concerned about future payoffs then he will invest more than his opponent. This is generally confirmed in our numerical analysis, for instance, in Fig. 1 and in Table 2 (where $r_{i}\leqslant r_{j}$, recall the values $r_{i}$ and $r_{j}$ are in the second column of each cell). However, Table 3 shows that the investment plans are surprising similar when players have the same between-cake discount factor or probability of game continuation (in all the cells either $r_{i}\,\,=\,\,r_{j}$ or $r_{i}\simeq r_{j})$. Differences in time preferences affect their consumption shares, but the long-run variable of our model, investment, is crucially determined by the probability of game continuation.

Table 3 Player i’s (j’s) MPE demands ($x_{i}$, $r_{i}$) in the first (second) line, for $\delta _{i}\,\,=\,\,0.9$, $\delta _{j}\,\,=\,\,0.95$ and $l\,\,=\,\,0.7$

In the next two remarks, we summarize the effects of a change in a party’s level of patience on the MPE investment strategies (Remark 3) and payoffs (Remark 4). As highlighted below, more patience may imply less investment.

Fig. 2

MPE demands for $\eta \,\,=\,\,1/2,$ $l\,\,=\,\,1.1$ and ($\alpha _{i},\delta _{i})\,\,=\,\,(0.8,0.9)$

Remark 3

If a party becomes more patient, both parties invest more, only when sufficiently similar, otherwise they decrease their investment plans.

Figure 2 presents the effect of a change in player j’s patience on the MPE demands, for $\eta \,\,=\,\,1/2,$ $l\,\,=\,\,1.1,$ $(\alpha _{i},\delta _{i})\,\,=\,\,(0.8,0.9).$ The x-axis represents player j’s within-cake discount factor, $\delta _{j}$ ($\alpha _{j}$ varies accordingly, see footnote 17). The effect on the consumption shares ($x_{i}$ and $x_{j}$) is simple here: when player j becomes more patient he can consume a larger share ($x_{j}$ increases) while his opponent consumes less ($x_{i}$ decreases), in line with standard bargaining theory.²¹ Instead, the effect of a change in player j’s patience on the investment shares is less straightforward. Figure 2 shows that starting from low levels of patience for player j, while he becomes more patient he reduces investment ($r_{j}$ decreases), similarly, for his opponent ($r_{i}$ decreases). However, as player j’s level of patience increases further ($\delta _{j}\geqslant 0.4$), he invests more and eventually also his opponent becomes willing to increase his investment plan ($\delta _{j}$ is required to be larger than 0.5). This effect is interesting, because generally, we would expect that if a party becomes more patient, he would invest more (since his future payoffs are discounted less heavily) and subsequently his rival will also invest more (as shown, for instance, in Table 2, when we move along each row, $r_{i}$ and $r_{j}$, the values in the second column of each cell, increase with player j’s patience). Clearly, though, this is a key incentive only when players’ asymmetry is mild. With pronounced asymmetries, instead, there is a tension between a patient player willing to invest a large share and an impatient one forced to accept smaller shares of the residual surplus. The key underlying driver of this result is that when counteroffers become cheaper for the impatient party (his between-cake discount factor increases, ceteris paribus), this allows him to increase his consumption level (by demanding a larger share and reducing his investment plan). As a result, his more patient opponent is forced to make larger concessions (by reducing both his investment and consumption plans).²²

In accumulation games with simpler bargaining structures, it has been shown that, differently from standard bargaining theory, patience is weakness. In our model, we can re-establish the result that patience is strength and demonstrate that patience can make a rival better off, under certain conditions, as shown next.

Fig. 3

a MPE for $\eta \,\,=\,\,2/3,$ $l\,\,=\,\,1.2$ and $(\alpha _{j},\delta _{j})\,\,=\,\,(0.8,0.95)$ b MPE for $\eta \,\,=\,\,2/3,$ $l\,\,=\,\,1.3$ and $(\alpha _{j},\delta _{j})\,\,=\,\,(0.8,0.95)$

Remark 4

Let player i be less patient than j, but his patience increases. Then, player j, consumes more and is overall better off, if l is sufficiently large and the production stage is sufficiently longer than a bargaining round.

Figure 3a and b show the effect of an increase in player i ’s patience on the MPE demands (first panel) and payoffs coefficients (second and third panel) for $(\alpha _{j},\delta _{j})\,\,=\,\,(0.8,0.95),$ when the production stage is relatively long (that is, a party’s between-cake discount factor is significantly lower than his within-cake discount factor, see also footnote 19). In terms of parameter constellations, the only difference between Fig. 3a and b is that in the former l is lower ($l\,\,=\,\,1.2$ in Fig. 3a and 1.3 in Fig. 3b). This is a crucial difference: while for $l\,\,=\,\,1.2$, we obtain the standard result that as a player (say i) gets more patient, his rival is worse off (the value function coefficients, $\phi _{j}$ and $\mu _{j}$ decrease, see the middle panel of Fig. 3a), for $l\,\,=\,\,1.3$, player j becomes better off ($\phi _{j}$ and $\mu _{j}$ increase for $\delta _{i}>0.85$, see the middle panel of Fig. 3b).

To understand this result, we look into the effect of patience on the MPE strategies. In contrast with Fig. 3a (and Fig. 2), Fig. 3b shows that proposer j is able to consume a higher share ($x_{j}$ increases) despite his opponent becoming more patient. In particular, while in Fig. 3a (and Fig. 2), for relatively low l, $x_{j}$ decreases monotonically, in Fig. 3b, with a higher l, $x_{j}$ increases with patience, for $\delta _{i}$ sufficiently large ($\delta _{i}>0.88$). The key force behind this result is that while the asymmetry between players softens, investment rates are converging and increasing ($r_{i}$ increases for $\delta _{i}>0.66$ and $r_{j}$ increases for $\delta _{i}>0.74$ in Fig. 3b) for a large rate of return ($l\,\,=\,\,1.3$). Hence, the patient player, j, who was forced to make concessions when player i was still significantly more impatient (see also Remark 3 and the following discussion), can now exploit the prospect of high future consumption levels, due to the high investment plans, and extract a larger share of the current surplus.²³

Finally, following Muthoo (1999, p. 307), we can interpret the value functions as a measure of overall bargaining power in long-run relationships.²⁴ Then, Fig. 3a and b show that, despite the concessions that a patient player must make in equilibrium, such a player maintains the highest bargaining power both as a proposer and as a responder (that is, $\phi _{j}>\phi _{i}$ and $\mu _{j}>\mu _{i}$, for any $\delta _{i}<\delta _{j}\,\,=\,\,0.95$, in Fig. 3a and b, middle and bottom panels).

3.2 MPE with Extreme Demands

In this section, we focus on MPE with extreme demands. We are interested in cases where parties are still relatively patient. Despite being relatively patient, there is an equilibrium in which both players are able to consume all the residual surplus (this is the polar consumption MPE) and it is analyzed in the next subsection. The case in which only one player is able to consume all the residual surplus (this is the hybrid MPE) is briefly considered last. We find that the different types of MPE cannot coexist for the same parameter constellation.

3.2.1 Polar Consumption MPE

Let

$$\begin{aligned} b_{i}\,\,=\,\,[\alpha _{i}^{\eta }(\alpha _{j}l)^{1-\eta }]^{\frac{2}{2\eta -1}} \end{aligned}$$

with $\eta \ne 1/2$ and²⁵

$$\begin{aligned} D\,\,=\,\, & {} \left\{ (\alpha _{i},\delta _{i},l)|\alpha _{i},\delta _{i}\in (0,1),l>0,\delta _{j}\le \alpha _{j}\left( lb_{i}\right) ^{1-\eta }, b_{i}\in (0,1)\right. \\&\left. \text {for }i,j\,\,=\,\,1,2,i\ne j\right\} \end{aligned}$$

Proposition 2

If $\eta \in (1/2,1)$ and $(\alpha _{i},\delta _{i},l)\in D$ there is a unique (linear) MPE in which each proposer consumes all the surplus not invested ($x_{i}\,\,=\,\,1$) and his investment plan is

$$\begin{aligned} r_{i}\,\,=\,\,lb_{i} \end{aligned}$$

(35)

The value function coefficients are

$$\begin{aligned} \phi _{i}\,\,=\,\,\frac{l^{1-\eta }}{(1-b_{i})^{\eta }}\text { and }\mu _{i}\,\,=\,\,\frac{ b_{i}^{\eta }}{(1-b_{i})^{\eta }\alpha _{i}} \end{aligned}$$

(36)

for $i,j\,\,=\,\,1,2$ with $i\ne j.$

Proof

In Appendix.²⁶$\square$

Polar consumption MPE can exist in our model when players are relatively patient, because a proposer can compensate a responder, who has a zero per-period consumption, by investing sufficiently therefore increasing his future consumption levels (as a proposer). A key role is played by the elasticity of intertemporal substitution, which is required to be sufficiently small ($\eta >1/2$). This measures the player’s willingness to substitute future consumption for present consumption. When it is low enough, extreme demands are acceptable. In other words, the curvature of the utility function in (3) decreases when consumption levels increase, but decreases less when $\eta$ is large. As a result, a player’s utility is higher for any positive level of consumption, when $\eta$ is larger. Therefore, the higher $\eta$, the higher the compensation a player will obtain after accepting an extreme demand. Hence, for $\eta >1/2$ the responder can defer consumption and accept a polar consumption proposal that gives him zero current consumption, while for $\eta \le 1/2$ responders cannot accept polar consumption proposal.

The investment path under the polar consumption MPE is simpler than the one highlighted in Remark 3. The investment rates in (35) increase with players’ patience. Therefore, if player i becomes more patient not only does he increase his investment plan but so does his opponent. This clear-cut effect is due to that fact that only the between-cake discount factors affect the size of $r_{i}$ [see (35)].²⁷ Moreover, the overall effect on player j’s payoff is positive [using (36), it can be shown that the coefficients for j’s value functions both as a proposer, $\phi _{j}$, and as a responder, $\mu _{j}$, are increasing with $\alpha _{i}$].²⁸ However, as for the interior MPE, also in the polar consumption MPE, there is underinvestment. That is, for $h_{1}\,\,=\,\,h_{2}$, the investment rates in (35) are lower than the socially optimal rate $r\,\,=\,\,(\alpha l)^{1/\eta }$ (see proof of Corollary 1, since $\alpha l^{1-\eta }<1$).

It has been shown that in long-run relationships without dynamic accumulation (see Muthoo 1995), players can have extreme forms of bargaining power where proposers consume all the residual surplus, although, only under unlikely conditions (in which the production stage is quicker than the length of a bargaining round, $\Delta \ge \tau ,$ see Muthoo 1999, p. 594). In our dynamic framework, a polar consumption MPE can be sustained under less restrictive conditions (that is, $\Delta <\tau$), as long as the investment rates are sufficiently large ($r_{i}\,\,=\,\,lb_{i}\ge (\delta _{j}/\alpha _{j})^{1/(1-\eta )}$) so as to compensate a responder for accepting extreme proposals. However, there must be some frictions in the bargaining stage. If, instead, counteroffers can be made instantaneously (the interval $\Delta$ tends to 0), extreme demands are not sustainable in equilibrium. To see this, we re-write the last two conditions in the feasibility set D as follows

$$\begin{aligned}&\frac{\delta _{j}^{2\eta -1}}{\alpha _{j}^{1-2\eta +2\eta ^{2}}\alpha _{i}^{2\eta (1-\eta )}}\le l^{1-\eta }<\frac{1}{\alpha _{i}^{\eta }\alpha _{j}^{1-\eta }} \end{aligned}$$

(37)

$$\begin{aligned}&\delta _{j}<\left( \frac{\alpha _{j}}{\alpha _{i}}\right) ^{\eta } \end{aligned}$$

(38)

At the limit for $\Delta$ that tends to 0, condition (38) cannot hold for both $i,j\,\,=\,\,1,2$ with $i\ne j.$ Intuitively, when counteroffers can be made quickly, extreme demands are not acceptable (investment levels cannot be large enough) and, as a result, a proposer must make some concessions (and leave a positive share of the surplus to the responder).

To give an idea of the support for the polar consumption MPE in Proposition 2, we consider the case of symmetric players, then, conditions (37) and (38), can be written as

$$\begin{aligned} \delta \le (\alpha l^{1-\eta })^{\frac{1}{2\eta -1}}<1 \end{aligned}$$

(39)

The first inequality in (39) ensures that the surplus generated is sufficiently large, so that fairly patient parties still accept consuming nothing when they are responders, while the second inequality in (39) ensures that the equilibrium payoffs are finite. Obviously, the conditions in (39) are less stringent when $\Delta \ge \tau .$ For instance, if after an agreement another bargaining stage can start straightaway ($\tau \rightarrow 0)$ then the upper bound for the discount factor $\delta$ is simply $l^{\frac{1-\eta }{2\eta -1}}$ and l is required to be less than 1. Assume, instead, it is quicker to make a counteroffer than producing a surplus ($\Delta <\tau )$. Then, l must be larger than 1 (from (39), since $\delta ^{2\eta -1}/\alpha >1).$ Hence, it is possible to accept extreme demands when counteroffers can be made relatively quickly only if capital is productive enough.

3.2.2 Hybrid MPE

In addition to the polar consumption MPE, there can be other solutions of the problem, in which only one player (say, 1) is able to make extreme offers (that is, $x_{1}\,\,=\,\,1$ while $x_{2}<1)$ without facing a rejection. Intuitively, this requires sufficiently asymmetric players (so that the most impatient party accepts an extreme proposal and makes concessions to the opponent when proposing). Indeed, this is what we can show numerally. However, we omit the numerical analysis, since the most interesting MPE remains the interior solution. For completeness, we present the characterization of the hybrid MPE in the Appendix.

4 Final Remarks

The novelty of our framework is that it addresses the problem of dynamic accumulation within a bargaining game, following a fully non-cooperative approach, where counteroffers are allowed and players can directly affect the future potential benefits which can arise from their long-run relationship. We have shown that when investment is introduced within a bargaining game, the interplay of the forces can be very complex and that various lessons from standard bargaining theory can be overturned. An additional novelty of our model is that polar consumption shares can be an equilibrium phenomenon, even with modest frictions, since a proposer can invest enough to compensate a responder for accepting a proposal that gives him zero current consumption. Moreover, although generally the investment strategy can give a proposer the ability to obtain an acceptance without making large concessions to his opponent, players will never over-invest. Indeed, they will typically under-invest. Only with frictionless bargaining, players can achieve the efficient level of investment.

In addition, when players are asymmetric, they agree on dynamically inefficient divisions, since typically they will share the surplus not invested. Instead, it would be Pareto superior to let only the impatient player consume a positive share of the initial N surpluses and let only the patient party consume afterwards. Although the solution is dynamically inefficient, it is dynamically consistent. Dynamic consistency emerges from the fact that players do not commit to future behaviors, in each period they simply optimize their behavior taking into account the effect of current decisions.

Institutions could re-establish efficiency. For instance, assuming players with similar rates of time preference, if they could commit to share all the residual surpluses equally, then, even if impatient they can behave efficiently (regardless of the bargaining procedure adopted). Suppose, for instance, that before entering a business, two partners could sign a contract that specifies that each will obtain half of the profits not re-invested. Then, their investment plan would be efficient. Accordingly, policy makers may wish to create institutions which guarantee an appropriate division of mutual gains to encourage efficient investment paths in ongoing negotiations.

Appendix

Proof of Lemma 1

²⁹

Consider any subgame where player i proposes first. Let $k_{t}$ be the state variable and $V_{i}(k_{t})$ ($W_{j}(k_{t})$) the sum of discounted payoffs to player i (j) in an arbitrary MPE, with $i,j\,\,=\,\,1,2$ and $i\ne j.$ First, we show that the sum of discounted utilities $V_{i}(k_{t})$ and $W_{i}(k_{t})$ are bounded,

$$\begin{aligned} V_{i}(k_{t}),W_{i}(k_{t})\in \left[ 0,\frac{k_{t}^{1-\eta }}{1-\eta }\frac{ l^{1-\eta }}{\left( 1-\left( \alpha _{i}l^{1-\eta }\right) ^{1/\eta }\right) ^{\eta }}\right] \end{aligned}$$

if $\alpha _{i}l^{1-\eta }<1.$ The upper bound has been derived by assuming that the investment and consumption paths are to maximize player i’s payoff as in a standard saving model (with one decision maker). Using the value function iteration method, it can be shown that the per-period consumption for player i is given by

$$\begin{aligned} l\left( 1-\left( \alpha _{i}l^{1-\eta }\right) ^{1/\eta }\right) k_{t} \end{aligned}$$

(40)

and all the surplus not consumed by player i is invested. The condition $\alpha _{i}l^{1-\eta }<1$ must hold to have the convergence of the sum of discounted payoffs.

Next, we show that delays cannot be part of an MPE. Consider an arbitrary stationary MPE, where player i proposes ($x_{i},\varphi _{i}$) to player j, with $i,j\,\,=\,\,1,2$ and $i\ne j$. If player j accepts the offer ($x_{i},\varphi _{i}$) and the state is $k_{t}$, his payoff is

$$\begin{aligned} u_{j}(x_{i},\varphi _{i},k_{t})+\alpha _{j}V_{j}(k_{t+1}) \end{aligned}$$

while, if he rejects it, he obtains $\delta _{j}V_{j}(k_{t}).$ Therefore, the proposal ($x_{i},\varphi _{i}$) is accepted if and only if

$$\begin{aligned} u_{j}(x_{i},\varphi _{i},k_{t})\ge \delta _{j}V_{j}(k_{t})-\alpha _{j}V_{j}(k_{t+1}) \end{aligned}$$

(41)

We now distinguish three scenarios: depending on whether (41) holds for at least one player or not. In the first case, (41) does not hold for any player, or $W_{j}(k_{t})<\delta _{j}V_{j}(k_{t})$ with $j\,\,=\,\,1,2$. If players always reject the offer, when the state is $k_{t}$, then the state $k_{t+1}$ is never reached and

$$\begin{aligned} V_{j}(k_{t})\,\,=\,\,V_{j}(k_{t+1})\,\,=\,\,W_{i}(k_{t})\,\,=\,\,W_{i}(k_{t+1})\,\,=\,\,0 \end{aligned}$$

for any $i,j\,\,=\,\,1,2,$ which leads to a contradiction.

In the second case, (41) holds only for one player, without loss of generality, say $j\,\,=\,\,1$ and $i\,\,=\,\,2.$ Then, player 2 makes an acceptable offer (while 1 does not). Player 2 prefers to make an acceptable offer if the sum of his discounted payoff, when making the offer, $V_{2}(k_{t})$, is not smaller than his discounted payoffs in the case of a rejection, or

$$\begin{aligned} u_{2}(x_{2},\varphi _{2},k_{t})+\alpha _{2}W_{2}(k_{t+1})\ge \delta _{2}W_{2}(k_{t}) \end{aligned}$$

(42)

with $k_{t+1}\,\,=\,\,(1+\lambda +\varphi _{2})k_{t}$. Instead, player 1 prefers to make an unacceptable offer if

$$\begin{aligned} u_{1}(x_{1},\varphi _{1},k_{t})+\alpha _{1}W_{1}(k_{t+1})<\delta _{1}W_{1}(k_{t}) \end{aligned}$$

(43)

Then, the offer must be such that player 2 prefers to reject it, $W_{2}(k_{t})<\delta _{2}V_{2}(k_{t}).$ Next, we show that this case cannot hold. Assume player 1 proposed the same division as player 2, $(x_{1},\varphi _{1})\,\,=\,\,(1-x_{2},\varphi _{2}),$ this would be accepted and player 1 would be strictly better off, since a delay is avoided (and $\delta _{1}<1$),

$$\begin{aligned} u_{1}(x_{1},\varphi _{1},k_{t})+\alpha _{1}W_{1}(k_{t+1})>\delta _{1}\left( u_{1}(x_{2},\varphi _{2},k_{t})+\alpha _{1}W_{1}(k_{t+1})\right) \end{aligned}$$

Therefore, there is a contradiction. We can conclude that delays cannot be part an MPE.

In the third case, (41) holds for both players when responding to an offer, in other words, regardless of who makes the offer at $k_{t}$, the other party accepts the offer. The rest of the paper focuses on this case.

Derivation of the First Order Conditions

Player i’s Lagrangian in (11) becomes

$$\begin{aligned}&\underset{\varphi _{i}\in [-(1-\lambda ),G]}{\underset{x_{i}\in [0,1]}{max}}\frac{(x_{i}(G-\varphi _{i})k_{t})^{1-\eta }}{1-\eta } +\alpha _{i}\mu _{i}\frac{((\varphi _{i}+1-\lambda )k_{t})^{1-\eta }}{1-\eta } \\&\quad +m_{i}\left[ \frac{((1-x_{i})(G-\varphi _{i})k_{t})^{1-\eta }}{1-\eta } +\alpha _{j}\phi _{j}\frac{((\varphi _{i}+1-\lambda )k_{t})^{1-\eta }}{1-\eta }+\right. \\&\quad \left. -\delta _{j}\left( \frac{(x_{j}(G-\varphi _{j})k_{t})^{1-\eta }}{ 1-\eta }+\alpha _{j}\mu _{j}\frac{((\varphi _{j}+1-\lambda )k_{t})^{1-\eta } }{1-\eta }\right) \right] \end{aligned}$$

The first order conditions with respect to the controls are

$$\begin{aligned}&\frac{1}{x_{i}^{\eta }}-\frac{m_{i}}{(1-x_{i})^{\eta }}\,\,=\,\,0 \end{aligned}$$

(44)

$$\begin{aligned}&-\frac{x_{i}{}^{1-\eta }+m_{i}(1-x_{i})^{1-\eta }}{(G-\varphi _{i})^{1-\eta } }+\frac{\alpha _{i}\mu _{i}+m_{i}\alpha _{j}\phi _{j}}{(\varphi _{i}+1-\lambda )^{\eta }}\,\,=\,\,0 \end{aligned}$$

(45)

while, with respect to the multiplier,

$$\begin{aligned} \mu _{j}-\delta _{j}\phi _{j}\geqslant 0, \quad m_{i}(\mu _{j}-\delta _{j}\phi _{j})\,\,=\,\,0 \end{aligned}$$

Then, using (44), we can obtain (16). Moreover, (16) in (45) gives the optimal for $\varphi _{i}$, as in (17). $\square$

Proof of Proposition 1

For $\eta \,\,=\,\,1/2$ and $h_{i}\,\,=\,\,h$, system (24)–(25) has a unique symmetric solution, which is given by (29) and (32). Then, the MPE demand (16) becomes (27), while using (32), the MPE investment plan (26) can be written as (28). Moreover, the payoff coefficients (30) and (31) follow from (22), given

$$\begin{aligned} g_{i}\,\,=\,\,\left( \psi _{i}-(1+m_{i}^{2})\right) ^{1/2} \end{aligned}$$

Finally, the support set M can be replaced by the condition $\alpha ^{2}l<1,$ given $\alpha ,\delta \in (0,1)$ and $l>0.$ $\square$

Proof of Corollary 2

The multiplier decreases with $\alpha$ and increases with $\delta ,$ since,

$$\begin{aligned} \frac{\partial m}{\partial \alpha }\,\,=\,\, & {} \frac{2l\alpha (1-\delta ^{2})\left( (1+l\alpha ^{2})(1-\delta ^{2})-\Gamma ^{\frac{1}{2}}\right) }{\delta (1-l\alpha ^{2})^{2}\Gamma ^{\frac{1}{2}}}<0 \\ \frac{\partial m}{\partial \delta }\,\,=\,\, & {} \frac{(1+\delta ^{2})(1+l\alpha ^{2})\left( \Gamma ^{\frac{1}{2}}-(1+l\alpha ^{2})(1-\delta ^{2})\right) }{ 2(1-l\alpha ^{2})\delta ^{2}\Gamma ^{\frac{1}{2}}}>0 \end{aligned}$$

for any $\alpha ,\delta$ in (0, 1) and $l\alpha ^{2}<1.$ Therefore the MPE demand (27) increases with $\alpha$ and decreases with $\delta$. $\square$

The effect of patience on the multiplier can be either positive or negative, as shown next. The derivative of the multiplier m with respect to h is

$$\begin{aligned} \frac{\partial m}{\partial h}\,\,=\,\,\frac{\partial m}{\partial \alpha }\frac{ \partial \alpha }{\partial h}+\frac{\partial m}{\partial \delta }\frac{ \partial \delta }{\partial h} \end{aligned}$$

with $\partial \alpha /\partial h\,\,=\,\,-\tau e^{-h\tau }$ and $\partial \delta /\partial h\,\,=\,\,-\Delta e^{-h\Delta }$. Hence,

$$\begin{aligned} \frac{\partial m}{\partial h}\,\,=\,\,\frac{a\left( \Gamma ^{\frac{1}{2}}-b\right) }{ \left( 1-f\right) ^{2}e^{-h\Delta }\Gamma ^{\frac{1}{2}}} \end{aligned}$$

where

$$\begin{aligned} a\,\,=\,\, & {} -\Delta \left( 1+(e^{-h\Delta })^{2}\right) \left( 1-f^{2}\right) +4\tau f(1-(e^{-h\Delta })^{2}) \\ b\,\,=\,\, & {} (1-(e^{-h\Delta })^{2})(1+f) \\ f\,\,=\,\, & {} (e^{-h\tau })^{2}l \end{aligned}$$

and $\Gamma$ as defined in Proposition 1. Next, we show that the sign of the derivative $\partial m/\partial h$ can be either positive or negative (depending on the sign of a,  as all the other factors in $\partial m/\partial h$ are non-negative). First, if l tends to 0, it is straightforward that the derivative $\partial m/\partial h$ is always negative ($\lim \partial m/\partial h\,\,=\,\,-2\Delta e^{-h\Delta }$), similarly for $\tau \rightarrow \infty$. Instead, if production is sufficiently short and l is sufficiently large (with $\alpha ^{2}l<1$), the derivative $\partial m/\partial h$ can be positive. For instance, in the case of $l\,\,=\,\,2$, $\tau \,\,=\,\,1.1,$ $\Delta \,\,=\,\,1$ and $h\,\,=\,\,0.5$, then $\partial m/\partial h\,\,=\,\,1.07$.

For the MPE investment (28),

$$\begin{aligned} \frac{\partial r}{\partial \alpha }\,\,=\,\,\frac{8(1+\delta ^{2}+l\alpha ^{2}\left( 1-3\delta ^{2})-\Gamma ^{\frac{1}{2}}\right) (1+\delta ^{2})(1-l\alpha ^{2})z}{ \Gamma ^{\frac{1}{2}}\left( 3-\delta ^{2}-l\alpha ^{2}(1+\delta ^{2})-\Gamma ^{ \frac{1}{2}}\right) ^{3}\alpha ^{3}\delta ^{2}} \end{aligned}$$

(46)

with

$$\begin{aligned} z\,\,=\,\,1+\delta ^{2}+l\alpha ^{2}(1+\delta ^{4}-6\delta ^{2}+l\alpha ^{2}\delta ^{2}(1+\delta ^{2}))-\Gamma ^{\frac{1}{2}}(1-\delta ^{2}l\alpha ^{2}) \end{aligned}$$

It can be shown that all terms in (46) are positive. Therefore, the MPE investment (28) increases with $\alpha$.

Finally,

$$\begin{aligned} \frac{\partial r}{\partial \delta }\,\,=\,\,\frac{8(1-\delta ^{2})(1+l\alpha ^{2})w}{ \alpha ^{2}\Gamma ^{\frac{1}{2}}(\Gamma ^{\frac{1}{2}}-3+\delta ^{2}+l\alpha ^{2}(1+\delta ^{2}))^{2}\delta ^{2}} \end{aligned}$$

(47)

with

$$\begin{aligned} w\,\,=\,\,(1+\delta ^{2})(1+\alpha ^{4}l^{2}\delta ^{2})+l\alpha ^{2}((1-\delta ^{2})^{2}-4\delta ^{2})-\Gamma ^{\frac{1}{2}}(1-\delta ^{2}l\alpha ^{2}) \end{aligned}$$

It can be shown that all the terms in (47) are positive, then the MPE investment (28) increases with $\delta$.$\square$

Proof of Proposition 2

Using the first order conditions of the general problem (11), in (16)–(18), $x_{i}\,\,=\,\,0$ if and only if $m_{i}\,\,=\,\,0$. By the complementary slackness condition, see (18), then $\mu _{j}\ge \delta _{j}\phi _{j}$. Next, we find under which conditions on the parameters of the model the corner solution is an equilibrium. The first order conditions (16) and (17) for $m_{i}\,\,=\,\,0$ become

$$\begin{aligned} \varphi _{i}\,\,=\,\, & {} \frac{(\alpha _{i}\mu _{i})^{1/\eta }G-(1-\lambda )}{(\alpha _{i}\mu _{i})^{1/\eta }+1} \end{aligned}$$

(48)

$$\begin{aligned} x_{i}\,\,=\,\, & {} 1 \end{aligned}$$

(49)

We now input the first order condition in the Bellman equation (12) and after simplifying we obtain that $\phi _{i}\,\,=\,\,\psi _{i}^{\eta }l^{1-\eta }$ with $\psi _{i}\,\,=\,\,1+(\alpha _{i}\mu _{i})^{1/\eta }$.

The rate of investment (48) can now be written as $\varphi _{i}\,\,=\,\,G-\frac{l}{\psi _{i}}$ or $r_{i}\,\,=\,\,l\left( 1-\frac{1}{\psi _{i}}\right)$. Consequently, the responder’s MPE payoff coefficient is

$$\begin{aligned} \mu _{j}\,\,=\,\,\alpha _{j}\phi _{j}r_{i}^{1-\eta } \end{aligned}$$

This and the definition of $\psi _{i}$, that is $(\psi _{i}-1)^{\eta }\,\,=\,\,\alpha _{i}\mu _{i}$, implies the following system

$$\begin{aligned} \alpha _{j}^{2}l^{2(1-\eta )}\left( \frac{\psi _{i}-1}{\psi _{i}}\right) ^{1-\eta }\,\,=\,\,\left( \frac{\psi _{j}-1}{\psi _{j}}\right) ^{\eta } \end{aligned}$$

For $\eta \in (1/2,1),$ there is a unique solution given by

$$\begin{aligned} \psi _{i}\,\,=\,\,\frac{1}{1-b_{i}} \end{aligned}$$

(50)

with $b_{i}\in (0,1).$³⁰ This defines an acceptable offer if the responder is better off in accepting rather than rejecting the offer

$$\begin{aligned} \alpha _{j}\phi _{j}l^{1-\eta }\left( 1-\frac{1}{\psi _{i}}\right) ^{1-\eta }\ge \delta _{j}\phi _{j} \end{aligned}$$

that is, $\alpha _{j}(lb_{i})^{1-\eta }\ge \delta _{j}$ for $i,j\,\,=\,\,1,2$ with $i\ne j.$ The latter, together with $b_{i}\in (0,1),$ implies the conditions set in (37) and (38) or the set D. Under such conditions, also the transversality condition is satisfied (since $\alpha _{i}^{2}(l^{2}b_{i}b_{j})^{1-\eta }<1$ implies the second inequality in (37)). Finally, given (50), the coefficients $\phi _{i}\,\,=\,\,\psi _{i}^{\eta }l^{1-\eta }$ and $\mu _{i}\,\,=\,\,(\psi _{i}-1)^{\eta }/\alpha _{i}$ can be written as in (36).$\square$

The System Characterizing the Hybrid MPE

The Bellman equations are given by (12) with $x_{1}\,\,=\,\,1$ and $x_{2}<1.$ In other words, the constraint of the acceptance condition (13) is not binding for player 2 (i.e., $m_{1}\,\,=\,\,0),$ while it must be binding for player 2 ($m_{2}>0).$ Let $c_{1}\,\,=\,\,(\alpha _{1}\delta _{1}l)^{^{\frac{1-\eta }{\eta }}}$ and³¹

$$\begin{aligned} C\,\,=\,\, & {} \left\{ (\psi _{2},m_{2},c_{1})|\frac{\delta _{2}}{\alpha _{2}}\le c_{1}<l^{^{1-\eta }},\psi _{2}>1+m_{2},m_{2}>0,\right. \\&\left. c_{1}\alpha _{1}^{2}\left[ \left( 1-\frac{1+m_{2}^{1/\eta }}{\psi _{2}}\right) l\right] ^{1-\eta }<1\right\} \end{aligned}$$

where $\psi _{2}\,\,=\,\,(\alpha _{2}\mu _{2}+m_{2}\alpha _{1}\phi _{1})^{1/\eta }+1+m_{2}^{1/\eta }$, as in (23). Using the first order condition of the Lagrangian (11), that is, (16) and (17) with $m_{1}\,\,=\,\,0,$ we obtain

$$\begin{aligned} x_{1}\,\,=\,\, & {} 1\text { and }r_{1}\,\,=\,\,\frac{l(\alpha _{1}\mu _{1})^{1/\eta }}{(\alpha _{1}\mu _{1})^{1/\eta }+1} \end{aligned}$$

(51)

$$\begin{aligned} x_{2}\,\,=\,\, & {} \frac{1}{1+m_{2}^{1/\eta }}\text { and }r_{2}\,\,=\,\,l\left( 1-\frac{ 1+m_{2}^{1/\eta }}{\psi _{2}}\right) \end{aligned}$$

(52)

Then, after some manipulations, the equilibrium coefficients can be re-written as

$$\begin{aligned} \phi _{1}\,\,=\,\, & {} l^{1-\eta }(1+(\alpha _{1}\mu _{1})^{1/\eta })^{\eta } \end{aligned}$$

(53)

$$\begin{aligned} \phi _{2}\,\,=\,\, & {} \frac{l^{1-\eta }}{\psi _{2}}\left[ 1+\alpha _{2}\mu _{2}(\psi _{2}-1-m_{2}^{1/\eta })^{1-\eta }\right] \end{aligned}$$

(54)

$$\begin{aligned} \mu _{1}\,\,=\,\, & {} \frac{l^{1-\eta }}{\psi _{2}}\left[ m_{2}^{\frac{1-\eta }{\eta } }+\alpha _{1}\phi _{1}(\psi _{2}-1-m_{2}^{1/\eta })^{1-\eta }\right] \end{aligned}$$

(55)

$$\begin{aligned} \mu _{2}\,\,=\,\, & {} \alpha _{2}\phi _{2}\left[ \frac{l(\alpha _{1}\mu _{1})^{1/\eta } }{1+(\alpha _{1}\mu _{1})^{1/\eta }}\right] ^{1-\eta } \end{aligned}$$

(56)

Given the indifferent condition for player 1, $\mu _{1}\,\,=\,\,\delta _{1}\phi _{1},$ then (53) becomes

$$\begin{aligned} \phi _{1}\,\,=\,\,\frac{l^{1-\eta }}{\left( 1-(\alpha _{1}\delta _{1}l^{1-\eta })^{ \frac{1}{\eta }}\right) ^{\eta }} \end{aligned}$$

(57)

Hence, using (57) and $\mu _{1}\,\,=\,\,\delta _{1}\phi _{1},$ $r_{1}$ in ( 51) becomes

$$\begin{aligned} r_{1}\,\,=\,\,c_{1}^{\frac{1}{1-\eta }} \end{aligned}$$

(58)

and (56) can be re-written as

$$\begin{aligned} \mu _{2}\,\,=\,\,\alpha _{2}\phi _{2}c_{1} \end{aligned}$$

The latter in (54) implies

$$\begin{aligned} \phi _{2}\,\,=\,\,\frac{l^{1-\eta }}{\psi _{2}^{1-\eta }-\alpha _{2}^{2}l^{1-\eta }c_{1}(\psi _{2}-1-m_{2}^{1/\eta })^{1-\eta }} \end{aligned}$$

Now, both $\phi _{2}$ and $\mu _{2}$ are written in terms of $\psi _{2}$ and $m_{2}$ (while $\phi _{1}$ and $\mu _{1}$ are already solved for). The equilibrium $\psi _{2}$ and $m_{2}$ are given by the solution of the following system

$$\begin{aligned} \left\{ \begin{array}{c} \psi _{2}\,\,=\,\,(\alpha _{2}\mu _{2}+m_{2}\alpha _{1}\phi _{1})^{1/\eta }+1+m_{2}^{1/\eta } \\ \mu _{1}\,\,=\,\,\delta _{1}\phi _{1} \end{array} \right. \end{aligned}$$

(59)

with $\phi _{1},$ $\mu _{1}$ and $\mu _{2}$ as in (57), (55) and (56) respectively. Numerically, we find that a solution $(\psi _{2},m_{2},c_{1})\in C$ cannot coexist with either an interior or a polar consumption MPE.