Seeking the real item difficulty: bias-corrected item difficulty and some consequences in Rasch and IRT modeling

Abstract

When the response pattern in a test item deviates from the deterministic pattern, the percentage of correct answers (p) is shown to be a biased estimator for the latent item difficulty (π). This is specifically true with the items of medium item difficulty. Four elements of impurities in p are formalized in the binary settings and four new estimators of π are proposed and studied. Algebraic reasons and a simulation suggest that, except the case of deterministic item discrimination, the real item difficulty is almost always more extreme than what p indicates. This characteristic of p to be biased toward a medium-leveled item difficulty has a strict consequence to item response theory (IRT) and Rasch modeling. Because the classical estimator of item difficulty p is a biased estimator of the latent difficulty level, the item parameters A and B and the person parameter θ within IRT modeling are, consequently, biased estimators of item discrimination and item difficulty as well as ability levels of the test takers.

1 Introduction: deterministic pattern and proportion of correct answers as an indicator of item difficulty

One of the less discussed underlying thinking in the modern test theory is that, latent to each observed item, there is an unobservable theoretical (image of the) item which the observed pattern of responses reflects. In Rasch models (Rasch 1960 onwards) and wider item response theory (IRT) models (Birnbaum 1968 and Lord and Novick 1968 onwards) as well as in nonparametric IRT (NIRT) models (Mokken 1971 onwards), this latent image is a deterministically discriminating (latent) item. With binary items, this is called Guttman-patterned item (GP¹; named after the legacy of Louis Guttman’s idea of scaling²; Guttman 1944, 1947, 1950). This latent connection is discussed, specifically, within Rasch modeling (e.g., Andrich 1985; Linacre 1992; 2000; Linacre et al. 2003; Linacre and Wright 1994; 1996; Pedler et al. 2011; Roskam and Jansen 1992; Van Schuur 2003). However, the phenomenon is not restricted to the Rasch model only. With IRT models using two or more parameters addition to the B-parameter (difficulty), this latent image may also be thought to be a perfectly discriminating item. In these settings, this latent image is reflected as a theoretical, non-estimable, indefinitely high estimate for the A-parameter (discrimination) and as a non-zero value for the C-parameter (guessing) indicating an obvious deviation from this latent image of deterministic item discrimination.

Because of the deterministic nature in the GP items, there is a fundamental difference between the Guttman model in comparison with non-deterministic or stochastic Rasch-, IRT-, and NIRT models (Curtis 2004). Also recall the mathematical connection between Guttman pattern and Mokken pattern (Mokken 1971) through Loevinger’s H (Loevinger 1948) which basically measures the number of errors in the Mokken pattern; when H equals 1, there are no errors in the Mokken pattern, and it equals with the Guttman pattern (van Onna 2004).

The deterministic nature of the Guttman pattern determines two things. First, the extreme nature of a GP item is seen in the fact that it discriminates the higher and lower scoring test takers from each other in a deterministic manner (e.g., Linacre and Wright 1994; Metsämuuronen 2020b). Second, important for the rest part of the article, GP items have unambiguous item “difficulty” π.³ The latter character of GP-items is specifically discussed and studied in the article.

The proportion of correct answers in a test item (p = observed score in an item divided by the maximum possible score in the item) is the key estimator of π in the classical test theory (e.g., Lord and Novick 1968).⁴ The sample-dependent p is also an elementary part of the modern test theory because p is a sufficient statistic for the difficulty parameter B (e.g., Embretson and Reise 2000; Fox 2010). In the simplest case, B is a logistic function of p, and all main transformation procedures of B use p in some form (e.g., Guo et al. 2009). Because p is strictly related to the observed values in the item, the raw score X used as a sufficient statistic for the latent ability θ (e.g., Embretson and Reise 2000; Fox 2010; Samejima 1969; Sijtsma and Henker 2000) is also strictly related to the response patterns forming p. In a two-parameter IRT-model, p is also used in estimating the item discriminating parameter A (Sijtsma and Henker 2000).

As an estimator of item difficulty, p appears to face two challenges. One is when the data consists of missing values and these are, conventionally, imputed as “wrong answer” with 0, this obviously changes the estimate of the true item mean. In their simulation, Rose et al. (2010) noted that re-coding the missing data as “answered incorrectly” leads to a biased estimator that systematically over estimates the true item mean. The resulting bias appears to increase with the difficulty of the item. This aspect, however, is not focused on in this article. This article focuses on the more obvious challenge related to p: although p is an accurate indicator of the number of correct answers of the observed test takers, it is not accurate in indicating π if the item deviates from the deterministic pattern.

There are two basic sources of bias in p: either there are unexpected correct answers in the lower part of the ordered dataset (“lucky guessing”, “specific knowledge” or “imputed outlier” in the typology by Linacre and Wright 1994; impurity 1 in Table 1) or unexpected incorrect answers in the upper part of the ordered dataset (“carelessness”, “sleeping”, or “slipping” in Linacre and Wright 1994; impurity 2 in Table 1). Obviously, both can be obtained simultaneously (impurity 3 in Table 1) Another source of impurity, necessary for the statistical processes based on stochastic errors, are the patterns where the middle-ranged test-takers make random errors because of ignorance or by being careless (impurities 4 and 5 in Table 1) and separating these necessary sources of impurity from the unwanted and unnecessary patterns may be difficult. However, by modeling the probability of the test-takers giving the correct answer, we would conclude that the probability of a very low-achieving test-taker to know the correct answer in a difficult item without a random correct guessing would be very low and the probability of a very high-achieving test-taker to give an incorrect answer in an easy item would be very low.

Table 1 Typology of the source of biasness in p

We may rationalize that because the classical estimator of item difficulty p is a biased estimator of the latent difficulty level, the item parameters A and B and the person parameter θ within IRT modeling are, consequently, biased estimators of item discrimination and item difficulty as well as ability levels of the test takers. It seems obvious that the more these illogical patterns are actualized in the item, the less the observed B reflects the “true” π and the latent item difficulty β and the less X reflects the “true” θ.⁵

2 Research questions

Whenever incidents of “lucky guessing” or “carelessness” in the dataset are obtained, relevant questions are, first, what the real item difficulty is, second, how to estimate that, and third, what are its possible consequences in the further processes of item analysis. The elements of impurities in p are formalized and four alternative solutions to estimate the “bias-corrected item difficulty” are proposed in four phases. First, the characteristics of GP items are discussed and defined. Second, the impurities in p are formalized. Third, four procedures to estimate the latent item difficulty are proposed for real-world items with non-deterministic patterns. Fourth, the behavior of the four estimators is studied using a simulation of a real-world dataset.

3 Deterministic pattern and unbiased and biased item difficulty

3.1 PES, cut-offs, and COC

In what follows, the mechanism familiar from Kelley’s discrimination index (DI; Kelley 1939; Long and Sandiford 1935) used with binary items and Metsämuuronen’s Generalized DI (GDI; Metsämuuronen 2017, 2020a) for binary and polytomous items are used later as a tool to detect the latent item difficulty. In comparison with other indices of item discrimination power, the computation of DI and GDI embed peculiarity that they use only the extreme cases of the sorted dataset in the estimation. Because of the mechanism of selecting only the extreme cases to the analysis, the different cut-offs for the extreme groups have been actively discussed during the years.⁶ Forlano and Pinter (1941), for example, after studying the cut-offs of upper and lower 50, 33, 27, 16, and 7% of the cases, concluded that no method can be ranked over the other. However, they preferred 27% because it was a simple and rapid, rough, and ready method suggested already by Kelley (1939) as 27% cut-off maximizes the differences in population if the item difficulty is p = 0.50. Traditionally, either 27% (e.g., Ebel 1967; Kelley 1939; Pemberton 1951; Ross and Weitzman 1964; Wiersma and Jurs 1990) or 25% (e.g., D’Agostino and Cureton 1975; Mehrens and Lehmann 1991; Metsämuuronen 2017, 2020a) of the extreme test-takers of the ordered data are suggested for the calculation of DI. Notably, while Kelley’s DI discussed above uses fixed cut-offs, GDI uses all cut-offs and a routine called the procedure of exhaustive splitting (PES) (see, Metsämuuronen 2020a) discussed in what follows.

To illustrate the phenomenon that a GP item detects the item discrimination and item difficulty π in a deterministic manner, the procedure of exhaustive splitting (PES) using all possible cut-offs of the extreme cases in the ordered dataset is employed and the related cut-off curves (COC; Metsämuuronen 2017; 2020a; see also Metsämuuronen 2022) are studied. PES (Metsämuuronen 2020a) is a simple routine where all possible cut-offs of the dataset are used to estimate the item discrimination by GDI. Although DI and GDI are used as indicators of item discrimination by Metsämuuronen (2020a) and here, PES is obviously not restricted to DI or GDI. In Metsämuuronen (2017), PES is used to illustrate differences in the estimates between point-biserial correlation and item–rest correlation (Henrysson 1963). The routine of PES is as follows:

• 1. Take the extreme highest and lowest observations from the sorted data and calculate the indices of interest. Save the result.

• 2. Take two highest and lowest observations from the sorted data and calculate the indices of interest (as in 1). Save the result.

• 3. Repeat Step 2, increasing the number of observations and gradually building up to ½N = 50% of the observations at both extremes. When there are odd number of cases, the median case is not considered for the procedure. A graphical tool, COC, can be used to visualize the characteristics of the item (see Figs. 1 and 2).

Fig. 1

Cut-off curve of a hypothetical GP item

Fig. 2

Cut-off curve of NGP item with minor stochastic error

In what follows, GDI is used as the indicator of item discrimination power because its form appears to have a close connection with the estimators of the latent π. GDI can be expressed as

$$ GDI_{a} = \frac{{R_{a}^{U} - R_{a}^{L} }}{{\tfrac{1}{2}T_{a} }} = 2\left( {p_{a} - 2p_{a}^{L} } \right). $$

(1)

(Metsämuuronen 2017, 2020a) where a refers to the number (or percent or proportion) of cases in half of the cut-off of the ordered dataset and, traditionally with binary items, $R_{a}^{U}$ and $R_{a}^{L}$ are the number of correct answers in the upper and lower half of the cut-off of 25% or 27% of the extreme test takers and T_a refers to the total number of observations in the two parts together.⁷ Consequently, p_a refers to the proportion of correct answers in the reduced dataset as a whole and $p_{a}^{L}$ is the proportion of correct answers in the lower half of the reduced dataset.

3.2 Deterministic pattern and unbiased item difficulty

Let us use a GP item with 24 respondents and four correct answers as an example of locating π. Ordered from the lowest to the highest test-taker based on the (unseen) test score, the pattern is as follows: (000000000000000000001111). The classical item difficulty is p = 4/24 = 0.167. After employing PES with Eq. (1) starting from the most extreme respondents (a = 1 or a = 0.042 or a = 4.2%) of the cases in half of the cut-off), the relevant figures and indices are collected in Table 2. Figure 1 shows the corresponding COC.

Table 2 All symmetric cut-offs of a GP item with the pattern (000000000000000000001111)

Three points are worth highlighting. First, from the visual viewpoint, COC detects the item difficulty (p = 0.167) at the threshold point of the curve. Also, at the threshold point, the item discrimination is perfect (GDI = 1) as should be because of the deterministic nature of the item. Second, it is not a coincident that the last value in Table 1 and COC is GDI_50% = 0.333. When multiplying this value with ½ we get the value ${{0.333} \mathord{\left/ {\vphantom {{0.333} {2 = 0.167}}} \right. \kern-\nulldelimiterspace} {2 = 0.167}}$, that is, the item difficulty $\pi_{s} =$ 0.167, where the index a = s = 4 refers to the number of the elements in the string of 1 s of the extreme test-takers in the ordered dataset. This is formalized in Theorem 1 in what follows. Third, in all cut-offs after a = s, that is, a = s+ , we detect the same item difficulty of the GP item $\pi_{s}$:

$$ \pi_{s + } = \frac{{R_{s + }^{U} - R_{s + }^{L} }}{N} = \frac{{\tfrac{1}{2}T_{s + } }}{N} \times GDI_{s + } = \pi_{s} . $$

(2)

(See the last column of Table 1). The phenomenon is important because it can be generalized to any cut-off of any GP item, and this has a consequence for the non-Guttman-patterned (NGP) items: we can detect $\pi_{s}$ of the latent GP item or any NGP item at any point of COC after the threshold cut-off a = s+ . This is formalized in Theorems 2 and 3 in what follows.

3.3 Non-deterministic pattern and the biased item difficulty

A simple example of a biased estimate of the latent item difficulty is given by an NGP item with a minor erroneous pattern (000000000000000010000111). Using PES, the corresponding COC is seen in Fig. 2 with the COCs of the GP items of π_s = 0.125 and π_s+1 = 0.167 as dashed lines.

Two points are noteworthy. First, comparing Fig. 1 with a GP item and Fig. 2 with an NPG item, we see that, in the latter, there are more than just one unique option for the latent GP item with the latent π: the first threshold point (π_s) suggests π = 0.125 while the last measurement point suggests π = 0.167. Although the exact magnitude is not known, the latent π seems to be somewhere between π_s = 0.125 and π_s+1 = 0.167 rather than uniquely p = 0.167 or p = 0.125. Second, although the observed COC (the solid line) does not follow all the way to the COC of one GP item, it follows the COC of some of the underlying theoretical GP items in each cut-off. This phenomenon appears to be important in estimating the latent item difficulty of the observed NGP item: when we know the latent GP item in each cut-off, π of these latent GP items could be used in estimating a plausible alternative for the “bias-corrected item difficulty” of the observed NGP item. This is formalized later in Theorem 2.

4 Formalizing the elements of impurity in p

4.1 Basic definitions related to binary dataset

The treatment uses mainly the same symbols as in Eq. (1) with DI and GDI. When splitting an item in an ordered dataset into two halves (a 50% split), in the binary case, traditionally, the symbol T refers to the total number of test-takers usually symbolized by N; R^U refers to the number of correct answers (1s) in the upper half (U); and R^L refers to the number of correct answers (1s) in the lower half (L). Then,

$$ {{R^{U} } \mathord{\left/ {\vphantom {{R^{U} } T}} \right. \kern-\nulldelimiterspace} T} = p^{U} \,{\text{and}}\,{{R^{L} } \mathord{\left/ {\vphantom {{R^{L} } T}} \right. \kern-\nulldelimiterspace} T} = p^{L} , $$

(3)

where p^U and p^L refer to the proportions of correct answers in the upper (U) and lower (L) halves of the ordered dataset, respectively. Let us denote the number of 1s in the item with C and the number of 0s with Z. Then,

$$ C = \, R^{U} + R^{L} , $$

(4)

$$ Z = T{-}C, $$

(5)

$$ {C \mathord{\left/ {\vphantom {C T}} \right. \kern-\nulldelimiterspace} T} = p, $$

(6)

and, because of (5) and (6)

$$ {Z \mathord{\left/ {\vphantom {Z T}} \right. \kern-\nulldelimiterspace} T} = {{\left( {T - C} \right)} \mathord{\left/ {\vphantom {{\left( {T - C} \right)} T}} \right. \kern-\nulldelimiterspace} T} = 1 - p, $$

(7)

For a later use, we note that, because of (4),

$$ \, R^{U} - R^{L} = \left\{ {\begin{array}{*{20}c} {C - 2R^{L} } \\ {2R^{U} - C} \\ \end{array} } \right., $$

(8)

and because of (3), (6) and (8)

$$ \, \frac{{R^{U} - R^{L} }}{T} = \left\{ {\begin{array}{*{20}c} {{{\left( {C - 2R^{L} } \right)} \mathord{\left/ {\vphantom {{\left( {C - 2R^{L} } \right)} {T = p - 2p^{L} }}} \right. \kern-\nulldelimiterspace} {T = p - 2p^{L} }}} \\ {{{\left( {2R^{U} - C} \right)} \mathord{\left/ {\vphantom {{\left( {2R^{U} - C} \right)} {T = 2p^{U} - p}}} \right. \kern-\nulldelimiterspace} {T = 2p^{U} - p}}} \\ \end{array} } \right.. $$

(9)

Finally, the number of test-takers T can be divided into two equally long parts denoted by T^U and T^L respectively for the number of cases in the upper and lower halves of the ordered dataset:

$$ T^{U} = T^{L} = \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} T = \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} N. $$

(10)

4.2 Basic definitions related to GP items

The preliminary definition concerns the location of the item difficulty π of the GP item. With binary items, in an ordered dataset, π is located where the leading substring of 0s turns to the trailing substring of 1s. Although not being intuitively obvious, the special string of interest is the shorter of the two extreme strings of 1s and 0s:

Definition 1

The shorter one of the extreme strings of 1s and 0s indicates the item difficulty π of GP items.

This definition is caused by selecting symmetric cut-offs as a basis of the treatment.⁸ From the viewpoint of cut-offs, this specific string is denoted by the cut-off a = s. Either the number or the proportion of the test takers in the cut-off could be taken as a basis for the scale. In what follows, the proportions are used to maintain the connection to the traditional p value.

Definition 2

With the GP items, because of Definition 1,

$$ \pi_{s} = \left\{ {\begin{array}{*{20}c} {p,{\text{\quad{when} }}p{ < 0}{\text{.50}}} \\ {1 - p,{\text{\quad{when} }}p \ge {0}{\text{.50 }}} \\ \end{array} } \right.. $$

(11)

4.3 Elements of impurity in p

The proportion of the correct answers includes several elements of impurity depending on the location of the erroneous observations (see Table 1). Two of these are handled explicitly in Theorem 1.

Theorem 1

With GP items, the item difficulty π is.

$$ \pi_{s} = \frac{{R^{U} - R^{L} }}{T} = \left\{ {\begin{array}{*{20}c} {p - 2p^{L} ,{\text{\quad{when} }}p{ < 0}{\text{.50 }}} \\ {p + \left( {1 - 2p^{U} } \right){\text{,\quad{when} }}p \ge {0}{\text{.50}}} \\ \end{array} } \right.. $$

(12)

where, in the binary case, T refers to the total number of test-takers usually symbolized by N; R^U refers to the number of correct answers (1s) in the upper half (U); R^L refers to the number of correct answers (1s) in the lower half (L); and p^U and p^L refer to the proportions of correct answers in the upper (U) and lower (L) halves of the ordered dataset, respectively.

Proof

Theorem 1 is proved with two lemmas; Lemma 1 handles the case of p ≥ 0.50 and Lemma 2 the case of p < 0.50.

Lemma 1

When p ≥ 0.50,$\pi_{s} = \left\{ {\begin{array}{*{20}c} {p - 2p^{L} } \\ {2p^{U} - p} \\ \end{array} } \right.$

Proof

Suppose a GP item with p ≥ 0.50. Then the shorter of the extreme strings of 0s and 1s indicating the item difficulty π is the one with 0s, that is,

$$ \pi_{s} = {Z \mathord{\left/ {\vphantom {Z T}} \right. \kern-\nulldelimiterspace} T}. $$

(13)

Because of the deterministic pattern, all test takers in the upper half of the ordered data set give the correct answer and, hence,

$$ T^{U} = R^{U} . $$

(14)

Because all 0s are in the lower half,

$$ T^{L} = R^{L} + Z. $$

(15)

Because of (15), Z can be manipulated as follows:

$$ \begin{gathered} Z = Z + T^{U} - T^{U} = Z + T^{U} - T^{L} \\ = T^{U} - \left( {T^{L} - Z} \right). \\ \end{gathered} $$

(16)

and because of (16), (14), (15), and (8)

$$ Z = R^{U} - R^{L} = C - 2R^{L} = 2R^{U} - C. $$

(17)

Therefore, when p ≥ 0.50, because of Eqs. (13), (17), (7), and (9),

$$ \pi_{s} = \frac{Z}{T} = \frac{{R^{U} - R^{L} }}{T} = \frac{{C - 2R^{L} }}{T} = \frac{{2R^{U} - C}}{T} = \left\{ {\begin{array}{*{20}c} {p - 2p^{L} } \\ {2p^{U} - p} \\ \end{array} } \right.. $$

(18)

This ends the proof of Lemma 1. □

Lemma 2

When p < 0.50,$\pi_{s} = p = \left\{ {\begin{array}{*{20}c} {p - 2p^{L} } \\ {2p^{U} - p} \\ \end{array} } \right.$

Proof

Suppose a GP item with p < 0.50. Then, the shorter of the extreme strings of 0s and 1s indicating the item difficulty π is the one with 1s, that is,

$$ \pi_{s} = {C \mathord{\left/ {\vphantom {C T}} \right. \kern-\nulldelimiterspace} T}. $$

(19)

Assuming p < 0.50, there are no correct answers in the lower half of the ordered GP item. Then,

$$ R^{L} = \, 0,{\text{ when}}p < \, 0.{5}0. $$

(20)

Because of Eqs. (6), (4), (9), and (20)

$$ \pi_{s} = \frac{C}{T} = \frac{{R^{U} }}{T} = \frac{{R^{U} - R^{L} }}{T} = \frac{{C - 2R^{L} }}{T} = \frac{{2R^{U} - C}}{T} = \left\{ {\begin{array}{*{20}c} {p - 2p^{L} } \\ {2p^{U} - p} \\ \end{array} } \right. $$

(21)

This ends the proof of Lemma 2. □

Because of Lemma 1 and Lemma 2, when a GP item is either difficult (p < 0.50) or easy (p ≥ 0.50), the item difficulty equals with

$$ \pi_{s} = \frac{{R^{U} - R^{L} }}{T} = \left\{ {\begin{array}{*{20}c} {p - 2p^{L} } \\ {2p^{U} - p} \\ \end{array} } \right., $$

(22)

where, in the binary case, T refers to the total number of test-takers usually symbolized by N; R^U refers to the number of correct answers (1s) in the upper half (U); R^L refers to the number of correct answers (1s) in the lower half (L); and p^U and p^L refer to the proportions of correct answers in the upper (U) and lower (L) halves of the ordered dataset, respectively. Because of Definition 2 and Lemmas 1 and 2, with GP items,

$$ \pi_{s} = \left\{ {\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {p - 2p^{L} } \\ {2p^{U} - p} \\ \end{array} } \right.,{\text{\quad{when} }}p{ < 0}{\text{.50 }}} \\ {\left\{ {\begin{array}{*{20}c} {2p^{L} + \left( {1 - p} \right)} \\ {p + \left( {1 - 2p^{U} } \right)} \\ \end{array} } \right.{\text{,\quad{when} }}p \ge {0}{\text{.50}}} \\ \end{array} } \right.. $$

(23)

This ends the proof of Theorem 1. □

4.4 Notes on Theorem 1

Four points on Theorem 1 are worth highlighting. First, the elements of $2p^{L}$ and $\left( {1 - 2p^{U} } \right)$ refer directly to the bias-causing elements in the p value: the former to the proportions of correct answers in the lower part of the difficult item and the latter to the proportion of incorrect answers in the upper part of an easy item. With GP items, $2p^{L} = \left( {1 - 2p^{U} } \right) = 0$ because there are no additional correct or incorrect answers in the lower and upper part of the dataset outside the perfect strings of 0s and 1s. However, if we find any correct answer in the lower part of the ordered dataset ($2p^{L}$) with a difficult item (“lucky guessing”) or any incorrect answer at the upper part $\left( {1 - 2p^{U} } \right)$ of an easy item (“sleepiness” or “carelessness”), $\pi_{s} \ne p$, and, then, p appears to be a biased estimator for the latent item difficulty. This always happens with NGP items. Notably, also, the more these responses break the deterministic pattern, the higher get $2p^{L}$ and $\left( {1 - 2p^{U} } \right)$, and the further p deviates from π. Because the elements $2p^{L}$ and $\left( {1 - 2p^{U} } \right)$ indicate the magnitude of the bias in p in relation to π, Eq. (12) may be taken as the “bias-corrected item difficulty”.

Second, when the item is a difficult one (p < 0.5), there may appear to be unexpected correct answers in the upper middle range of the ordered dataset (impurity 4 in Table 1). Also, when the item is an easy one (p > 0.5), there may appear unexpected incorrect answers in the lower middle range of the dataset (impurity 5 in Table 1). Although these two patterns of impurity are not explicit in Theorem 1, they are implicit because they strictly affect the magnitude of p.

Third, with NGP items, always, $\left| p \right| < \left| \pi \right|$ because the impurity elements in Theorem 1, whenever found, tend to affect p to be closer to p = 0.50 in comparison with π. This means that the observed p is always deflated in a sense that the magnitude of π is always more extreme than that of the observed p. The closer the response pattern is to the deterministic pattern, the less is the difference between π and p. Notably, the probability of such pattern-breaking responses is lower in items with extreme difficulty in comparison with items with medium difficulty. Hence, it is expected that the difference between p and π will be greater in items with medium difficulty than in items with extreme difficulty.

Fourth, if the outcome of $R^{U} - R^{L}$ appears to be negative (leading to negative item discrimination), the estimate of π would get an out-of-range value when p > 0.50. Namely, if $p - 2p^{L} < 0$, then $1 - \left( {p - 2p^{L} } \right) = \pi_{s} > 1$. In such a case, the value of the estimate could be changed to 1 the same manner as is customary with out-of-range estimates by omega- and epsilon squared in settings related to general linear modeling; the negative explaining powers are replaced by 0 (see Cohen 1973; Okada 2017).

4.5 Item difficulty π of GP items in the cut-offs a = s+ 

An important characteristic of any GP item is that whichever partition of the extreme test-takers is considered, the reduced dataset is patterned with a string of 0s followed by a string of 1s when the respondents are ordered by the test score. This obviously means that the reduced dataset of extreme test-takers of a GP item carries the characteristic of GP item. Then, Theorem 1 is valid in every cut-off of a GP item.

Let us denote the cut-offs for the reduced datasets of extreme test-takers by a = 1,…, s, s + 1,…, ½T = ½N and the cut-offs after the threshold cut-off a = s by a general subscript a = s+ . Theorem 2 relates with the phenomenon seen in Fig. 2: the latent difficulty level of an item (π_s) can be detected in any cut-off after the threshold cut-off a = s+ .

Theorem 2

With GP item, $\pi_{s + } = \pi_{s}$.

Proof

Assume a GP item ordered by the score. Let us denote the cut-offs for the reduced datasets of extreme test-takers by a = 1,…, s, s + 1,…, ½T = ½N and the cut-offs after the threshold cut-off a = s by a general subscript a = s+ . In each cut-off after the previous one (a + 1), the single observations of the next pair of individual test-takers in the upper and lower halves are denoted by $O_{a + 1}^{U} = \left\{ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right.$ and $O_{a + 1}^{L} = \left\{ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right.$, respectively.

When a = s+ ,

$$ R_{s + }^{U} = R_{s}^{U} + O_{s + 1}^{U} + ... + O_{s + }^{U} = R_{s}^{U} + \sum\limits_{i = s + 1}^{s + } {\left( {O_{i}^{U} } \right)} , $$

(24)

and

$$ R_{s + }^{L} = R_{s}^{L} + O_{s + 1}^{L} + ... + O_{s + }^{L} = R_{s}^{L} + \sum\limits_{i = s + 1}^{s + } {\left( {O_{i}^{L} } \right)} , $$

(25)

Always with GP items, when p ≥ 0.5,

$$ O_{S + }^{U} = O_{S + }^{L} = { 1} $$

(26)

and, when p < 0.5,

$$ O_{s + }^{U} \, = \,O_{s + }^{L} \, = \,0, $$

(27)

because there are no additional 1s or 0s outside the perfect strings of 0s and 1s. Hence, because of Eqs. (26) and (27), always with GP item,

$$ O_{s + }^{U} - O_{s + }^{L} = 0 $$

(28)

and

$$ R_{s + }^{U} - R_{s + }^{L} = R_{s}^{U} - R_{s}^{L} + \left( {O_{s + 1}^{U} - O_{s + 1}^{L} } \right) + ... + \left( {O_{s + }^{U} - O_{s + }^{L} } \right) = R_{s}^{U} - R_{s}^{L} + 0 = R_{s}^{U} - R_{s}^{L} , $$

(29)

Then, with the GP items,

$$ \, \pi_{s + } = \frac{{R_{s + }^{U} - R_{s + }^{L} }}{T} = \frac{{R_{s}^{U} - R_{s}^{L} }}{T} = \pi_{s} = \left\{ {\begin{array}{*{20}c} {p - 2p^{L} ,{\text{when }}p{ < 0}{\text{.50 }}} \\ {p + \left( {1 - 2p^{U} } \right){\text{,when }}p \ge {0}{\text{.50}}} \\ \end{array} } \right.. $$

(30)

This ends the proof of Theorem 2. □

Hence, the threshold cut-off a = s leading to a form $\left( {R_{s}^{U} - R_{s}^{L} } \right)$ related to Eqs. (8), (18), and (21) always refers—even with NGP items—to the condition where Theorem 1 is valid. Further, because of Theorem 2, with GP items, $\left( {R_{s}^{U} - R_{s}^{L} } \right) = \left( {R_{s + }^{U} - R_{s + }^{L} } \right) = \left( {R_{{\tfrac{1}{2}T}}^{U} - R_{{\tfrac{1}{2}T}}^{L} } \right)$ because, after the cut-off a = s, the number of correct answers are fixed both in the upper half of the dataset $R_{s}^{U} = R_{s + }^{U} = R^{U}$ and in the lower half $R_{s}^{L} = R_{s + }^{L} = R^{L}$. This was seen also in Table 2.

4.6 Connection of GDI and π _s

Notably, the notation used above follows the notation familiar from GDI (Eq. 1); the π_s of an GP item latent to any NGP item can be detected strictly by knowing the magnitude of GDI at any cut-off after the threshold cut-off a = s.

Theorem 3

With GP item, $\pi_{s + } = \frac{{\tfrac{1}{2}T_{s + } }}{T} \times \frac{{R_{s + }^{U} - R_{s + }^{L} }}{{\tfrac{1}{2}T_{s + } }} = \frac{{\tfrac{1}{2}T_{s + } }}{T} \times GDI_{s + } = \frac{{\tfrac{1}{2}T_{s + } \times GDI_{s + } }}{N} = \pi_{s}$.

Proof

Strictly from Eqs. (30) and (1) it is known that, with GP items,

$$ \pi_{s} = \pi_{s + } = \frac{{R_{s + }^{U} - R_{s + }^{L} }}{T} = \frac{{\tfrac{1}{2}T_{s + } }}{T} \times \frac{{R_{s + }^{U} - R_{s + }^{L} }}{{\tfrac{1}{2}T_{s + } }} = \frac{{\tfrac{1}{2}T_{s + } }}{T} \times GDI_{s + } = \frac{{\tfrac{1}{2}T_{s + } \times GDI_{s + } }}{N}. $$

(31)

This ends the proof of Theorem 3. □

4.7 Initial numeric example of Theorems 1, 2, and 3

Theorems 1 and 2 have a strict relevance in estimating the latent π for NGP items. First, because of Theorem 1, the π of any latent GP item can be detected unambiguously. Second, because of Theorem 2, the π of any GP item can be calculated unambiguously at any cut-off after the threshold cut-off a = s. Third, because, in each cut-off, the COC of an NGP item strictly follows the COC of a known GP item, the latent π_s can be detected in each cut-off for any NGP item. This is first illustrated with a hypothetic nontrivial NGP item and later by a simulation with real-world items.

Let us take a nontrivial NGP item with N = 24 test takers and 15 correct answers with the structure of (000100101011│111111001111) after ordered by the (unseen) test score (Table 3; Fig. 3; the bar indicates the middle point of the ordered item where the procedure of splitting stops). The lighter curves in Fig. 3 are COCs of the underlying GP items.

Table 3 All symmetric cut-offs of an NGP item with the pattern (000100101011111111001111)

Fig. 3

Cut-off curve for a hypothetical NGP item with N = 24 in Table 3

From the viewpoint of Theorem 1, the last point-estimate of π in Table 3 and in Fig. 3 is $\pi = {{\left( {R_{50\% }^{U} - R_{50\% }^{L} } \right)} \mathord{\left/ {\vphantom {{\left( {R_{50\% }^{U} - R_{50\% }^{L} } \right)} {N = 5/24 = 0.208}}} \right. \kern-\nulldelimiterspace} {N = 5/24 = 0.208}}$ referring to the threshold of the latent GP item with the item difficulty π_s+2 in Fig. 3. From the viewpoint of Theorem 2, we may take any of the cut-offs after the threshold cut-off a = s, and the value by $\pi_{s + } = {{\left( {R_{s + }^{U} - R_{s + }^{L} } \right)} \mathord{\left/ {\vphantom {{\left( {R_{s + }^{U} - R_{s + }^{L} } \right)} T}} \right. \kern-\nulldelimiterspace} T} = {{\left( {R_{s + }^{U} - R_{s + }^{L} } \right)} \mathord{\left/ {\vphantom {{\left( {R_{s + }^{U} - R_{s + }^{L} } \right)} N}} \right. \kern-\nulldelimiterspace} N}$ leads us to item difficulty π characteristic to the latent GP item in each cut-off. Hence, the last three estimates of the observed (NGP) item in Table 3 point to the latent variable characterized by π = π_s+2 = 0.208 and next two ones to π = π_s+1 = 0.167, while the cut-offs a = s to s + 4 point to the latent variable with π = π_s = 0.125. From the viewpoint of Theorem 3, the last value of GDI, as an example, leads to $\left( {{{\tfrac{1}{2}T_{50\% } } \mathord{\left/ {\vphantom {{\tfrac{1}{2}T_{50\% } } N}} \right. \kern-\nulldelimiterspace} N}} \right) \times GDI_{50\% } = \left( {{{12} \mathord{\left/ {\vphantom {{12} {24}}} \right. \kern-\nulldelimiterspace} {24}}} \right) \times 0.4167 = 0.208 = \pi_{s + 2}$ as well as the second last: $\left( {{{\tfrac{1}{2}T_{45.8\% } } \mathord{\left/ {\vphantom {{\tfrac{1}{2}T_{45.8\% } } N}} \right. \kern-\nulldelimiterspace} N}} \right) \times GDI_{45.8\% } = \left( {{{11} \mathord{\left/ {\vphantom {{11} {24}}} \right. \kern-\nulldelimiterspace} {24}}} \right) \times 0.455 = 0.208 = \pi_{s + 2}$.

Notably, we have several options for the latent item difficulty: π_s points to the threshold cut-off 3/24 = 0.125, π_s+1 to 4/24 = 0.167, and π_s+2 to 5/24 = 0.208 which turn to be π_s = 1 – 0.125 = 0.875, π_s+1 = 1 – 0.167 = 0.833, and π_s+2 = 1 – 0.208 = 0.792 because the observed p = 0.625 > 0.5. A relevant question is, how to determine the most credible estimate of π? Four alternatives of estimating π, or “bias-corrected item difficulty”, are discussed below with numerical examples.

5 Four alternatives to estimate the latent item difficulty

5.1 Option 1 ( $\pi_{1}$ ): estimator based on the mean of $\hat{\pi }_{s + }$

The first alternative for the procedure of estimating the latent item difficulty of a real-world item is based on Theorem 2: the average of the suggested estimates $\hat{\pi }_{s + }$ in the cut-offs a = s, s + 1,…,$\tfrac{1}{2}T = \tfrac{1}{2}N$, where a = $\tfrac{1}{2}N$ = a_50%. The latent item difficulty $\hat{\pi }_{s}$, $\hat{\pi }_{s + 1}$,…,$\hat{\pi }_{{\tfrac{1}{2}T}} = \hat{\pi }_{{\tfrac{1}{2}N}}$ is suggested in each cut-off. The number of these cut-offs is $\tfrac{1}{2}N - \left( {s - 1} \right)$. Then, following Theorem 2 and Definition 2, $\pi_{1}$ is the mean of these point estimates:

$$ \pi _{1} = \left\{ {\begin{array}{*{20}l} {\bar{\hat{\pi }}_{{s + }} = \frac{{\sum\limits_{{a = s}}^{{\tfrac{1}{2}N}} {\hat{\pi }_{a} } }}{{\tfrac{1}{2}N - \left( {s - 1} \right)}} = \frac{{\sum\limits_{{a = s}}^{{\tfrac{1}{2}N}} {\left( {p_{a} - 2p_{a}^{L} } \right)} }}{{\tfrac{1}{2}N - \left( {s - 1} \right)}}{\text{, when }}p\, < \,0.50{\mkern 1mu} } \hfill \\ {1 - \bar{\hat{\pi }}_{{s + }} = 1 - \frac{{\sum\limits_{{a = s}}^{{\tfrac{1}{2}N}} {\hat{\pi }_{a} } }}{{\tfrac{1}{2}N - \left( {s - 1} \right)}} = 1 - \frac{{\sum\limits_{{a = s}}^{{\tfrac{1}{2}N}} {\left( {p_{a} - 2p_{a}^{L} } \right)} }}{{\tfrac{1}{2}N - \left( {s - 1} \right)}}{\text{, when }}p \ge 0.50} \hfill \\ \end{array} } \right.. $$

(32)

where $\hat{\pi }_{a}$ is the point estimate at a cut-off a. Variance of the estimate can be calculated as

$$VAR\left( {\pi _{1} } \right) = \frac{{\sum\nolimits_{{a = s}}^{{\tfrac{1}{2}N}} {\left( {\hat{\pi }_{a} - \bar{\hat{\pi }}_{{s + }} } \right)^{2} } }}{{\tfrac{1}{2}N - \left( {s - 1} \right)}}, $$

(33)

For the item in Table 3 and Fig. 3, because p ≥ 0.50, the routine in Eqs. (32) and (33) suggests the latent item difficulty as

$$ \pi_{1} = 1 - \hat{\pi } = 1 - \overline{\hat{\pi }}_{s + } = 1 - \frac{{\left( {5 \times {3 \mathord{\left/ {\vphantom {3 {24}}} \right. \kern-\nulldelimiterspace} {24}} + 2 \times {4 \mathord{\left/ {\vphantom {4 {24}}} \right. \kern-\nulldelimiterspace} {24}} + 3 \times {5 \mathord{\left/ {\vphantom {5 {24}}} \right. \kern-\nulldelimiterspace} {24}}} \right)}}{12 - 3 + 1} = 1 - \frac{{{{38} \mathord{\left/ {\vphantom {{38} {24}}} \right. \kern-\nulldelimiterspace} {24}}}}{10} = 1 - 0.158 = 0.842 $$

with the variance.

$$ VAR\left( {\hat{\pi }_{1} } \right) = \frac{{\left[ {5 \times 0.0011 + 2 \times 0.00007 + 3 \times 0.0025} \right]}}{10} = \frac{0.0132}{{10}} = 0.0013, $$

where 0.0011 = $\left( {\left( {{{1 - 3} \mathord{\left/ {\vphantom {{1 - 3} {24}}} \right. \kern-\nulldelimiterspace} {24}}} \right) - 0.842} \right)^{2}$, 0.00007 = $\left( {\left( {{{1 - 4} \mathord{\left/ {\vphantom {{1 - 4} {24}}} \right. \kern-\nulldelimiterspace} {24}}} \right) - 0.842} \right)^{2}$, and 0.0025 = $\left( {\left( {{{1 - 5} \mathord{\left/ {\vphantom {{1 - 5} {24}}} \right. \kern-\nulldelimiterspace} {24}}} \right) - 0.842} \right)^{2}$. To calculate $\pi_{1}$, the threshold cut-off a = s needs to be detected. This can be done two ways: either by detecting strictly the shorter of the extreme strings or by calculating GDI and detect the last cut-off showing the perfect item discrimination GDI = 1. This is illustrated in Sect. 5.6.

5.2 Option 2 ($\pi_{2}$): estimator based on all cut-offs

A somewhat rougher routine based in Theorem 2 is to use all cut-offs in the estimation. The advance in this exhaustive alternative is that the number of point-estimates (½N) is the same for all items and, hence, there is no need to seek the specific threshold cut-off a = s. Using the same logic as in $\pi_{1}$, the estimator is

$$ \pi _{2} = \left\{ \begin{gathered} \bar{\hat{\pi }} = \frac{{\sum\nolimits_{{a = 1}}^{{\tfrac{1}{2}N}} {\hat{\pi }_{a} } }}{{\tfrac{1}{2}N}} = \frac{{\sum\nolimits_{{a = 1}}^{{\tfrac{1}{2}N}} {\left( {p_{a} - 2p_{a}^{L} } \right)} }}{{\tfrac{1}{2}N}}{\text{, }}\,\,{\text{when }}p\, < 0.50 \hfill \\ 1 - \bar{\hat{\pi }} = 1 - = \frac{{\sum\nolimits_{{a = 1}}^{{\tfrac{1}{2}N}} {\hat{\pi }_{a} } }}{{\tfrac{1}{2}N}} = 1 - \frac{{\sum\nolimits_{{a = 1}}^{{\tfrac{1}{2}N}} {\left( {p_{a} - 2p_{a}^{L} } \right)} }}{{\tfrac{1}{2}N}}{\text{, when }}p \ge 0.50, \hfill \\ \end{gathered} \right. $$

(34)

Parallel to $\pi_{1}$, the variance of the estimate is

$$ VAR\left( {\hat{\pi }_{2} } \right) = \frac{{\sum\nolimits_{{a = 1}}^{{\tfrac{1}{2}N}} {\left( {\hat{\pi }_{a} - \bar{\hat{\pi }}} \right)^{2} } }}{{\tfrac{1}{2}N}}. $$

(35)

For the item in Table 3 and Fig. 3, because p ≥ 0.50, the routine in Eqs. (34) and (35) suggests the latent item difficulty as

$$ \hat{\pi }_{2} = 1 - \hat{\pi } = 1 - \overline{\hat{\pi }} = 1 - \frac{{\left( {1 \times {1 \mathord{\left/ {\vphantom {1 {24}}} \right. \kern-\nulldelimiterspace} {24}} + 1 \times {2 \mathord{\left/ {\vphantom {2 {24}}} \right. \kern-\nulldelimiterspace} {24}} + 5 \times {3 \mathord{\left/ {\vphantom {3 {24}}} \right. \kern-\nulldelimiterspace} {24}} + 2 \times {4 \mathord{\left/ {\vphantom {4 {24}}} \right. \kern-\nulldelimiterspace} {24}} + 3 \times {5 \mathord{\left/ {\vphantom {5 {24}}} \right. \kern-\nulldelimiterspace} {24}}} \right)}}{12} = 1 - \frac{{{{41} \mathord{\left/ {\vphantom {{41} {24}}} \right. \kern-\nulldelimiterspace} {24}}}}{12} = 1 - 0.142 = 0.858 $$

with the variance.

$$ VAR\left( {\hat{\pi }_{2} } \right) = \frac{{\left[ {1 \times 0.0101 + 1 \times 0.0035 + 5 \times 0.0003 + 2 \times 0.0006 + 3 \times 0.0043} \right]}}{12} = \frac{0.02937}{{12}} = 0.0024, $$

where 0.0101 = $\left( {\left( {{{1 - 1} \mathord{\left/ {\vphantom {{1 - 1} {24}}} \right. \kern-\nulldelimiterspace} {24}}} \right) - 0.858} \right)^{2}$, for example.

5.3 Option 3 ($\pi_{3}$): rough estimator based on the cut-off of 25% or 27% of the test-takers

In practical settings, the possible manual calculations of many point estimates for π are laborious and this may not encourage one to estimate the latent π. A simpler option would be to use the traditional cut-off for the DI, that is 25% (or 27%) of the test takers in estimation. This cut-off could be a reasonable option because it uses the median point estimate of the cut-offs and it also relates with the traditional cut-off of estimating DI. The suggestion based on Theorem 3 is

$$ \pi _{3} = \left\{ \begin{gathered} \hat{\pi } = \hat{\pi }_{{25\% }} = p_{{25\% }} - 2p_{{25\% }}^{L} = \frac{{\tfrac{1}{2}T_{{25\% }} }}{N} \times GDI_{{25\% }} {\text{, when }}p < \,0.50 \hfill \\ 1 - \hat{\pi } = 1 - \hat{\pi }_{{25\% }} = 1 - p_{{25\% }} + 2p_{{25\% }}^{L} = 1 - \frac{{\tfrac{1}{2}T_{{25\% }} }}{N} \times GDI_{{25\% }} {\text{, when }}p \ge 0.50 \hfill \\ \end{gathered} \right.\, $$

(36)

From Table 3, it is known that π_25% = 0.125, that is, $\hat{\pi }_{3}$ = $1{-}\hat{\pi } _{25\% }$ = 0.875.

5.4 Option 4 ($\pi_{4}$): rough estimator based on the largest cut-off

The fourth estimator, comparable to $\pi_{3}$, is to use the cut-off of 50%, that is, all the respondents in the estimation (T_50% = N). From the simplicity viewpoint, this routine may serve as a starting point when one is willing to have a rough idea of the latent item difficulty. The suggestion based on Theorem 1 is

$$ \pi _{4} = \left\{ \begin{gathered} \hat{\pi } = \hat{\pi }_{{50\% }} = p - 2p^{L} {\text{, }}\,\,\,{\text{when }}p < \,0.50 \hfill \\ {\mkern 1mu} 1 - \hat{\pi } = 1 - \hat{\pi }_{{50\% }} = 1 - \left( {p - 2p^{L} } \right){\text{, }}\,{\text{when }}p \ge 0.50. \hfill \\ \end{gathered} \right. $$

(37)

From Table 3 it is known that π_50% = 0.208, that is, $\hat{\pi }_{4}$ = 1 – π = 0.792.

5.5 General evaluation of the estimators

Above, four options to estimate the latent π of a real-world item is given; several other options of the procedures could have been offered. Anyhow, above, we obtained four estimates of the latent, bias-corrected item difficulty: $\hat{\pi }_{1} = 0.842$, $\hat{\pi }_{2} = 0.858$, $\hat{\pi }_{3} = 0.875$, and $\hat{\pi }_{4} = 0.792$. Of these four, assumingly, $\pi_{1}$ reaches the closest to the “true” latent item difficulty in the given dataset. Although no such actual proportion of correct answers nor GP item pointing to $\hat{\pi }_{1}$ = 0.842 exists in Table 3 and Fig. 3, the result seems quite a credible reflection of the image we obtain from Fig. 3: a plausible π of a theoretical latent Guttman-patterned item is somewhere close to π = 0.167 which turns to be π = 1 – π = 0.833 on p-scale. The estimate by $\pi_{2}$ comes quite close to $\pi_{1}$ so that the estimates from the cut-offs a = 1 to a = s – 1 seem to cause the magnitude of the estimate to be lower than those by $\pi_{1}$ and, hence, seemingly, $\hat{\pi }_{2} \le \hat{\pi }_{1}$. However, this is not a general result as seen in the comparison of the estimators in the larger dataset below. Of the simple estimators $\pi_{3}$ and $\pi_{4}$, the estimate by $\pi_{3}$, that is, the median estimate of all estimates $\hat{\pi }_{a}$, comes close the “true” estimate $\hat{\pi }_{1}$ while the estimate by $\pi_{4}$ comes closer the original p = 0.625. The simpler routines offer us a simple access to assess how far the observed structure of the item is from the pattern of a GP item.

5.6 Numerical example of the computing of the estimators with a small real-world dataset

As a simple numerical example of computing the estimators of the latent item difficulty and, consequently, the form of the latent item in the real-life settings, let us consider a random sample of n = 26 test takers of mathematics test of originally 30 items of N = 4,023 grade 9 students (FINEEC 2018). Of the 30 items, seven are selected in Table 4a just as examples of the process and the outcomes. Table 4b shows the estimates of GDI in different cut-offs a using PES, and Table 4c shows the estimates of $\hat{\pi }_{a}$. For example, the value GDI in item V2 highlighted in Table 4b, is obtained by ${{\left( {\left( {1 + 1 + 1} \right){-}\left( {0 + 0 + 1} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {\left( {1 + 1 + 1} \right){-}\left( {0 + 0 + 1} \right)} \right)} 3}} \right. \kern-\nulldelimiterspace} 3}$ = 0.667 and the corresponding $\hat{\pi }_{3}$ = ${{1 - \left( {\left( {1 + 1 + 1} \right){-}\left( {0 + 0 + 1} \right)} \right)} \mathord{\left/ {\vphantom {{1 - \left( {\left( {1 + 1 + 1} \right){-}\left( {0 + 0 + 1} \right)} \right)} {26}}} \right. \kern-\nulldelimiterspace} {26}}$ = $1 - {2 \mathord{\left/ {\vphantom {2 {26}}} \right. \kern-\nulldelimiterspace} {26}}$ = 0.923; these are highlighted in Table 4c. Notably, Table 4b is needed only for detecting the perfect item discrimination and, consequently, the specific threshold a_s to compute the estimate by π₁. Table 4d collects the estimates for the latent, “biased-corrected item difficulty”. In Table 4a, a rough weighting system was used to make the order in the score (X) as unambiguous as possible (see Table 4a).

Table 4 a Numerical example of latent variables with a biased-corrected item difficulty. b Estimates of GDI in each cut-off a. c Estimates of $\hat{\pi }_{a}$ in each cut-off for the biased-corrected item difficulty. d Estimates of latent item difficulty

Item V1 is taken here as an example of the calculation of the estimates. Knowing that p > 0.50, based on Eq. (32) and Table 4c, the estimate by $\pi_{1}$ for V1 is computed as the mean of the estimates from the threshold cut-off for the last GDI = 1 in PES (a_s) onwards including the estimate for the cut-off itself:

$$ \begin{gathered} \pi _{1} = 1 - \bar{\hat{\pi }}_{{s + }} = 1 - \frac{{\sum\nolimits_{{a = s}}^{{\tfrac{1}{2}N}} {\hat{\pi }_{a} } }}{{\tfrac{1}{2}N - \left( {s - 1} \right)}} \hfill \\ \,\,\,\,\,\, = 1 - \frac{{\left( {0.885 + 0.885 + ... + 0.885 + 0.885} \right)}}{{13 - 3 + 1}} \hfill \\ \,\,\,\,\,\, = 1 - \frac{{9.731}}{{11}} = 0.885. \hfill \\ \end{gathered} $$

The estimate by $\pi_{2}$ for V1 is computed as the mean of all estimates using Eq. (34) and Table 4c:

$$\pi _{2} = 1 - \bar{\hat{\pi }} = 1 - \frac{{\sum\nolimits_{{a = 1}}^{{\tfrac{1}{2}N}} {\hat{\pi }_{a} } }}{{\tfrac{1}{2}N}} = 1 - \frac{{\left( {0.962 + 0.923 + ... + 0.885 + 0.885} \right)}}{{13}} = 0.893. $$

The point-estimate of 25–27% cut-off by $\pi_{3}$ for V1 is read from the closest cut-off to 0.27 (a = 7). using Eq. (36) and Table 4c, this leads to an estimate $\pi_{3} = 1 - \hat{\pi }_{27\% } = 0.885$. Finally, the point-estimate of 50% cut-off by $\pi_{4}$ for V1 is read from the cut-off 0.50 (a = 13), that is, using Eq. (37) and Table 4c, the estimate is $\pi_{4} = 1 - \hat{\pi }_{50\% } = 0.885$.

We note that the item V1 in the sample was, factually, a Guttman-patterned item to start with. Hence, the original p detects this correctly as do the estimators $\pi_{1}$, $\pi_{3}$, and $\pi_{4}$. The estimator $\pi_{2}$ seems to overestimate this sample estimate slightly. However, all the estimates above are notably lower than the population estimate (π₁ = 0.946) estimated from the original dataset of 4,022 test takers using the protocol π₁ (Eq. 32). The population value, the “true” latent item difficulty or “true” π is, notably, more extreme than the traditional p value (0.885). This and the fact that the estimate by $\pi_{2}$ is closer to the “true” π than the other estimators are discussed with a larger simulation discussed in what follows.

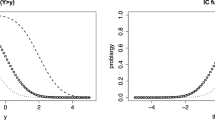
Three notes are made concerning Tables 4a and 4d. First, estimators by the procedures of Eq. (32), (34), (36) and (37) tend to produce estimates that are more extreme than the traditional estimate (see Figs. 4 and 5). More extreme estimates are expected because each “illogical” observation in the dataset, after being corrected by the process, leads to a more extreme outcome. The observed item characteristic curves (ICCs; see the discussion of the graph format in Metsämuuronen 2022) in Fig. 5 are obtained using five groups of ability levels with five cases in each plus two additional groups in the extremes with two cases.

Fig. 4

Population and sample estimates

Fig. 5

Observed ICCs and shift in the estimate of the latent item difficulty

Second, with item V28 with a difficulty level of very close to p = 0.50, all the sample estimates seem to be far off the population value. This is caused by the fact that when the difficulty level is very close to p = 0.50 and the sample size is small, even one case may turn the p-value from p < 0.5 to p > 0.5 or vice versa, and this may have a radical effect to the outcome if the p-value is used as a switch element in the process. This issue is discussed further in the next section with a larger dataset.

Third, by taking the estimate by $\pi_{1}$ a credible estimate of the item difficulty, Table 4a shows the latent, deterministically discriminating images of the selected items. We notice that the procedure makes, factually, suggestions which of the observations should be changed as being illogical from the ability level viewpoint.

Table 4a and related discussion is, obviously, just an example of how the estimates are computed and what kind of output we may expect in the process. Next section studies the characteristics of the estimators using a larger dataset.

5.7 Numerical simulation of the estimators with a larger real-world dataset

As a larger numerical example of the difference between p and π and the estimators of π in a real-world dataset, a test with 30 binary items with multiple choice questions (MCQ) from a mathematics test with 4,023 test-takers (FINEEC 2018) is used. The original item difficulties varied 0.24 < p < 0.95 with average $\overline{p}$ = 0.63. The estimates from this dataset are taken as “true p” and “true π”. The true p is the p value in the “population”. The true π is calculated using the protocol π₁ (Eq. 32) in the “population” as above. A rough weighting systemic was used to make the order in the score (X) as unambiguous as possible: before summing up, each item (g_i) was weighted by ${1 \mathord{\left/ {\vphantom {1 p}} \right. \kern-\nulldelimiterspace} p}_{i}$, that is, $X = \sum\nolimits_{{i = 1}}^{k} {w_{i} g_{i} } = \sum\nolimits_{{i = 1}}^{k} {\frac{{g_{i} }}{{p_{i} }}}$. The logic corresponds with the logic of Rasch and IRT models: demanding items have more effect on the score than the less demanding items. Consequently, instead of 30 categories in the unweighted score the weighted score included 3571 categories. Notably, a two-parameter logistic model would have given roughly the same number of categories. Pearson correlation between the scores is r = 0.994. Figure 6 summarizes the differences between the true p and π.

Fig. 6

Relation of p and π in the population (N = 4022)

As expected from Theorems 1 and 2, the estimates by π₁ are more extreme than those by p. The correlation between the true p and π is reasonably high: r = 0.760 for all items and r = 0.521 for items with p > 0.50. The nearer p is to p = 0.50 the further the response pattern deviates from the pure Guttman-pattern. This is caused by the fact that, with a medium item difficulty, the probability to obtain patterns that break the deterministic pattern is much higher than with items of extreme item difficulties.

From the viewpoint of estimating the person parameter θ using Rasch and IRT modeling, the order of the item difficulties is an important character of a set of test items because it defines the weight of an individual item in the summing process. Notably, both Somers delta (D; Somers 1962) and Goodman–Kruskal gamma (G; Goodman and Kruskal 1954), which indicate the probability of the pairs of cases in two variables to be in a same order (e.g., Van der Ark and Van Aert 2015) as well as the proportion of logically located cases in one variable after they are ordered by the other (Metsämuuronen 2021), show insignificant association between the true p and π. With the items with p > 0.50 (k = 27), although the covariance between the true p and π is reasonably high (r = 0.521, p < 0.001), the proportion of the items with the same order in both p and π is insignificantly low (D = G = 0.217; p = 0.225).

If we take π as a less biased estimator of the latent item difficulty, the order of the item difficulties obtained by p is radically biased too. This may mean that p is a remarkably less sufficient estimator of the latent item difficulty than traditionally has been considered within Rasch and IRT modeling. Larger, systematic simulations may enrich our knowledge of the matter.

From the original dataset, 20 random samples of size n = 2000, 1000, 500, 200, 100, 50, and 26 were picked and 20 × 7 = 140 estimates were calculated for each item by the estimators $\pi_{1}$, $\pi_{2}$, $\pi_{3}$, and $\pi_{4}$. The average estimates are collected in Fig. 7 for the items with p > 0.50 to highlight the essential patterns. The datasets are available in CSV format at http://dx.doi.org/10.13140/RG.2.2.34357.35042 and in SPSS format at http://dx.doi.org/10.13140/RG.2.2.12546.96968.

Fig. 7

Comparison of the estimates by different estimators of π (items with p > 0.50)

Four points are highlighted. First, although single estimates in the samples may be lower or higher than the true π, the average estimates of all estimators tend to be less extreme than the true value. Partly, the phenomenon is related to the sample size: the deviance between the true π and the estimated values tends to be wider with smaller sample sizes. The reason is mainly mechanical: the higher is the sample size, the more probable it is to find response patterns that break the deterministic pattern which causes the estimate to be more extreme.

Second, the estimates related to the means of point estimates (π₁ and π₂) are closer the true π than the single point estimates of 25% and 50% of the test-takers. Of the first two, as a surprise, the estimator that uses all cut-offs in estimation (π₂) tends to give estimates that are closer to the true π for items with a medium item difficulty. The point estimates related to the median cut-off of 25% (π₃) are quite near the estimates by π₁ and π₂. The point estimates related to the whole dataset (π₄) are the furthest from the true π with all items although the difference is not wide for items with extreme p to start with; in these items there are less possibilities to obtain additional 1s and 0s outside the perfect strings obtained from the extreme test-takers.

Third, when the item difficulty is around p ≈ 0.5 slightly higher or lower, the sample may appear to show opposite direction than the population in item difficulty. Small samples are more prone to this phenomenon. Then, the outcome of 1 – (p – 2p^L) may cause a radical deviance between the population value and the estimate. In the simulation, 108 of the estimates (2.5%) were found to be obvious outliers in comparison with the true value. Of these, 52% came from samples with n = 50 and n = 26. A reflection of this phenomenon is seen in the 4th item in Fig. 7 where all estimates differ from the true value in an obvious manner.

Fifth, out of 4200 estimates in the simulation, two point-estimates by π₃ and nine by π₄ showed an out-of-range value ($\hat{\pi } > 1$). In estimators π₁ and π₂ such outliers were not found. The mechanics of this phenomenon is related to negative item discrimination discussed with Theorem 1. When R^U < R^L, (p – 2p^L) < 0 and, then, consequently, 1 – (p – 2p^L) = π₄ > 1. Although the number and magnitude of out-of-range estimates in the samples is small (all estimates < 1.040), the phenomenon must be noted. A possible solution is that, whenever obtained, the values $\hat{\pi } > 1$ can be replaced by $\hat{\pi } = 1$ unless the real reason for the phenomenon is “miskey” (as typologized by Linacre and Wright 1994), that is, if the wrong answers are marked, mistakenly, as the correct ones leading to mechanical negative item discrimination.

6 Discussion

6.1 Results in a nutshell

This article had three starting points. First, latent to each test item there is a theoretical (image of an optimal) item that the observed pattern of responses reflects. As often is the case in Rasch-, IRT-, and NIRT modeling settings with binary items, this latent item is thought to be an item with a deterministic pattern with the item difficulty π. Second, the classical parameter used for the item difficulty (p) can locate the item difficulty unambiguously only with Guttman-patterned, deterministic items; with non-GP items, there are several options for the latent π. Third, it is known that the cut-off-curve of any NGP item at any cut-off a follows the COC of some of the latent GP items. The task is, then, to estimate which of the latent GP items would be the most credible (latent) image of the observed, manifested item.

Two of the four elements of impurity in p were formalized in the article while the other two are implicit in the formulae. Theorem 1 shows that the item difficulty of a GP item can be reached by $\pi = \left\{ {\begin{array}{*{20}c} {p - 2p^{L} ,{\text{when }}p{ < 0}{\text{.50 }}} \\ {p + \left( {1 - 2p^{U} } \right){\text{,when }}p \ge {0}{\text{.50}}} \\ \end{array} } \right.$ where the elements of impurity, $2p^{L}$ and $\left( {1 - 2p^{U} } \right)$, are explicit. For real-world items with a non-deterministic pattern, this means that if we find any correct answers in the lower half of the ordered dataset ($2p^{L}$) of a difficult item (that is, the pattern of “lucky guessing”) or any incorrect answer in the upper half of the ordered dataset $\left( {1 - 2p^{U} } \right)$ of an easy item (that is, the pattern of “carelessness” or “sleepiness”), p is a biased indicator of the “real” item difficulty. Four estimators of the latent π, or “bias-corrected item difficulty”, are discussed and studied in this article. A simulation indicates that p in the sample may be a radically misleading indicator of π, especially, when the item is of medium item difficulty with p ≈ 0.50.

6.2 Some reflections of the biasness in p within the Rasch- and IRT modeling

Because p can locate the latent item difficulty π correctly only with GP items, we may reason that the higher is the number of erroneous patterns of 1 s and 0 s in the data structure the less p reflects the latent π. The simulation shows that, specifically, with items with a medium item difficulty, p may deviate radically from π. Because p is used as a sufficient starting point for the estimation of the B parameter in Rasch- and IRT modeling, B seems to be radically biased with items of medium item difficulty. Further, if p is a biased indicator of the item difficulty implying that the 0s and 1s in the dataset are not logically patterned, it seems that the total score is a biased estimator of the latent ability because it is based directly on the correct and incorrect responses in the data. From the real-world dataset we know that the order of the item difficulties may differ radically depending on whether the (biased) p or (unbiased) π is used as the indicator of the order. If we take π as a less biased estimator of the latent item difficulty, the order of the item difficulty obtained by p may be radically biased. This may have some consequences in using p as a sufficient estimator of latent item difficulty in Rasch and IRT modeling.

Another, related question is how are the patterns of “lucky guessing” or “carelessness” in the dataset and the proposed procedures of estimating the bias-corrected estimators of item difficulty related to the difficulty parameter in the three-parameter logistic model with the guessing parameter? Four points are discussed here. First, technically, the proposed methods suggested to be used to estimate the latent or “real” item difficulty are not dependent on the response patterns. However, as discussed above, the patterns of “lucky guessing” and “carelessness” always seem to lead the procedures to react so that the magnitude of the estimates of the “biased-corrected” p are more extreme than those of observed p values. Second, the concept of “guessing” within three-parameter IRT modeling seems to be widely understood incorrectly; in many cases, the high “guessing” plainly indicates that the item is an easy one. Then, factually, there was not necessarily “guessing” per se. To give a blunt example, assume we have 1000 test takers of which only one gave the incorrect answer and this case was the lowest scoring test-taker. In this case, we need to conclude that no “guessing” was obtained in the dataset nor obvious “lucky guessing”. In this case, however, the “guessing” parameter C in the three-parameter IRT model would indicate that that “guessing” is (misleadingly) quite high. Hence, third, with an easy item, it would be important to make a difference between a real correct answer and a “lucky guessing”—separating these is not an obvious task as discussed above. The practicalities related to “lucky guessing” with an easy item in the sense discussed in the article are related to the fact whether we obtained at least one correct and one incorrect answer in the dataset within those test takers that are ranked lower than the potential case with a “lucky guessing” (see impurity 1 and 3 in Table 3). Fourth, consequently, maybe the new way of thinking the item difficulty would lead to a new thinking of item discrimination and guessing?

Although using p in estimating A, B, and θ has a long and steady history in IRT- and Rasch models, it feels valuable to try to use estimates that would reflect as close as possible the “real” latent item difficulty in the process. A relevant question is, how the “bias-corrected item difficulty” π could or should be used in the item analysis and measurement modeling? Some ideas are discussed in what follows.

6.3 Options for the further studies

The results obtained in this article provide a new kind of tool that can be used, first, in locating the bias-corrected item difficulty and, second, detecting a plausible cut-off in the dataset for estimating the item discrimination in the settings related to DI and GDI. This may open possibilities on building up firmer bridges between the classical test theory and Rasch- and IRT modeling (cl., Bechger et al. 2003, Macdonald and Paunonen 2002).

The procedures presented in the article raise several questions and ideas for further development of both the older and the new paradigms. Some questions concerning Rasch- and IRT modeling were already raised above. Two sets of questions can be asked concerning the topic discussed in this article.

First, what are the strict consequences of the results to Rasch- and IRT modeling? Should we change the procedures in some way to consider the biasness in p? Would it be possible, maybe even valuable, to utilize the “bias-corrected item difficulty” in the estimation processes? From this viewpoint, using π₄ = p – 2p^L as a rough estimator instead of p could be an option worth studying further. Second, if the p-value is severely biased, it means that some values in the dataset are not logical and there may be a need to consider what is the effect of this on the test score. What are the consequences of the results in person parameter that depends on the total score, which now has revealed to be biased, too? Third, studies of the optimal weighting mechanism would be beneficial in respect of the new set of estimators; the order of the cases is a crucial matter in determining the latent item difficulty. If the p value is biased, also the person parameter θ is biased. What would be an optimal procedure to find the most credible order of the cases to start the process?

Obviously, larger simulations of the estimators of π would enrich our knowledge. Maybe new, better estimators could or should be developed? It may be valuable to create enhanced procedures to estimate A, B, and θ using $\hat{\pi }$ instead of p. After this, comparisons with the new kind of estimators of “bias-corrected” B and θ should be compared with the traditional ones.

6.4 Some known limitations of the approach

Four main limitations of the procedure may be worth highlighting. First, estimating the latent π using the procedures proposed in this article are strictly based on the “correct” or plausible order of the test-takers. In the article, a simple weighting system based on the biased p was used. It led to a reasonable solution from the viewpoint that it was possible to give almost all test-takers their unique rank instead of being bound to 30 categories based on the unweighted score. Relevant questions are, how do we know which order of the item difficulties would be the “most correct” option to lead us to the plausible estimates of person parameters?; and, Could we consider some alternative ways to solve the original ranking in the initial phase?

Second, the formulae in Theorems 1and 2 lead to a kind of “purified” dataset where all responses caused by “lucky guessing” and “carelessness” are omitted from the dataset and the estimation of the latent item difficulty is done without these cases. Because of this, the routines in Eqs. (32), (34), (36), and (37) tend to lead to a situation in which the “bias-corrected item difficulty” is always more extreme—sometimes radically—than the original p indicates. This is relevant for items with medium item difficulties where we expect to see many patterns deviating from a pure deterministic pattern. A relevant question is, could there be some lighter possibilities that would not exclude all the cases that break the deterministic pattern to also leave some stochastic error in the dataset? Would it be possible to derive the elements of impurity other than discussed in this article, or to estimate the π in some other way to make possible to estimate the latent item difficulties so that the estimates are not that extreme? Maybe just the extreme cases with clear guessing or sleepiness should be omitted from the analysis? The mechanism presented in this article does not provide these tools although those may be possible to develop.

Third, when the response pattern follows the so-called “special knowledge” pattern (see Linacre and Wright 1994) one needs to be cautious. In this pattern, there are several theoretically pathological cases characterized by a pattern where in the middle of the sequence, test-takers with a higher score fail to give the correct answer while some test-takers with a lower score but with the “special knowledge” give correct answers, all the estimators $\pi_{1}$, $\pi_{2}$, $\pi_{3}$, and $\pi_{4}$ may fail to locate a plausible π.

Fourth, the approach in this article was restricted to binary items. To derive the Theorems 1 and 2 for polytomous items seems possible because Eq. (1) can be used also with polytomous items (see examples in Metsämuuronen 2020a). Although the derivations would not be that simple as they are in the binary case those would be a valuable to do.