Abstract
Temporal networks are networks whose topology changes over time. Two nodes in a temporal network are connected at a discrete time step only if they have a contact/interaction at that time. The classic temporal network prediction problem aims to predict the temporal network one time step ahead based on the network observed in the past of a given duration. This problem has been addressed mostly via machine learning algorithms, at the expense of high computational costs and limited interpretation of the underlying mechanisms that form the networks. Hence, we propose to predict the connection of each node pair one step ahead based on the connections of this node pair itself and of node pairs that share a common node with this target node pair in the past. The concrete design of our two prediction models is based on the analysis of the memory property of real-world physical networks, i.e., to what extent two snapshots of a network at different times are similar in topology (or overlap). State-of-the-art prediction methods that allow interpretation are considered as baseline models. In seven real-world physical contact networks, our methods are shown to outperform the baselines in both prediction accuracy and computational complexity. They perform better in networks with stronger memory. Importantly, our models reveal how the connections of different types of node pairs in the past contribute to the connection estimation of a target node pair. Predicting temporal networks like physical contact networks in the long-term future beyond short-term i.e., one step ahead is crucial to forecast and mitigate the spread of epidemics and misinformation on the network. This long-term prediction problem has been seldom explored. Therefore, we propose basic methods that adapt each aforementioned prediction model to address classic short-term network prediction problem for long-term network prediction task. The prediction quality of all adapted models is evaluated via the accuracy in predicting each network snapshot and in reproducing key network properties. The prediction based on one of our models tends to have the highest accuracy and lowest computational complexity.
Similar content being viewed by others
Introduction
Complex systems can be represented as networks, where nodes represent the components of a system and links denote the interaction or relation between the components. The interactions are, in many cases, not continuously active. For example, individuals connect via email, phone call, or physical contact at specific times instead of constantly. Temporal networks (Holme and Saramäki 2012; Masuda and Lambiotte 2016; Holme 2015) could represent these systems more realistically with time-varying network topology.
The classic temporal network prediction problem aims to predict the interactions (or equivalently the network) one step ahead based on the network observed in the previous L steps. This problem is also equivalent to problems in recommender systems, e.g., predicting which user will purchase which product, which individuals will become acquaintances at the next time step (Kumar et al. 2019; Dhote et at. 2013). The temporal network prediction problem is more challenging than the static network prediction problem, which aims to predict the missing links or future links based on the links observed (Lü and Zhou 2011; Kumar et al. 2020; Cui et al. 2017; Zou et al. 2021; Zhan et al. 2020). Recently, machine learning algorithms have been developed to predict temporal networks. Embedding algorithms embed each node in a low-dimensional space based on the network observed. If the learned representations of two nodes are closer in the vector space, it is more likely to have a contact between this node pair one time step ahead (Kumar et al. 2019; Kazemi et al. 2020; Zhou et al. 2018; Wang et al. 2021; Rahman et al. 2018; Xu et al. 2020). Restricted Boltzmann machine (RBM) based methods (Li et al. 2014) and Graph neural networks (Pareja et al. 2020; Wu et al. 2022; Ma and Tang 2021) have also been developed for this prediction task and they can achieve high prediction accuracy. These methods, however, are at the expense of high computational costs and are limited in providing insights regarding which mechanisms enable the prediction and thus could possibly form temporal networks.
Network-based methods have been proposed to predict new links, i.e., the node pairs that will have contact in the future but have not had any contact in the past, instead of predicting all contacts at a specific future time step. These network-based methods consider a network property, also called similarity, of a node pair as the tendency that a new link will appear between the node pair (Liben-Nowell and Kleinberg 2003; Ahmed et al. 2016; Xu and Zhang 2013). Network-based methods tell directly which mechanisms or properties are used for the prediction and tend to have a low computational complexity. Recently, network properties of a node pair have been combined with learning algorithms to address the classic temporal network prediction problem (Li et al. 2019).
In this work, we aim to design network-based methods to solve the classic temporal network prediction problem and to unravel which mechanisms and network properties enable the prediction.
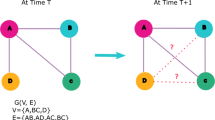
A temporal network measured at discrete times can be represented as a sequence of network snapshots \(G=\{G_1, G_2,..., G_T\}\), where T is the duration of the observation window, \(G_t=(V; E_t)\) is the snapshot at time step t with V and \(E_t\) being the set of nodes and contacts, respectively. If node j and k have a contact at time step t, \((j,k)\in E_t\). We assume all snapshots share the same set V of nodes. The time aggregated network \(G^w\) contains the same set V of nodes and set of links \(E=\cup _{t=1}^TE_t\). That is, a pair of nodes is connected with a link in the aggregated network if at least one contact occurs between them in the temporal network. We give each link in the aggregated network an index i, where \(i\in [1, M]\) and \(M=|E|\) is the total number of links. The temporal connection or activity of link i over time could then be represented by a T-dimension vector \(\mathbf {x_{i}}\) whose element is \({x_{i}(t)}\), where \(t\in [1,T]\), \(x_{i}(t)=1\) when link i has a contact at time t and \(x_{i}(t)=0\) if no contact occurs at t. A temporal network can be thus equivalently represented by its aggregated network, where each link i is further associated with its activity time series \(\mathbf {x_{i}}.\)
Specifically, the prediction task is to predict the activation/connection tendency of each link i at the next time step \(t+1\) based on the network observed in the previous L steps \([t-L+1,t]\), where \(1 \le t-L+1<t \le T\). The aggregated network \(G^w\) is assumed to be known in the prediction problem because it represents social relationships and varies relatively slowly in time compared to contacts. The prediction accuracy is evaluated via the area under the precision-recall curve (AUPR), which compares the predicted activity tendency and the ground-truth connection of each link at the prediction time step.
Firstly, we explore the structural similarity between two network snapshots at any two time steps with a given time lag. We find the similarity or so-called network memory is relatively high when the time lag is small and decays as the time lag increases in the seven real-world physical contact networks considered. Based on this observed time-decaying memory in temporal networks, we design two network-based temporal network prediction models.
The self-driven (SD) model assumes that the activation tendency of a link at a prediction step is solely influenced by its past activity states, with a stronger influence from more recent states. This concept is not new (Li et al. 2019; Jo et al. 2015). The SD model is emphasized as one model here because we will explore in depth the choice and interpretation of its parameter and it is the basis to build our self- and cross-driven (SCD) model (Zou et al. 2023). In the SCD model, the activity tendency is firstly derived for each link at the prediction time step based on SD model. SCD assumes the connection tendency of a target link at a prediction step depends not only on the SD activity tendency of the link itself at the same prediction step but also of the neighboring links (links share a common end node with the target link) in the aggregated network. State-of-the-art models that allow interpretation are considered as baselines: Common Neighbor, Lasso Regression, Correlated Discrete Auto-regression model, and the Markov model. In several real-world contact networks, we find that SCD outperforms SD model and both SCD and SD models perform better than the baselines. Both SD and SCD perform better in networks with a stronger memory. Additionally, the SCD model allows us to understand how different types of neighboring links (depending on whether they form a triangle with the target link or not) contribute to the prediction of a target link’s future activity.
It is essential to predict the contact network in the long-term future, instead of one step ahead, in order to develop strategies to mitigate the epidemic or information spreading on the network. However, this long-term prediction problem on temporal networks remains unexplored. Hence, we further propose basic methods that adapt the aforementioned models for short-term network prediction to solve the long-term network prediction problem. Specifically, the long-term temporal network prediction problem is to predict the network (activities of all links) at each time step within the prediction period \([t+1,t+L^*]\) based on the network observed within \([t-L+1,t]\). Moreover, the aggregated network \(G^w\) and the total number of contacts at each time step within the prediction period are assumed to be given. The latter assumption aims to simplify the problem, also because the number of contacts can be influenced by factors like weather and policy other than the network observed in the past. The prediction quality is evaluated via whether the predicted network within the prediction period is precise and could reproduce key network properties. We find in general, the adapted SD model performs the best among all models in all data sets. Its prediction accuracy decays as the prediction step is further ahead in time and this decay speed is positively correlated with the decay speed of network memory. Finally, networks predicted by various models respectively within the prediction period have a heterogeneous distribution of inter-event time of contacts along a link, similar to real-world networks.
The rest of the paper is organized as follows. We will introduce real-world temporal networks to be used to design and evaluate temporal network prediction methods in section "Empirical data sets". Key temporal network properties will be analyzed in section "Memory in temporal networks" to motivate our network-based models (Section "Short-term network prediction methods") for the classic short-term network prediction problem. The proposed models will be evaluated and interpreted in section "Performance analysis in short-term prediction". Finally, our network-based models and baseline models will be further developed and evaluated for the long-term prediction problem in sections "Long-term prediction methods" and "Performance analysis in long-term prediction" respectively.
Empirical data sets
To design and evaluate temporal network prediction methods, we consider seven empirical physical contact networks: Hospital (Vanhems et al. 2013), Workplace (Génois and Barrat 2018), PrimarySchool (Stehlé et al. 2011), HighSchool (Mastrandrea et al. 2015), LH10 (Génois and Barrat 2018), SFHH (Rossi and Ahmed 2015) and Hypertext2009 (Isella et al. 2011). The basic properties of these data sets are given in Table 1. The time steps at which there is no contact in the whole network have been deleted.
Memory in temporal networks
In this section, we explore whether a temporal network has memory, i.e., the network observed at different times share certain similarity. Such memory property may inspire the design of network-based temporal network prediction methods and influence prediction quality.
Auto-correlation Firstly, we explore the correlation of the activity of a link at two times with a given interval \(\Delta \), called time lag, via the auto-correlation of the activity series of each link. The auto-correlation of a time series is the Pearson correlation between the given time series and its lagged version. We compute, for each link i, the Pearson correlation coefficient \(R_{x_{i}x_{i}}(\Delta )\) between \(\{x_{i}(t)\}_{t=1,2,...,T-\Delta }\) and \(\{x_{i}(t)\}_{t=\Delta +1,\Delta +2,...,T}\) as its auto-correlation coefficient. Figure 1a shows that the average auto-correlation coefficient over all links decays with the time lag \(\Delta \) in every real-world network. The average auto-correlation decays slower as the time lag increases.
Jaccard similarity Furthermore, the similarity of the network at two times with a given time lag \(\Delta \) is examined via Jaccard similarity (JS). JS measures how similar two sets are by considering the percentage of shared elements between them. Given two snapshots of a temporal network \(G_t\) and \(G_{t+\Delta }\), their Jaccard similarity is defined as the size of their intersection in contacts divided by the size of the union of their contact sets, that is, \(JS(G_t,G_{t+\Delta })=\frac{E_t\cap E_{t+\Delta }}{E_t\cup E_{t+\Delta }}\). Large JS means a large overlap/similarity between the two snapshots of the temporal network. Figure 1b shows the average Jaccard similarity over all possible pairs of temporal network snapshots that have a time lag \(\Delta \). Similar to auto-correlation in link activity, the similarity between temporal snapshots decays with their time lag in all empirical data sets, manifesting the time-decaying memory of real-world temporal networks.
Short-term network prediction methods
In this subsection, we will propose two network-based prediction models and four baseline models for the classic short-term temporal prediction problem, that is, predicting the activation tendency of each link in the aggregated network \(G^w\) (\(G^w\) is given) at the next time step \(t+1\) based on the network observed in the previous L steps within \([t-L+1,t]\).
Our network-based models
Inspired by the time-decaying memory of temporal networks, we propose two network-based temporal link prediction models. In our previous work (Zou et al. 2022) that uses Lasso Regression for short-term prediction explained in “Lasso regression” section, it has been found that a link’s state at the next step is largely determined by the current state of the link itself and of the neighboring links that share a common node with the target link in the aggregated network. Hence, our two network-based models will estimate a link’s activity tendency one step ahead based on the past activities of the link itself and of its neighboring links respectively by taking the memory effect into account.
Self-driven (SD) model
The self-driven (SD) model predicts the tendency \(w_{i}(t+1)\) of the link i to be active at the prediction time \(t+1\) as:
where the decay factor \(\tau \) controls the rate of the memory decay and \(x_i(k)\) is the state of link i at time step k. A large \(\tau \) corresponds to a fast decay of memory, such that a small number of previous states affect the tendency of connection. When \(\tau =0\), all past states have equal influence on the future connection tendency, and \(w_i(t+1)\) reduces to the total number of contacts of link i during the past L steps. Such exponential decay has also been considered in Li et al. (2019), Yu et al. (2017). In “Model evaluation” section, we will show that the SD model performs well for a common wide range of the decay factor \(\tau \) among all real-world networks considered and we do not need to learn \(\tau \) from the temporal network observed in the past.
Self- and cross-driven (SCD) model
Furthermore, we generalize the SD model to a self- and cross-driven (SCD) model. The SCD model assumes that the activity tendency of a target link one step ahead depends on the SD connection tendency defined in Eq. (1) of the link itself and also of neighboring links that share an end-node node with the target link in the aggregated network. The union of the target link and its neighboring links is also called the ego-network centered at the target link, exemplified in Fig. 2. Furthermore, we differentiate three types of links in an ego-network, colored differently in Fig. 2: the target link itself (in grey in Fig. 2), links that form a triangle with the target link (in blue), and the remaining links (in green). We assume that the previous states of these three types of links may contribute differently to the connection tendency of the target link. This is motivated by a) our finding that, when Lasso Regression is used to estimate connection tendency (Zou et al. 2022), the previous activity of the target link itself contributes more than that of the neighboring links, b) the common neighbor similarity method in static network prediction and c) the observation of temporal motifs (e.g., three contacts that happen within a short duration with a specific ordering in time, and form a triangle in topology) in temporal networks (Paranjape et al. 2017; Saramäki and Moro 2015).
Specifically, our SCD model assumes that the tendency \(h_i(t+1)\) for link i to be active at time step \(t+1\) is a linear function
of the contributions of the link itself \(w_i(t+1)\) as defined in Eq. (1), the neighboring links that form a triangle with the target link \(u_i(t+1)\) and the other neighboring links \(g_i(t+1)\). The latter two factors \(u_i(t+1)\) and \(g_i(t+1)\) will be defined soon as a function of the SD tendency at \(t+1\) of links in the ego-network.
The contribution \(u_i(t+1)\) of the neighboring links that form a triangle with the target link i is defined as follows. For each pair of neighboring links j and k that form a triangle with the target link i, the geometric mean \(\sqrt{w_j(t+1) \cdot w_k(t+1)}\) suggests the strength that the two end nodes of link i interact with the corresponding common neighbor. We define \(u_i(t+1)\) as the average geometric mean over all link pairs that form a triangle with the target link. This design of \(u_i(t+1)\) aims to capture the weighted version of common neighbor similarity. The contribution of the other links \(g_i(t+1)\) in the ego-network is defined as the average of their SD activity tendency. For each prediction time step \(t+1\), a set of coefficients \(\beta _0^*\), \(\beta _1^*\), \(\beta _2^*\), and \(\beta _3^*\) in Eq. (2) will be learned through Lasso Regression from the temporal network observed in the past L steps for all possible target links.
Baseline models
Our goal is to develop network-based models for predicting temporal networks. This is because they usually have low computation complexity and allow us to understand the underlying mechanism that enables the prediction, thus mechanism that potentially forms temporal networks. Hence, as baselines, we introduce four models that are relatively interpretable in their mechanisms of prediction.
Common neighbor
We generalize the common neighbor method from static network prediction (Liben-Nowell and Kleinberg 2003) to the temporal network prediction problem. The number of common neighbors of a target node pair can be computed for each of the previous L snapshots. The total number of common neighbors (CN) over the past L snapshots is used as the target node pair’s tendency of connection at the prediction time step \(t+1\).
Scholz et al. (2013) and Tsugawa et al. (2013) have used the number of common neighbors (CN\(_{agg}\)) of a target node pair in the unweighted aggregated network over the past L snapshots to estimate if there will be a new link between this node pair at the prediction time step. Later, we will show that the CN\(_{agg}\) method performs overall worse than the CN method in all real-world networks.
Lasso regression
Lasso Regression (Zou et al. 2022) assumes that the activity of link i at time \(t+1\) is a linear function of the activities of all the links at time t, i.e.,
The objective is
where M is the number of features, as well as the number of links in the aggregated network, \(c_{i}\) is the constant coefficient, and \(\beta _i=\{\beta _{i1}, \beta _{i2}, \cdots , \beta _{iM}\}\) are the regression coefficients of all the features for link i. The coefficients will be learned from the temporal network observed in the past L steps for each link. We use L1 regularization, which adds a penalty to the sum of the magnitude of coefficients \(\sum _{j=1}^M|\beta _{ij}|\). The parameter \(\alpha \) controls the penalty strength. The regularization forces some of the coefficients to be zero and thus leads to models with few non-zero coefficients (relevant features). The optimal \(\alpha \) that achieves the best prediction is chosen by searching 50 logarithmically spaced points within \([10^{-4},10]\).
CDARN model
The correlated Discrete Auto-Regression Network (CDARN) model has been shown to be able to capture the non-Markovian evolution of temporal networks and also the correlation between links in their activities (Williams et al. 2022). It assumes that the state of a link at each time step t is either a copy of a previous state of the link itself or another link or is a Bernoulli random variable. The dynamics of each link i is governed by the process:
where \(Q_i(t) \sim {\mathscr {B}}(q_1)\) is a Bernoulli variable and \(Q_i(t)=1\) (or \(Q_i(t)=0\)) with probability \(q_1\) (or \(1-q_1\)), the current state \(x_i(t)\) of a link i is equal to the state of link \(C_i(t)\) at a past time \(t-Z_i(t)\) if \(Q_i(t)=1\), and \(Y_i(t)\sim {\mathscr {B}}(q_2)\) is a Bernoulli variable with average \(q_2\) controlling the density of the network.
\(Z_i(t)\) is a discrete random variable that is uniformly distributed within \(\{1,2,\dots , P\}\) and it means that states of previous P steps have equal probability to be chosen as \(x_i(t)\). This random variable \(C_i(t)\) encodes which link’s state would be copied by link i and distributed as
where \(\Gamma _i\) is the set of neighboring links of link i in the aggregated network \(G^w\). Two links in the aggregated network are neighboring links if they share a common end node.
At any time t, \(Q_i(t)\) is an independent and identically distributed random variable. The same holds for \(C_i(t)\), \(Z_i(t)\) and \(Y_i(t)\). The parameters \(q_1\), \(q_2\), and c can be estimated via Maximum Likelihood Estimation as described in Williams et al. (2022) based on the network topology observed in the previous L steps. The same as Lasso Regression models, we confine ourselves to the CDARN model with memory length \(P=1\), where a link’s current state is determined probabilistically by the states of the link itself or its neighboring links at the previous time step. This choice is also motivated by the high computational cost of CDARN.
Based on the estimated parameters (\(q_1\), \(q_2\) and c), the CDARN tendency for each link i to be active at \(t+1\) has been derived in Williams et al. (2022) for link prediction task, as
with
where \(\delta (a,b)\) is the Kronecker delta, equal to 1 if \(a=b\), otherwise 0, and \(\Gamma _i\) is the set of neighboring links of link i in the aggregated network. The term \({{\tilde{\textrm{C}}}}_i(t+1)\) represents the fraction of active links among all the neighboring links of link i at t. The term \((1-c){{\tilde{\textrm{D}}}}_i(t+1)+c{{\tilde{\textrm{C}}}}_i(t+1)\) interprets the probability that the state of link i at \(t+1\) is active given it is a copy of a previous state of the link itself or its neighboring links.
Markov model
Markov model (Kemeny and Snell 1976; Tang et al. 2020) assumes that the activity or time series of a link in a temporal network is independent of that of other links and a link’s activity at the current time step depends only on its state at the previous time step. For each link, we can obtain a \(2\times 2\) transition matrix, where each element represents the transition probability from each possible state (either 0 or 1) at any time step to each possible state at the next consecutive time step, based on the states of the link observed in the last L steps. The Markov tendency for each link being active at \(t+1\) is the transition probability from its state at t to an active state.
Performance analysis in short-term prediction
In this section, we will evaluate and interpret the performance of these short-term network prediction models in the aforementioned set of real-world physical contact networks.
Model evaluation
We first introduce the method to evaluate the prediction accuracy of a model. Secondly, we explore how to choose the decay factor in the SD model. Thirdly, we compare the performance of all the models.
Temporal network prediction accuracy of short-term prediction
Each model predicts the activation tendency of each link at time step \(t+1\) based on the temporal network observed in the past L steps. The prediction step \(t+1\) is sampled 1000 times from \([T/2+1, T]\) with equal space.
The average proportion of the M links that are active at a time step is lower than \(1\%\) in all the real-world networks we considered. The classification labels (the number of active links and inactive links per time step) are imbalanced. Hence, we evaluate the prediction accuracy via the area under the precision-recall curve (AUPR) (Davis and Goadrich 2006). An AUPR can be derived for the prediction of each network snapshot, using the connection tendency of each link derived by a given model and the actual network snapshot. AUPR provides an aggregated accuracy across all possible classification thresholds. The average AUPR of a model over the 1000 prediction snapshots quantifies the prediction accuracy of the model. A high AUPR means high prediction accuracy.
Choice of decay factor
How to choose the decay factor \(\tau \) will be motivated by comparing two possibilities. We first consider a simple case where \(\tau \) is a control parameter and does not vary over time, i.e., remaining the same for the 1000 samples of the prediction time step \(t+1\). Given a \(\tau \), the tendency \(w_i(t+1)\) (\(i\in [1,2,...,M]\)) can be obtained at each prediction step based on Eq. (1). Figure 3 shows that the decay factor \(\tau \) indeed affects the prediction accuracy AUPR of the SD model. A universal pattern is that the optimal performance is obtained by a common and relatively broad range of \(\tau \in [0.5,5]\) in all networks. This implies that our real-world physical contact networks measured at school, hospital, workplace, etc., may be formed by a universal class of time-decaying memory. Hence, \(\tau \) can be chosen arbitrarily within [0.5, 5].
In the second method of choosing \(\tau \), a \(\tau (t+1)\) for each prediction step \(t+1\) is learned from the network observed in the past L steps. The \(\tau (t+1)\) is chosen as the one that allows the SD model to best predict the temporal network at t based on the network observed in the past L steps. The prediction accuracy achieved by the first (second) method of choosing \(\tau \) is 0.63 (0.61), 0.68 (0.67), 0.69 (0.63), 0.75 (0.74), 0.68 (0.67), 0.34 (0.33) and 0.65 (0.63), for the seven data sets, respectively.
Hence, \(\tau \) could be chosen arbitrarily from [0.5, 5], which has lower computational complexity and better prediction accuracy than learning \(\tau \) dynamically over time. We consider \(\tau =0.5\) to derive the SD tendency and SCD tendency in the rest analysis.
Comparison of models
Temporal network prediction accuracy AUPR of Common Neighbor model (CN and CN\(_{agg}\)), Lasso Regression (LR), CDARN model, Markov model, SD model, and SCD model. All methods consider \(L=T/2\) and \(\tau =0.5\) except for SD (\(\tau =0.5\), \(L=3\)), which is needed only for “Duration L of past observation” section
We further compare the prediction accuracy of all models. As shown in Fig. 4, both SD and SCD models perform better than the baselines. The SCD model, which predicts a link’s connection utilizing SD tendency of the neighboring links and of the link itself, indeed performs better than the SD model that uses only the SD tendency of the link itself. Moreover, the SD and SCD models perform the best (worst) in LH10 (PrimarySchool), in line with the strongest (weakest) memory/similarity of LH10 (PrimarySchool) observed in Fig. 1.
Previous studies have shown that the number of common neighbors (CN\(_{agg}\)) in the unweighted aggregated network over the past observation period could relatively accurately predict new links to appear in the aggregated network (Scholz et al. 2013; Tsugawa and Ohsaki 2013). However, our CN method, though performs better than the CN\(_{agg}\), performs poorly in the short-term network prediction problem. This is likely because when the neighboring links that form a triangle with the target have contacts is crucial for the short-term network prediction problem, but largely ignored by CN and CN\(_{agg}\) methods. The SCD model, in contrast, weighs events that happen earlier in time less and estimates implicitly the chance those two neighboring links have contacts at the same time, giving rise to its superior performance. CN method uses the sum of the number of common neighbors over the past L snapshots to estimate a target node pair’s tendency of connection at the prediction time step. In this case, every two contacts of a node with the target node pair respectively at the same time contribute to the connection tendency. The CN method taking into account more time information of contacts than CN\(_{agg}\), performs better than CN\(_{agg}\).
Model interpretation
In this subsection, we interpret firstly the SCD model, to understand how the past states of different types of links in the ego-network (neighborhood) of a target link contribute to the activation tendency of the target link. Afterwards, we interpret the decay factor \(\tau \) and the duration L of past observation to understand how past contacts over time contribute to the prediction.
Interpretation of SCD model
As defined in Eq. (2), SCD model predicts a link’s future connection, based on the SD tendency of the link itself, links that form a triangle with the link, and the rest of the links that share a common node with the link. The contributions of these three types of links are reflected in the learned coefficients in Eq. (2). The average of each coefficient over all prediction steps is given in Table 2. In all networks except for Primary School, \(|\beta _1^*|>|\beta _2^*|>|\beta _3^*|\approx 0\). This means that the activity of a target link in the future is mainly influenced by the past activity of the link itself, slightly influenced by the activity of the neighboring links that form a triangle with the target link, and seldom affected by the activity of the other neighboring links. The predictive power of neighboring links that form a triangle with the target link may come from the nature of physical contact networks: contacts are often determined by physical proximity; two people that are close to a third but not yet close to each other are likely to already be in relatively close proximity.
One exception is the PrimarySchool, where \(\beta _2^*>\beta _1^*\). Table 2 shows the aggregated network of PrimarySchool has the largest clustering coefficientFootnote 1 in the aggregated network as shown in Table 2. In general, we find the contribution \(\beta _2^*\) of links that form a triangle with the target link tends to be more significant in temporal networks with a larger clustering coefficient cc.
Duration L of past observation
According to the definition of SD tendency of connection in Eq. (1), only the coefficients/contributions \(e^{-\tau (t-k)}\) of the previous 24 steps (3 steps) are larger than \(10^{-5}\) when \(\tau =0.5\) (\(\tau =5\)), out of \(L=T/2>1000\) previous steps observed. We wonder whether considering only a few previous steps instead of \(L=T/2\) steps would be sufficient for a good prediction. As shown in Fig. 4, the prediction accuracy of SD model when \(L=3\) and \(\tau =0.5\) is worse than that when \(L=T/2\) and \(\tau =0.5\). This suggests that although the contribution of each early state of a target link is small, the accumulated contribution of many early states improves the prediction accuracy. The prediction accuracy of the SD model when \(L=3\) and \(\tau =0.5\), whose computational complexity is extremely low, is still better or similar to that of Lasso Regression, reflecting the prediction power of recent states of a link.
The choice of L may influence the prediction accuracy of all models. Hence, we compare further the prediction accuracy of all models when \(L=T/4\) in Fig. 5. We find the same conclusion holds as that when \(L=T/2\): both SD and SCD models perform better than the baselines, and SCD performs better than SD model. Additionally, we observe a significant decrease in prediction accuracy when L decreases from \(L=T/2\) to \(L=T/4\) for both Lasso Regression and CDARN models, likely because these learning models need a sufficiently long period of observation for training. In contrast, the prediction accuracy remains relatively stable for the SD, SCD, Makrov, and CN models, despite the change in L. This suggests that the SD, SCD, Markov, and CN models are more resilient to variations in L compared to Lasso Regression and CDARN models.
Link prediction accuracy AUPR of all models when \(L=T/4\), and \(\tau =0.5\) in seven data sets. The prediction accuracy is averaged over 1000 prediction snapshots for all models except that the accuracy of the CDARN model is averaged over 100 prediction snapshots due to its computational complexity
Long-term prediction methods
Strategies to mitigate epidemics or information spreading are supposed to be carried out for a relatively long period instead of only one time step. Hence, predicting the temporal network in the long-term future is essential for the development of mitigating strategies.
The long-term prediction problem is to predict the temporal network in the long-term future within \([t+1,t+L^*]\) based on the network topology observed in the past L time steps within [\(t-L+1,t\)]. The number of contacts \(m(t+\Delta t)\) at each prediction step and the aggregated network over the whole time window [1, T] of each data set are known. We introduce two basic methods that adapt each short-term network prediction model for the long-term prediction task: recursive long-term prediction and repeated long-term prediction. The common neighbor model is not considered in view of its low performance in short-term prediction.
Recursive long-term prediction
In short-term prediction, the SD model differs from all the other models in the sense that SD model has only one parameter \(\tau \), which can be chosen arbitrarily from [0.5, 5] to achieve approximately the optimal performance, whereas parameters for the other models (Eq. 2 for SCD model, Eq. 3 for Lasso Regression, Eq. 7 for CDARN model, and transition matrix for Markov model) need to be trained from the network observed in the past. Hence, we will explain how to make recursive long-term predictions using these two kinds of models respectively.
For SD model, the SD connection tendency for each link at \(t+1\) can be obtained according to Eq. 1 based on the network observed in the past [\(t-L+1,t\)] and \(\tau =0.5\). Since the number of contacts \(m(t+1)\) is known, we predict the temporal network by considering the \(m(t+1)\) links with the highest connection tendency as contacts. The predicted network \(G_{t+1}'\) at \(t+1\) could be represented by the predicted state of each link \(\{x_1'(t+1),x_2'(t+1),\dots ,x_M'(t+1)\}\) at \(t+1\). The predicted network \(G_{t+1}'\) at \(t+1\) and the network observed within [\(t-L+2,t\)] will be used to compute the SD connection tendency of each link at \(t+2\) and to derive further the predicted network \(G_{t+2}'\) at \(t+2\), equivalently the \(m(t+2)\) contacts. The connection tendency of each link at each future step \(t+\Delta t\), where \(2\le \Delta t\le L^*\) is derived recursively using the network observed in [\(t+\Delta t-1-L,t\)] and network predicted in [\(t+1,t+\Delta t -1\)] according to
The SD connection tendency of each link and the given number of contacts at each future step \(t+\Delta t\) are used to predict the temporal network at that time step.
For SCD model, Lasso Regression, CDARN model, and Markov model, we train each model only once based on the network observed in the past L steps within [\(t-L+1,t\)] to obtain its parameters. Each trained model will be used to derive the activation tendency of each target link at \(t+1\) using the network observed at t. Then we predict the temporal network at \(t+1\) by considering the \(m(t+1)\) links with the highest connection tendency to be active. The same trained model will be applied recursively to derive the activation tendency at \(t+\Delta t\) using the network \(G_{t+\Delta t-1}'\) predicted at \(t+\Delta t-1\) and predict the network \(G_{t+\Delta t}'\) as the set of contacts along the \(m(t+\Delta t)\) links with the highest connection tendency.
Repeated long-term prediction
The repeated long-term prediction based on each of the aforementioned models is defined as follows. We firstly derive the connection tendency of each link at \(t+1\) in the same way as in short-term prediction based on the network observed within [\(t-L,t\)] using a given model. Then the connection tendency of each link at any prediction step \(t+\Delta t\) where \(\Delta t \in [2, L^*]\) is assumed to be the same as the connection tendency of that link at \(t+1\). Given the connection tendency of each link at any prediction step \(t+\Delta t\) where \(\Delta t \in [1, L^*]\), we predict the network \(G_{t+\Delta t}'\) by considering the \(m(t+\Delta t)\) links with the highest connection tendency to be active.
Our short-term prediction models can be applied thus either recursively or repeatedly to predict the network in the long-term future. The repeated long-term prediction assumes that the connection tendency of each link remains the same over the long-term prediction period. In contrast, the recursive long-term prediction uses both the observed network and predicted network to predict the network further in time. Hence, it possibly captures the evolving nature of the network over time but leads to accumulative prediction error over time.
Performance analysis in long-term prediction
In this section, we explore the performance of different models applied either repeatedly or recursively in long-term prediction and its relation with the memory property of temporal networks.
The prediction quality of any method is evaluated via the accuracy in 1) predicting the network at each prediction step within the prediction period [\(t+1, t+L^*\)], 2) predicting the weighted aggregated network over the prediction period and 3) reproducing the inter-event time distribution of contacts along a link within the prediction period. The accuracy in these three perspectives is, in general, desirable for long-term network prediction since the network per snapshot, the aggregated network, and the distribution of inter-event time of contacts along a link affect evidently spreading processes unfolding on the network (Scholtes et al. 2014; Vazquez et al. 2007; Newman 2003; Horváth and Kertész 2014).
The prediction length \(L^*\) is chosen as \(10\%T\), and the starting point \(t+1\) of each prediction period \([t+1,t+L^*]\) is sampled 1000 times from [\(T/2+1, 90\%T\)] with equal space, to illustrate our method.
Network snapshot
Model evaluation
Since the number of contacts \(m(t+\Delta t)\) in each prediction step \(t+\Delta t \in [t+1, t+L^*]\) is given, the number of contacts in the network predicted \(G_{t+\Delta t}'\) at time step \(t+\Delta t\) is the same that of the real-world network (ground-truth) \(G_{t+\Delta t}\). Hence, we evaluate the accuracy of the network predicted at each time step \(t+\Delta t \in [t+1, t+L^*]\) via recall, the number of contacts that exist both in the predicted network snapshot \(G_{t+\Delta t}'\) and the real-world network \(G_{t+\Delta t}\) divided by \(m(t+\Delta t)\).
Firstly, we compare the prediction accuracy recall of each model using the recursive and repeated prediction methods respectively, as a function of prediction time gap \(\Delta t\), the number of time steps that the prediction step \(t+\Delta t\) is ahead of the observation window \([t-L+1,t]\). For each \(\Delta t \in [1, L^*]\), the prediction accuracy recall is averaged over the 1000 samples of the prediction period. From Fig. 6 (for network Hospital) and Fig. 11 (for other networks) in the Appendix, we could not recognize any difference between the repeated and recursive methods for SD and SCD models, while Lasso Regression, CDARN, and Markov model tend to perform better using the repeated prediction method.
The similar performance of the SD model when it is applied recursively and repeatedly can be explained by the following. When SD model is applied recursively to predict the network at step \(t+1\), the \(m(t+1)\) links with the highest connection tendency are predicted to have contacts, which in return makes their connection tendency at \(t+2\) higher than the other links. In this way, the ranking of links in connection tendency at each prediction time step within [\(t+1, t+L^*\)] remains nearly the same, as in the SD model applied repeatedly. At any prediction step, it is the ranking of links in connection tendency that decides the predicted network.
The prediction accuracy of Lasso Regression, CDARN model, and Markov model is low in short-term prediction. When we use the network predicted by any of these models at \(t+\Delta t\) to predict a network at \(t+\Delta t+1\) using the recursive prediction method, the prediction error is accumulated. This is likely why these three models tend to perform better using the repeated prediction method. We consider the repeated prediction method in the rest analysis of this section.
Secondly, we compare the performance of all models using the repeated prediction method in each data set. Figure 7 shows the average Recall decreases as the prediction gap \(\Delta t\) increases for all models in all temporal networks. In general, SCD performs the best among all models in all data sets when \(\Delta t=1\), as observed in the short-term prediction in “Model evaluation” section. When \(\Delta t>2\), SD achieves roughly the best prediction accuracy.
The prediction accuracy, Recall, for SD, SCD, Lasso Regression, CDARN, and Markov model applied repeatedly, respectively in seven temporal networks at each prediction step \(t+\Delta t\). In the Random model, the \(m(t+\Delta t)\) predicted contacts are randomly chosen at the prediction step \(t+\Delta t\)
Prediction accuracy in relation to network memory
As SD achieves roughly the best prediction accuracy among all models, we further explore the relation between the prediction accuracy of SD model and the memory property of temporal networks, aiming to understand in which kind of temporal networks the SD model predicts better.
The prediction accuracy recall of SD model in general decreases as the prediction time gap \(\Delta t\) increases. The decrease is faster when \(\Delta t\) is smaller, as shown in Fig. 7. We will focus on the prediction gap within [1,\(1\%T\)] since the prediction accuracy is too low when \(\Delta t>1\%T\).
Intuitively, it’s probably difficult to predict a temporal network if the network has a weak memory, i.e., the network observed at different times shares low similarity, especially for models like SD and SCD that utilize network memory in network prediction. Hence, we explore the relation between the prediction accuracy of the SD model and the memory property of the temporal network. Figure 8a shows the recall of SD model as a function of the normalized prediction time gap \(\frac{\Delta t}{1\%T}\). Figure 8b illustrates the average Jaccard similarity of two snapshots of a temporal network when their time lag equals \(\frac{\Delta t}{1\%T}\). We observe that approximately the prediction accuracy tends to be better in networks with stronger memory (Jaccard similarity). For example, the recall is the largest (smallest) in LH10 (PrimarySchool, Workplace, and Hospital), whose Jaccard similarity is also the largest (smallest). Furthermore, the decay rate of the prediction accuracy with prediction time gap \(\frac{\Delta t}{1\%T}\) in Fig. 8 seems to be related to the decay rate of Jaccard similarity with the time lag \(\frac{\Delta t}{1\%T}\) in Fig. 8b. The decay rate of recall within the interval [\(\frac{1}{1\%T}\), \(\frac{\Delta t}{1\%T} \)] is defined as \(\frac{Recall(\frac{\Delta t}{1\%T})-Recall(\frac{1}{1\%T})}{\frac{\Delta t}{1\%T}-\frac{1}{1\%T}}\), and the same definition holds for the decay rate of Jaccard similarity. Figure 8c and d show the decay rate of recall and JS respectively within \([\frac{1}{1\%T},\frac{\Delta t}{1\%T}]\) as a function of \(\frac{\Delta t}{1\%T}\). We find the ranking of the real-world networks in the decay rate of recall approximates that in decay rate of JS at any \(\frac{\Delta t}{1\%T}\). This means that the prediction accuracy of SD model decays fast in networks with fast decaying memory.
Aggregated network
We evaluate further the precision of the predicted aggregated network \(G'_{w}(t+1, t+L^*)\), which is the network predicted per time step aggregated within the prediction period \([t+1,t+L^*]\). The aggregated network \(G_{w}(t+1, t+L^*)\) of the real-world network is constructed as follows. Two nodes are connected by a link in \(G_{w}(t+1, t+L^*)\), if the two nodes have at least a contact in the real-world network within [\(t+1, t+L^*\)]. Moreover, the weight of each link is defined as the number of contacts along the link within [\(t+1, t+L^*\)]. The weighted aggregated network \(G_{w}(t+1, t+L^*)\) could be represented by a weighted adjacency matrix \(A_{G_{w}(t+1, t+L^*)}\) whose element in row i and column j is the number of contacts between node i and node j within [\(t+1, t+L^*\)]. Similarly, we can construct the predicted aggregated network \(G'_{w}(t+1, t+L^*)\), a weighted network, based on the network predicted within [\(t+1, t+L^*\)] and represent it by the weighted adjacency matrix \(A'_{G_{w}(t+1, t+L^*)}\). Note that the number of contacts in the predicted network is the same as that in the real-world network at any prediction step.
We evaluate the accuracy in predicting the aggregated network via the generalized recall (\(Recall_{wei}\)):
which measures the extent that the two weighted aggregated networks \(G'_{w}(t+1, t+L^*)\) and \(G_{w}(t+1, t+L^*)\) overlap.
We first compare the generalized recall of each model using the recursive and repeated prediction methods respectively, as a function of the prediction period \(L^*\). Instead of considering \(L^*=10\%T\) as in the previous sections, we consider the general scenario where \(L^*\) is a variable \(L^*\in [1, 10\%T]\). We have observed the same when evaluating the prediction accuracy per snapshot and per aggregated network. We could not recognize any difference in prediction accuracy between the repeated and recursive methods for both SD and SCD models, while Lasso Regression, CDARN, and Markov model tend to perform better using the repeated prediction method (see Fig. 12 in Appendix).
When all models are applied repeatedly, SD achieves roughly the best prediction accuracy (see Fig. 13 in Appendix). The SD model tends to predict better in networks with a strong memory, and the prediction accuracy of SD model decays fast in networks with fast-decaying memory as shown in Fig. 14 in Appendix.
The distribution of inter-event time
The scaled probability density function \(\Lambda _0f_{\Lambda }(x)\) of the inter-event times derived from each group of links as a function of \(x/\Lambda _0\), where \(\Lambda _0\) is the average inter-event time of the same group, in each real temporal network (circle) and network predicted by SD model (asterisk). Different colors indicate the distribution derived from different groups of links. Links are sorted into 10 groups with a logarithmically increasing width based on their number of contacts
The inter-event time (\(\Lambda \)) is the time between two consecutive contacts of a link. Firstly, we derive the inter-event distribution of a real-world (predicted) temporal network within \([t+1, t+L^*]\) from the inter-event times collected from all links that have at least two contacts within \([t+1, t+L^*]\). The objective is to explore whether the predicted network and corresponding real-world network during the prediction period have a similar inter-event distribution. Figure 9 (Fig. 15 in Appendix) shows the inter-event time distribution in each real-world network and the corresponding predicted networks when each model is applied repeatedly (recursively). In each data set, the networks predicted by various models possess almost the same heterogeneous inter-event time distribution, which can be explained as follows.
For repeated prediction, the tendency for each link to be active at each prediction time step \(t+\Delta t\) (\(\Delta t \in [2, L^*]\)) is the same as its activation tendency at \(t+1\), and \(m(t+\Delta t)\) links with the highest connection tendency are considered to have contacts at \(t+\Delta t\). When no links have the same rank in tendency, the total number of contacts in the network at each time step over time decides the distribution of inter-event time. The link whose connection tendency is the rth largest among all links will be active at a prediction step if the total number of contacts at that prediction step is no less than r. Links with high (low) link tendency are likely to be active (inactive) at each time step, leading to many (few) small (large) inter-event times, which leads to a heterogeneous distribution of inter-event time. The distribution of inter-event time observed in predicted networks approximates roughly the distribution in the corresponding real-world network.
Still, this does not mean that predicted networks have the burstiness of inter-event time as observed in real-world networks: contacts between a pair of nodes usually occur in bursts of many contacts close in time followed by a long period of inactivity. To systematically explore the burstiness property of inter-event time along a link, we group links based on their total number of contacts within \([t+1,t+L^*]\) as in the method of Goh and Barabási (2008) and derive the probability density function \(f_{\Lambda }(x)\) of inter-event times (\(\Lambda \)) collected from all links in each group. Figure 10 shows the scaled probability density function \(\Lambda _0f_{\Lambda }(x)\) for each group of links as a function of \(x/\Lambda _0\), where \(\Lambda _0\) is the average inter-event time of the same group. As shown in Fig. 10, the distributions of inter-event time of all groups in both the real-world network and the network predicted by SD model follow a similar heavy-tail distribution. Networks predicted by our SD model reproduce approximately the burstiness of inter-event times as observed in real-world networks.
Conclusion
In this work, we propose two network-based models to solve the short-term temporal network prediction problem. The design of these models is motivated by the time-decaying memory observed in temporal networks. The proposed self-driven (SD) model and self- and cross-driven (SCD) model predict a link’s future activity based on the past activities of the link itself, and also of the neighboring links, respectively. Both models perform better than the baseline models. Interestingly, we find that SD and SCD models perform better in temporal networks with a stronger memory.
The SCD model reveals that a link’s future activity is mainly determined by (the past activities of) the link itself, moderately by neighboring links that form a triangle with the target link, and hardly by other neighboring links. However, if the temporal network has a high clustering coefficient in its aggregated network, the contribution of the neighboring links that form a triangle with the target link tends to be significant and possibly dominant.
We further apply these short-term network prediction models either recursively or repeatedly to make the long-term network prediction., that is the prediction of the temporal network in the long-term future based on the network topology observed in the past and given the number of contacts at each prediction step. The accuracy of long-term prediction accuracy is evaluated from the perspective of the network predicted per snapshot and the predicted aggregated network. The repeated method performs, in general, better for all prediction models. This is likely because the iterative method uses both the observed network and the predicted network which is not precise enough to predict the network further in time. In general, SD model performs the best among all models in all data sets. It predicts better in networks with a stronger memory. The prediction accuracy decays as the prediction step is further ahead in time and this decay speed is positively correlated with the decay speed of network memory. Finally, networks predicted by various models respectively have a heterogeneous distribution of inter-event time similar to real-world networks, and also the burstiness of inter-event times of a link.
Our work is a starting point to explore network-based temporal network prediction methods. Our findings may shed light on the modeling of the formation of temporal networks which is crucial in understanding and controlling the dynamics of and on temporal networks. Our finding that activities of neighboring links that form a triangle with a target link have prediction power on the connection of the target link may suggest that higher-order events (Ceria and Wang 2023; Benson et al. 2018) like triangles in each network snapshot may contribute to the prediction of (pairwise and higher-order) temporal networks. It is also interesting to evaluate the prediction accuracy of network-based prediction methods in comparison with state-of-the-art machine learning methods that target at high accuracy.
Availability of data and materials
The data sets used are publicly available. More information can be found in the corresponding references.
Notes
The clustering coefficient of a network is the probability that two neighbors of a node are connected.
References
Ahmed NM, Chen L, Wang Y, Li B, Li Y, Liu W (2016) Sampling-based algorithm for link prediction in temporal networks. Inf Sci 374:1–14
Benson AR, Abebe R, Schaub MT, Kleinberg J (2018) Simplicial closure and higher-order link prediction. PNAS 115:E11221–E11230
Ceria A, Wang H (2023) Temporal-topological properties of higher-order evolving networks. Sci Rep 13:5885
Cui P, Wang X, Pei J, Zhu W (2017) A survey on network embedding. IEEE Trans Knowl Data Eng 31:833–852
Davis J, Goadrich M (2006) The Relationship between Precision-Recall and ROC Curves. In: The 23rd international conference on machine learning, vol 8. Association for Computing Machinery, New York, pp 233–240
Dhote Y, Mishra N, Sharma S (2013) Survey and analysis of temporal link prediction in online social networks. In: Proceedings of the 2013 international conference on advances in computing, communications and informatics (ICACCI), Mysore, India, pp 1178–1183
Génois M, Barrat A (2018) Can co-location be used as a proxy for face-to-face contacts? EPJ Data Sci 7:1–18
Génois M, Barrat A (2018) Can co-location be used as a proxy for face-to-face contacts? EPJ Data Sci 7:11
Goh KI, Barabási A-L (2008) Burstiness and memory in complex networks. EPL 81:48002
Holme P (2015) Modern temporal network theory: a colloquium. Eur Phys J B 88:234
Holme P, Saramäki J (2012) Temporal networks. Phys Rep 519:97–125
Horváth DX, Kertész J (2014) Spreading dynamics on networks: the role of burstiness, topology and non-stationarity. New J Phys 16:073037
Isella L, Stehlé J, Barrat A, Cattuto C, Pinton J-F, den Broeck WV (2011) What’s in a crowd? Analysis of face-to-face behavioral networks. J Theor Biol 271:166–180
Jo H-H, Perotti JI, Kaski K, Kerteéz J (2015) Correlated bursts and the role of memory range. Phys Rev E 92:022814
Kazemi SM, Goel R, Jain K, Kobyzev I, Sethi A, Forsyth P, Poupart P (2020) Representation learning for dynamic graphs: a survey. J Mach Learn Res 21:1–73
Kemeny JG, Snell JL (1976) Markov chains. Springer-Verlag, New York
Kumar A, Singh SS, Singh K, Biswas B (2020) Link prediction techniques, applications, and performance: a survey. Phys A: Stat Mech 553:124289
Kumar S, Zhang X, Leskover J (2019) Predicting dynamic embedding trajectory in temporal interaction networks. In: Proceedings of the 25th ACM SIGKDD international conference on knowledge discovery & data mining. Association for Computing Machinery, Anchorage, AK, USA, pp 1269–1278
Liben-Nowell D, Kleinberg J (2003) The link prediction problem for social networks. In: The twelfth international conference on information and knowledge management, vol 4. Association for Computing Machinery, New York, , pp 556–559
Li X, Du N, Li H, Li K, Gao J, zhang A (2014) A deep learning approach to link prediction in dynamic networks. In: 2014 SIAM international conference on data mining, pp 289–297
Li X, Liang W, Zhang X, Liu X, Wu W (2019) A universal method based on structure subgraph feature for link prediction over dynamic networks. In: 39th International Conference on Distributed Computing Systems, pp. 1210-1220. IEEE, Dallas, USA
Lü L, Zhou T (2011) Link prediction in complex networks: a survey. Phys A: Stat Mech 390:1150–1170
Ma Y, Tang J (2021) Deep learning on graphs. Cambridge University Press, Cambridge
Mastrandrea R, Fournet J, Barrat A (2015) Contact patterns in a high school: a comparison between data collected using wearable sensors, contact diaries and friendship surveys. PLoS ONE 10:e0136497
Masuda N, Lambiotte R (2016) A guide to temporal networks. In: Series on complexity science, vol 4. World scientific, Europe, p 252
Newman MEJ (2003) The structure and function of complex networks. SIAM Rev 45:167–256
Paranjape A, Benson AR, Leskovec J (2017) Motifs in temporal networks. In: Tenth ACM international conference on Web Search and Data Mining. Association for Computing Machinery, Cambridge, pp 601–610
Pareja A, Domeniconi G, Chen J, Ma T, Suzumura T, Kanezashi H, Kaler T, Schardl TB, Leiserson CE (2020) EvolveGCN: evolving graph convolutional networks for dynamic graphs. In.: Proceedings of the AAAI conference on artificial intelligence, vol 34. AAAI Press, California, pp 5363–5370
Rahman M. Saha TK, Hasan MA, Xu KS, Reddy CK (2018) DyLink2Vec: effective feature representation for link prediction in dynamic networks. ArXiv
Rossi RA, Ahmed K (2015) The network data repository with interactive graph analytics and visualization. In: The twenty-ninth AAAI conference on artificial intelligence. AAAI Press, Palo Alto, California, pp 4292–4293
Saramäki J, Moro E (2015) From seconds to months: an overview of multi-scale dynamics of mobile telephone calls. Eur Phys J B 88:164
Scholtes I, Wider N, Pfitzner R, Garas A, Tessone CJ, Schweizer F (2014) Causality-driven slow-down and speed-up of diffusion in non-Markovian temporal networks. Nat Commun 5:5024
Scholz C, Atzmueller M, Barrat A, Cattuto C, Stumme G (2013) New insights and methods for predicting face-to-face contacts. In: Proceedings of the seventh international AAAI conference on weblogs and social media, vol 7(1), pp 563–572
Stehlé J, Voirin N, Barrat A, Cattuto C, Isella L, Pinton JF, Quaggiotto M, Van den Broeck W, Régis C, Lina B et al (2011) High-resolution measurements of face-to-face contact patterns in a primary school. PLoS ONE 6:e23176
Tang D, Du W, Shekhtman L, Wang Y, Havlin S, Cao X, Yan G (2020) Predictability of real temporal networks. Natl Sci Rev 7:929–937
Tsugawa S, Ohsaki H (2013) Effectiveness of link prediction for face-to-face behavioral networks. PLoS ONE 8(12):e81727
Vanhems P, Barrat A, Cattuto C, Pinton JF, Khanafer N, R’egis C, Kim Ba, Comte B, Voirin N, (2013) Estimating potential infection transmission routes in hospital wards using wearable proximity sensors. PLoS ONE 8:e73970
Vazquez A, Rácz B, Lukács A, Barabási A-L (2007) Impact of non-Poissonian activity patterns on spreading processes. Phys Rev Lett 98:158702
Wang Y, Chang Y-Y, Liu Y, Leskovec J, Li P (2021) Inductive representation learning in temporal networks via causal anonymous walks. arXiv:2101.05974
Williams OE, Mazzarisi P, Lillo F, Latora V (2022) Non-markovian temporal networks with auto- and cross-correlated link dynamics. Phys Rev E 105:034301
Wu L, Cui P, Pei J, Zhao L (2022) Graph neural networks: foundations, frontiers, and applications. Springer, Singapore
Xu HH, Zhang LJ (2013) Application of link prediction in temporal networks. Adv Mater Res 2231:756–759
Xu D, Ruan C, Korpeoglu E, Kumar S, Achan K (2020) Inductive representation learning on temporal graphs. arXiv:2002.07962
Yu W, Cheng W, Aggarwal CC, Chen H, wang W (2017) Link prediction with spatial and temporal consistency in dynamic networks. In: The twenty-sixth international joint conference on artificial intelligence. International Joint Conferences on Artificial Intelligence, Melbourne, Australia, pp 3343–3349
Zhan X-X, Li Z, Masuda N, Holme P, Wang H (2020) Susceptible-infected-spreading-based network embedding in static and temporal networks. EPJ Data Sci 9:30
Zhou L, Yang Y, Ren X, Wu F, Zhuang Y (2018) Dynamic network embedding by modeling triadic closure process. In: 32nd AAAI conference on artificial intelligence. AAAI Press, California, , pp 571–578
Zou L, Wang C, Zeng A, Fan Y, Di Z (2021) Link prediction in growing networks with aging. Soc Netw 65:1–7
Zou L, Zhan X-X, Sun J, Hanjalic A, Wang H (2022) Temporal network prediction and interpretation. IEEE Trans. Netw. Sci. Eng. 9:1215–1224
Zou L, Wang A, Wang H (2023) Memory based temporal network prediction. In: Complex networks and their applications XI. Springer, Cham, pp 661–673
Funding
The authors would like to thank the support of the Netherlands Organisation for Scientific Research NWO (TOP Grant no. 612.001.802, project FORT-PORT no. KICH1.VE03.21.008), NExTWORKx, a collaboration between TU Delft and KPN on future telecommunication networks and the China Scholarship Council.
Author information
Authors and Affiliations
Contributions
LZ and HW designed the research and wrote the manuscript. LZ, AC, and HW analyzed the results. LZ performed the experiments and prepared all the figures and tables. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: The prediction accuracy in long-term network prediction
Appendix: The prediction accuracy in long-term network prediction
See Figs. 11, 12, 13, 14 and 15.
a The accuracy, \(Recall_{wei}\), of SD model applied repeatedly in predicting the aggregated network over \([t+1,t+\Delta t]\), b the Jaccard similarity (JS), c the decay rate of \(Recall_{wei}\) and d the decay rate of JS as a function of the normalized prediction time gap \(\frac{\Delta t}{1\%T}\)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zou, L., Ceria, A. & Wang, H. Short- and long-term temporal network prediction based on network memory. Appl Netw Sci 8, 76 (2023). https://doi.org/10.1007/s41109-023-00597-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41109-023-00597-w