Unsupervised relational inference using masked reconstruction

Abstract

Problem setting

Stochastic dynamical systems in which local interactions give rise to complex emerging phenomena are ubiquitous in nature and society. This work explores the problem of inferring the unknown interaction structure (represented as a graph) of such a system from measurements of its constituent agents or individual components (represented as nodes). We consider a setting where the underlying dynamical model is unknown and where different measurements (i.e., snapshots) may be independent (e.g., may stem from different experiments).

Method

Our method is based on the observation that the temporal stochastic evolution manifests itself in local patterns. We show that we can exploit these patterns to infer the underlying graph by formulating a masked reconstruction task. Therefore, we propose GINA (Graph Inference Network Architecture), a machine learning approach to simultaneously learn the latent interaction graph and, conditioned on the interaction graph, the prediction of the (masked) state of a node based only on adjacent vertices. Our method is based on the hypothesis that the ground truth interaction graph—among all other potential graphs—allows us to predict the state of a node, given the states of its neighbors, with the highest accuracy.

Results

We test this hypothesis and demonstrate GINA’s effectiveness on a wide range of interaction graphs and dynamical processes. We find that our paradigm allows to reconstruct the ground truth interaction graph in many cases and that GINA outperforms statistical and machine learning baseline on independent snapshots as well as on time series data.

Introduction

Stochastic dynamical systems in which local interactions give rise to complex emerging phenomena are ubiquitous in nature and society. However, their analysis remains challenging. Traditionally, the analysis of complex systems is based on models of individual components. This reductionist perspective reaches its limitations when the interactions of the individual components—not the components themselves—become the dominant force behind a system’s dynamical evolution. Inferring the functional organization of a complex system from measurements is relevant for their analysis (Fornito et al. 2015; Prakash et al. 2012; Amini et al. 2016; Finn et al. 2019), design (Zitnik et al. 2018; Hagberg and Schult 2008; Memmesheimer and Timme 2006), control (Gu et al. 2015; Großmann et al. 2020), and prediction (Kipf et al. 2018; Zhang et al. 2019).

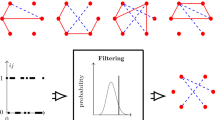
In this work, we focus on the internal interaction structure (i.e., graph or network) of a complex system. We propose a machine learning approach to infer this structure based on observational data of the nodes (i.e., components or constituent agents). We refer to these observations as snapshots and assume that the observable states of all components are measured simultaneously (see Fig. 1 for an overview). However, we make no prior assumption about the relationship between snapshots. Specifically, snapshots are not labelled with time stamps. They may be taken from different experiments with varying initial conditions.

Most recent work on graph inference focuses on time series data, where observations are time-correlated and the interaction graph is inferred from the joint time evolution of the node-states (Zhang et al. 2019; Kipf et al. 2018). Naturally, time series data contains more information on the system’s internal interactions than snapshot data. However, in many cases, such data is not available: In some cases, one has to destroy a system to access its components (e.g., slice a brain (Rossini et al. 2019), observe a quantum system (Martínez et al. 2019), or terminate a cell (Chan et al. 2017)). Sometimes, the relevant time scale of the system is too small (e.g., in particle physics) or too large (e.g., in evolutionary dynamics) to be observed. Often, there is a trade-off between spatial and temporal resolution of a measurement (Sarraf and Sun 2016). And finally, measurements may be temporally decoupled due to large observation intervals and thus become unsuitable for methods that exploit correlations in time. Yet, machine learning techniques for graph inference from independent data remain underexplored in the literature.

Fig. 1

Schematic illustration the problem setting. We are interested in inferring the latent (unweighted and undirected) interaction graph from observational data of the process

In contrast to many state-of-the-art approaches, our method makes no prior assumptions about the dynamical laws. Conceptually, our analysis is founded on identifying patterns within the snapshots. These patterns are spatial manifestations of the temporal co-evolution of neighboring nodes. Thus, they carry information about the underlying connectivity.

We propose an approach based on ideas recently popularized for time series-based network inference (Zhang et al. 2018; Kipf et al. 2018). It provides an elegant way of formalizing the graph inference problem with minimal parametric assumptions on the underlying dynamical model. The core assumption is that the interaction graph “best describing” the observed data is the ground truth. In the time series setting, this means that it enables time series forecasting.

Here, we assume that time series data is not available. Hence, we aim at finding the graph that best enables us to predict a node’s state based on its direct neighborhood within a snapshot (not at future times). This technique is commonly referred to as masking (Mishra et al. 2020). That is, we mask (i.e., erase) the state of a node and then try to recover it by looking at its neighbors. To this end, we use a prediction model to learn a node’s observable state (i.e., the node-state) given the joint state of all adjacent nodes. Then we maximize the prediction accuracy by jointly optimizing the interaction graph and the prediction model. In essence, we assume that the information shared between a node and its complete neighborhood is higher in the ground truth graph than in other potential graphs.

However, in a trivial implementation, the network that enables the best node-state prediction is the complete graph because it provides all information available in a given snapshot. This necessitates a form of regularization in which edges that are present but not necessary reduce prediction quality. We do this using a counting neighborhood aggregation scheme that acts as a bottleneck of information flow.

For an efficient solution to the graph inference problem, we propose GINA. GINA is inspired by graph neural network architectures and combines a simple neighborhood aggregation and an efficient weight-sharing mechanism between nodes with a differentiable graph representation. This enables the application of our methods to systems with hundreds of nodes. GINA is both, model-free, (apart from the inductive biases from the constituent neural networks, it can learn arbitrary patterns in snapshots) and threshold-free (implicit thresholding is done during training, no arbitrary edge binarization is needed afterwards). However, the way the dynamics is encodes is inspired by the theory of multi-state processes. These provide a powerful description for many relevant dynamical models of interacting systems (Gleeson 2011; Fennell and Gleeson 2019) (a similar model-class is studied under the name Stochastic Automata Networks (Langville and Stewart 2004; Plateau and Stewart 2000)).

In summary, we conceptualize and test the hypothesis that network reconstruction can be formulated as a prediction task. In this contribution (i) we propose a masking technique to formalize the prediction problem, (ii) propose a suitable neighborhood aggregation mechanism that automatically acts as a regularization mechanism, (iii) develop the neural architecture GINA to efficiently solve the prediction and reconstruction task, and (iv) we test our hypothesis using synthetically generated snapshots using various combinations of graphs and diffusion models.

Foundations and problem formulation

Fig. 2

Schematic architecture using 4-node graph with ${\mathcal {S}} = \{(0,1),(1,0)\}$. Nodes are color-coded, node-states are indicated by the shape (filled: I, blank: S). First, we compute ${\textbf{m}}_i$ for each node $v_i$ (stored as ${\textbf{M}}$), then we feed each ${\textbf{m}}_i$ into a predictor that predicts the original state

Notation

The goal is to find the latent interaction graph of a complex system with n agents/nodes. A graph is represented as a binary adjacency matrix ${\textbf{A}}$ of size $n \times n$ (with node set $\{v_i \mid 1 \le i \le n \}$). An entry $a_{ij} \in \{0,1\}$ indicates the presence ($a_{ij}=1$) or absence ($a_{ij}=0$) of an edge between node $v_i$ and $v_j$. We assume that ${\textbf{A}}$ is symmetric (the graph is undirected) and the diagonal entries are all zero (the graph has no self-loops). We use ${\textbf{A}}^*$ to denote the ground truth matrix.

Each snapshot assigns a node-state to each node. The finite set of possible node-states is denoted ${\mathcal {S}}$. For convenience, we assume that the node-states are represented using one-hot encoding. For instance, in an epidemic model a node might be susceptible or infected. Since there are two node-states, we use ${\mathcal {S}} = \{(0,1),(1,0)\}$. Each snapshot ${\textbf{X}} \in \{0,1\}^{n \times |{\mathcal {S}}| }$ can then conveniently be represented as a matrix with n rows, each row describing the corresponding one-hot encoded node-state (cf. Fig. 2 left). We use ${\mathcal {X}}$ to denote the set of independent snapshots. We make no specific assumption about the underlying distribution or process behind the snapshots or their relationship to another.

For a node $v_i$ (and fixed snapshot), we use ${\textbf{m}}_i \in {\mathbb {Z}}^{|{\mathcal {S}}|}_{\ge 0}$ to denote the (element-wise) sum of all neighboring node-states, referred to as neighborhood counting vector. Let’s return to our previous example, where ${\mathcal {S}} = \{(1,0),(0,1)\}$. The state ${\textbf{m}}_i=(10,13)$ tells us that node $v_i$ has 10 susceptible ((1, 0)) and 13 infected ((0, 1)) neighbors. Note that the sum over ${\textbf{m}}_i$ is the degree (i.e., number of neighbors) of that node (here, $10+13=23$). The set of all possible neighborhood counting vectors is denoted by ${\mathcal {M}} \subset {\mathbb {Z}}^{|{\mathcal {S}}|}_{\ge 0}$. We can compute neighborhood counting vectors of all nodes using ${\textbf{M}} = {\textbf{A}}{\textbf{X}}$, where the matrix ${\textbf{M}}$ is such that its i-th row equals ${\textbf{m}}_i$ (cf. Fig. 2 center).

Idea

We feed each counting vector ${\textbf{m}}_i$ into a machine learning model that predicts (resp. recovers) the original (masked) state of $v_i$ in that snapshot. Specifically, for each node $v_i$, we learn a function $F_{i}: {\mathcal {M}} \rightarrow \texttt {Cat}({\mathcal {S}})$, where $\texttt {Cat}({\mathcal {S}})$ denotes the set of all probability distributions over ${\mathcal {S}}$ (in the sequel, we make the mapping to a probability distribution explicit by adding a $\texttt {Softmax}(\cdot )$ function). To evaluate $F_{i}(\cdot )$, we use some loss function to quantify how well the distribution predicts the true state and minimize this prediction loss. Practically, we assume that $F_{i}(\cdot )$ is implemented using a neural network. Hence, we assume that $F_{i}(\cdot )$ is fully parameterized by node-dependent parameters $\theta _i$ (e.g., in a NN, $\theta _i$ contains the weights and biases of all layers). For simplicity, we still write $F_{i}(\cdot )$ instead of $F_{\theta _i}(\cdot )$. We also simply use ${\theta }=\{\theta _1, \dots , \theta _n\}$ to denote the weights for all nodes. We define ${F}_{\theta }(\cdot )$ as a node-wise application of $F_{i}(\cdot )$, that is,

$$\begin{aligned} F_{\theta }({{\textbf {m}}}_1, {{\textbf {m}}}_2, \dots , {{\textbf {m}}}_n) = \big (F_{1}({{\textbf {m}}}_1), F_{2}({{\textbf {m}}}_2), \dots ,F_{n}({{\textbf {m}}}_n) \big ) \;\;. \end{aligned}$$

(1)

The hypothesis is that the ground truth adjacency matrix ${\textbf{A}}^*$ provides the best foundation for $F_{i}(\cdot )$, ultimately leading to the smallest prediction loss. Under this hypothesis, we can use the loss as a surrogate for the accuracy of candidate ${\textbf{A}}$ (compared to the ground truth graph). The number of possible adjacency matrices of a system with n nodes (assuming no self-loops and symmetries) is $2^{n(n-1)/2}$. Thus, it is hopeless to simply try all possible adjacency matrices. Hence, we additionally assume that smaller distances between ${\textbf{A}}$ and ${\textbf{A}}^*$ (we call this graph loss) lead to smaller prediction losses. This way, the optimization becomes feasible and we can follow the surrogate loss in order to arrive at ${\textbf{A}}^*$.

Masked reconstruction

Next, we formulate the graph inference problem using a simple neural network, denoted $\psi (\cdot )$, which loosely resembles an autoencoder architecture: For each snapshot ${{\textbf {X}}}$, we predict the node-state of each node using only the neighborhood of that node. Then, we compare the prediction with the actual (known) node-state. The model $\psi (\cdot )$ can be seen as a elementary graph neural network (as discussed in the next section).

For a given adjacency matrix (graph) ${\textbf{A}} \in \{0,1\}^{n\times n}$ and MLP parameters $\theta$, we define $\psi (\cdot )$, applied to a snapshot ${\textbf{X}} \in \{0,1\}^{n \times |{\mathcal {S}}|}$ as:

$$\begin{aligned}&\psi _{\theta ,{\textbf{A}}}: \{0,1\}^{ n\times |{\mathcal {S}}|} \rightarrow {\mathbb {R}}^{n \times |{\mathcal {S}}|} \\&\psi _{\theta ,{\textbf{A}}}: {\textbf{X}} \mapsto \texttt {Softmax} \big (F_{\theta }( {\textbf{A}}{\textbf{X}})\big ) \;, \end{aligned}$$

(2)

where $\texttt {Softmax} (\cdot )$ and $F_{\theta }(\cdot )$ are applied row-wise. Thus, $\psi _{\theta ,{\textbf{A}}}({\textbf{X}})$ results in a matrix where each row corresponds to a node and models a distribution over node-states. Similar to the auto-encoder paradigm, input and output are of the same form and the network learns to minimize the difference. The absence of self-loops in ${\textbf{A}}$ is critical as it means that the actual node-state of a node is not part of its own neighborhood aggregation (i.e., it is masked). As we want to predict a node’s state, the state itself cannot be part of the input.

We will refer to the matrix multiplication ${\textbf{A}}{\textbf{X}}$ as graph layer and to the application of $\texttt {Softmax}(F_{\theta }( \cdot ))$ as prediction layer.

Relationship to GNN architectures

The function $\psi (\cdot )$ can be seen as a single-layer graph neural network (GNN). GNNs are the de-facto standard machine learning method to process graph-structured data. A GNN can take graphs of arbitrary size as input. The output typically fulfills some form of invariance to the node-ordering of the input (e.g., two isomorphic graphs might be guaranteed to produce the same output). Seminal work in their development was done by Duvenaud et al. (2015) who proposed an elementary GNN architecture to learn representations of molecular graphs and by Kipf and Welling (2016) who provide additional theoretical insights and an efficient solution of the graph convolution operator to learn node representations.

Most modern GNN architectures follow the message-passing scheme developed by Gilmer et al. (2017). Each layer performs an aggregate$(\cdot )$ and a combine$(\cdot )$ step. The aggregate$(\cdot )$ step computes a neighborhood embedding based on a permutation-invariant function of all neighboring nodes. The combine$(\cdot )$ step combines this embedding with the actual node-state. In our architecture, the aggregation-step is the element-wise sum (given by the multiplication of the adjacency matrix and the neighborhood counting matrix). In principle, other permutation-invariant aggregation functions like the element-wise mean or maximum/minimum would also be possible. We choose a sum because it corresponds to the multi-state paradigm (Gleeson 2011; Fennell and Gleeson 2019), empirically works well, and is also more informative than comparable aggregators. Importantly, the combine$(\cdot )$ step needs to purposely ignore the node-state (in order for the prediction task to make sense).

We also only perform a single application of the graph layer on purpose, which means that only information from the immediate neighborhood can be used to predict a node-state. Recall that we define the ground truth network such that interactions only happen along edges. While using n-hop neighborhoods would increase the network’s predictive power, it would be detrimental to graph reconstruction. Another possibility to increase the accuracy of the prediction is by learning attention weights for each individual neighbor of a node (instead of simply using a sum-aggregation). The problem with that is that a variable interaction strength necessities an (arbitrary) thresholding to get a binarized adjacency matrix. Using a simple sum enforces that edges that are present, but not necessary, hurt the prediction performance because the network cannot learn to ignore these.

It is also worth noticing that $F_{i}( \cdot )$ is specific to node $v_i$ (hurting the permutation-equivariance that is typically guaranteed by GNNs). This is possible because the snapshots identify each node unambiguously. However, the aggregation function needs to be permutation-invariant following our premise that a node’s neighbors are only distinguishable by their respective node-states.

Prediction loss

We assume a loss function $L(\cdot )$ that is applied independently to each snapshot:

$$\begin{aligned}&L: \{0,1\}^{ n\times |{\mathcal {S}}|} \times {\mathbb {R}}^{n \times |{\mathcal {S}}|} \rightarrow {\mathbb {R}} \end{aligned}$$

(3)

The prediction loss L compares the input (actual node-states) and output (predicted node-states) of $\psi _{\theta ,{\textbf{A}}}(\cdot )$. We define the loss on a set of independent snapshots ${\mathcal {X}}$ as the sum over all constituent snapshots:

$$\begin{aligned} L \big ({\mathcal {X}}, \psi _{\theta ,{\textbf{A}}}({\mathcal {X}}) \big ) {:}{=}\sum _{{\textbf{X}} \in {\mathcal {X}}} L \big ({\textbf{X}}, \psi _{\theta ,{\textbf{A}}} ({\textbf{X}}) \big ) \;. \end{aligned}$$

(4)

In our experiments, we use row-wise MSE-loss.

Note that, in the above sum, all snapshots are treated equally independent of their corresponding initial conditions or time points at which they were made. Formally, this is reflected in the fact that the loss function is invariant to the order of the snapshots.

Graph inference problem

We define the graph inference problem as follows: For given set of m snapshots ${\mathcal {X}} = \{ {\textbf{X}}_1, \dots , {\textbf{X}}_m \}$ (corresponding to n nodes), find an adjacency matrix ${\textbf{A}}' \in \{0,1\}^{n\times n}$ and MLP parameters $\theta '$ minimizing the prediction loss:

$$\begin{aligned} (\theta ', {\textbf{A}}') {:}{=}\mathop {\mathrm {arg\,min}}\limits _{\theta , {\textbf{A}}} L \big ({\mathcal {X}}, \psi _{\theta ,{\textbf{A}}}({\mathcal {X}}) \big ) \,. \end{aligned}$$

(5)

Thus, solving the graph inference problem requires simultaneously optimizing over a discrete space (graphs) and a continuous space (weights). In the next section, we explain how to achieve this by relaxing the discrete space.

Note that, in general, we cannot guarantee that ${\textbf{A}}'$ is equal to the ground truth matrix ${\textbf{A}}^*$. Regarding the computational complexity, it is known that network reconstruction for epidemic models based on time series data is $\mathcal{N}\mathcal{P}$-hard when formulated as a decision problem (Prasse and Van Mieghem 2018). We believe that this carries over to our setting but leave a proof for future work.

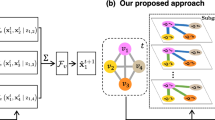
Our method: GINA

Fig. 3

Illustration of GINA. Snapshots are processed independently. Each input/snapshot associates each node with a node state (blue, pink). The output is a distribution over states for each node. During training, this distribution is optimized w.r.t the input. The output is computed based on a multiplication with the current adjacency matrix candidate (stored as C) and the application of a node-wise MLP. Ultimately, we are interested in a binarized version of the adjacency matrix. Color/filling indicates the state, shape identifies nodes

As explained in the previous section, it is not possible to solve the graph inference problem by iterating over all possible graphs/weights. Hence, we propose GINA (Graph Inference Network Architecture). GINA efficiently approximates the graph inference problem by jointly optimizing the graph ${\textbf{A}}$ and the prediction layer weights $\theta$ using stochastic gradient descent.

Therefore, we adopt two tricks: Firstly, we impose a relaxation on the graph adjacency matrix representing its entries as real-valued numbers. Secondly, we use shared weights in the weight matrices belonging to different nodes. Specifically, each node $v_i$ gets its custom MLP, but weights of all layers, except the last one, are shared among nodes. This allows us to simultaneously optimize the graph and the weights using back-propagation. Note that traditional GNN architectures need to have shared weights to achieve permutation invariant. Here, we can freely combine shared and note-specific weights to achieve to balance predictive power and generalizability/efficiency. Apart from that, we still follow the architecture from the previous section. That is, a graph layer maps a snapshot to neighborhood counting vectors, and each neighborhood counting vector is pushed through a node-wise MLP.

Graph layer

Internally, we store the interaction graph as a real-valued upper triangular matrix ${{\textbf {C}}}$ that can contain arbitrary values. During each forward pass, we deterministically translate ${{\textbf {C}}}$ into an adjacency matrix representing the interaction graph. Specifically, in each step, we (i) compute ${{\textbf {B}}} = {{\textbf {C}}} + {{\textbf {C}}}^\top$ to enforce symmetry, (ii) compute ${{\textbf{A}}'} = \mu ({{\textbf {B}}})$ to enforce a reasonable range, and (iii) set all diagonal entries of ${{\textbf{A}}'}$ to zero, yielding $\hat{{\textbf{A}}} = \text {mask}({\textbf{A}}')$. Setting the diagonal entries to zero using $\text {mask}(\cdot )$ is important to ensure that no information leaks from the node itself to the prediction of its state.

Here, $\mu (\cdot )$ is a differential function that is applied element-wise and maps real-valued entries to the interval [0, 1]. It ensures that $\hat{{\textbf{A}}}$ approximately behaves like a binary adjacency matrix. Thus, it can be seen as a differentiable edge binarization (the hat-notation indicates relaxation). Specifically, we use a nested Sigmoid-type function $f(\cdot )$ that is parametrized by a sharpness parameter v:

$$ \begin{aligned}&\mu : {\mathbb {R}} \rightarrow [0,1] \\&\mu : x \mapsto f \Big ( \big (f(x)-0.5 \big ) \cdot v \Big ) \;, \end{aligned}$$

(6)

where we choose $f(x)=1/(1+ \texttt {exp}(-x))$ and increase the sharpness v over the course of the training. Increasing the sharpness means that the entries of $\hat{{\textbf{A}}}$ move closer and closer to 0 or 1 during the training. Note that the masking is done implicitly if we ensure that diagonal entries in ${{\textbf {C}}}$ are zero and $\mu (0)=0$.

Finally, $\hat{{\textbf{A}}}$ is multiplied with the snapshot which yields a relaxed version of the neighborhood counting abstraction. The output $\hat{{\textbf{M}}} = \hat{{\textbf{A}}}{{\textbf {X}}}$ is a relaxed version of the neighborhood counting matrix ${{\textbf {M}}}$.

In summary, for a snapshot ${{\textbf {X}}}$, the graph layer computes:

$$\begin{aligned} \hat{{\textbf{M}}} = \hat{{\textbf{A}}}{{\textbf {X}}} = \text {mask}(\mu ({{\textbf {C}}} + {{\textbf {C}}}^\top )){{\textbf {X}}}, \end{aligned}$$

(7)

where ${{\textbf {C}}}$ is optimized during training. Note that the process is differentiable and the overall loss can be back-propagated to ${{\textbf {C}}}$ (cf. Fig. 3).

For the final results (and comparison with the ground truth), we threshold the adjacency matrix ${{\textbf {A}}}$ at 0.5. That is, we complete the differentiable thresholding of $\mu (\cdot )$ with a final hard cut of.

Prediction layer

We use MLPs to implement the prediction layer $F_{\theta }(\cdot )$ that transforms the output of the graph layer ($\hat{{\textbf{M}}}$) into a predictions of node-states. In $\hat{{\textbf{M}}}$, each row corresponds to one node. Thus, we apply the MLPs independently to each row. We use $\mathbf {\hat{m}}_i$ to denote the row corresponding to node $v_i$ (i.e., the neighborhood counting relaxation of $v_i$). Let $FC_{i,o}(\cdot )$ denote a fully-connected (i.e., linear) layer with input (resp. output) dimension i (resp. o). We use $\texttt {ReLu}$ and Softmax activation functions. Each node-wise prediction layer MLP contains four sub-layers and is given as:

$$ \begin{aligned}&o^1_i = \texttt {ReLu} (FC_{|{\mathcal {S}}|,10}(\mathbf {\hat{m}}_i)) \\&o^2_i = \texttt {ReLu} (FC_{10,10}(o^1)) \\&o^3_i = \texttt {Softmax} (FC_{10,|{\mathcal {S}}|}(o^2)) \\&o^4_i = \texttt {Softmax} (FC_{|{\mathcal {S}}|,|{\mathcal {S}}|}(o^3)) \;. \end{aligned} $$

(8)

In our implementation, only the last sub-layer ($o^4_i$) contains node-specific weights. This enables a node-specific shift of the probability computed in the previous layer. In other words, the $o^3_i$ already contains valid predictions for each node, but the probably distribution is fine-tuned in the last layers. All other weights are shared among nodes which results in strong regularization. Thus, $F_{i}(\cdot )$ applies the MLP of node $v_i$ . Note that we use a comparably small dimension (i.e., 10) for internal embeddings, which has shown to be sufficient in our experiments. The node-specific weights lead to a small, but consistent, improvement of the graph reconstruction. All node-specific weights can be updated efficiently in parallel in a single forward-backward pass.

Training

To solve the graph inference problem, we use a relaxed graph representation to compute neighborhood vectors (Eq. (7)). We evaluate these using node-specific MLPs (Eq. (8)). The loss compares the input with the output using node-wise MSE. During training, the loss back-propagates to the graph representation and the MLP weights, which are updated accordingly (Eq. (4)).

We empirically find that over-fitting is not a problem and therefore do not use a test set. However, a natural approach would be to split the snapshots into a training and test set and optimize $\hat{{\textbf{A}}}$ and $\theta$ on the training set until the loss reaches a minimum on the test set. Another important aspect during training is the usage of mini-batches. For ease of notation, we ignored batches so far. In practice, mini-batches of snapshots are crucial for fast and robust training. A mini-batch of size b, can be created by concatenating b snapshots (in the graph layer) and re-ordering the rows accordingly (in the prediction layer).

Limitations

There are some relevant limitations to GINA. Firstly, we can provide no guarantees that the ground truth graph is actually the solution to the graph inference problem. In particular, simple patterns in the time domain (that enable trivial graph inference using time series data) might correspond to highly non-linear patterns inside a single snapshot (yet, in practice, the spatial patterns seem to be easier to recognize). Secondly, GINA is only applicable if statistical associations among adjacent nodes manifest themselves in a way that renders the counting abstraction meaningful. Statistical methods are more robust in the way they can handle different types of pair-wise interactions but less powerful regarding non-linear combined effects of the complete neighborhood. Another relevant design decision is to use one-hot encoding which renders the forward pass extremely fast but will reach limitations when the node-state domain becomes very complex. We also assume that all agents behave reasonably similar to another which enables weight sharing and therefore greatly increases the efficiency of the training and reduces the number of required samples.

Experiments

Fig. 4

Examples of typical equilibrium snapshots on a $10\times 10$ grid graph. Different dynamics give rise to different types of cluster formations

We conduct three experiments using synthetically generated snapshots. In Experiment 1, we analyze the underlying hypothesis that the ground truth graph enables the best node-state prediction. In Experiment 2, we compare GINA to statistical baselines on independent snapshots. In Experiment 3, we test GINA on time series data and compare with machine learning baselines.

Setup.

Our prototype of GINA is implemented using PyTorch (Paszke et al. 2019) and is executed on a standard desktop computer with 32 GB of RAM and an Intel i9-10850K CPU.

Accuracy and loss.

We quantify the performance of GINA using the graph loss and the prediction loss. The graph loss measures the quality of an inferred graph. It is defined as the $L_1$ (Manhattan) distance of the upper triangular parts of the two adjacency matrices (i.e., the number of edges to add/remove). We always use a binarized version of inferred graph $\hat{{{\textbf {C}}}}$ for comparison with the ground truth ${{\textbf {A}}}^*$. The prediction loss measures how well GINA predicts masked node-states and follows the definition in Section Prediction loss . All results are based on a single run of GINA, performing multiple runs and using the result with the lower prediction loss, might further improve GINA’s performance. For more details regarding the architecture and hyperparameters of GINA, we refer the reader to Appendix A: Technical details of GINA .

Dynamical models

We study six models. A precise description of dynamics and parameters is provided in Appendix B: Dynamical models section . We focus on stochastic processes, as probabilistic decisions and interactions are essential for modeling uncertainty in real-world systems. The models include a simple SIS-epidemic model where infected nodes can randomly infect susceptible neighbors or become susceptible again. In this model, susceptible nodes tend to be close to other susceptible nodes and vice versa. This renders network reconstruction comparably simple. In contrast, we also propose an Inverted Voter model (InvVoter) where nodes tend to maximize their disagreement with their neighborhood (influenced by the original Voter model (Campbell et al. 1954)). Nodes hold one of two opinions (A or B) and A-nodes switch to B faster the more A-neighbors they have and vice versa. For even more complex emerging dynamics, we study a system loosely inspired by Conway’s Game of Life. Nodes (cells) are either dead (D) or alive (A). Living conditions are good (i.e., nodes tend to stay alive or be born) when roughly half of an node’s neighbors are alive. Likewise, they tend to die (or stay dead) when the neighborhood is highly unbalanced. That is, almost all neighboring cells are either dead (underpopulation) or alive (overpopulation). We also examine a rock-paper-scissors (RPS) model to study evolutionary dynamics (Szabó and Fath 2007) and the well-known Forest Fire model (Bak et al. 1990) where a node (spot) can be empty (E), occupied by a tree (T), or occupied by fire (F) induced by stochastic lightning. Finally, we test a deterministic discrete-time dynamical model: a coupled map lattice model (CML) (Garcia et al. 2002; Kaneko 1992; Zhang et al. 2019) to study graph inference in the presence of chaotic behavior. As the CML model admits real node-values [0, 1], we performed discretization into 10 equally-spaced bins.

For the stochastic models, we use numerical simulations to sample from the equilibrium distribution. For CML, we randomly sample an initial state and simulate it for a random time period. We do not explicitly add measurement errors but all nodes are subject to internal noise (i.e., they spontaneously flip with a small probability). Figure 4 provides visualizations of typical equilibrium samples from the dynamical models.

Experiment 1: loss landscape

For this experiment, we generated 5000 snapshots for all dynamical models on the so-called bull graph (illustrated in Fig. 1). We then trained GINA and measured the prediction loss for all potential $5 \times 5$ adjacency matrices that represent a connected graph. Note that the ground truth graph has a graph distance of zero. During training, we fixed the graph layer and only optimized the prediction layer. We observe a large dependency between the prediction loss of a candidate graph and the corresponding graph loss (Fig. 5). We conclude that the hypothesis that graphs that are closer to the ground truth yield a better predictive performance is reasonable. The Game of Life dynamical model is the only example, where graph candidates exist that allow a better prediction than the ground truth graph (by an extremely small amount). Interestingly, this is one of the graph candidates that is furthest from ground truth.

Fig. 5

Exp. 1: [Lower is better.] Computing the loss landscape based on all possible 5-node graphs. x-axis: Graph distance to ground truth adjacency matrix. y-axis: Mean prediction loss of corresponding graph candidates. Error bars denote min/max-loss

Experiment 2: independent snapshots

Table 1 Exp. 2: [Lower is better.] Results of different graph inference methods

Next, we compare GINA with statistical baselines on independent equilibrium snapshots.

Ground truth graphs

To generate ground truth graphs we use Erdős-Renyi (ER) ($N=22$), Geometric (Geom) ($N=50$), and Watts-Strogatz (WS) ($N=30$). Moreover, we use a 2D-grid graph with $10 \times 10$ nodes ($N=100$, $|E| = 180$). We use 50 thousand samples. Graphs were generated the using networkX package (Hagberg et al. 2008) (cf. Appendix C: Random graph generation for details).

Baselines

As statistical baselines, we use Python package netrd (Hartle et al. 2020). Specifically, we use the correlation (Corr), mutual information (MI), and partial correlation (ParCorr) methods. The baselines only return weighted matrices. Hence, they need to be binarized using a threshold. To find the optimal threshold, we provide netrd with the number of edges of the ground truth graph. Notably, especially in sparse graphs, this leads to an unfair advantage and renders the results not directly comparable. We also tested an automated thresholding approach based on k-means clustering of the weighted matrices. The results were quite good, but consistently worse than when the edge count was provided (results not shown). Furthermore, netrd only accepts binary or real-valued node-states. This is a problem for the categorical models RPS and FF. As a solution, we simply map the three node-states to real values (1, 2, 3), breaking statistical convention. Interestingly, the baselines handle this well and, in most cases, identify the ground truth graph nevertheless. Results are shown in Table 1.

Fig. 6

Output of the prediction layer for a random node in the Watts-Strogatz network. We map neighborhood counting vectors to the probability of the node being instate S (SIS), A (InvVoter), or D (Game of Life)

Prediction layer visualization

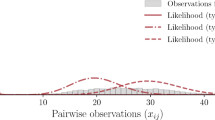
We can visualize the prediction layer for the 2-state models. It encodes the conditional probability to be in a specific node-state given the 2-dimensional neighborhood counting vector ${\textbf{m}}_i$. Figure 6 illustrates this conditional probability as a map from each possible neighborhood counting vectors. The results are given for a Watts-Strogatz graph (where each node has approximately degree 4). The prediction layer belonging to the same node was used for all three models. We observe that the prediction layer finds conditional probability distributions that capture the specific characteristics of the dynamical models. It also generalizes well (beyond degree 4).

Experiment 3: time series data

In contrast to approaches for network inference based on time series data, GINA can be used when there is no (known) temporal relationship between snapshots. However, we can still apply GINA when time series data is available. In this experiment, we generate a single trajectory of a stochastic process and observe it at an interval x ($x \in \{1,5,10,20\}$), e.g., $x=1$ means that we observe the process after every jump in the underlying stochastic process. The reason to test different intervals between observations is that time series analysis methods are, in principle, sensitive to the time resolution of the observations. If too many (or too few) nodes change their state from one observation to another, this could hinder these approaches’ capability of finding and exploiting temporal patterns. In practice, we observe little dependence on the temporal resolution.

Baseline

We compare GINA with the previous statistical baselines and with the machine learning approaches Automated Interactions and Dynamics Discovery (AIDD) (Zhang et al. 2021) and Gumbel Graph Network (GGN) (Zhang et al. 2019) which are both general frameworks to infer the network structure based on time series data (cf. Related work for more details).

Setup

We used 6000 samples (less were not possible without adapting the GGN code further) and a simple $5 \times 5$ grid graph (larger graphs made the GGN application too expensive). We used binary state dynamics because we could apply the baseline code off-the-shelf only to this format. We trained AIDD for 400 epochs and GGN for 40 epochs (we found that accuracy would not improve after that). For comparison, we made the results of the baselines symmetric and binary.

Results

Generally, we find that GINA outperforms the methods based on time series analysis (AIDD and GGN). This is surprising as, in principle, the temporal data should contain significantly more information on the connectivity than the individual snapshots. We can only speculate why GGN performs poorly, but hypothesize that the method is conceptually unsuited for stochastic dynamics of jump processes where only a single agent changes at a time (and not all agents at once). Less surprisingly, we find that GINA is many orders of magnitude faster than AIDD and GGN (ca. 40 to 70 times) while still processing many more epochs (up to 5000 in GINA vs 400 and 40 in AIDD and GGN, respectively).

Moreover, we find that GINA performs slightly better than the statistical methods. Interestingly, Mutual Information is the only baseline that performs well on all dynamical models, Corr and ParCorr fail on the InvVoter and GoL model (this happens consistently even when increasing the number of snapshots). Using automated thresholding (instead of providing netrd with the number of edges) prevents the “collapse” of the statistical methods, but lead a larger graph loss in general. Detailed results are shown in Table 2.

Table 2 Exp. 3: [Lower is better.] Results of different graph inference methods on time series data

Discussion

The results clearly show that graph inference based on independent snapshots is possible and that GINA is a viable alternative to statistical methods. Compared to the baselines, GINA performed best most often, even though we gave the baseline methods the advantage of knowing the ground truth number of edges. GINA performed particularly well in the challenging cases where neighboring nodes do not tend to be in the same (or in similar) node-states. GINA even performed acceptably in the case of CML dynamics despite the discretization and the chaotic and deterministic nature of the process.

Related work

Literature abounds with methods to infer the (latent) functional organization of complex systems that is often expressed using (potentially weighted, directed, temporal, multi-) graphs.

Most relevant for this work are previous approaches that use deep learning on time series data to learn the interaction dynamics and the interaction structure. Naturally, these approaches require consecutive snapshots but are otherwise conceptually similar to GINA. Zhang et al. designed a two-component GNN architecture, called Gumble Graph Network (GGN), where a graph generator network proposes interaction graphs and a dynamics learner learns to predict the dynamical evolution using the interaction graph (Zhang et al. 2019). Both components are trained alternately which is comparably slow. The conceptually similar, but newer, AIDD (framework for automated interaction network and dynamics discovery) (Zhang et al. 2021) scales significantly better with the size of the network.

Similarly, Kipf et al. propose NRI (neural relational inference) to learn the dynamics using an encoder-decoder architecture that is constrained by an interaction graph which is optimized simultaneously (Kipf et al. 2018). The technique popularized neural relational inference but is reported to scale poorly with the network size and seems to be unsuitable for stochastic discrete dynamics (see (Zhang et al. 2021) and literature referenced therein). Using our dynamical models from Experiment 3, NRI failed to reconstruct any graph.

Another state-of-the-art approach for this problem, based on regression analysis instead of deep learning, is the ARNI framework by Casadiego et al. (2017). This method, however, hinges on a good choice of basis functions.

Other methods to infer interaction structures aim at specific dynamical models and applications. Examples include epidemic contagion (Newman 2018; Di Lauro et al. 2020; Prasse and Van Mieghem 2020), gene networks (Kishan et al. 2019; Omranian et al. 2016), functional brain network organization (de Abril et al. 2018), and protein-protein interactions (Hashemifar et al. 2018). In contrast, our approach assumes no prior knowledge about the laws that govern the system’s evolution.

Statistical methods provide an equally viable and often very robust alternative. These can be based on partial correlation, mutual information, or graphical lasso (Tibshirani 1996; Friedman et al. 2008). These methods rely on pair-wise correlations among agents. Our method takes the joint impact of all neighboring agents into account, which is necessary in the presence of non-linear dynamical laws governing the system. Moreover, we directly infer binary (i.e., unweighted) graphs in order to not rely on (often unprincipled) threshold mechanisms.

Our method is also related to self-supervised machine learning, in particular to masking. Masking, in the form of masked language modeling, was popularized for the pre-training transformer-based models like Bert (Devlin et al. 2018). Masking image patches also results in state-of-the-art pre-training for image recognition (Chen et al. 2022). Likewise, node-attribute masking was successfully used as a GNN pre-training technique (Hu et al. 2019) and to improve the ability of a network to generalize (Mishra et al. 2020).

Another relevant research area is optimization over discrete structures (like graphs). While traditional methods use gradient-free techniques like greedy optimization (Netrapalli et al. 2010), genetic (Barman and Kwon 2018), or memetic (Wu et al. 2019) algorithms, SGD-based approaches gain popularity. For instance, Paulus et al. (2020) apply the Gumble-softmax-trick, Fu et al. (2020) use iterative refinement using a differential (GNN-based) loss function, and Bengio et al. (2021) directly predict a sample from a distribution over discrete objects that is implicitly specified by a reward signal.

Conclusions and future work

We propose a model-free and threshold-free paradigm for network reconstruction. Based on this paradigm, we develop GINA to infer the underlying graph structure of a dynamical system from independent observations in an efficient way. GINA is based on the principle that local interactions among agents manifest themselves in specific spatial patterns. These patterns can be found and exploited.

More generally, we show that the underlying hypothesis—that the ground truth graph best describes a set of snapshots—is a promising graph inference paradigm. We also show that node-attribute masking is a principled and practical approach to formalize and measure what it means to “best describe” the observational data. For small graphs, we demonstrate this by enumerating the whole search space (Experiment 1), and for larger graphs, we demonstrate this by showing that GINA beats statistical baselines in many cases (Experiment 2) and even beats machine learning baselines that have access to the temporal ordering of the snapshots (Experiment 3).

GINA explores the vast space of all possible graphs by utilizing a relaxation of the adjacency matrix. This makes the problem amenable to gradient-based methods. Other methods (e.g., based on genetic algorithms or Gumbel-softmax-based optimization) are also possible and worth exploring. We believe that the main challenge for future work is to find ways of inferring graphs when the types of interaction differ largely among all edges. Moreover, a deeper theoretical understanding of which processes lead to meaningful statistical associations, not only over time but also within snapshots, would be desirable.

Appendices

Appendix A: technical details of GINA

We start with a sharpness parameter $v=5.0$ and increase v after 50 epochs by 0.3. We train (maximally) for 5000 (1000 in Experiment 3) epochs but employ early stopping if the underlying (binarized) graph does not change for 500 epochs (measured each 50 epochs). Moreover, we use Pytorch’s Adam optimizer with an initial learning rate of 10^^{− 3}.

We use a mini-batch size of 100. For an efficient forward pass, we first stack the 100 snapshots horizontally, yielding a $n \times 100 |{\mathcal {S}}|$ matrix. We push it through the graph layer and get another $n \times 100 |{\mathcal {S}}|$ matrix. We then reshape it, yielding a $100 n \times |{\mathcal {S}}|$ matrix, and apply the prediction layer row-wise.

In Experiment 1, we use a fixed (pre-defined) binarized adjacency matrix and only optimize the weights of the prediction layer during training.

In contrast to standard GNN software (like Pytorch Geometric), we do not use a sparse representation of the underlying graph, because we optimize over all entries in the adjacency matrix. Moreover, our training set consists of snapshots rather than graphs, so we do not use any sort of graph batching as is common in GNN training.

We did not utilize hyperparameter optimization. Using a validation set to optimize the aforementioned parameters would likely noticeably increase the performance of GINA.

Appendix B: dynamical models

Except for the CML, we use continuous-time stochastic processes with a discrete state-space to generate snapshots. Specifically, these models have a continuous-time Markov chain (CTMC) semantics. Moreover, each node/agent occupies one of several node-states (denoted ${\mathcal {S}}$) at each point in time. Nodes change their state stochastically according to their neighborhood (more precisely, according to their neighborhood counting vector). We assume that all nodes obey the same rules/local behavior. We refer the reader to Kiss et al. (2017); Fennell and Gleeson (2019); Großmann and Bortolussi (2019) for a detailed description of the CTMC construction in the context of epidemic spreading processes.

SIS

Nodes are susceptible (S) or infected (I). Infected nodes can infect their susceptible neighbors or spontaneously become susceptible again. In other words, I-nodes become S-nodes with a fixed reaction rate $\mu$ and S-nodes become I-nods with a rate $\beta {{\textbf {m}}}[\text {I}]$, where ${{\textbf {m}}}[\text {I}]$ denotes the number of infected neighbors of the node and $\beta$ is the reaction rate parameter. Moreover, for all models, we add a small amount of stochastic noise $\epsilon$ to the dynamics. The noise not only mimics measurement errors but also prevents the system from getting stuck in trap state where no rule is applicable (e.g., all nodes are susceptible).

In the sequel, we use the corresponding notation:

$$\begin{aligned} \text {I}\xrightarrow []{\mu + \epsilon } \text {S} \text {S} \xrightarrow []{\beta {{\textbf {m}}}[\text {I}]+ \epsilon }\text {I}. \end{aligned}$$

The reaction rate refers to the exponentially distributed residence times and a higher rate is associated with a faster state transition. When the reaction rate is zero (e.g., when no neighbors are infected), the state transition is impossible.

The parameterization is $\mu = 2.0$, $\beta = 1.0$, and $\epsilon = 0.1$.

Inverted voter

describes two competing opinions (A and B) while nodes always tend to maximize their disagreement with their neighbors.

$$\begin{aligned} \text {A}\xrightarrow []{ {{\textbf {m}}}[\text {A}]+ \epsilon } \text {B} \text {B} \xrightarrow []{ {{\textbf {m}}}[\text {B}]+ \epsilon }\text {A}. \end{aligned}$$

We use $\epsilon = 0.01$.

Game of life

Nodes represent cells (resp. areas) that are either dead (D) (resp. unpopulated) or alive (A) (resp. populated). Living conditions are good when roughly half of the neighboring cells are alive. Otherwise, a cell tends to die due to either over- or underpopulation.

$$\begin{aligned} \text {A}\xrightarrow []{ |{{\textbf {m}}}[\text {A}]-{{\textbf {m}}}[\text {D}] | + \epsilon } \text {D} \text {D} \xrightarrow []{ k - |{{\textbf {m}}}[\text {A}]-{{\textbf {m}}}[\text {D}] | + \epsilon }\text {A}, \end{aligned}$$

where $k={{\textbf {m}}}[\text {A}]+{{\textbf {m}}}[\text {D}]$ is the degree of the node. We use $\epsilon = 0.01$.

Rock paper scissors

mimics a simple evolutionary process where three species compete and defeat each other in a ring-like relationship.

$$\begin{aligned} \text {R}\xrightarrow []{ {{\textbf {m}}}[\text {P}] + \epsilon } \text {P} \text {P}\xrightarrow []{ {{\textbf {m}}}[\text {S}]+ \epsilon } \text {S} \text {S} \xrightarrow []{ {{\textbf {m}}}[\text {R}]+ \epsilon } \text {R}. \end{aligned}$$

We use $\epsilon = 0.01$.

Forest fire

Spots/nodes are either empty (E), on fire (F), or have a tree on them (T). Trees grow with a growth rate g. Random lightning starts a fired on tree-nodes with rate $f_{\text {start}}$. The fire on a node goes extinct with rate $f_{\text {end}}$ leaving the node empty. Finally, fire spreads to neighboring tree-nodes with rate $f_{\text {spread}}$.

$$\begin{aligned} \text {T}\xrightarrow []{ f_{\text {start}} + {{\textbf {m}}}[\text {F}]f_{\text {spread}} + \epsilon } \text {F} \text {F}\xrightarrow []{f_{\text {end} +\epsilon } } \text {E} \text {E}\xrightarrow []{g +\epsilon } \text {T}. \end{aligned}$$

The parameterization is $g = 1.0$, $f_{\text {start}} = 0.1$, $f_{\text {end}} = 2.0$, $f_{\text {spread}} = 2.0$, and $\epsilon = 0.1$.

Coupled map lattice

Let $x_i$ be the value of node $v_i$ at time-step i. Each node starts with a random value (uniform in [0, 1]). At each time step all nodes are updated based on a linear combination of their own node-value and the node-values of neighboring nodes (Kaneko 1992):

$$\begin{aligned} x_{i+1} = (1.0-s) f(x_i) + \frac{s}{d_i} \sum _{j \in N(i)} f(x_j), \end{aligned}$$

(9)

where $d_i$ is the degree of $v_i$, N(i) denotes the set of (indices of) nodes adjacent to $v_i$, s is the coupling strength and f is the local map. Like (Zhang et al. 2019), we use the logistic function (May 2004):

$$\begin{aligned} f(x)= r \cdot x \cdot (1.0-x). \end{aligned}$$

(10)

where r modulates the complexity of the dynamics.

We use $s=0.1$ and $r=3.57$.

Appendix C: random graph generation

We use the Python NetworkX (Hagberg et al. 2008) package to generate a single instance (variate) of a random graph model and test GINA and the baselines on a large number of snapshots generated using this graph. In particular, we use Erdős-Renyi (ER) ($N=22$, $|E| = 33$) graph model with connection probability 0.15:

We also use Geometric Graph ($N=50$, $|E| = 278$):

and a Watts-Strogatz graph ($N=30$, $|E| = 69$) where each node has 4 neighbors and the re-wiring probability is 0.15:

After generation, the node-ids are randomly shuffled in order to guarantee that they do not leak information about connectivity to the training model.