1 Introduction

Since battery electric vehicles (BEV) stop being a niche product and gain increased importance in every passenger car segment, the OEMs have to design electrical machines for various requirements [2]. The task is to find the optimum design e.g. for segments like small city cars, middle and upper class sports cars, and SUVs. Each vehicle segment has a specific demand for the powertrain concerning speed and torque [4]. Furthermore, the operating points span a wide range of speed and torque depending on the use of the car. While the use in the city usually means low speeds, a car on a highway-ride should operate best at high speeds. Both the vehicle segment and the vehicle usage affect the propulsion system, the typical use of the car and its type, due to properties like weight and size. A manufacturer has to decide, whether to optimize a powertrain for every specific purpose, like a dedicated city car or a vehicle that serves best on a highway-ride. The second option is to design a powertrain that is the best compromise between all specifications. This, however, goes hand in hand with drawbacks in each use case when it comes to performance. On the other hand, the elevated quantity of similar powertrains can lead to economic benefits.

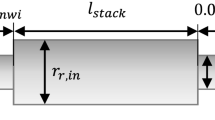
The electromagnetic properties of a permanent magnet synchronous machine depend on various factors like the shape and size of the magnets, flux barriers and stator teeth for example. Next to these parameters, the arrangement of the windings plays an important role, including the number of Turns per Coil (\(TC\)). For similar machine dimensions, different electromagnetic characteristics can be achieved by changing the \(TC\) value. Another way to scale the performance without expensively redesigning the machine is changing its length. The maximum length is usually only set by bending loads and the available space [14]. Scaling the performance by changing the diameter requires a re-calculation of the electromagnetic behavior and mechanical limitations have to be considered. For every application, the exact dimensions in the rotor and stator would have to be optimized in order to achieve the desired torque and power at maximum system efficiency. Since this is complex and time-consuming [7,8,9,10], first studies can be done by scaling the machine radially without any further adaptions of the geometry. Radial scaling of the electric machine is illustrated in Fig. 1. Since the general shape of magnets and flux barriers remains the same, the iron-bridge thickness increases with increasing diameter of the machine. For large diameters, this can lead to magnetic short circuits and therefore bad electromagnetic performance. Small diameters, by contrast, decrease the thickness of supporting iron-bridges. The lower limit of the diameter is therefore set by production limits.

Fig. 1
figure 1

Visualization of the scaling of the diameter of a permanent magnet synchronous machine

Full size image

The present work demonstrates how the respective optimal design within the above mentioned design boundaries of a PMSM can be derived from a reference machine design by scaling it in length, diameter and turns per coil. First, the design space will be defined and boundary conditions will be introduced, as well as the characteristics of driving cycles and vehicle types under investigation. Next, the applied model is defined. The results are divided in three subsections: a sensitivity analysis describes the influence of the design parameters on torque, power and efficiency of the PMSM. The energy consumption of the machine designs is then evaluated for the six different use cases.

1.1 Boundary conditions

In this work the length, diameter and turns per coil are changed in a parameter study. The length is varied from 6 to 20 cm and the diameter from 16 to 25 cm, each in 1 cm steps. In addition, numbers of turns per coil between 5 and 15 are evaluated. Furthermore, the study considers a maximum current of \(I=650\) A of the power electronics and a maximum current density \(J= 29\) A/mm2. The limit of the current density arises from the requirement of the time that the machine has to be able to operate at peak torque. In all investigations, the constant Voltage \(U=350\) V is applied.

First, the influence of the three parameters on torque, power and efficiency of the PMSM is discussed. For the sensitivity analysis, FE-Analysis and a Matlab model is applied. Second, the performance of the different scaled PMSM in different scenarios, are investigated. Torque characteristics as well as loss maps form the previous sensitivity analysis are integrated in a Matlab/Simulink backward model that simulates the vehicle behavior. A city car and a highway car are compared in three different cycles: City (CC), Highway (HC) and the Worldwide Harmonized Light Vehicle test Cycle (WLTC). Mohan et al. demonstrated the suitability of backward models for the powertrain component sizing of combustion engines [11]. The characteristics of both cars and the cycles are summarized in Tables 1 and 2. Typically, a car used in the city has to accelerate and decelerate frequently at low speeds and operates at low powers. Opposed to that, on a highway the electric machine operates at high speeds and high power requirements. The WLTC cycle tries to reflect the average use of a car and has moderate torque and power requirements with maximum speeds of about 130 kph. The different use cases differ largely in their profile of requirements towards the powertrain [4]. Accordingly, the optimum machine design is different in each case. Another influence on the requirements for the electric machine result from the choice of the car. Similar values for the drag coefficient \(c_\mathrm{w}\) and friction \({f}_\mathrm{r}\) are considered for a city car and a highway car. However the latter has both, a bigger cross-sectional area \(A_\mathrm{x}\), and a higher mass \(m\). It further has a higher top speed requirements \({v}_{\mathrm{max}}\) and longer acceleration times \({t}_{0-100}\) from 0 to 100 kph. The powertrain and driving characteristics are simulated in a Matlab/Simulink model and consider a gearbox with a gear ratio that is chosen in a way that the maximum speed of the PMSM is sufficient for a vehicle velocity of 140 kph for a city car and 180 kph for a highway car. The torque required for a given acceleration is calculated by Newton’s second law and a force balance taking into account aerodynamic drag \({F}_{\mathrm{d}}\), friction of the tires \({F}_{\mathrm{t}}\), as well as mechanical losses in the transmission and in the side shafts [5].

Table 1 Characteristics of the three different driving cycles under investigation
Full size table
Table 2 Characteristics of the two different vehicle types under investigation
Full size table

1.2 Powertrain model

1.2.1 Electromagnetic model

The majority of losses in electric machine occur in the copper windings, stator iron, rotor iron, and magnets. The ohmic losses \({P}_{\mathrm{v},\mathrm{ohm}}\) in the windings depend on the ohmic resistance \({R}_{\mathrm{ohm}}\) and the electric current \(I\). The latter can also be expressed by the current density \(J\) and the conducting cross sectional copper-area \({A}_{\mathrm{Cu}}^{\mathrm{ph}}\). The ohmic resistance itself depends on the specific resistance \({\rho }_{\mathrm{el}}\) of the conductor, its cross-sectional area \({A}_{\mathrm{wire}}\) and its length \({l}_{\mathrm{wire}}\) [12].

$${P}_{l,\mathrm{ohm}}={R}_{\mathrm{ohm}}\cdot {I}^{2}={\rho }_{\mathrm{el}}\cdot \frac{{l}_{\mathrm{wire}}}{{A}_{\mathrm{wire}}}\cdot {\left(J\cdot {A}_{\mathrm{Cu}}^{\mathrm{ph}}\right)}^{2}$$
(1)

The area \({A}_{\mathrm{Cu}}^{\mathrm{ph}}\) depends on the area per phase of the stator slots that is filled with copper. Typically, the area of copper in a slot is significantly lower than the one of the slot \({A}_{\mathrm{slot}}\) itself. This is considered by the filling factor

$${ff}_{\mathrm{el}}=\frac{n\pi \frac{{d}_{\mathrm{wire}}^{2}}{4}}{{A}_{\mathrm{slot}}}$$
(2)

with the number of wires \(n\) and wire diameter \({d}_{\mathrm{wire}}\) [15]. Both the necessary electrical insulation and the round shape of the conductors with diameter \({d}_{\mathrm{Cu}}\) decrease maximum number of \(n\) wires that fit in the slot. Typically filling factors between \(45 \%\) and \(55 \%\) are achieved in electrical machines [13] [3]. A filling factor for a reference machine is calculated and kept constant for all further studies in this paper.

An increase in machine diameter considered in this paper also increases the slot area \({A}_{\mathrm{slot}}\) and therefore the wire diameter \({d}_{\mathrm{wire}}\) can be bigger if the number of turns per coil \(TC\) remains constant. If the number of turns per coil \(TC\) is increased instead, the wire diameter has to be decreased in order to the fit more wires in the constant slot area \({A}_{\mathrm{slot}}\) for a given machine diameter. Considering the constant filling factor the product of turns per coil and wire area has to be constant resulting in

$${d}_{\mathrm{wire},\mathrm{i}}={d}_{\mathrm{wire},0}\cdot \sqrt{\frac{T{C}_{0}}{T{C}_{\mathrm{i}}}}$$
(3)

Equation (3) describes the scaling of the wire diameter \({d}_{\mathrm{wire},\mathrm{i}}\) relative to a reference diameter \({d}_{\mathrm{wire},0}\) if the turns per coil are changed from a reference \(T{C}_{0}\) to \(T{C}_{\mathrm{i}}\). Equation (3) indicates, that the current density \(J\) increases with increasing \(TC\)-values at a constant current \(I\) or vice versa, since the turns per coil describe the number of wires in a slot that are connected in series. This has to be taken into account in the further investigations of this paper, as well as the fact that the diameter of the wires changes with the number of turns per coil according to Eq. (2) and thus the ohmic losses change according to Eq. (1).

Next to the conducting copper area in the slots, the turns per coil also affect the magnetic flux of the coils:

$${\Psi }_{\mathrm{coil}}=B\cdot {A}_{\mathrm{coil}}=\mu \cdot TC\cdot I\cdot \frac{{A}_{\mathrm{coil}}}{{l}_{\mathrm{coil}}}$$
(4)

with magnetic flux density \(B\), magnetic permeability \(\mu\), area of the coil \({A}_{\mathrm{coil}}\), and length of the coil \({l}_{\mathrm{coil}}\) [12]. Accordingly, the same torque can be generated with less current, if the turns per coil are increased. Furthermore, with increasing \(TC\) the voltage limit of the electrical drive system is reached at lower speeds and the field weakening area is shifted accordingly.

Next to the ohmic losses in the conductors, the losses in the rotor and stator iron \({P}_{\mathrm{l},\mathrm{Fe}}\) represent the main loss source. For a sinusoidal excitation, the specific iron losses can be calculated as

$${p}_{l,\mathrm{Fe}}=\frac{{\pi }^{2}\sigma {d}^{2}}{6\rho }{\left({B}_{\mathrm{max}}f\right)}^{2}+k\frac{4{H}_{c}}{\rho }{B}_{\mathrm{max}}f+\frac{C}{\rho }{\left({B}_{\mathrm{max}}f\right)}^{3/2}$$
(5)

with the electrical conductivity of the iron \(\sigma\), the density \(\rho\), the coercivity \({H}_{\mathrm{c}}\), a material specific constant \(C\), the maximum of the magnetic flux density \({B}_{\mathrm{max}}\), the form factor \(k\), the thickness of the iron sheets \(d\) and the frequency \(f\) [1]. The magnetic flux density in rotor and stator depends on the specific machine design as well as the speed and torque of each operating point. A finite element analysis (FEA) is used in this work to evaluate the flux density for all operating points for every machine diameter. Since parts in the machine center are not affected by the axial ends, the length shows not influence on the magnetic flux density distribution. Therefore, it is considered similar for each diameter at different machine lengths. The same assumption is made for the magnet losses that can be calculated similar to the iron losses, considering only the eddy currents. These are described by the first summand in Eq. (5). The overall loss \({P}_{\mathrm{l}}\) of a PMSM is the sum of the losses in copper, iron and magnets. Compared to the specific losses described in Eq. (1) and (5), the overall losses are weighted with the mass of the respective machine parts.

1.2.2 Mechanical model

Since the energy content of automotive batteries is lower than that of fuel tanks in conventional vehicles, driving range and thus powertrain efficiency is a crucial characteristic value in battery electric vehicles [6]. The efficiency of an electric machine in motor and generator operation is defined by the mechanical power \({P}_{\mathrm{mech}}\) and the electrical AC power \({P}_{\mathrm{AC}}\):

$${\eta }_{\mathrm{mot}}=\frac{{P}_{\mathrm{mech}}}{{P}_{\mathrm{AC}}}$$
$${\eta }_{\mathrm{gen}}=\frac{{P}_{\mathrm{AC}}}{{P}_{\mathrm{mech}}}$$
(6)

The difference between mechanical and electrical power equals the losses \({P}_{l}\) of the machine. In the applied backwards model, the driving maneuver determines the mechanical power of the machine. For a given vehicle with the vehicle mass \({m}_{\mathrm{vehc}}\), the deceleration caused by drag forces and rolling resistance of the wheels and the desired acceleration result in a necessary accelerating force. This force equals a torque that has to be provided by the electrical propulsion system as an output torque of the electrical machine. The required torque mainly depends on the dynamic wheel diameter, mechanical losses and the gear ratio of the transmission. Similarly, the rotational speed of the electrical machine depends on the vehicle velocity, the wheel diameter and the gear ratio. Thus, for a given driving cycle and given vehicle properties, the required machine torque and speed are well defined. The energy consumption defined as the integral of the losses over time during a driving cycle allows an evaluation of the possible driving range with different propulsion systems. Focus of this paper is the influence of different machine properties on the vehicle consumption.

In this work, the gear ratio is adapted to the machine diameter \(D\) in a way that the maximum rotational speed is not exceeded. The mechanical design of the rotor is chosen in a way that the rotor can endure a speed that is the maximum required speed times a safety factor. For a constant maximum required vehicle velocity \({v}_{\mathrm{max}}\), the gear ratio has to be decreased if the rotor diameter increases in order to compensate for higher centrifugal forces.

2 Results

2.1 Electromagnetic sensitivity analysis

Before discussing the scaled PMSMs in a certain use case, the specific influence of each parameter, namely diameter, length and \(TC\) will be investigated, considering torque, power and efficiency. As boundary conditions, a diameter of 220 mm and eight turns per coil are chosen for the investigation of the influence of different lengths. Figure 2 shows the results as the normalized peak torque (top left), normalized peak power (middle left) and normalized efficiency (bottom left) plotted over the normalized speed in each case for every considered length of the machine. On the right hand side the normalized maximum torque, power and efficiency (top to bottom) at each machine length are depicted. All three PMSM characteristics increase with the machine length. However, there is a saturation in efficiency and power that cannot be discovered in the linearly increasing torque. The field-weakening area shifts to lower speeds with increasing length, since the BEMF increases. This cancels out the rise in torque leading a flattening gradient of the power. Decreasing the required current at a given operating point, the maximum efficiency increases with increasing lengths. In addition, the isocurve of maximum \(\eta =96 \%\) covers an increasing area and shifts to lower speeds.

Fig. 2
figure 2

Sensitivity analysis of the active length with diameter \(D=22\) cm and \(TC=8\). Influence on normalized torque, power, maximum efficiency and 96%-efficiency

Full size image

Varying the diameter instead of the length leads to the results shown in Fig. 3 following the same logic as before. The maximum motor-torque increases with diameter and the field-weakening area shifts to lower speeds. However, the latter effect is less pronounced than for the variation in length. Accordingly, the impact of the diameter on the power is stronger in this investigation. A lower gradient can be identified at big diameters for torque and power in the respective diagrams on the right. This matches with the decreasing growth in maximum torque. In these cases, the power electronics limits the performance with the maximum current of \(I=650\) A. As discussed in Sect. 3, the diameter of the wires increases with the machine diameter and therefore the current density decreases for a given current. At a diameter \(22 \mathrm{cm}<D<23 \mathrm{cm}\), the maximum current limits the peak torque instead of the current density. The maximum efficiency shown in the last diagrams hardly seems to be affected by the machine diameter. However, the area covered by \(\eta >96 \%\) is growing with increasing diameter, partly because the flux density decreases due to the increase in iron cross-section.

Fig. 3
figure 3

Sensitivity analysis of the active diameter with length \(L =16\) cm and \(TC=8\). Influence on normalized torque, power, maximum efficiency and 96%-efficiency

Full size image

A third sensitivity analysis is dedicated to the turns per coil. Results are summarized in Fig. 4. The turns per coil show no effect on the maximum torque for the given machine dimensions, except for the minimum number of \(TC=5\). According to Eq. (3), the wire diameter increases with decreasing turns per coil. At \(TC=5\), the increase in wire diameter is big enough, so that the current limit of the power electronics is limiting the torque. For differently sized slots, this can be the case at different numbers of turns per coil and therefore has to be considered for every machine diameter. As introduced with Eq. (4), the flux induced by the windings is linked to the number of turns per coil as well. This causes a beginning of the field-weakening area at lower speeds. Corresponding to the findings above, the maximum power decreases with the number of turns per coil. Although the maximum efficiency of the machine is hardly affected by the number of turns per coil, the area of efficiencies above \(96 \%\), decreases when \(TC\) is increased due to saturation effects in the iron. The results of the different investigations are summarized in Table 3.

Fig. 4
figure 4

Sensitivity analysis of the turns per coil with length \(L =20\) cm and \(D=18\) cm. Influence on normalized torque, power, maximum efficiency and 96%-efficiency

Full size image
Table 3 Isnfluence of the investigated parameters on the performance of the permanent magnet synchronous machine
Full size table

2.2 Driving cycle efficiency

2.2.1 Highway car energy consumption

For the different cycles, and vehicles, the evaluation criterion is the system efficiency reflected by the energy consumption. Each drive cycle is calculated with all the machines characterized by diameter, length and \(TC\) introduced above. The consumption is compared to the most efficient machine in each case. Then the relative difference in consumption is plotted over active diameter and active length in Fig. 5 (top) for a highway car in the WLTC. Different turns per coil lead to different consumptions at constant active dimensions of the machine. High lengths perform best when combined with low \(TC\), whereas high \(TC\) have an advantage for short machines. The surface connecting the most efficient combinations at the different machine dimensions is depicted in Fig. 5 (bottom). Those machines, that do not meet the specified operating points of the drive cycle due exceedance of the maximum current density, are not plotted, resulting in blank spaces in the diagrams. It can be seen that the WLTC is designed in such a way, that small machines are beneficial in terms of efficiency. In addition, the isocurves of constant active volume show that high lengths and small diameters are slightly better than machines with the same active volume but higher diameters. These results are a direct consequence of the efficiency of the electrical machine improving in the area where the machine is operated during WLTC.

Fig. 5
figure 5

Impact of the machine design on the consumption of a highway car in WLTC

Full size image

The same investigation is made for the highway car in the city cycle and in the highway cycle. Results are shown in Fig. 6 on the left and on the right, respectively. The 3D-plot is not shown but only the isosurface of the machines with the optimum TC at every geometry. Similar to the WLTC, small machines perform best in the highway cycle, whereas in the city cycle, large machines have less consumption than small ones. Again only machines that are able to perform the drive cycle are plotted. The differences are most pronounced in the highway cycle with an additional consumption of more than 12% compared to the best case. It becomes clear, that no machine exists, that suits all three cycles perfectly. Therefore, manufacturers have to decide, whether to build cars with machines dedicated for one of the use cases or to build ones that are a compromise.

Fig. 6
figure 6

Impact of the machine design on the consumption of a highway car in city cycle (left) and in highway cycle (right)

Full size image

2.3 City car energy consumption

In contrast to a highway car, city cars are smaller and lighter (see Table 2). Therefore, the drag force at a certain velocity is less than with a highway car and the same acceleration requires less force. Performing the same evaluation as above on a city car therefore leads to different results, as outlined in Figs. 7 and 9. Because of the reduced torque required for accelerating lighter vehicles, more machines are able to perform the drive cycles with the given current density limit. Again small machines perform best, when it comes to the consumption and again the isocurves indicate that at the same volume, it is favorable to reduce the diameter rather than the length in the design space under investigation. An exception of the above stated conclusions is the city car in the city cycle. At the same active volume, big lengths are still favorable compared to big diameters. However, there is not a monotonous decrease in consumption with the machine length. Areas of high efficiency shift away from the operating points of the city cycle again.

Fig. 7
figure 7

Impact of the machine design on the consumption of a city car in WLTC and in city cycle

Full size image

Comparing highway and city cars, the latter show a bigger difference in fuel consumption between best and worst case since the utilization of the machines decreases and a larger number of machines of the design space meet the specifications. Note, that for example in the highway cycle, the consumption increases approximately by one third between the best machine and the worst with the right choice of the coils per turn. When the worst choice of coils per turn is taken into account, however, the consumption almost doubles as depicted in the 3D-plot of Fig. 8 (top).

Fig. 8
figure 8

Impact of the machine design on the consumption of a city car in highway cycle

Full size image

2.4 Overall energy consumption

The results above demonstrate, how an optimum machine design can be found in a given design space for a certain vehicle type and drive cycle. Consumption differs significantly between the different modifications which has a direct impact on vehicle range for a given battery capacity. However, the optimum machine for each purpose is different. This raises the question, which is the machine that would be the best compromise between the different cycles for example. Adding the consumption per kilometer for all driving cycles for each machine and calculating the relative difference compared to the best case

$$\Delta {C}_{i}=\sum_{\mathrm{cycle}}\frac{{C}_{\mathrm{cycle}}^{i}-{C}_{\mathrm{cycle}}^{*}}{{C}_{\mathrm{cycle}}^{*}}$$
(7)

results in the diagrams in Fig. 9 for the highway car (left) and city car (right), respectively. Here \(C\) represents the powertrain consumption of powertrain \(i\), the asterisks represents the optimal design, and \(\mathrm{cycle}\) represents the city cycle, the highway cycle and the WLTC. Again, only the isosurface of the best \(TC\) for every diameter-length-combination is plotted. Compared to the results for a single driving cycle, this time the \(TC\) has to be selected in a way, that all driving cycles are feasible. Table 4 shows the machines that minimize the energy consumption for all drive cycles with the highway car and the city car, respectively. For the heavy and large car investigated in this study, the designer should choose a long machine with a small diameter and low TC. However, using this machine in the city car would result in \(5 \%\) more losses than with the machine specifically designed for this use case. For this purpose, it is be beneficial to select a shorter machine which has advantages concerning weight, space and price at the same time. The requirements for the highway car cannot be met with the small machine.

Fig. 9
figure 9

Impact of the machine design on the consumption of a highway car (left) and a city car (right) in all drive cycles

Full size image
Table 4 Results of the machine optimization for the highway car and the city car
Full size table

While for single drive cycles small numbers of turns per coil seemed beneficial, the overall consumption can be minimized with higher values. Again, the difference is more pronounced for city cars. With a highway car, the differences in the driving cycles cancel out each other so that the machine design has a lower impact on the consumption than with a city car under the assumptions made in this paper. It further has to be noted that again only the isosurface over the \(TC\) that lead to the lowest energy consumption is plotted in Fig. 9. A bad choice of \(TC\) can still lead to significant differences in energy consumption with a highway car. The increased variance in overall city car consumption is partially linked to the increased amount of powertrains that fulfill the requirements of the driving cycles. In accordance with the single driving cycles, a small machine is also best in the combined use case.

3 Conclusion

In this paper, a sensitivity analysis for the design of a permanent magnet synchronous machine was demonstrated. For given voltage, current and current density limits, the influence of machine length, machine diameter and turns per coil were evaluated. After demonstrating the impact on maximum torque, power and efficiency, the optimum design for a highway car and a city car was identified. Big differences in the machine consumption of up to \(\Delta C=100\) % were detected in the highway cycle with a city car. Even if only the optimum number of turns per coil was taken into account for every machine dimension, there was a difference in consumption of more than \(30\) %. It was then demonstrated, that the difference becomes less pronounced, yet must not be neglected, if an overall consumption in all driving cycles is taken into account. However, the optimum machine design differs largely with the different driving requirements. The designer has to choose a compromise for all different scenarios. Including thermal requirements, weight, space and price considerations makes the optimization even more challenging. This will be investigated in future work. The investigation described in this paper serves the main purposes to demonstrate the impact of vehicle type and vehicle use case on the optimum machine design with respect to energy consumption.