1 Introduction

Climate change and air pollution are more than ever discussed topics in the line with engine development. CO\(_{2}\) output of passenger cars contribute to global warming especially when using fossil fuels. To increase efficiency and reduce fuel consumption downsizing have been established in the market during the last years. By reducing the Displacement a higher specific load leads to less gas exchange losses. But the smaller combustion chambers also imply disadvantages. Because of the reduced free path for the fuel spray interaction with combustion chamber walls (liner and piston) is intensified. As a result combustion chamber deposit (CCD) formation can be increased resulting in various effects. The most important ones are described by Kalghatgi [1]. The main process to form CDD is a polymerization of fuel and to some extend oil which is attached to hot surfaces. The surface temperature and the extent of fuel-wall-interaction are major influences on CCD growth and structure.

CCD also affects engine out emissions. It is reported that CO\(_{2}\) output decreases with higher amount of CCD as a result of higher efficiency because of their thermal insulation and decrease of heat loss. On the other hand NO concentrations increase as a result of the higher in-cylinder temperatures. No clear statement can be made concerning HC. CDD can reduce crevice volume and hence reduce unburned HC from these sources. However, the porous structure can store unburned or partial burned HC and thus increase their emission. Furthermore the stored HC can burn in a diffusive flame and increase the soot formation.

CDD vary in their composition. Carbon dominates with a share of more than 60%. Usually small quantities of Ca, Zn and Mg can be found which come from lubricant additives. They mostly occur in the form of sulphates or phosphates. Compared to the deposits in the cylinder head, CCD on the piston top have higher concentrations of these elements, suggesting that oil plays a bigger role in forming piston deposits.

Average densities are between 1100 and 2000 kg/m\(^{3}\) and heat capacities are between 0.84 and 1.84 kgK. Values for thermal conductivity are reported between 0.17 and 0.8 W/(mK). However, these values depend on the measurement procedure, the way of preparation and the structure of the deposits. Hence, an in-situ measurement is recommended. For comparison: pure aluminum has a thermal conductivity of 236 W/(mK). Therefore CCD can be described as a thermal insulating layer. The consequently higher temperatures in the combustion chamber increase the octane requirement or can lead to abnormal combustion phenomena such as knocking or pre-ignition. Therefore this work deals with the surface structure of CCD and their influence on heat transfer. A kind-of in-situ measurement is used to determine the thermal conductivity of CCD depending on the operation point of the engine.

Outline of the paper:

In Sect. 2 the state of the art on CCD in internal combustion engines and fundamentals on wall heat transfer is described. A brief introduction in DNS simulation of flow and heat transfer near rough walls is given.

Section 3 describes the experimental setup of the engine and the measurement techniques used to characterize the CCD surface and to measure the temporally resolved wall temperature. An analytical method to calculate the wall heat flux and two a derived methodologies to calculate the CCD layer thickness are shown. In Sect. 4 the results are presented. At first the surface roughness, structure and composition of CCD on the piston and the cylinder head is described. With the roughness values a DNS of the near wall flow was performed to assess whether the surface structure affects the convective heat transfer or not. Using characteristic CCD properties given in the literature the calculated deposit layer thickness on the cylinder head is shown and compared to measured values. Finally the thermal conductivity as a function of heat capacity and CCD density is calculated. Section 5 provides a short summary and some conclusions.

2 State of the art

2.1 Combustion chamber deposits

CCD can have various effects on engine operation. Pinto da Costa [2] states that CCD can increase knocking tendency. Deposit flakes can be heated up by combustion and lead to self-ignition. Additionally, the wall heat transfer can be reduced by the insulation effect of CCD. The surface temperature increases and forms hot spots which can additionally host reactive species in the CCD structure and consequently support knocking combustion [3]. In extreme cases strong deposits increase knocking by increasing the effective compression ratio.

Especially in investigations of DI engines with homogeneous charge and compression ignition the thermal insulation of CCD plays a major role. Because of thermal insulation of the combustion chamber the gas temperature and hence the ignition timing changes [4]. Hensel et al. showed that conventional heat transfer models have to be adapted for HCCI engines because the maximum heat flux occurs at later crank angles than predicted by existing models [5]. Hoffman and Filipi showed in [6] that the limited operational range of low temperature combustion is influenced by near-wall conditions. They investigated the influence of CCD on thermal insulation effect which was measured in-situ by thermocouples. They found that the porosity of the CCD is decisive for the insulation effect rather than fuel trapped in the pores.

CCD can also support fuel film formation on the piston. Drake et al. [7] summarized that smoke emissions are probably formed by mainly three sources: (1) locally rich gaseous mixtures, (2) incompletely volatilized liquid fuel drops, and (3) pool fires fed by fuel films from the piston top and other surfaces. The surface properties are of importance considering the fuel-wall-interaction and the resulting fuel films. It is a difference whether the fuel spray contacts a clean metal piston surface or for example a porous structure of deposits which can act like a sponge and store fuel. Kopple et al. investigated the correlation between liquid fuel films, piston top temperatures and soot formation. Especially during load steps they identified the interaction of fuel spray and piston surface as major soot source, because the relatively low piston top temperature supports fuel film formation and its diffusive burning [8]. Han et al. [9] showed that the amount of fuel in a film on the piston surface is linked to the amount of formed soot. Drake et al. investigated fuel film masses in a DISI Engine under stratified operation. Depending on the injection system they found between 0.1 and 1% of the injected fuel as film on the piston top. The diffusive burning of these fuel films in pool fires persisted past 60ATDC and was the main source of soot emissions. In this investigation the fuel films contributed between 2 and 15% to the HC emissions. Jiao and Reitz [10] supported these findings by modelling spray-wall-interaction and soot formation process. In their work the Lagrangian particle approach proposed by O’Rourke and Amsden [11, 12] was used. In the near wall regions, film vaporization alters the structure of the turbulent boundary layers above wall films due to the existence of gas velocities normal to the wall induced by vaporization and the consequent convective transport of mass, momentum, and energy away from the film. The influence of the surface structure of the piston top cannot be considered.

In Dessouter et al. [13] state that turbulent, chemical reactive multiphase flows are influenced by the combustion chamber walls in IC engines. CCD have an impact on heat flux, flow conditions and reaction conditions. The change of the near wall conditions by formation of CCD are so far not understood although they affect emission formation through the change of turbulent momentum and heat transport. Experimental studies on the heat transfer in combustion engines are numerous, but only a few experimental studies on the influence of wall deposits in Gasoline and diesel engines are known [13, 14]. Numerical investigations of heat transfer in combustion engines have so far been carried out exclusively without wall deposits [15, 16].

It has been known for a long time that a hydrodynamically rough wall leads to a shift of the average velocity profile in the direction of the wall. To assess the change in Reynolds stresses and dissipation DNS of turbulent flows over rough walls were performed. These simulations are generally limited to spatially periodic roughness which is a simplification compared to real CCD surface structures [17]. In addition to spatially inhomogeneous boundary conditions, statistically unsteady flow conditions are characteristic for combustion engines. In the literature, a few studies on the influence of the flow under unsteady operating conditions are known [18]. The combination with spatially varying surface characteristics has so far not been investigated. An assessment of the global influence of the flow through local changes in the surface is needed to understand near-wall processes [19]. For this purpose, knowledge of the CCD properties and their influence on wall heat flux, as shown in this work, is necessary.

2.2 Wall heat transfer

A variety of models describe the convective heat transfer at the combustion chamber wall based on Newton’s law of cooling:

$$\begin{aligned} {\dot{Q}}({\varphi })={\dot{q}}({\varphi })\,A={\alpha }({\varphi })\,A\,(T_\mathrm {G}({\varphi }) - T_\mathrm {W}), \end{aligned}$$
(1)

where the heat flux \(\dot{Q}({\varphi })\) is described as a function of the heat flux density \(\dot{q}\) across the surface A that contributes to the heat transfer and \(\dot{Q}({\varphi })\) is proportional to the difference in process gas temperature \(T_\mathrm {G}\) and wall temperature \(T_\mathrm {W}\). A plethora of studies were designed to determine the heat transfer coefficient \(\alpha ({\varphi })\) empirically [20,21,22]. Analytical solutions describe the heat transfer coefficient based on the theory of duct flow using the Nusselt number:

$$\begin{aligned} Nu=f(Re,Pr)=C\,Re^{m}\,Pr^n \end{aligned}$$
(2)
$$\begin{aligned} Nu=\frac{\alpha \,l}{\lambda }\quad Re=\frac{w\,l\,\rho }{\eta }\quad Pr=\frac{\nu }{a} \end{aligned}$$
(3)
$$\begin{aligned} \alpha =C\, \lambda \, (l_\mathrm {char})^{m-1} \left( \frac{w_\mathrm {char}\,\rho }{\eta } \right) ^m \end{aligned}$$
(4)

Another analytical approach takes advantage of the correlation between heat transfer and velocity gradient at the combustion chamber wall [23, 24]:

$$\begin{aligned} \alpha =\frac{1}{2}{\lambda }_r{w}_\mathrm {char}\rho {c_p}. \end{aligned}$$
(5)

Based upon these analytical observations, Woschni [25,26,27] and Huber [28] derived integral models (for spark ignition and diesel engines, respectively) describing the heat transfer coefficient as a function of velocity w, cylinder pressure p, local gas temperature T, and displacement \(V_\mathrm {h}\)

$$\begin{aligned} \alpha =130 d^{-0.2} p^{0.8} T^{-0.53}(C_1 w)^{0.8}, \end{aligned}$$
(6)

with the prevailing difference between Huber’s and Woschni’s model being the calculation of the velocity term w.

Hohenberg developed a similar model for Diesel engines [29] which takes into account the turbulent flow during combustion. Bargende [30] extended the combustion term such that it accounts for the temperature difference between burnt and unburned gas and combustion chamber wall, respectively, considering at the same time the transient flow in the combustion chamber of spark ignition engines.

Hensel [5] developed an approach to describe the heat transfer in homogeneous charge compression ignition engines based upon the work of Hohenberg and Bargende. His modifications include the consideration of air mass flow and intake velocity as well as the formulation of a combustion term generating a reduced rate of temperature change close to the combustion chamber wall after ignition.

Quasi-dimensional models designed to examine the spatially resolved heat transfer are usually implemented by discretizing the combustion chamber based on local fluid mechanical and thermodynamic properties. In these models, the heat transfer coefficient for each discretisational element is derived from the local flow field as well as the progress in combustion.

The two-zone model implemented by Morel and Keribar [31] applies a gas temperature which is calculated as mass-weighted average of the unburnt and burnt zones of the combustion chamber. In this model, the effective velocity of the gas in each zone is based on its average flow velocity and the turbulent kinetic energy. Eiglmeier [32] divides the combustion chamber into isothermal areas, thereby causing a finer discretisation compared to two-zone models. His model for the wall heat transfer of Diesel engines accounts for soot radiation and deposits. Kleinschmidt [33] developed a transient model for the heat transfer calculating the one-dimensional heat transfer iteratively from a superposition of pressure and temperature dynamics. His approach is the first to account for thermal conduction of the combustion chamber wall.

2.3 DNS simulation of flow and heat transfer near the rough walls

For the simulation of flow and heat transfer near the rough walls, models based on equivalent sand roughness (e.g. Aupoix [34]) are predominantly used in the industry due to their low computational cost. These models, however, do not reproduce the physics of near wall flow and rely on an a priori knowledge of the equivalent sand roughness value. In comparison to that, simulations based on discrete element approach (Taylor et al. [35]; Stripf et al. [36]), in which the governing equations are solved below the roughness crest, provide a higher fidelity. Nevertheless, in this kind of approach the fluid-solid interface is not resolved, but effectively modeled, hence cannot be considered fully physical. The highest fidelity approach is to calculate the flow using DNS in which the interface is resolved. Due to high computational cost, there are a very limited number of such calculations reported in literature. Most of these studies are based on simple roughness geometries. For example Nagano et al. [37] simulated heat transfer over square transverse ribs in a channel in a relatively low Reynolds number. Orlandi et al. [38] solved conjugate heat transfer in a channel with transverse ribs and cubes attached to the wall. Recently, Forooghi et al. [39] reported the first DNS based on realistic CCD geometry on a piston head. These authors conducted simulations in a channel geometry and focused on the characterization roughness and its effect on flow and heat transfer.

3 Experimental setup, measurement techniques, and analytical methods

3.1 Experimental setup

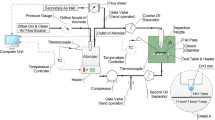
The experiments shown in this paper have been conducted using a single cylinder research engine. The base engine is a single cylinder motorcycle engine which is used in BMW F650. The engine has been equipped with a prototype aluminum cylinder head which features a pent roof combustion chamber with four squish areas. The cylinder head has been equipped with four endoscopic optical accesses. To one of these accesses a fast response surface thermocouple has been applied in order to be able to measure the surface temperature for the heat flux calculation. The engine is equipped with a centrally mounted injector. The spark plug and the injector are aligned longitudinal to the crankshaft. The basic engine data is shown in Table 1 and the layout of the engine setup can be seen in Fig. 1. The injector is a production-model solenoid actuated, multihole injector. For all experiments an engine speed of 2000/min, a coolant temperature of 90\(^{\circ }\)C, an oil temperature of 80\(^{\circ }\)C and a stoichiometric air-fuel ratio (\(\lambda\) = 1) was used. The engine was operated using a single injection during the intake stroke resulting in a homogeneous operation. The fuel was conventional gasoline with 5% ethanol content. The fuel properties are given in Table 2.

Table 1 Engine data
Full size table
Table 2 Fuel properties
Full size table
Fig. 1
figure 1

Experimental setup

Full size image
Fig. 2
figure 2

Measuring process

Full size image

The in-cylinder pressure is measured using a Kister 6045 piezo-electrical pressure transducer, the low pressure traces are measured using piezo-resistive transducers (intake Kistler 4045, exhaust Kistler 4045). The high pressure data is used to calculate the in-cylinder temperature according to the ideal gas law. For each measurement point 250 consecutive cycles with a resolution of 3600 pulses per revolution were recorded.

For each operating point the engine was run for 8 h under fired operation during the tests for the deposit evaluation on the fast response surface thermocouples. The time interval of 8 h was sliced into shorter periods of 1 h enclosed by motored operation in order to be able to calculate the deposit properties. During fired operation approximately every five minutes a measurement was performed. Additional measurement points were recorded during motored operation shortly before and after fired operation. The measuring process is shown in Fig. 2.

For the evaluation of the piston deposits a simpler approach was used. The engine was operated for 4 h under the above-mentioned conditions without any breaks.

3.2 Measurement techniques

3.2.1 Setup for the measurement of CCD on the piston head

To get information about CCD the piston of the test engine is equipped with a slot for an exchangeable sample probe plate. The dimension of the plates is 77 mm \(\times\) 37 mm. Figure 3 shows the piston head with the rectangular slot for the plate. To ensure the heat transfer between the piston and the sample probe plate both surfaces were machined very precisely. Nevertheless there might be a slight change in surface temperature. A possible higher surface temperature would increase the deposit oxidation and decrease the layer thickness. Pilot tests with heat transfer paste showed that the paste is expelled from the gap underneath the plate. The paste which conglomerates on top of the plate might influence the deposit formation and the EDX measurements as well as the change in surface temperature. Therefore no heat transfer paste was used for the experiments. Optical investigations showed that the sample probe plate had no major visible influence on the surface structure or the speed of the deposit formation. After each test run the engine was disassembled to remove the laden sample probe plates from the piston and to clean the piston head surface for subsequent experiments [40].

Fig. 3
figure 3

Piston with rectangular slot for sample probe plate after engine experiment [40]

Full size image

3.2.2 Fast response surface thermocouples

In order to be able to calculate the instantaneous heat flux the surface temperature has to measured with a high temporal resolution. Therefore the instantaneous surface temperatures were measured using fast-response surface-thermocouples. The thermocouples were inserted into the cylinder head using removable sample plugs. For the investigations modified type K thermocouples with a diameter of 0.5 mm were used. During the manufacturing process the thermocouple was clued into the sample plug and milled flush with the surface. Hence the thermocouple junction was disconnected. Afterwards the surface was coated with chromium and gold in order to rebuild the thermocouple junction again. The manufacturing process of these thermocouples is described in detail in [41].

The properties of the new junction are unknown and might differ from the original properties. Therefore the surface-thermocouples were calibrated using an ice bath and an oven. A resistance thermometer (Pt 100) was used as reference. The maximum temperature deviation between the surface-thermocouple and the resistance thermometer in the investigated temperature range, which ranges from 0\(^{\circ }\)C to approximately 155\(^{\circ }\)C was below 2.2 K and therefore smaller than the allowed temperature deviation using commercially available tolerance class two thermocouples.

According to Eq. 12 the heat penetration coefficient b has to been known in order to be able to calculate the instantaneous heat flux. The fast-response surface thermocouples are made from a combination of different materials. Therefore the heat penetration coefficient can not be determined by a theoretical approach. Huber [28] described an experimental approach to measure the heat penetration coefficient. If two semi-infinite slabs with different temperatures are brought into contact a time-independent contact-temperature is reached. If this contact-temperature and further variables are measured the heat-penetration coefficient can be calculated according to Eq. 7. The sample plugs which carry the fast-response thermocouples have been calibrated using a water bath. Figure 4 shows a typical temperature trace of the experiment for the determination of the heat-penetration coefficient. To reduce the influence of the signal noise the temperature trace has been averaged in the red marked area.

$$\begin{aligned} b_1=b_2\frac{T_2-T_K}{T_K-T_1} \end{aligned}$$
(7)
Fig. 4
figure 4

Temperature trace for the determination of the heat penetration coefficient

Full size image

3.2.3 Optical profiler

A nanofocus \(\mu\) surf expert confocal 3D microscope was used to analyse the surface structure of the removable sample plugs. For the measurements a 10\(\times\) magnification was applied. In order to be able to study a wide area the automated axis drive in x- and y-direction was used. The error which was introduced due to a tilted surface of the specimen was corrected be means of built-in software functions.

Fig. 5
figure 5

Example of the surface roughness measurement (upper figure before engine operation, lower figure after 8 h of engine operation)

Full size image

Figure 5 shows the surface roughness of one of the sample plugs as-fabricated and after the 8 h test run. In the middle of the 6 mm \(\times\) 6 mm patch the modified thermocouple can be clearly seen. It must be considered that the sample plugs are not aligned in the same way due to the restricted positioning accuracy of the measuring device. The arithmetic average roughness differs by a factor of two but nevertheless both surfaces can be considered hydraulically smooth in the context of internal combustion engines. Therefore the change in surface roughness does not change the convective heat transfer and is not considered for the heat flux calculation.

In the addition to the surface roughness measurements the optical profiler has been used to measure the deposit hight. In a small area of the sample the deposit layer has been scratched of the surface, exposing the metal surface of the sample plug. Afterwards the profiler measured the surface profile which was used to calculate the hight of the generated step. Although this technique appears simple it produces valuable information. Because the edge produced by the scratching routine is not very defined the evaluated areas had to be selected manually. Figure 6 shows the steps after scratching of the deposit layer partly. The areas which are are used for the determination of the layer thickness are marked in red. To reduce noise the the sample points of the lower and higher step are averaged.

Fig. 6
figure 6

Example of the evaluated areas for the deposit layer thickness calculation

Full size image

3.2.4 SEM/EDX

In order to be able to investigate the microstructure of the deposits, scanning electron microscope (SEM) measurements have been conducted. During the measurement the sample surface is scanned by a focused beam of electrons. The electrons interact with the sample surface and produce signals which can be used image the surface topography. Due to charge effects the measurements had been made using the environmental scanning electron microscope (ESEM) mode of the measuring device at a pressure of 70–120 Pa. Magnifications between 100\(\times\) and 10,000\(\times\) haven been used for the studies presented in this Paper.

In addition to the SEM measurements Energy-dispersive X-ray spectroscopy measurements have been conducted to characterise the chemical composition of the deposits. This information is especially useful if it is unclear whether the the deposits are fuel or oil derived.

3.3 Analytical methods

Based on the measured temperature oscillations, the transient heat flux is derived as described in [5, 27,28,29,30, 32]. Assuming the temperature field to be of one-dimensional character, the Fourier differential equation for transient temperature fields narrows down to:

$$\begin{aligned} \frac{\partial T}{\partial t}=a \frac{\partial ^2 T}{\partial x^2}. \end{aligned}$$
(8)

Assuming a semi-inifinite wall and a steady state heat flux, the solution for Eq. 8 can be formulated in closed-form using Fourier series:

$$\begin{aligned} T(x,t) = T_{m} - \frac{{\dot{q}_{m} }}{\lambda }x + \sum\limits_{{i = 1}}^{\infty } {e^{{ - x\sqrt {\frac{{i\omega }}{{2a}}} }} } \left[ {A_{i} \cos \left( {i\omega t - x\sqrt {\frac{{i\omega }}{{2a}}} } \right)} \quad + B_{i} \sin \left( {i\omega t - x\sqrt {\frac{{i\omega }}{{2a}}} } \right)\right]. \\ \end{aligned}$$
(9)

Considering the one dimensional character of the heat flux means:

$$\begin{aligned} \dot{q} = -\lambda \frac{\partial T}{\partial x}\text {,} \end{aligned}$$
(10)

and Eq. 9 can be derived to

$$\begin{aligned} \dot{q}(x,t) = \dot{q}_{m} + \lambda \sum\limits_{{i = 1}}^{\infty } {\sqrt {\frac{{i\omega }}{{2a}}} } e^{{ - x\sqrt {\frac{{i\omega }}{{2a}}} }} \left[ {A_{i} \cos \left( {i\omega t - x\sqrt {\frac{{i\omega }}{{2a}}} } \right)} + B_{i} \sin \left( {i\omega t - x\sqrt {\frac{{i\omega }}{{2a}}} } \right)\right]. \\ \end{aligned}$$
(11)

Using Eq. 11, it is possible to evaluate the heat flux at any given position x in the combustion chamber wall. Focussing on the derivation of the heat flux at the combustion chamber surface (\(x= 0\)), the thermal conductivity \(\lambda\) and the thermal diffusivity a in Eq. 11 can be substituted with the experimentally determined heat penetration coefficient b:

$$\begin{aligned} b = \sqrt{\lambda \rho c_{\text {p}}} = \frac{\lambda }{\sqrt{a}}. \end{aligned}$$
(12)

Accordingly, the heat flux at the surface thermocouple can be described as

$$\begin{aligned} & \dot{q} = \dot{q}_{\text {m}} + b \sum _{i=1}^\infty \sqrt{\frac{i \omega }{2}} \nonumber \\&\quad \left[ \left( A_i +B_i \right) \cos \left( i \omega t \right) + \left( A_i - B_i \right) \sin \left( i \omega t \right) \right] \end{aligned}$$
(13)

where \(A_i\) and \(B_i\) can be determined from the measured temperature oscillations using a fast Fourier transform. Whenever the gas temperature equals the surface temperature, the instantaneous heat flux is assumed to be negligible. Thus, \(\dot{q}_{\text {m}}\) is evaluated using the calculated bulk gas temperature as described in [42, 43]. In order to account for the difference in the thermal properties of combustion chamber [29] and deposit layer, an analytical approach enabling the calculation of heat conduction in a composite slab subject was used [5]. According to [44], measured temperatures at the thermocouple surface are typically overestimated due to the difference in the material properties between thermocouple and engine. Decent results for the calculated transient heat flux using the experimentally determined heat penetration coefficient b were reported in  [5, 28, 32].

3.4 Deposit layer thickness calculation according to Hopwood [45]

In clean condition the temperature on the metal surface of a combustion chamber wall can be measured by means of a fast thermocouple. In a cycle a temperature swing with a maximum during combustion will be detected. When deposits grow on the surface the measured temperature is no longer the surface temperature. As the deposit is a thermal insulator compared to the metal surface the measured temperature curve is damped. Its maximum decreases and is shifted towards later crank angles. The bigger the deposit layer thickness is the later the temperature maximum at the thermocouple occurs. Hopwood has derived a semi-empirical correlation between the thermal diffusivity and the shift of the temperature maximum as shown in the following equation

$$\begin{aligned} \begin{array}{ll} T(x,t)= 2 \exp &{}\left( -x \sqrt{\frac{\pi }{\alpha _{CCD} t_{0}}}\right) \\ &\cos \left( \frac{2\pi (t-\frac{t_0}{12})}{t_0} -x \sqrt{\frac{\pi }{\alpha _{CCD} t_{0}}} \right) \\ &2 \exp \left( -x \sqrt{\frac{2\pi }{\alpha _{\text {CCD}} t_{0}}}\right) \\ &\sin \left( \frac{4\pi (t-\frac{t_0}{12})}{t_0} -x \sqrt{\frac{2\pi }{\alpha _{\text {CCD}} t_{0}}} \right) \\ \end{array} \end{aligned}$$
(14)

The term \((-t_0/12)\) insures that the temperature maximum at the surface always occurs at TDC. The measured position of the temperature maximum behind the deposit layer \(t_{T_{\text {max}}}\) is then equal to the time shift of the temperature maximum \(\Delta t\). After derivation of Eq. 14 dT/dt is set to zero and it follows

$$\begin{aligned} \begin{array}{ll} \exp &{} \left( (1-\sqrt{2})x \sqrt{\frac{\pi }{\alpha _{\text {CCD}}t_0}}\right) \\ \sin &{} \left( \frac{\pi }{6} + \frac{4 \pi t_{T_{\text {max}}}}{t_0} -x \sqrt{\frac{\pi }{\alpha _{\text {CCD}} t_{0}}} \right) \\ &{}=\sin \left( \frac{\pi }{6} + \frac{2 \pi t_{T_{\text {max}}}}{t_0} +x \sqrt{\frac{\pi }{\alpha _{CCD} t_{0}}} \right) \end{array} \end{aligned}$$
(15)

With the assumption of thin deposit layers the following applies:

$$\begin{aligned} \exp \left( (1-\sqrt{2})x \sqrt{\frac{\pi }{\alpha _{\text {CCD}}t_0}}\right) \approx 1 \end{aligned}$$
(16)

If \(t_{T_{\text {max}}}\) is replaced by \(\Delta t\) and x by the layer thickness d, the thermal diffusivity can be calculated by the following equation

$$\begin{aligned} \alpha _{\text {CCD}}=\left( \frac{d}{\Delta t} \right) ^2 \frac{t_0}{\pi } 0.209 \left( 1- \frac{\Delta t}{4t_0} \right) ^{-2} \end{aligned}$$
(17)

Hence, at a given \(\Delta t\) and \(t_0\) the thermal diffusivity is proportional to the square of the layer thickness. To finally calculate the thermal conductivity \(\lambda\) the specific heat capacity c and the material density \(\rho\) is needed:

$$\begin{aligned} \lambda _{\text {CCD}} = \alpha _{\text {CCD}} \cdot \rho _{\text {CCD}} \cdot c_{\text {CCD}}. \end{aligned}$$
(18)

3.5 Deposit layer thickness calculation according to the two-layer-method

The two-layer-method it is feasible to calculate the current thickness of the deposit layer and the real heat flux at the deposit surface. It is an analytical approach that allows calculation of heat conduction in a composite slab subject with periodic temperatures. The heat transfer equations for multiple layers with different material properties are solved by Laplace-transformation. A detailed explanation of this method can be found in [46]. It was originally developed with the focus on heat transfer problems of buildings. For the first time, this approach was used to determine the deposit thickness and the heat flux at the surface of the deposit in combustion chambers of engines in [5].

4 Results

4.1 Characterization of CCD on piston and cylinder head

Fig. 7
figure 7

Optical detection of fuel spray piston surface interaction IMEP = 4 bar, SOI = 300 \(^{\circ }\) CA bTDCf

Full size image
Fig. 8
figure 8

Top: CCD on piston plate, bottom: CCD on cylinder head probe (partly removed for layer thickness measurement) IMEP = 4 bar/SOI = 300 \(^{\circ }\)CA bTDCf

Full size image
Fig. 9
figure 9

Roughness measurement, top: clean plate; bottom: plate with CCD, IMEP = 4 bar, SOI = 300 \(^{\circ }\)CA bTDCf

Full size image
Fig. 10
figure 10

Top: clean probe with thermocouple in center; bottom: probe with CCD, IMEP = 4 bar, SOI = 300 \(^{\circ }\)CA bTDCf

Full size image

Focus of these investigations was the influence of operation conditions on CDD structures and their effects on heat transfer through cylinder walls. Generally there are several outstanding issues on the interaction between CCD and the different in-cylinder processes such as mixture formation (spray-wall-interaction), fuel storage in CCD with resulting soot formation, heat flux reduction and boundary layer influence on near wall flow and convective heat transfer as described in the section motivation and state of the art. To investigate the influence of operation conditions the engine was operated at three loads with IMEP = 2 ,4 ,and 6 bar. At IMEP = 4 bar the start of Injection was varied from early timing at 300 \(^\circ\)CA bTDCf to later timing at 260 \(^\circ\)CA bTDCf to investigate the effect of fuel spray piston surface interaction. In Fig. 7 the fuel spray is shown 9 \(^\circ\)CA after start of injection. The injector is a Bosch HDEV 5.2 with 6 holes. The white lines depict the spray impingement on the piston. Hence, fuel droplet on piston surface interaction is at least partly responsible for CCD formation on the investigated piston plate which is shown in Fig. 8.

To assess different formation processes a screwable adapter was mounted on the piston and in the cylinder head as described in Sects. 3.2.1 and 3.2.2. The position of the cylinder head sample plug was in the endoscopic access which was used for the optical detection of the fuel spray in Fig. 7. By the optical measurements it could be proofed that there is no direct contact of liquid fuel at this position of the cylinder head. As described in [47, 48] it is assumed that CCD at this part of the combustion chamber possibly comes from oxidation products of the fuel combustion and to some extent oil combustion which condense on the combustion chamber surface and subsequently undergo a polymerization process. The CCD act as a thermal insulating layer by decreasing the thermal conductivity. This work also addresses the question if the surface structure essentially affects the near wall gas flow and if the resulting change in the convective heat transfer has to be taken into account. This question could be answered by direct numerical simulations in the following chapter. To measure the heat flux the cylinder head adapter was equipped with a fast thermocouple. This allows to calculate the layer thickness using the model of Hopwood [45] and by comparison with the measured thickness the value for the thermal conductivity as a function of density and heat capacity of the CCD layer can be calculated. This is shown in Sect. 3.4. Therefore the measurements of the layer thickness and the roughness are carried out in the area of the thermocouple position.

In Fig. 8 the area in which the CCD is characterized is shown in blue on the piston plate (top) and the cylinder head adapter (bottom). In both cases the colors of the CCD vary from middle brown to black. Without any magnification the CCD appears smooth and apart from the color—homogeneous in its structure. Only at the right part of the intake side of the piston plate an inhomogeneous structure can be noticed. A kind of single black flakes or islands with higher structure heights occur. Before characterizing the CCD surface roughness it is important to know the Structure of the ground material to judge whether the CCD layer forms its own structure or just copies the structure of the material surface below. The CCD formation process was monitored by a camera through the endoscopic access. After operation of 2 h no change in the CCD could optically be detected. The engine then was operated for another 2 h. After this test the CCD was considered to be in stationary state.

Fig. 11
figure 11

SEM surface images, magnification \(\times\)100, upper row: cylinder head, lower row: piston, 1. Column: IMEP = 4 bar/SOI = 300 \(^{\circ }\)CA bTDCf, 2. Column: IMEP = 4 bar/SOI = 260 \(^{\circ }\)CA bTDCf, 3. Column: IMEP = 6 bar/SOI = 300 \(^{\circ }\)CA bTDCf, 4. Column: IMEP = 2 bar/SOI = 300 \(^{\circ }\)CA bTDCf

Full size image
Fig. 12
figure 12

SEM surface images, magnification \(\times\)1000, upper row: cylinder head, lower row: piston, 1. Column: IMEP = 4 bar/SOI = 300 \(^{\circ }\)CA bTDCf, 2. Column: IMEP = 4 bar/SOI = 260 \(^{\circ }\)CA bTDCf, 3. Column: IMEP = 6 bar/SOI = 300 \(^{\circ }\)CA bTDCf, 4. Column: IMEP = 2 bar/SOI = 300 \(^{\circ }\)CA bTDCf

Full size image
Fig. 13
figure 13

SEM surface images, magnification \(\times\)10,000, upper row: cylinder head, lower row: piston, 1. Column: IMEP = 4 bar/SOI = 300 \(^{\circ }\)CA bTDCf, 2. Column: IMEP = 4 bar/SOI = 260 \(^{\circ }\)CA bTDCf, 3. Column: IMEP = 6 bar/SOI = 300 \(^{\circ }\)CA bTDCf, 4. Column: IMEP = 2 bar/SOI = 300 \(^{\circ }\)CA bTDCf

Full size image
Table 3 Roughness and structure heights on piston and cylinder head
Full size table
Table 4 Lubricating oil characteristics
Full size table

Figure 9 (top) shows the topography of the piston plate. It has an average roughness of \(R_{\text {a}}\) = 1.6 \(\upmu\)m. The scoring of the manufacturing process can clearly be seen in the vertical direction. The maximum structure height is around 10 \(\upmu\)m. On the right the roughness measurement of the CCD surface is shown. The scoring of the plate structure can still slightly be noticed. But most of the basic structure is filled with CCD and the maximum structure height is around 5 times of that of the unladen plate. The mean roughness of the deposit layer is \(R_{\text {a}}\) = 4.7 \(\upmu\)m. Obviously, the basic structure of the piston surface is not decisive for the structure of the CCD under these conditions. The SEM image with 100\(\times\) magnification also shows a homogeneous structure that seems to have equally distributed elevations on a smooth ground Fig. 11 (column below). At higher magnifications [Figs. 12 and 13 (column below)] it can be noticed that many small more or less globular particles form clusters which result in a rugged and porous surface. At the cylinder head the CCD roughness is half of that on the piston. Again the surface structure of the CCD significantly differs from the ground material as can be seen in Fig. 10. The roughness of the clean adapter is \(R_{\text {a}}\) = 1.28 \(\upmu\)m whereas the CCD shows roughly the double value of \(R_{\text {a}}\) = 2.45 \(\upmu\)m. On the SEM image in Fig. 11 (1. column above) a inhomogeneous surface can be seen. Especially with higher magnifications in Figs. 12 and 13 the surface appears to consist of single structures like ice-floes which show clear cracks on the upper right side. The floes itself seem to be very even and smooth.

To investigate the influence of fuel impingement on the piston surface the SOI was shifted from 300 to 260 \(^\circ\)CA bTDCf at IMEP of 4 bar. A late injection results in little interaction between the fuel spray and the piston head. At low magnification the surface looks similar to that at SOI = 300 \(^\circ\)CA bTDCf (Fig. 11 (2. column below)). At a second glance at higher magnifications (Figs. 12, 13) again clustered structures can be seen which are noticeably separated this time and the roughness is slightly higher at \(R_a\) = 5.8 \(\upmu\)m. At the cylinder head again the ice-floe like structure appears. This time no cracks are visible. The roughness is almost the same with \(R_a\) = 2.0 \(\upmu\)m. But at higher magnifications a clear difference can be noticed. The floes do not have a smooth and compact surface but consist of a very small, branched skeletal substructure.

An important parameter for CCD formation is the surface temperature of the combustion chamber walls. It influences the condensation of combustion products and their polymerization process on the surface. The surface temperature correlates with the engine load. The higher the load is, the higher the temperatures are. Therefore, a load variation was conducted. Starting from the base point at 4 bar IMEP the load was increased to 6 bar and decreased to 2 bar. The SOI was 300 \(^\circ\)CA bTDCf in all three cases. At the high load of IMEP = 6 bar the smoothest surface of all can be found. \(R_a\) is only 1.4 \(\upmu\)m and thus in the range of the ground plate. The microstructure at highest magnification in Fig. 13 (3. column below) looks like a mixture between those of IMEP = 4 bar. On the cylinder head adapter the floe-like structure can be seen again. This time with many cracks and a different microstructure compared to the last two cases. The floes seem to consist of very small granular particles. The roughness of \(R_a\) = 2.2 \(\upmu\)m does not significantly differ from the roughness values at IMEP = 4 bar. However, an essential difference appears at the low load of IMEP = 2 bar. At the piston plate the roughness increases to \(R_a\) = 18.7 \(\upmu\)m, the far highest value of all surfaces. Additionally noticeable is the maximum height of single structures up to 400 \(\upmu\)m. In the SEM image at highest magnification (Fig. 13 (4. column below)) it seems like isolated structures grow on a smooth and even ground. At the cylinder head again the floe-like structure is visible. As on the piston the highest roughness of all cases of \(R_a\) = 4.2 \(\upmu\)m was measured. In contrast to the piston plate no conspicuous high structure element can be found. The microstructure differs from the other three operating points. The floes consist of small beads that form regular small clusters. All roughness values and maximum structure heights are summarized in Table 3. Within the Collaborative Research Center, in which this work was performed, the viscous length scale in wall proximity was estimated to be between 7 and 19 \(\upmu\)m. The highest deposit peaks at the piston significantly tower above this viscous layer, the deposit peaks at the cylinder head at least partly do so. Hence, a rough wall exists on the surface of the CCD which might affect the convective heat transfer at the deposit surface. A DNS approach to assess this effect is described in Sect. 4.2.

Additionally to the roughness measurement and the surface characterization EDX measurements (energy dispersive X-ray spectroscopy) were performed to judge the oil contribution to the CCD formation. The additive concentrations of the lubricating oil are shown in Table 4. A very high content of sulfur and calcium can be noticed. Figure 14 shows the main components of the CCD on the cylinder head (above) and piston (below) measured by means of EDX. The absolute value of CPS/eV on the Y-axis is not of importance and therefore is not plotted. The CCD consist mostly of carbon and oxygen. Crucial is the occurrence of significant Ca- and S-Peaks. These elements can clearly be assigned to the engine oil. On the cylinder head these peaks are not noticeable. This is in accordance to the literature. In many studies it is stated that engine oil contributes rather to the piston CCD than to the cylinder head CCD [1].

Fig. 14
figure 14

Main components of CDD on cylinder head (above) and piston (below) measured with EDX

Full size image

It seems that the oil contribution leads to a higher roughness—not only when comparing the piston and cylinder head CDD. In a random trial at the base operating point of IMEP = 4 bar and n = 2000 rpm a valve stem seal with less pre-stress was used to increase the entry of oil into the combustion chamber. Figure 15 shows the surface roughness compared to the base point. The arithmetic average roughness Ra increases from 4.7 to 22.1 \(\upmu\) m which is the highest value of all measurements. The detailed results can be found in [40].

Fig. 15
figure 15

Surface structure with low oil entry (above) and increased oil entry (below), IMEP = 4 bar/SOI = 300 \(^{\circ }\)CA bTDCf

Full size image

4.2 DNS approach for flow and heat transfer near the rough walls

Direct Numerical Simulation is used to understand the effect of CCD roughness on flow and heat transfer. A full description of the solutions is available in Forooghi et al. [39], hence only the important aspects are briefly discussed here. The DNS is based on two surface maps extracted from a piston head. The average peak to valley roughness height of these surfaces is about (\(R_{\text {z}}\) =125 \(\upmu\)m) (\(R_{\text {a}}\) = 12–22 \(\upmu\)m). The exact fluid-solid interface geometry is reproduced in the simulations using an immersed boundary method, and the incompressible Navier Stokes and energy equations in the fluid domain are solved using a pseudo-spectral solver. The simulations are carried out in a standard channel DNS configuration, i.e. with periodic boundary conditions in the streamwise and spanwise directions. Isothermal boundary conditions are applied on the channel walls (one hot and one cold wall).

By varying the friction Reynolds number and roughness to channel height ratio, different values of roughness height \(k^+\) in viscous units (plus subscript indicates viscous units) are realized in the DNS, thereby transitionally and fully rough regimes as well as the value of equivalent sand roughness can be estimated. The results suggest that the equivalent sand roughness height of the simulated roughness geometries is about \(k_{\text {s}}=300\), i.e. approximately \(2.4R_{\text {z}}\). Based on available in-cylinder flow measurements, Forooghi et al. [39] estimated this to correspond to \(k_{\text {s}}^+\) values between 15 and 40. They also estimated a maximum two-fold increase in the convective heat transfer coefficient compared to a smooth wall for their specific Reynolds numbers.

The peak to valley roughness height of the cylinder-head deposits studied in the present paper is in the order of 10 \(\upmu\)m. By comparison to the DNS results, it is estimated that for this roughness \(k_{\text {s}}^+<5\), which corresponds to the hydraulically smooth regime; therefore, it can be argued that the presence of roughness in this problem has no influence on the convection heat transfer at the fluid-solid interface.

4.3 Deposit layer thickness calculation

As shown in Sects. 3.4 and 3.5 different approaches can be used to calculate the deposit layer thickness on top of the fast response surface thermocouples. Figures 16, 17, 18 and 19 show the calculated and measured deposit thickness. In addition to to symbols explained in the legend the red circle indicates the last value of the fitted data calculated according to Hopwood and the red square marks the measured deposit thickness. The best-fit curve has bee calculated using a polynomial function of degree 2 and a least square approach. The deposit thickness calculated during motored operation has been averaged over all measuring points recorded during this section of the test run. The most important parameters for the calculations are given in Table 5. The calculation according to Hopwood during fired operation is used as a reference, because the most data was recorded and evaluated under these operating conditions.

Fig. 16
figure 16

Calculated and measured deposit layer thickness, IMEP = 4 bar/SOI = 300 \(^{\circ }\)CA bTDCf

Full size image
Fig. 17
figure 17

Calculated and measured deposit layer thickness, IMEP = 4 bar/SOI = 260 \(^{\circ }\)CA bTDCf

Full size image
Fig. 18
figure 18

Calculated and measured deposit layer thickness, IMEP = 6 bar/SOI = 300 \(^{\circ }\)CA bTDCf

Full size image
Fig. 19
figure 19

Calculated and measured deposit layer thickness, IMEP = 2 bar/SOI = 300 \(^{\circ }\)CA bTDCf

Full size image

For the base point IMEP = 4 bar/SOI = 300 CA bTDCf the deposit increase shows a linear behavior regarding the calculation according to Hopwood during fired engine operation with only small deviations from the best fit curve. There is no indication that the deposit growth has reached steady-state or that there is a deceleration in the deposit growth rate. The calculation using the motored measuring points match the calculation during fired operation quite well during the first 4 h of operation. For longer operation times the calculation according to Hopwood using motored measuring point underestimates the best fit curve by a factor of about two whereas the two-layer method overestimates the reference. The deposit thickness measurement matches the thickness calculated according to Hopwood during motored operation very well.

Compared to the base point the deposit growth rate of the other operating conditions is increasing during prolonged engine operation. Therefore it can be assumed that the rate of growth has also not reached steady state for these operating points.

The start of injection has only a minor influence on the deposit thickness after 8 h of engine operation which can been seen in Fig. 17. The calculation as well as the measurements show only very small deviations from the base point measurements. The calculation according to Hopwood during motored operation underestimates the calculation during fired operation again. The calculation using the two layer method matches the calculated reference quite well. All calculation methods overrate the measured deposit thickness.

In contrast to the injection timing the engine load has a major influence on the deposit layer thickness. In the IMEP = 6 bar test run shown in Fig. 18 the deposit thickness is considerable smaller than in all other cases. In this case the calculation using the data recorded during motored operation overestimates the base calculation. The thickness measurement is overestimated by a factor of more than two. For the IMEP = 2 bar case no clear difference from the reference test run can be seen. Therefore there might be a threshold above which the increased surface temperature caused by a higher load leads to a oxidation of the deposit layer which decreases the rate of deposit formation.

For all shown parameter variations the measured deposit thickness is overestimated. Therefore it can be assumed that the parameters for the calculation which were chosen according to Hohenberg [29] do not match the properties of the deposit layer. A explanation of the correlation of the thermal properties and the deposit layer thickness can be found in Sects. 3.4 and 3.5.

Figure 20 shows the influence of the CCD density and the heat capacity on the thermal conductivity (IMEP = 4 bar/SOI = 300CA). According to Kalghatgi [15] there is a much wider range for the properties than stated by Hohenberg [29]. The values for the thermal conductivity calculated by the measured deposit thickness are in the range of 0.57–0.80 mK and therefore almost four times smaller than stated by Hohenberg. The values which were used for the calculations shown in this study (red square) are at the boundary of the reasonable range. Therefore it becomes obvious that care must be taken to ensure that the parameters chosen for the calculations match the properties of the deposits. This must be especially taken into account if the calculations are used to determine the surface temperature for heat flux calculations.

Table 5 Parameters used for the deposit thickness calculation
Full size table
Fig. 20
figure 20

Calculated influence of density and heat capacity on thermal conductivity, IMEP = 4 bar/SOI = 300 \(^{\circ }\)CA bTDCf

Full size image

5 Summary and conclusions

The study in this paper deals with the question how the operating conditions of an combustion engines influences the thermal properties of combustion chamber deposits. To generate deposits a single cylinder engine was operated with direct injection at an engine speed of 2000/min and three different loads (IMEP 2, 4 and 6 bar) and two injection timings (300 and 260 \(^\circ\)CA bTDCf). The piston was equipped with a removable sample plate on its surface to collect and characterize CCD on the piston top. In the cylinder head a removable cylindrical adapter was mounted which was equipped with a fast response thermocouple to again characterize the CCD at this position in the combustion chamber and to additionally measure the temporally resolved temperature at the surface of the cylinder head. By means of an optical profiler the roughness of the CCD surface was measured. With a scanning electron microscope the structure of the surfaces was depicted.

The results show that the roughness on the piston in most cases is bigger than on the cylinder head. On the piston the average roughness ranges from 1.4 to 18.7 \(\upmu\)m and valley to peak heights from 20 to 400 \(\upmu\)m. On the cylinder head average roughness is between 2.0 and 4.2 \(\upmu\)m and valley to peak heights 10–15 \(\upmu\)m. On the piston as well as on the cylinder head the biggest roughness occurs at low load whereas the influence of SOI plays a minor role. The analysis of the deposit composition suggests a contribution of lubricating oil to the CCD formation only on the piston top. With an additional random trial with increased oil entry into the combustion chamber a trend can be recognized that oil leads to higher roughness values of the CCD.

Using the measured roughness values a DNS was performed to simulate the near wall flow. The result showed that the CCD surface has to be considered as a rough wall which affects the near wall flow. But the influence on the convective heat transfer can be neglected compared to the influence of the thermal insulation on the heat flux through the deposit layer. Consequently only the thermal properties of CCD are important regarding the wall heat losses but not their structure. CCD influence on wall heat losses is merely a conductive heat transfer problem.

Applying the method from Hopwood the thickness of the CCD layer was calculated on the base of the measured attenuation of the temperature oscillation on the surface of the cylinder head adapter containing fast thermocouples. Basic CCD properties such as density, thermal conductivity and heat capacity were taken from the literature [29]. Compared to the measured thickness values the calculation overestimates the thickness in all cases. It seems that the literature value for the thermal conductivity is noticeably too high. Taking into account the whole range of values for the density (1100–2000 kg/m\(^3\)) and heat capacity (840–1840 J (kg/K) of the CCD given in the literature [15] the thermal conductivity reaches values between 0.23 W/(mK) (at IMEP = 4 bar and SOI = 300 \(^\circ\)CA bTDCf) and 1.34 W/(mK) (at IMEP = 4 bar and SOI = 260 \(^\circ\)CA bTDCf). A correlation between the thermal conductivity and the CCD surface properties could not be observed.