Multi-armed bandits for performance marketing

Abstract

This paper deals with the problem of optimising bids and budgets of a set of digital advertising campaigns. We improve on the current state of the art by introducing support for multi-ad group marketing campaigns and developing a highly data efficient parametric contextual bandit. The bandit, which exploits domain knowledge to reduce the exploration space, is shown to be effective under the following settings; few clicks and/or small conversion rate, short horizon scenarios, rapidly changing markets and low budget. Furthermore, a bootstrapped Thompson sampling algorithm is adapted to fit the parametric bandit. Extensive numerical experiments, performed on synthetic and real-world data, show that, on average, the parametric bandit gains more conversions than state-of-the-art bandits. Gains in performance are particularly high when an optimisation algorithm is needed the most, i.e. with tight budget or many ad groups, though gains are present also in the case of a single-ad group.

1 Introduction

Digital advertising expense in the USA reached 189 billions USD in 2021, showing a staggering 35% year-over-year growth [25]. This was the highest level of growth seen since 2006 [26] and was to be partially imputed to COVID-19 restrictions and the consequent reliance on digital media: a deceleration in advertising revenues was thus to be expected. Moreover, the macroeconomic climate (high inflation rates, raising interest rates and economic uncertainty throughout 2022) impacted marketing budgets among others. Nevertheless, in 2022, far from decreasing, digital advertising expense reached a two-digit growth (10.8%) with respect to 2021, totalling 210 billions USD in the USA [26]. These numbers show that digital marketing is an ever so important expense item for brands. Moreover, the current shift in focus from growth to profitability due to raising costs and interest rates means it is vital to efficiently and effectively manage digital marketing budget.

This challenge has attracted the interest of the machine learning community for a manifold of reasons. Being fully digital, it is possible to reliably measure the impact of decisions, hence closing the data loop between action and reward. Moreover, tabular data consisting of many dimensions are appealing for learning algorithms, as opposed to human intuition. Finally, and crucially for this contribution, this endeavour can be seen as an exploration–exploitation dilemma: the algorithm in charge of optimising marketing expense (the agent) has to balance the need of gathering more data from the environment (exploration) to make sharper decisions and the need to limit the cost of data acquisition (exploitation).

Three digital advertising formats account for the overwhelming majority (93%) of the total spend: search ads (40%), display ads (30%) and digital video ads (23%). Major advertising platforms share the same basic strategy for choosing which ads get shown to internet users: every time a user is eligible for seeing an ad, compatible advertisers take part in an automated auction. For every ad, the advertiser is thus called to choose wisely a target (i.e. keywords and user profiles), a bid for the auctions and a maximum daily budget (i.e. the maximum total expense one wants to sustain for that ad in a day).

While a complete description of the different auction types is beyond the scope of this work, they mainly belong to three kinds: Generalized Second Price, VCG [35] and First Price [11]. Moreover, the advertiser can be charged on the basis of different principles, the most common of which are CPM (cost-per-mille, i.e. payments are based on the number of impressions, expressed in thousands), CPC (cost-per-click) and CPA (cost-per-acquisition, i.e. payments are based on the number of contacts or sales).

For definiteness, in this work we focus on Generalized Second Price auctions with CPC payments, typical of Search Engine Marketing. In this setting, the bid represents the maximum cost the advertiser is willing to pay if the user clicks on the ad. However, as will become apparent, the methods can be easily adapted to other kinds of auction and charging principles.

While it is often assumed [18, 37] that bidding one’s private value truthfully is the optimal strategy in second-price auctions, this holds only under the unrealistic assumption of infinite budget [24]. Moreover, and crucially in our setting, in order to truthfully bid the private value the bidder must know it, and this assumption is typically unrealistic [37]. It follows that the bidder must sequentially learn the optimal bids.

Search Engine Marketing ads are typically organised into three hierarchical levels [17]: campaigns, ad groups and the ads themselves. The primary purpose of this layered structure is to help advertisers organise their online advertising efforts. In particular, a campaign is usually associated to a specific advertising objective: for instance, two campaigns can be used to market different products sold by one advertiser. Moreover, for a fixed product, one can arrange several campaigns in order to segment the audience (i.e. to reach distinct demographic or geographic targets). Campaigns are sub-divided into ad groups: these serve as organisational units, in which advertisers group together ads that share a common theme, an aligned message or the same target audience and the associated keywords.

As an example, we can think of an advertiser that sets up two campaigns to market two coding courses, and each campaign is divided into two ad groups: one contains the ads that are targeted to students and the other one the ads targeted to professionals.

In major online advertising platforms, the daily budget is assigned at the campaign level. In other words, ad groups within a campaign share the budget allocated to the overall campaign. The bids are, instead, set at the ad group level. The budget applies to the entire campaign since it is associated with how much the advertiser is willing to spend to achieve a specific advertising objective; on the other hand, differing targets, ads and keywords (even within the same campaign) usually imply differing competition landscapes, hence bids are regulated at the more granular ad group level.

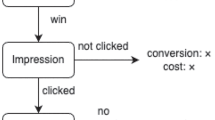
We consider here the common situation in which a total daily budget is given, and it must be split across a set of several campaigns. We will henceforth call such set a portfolio of campaigns.¹ The layered structure of a stylised digital advertising portfolio is depicted in Fig. 1.

Fig. 1

The structure of a portfolio of two campaigns, each of which contains two ad groups, in turn containing two ads each

Two recent works [21, 22] have cast the daily bid/budget optimisation as a multi-armed bandit problem. In particular, the goal is to maximise the long-term revenue, choosing daily the combination of bids and budgets for the whole portfolio over which the total budget is set. To this end, the whole combination of bids and budgets is the arm of the bandit that the learning agent plays.

In particular, the authors of [21] note that, when the agent plays one such combination, it does not observe just the total number of clicks and conversions gained by the portfolio over the day: it observes also the individual numbers of clicks and conversions totalled by each ad group. In other words, even if the space of possible actions is combinatorial in nature, a richer feedback with respect to the pure bandit feedback makes the problem manageable, as the agent can learn how to associate the bids and budget of a single campaign to the expected number of clicks. As the whole combination of bids a budgets can be seen as a collection of arms of single, simpler bandits (the campaigns and the ad groups), it is called the super arm of a combinatorial bandit [9, 28, 29]. Campaigns are in turn seen as static contextual bandits [1]: similar bid/budget combinations for a campaign share information. The fixed context (feature) vector is indeed given by the bids/budget pair.

The application of these results in practical settings is, however, limited by the following shortcomings:

• (i) The literature concentrates on campaigns without substructure (single-ad group campaigns). This means that, besides the budget, only one bid must be chosen per campaign. However, the typical campaign is divided into ad groups, thus requiring generalisation. Given the regression model introduced in [21], this generalisation is non-trivial.

• (ii) Agnostic nature of Gaussian processes (GPs) with respect to the functional form which links bid to observed clicks. While this method is very flexible, it also reflects in the need for more data to converge to a sensible posterior, if compared to a more informed model (in particular, a parametric model).

• (iii) The need to extrapolate, from the observed clicks, the so-called saturation clicks, i.e. the number of clicks we would have observed if we did not have budget constraints. The authors of [21] suggest using the time of the day when the daily budget finished and an estimate of the distribution of the number of clicks during the day to perform the extrapolation (see also [22] where the example of constant distribution is given). However, this information is not available, and ad frequency is explicitly reduced throughout the day to make sure the budget lasts until the end of the day [17]. Other metrics could be used to this end, but they are inherently noisy. Perhaps more importantly, this extrapolation method needs a certain share of the total budget to be always reserved for exploration (akin to $\varepsilon$-greedy strategies). The need for this missing data imputation stems from the use of vanilla GPs (i.e. with a Gaussian likelihood [38]). On the other hand, censored regression is a principled way to avoid the need for missing data imputation. While GPs can accommodate non-Gaussian likelihoods, this requires giving up exact update formulas, and switching to approximate methods [14].

Reasons (ii) and (iii) point to parametric regression, exploiting a functional form suggested by domain knowledge, as a way to use data more efficiently and without resorting to proxies. In this spirit, a recent work [16] has overcome aforementioned shortcomings making the following contributions:

• To address point (i) above, a multi-ad group generalisation of the relation between bid/budget and clicks was developed (Sect. 2), suitable regardless of the regression model one employs.

• To tackle points (ii) and (iii) above, an informed alternative to GP regression has been devised, namely a parametric regression model, which accounts for censoring in a principled way and with interpretable parameters (Sect. 3.1).

• The use of such a model in the context of bandits (and specifically Thompson sampling) has been explored (Sect. 3.2). In particular, bid and budget selection are recast as local constrained optimisation problems, as opposed to global optimisation required by GPs: this brings advantages both in terms of resource requirements and accuracy of the found optimum.

• To test and compare performances of the proposed approach, a simulation environment was developed, built on what is known about the inner workings of the auctions (Sect. 4.1). Numerical results reported in Sect. 4.2 confirm the advantages of the proposed method.

This paper extends [16] by making the following novel contributions:

• The performance of the approach proposed in [16] has been extensively tested on real-world data by exploiting the Criteo Attribution Modeling for Bidding Dataset [12] (described in Sect. 5.1).

• With an eye to applications, bootstrapped Thompson sampling [23, 28], an easy to implement approximated Bayesian inference method, has been adapted to our contextual bandit and tested (see Sect. 3.3).

• The impact of various parameters on model’s performance has been studied on the Criteo dataset. Furthermore, an ablation experiment, to study the effect of the model alone on single-ad group campaigns, has been performed (Sect. 5.2).

The paper is organised as follows: In Sect. 2, we set the notation and define the multi-ad group optimisation problem. In Sect. 3, we analyse how the optimisation can be carried out using a parametric Bayesian regression model. Section 4 is devoted to testing the proposed technique in an artificial simulated environment, while in Sect. 5 we test it on real-world data. Finally, we draw the conclusions and trace the next steps in Sect. 6.

2 Optimisation problem

In this section, we generalise the single-ad group model to multiple ad groups per campaigns. To do so, we first establish the notation in the single-ad group regime and proceed with the generalisation below.

We follow [21] and assume for now that we have a portfolio of N campaigns, each with just one ad group. Let’s call $n_j(b_j, B_j)$ the average number of clicks obtained by the j-th campaign with budget $B_j$ and bid $b_j$. Let $v_j$ be the average value of one click from the j-th campaign. The task of maximising the revenue can then be formulated as the following constrained optimisation problem:

$$\begin{aligned} \begin{aligned}&\max \sum _{j=1}^N v_j n_j(b_j, B_j)\\&\text {s.t.} \sum _{j=1}^N B_j \le B, \quad b_j \in [\underline{b}_j, \overline{b}_j]\, \forall j \end{aligned} \end{aligned}$$

(1)

where the maximum is taken over the budgets $B_1, \dots , B_N$ and the bids $b_1, \dots , b_N$, B is the total budget and $\underline{b}_j$ and $\overline{b}_j$ are the (possibly campaign-dependent) minimum and maximum allowed bids.

Both the functions $n_j$ and the values $v_j$ are unknown and must be estimated from the collected data, hence the need to balance exploration and exploitation. Early estimates could be inaccurate and lead to sub-optimal decisions, but one does not want to spend too many resources on data gathering either, since this comes at the expense of exploiting acquired knowledge.

Note that, in accordance with [21], we are here assuming stationarity, i.e. that the probability distributions of click value and number of clicks given a bid and budget don’t change with time. This is a realistic approximation only on short time spans: as detailed in Sect. 5, this motivates the need for fast-learning models, as the one we present in Sect. 3.1.

In order to reduce the burden of exploration, in [21] an ansatz for the form of $n_j$ is proposed, reducing the complexity of a two-variable regression to two one-variable functions:

$$\begin{aligned} n_j(b_j, B_j) \approx n^{\,\textrm{sat}}_j(b_j) \, \min \left( 1, \frac{B_j}{c^{\,\textrm{sat}}_j(b_j)} \right) . \end{aligned}$$

(2)

Here the function $n^{\,\textrm{sat}}_j$ denotes the saturation clicks, i.e. the number of clicks a campaign would obtain if there were no budget limits. Likewise, $c^{\,\textrm{sat}}_j$ denotes the saturation cost, i.e. the cost faced in the same situation. Since the right-hand side depends nonlinearly on $n^{\,\textrm{sat}}$ and $c^{\,\textrm{sat}}$, and given that we are speaking about averages, the equality in (2) strictly holds only in the deterministic case.

The issue in generalising the problem (1) to the multi-ad group setting is that the budget is shared by all the ad groups of the same campaign, as stated in Sect. 1. While we can let an index k run over ad groups and define $v_{jk}$ as the value of a click from the ad group k of campaign j and do similarly for the bid $b_{jk}$, we cannot define a corresponding click function $n_{jk}(b_{jk}, B_j)$: the number of clicks gathered by an ad group depends also on the bids of all the other ad groups belonging to the same campaign. Intuitively, raising the bid $b_{jk}$ will bring more clicks for the corresponding ad group, but it will also erode the budget $B_j$ more quickly, thus lowering the clicks received by the other ad groups. This difficulty can be circumvented introducing the total value function $V_j(\varvec{b}_j, B_j)$ of a campaign, which depends on the whole vector of bids $\varvec{b}_j$. Therefore, the optimisation problem (1) generalises to

$$\begin{aligned} \begin{aligned}&\max \sum _{j=1}^{N}V_j(\varvec{b}_j, B_j) \\&\text {s.t.} \sum _{j=1}^{N} B_j \le B, \quad b_{jk} \in [\underline{b}_{jk}, \overline{b}_{jk}]\, \forall j, k. \end{aligned} \end{aligned}$$

(3)

In order to preserve data efficiency, the ansatz (2) must be generalised too, linking the total value function to the corresponding saturation quantities. Note that the aforementioned interdependence among different ad groups is a consequence of a limited budget, while the dependence of saturation quantities $n^{\,\textrm{sat}}_{jk}$ and $c^{\,\textrm{sat}}_{jk}$ on the single bid $b_{jk}$ is well defined. If the j-th campaign contains $m_j$ ad groups, and we let

$$\begin{aligned} \begin{aligned} V^{\,\textrm{sat}}_j(\varvec{b}_j)&= \sum _{k=1}^{m_j} v_{jk}n^{\,\textrm{sat}}_{jk}(b_{jk}), \\ c^{\,\textrm{sat}}_j(\varvec{b}_j)&= \sum _{k=1}^{m_j} c^{\,\textrm{sat}}_{jk}(b_{jk}), \end{aligned} \end{aligned}$$

(4)

then ansatz (2) generalises to

$$\begin{aligned} V_j(\varvec{b}_j, B_j) \approx V^{\,\textrm{sat}}_j(\varvec{b}_j) \, \min \left( 1, \frac{B_j}{c^{\,\textrm{sat}}_j(\varvec{b}_j)} \right) . \end{aligned}$$

(5)

Since the right-hand side is not a sum over single-ad group contributions, this formula captures the interaction among different ad groups.

As a way to intuitively justify (5) for fixed bids and budget, we can think of the single $n^{\,\textrm{sat}}_{jk}$ as the sizes of “reservoirs”, one for each ad group, from which clicks are randomly drawn, up until the moment when the total cost paid matches the assigned budget. If the clicks pertaining to different ad groups are well mixed, each will bring approximately the same fraction of its saturation value $V^{\,\textrm{sat}}_{jk}(b_{jk}) = v_{jk}n^{\,\textrm{sat}}_{jk}(b_{jk})$ and saturation cost. The value of this fraction is found equating the total cost paid and the assigned budget $B_j$, hence (5).

3 Optimisation strategy

In the previous section, we established how the optimisation problem is formulated, generalising it to the multi-ad group domain, which contains single-ad group as a special case. In this section, we explore an efficient way to perform the optimisation itself.

As stated in Introduction (Sect. 1), we face here the exploration–exploitation dilemma, since the function we want to optimise must be learnt from the data. We will formulate, as in [22], this problem as a stochastic multi-armed bandit. One could argue that, dealing with auctions, an adversarial environment which adapts to the bidder’s strategy would better model the problem. However, we assume that advertising competitors are many and not coordinated: the stochastic setting is then justified by a mean-field approximation [3, 20] and is standard in the literature [36]. Even if each competitor implements a learning strategy, several quantities can be effectively modelled as random, e.g. time of entering the market, private values, ad quality (which is factored in to determine auction winners, see Sect. 4.1). Moreover, standard adversarial bandit algorithms focus on worst-case performance, without taking advantage of “nice” problem instances [4]: if one can assume a stochastic environment, stochastic bandit algorithms achieve lower regret. The (relatively slow) collective change in behaviour of competitors due to the added presence of the bidder can be modelled as a non-stationary stochastic bandit: we will touch upon non-stationarity in Sects. 5 and 6.²

Among stochastic bandit algorithms, Thompson sampling [33] is of particular interest to practitioners, due both to its performance [8], generality and conceptual simplicity [28].

In general, Thompson sampling involves two steps:

• 1. Making optimal use of the data gathered thus far with Bayesian inference, establishing a posterior distribution on the space of parameters (Sect. 3.1);

• 2. Sampling from the posterior distribution, and selecting the best arm acting as if the sample represented the reality (Sect. 3.2).

We investigate these steps separately in the upcoming subsections, while in Sect. 3.3 we show how Bayesian inference can be simplified with an approximated technique.

3.1 Parametric regression model

If we see the j-th campaign as a contextual bandit, Thompson sampling requires performing Bayesian regression on the correspondence between $(\varvec{b}_j, B_j)$ and the reward $r_j$. We can restrict the search space by placing few, sensible hypotheses on the shape of the functions $n^{\,\textrm{sat}}$ and $c^{\,\textrm{sat}}$, introduced in equations (5) and (4) (we are here dropping indices for simplicity). These hypotheses will lead us naturally to a parametric model: Bayesian regression can then be conducted with Markov chain Monte Carlo (MCMC) [31].

Clicks and cost paid are of course highly correlated, so to be able to perform separately the two regressions it is convenient to introduce the cost-per-click (CPC) function $\varphi (b) = \frac{c^{\,\textrm{sat}}(b)}{n^{\,\textrm{sat}}(b)}$. Both functions $n^{\,\textrm{sat}}$ and $\varphi$ must be positive, be monotonic increasing with the bid, saturate for high enough bid and vanish for vanishing bid. Moreover, $\varphi$ was empirically found to be linear for small bids (in accordance with the law of diminishing returns), and must be strictly smaller than the identity (because of the meaning of bid as maximum CPC). These considerations suggest to use a properly shifted and scaled logistic function. Starting from the saturation clicks,

$$\begin{aligned} n^{\,\textrm{sat}}(b)= & {} \underbrace{k (1 + e^{-ac})}_{\text {scale factor}} \cdot \biggl (\,\underbrace{\frac{1}{1+e^{-a(b-c)}}}_{\text {logistic function}} - \underbrace{\frac{1}{1+e^{ac}}}_{\text {vert. shift}}\biggr ). \end{aligned}$$

(6)

An example of this function is shown in Fig. 2a. The term in parentheses in the scale factor has the goal of providing a meaningful k, which is the saturation value, i.e. the maximum number of clicks one can expect when setting a very high bid. The coefficients a and c have the meaning of an inverted length scale and of a horizontal shift. In order to give them a more intuitive meaning (since it is required to place priors on them), we can link them to the elbows of the curve, which can be identified as the maximum and minimum of the second derivative of the function. The left elbow can be interpreted as the threshold below which the bid yields a negligible number of clicks, while above the right elbow the function effectively saturates. For a standard logistic function (with $a = c = 1$) such elbow points are: $x_{\pm } = \log (2 \pm \sqrt{3}).$ For a general logistic function, the elbows $b_-$ and $b_+$ are linked to the parameters a and c via: $a = \frac{x_+ - x_-}{b_+ - b_-}, \quad c = b_+ - \frac{x_+}{a}.$

Switching to the CPC function $\varphi$ (Fig. 2b), the additional hypothesis of being linear near the origin suggests the same functional form as (6), with $c=0$:

$$\begin{aligned} \varphi (b) = 2 \kappa \left( \frac{1}{1 + e^{-\alpha b}} - \frac{1}{2}\right) . \end{aligned}$$

(7)

Here $\kappa$ is the maximum CPC which can be paid, and the same considerations connecting $\alpha$ with elbows apply.

Fig. 2

Bayesian regression for models (6) and (7). Data have been simulated as in Sect. 4.1. Orange dots denote censored quantities: the number of saturation clicks is greater or equal than the observed number of clicks (see Sect. 3.1)

In order to perform regression, one needs to model the likelihood of the data given the parameters. Since $n^{\,\textrm{sat}}$ is a count of clicks at saturation, a natural choice is the Poisson distribution, centred around the mean given by (6). We note, however, that this count is often censored, i.e. only partially known: this happens when the assigned budget is less than the saturation cost. In these cases, all we know is that saturation clicks are greater than or equal to observed clicks, and one needs a principled way to take these data into account, without introducing systematic bias. In the bandit model, one can assume non-informative censoring [19]. Thus, just a simple change in the likelihood is needed: censored data enters the likelihood via the so-called survival function, i.e. the complementary of the Poisson CDF. Finally, a natural model for the CPC is offered by the lognormal distribution.

Summing up, this model has the following advantages: (i) lower variance (with a small bias increase), (ii) closed-form functions, (iii) it forces monotonicity, which helps optimisation to choose the next action, (iv) transparent hyperparameters make it easy to elicit priors, and finally (v) parametric Bayesian regression easily accommodates censoring.

Contextual bandits have been mostly studied in the linear [2, 10], generalised linear [13] and kernelised domain [30, 34]. More recently, deep neural networks have been explored for the regression step [27]; their expressive power is, however, balanced by the large need of data. To the best of our knowledge, this is the first work which uses full-fledged Bayesian regression on a parametric function which is not (generalised) linear.

3.2 Next super-arm selection

We now turn to the problem of sampling from the posterior distribution, and selecting the best arm accordingly: this means drawing a particular instance of the functions introduced in (4) and (5) and solving the optimisation problem (3) for those instances. As noted in [21], since the constraint acts only on the budgets, the optimisation problem (3) can be decoupled as follows:

$$\begin{aligned} \max \sum _{j=1}^{N}V_j(\varvec{b}_j, B_j) = \max _{B_1, \dots , B_N} \left( \sum _{j=1}^{N} \max _{\varvec{b}_j} V_j(\varvec{b}_j, B_j) \right) . \end{aligned}$$

In other words, if we are able to find the bid vector $\varvec{b}_j = \varvec{b}_j(B_j)$ which maximises the value $V_j(\varvec{b}_j, B_j)$ for a fixed budget $B_j$, we are then left only with the constrained optimisation on the budget splitting $B_1, \dots , B_N$.

While the grid search approach suggested in [21] works well in one dimension (i.e. for single-ad group campaigns), it scales badly with increasing dimensionality. If a GP regression model is employed, owing to the non-monotonic nature of extracted samples, one must recur to global methods, as opposed to local ones. On the other hand, employing the monotonic functions (6) and (7), the function $V_j(\varvec{b}_j, B_j)$ with fixed budget was empirically found to have only one local maximum, which is also global (see Fig. 3a). Therefore, optimisation is amenable to local methods: when applicable, these are both faster and more reliable. We now describe how such methods can be applied in practice. Starting from (5), $V_j(\varvec{b}_j, B_j)$ can be rewritten as a piecewise function:

$$\begin{aligned} V_j(\varvec{b}_j, B_j) = {\left\{ \begin{array}{ll} V^{\,\textrm{sat}}_j(\varvec{b}_j), \quad \!\! c^{\,\textrm{sat}}_j(\varvec{b}_j) \le B_j \\ B_j \frac{V^{\,\textrm{sat}}_j(\varvec{b}_j)}{c^{\,\textrm{sat}}_j(\varvec{b}_j)}, \quad \!\! c^{\,\textrm{sat}}_j(\varvec{b}_j) \ge B_j \end{array}\right. }. \end{aligned}$$

(8)

Fig. 3

Thompson sample of the total value function $V_j(\varvec{b}_j, B_j)$ of a campaign with two ad groups (click values $v_{jk}$ are set to 1 for simplicity)

Note that, on the boundary $\left\{ c^{\,\textrm{sat}}(\varvec{b}_j) = B_j \right\}$ between the two regions, the functions coincide. On the other hand, traversing the boundary the gradient changes abruptly, thus hindering the direct application of gradient-based optimisation methods. We will see, however, that a constrained optimisation on just one region is sufficient. First we note that, if both regions are non-empty, the global maximum of $V_j(\varvec{b}_j, B_j)$ is given by the maximum between the two maxima of the function on the two regions. Moreover, every directional derivative of $V^{\,\textrm{sat}}_j(\varvec{b}_j)$ (sum of monotonic single-variable functions) is strictly positive. If the boundary $\left\{ c^{\,\textrm{sat}}(\varvec{b}_j) = B_j \right\}$ is not empty, the maximum of $V^{\,\textrm{sat}}_j(\varvec{b}_j)$ then lies on said boundary. This, in turn, means that the maximum over the region $\left\{ c^{\,\textrm{sat}}(\varvec{b}_j) \le B_j\right\}$ is less than or equal to the maximum over the region $\left\{ c^{\,\textrm{sat}}(\varvec{b}_j) \ge B_j\right\}$, i.e. that, if the latter region is not empty, it suffices to search the maximum there.

Up to now, we dealt with finding the optimal bids for a campaign given the budget, thus finding a function $\varvec{b}_j = \varvec{b}_j(B_j)$. We must now solve the following optimisation problem:

$$\begin{aligned} \begin{aligned}&\max _{B_1, \dots , B_N} \sum _{j=1}^N V_j(\varvec{b}_j(B_j), B_j) \\&\text {s.t.} \sum _j B_j \le B. \end{aligned} \end{aligned}$$

(9)

Fig. 4

Flow chart of the whole bid/budget optimisation algorithm. On the first day of optimisation, the algorithm starts from the top left node, sampling from the priors (since no data have been gathered yet). Here, $n^{\textrm{sat}}$ and $\varphi$ are the click and CPC functions introduced in Sect. 2, and indices running over all ad groups and campaigns are dropped for simplicity, as in Sect. 3.1. Bayesian regression and sampling from posterior can be carried out either with MCMC or with Bootstrapped TS (Sect. 3.3)

The terms $V_j(\varvec{b}_j(B_j), B_j)$ in the sum are single-argument functions that depend only on the budget of the campaign. For budgets $B_j$ greater than the spending capability $c^{\,\textrm{sat}}_j(\overline{b}_{j1}, \dots \overline{b}_{jm_j})$ of the campaign, such functions become constant, as can be seen by (8). For budgets below the spending capabilities, the functions have been empirically found to be downwards concave (see Fig. 3b), in agreement with the law of diminishing returns. This also means that this optimisation step is amenable to local gradient methods too. If, however, the optimisation over bids is performed with numerical methods, extra care must be taken in choosing the step size over budgets: small errors in the first step translate to a small noise in the function $V_j(\varvec{b}_j(B_j), B_j)$. To control this issue, we developed an intuitive optimisation procedure which generalises the budget splitting strategy presented in [15] to the case of non-constant return on investment (i.e. non-linear functions): this procedure is outlined in Algorithm 1.

Algorithm 1

Local budget splitting optimisation

The procedure keeps subtracting budget from a campaign until the discrete derivative matches or becomes smaller than the discrete derivative of another. This means that the procedure effectively searches for the point in the budget splitting simplex where the derivatives are approximately equal: this is the solution of the Lagrange problem corresponding to (9).

A flow chart depicting the broad steps of the whole bid/budget optimisation algorithm, from data gathering to next super-arm selection, is given in Fig. 4.

3.3 Bootstrapped Thompson sampling

While Markov chain Monte Carlo [31] has become the de facto standard for Bayesian inference when no closed formula for the posterior exists, it presents challenges that could hinder applications. First, some tuning is often required on the models to ensure that the Markov process converges, and that the sampled data approximate the posterior well. Second, it is resource-intensive and requires much time to converge (if compared to maximum likelihood models). To bridge this gap, we adapted an approximated, lighter alternative, i.e. bootstrapped Thompson sampling [23, 28].

The main idea behind this method is to approximate sampling from the posterior with the statistical bootstrap. In the case of our parametric model, this would mean sampling with replacement from the history of data gathered so far, and finding the maximum likelihood estimate of the parameters for said sampled history. This procedure, however, would present two issues [28]: the prior over parameters is ignored and, more importantly, the uncertainty over parameters is underestimated in initial periods, when data points are scarce. Since Thompson sampling leverages this uncertainty to produce next action decisions, this naive application of the bootstrap is known to lead to linear regret [23]. In particular, in the first days of optimisation the agent could conclude that an ad group is underperforming with respect to the others just by chance, and stop allocating budget to that ad group altogether, never allowing it to recover.

To overcome this issue, we adapted Algorithm 3 of [23] with Bayesian bootstrapping to our setting. The adapted algorithm is reported in Algorithm 2.

Algorithm 2

Bootstrapped Thompson Sampling

4 Numerical simulations

In order to test the model and compare it with the state of the art, we designed and developed an environment which tries to capture what is disclosed about the ad placing auctions [17]. In Sect. 4.1, we introduce such environment, while in Sect. 4.2 we analyse the results of our simulations.

4.1 Simulation environment

We describe here the simulation environment: while some simplifying assumptions have been made, the click and CPC dependence on bids agrees with experience on actual auctions. Moreover, the goal is proving the ability of the optimiser to adapt to an environment which is similar enough to reality. In particular, we are avoiding simulating the distribution of the number of clicks using the same models that are being tested, in order not to introduce bias.

For every day, the number of searches compatible with an ad group is sampled from a Poisson distribution. Then, for each search we simulate an auction. The number of competing advertisers is again sampled from a Poisson distribution (with a different mean). The ads belonging to different advertisers are ranked according to the product of three quantities. The first is the bid: for competing advertisers, the bid is sampled from an exponential distribution. The second is a static quality score, which measures the intrinsic quality of the ad: it is sampled from a triangular distribution. The third is an instantaneous quality score, which measures the affinity between the single search and the ad group. It is modelled as an angle between vectors, which is extracted from a rescaled beta distribution; then, the quality score is calculated as the scalar product between said vectors.

After the ads have been ranked, the first ones appear on the search engine result page: whether they are clicked or not is determined by a Bernoulli distribution. Then, in keeping with the meaning of the bid as maximum CPC, the advertiser that has received a click pays the minimum amount necessary to appear in that position. The budget is then updated accordingly, until either available searches end or the budget is finished. A second Bernoulli distribution governs which clicks turn into contacts. What distinguishes various simulations are the parameters of the manifold of the probability distributions involved.

To run a comparison between the parametric regression model introduced in Sect. 3.1 and the GP model introduced in [21], the latter needs some additional metric to extrapolate the saturation clicks of the day from the observed clicks, as stated in Sect. 1. We have chosen lost impression share, an estimate of the fraction of times the ad was eligible for appearing in a search, but did not due to limited budget. To capture the fact that it is inherently a noisy quantity, a convex combination of the actual lost impression share with random fractions was used, with varying coefficients.

The code of the simulation environment is available at https://github.com/MarcoGigli/sem-simulation.

4.2 Simulation results

We run 120 experiments randomly drawing the parameters introduced in Sect. 4.1 (thus tripling the number of experiments reported in the preliminary version [16]). The number of campaigns of the portfolio varied between 2 and 8 and, for each campaign, the number of ad groups varied between 1 and 4. For each parameter setting, both the parametric and the GP model optimised the total value for 100 virtual days. We specify that in these numerical simulations we tested the parametric model with full-fledged Bayesian inference, performed with MCMC: we deferred testing the approximated bootstrapped Thompson sampling introduced in Sect. 3.3 to the real-world experiments (see Sect. 5.2).

Fig. 5

Time dependence of regret and relative regret suffered by the GP model when compared to the parametric model

To compare performances, we evaluated the regret of using the GP model instead of the parametric one, $R_n = \sum _{t=1}^{n} \left( r^{\text {par}}_t - r^{\text {GP}}_t \right) .$ Here $r^{\text {par}}_t$ and $r^{\text {GP}}_t$ represent the rewards received at day t using the parametric and GP model, respectively. In particular, it is given by the number of contacts. We also calculated relative regret $\rho _n = \frac{\sum _{t=1}^{n} \left( r^{\text {par}}_t - r^{\text {GP}}_t \right) }{\sum _{t=1}^{n} r^{\text {par}}_t}$ to meaningfully compare performances of experiments with different parameters.

In Fig. 5, the behaviour in time of regret and relative regret is shown for a particular set of parameters, i.e. one of the 120 experiments. After a short time in which, due to random fluctuations, the GP model gathers more contacts, the relative regret quickly raises to 40%. Then, as both models are given more data, the relative difference in performance gradually tapers off and converges to approximately 10%.

This example is typical, as can be seen in Fig. 6 and in table 1: at $n=10$ days, only in 11 experiments the regret is negative, and in most cases the relative regret ranges from 8% to 55%. Fast convergence is especially important if a sliding window strategy is employed to retroactively take time dependence into account, as in [22]. At $n=100$ days, the relative regrets are much less spread out and lower on average, and again they are negative only in roughly one in ten cases (13 runs). As hinted at in the preliminary version [16], upon closer inspection the most important feature in determining regret is the number of ad groups per campaign (see Fig. 7). This shows that the ability to efficiently search for the optimal bid combination given a certain budget (as described in Sect. 3.2) is crucial for the performance of the agent. Moreover, higher percentages of noise in the extrapolation metric are associated with a higher relative regret (especially at $n=100$ days), as is to be expected from the discussion of Sect. 3.1. Other features do not show a clear link with relative regret.

5 Real-world data

While the simulation environment described in Sect. 4.1 has the benefit of giving full control over the parameters of the simulation, it is at risk of being too idealised and relying too heavily on assumptions, particularly with regard to probability distributions and the presence of outliers. To counter this, we performed extensive experiments over the Criteo Attribution Modeling for Bidding Dataset [12], which contains one month worth of (subsampled) Criteo display advertising data. Dealing with real data, as opposed to synthetic, means we are not shielded from non-stationarity; moreover, the imposed 31-day time frame makes data efficiency all the more important.

In the following subsections, we first describe the dataset, and how it can be used to evaluate bandit performances (Sect. 5.1) and then we analyse the results of the experiments (Sect. 5.2).

5.1 The Criteo dataset

Every line of the dataset contains contextual features regarding the user, the website and the ad. These (anonymised) categorical features are used to feed a supervised model that predicts the probability of conversion (see [12] for details). This predicted probability is the analogue of the product of static and instantaneous quality score described in Sect. 4.1: it is multiplied by the bid to determine the ad rank and thus the right to be shown on page. The dataset was thus split in two: one half was used to train the predictive model, while the other half was used to test the bandit algorithms. The training set was also used to learn the priors, both over the parameters of the proposed Bayesian model and over the hyperparameters of the GPs.

The data points correspond to auctions that were won by the production policy; in other words, the dataset is truncated, since lines corresponding to lost auctions are absent. This selection bias means that the logged distribution of minimum winning bids is not representative of the true one. More generally, to evaluate the performance of competing bandit policies on logged data one would need a full counterfactual analysis [32], which could be unfeasible if the production policy is deterministic. In this case, however, it has become standard practice to tackle the problem of selection bias by injecting noise into the distribution of competing bids [7, 12], and we followed this simple approach.

It was thus possible to effectively replay the auctions. The bid chosen by the agent for a given day and ad group is compared, after multiplication by the predicted probability of conversion, with the best competing ad rank. If the auction is won and the ad in the dataset received a click, then the click count for that day is increased by one. The same holds for conversions.

Fig. 6

Distribution of the relative regret at n = 10 days and n = 100 days for all synthetic experiments. The boxes show the first quartile, median and third quartile

Table 1 Descriptive statistics of the relative regret at n = 10 days and n = 100 days

Fig. 7

Distribution of the relative regret at n = 10 days and n = 100 days varying the number of ad groups per campaign. The boxes show the first quartile, median and third quartile

As an ablation experiment, and to keep matters as close as possible to the original dataset, we fed the GP model with the actual lost impression share, without adding noise. This benefits the GP model, as one of the concerns raised in Sect. 1 was here removed. Nevertheless, we will see in Sect. 5.2 that the parametric Bayesian model performs best on average in every setting we studied.

Before delving into comparing the performances of the bandit algorithms on this dataset, we can study the two regression models taken in isolation. First note that the right hand side of formula (6) with $k=1$ is the probability of winning a single auction, as predicted by the parametric model. The actual probability of winning is given here by the cumulative distribution of competing ad ranks (which is unknown to the agent). A comparison of the two curves shows the expressive power of the proposed model (see Fig. 8 for an example).

Switching to the number of clicks in a day, one can compare the proposed parametric model with a GP trained on the same data (see Fig. 9). Here we see that the fewer restrictions placed on the GP (as mentioned in Sect. 1) mean much slower convergence to sensible shapes.

Fig. 8

Predicted versus actual dependence of the probability of winning an auction on the bid, for a campaign of the Criteo dataset

Fig. 9

Daily saturation number of clicks for a given bid with the prediction of the parametric model and the GP, for a campaign of the Criteo dataset

5.2 Results on the Criteo data

In order to study how the main parameters of the experiment affect the regrets, we varied them one at a time, keeping the others fixed: budget per ad group (Fig. 10a), number of campaigns (Fig. 10b), and number of ad groups per campaign (Fig. 10c).

For each parameter combination, we sampled 120 realisations from the Criteo dataset, i.e. we randomly extracted portfolios with the chosen number of campaigns and ad groups, and replayed its auction as described in Sect. 5.1. Since the campaigns of the Criteo dataset present no substructure, to test multi-ad group scenarios we treated them as ad groups, and randomly clustered them to form campaigns.

The experiments letting budget and number of campaigns vary were conducted with one ad group per campaign, to perform an ablation experiment and study the effect of the parametric model alone, independently of the multi-ad group generalisation introduced in Sect. 2.

Fig. 10

Behaviour of the average relative regret on the Criteo dataset varying one parameter at a time

Overall, in every setting we studied, the average regret suffered by either the GP method or Bootstrapped TS at the end of the simulation is positive. As shown in Fig. 10, the average percentage of conversions lost due to not using the parametric Bayesian method can reach in some settings 40% (Fig. 10c).

As can be seen from Fig. 10a, keeping the number of campaigns and ad groups fixed and increasing daily budget, relative regret quite steadily decreases both for GPs and Bootstrapped TS. This is to be expected, since increasing daily budget means moving closer to saturation cost, which in turn means that

• Errors in splitting budget have less impact,

• More budget is available for exploration, which means getting more accurate data.

Put differently, while the proposed method gathers more conversions on average for all the budgets we tested, its advantages are more clear cut when daily budget is tight.

The relative order between the two curves in Fig. 10a is in turn an effect of the relatively high number of campaigns involved, as can be seen in Fig. 10b: while the regret for GP is somewhat independent by the number of campaigns, bootstrapped TS suffers from increasing this number, so that the two curves cross.

If we instead let the number of ad groups per campaign vary (Fig. 10c), while both methods show increasing average relative regret with increasing number of ad groups, bootstrapped TS suffers less: while the Bayesian posterior is approximated, next action selection is the same as in the full-fledged parametric Bayesian algorithm and can thus benefit from the same local optimisation method.

The GP method and bootstrapped TS show comparable performances across the settings studied. One can interpret this as showing the separated effects of both a more efficient model (shared by bootstrapped TS and our method) and full Bayesian inference (shared by GPs and our method): one needs both in order to increase performance in this environment.

6 Conclusion and next steps

In this paper, we extended a state-of-the-art method for Search Engine Marketing optimisation to the multi-ad group domain, thus bridging a gap with application. Exploiting domain knowledge, we introduced a parametric Bayesian regression model to reduce the need of data with respect to GPs and to naturally account for censoring, further freeing up resources for both exploration and exploitation. Parameters are interpretable, hence allowing for the easy elicitation of priors on them. Benefiting from the properties of this model, we presented how the optimisation step in Thompson sampling can be carried out by local (as opposed to global) methods. To bridge the gap with applications and study the effect of exact Bayesian inference on Thompson sampling performance, we adapted a version of bootstrapped TS to static contextual bandits. In order to test the performance of competing models, we both built a simulation environment and replayed the auctions of a public digital advertising dataset. Finally, we run a host of simulations that show a clear improvement over the state of the art, especially over short times (implying a much faster convergence on average), when the budget is particularly constrained or the number of ad groups raises.

The following extensions will be addressed in future works:

• Although time effects are not explicitly included in the analysed models, the proposed method shows fast convergence on a real dataset, which is non-stationary. This means that a simple sliding window could be applied in real-world settings to discard data older than one month and keep the model up-to-date. We plan on exploring how state-of-the-art non-stationary bandit techniques fare on the various types of concept drift [5], including adaptive window size, that takes into account how fast the environment changes.

• This work assumes that the reward is immediate, i.e. that the agent is shown the reward of its past action before the next round occurs. In practical settings, this hypothesis works for optimising clicks and first contacts; on the other hand, further steps of the marketing funnel (sales in particular) can occur many days after the first interaction.

• As we have seen in Sect. 3, we are able to assume a stochastic (as opposed to adversarial) environment thanks to the mean-field approximation, in turn justified by a large number of competitors. An interesting question is what would happen if all competitors were to use the proposed method to choose bids. We plan on studying this setting, letting the number of competitors vary, to empirically verify the onset of the mean-field approximation as the number of competitors grows.