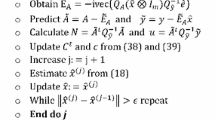1 Introduction

Optimal spatial alignment of one high-dimensional data set to another has been explored through the literature by the use of an Orthogonal Procrustes Rotation [1]. Numerous “flavors” of Procrustes-type methods exist; however, the Procrustes methods discussed herein apply to linear transformations of the data set, hence an orthonormal rotation, which differs from projection problems, transformations by non-square, orthonormal, matrices. The name originates back to Greek mythology. Procrustes was a giant who had an iron bed (or, according to some accounts, two beds) on which he compelled his victims to lie. If the victim was shorter than the bed, Procrustes stretched them by hammering or racking the body to fit. Alternatively, if the victim was longer than the bed, Procrustes would cut off the legs to make the body fit the bed’s length. In either event, the victim died [2, 3]. In a similar, but less gruesome manner, Procrustes Analysis or Procrustes methods refer to a set of least squares mathematical techniques used to perform transformations among corresponding points belonging to a generic m-dimensional space, to satisfy some maximum agreement [3].

2 Motivation, applications, and preview

2.1 Motivation

Little literature exists as to how errors are propagated through Procrustes-type problems, each piece of literature is highly dependent on the structure of the problem. Maset, Crosilla, and Fusiello provided an Errors-In-Variables model in the anisotropic, row-scaling Procrustes analysis with a solution that can deal with the uncertainty affecting both sets of observations [4]. Others have looked at the problem through estimating the probability distributions over the set of 3D rotations \(\textrm{SO}(3) \) using a von Mises–Fisher distribution in \(\mathbb {R}^3\) [5]. A full uncertainty characterization of the optimization problem of obtaining the transformation between corresponding m-dimensional point sets and their closed-form solution while considering point sets perturbed by anisotropic noise and points that are not required to be independent nor identically distributed has been analyzed for the Procrustes problem without scaling [6]. Random sample consensus (RANSAC) methods for outlier detection have been utilized for various computer vision problems ranging from 2D homography estimation to video stabilization [7,8,9]. Therefore, it seems appealing to find a methodology to combine the outlier detection and robustness of RANSAC with Procrustes methods.

This paper covers the statistical nature of Orthogonal Procrustes Analysis (OPA) and Orthogonal Anisotropic Procrustes Analysis (OAPA). Analytic solutions will be provided for how the residuals are distributed in OAPA, see the Appendix. Studying the statistical properties of Procrustes techniques provides the justification for maximum likelihood estimation (MLE) as a method for modeling the residuals in order to classify data points as inliers or outliers. This paper also provides useful information about how to combine Procrustes methods with parametric and nonparametric statistical models within RANSAC frameworks for robustness. Procrustes methods are susceptible to errors when outliers corrupt the data; thus, robustness needs to be imparted on them to ensure that the results are minimally impacted by outliers.

2.2 Applications and examples

The intended application for the methodology is to robustly automate the rotation of populations of experimentally collected triaxial accelerometer data sets to a single global coordinate system. The term population is intended to imply that multiple accelerometers are located within or on a particular test body and that each accelerometer might not be aligned with the global coordinate system of the test body. In the context of mechanical vibration and shock, outliers represent non-rigid body responses, environmental noise, and/or sensor and data acquisition issues. Inlier data are rigid body responses collected from the triaxial accelerometers such that the test body does not deform under the action of the applied forces. Thus, outliers are the complement of the set of inliers. Common sensor issues causing outliers often manifest themselves as corrupt/faulty sensors, clipping, or saturation of a sensor due to a measured response greater than what the sensor is calibrated for. Scaling of the data is required to correct the case when the voltages of the accelerometer sensors were improperly calibrated.

A challenging synthetic data set along with a real data set from a shock experiment will be used to exemplify the efficacy of the methodology presented herein. Analysts using these methodologies will be able to greatly reduce their errors by avoiding any manual estimation of a rotation while also reducing the time needed to analyze and validate the data. When the data does not appear to be correct, the analyst is faced with correctly identifying whether that the data is valid but the rotations and/or scalings are wrong or the data is invalid, regardless of the rotations and/or scalings. Installation errors such as polarity swaps (180\(^\circ \) rotations) or spatial directions swaps (90\(^\circ \) rotations) can be discovered when the estimated rotation matrices do not match the rotation matrices provided in the part drawings. Part drawings define how each accelerometer is to be installed and what its local orientation is in reference to the coordinate system of the test body.

2.3 High level preview

The procedures listed in the paper follow a sequence of several algorithms which are detailed in various sections herein. To help facilitate the reader’s understanding, a brief overview of all the components of the full algorithm will be detailed. The underlying goal of this paper is a methodology that provides a robust and optimal rotation of multiple objects to a single coordinate system. For the rotation, and possible scaling of the object, a variety of Procrustes-type methods will be implemented. The authors have successfully incorporated a RANSAC framework within the Procrustes methods to impart robustness. RANSAC requires subsampling from the initial data many times, with the goal of getting at least one subsample that is entirely outlier free. A Procrustes method will be performed over all these subsamples yielding many possible Procrustes models. A Procrustes model is a rotation, and possibly a scaling matrix (depending on the Procrustes method). The Procrustes distinction is to help alleviate confusion between the statistic model architectures: MLE mixture or the nonparametric order-based model. Residuals can then be calculated for every Procrustes model using one of the architectures listed above. Analysis of these residuals provides a method in classifying them and their respective data points, time points for the applications provided here, as either inliers or outliers.

Two statistical architectures are suggested on how to model the distribution of the residuals. A maximum likelihood estimation approach using a mixture model on the residuals where inliers are modeled as one distribution and outliers as another distribution. The second version is a nonparametric approach utilizing order statistics on the residuals to remove potential outliers. The statistical architectures above provide a heuristic that is used to rank the numerous Procrustes models generated from the subsampling procedure. A few top Procrustes models are kept from the initial RANSAC subsampling procedure, these top Procrustes models are further optimized utilizing their inliers with a procedure known as locally optimized RANSAC (LO-RANSAC) [7, 8]. The following sections will go in depth for each of the concepts described above.

For the context of this paper, the Procrustes models are first formed by GOPA using RANSAC and LO-RANSAC. After iterating over each object, the group average \(G_h\) is updated, this is performed until the group average has converged, denoted as G. GOPA is first used to calculate the initial rotations, \(Q_{i}\), along with the group average, G. Finally, an OAPA model with the target object now being the group average will be performed for each object, \(A_i\). OAPA using RANSAC and LO-RANSAC will subsequently provide the optimal rotation, \(Q_{i}\), and scaling, \(\Lambda _{i}\), for each object with respect to G. The reasoning behind this series of algorithms will be explained in the Complete Methodology section.

3 Mathematical background

3.1 Orthogonal anisotropic procrustes analysis

The easiest example of OAPA is simultaneously finding the optimal 3D rotation of one object, \(A_1\), with respect to a target object, \(A_2\), while also finding the optimal scaling matrix, \(\Lambda \). The orthogonal Procrustes problem focuses on the optimal rotation matrix, Q, out of the solution space of all rotation matrices that minimizes the error between two objects represented as matrices: \(\{A_1,A_2\}\). The term anisotropic come from the diagonalization of \(\Lambda \), which provides different scaling factors for the columns of \(A_1\). In the case of triaxial accelerometer data, \(A_{(i=1,2)}\in \mathbb {R}^{(m \textrm{x} 3)}\), with m rows corresponding to m number of responses in three spatial coordinates with respect to time. OAPA takes the following form:

$$\begin{aligned} F(Q, \Lambda )= & {} ||A_1 \Lambda Q - A_2 ||_F^2 \quad | \quad Q^T Q = I_3, \nonumber \\ \Lambda= & {} \begin{bmatrix} \lambda _{x} &{} 0 &{} 0\\ 0 &{} \lambda _{y} &{} 0\\ 0 &{} 0 &{} \lambda _{z} \end{bmatrix}, \end{aligned}$$
(1)

where \(|| \bullet ||_F\) refers to the Frobenius norm, and \(I_3\) is the identity matrix in \(\mathbb {R}^3\). Methodologies to minimize \(F(Q, \Lambda )\) require simultaneously optimizing for Q and \(\Lambda \) through the use of block relaxation methods, two-block least squares, also known as alternating least squares [1, 10].

If one assumes that the noise found in both \(A_1\) and \(A_2\) follows a normal random distribution, independent of spatial direction, then the resulting residuals after the affine transformation in (1) will also follow a normal random distribution. The results found in the Appendix exhibit the underlying property that the sum of independent normal random variables also have a normal distribution. In the case where the original signal noise was not independent of channel direction, this leads to a trivariate normal distribution, \(\Psi _1 \sim \mathcal {N}( \varvec{ \mu }, \varvec{\Sigma })\), implying nonzero entries in the off-diagonal of the covariance matrix. However, linear combinations of multivariate normal random variables preserve the statistical structure and still are multivariate normal random variables. The normality of the residuals is useful in the context that a mixture model can then be built with the assumption that the inliers follow this distribution.

3.2 General orthogonal procrustes analysis

The term generalized for Procrustes analysis is used when there are at least two objects, \(n \ge 2\), to be matched [11]. When there are just two objects in Procrustes analysis, this implies matching of one object (matrix) onto a target object. General Orthogonal Procrustes Analysis (GOPA) has the goal of minimizing the quantity proportional to the sum of squared norms of pairwise differences,

$$\begin{aligned} F(Q_1,\ldots , Q_n) = \frac{1}{n} \sum _{i=1}^{n} \sum _{j=i+1}^{n} ||A_i Q_i - A_j Q_j ||_F^2. \end{aligned}$$
(2)

Equation (2) can be rewritten in an equivalent form seen in (3), which is matching all transformed objects to their group average, G [12]

$$\begin{aligned} F(Q_1,\ldots , Q_n)&= \frac{1}{n} \sum _{i=1}^{n} || A_i Q_i - G ||_F^2, \nonumber \\ G&= \frac{1}{n} \sum _{i=1}^{n} A_i Q_i. \end{aligned}$$
(3)

GOPA can be viewed as iterating over each object many times and performing OPA with the target object as the group average, G. GOPA requires multiple iterations over all objects as convergence of G is dependent on all the subsequent rotations, just as the convergence of \(Q_i\) is dependent on convergence of the G.

Implementations for any of the General Procrustes methods, GOPA and GOAPA (explained in the following section), require multiple iterations over all the objects. One could update the group average incrementally after estimating each \(Q_i\) or one could incrementally update the group average after estimating all \(Q_1,\ldots ,Q_n\); the authors have chosen the later approach. To denote how the group average changes over each iteration, the notation, \(G_h\), is used where, h, denotes how many times the group average has been estimated. At the very start of general Procrustes methods, \(h=1\), the group average, \(G_1\), is not defined. The authors arbitrarily initialize the group average as the first object, \(G_1=A_1\).

Stopping criteria for the group average in this paper is performed two ways. A tolerance on the error is defined as \(\varepsilon _{groupTol}\). When the Frobenius norm between the current group average and the subsequent group average is less than the convergence criterion, the algorithm stops: \( ||G_h - G_{h-1} ||_F^2 < \varepsilon _{groupTol}\). Occasionally, convergence of the group average does not reach the tolerance and the error becomes cyclical between iterations. A maximum number of iterations is defined as nGroupIter to avoid an infinite loop.

For OPA and GOPA based problems, \(\Lambda \) is simply the identity matrix in \(\mathbb {R}^3\). The method for solving \(Q_i\) reduces to just a singular value decomposition problem as shown in (4) where T implies transpose,

$$\begin{aligned} B= & {} A_i^T G \nonumber \\ B= & {} U S V^T \nonumber \\ Q_i= & {} V U^T. \end{aligned}$$
(4)

For OPA, simply replace the G with the target object, such as \(A_2\).

3.3 General orthogonal anisotropic procrustes analysis

General Orthogonal Anisotropic Procrustes Analysis (GOAPA) is similar to GOPA with the goal of minimizing the quantity proportional to the sum of squared norms of pairwise differences but subject to some constraint to prevent the trivial solution for all the anisotropic scalings being \(\textbf{0}\),

$$\begin{aligned}{} & {} F(\Lambda _1,\ldots ,\Lambda _n, \; Q_1, \ldots , Q_n) \nonumber \\{} & {} \quad =\frac{1}{n} \sum _{i=1}^{n} \sum _{j=i+1}^{n} ||A_i \Lambda _i Q_i - A_j \Lambda _j Q_j ||_F^2. \end{aligned}$$
(5)

Equation (5) can be rewritten in an equivalent problem, which is matching all transformed objects to their average [12]:

$$\begin{aligned}{} & {} F(\Lambda _1,\ldots ,\Lambda _n, \; Q_1, \ldots , Q_n) \nonumber \\{} & {} \quad =\frac{1}{n} \sum _{i=1}^{n} ||A_i \Lambda _i Q_i - G ||_F^2, \nonumber \\{} & {} G = \frac{1}{n} \sum _{i=1}^{n} A_i \Lambda _i Q_i. \end{aligned}$$
(6)

The methodologies to minimize \(F(Q_1,\ldots ,Q_n, \, \Lambda _1,\ldots ,\Lambda _n)\) for GOAPA still require the use of block relaxation methods used in OAPA, albeit with multiple iterations over all objects. This is because the group average, G, is now dependent on all the rotations and anisotropic scalings. Constraining GOAPA with \(\Lambda _i= I_3, \forall \; i=1,\ldots ,n\) causes the method to collapse to just GOPA.

4 Imparting robustness to procrustes methods through random sample consensus

All of the four Procrustes methods presented in Sect. 3 are susceptible to outliers affecting their results. The approach used in this paper implements a RANSAC framework to alleviate the effects of outliers to any of the Procrustes Methods. The only difference in the implementation of RANSAC with any of the Procrustes methods described above is purely in how the residuals are calculated; all other aspects of the RANSAC framework are identical.

4.1 Stopping criteria

RANSAC requires numerous subsampling from the initial data, with the goal of getting at least one subsample that is entirely outlier free. The purpose of this subsection is to calculate how many times one ought to perform the subsampling. The total number of subsamples required before stopping RANSAC is denoted as, M. Calculating M requires some initial worst-case estimate of the inlier fraction, \(\gamma \), and the number of subsamples or data points needed to generate a Procrustes model, L.

L is the minimum, or close to minimum, number of data points or samples required to estimate the model parameters and is dependent on the problem space. For Procrustes models, the model parameters would either be rotations or rotations and scalings. In ordinary linear regression the minimum sample size is \(L=2\) in \(\mathbb {R}^2\) because only two data points from the entire data set are necessary to define a line. For all Procrustes models, general or not, anisotropic or isotropic, the authors have found that \(L=9\) provides a balance. There is a trade-off between good initial rotation or scaling estimates from a subsample with more samples and a higher value of M required to assure, with some confidence, that the entire subsample is outlier free. For the Procrustes problems presented here, the subsample, \(D_i\), would contain nine time points from the data in \(\mathbb {R}^3\), forming a matrix, \(D_i \in \mathbb {R}^{ 9 \textrm{x} 3}, \; D_i \subset A_i\).

The probability of obtaining a subsample of the data without outliers is calculated by [13, 14]:

$$\begin{aligned} \Gamma (\gamma , L, M) = 1 - (1-\gamma ^L )^M. \end{aligned}$$
(7)

\(\Gamma (\gamma , L, M)\) is the probability that an outlier-free sample has already been selected after M iterations. One must compute the number of iterations, M, using a rough estimate about the inlier fraction, \(\gamma \), for the data set and stop only after all M hypotheses are selected and tested. For the examples provided herein, \(\gamma = 0.95\), which implies that the authors assume that at least 95% of the data are inliers. Ideally, one wants \(\Gamma (\gamma , L, M) \ge c\), where c is the desired confidence, typically between 95 and 99%, of selecting a subsample that contains only inliers. One can calculate M as:

$$\begin{aligned} M = \left\lceil \frac{\log {(1-c)}}{\log {(1-\gamma ^L)}}\right\rceil , \end{aligned}$$
(8)

where \(\lceil \bullet \rceil \) denotes the ceiling operator.

The other stopping criterion that must be addressed is for LO-RANSAC. The stopping procedure can be defined when a certain threshold or convergence criteria are met within the local optimization. Experimentally, the authors found the local optimization for the Procrustes methods described here converges rather quickly by the second or third iteration as the number of inliers within that Procrustes model converges. The authors chose a LO-RANSAC stopping criterion after three iterations, \(nLOSAC = 3\), see Algorithm 3. However, one could also stop using different criteria depending on the problem.

4.2 Subsample from the entire data and generate a Procrustes model consistent with this subsample

After M is calculated, the algorithm follows by taking a subsample of size, L, from the entire data set to form \(D_{(i,j)}\), where the first subscript, i, denotes from which object and/or matrix it was sampled from, and the second subscript denotes the iteration, j, out of M iterations. One then calculates a Procrustes model, either \(Q_{(i,j)}\) or \(Q_{(i,j)}\) and \(\Lambda _{(i, j)}\), from \(D_{(i,j)}\) using the corresponding sample from the group average denoted \(G_{(h,j)}\). Corresponding in this context implies that the row indices r used to subsample \(A_i\) to form \(D_{(i,j)}\) are the same row indices used to subsample \(G_h\) to form \(G_{(h,j)}\). The row indices, r, are a random sample of the integers from 1 to m without repeating elements. This additional step is necessitated by the fact that the Procrustes methods require that the two objects have the same dimension.

4.3 Apply the procrustes model to the entire data set

The next step is to apply the Procrustes model, either \(Q_{(i,j)}\) or \(Q_{(i,j)}\) and \(\Lambda _{(i, j)}\), to the entire data of its respective object, \(A_i\). For RANSAC applications described here, the residuals are used to help rank the different Procrustes models created after each subsample iteration. The residual matrix, \(\Xi _{(i, j)} \), in the context of GOPA or GOAPA is defined as:

$$\begin{aligned} \Xi _{i, j} = A_i \Lambda _{(i,j)} Q_{(i,j)} - G_{h}, \end{aligned}$$
(9)

due to the inclusions of the group average, \(G_{h}\). For GOPA, \(\Lambda _{(i, j)}=I_3 \; \forall \; i,j\). If the group average is already converged, \(G_{h}\) can be replaced by G which now becomes the target object. Thus, the form of (9) is suitable for all the Procrustes methods described above.

4.4 Rank the Procrustes models through some heuristic

Many different heuristics are available for ranking the Procrustes models generated by the RANSAC subsampling procedure. For linear regression, a common method is based on a threshold distance between a data point and the regressed line [15]. If the data point is beyond a certain threshold, it is considered an outlier, and if the data point is within the threshold, it is considered an inlier. The linear model that selects the least number of outliers, i.e., the greatest number of inliers, is then chosen. The problem with this heuristic is that it predicates on knowing what a good threshold value is, which may change depending on the variance and magnitude of the data. A robust heuristic would account for the variance and magnitude of the data, adjusting the threshold to account for them. Parametric models for the residuals of the data, such as utilizing the Gaussian distribution, have a dedicated term, \(\sigma \), to account for this variance. The subsequent sections will provide details on two different architectures for modeling the residuals generated using Procrustes methods.

4.4.1 Maximum likelihood estimation for the residuals

It is assumed that the residuals from each spatial direction are independent from each other and that the residuals are independent in time. If these conditions are met, one can decompose the residual matrix, \(\Xi _{(i, j)}\), for the \(i^\textrm{th}\) object, for the \(j^\textrm{th}\) iteration, into residual vectors, \(\varvec{\epsilon }_{(i, j, k)}: k=\{x, y, z \}\), for each of the three spatial directions,

$$\begin{aligned} \Xi = \left[ \varvec{\epsilon }_{x}, \varvec{\epsilon }_{y}, \varvec{\epsilon }_{z} \right] . \end{aligned}$$
(10)

For the remainder of the MLE section, the \(i^\textrm{th}\) object for the \(j^\textrm{th}\) iteration will be dropped for brevity, but are still implicitly there, until explicitly needed for clarity.

Due to the property that the residuals follow a normal distribution, one could then use a MLE method where the inliers for each spatial direction follow their respective normal distribution. However, in the case where outliers are incorrectly identified, the Student’s t-distribution provides a better alternative. Thus, an MLE method will be utilized where the inliers for each spatial direction will be modeled as a three-parameter Student’s t-distribution denoted as \(f_t\),

$$\begin{aligned}{} & {} f_t(\epsilon _{k,l} | \mu _k, \sigma _k, \nu _k) \nonumber \\{} & {} \quad =\frac{\Gamma ({\frac{\nu _k + 1}{2}})}{\sigma _k \sqrt{\nu _k \pi } \; \Gamma ({\frac{\nu _k}{2}})} \left( \frac{\nu _k + (\frac{ \epsilon _{k, l} - \mu _k}{\sigma _k})^2 }{\nu _k} \right) ^{-\left( \frac{\nu _k + 1}{2}\right) } \nonumber \\{} & {} \quad : k = \{x,y, z\}. \end{aligned}$$
(11)

The t-distribution has been used in Bayesian analysis because of its robustness to outliers [16,17,18]. Even when the data is Gaussian, as the parameter \(\nu \) approaches \(\infty \), the t-distribution converges to a Gaussian distribution. Modeling inliers within RANSAC has predominately been done through a Gaussian distribution [9, 13, 14].

Ultimately, the residuals are expected to follow a normal distribution when all the outliers are correctly identified. The use of the Student’s t-distribution is purely used as an additional level of robustness against false negatives, true outliers that incorrectly got classified as inliers. When the Procrustes methods are OPA or OAPA, and the underlying noise is normally distributed, the choice of using of using t-distribution compared to the Gaussian distribution is justified above. Nevertheless, with any of the general Procrustes methods the choice of the inlier distribution may alter the underlying group average and thus all the subsequent rotations. Due to the iterative nature of estimating the group average, proving the exact distribution of the residuals is challenging. Little to no literature exists on these nuances, but the examples provided in the Sect. 5 provide evidence that the methodologies and assumptions presented in this section are satisfactory.

In (11), \(\epsilon _{k,l}\) refers to the \(l^\textrm{th}\) time point out of m within one of the three spatial residual vectors. For the context of this paper, it is assumed that the residuals for each spatial direction have a mean of 0, \(\mu _k=0\), which reduces the parameter space for the student’s t-distribution into just two variables: \(\sigma _k\), for the variance and \(\nu _k\), for the degrees of freedom. Thus, the noncentral t-distribution is simplified to a standard t-distribution.

Outliers follow a uniform distribution, \(f_U\), which is defined as the reciprocal of the difference between the largest and smallest residual error for a spatial direction,

$$\begin{aligned} f_U(\epsilon _k) = \frac{1}{\Omega }: \; \Omega = \max (\varvec{\epsilon }_k) - \min (\varvec{\epsilon }_k). \end{aligned}$$
(12)

\(\Omega \) must be defined ahead of time for the mixture model because the maximum likelihood for the uniform distribution does not provide the necessary smoothness required for differentiation to solve for the support of the distribution [19]. The inlier and outlier probabilities are combined into the following mixture model:

$$\begin{aligned} \textrm{Pr}(\epsilon _{k,l} | \varvec{\theta }_k) = \phi _k f_t + (1-\phi _k)f_U\; : \; 0 \le \phi _k \le 1. \end{aligned}$$
(13)

\(\phi _k\) represents the estimated fraction of inliers by the mixture model for a spatial direction. If the data in all three spatial directions follows the statistical model defined above, then one expects \(\phi _k \approxeq \gamma \), the true inlier fraction, used to estimate the RANSAC subsampling stopping criterion in Sect. 4.1. For succinctness, \(\varvec{\theta }_k = (\sigma _k, \nu _k, \phi _k)\) is used. Finally, the likelihood can be represented as,

$$\begin{aligned} \mathscr {L}(\varvec{\theta }_k | \varvec{\epsilon }_k) = \prod _{l=1}^m \textrm{Pr}(\epsilon _{k,l} | \varvec{\theta }_k) \, \end{aligned}$$
(14)

which describes multiplying all the probabilities at every point l up to the number of rows or observations, m.

Maximizing the log-likelihood of (14) provides estimates for \(\varvec{\theta }_k\) while providing a metric to which one can compare one Procrustes model to all other M Procrustes models. Optimization of the mixture model defined here is relatively straightforward due to simplicity of \(f_U(\epsilon _k)\) and utilizing a standard t-distribution compared to a noncentral t-distribution. These modifications provide three equations and three unknowns leading a well-posed optimization problem. The global metric, \(\mathcal {M}\), is the sum of the negative log-likelihood from each mixture model representing one of the three spatial directions,

$$\begin{aligned} \mathcal {M}_j&= -\log {(\mathscr {L}({\varvec{\theta }}_{x,y,z} | \varvec{\epsilon }_x, \varvec{\epsilon }_y, \varvec{\epsilon }_z})) \nonumber \\&= -\log {(\mathscr {L}(\varvec{\theta }_x | \varvec{\epsilon }_x))} - \log {(\mathscr {L}(\varvec{\theta }_y | \varvec{\epsilon }_y))}\nonumber \\&\quad \, \ - \log {(\mathscr {L} (\varvec{\theta }_z} | \varvec{\epsilon }_z)). \end{aligned}$$
(15)

The best fitting MLE mixture model for the residuals from (15) has the lowest negative log-likelihood value while the worst fit model has the largest negative log-likelihood value. Thus, for every j out of M iterations of the RANSAC subsampling procedure, one verifies whether the newest Procrustes model has a lower combined negative log-likelihood than the previous one, i.e., \(\mathcal {M}_{j} < \mathcal {M}_{j-1}\).

It is possible to represent the likelihood defined in (15) as a joint, multivariate, distribution over the three spatial directions instead of three separate, uncorrelated, distributions. A joint, multivariate, normal or t-distribution has the benefit of including possible correlations among the spatial direction, but it also brings additional complexities. The mixture model utilizing any of the multivariate distributions becomes rather cumbersome as it now requires a multivariate uniform distribution. Optimizing univariate mixture models provide sufficient challenges on their own, let alone multivariate mixture models. Computational speed is also important as numerous MLE optimizations occur for each subsample within the RANSAC framework, which further inhibits using a multivariate mixture problem. Therefore, the authors chose to analyze the residuals for each spatial direction as their own distinct MLE mixture problem until summing their negative log-likelihood at the very end.

4.4.2 Nonparametric (order statistics) for the residuals

When the residuals of (10) cannot be adequately modeled by the mixture model of (13), a nonparametric approach can be taken. From the authors’ experience, a nonparametric model works well on accelerometer data originating from a shaker table driven by a sinusoidal input. A shaker table is a table that is utilized for general vibration testing of components to vibration testing of an entire test body. The residuals from this type of data were multi-modal distributed making it difficult to fit any elementary mixture model to them.

The ranking metric for a nonparametric inlier model was chosen as the absolute value, denoted with vertical bars \(|\bullet |\), of the median of the residuals for each spatial direction. The global metric is then the sum of absolute value of each direction’s median residuals,

$$\begin{aligned} \mathcal {M}_j = |\textrm{median}(\varvec{\epsilon }_x)| + |\textrm{median}(\varvec{\epsilon }_y)| + |\textrm{median}(\varvec{\epsilon }_z)|. \end{aligned}$$
(16)

Intuitively, better Procrustes models ought to return smaller residuals, and the median should be more robust to outliers than the mean. In a similar manner, the median of the residuals has been used to help model the variance of parametric models [20]. The assumption with this approach is that over half the time points are inliers. As previously mentioned, for every j out of M iterations of the RANSAC subsampling procedure, one verifies whether the newest Procrustes model is a better than the previous one.

4.5 Classification of inliers and outliers—use the residuals

In the previous section, two heuristics were provided for ranking RANSAC models that utilized the residuals from a Procrustes model. This section describes how one can utilize the residuals to classify whether a single time point is either an inlier or an outlier. Checking all the time points for each object will result in a logical vector denoting inliers as 1, true, and outliers as 0, false. The logical vector constructed by the inliers and outliers will be utilized in Section 4.7 and its corresponding LO-RANSAC algorithm for local optimization.

A quick discussion about joint confidence statements is required to account for controlling multiple hypotheses. When the residuals are statistically independent, this surmounts to solving for p given the probability of a joint confidence statement denoted as \(p_J\) [21]:

$$\begin{aligned} p_J = p^3. \end{aligned}$$
(17)

For example, if one desires a joint confidence of 95% that all three spatial directions are inliers, then \(p_J=0.95\); thus, this will require \(p=0.983\) because \( (0.983)^3=0.95\). The joint significance level, \(\alpha _J\), is defined to correct for the family-wise error rate described above, \(\alpha _J = 1-p_J\). The adjustment for multiple hypotheses is required because the framework above treats modeling the residuals independently from each other.

4.5.1 Classification within the MLE framework

Inlier and outliers for each channel direction are then classified using the quantile function, \(\textrm{Qn}(\bullet )\). For the student’s t-distribution, this is given by:

$$\begin{aligned} \rho _{i,j,k,l} (\epsilon _{i,j,k,l}) = {\left\{ \begin{array}{ll} 1 &{} \text {if}\quad F(\alpha _J, \epsilon _{i,j,k,l}) \\ 0 &{} \text {otherwise } \\ \end{array}\right. }, \end{aligned}$$
(18)

where \( F(\alpha _J, \epsilon _{i,j,k,l})\) is defined as:

$$\begin{aligned}{} & {} F(\alpha _J, \epsilon _{i,j,k,l}) \\{} & {} \quad =\textrm{Qn}(\alpha _J | \varvec{\theta }_{i,j,k})< \epsilon _{(i,j,k,l)} < \textrm{Qn}(1 - \alpha _J | \varvec{\theta }_{i,j,k} ). \end{aligned}$$

Inliers are classified globally when a single data point has inliers in all three spatial directions by,

$$\begin{aligned} \rho _{(i,j,l)} = {\left\{ \begin{array}{ll} 1 &{} \text {if}\quad \rho _{(i,j,x,l)} \wedge \rho _{(i,j,y,l)} \wedge \rho _{(i,j,z,l)}\\ 0 &{} \text {otherwise} \end{array}\right. } \, \end{aligned}$$
(19)

with \(\wedge \) denoting the \(\text {AND}\) operator [22]. Utilizing (19), the dimension of \(\rho _{(i,j)}\) over all data points, l, and over all the spatial directions, is simply an \(m\,\textrm{x}\,1\) vector of ones and zeros.

4.5.2 Classification within the nonparametric framework

For the nonparametric architecture, outliers and inliers are based on sorting the absolute value of the residuals for each spatial direction into their order statistics. The order is denoted as an individual subscript with a parenthesis, \(X_{(1)},\ldots ,X_{(m)}\) [23]. An individual subscript with a parenthesis, \(X_{(i)}\), is not to be confused with multiple subscripts, \(X_{i, j, k}\), for which the later notation is used to denote the use of multiple subscripts. When using the order statistic notation along with additional subscripts, \(X_{i, j, k, (l)}\), no additional parenthesis around all the subscripts will be used to avoid potential confusion. As is tradition, the first-order statistic is always the minimum of the sample, \(X_{(1)} = \min {(| X_1,\ldots ,X_m |)}\), while the last order statistic is the largest of the sample, \(X_{(m)} = \max {(| X_1,\ldots ,X_m |)}\). In the rare case of ties for double precision values, a tied ranking scheme is implemented. For example, if counting from smallest to largest, there exists two identical values, which happen to be the second and third values, then they both get the rank of 2.5 (average of 2 and 3). The ordinal index ranking threshold, \(\delta \), can be calculated as:

$$\begin{aligned} \delta = \lfloor {m \gamma }\rfloor , \end{aligned}$$
(20)

where the floor operator is denoted as \(\lfloor {\bullet }\rfloor \).

Outliers for each channel direction, \(k \in \{x,y,z\} \), are then classified using order statistic by:

$$\begin{aligned} \rho _{i,j,k,l}(X_{i,j,k,(l)}) = {\left\{ \begin{array}{ll} 1 &{} \text {if}\quad X_{i,j,k,(l)} < X_{i,j,k,(\delta )}\\ 0 &{} \text {otherwise} \end{array}\right. }. \end{aligned}$$
(21)

Inliers are classified globally when a single data point has inliers in all three spatial directions using (19). There are two main benefits of using a nonparametric model compared to a parametric model in RANSAC. One is the speed compared to parametric models that require extensive minimizing of the negative log-likelihoods M times for each of the three spatial directions. This is in contrast to simply sorting and ranking numbers M times for each of the three spatial directions. Two, the robustness of the nonparametric methods allows it to generalize regardless of underlying noise distribution.

The biggest drawback for nonparametric methods compared to parametric methods, in this context, is that the number of inliers for all objects will never be greater than the estimated inlier fraction, \(\gamma \). If the real inlier fraction is much larger than the estimate, a lot of data is excluded from the calculations to estimate the scaling or rotations. If one overestimates the inlier fraction, the nonparametric approach does not adapt which would imply some outliers are now included in the estimates. Even if one guessed \(\gamma \) correctly and only one object has an inlier fraction of 0.5 while the remaining objects have a much higher inlier fraction of 0.99, the nonparametric method will still impose that all the remaining objects have an inlier fraction of 0.5. To avoid this, it would possible to assign an estimated inlier fraction for every object,\(\gamma _{i}\),within the nonparametric approach, but this provides additional complexity as each object now requires a different stopping criterion, \(M_{i}\). Parametric models are more flexible in the context of this paper because the inlier fraction is estimated for every object compared to globally imposed over all objects.

4.6 Imparting robustness to the group average

If the parametric or nonparametric architectures above provide false negatives for the outliers, the subsequent rotations will be affected. The formation of the group average utilizes each object and its respective rotation. If the rotations are affected by outliers, this could inevitably cause the group average to be contaminated. To alleviate this problem, the group average is calculated by using the spatial median instead of the mean [24]. Using the median compared to the mean has precedence from Crosilla and Beinat who used the median to form the initial centroid in their Iterative Forward Search approach for robust Procrustes analysis [25]. In this paper, the authors use the Weiszfeld method for calculating the spatial median for the group average [26]. The spatial median is calculated for every time point using the corresponding time point in \(\mathbb {R}^3\) from every object.

The group average implemented here utilizes all data from each object when applying the spatial median. This contrasts with utilizing only inliers from each object. Forming the group average using only the inliers adds significant complexity to the framework. It is possible that all the objects classify a single time point as an outlier. Similarly, for a single time point to not have enough inliers to form the spatial median. Both issues must be addressed further down the algorithm pipeline as the group average now has a different dimension than the objects. Calculating the group average using all the data is often justified when the data set has numerous objects and a moderate fraction of inliers, as shown in the examples provided here.

4.7 LO-RANSAC

Using a Procrustes model from the initial subsampled data from RANSAC may not yield an optimal Procrustes model, particularly if the subsampled data has inliers that are not ideally representative of the entire data. Local optimization of the Procrustes models, known as LO-RANSAC is then implemented after the initial RANSAC steps. The purpose of the local optimization is to refit the Procrustes model to only inliers and iterate until either the Procrustes model converges and/or the number of inliers converges. For the Procrustes models in this paper, the convergences stated above occurs within three iterations, hence why the stopping criterion for the LO-RANSAC algorithm is \(nLOSAC = 3\).

The number of top Procrustes models to further refine using LO-RANSAC is denoted by the variable K. The LO-RANSAC implementation used here uses, \(K=10\). Lowercase, k, in Algorithm 3, is the \(k^\textrm{th}\) locally optimized Procrustes model out of K. \(\mathfrak {M}\) are the K global metrics from each Procrustes model that has completed the local optimization procedure. The locally optimized Procrustes model with the minimum global metric, \(\mathcal {M}_{i}\), in \(\mathfrak {M}\), is the final and best Procrustes model. The final Procrustes model thus provides the best \(Q_{i}\) or \(Q_{i}\) and \(\Lambda _{i}\), depending on the Procrustes method.

In summary, each individual Procrustes model from the top ten is locally optimized and the best Procrustes model after local optimization is chosen. Local optimization significantly improves the accuracy of Procrustes models because of the vast increase in inlier data compared to the minimum or close to minimum sample size, L, used in the initial RANSAC algorithm.

4.8 Complete methodology

One might expect a generalization of the statistical properties of OAPA to apply to GOAPA. However, the authors have found issues with coupling a MLE architecture within a RANSAC framework for GOAPA. The additional complexity of solving for the scaling factors is the source of the problem. The group average, rotations, and scaling matrices are iterated until convergence. The residuals from the MLE models are affected by this iteration process. Unfortunately, the authors have found that fitting on these “transient” residuals leads to selecting false MLE models, which eventually yields an incorrect group average. This problem is not present when coupling a MLE architecture within a RANSAC framework for GOPA, which uses unity scaling factors.

To work around these issues, GOPA is implemented first using a MLE or nonparametric architecture within RANSAC and LO-RANSAC. The group average, \(G_h\), is updated after iterating through all the objects, A1, ..., An, , before returning to another loop over all the objects, Algorithm 2. This continues until the group average, \(G_h\), has met either the convergence criterion or maximum iteration threshold. The authors have found that a tolerance on the group average convergence of \(\varepsilon _{groupTol}={1\textrm{e}-6}\) works well. The maximum number of iterations is defined as \(nGroupIter=10\). Experimentally, a value of 10 seems to provide enough iterations for either the convergence criterion to be met or to avoid an infinite loop. The GOPA algorithm returns a converged group average, G, which now can be utilized in the OAPA algorithm. In the OAPA algorithm, a final pass over all the objects is performed utilizing the converged group average as the target object, Algorithm 4. The only assumption of doing OAPA after GOPA is that most of the objects only require unity scaling, and the minority will require anisotropic scaling. The OAPA algorithm returns the final rotations and scalings for all the objects. The entire framework is succinctly provided in algorithm 1.

Algorithm 1
figure a

- Final Robust General Procrustes Framework with Anisotropic Scaling

Full size image
Algorithm 2
figure b

- GOPA Algorithm using a MLE/Nonparametric architecture and RANSAC Framework. The randperm function returns a vector r containing L unique integers selected randomly from 1 to m without repeating elements. The vector r is used as indices to randomly subsample the data and corresponding group average. The spatialMedian function returns the spatial median of all the rotated objects \((A_iQ_i,\ldots ,A_nQ_n)\) utilizing the Weiszfeld method described in section 4.6. The global metrics and inlier masks on line 13 of the algorithm are needed for local optimization, Algorithm 3.

Full size image
Algorithm 3
figure c

- LO-RANSAC Algorithm. \(\mathcal {M}_{(i, \ j,\ldots , M)}\) a is a vector of global metrics from all M iterations, for the \(i^\textrm{th}\) object, within the RANSAC subsampling routine. The minK function returns the K smallest global metrics for a particular object. The K smallest global metrics are directly associated with the top K Procrustes models. The inlier mask associated with each of the K smallest global metrics is utilized to resample the data at the start of their local optimization procedure. This contrast with the small, randomized, sampling procedure in step 6 of Algorithm 2. The inlier mask, \(\rho _{i, ii}(\Xi _{i, ii})\), for a particular object and associated Procrustes model is updated in the LO-RANSAC procedure; as the number of identified inliers increases after each iteration, the estimates for the rotation or scalings subsequently improve due to the increased amount of data. Lowercase, k, is the \(k^\textrm{th}\) locally optimized Procrustes model out of K. \(\mathfrak {M}\) are the K global metrics from each Procrustes model that has completed the local optimization procedure. The locally optimized Procrustes model with the minimum global metric, \(\mathcal {M}_{i}\), in \(\mathfrak {M}\), is the final and best Procrustes model. The final Procrustes model thus provides the best \(Q_{i}\) or \(Q_{i}\) and \(\Lambda _{i}\), depending on the Procrustes method.

Full size image
Algorithm 4
figure d

- Final OAPA algorithm using OAPA with the Group Average as the target object. Utilizing a MLE/Nonparametric architecture and RANSAC Framework.

Full size image

5 Results

5.1 Synthetic data example

To illustrate the effectiveness of the methodology presented here, a challenging synthetic data set will be used. Five objects, representing five accelerometers, will need to be robustly and optimally rotated and scaled. Each object represents a triaxial accelerometer, where the columns represent the triaxial acceleration in \(\mathbb {R}^3\) and the rows represent a response in time. The inlier fraction of the response represents rigid body motion experienced by all members of the population. The fourth accelerometer will be anisotropically scaled, while the fifth accelerometer will have outliers consisting of half of the entire time series. The underlying time domain ranges from 0 to \(4\pi \) with a discrete step size of \(\Delta t=0.01, \; t=[ 0,4\pi ]\). Three trigonometric functions are applied to the time domain, which forms the columns of the matrix, \(A_{\textrm{true}} \in \mathbb {R}^{1257 \textrm{x} 3}\), defined as:

$$\begin{aligned} A_{\textrm{true}} = [\sin (3t),\quad 2\cos (2t),\quad 3\cos (t)]. \end{aligned}$$
(22)

The data are generated by applying the inverse of a unique random rotation, \(R_i\), to each of the true accelerometer data. Randomly generated noise is added to each of them as defined by \(\Psi \). The fourth accelerometer was anisotropically scaled after the rotation, \( \textrm{diag}( \Lambda _4^{-1}) = [2,4,6] \). The fifth accelerometer is further perturbed by setting the first half of the signal in all spatial directions to a constant one, with noise, to emulate faulty data or outliers. The generate data can succinctly be written as:

$$\begin{aligned}&A_i = A_{\textrm{true}} R_i^{-1} + \Psi _{i} : i=1,\ldots ,5, i\ne 4 \nonumber \\&A_4 = A_{\textrm{true}} R_4^{-1} \Lambda _4^{-1} + \Psi _{4} \nonumber \\&\Psi \sim \mathcal {N} \left( \textbf{0}, \varvec{\Sigma }=\begin{bmatrix} 0.01^2 &{} 0 &{} 0\\ 0 &{} 0.02^2 &{} 0\\ 0 &{} 0 &{} 0.03^2 \end{bmatrix} \right) . \end{aligned}$$
(23)

For each channel direction, an individual confidence value of \(p=0.983\) was chosen to provide a joint confidence value of 95%, \(p_J=0.95\). The figures in this section refer to a single instance of a simulated data set. The synthetic data example has been purposely curated with various issues that are more severe than most real data sets. The proceeding subsection will highlight a real data example coming from a series of shock experiments.

A robust methodology for the optimal alignment of this high-dimensional data set should return the optimal rotations, \(Q_i\), for all five objects while excluding the faulty signal content of the first half of \(A_5\). The methodology should also return the correct anisotropic scaling for \(A_4\), i.e., \(\textrm{diag}( \Lambda _4) = [\frac{1}{2}, \frac{1}{4}, \frac{1}{6}]\).

The first row of Fig. 1 exhibits the true signal comprising of the trigonometric functions in the global coordinate system. The second row exhibits the original function now in arbitrary coordinate systems with perturbations. Figure 2, first row, demonstrates the efficacy of the methodology with all the objects correctly rotated to match the true signal, even if \(A_1\), \(A_2\), and \(A_3\) are difficult to see behind \(A_4\) and \(A_5\). Figure 2, second row, highlights the accuracy of the methodology in estimating the group average even in the presence of anisotropy and outliers. Figure 3 provides additional information on what inliers were selected from \(A_5\). The true outlier fraction was 0.5, and the estimated inlier fraction for \(A_5\) is shown in Table 1, with a value of \(\hat{\gamma }=0.496\). More importantly, the true positive outliers were all selected with only a small proportion of false positives being selected because of the underlying noise. One interesting observation is the individual channel direction outlier fractions were much higher than 0.5, but the joint condition of all three spatial directions requiring to be inliers corrected for this. The rotational errors are all less than a Frobenius norm of \({1\textrm{e}-4}\), Table 1. The anisotropic scaling estimates are sufficiently accurate with an error of less than \({1\textrm{e}-2}\).

Fig. 1
figure 1

\(A_{\textrm{true}}\) with \(A_1,\ldots ,A_5\) generated from using (23). \(A_4\), purple line with squares, has anisotropic scaling. \(A_5\), green line with hollow circles, has an almost constant value for the first half the signal that represents a corrupt signal with noise. The second half of the signal, light blue with hollow circles, represents the remaining uncorrupt portion

Full size image
Fig. 2
figure 2

Accelerometers \(A_1,\ldots ,A_5\) rotated into the global coordinate system using the optimal rotation matrices from running GOPA and OAPA with MLE within a RANSAC framework. \(A_4\) on the first row also uses the correct anisotropic scaling to correct the signal. \(A_5\) on the first row correctly identifies that the first half of the signal is corrupt and excludes that portion with the exclusion of the purple signal content from Fig. 1 The second row demonstrates how well the group average matches the ground truth even in the presence of outliers and incorrectly scaled data

Full size image
Table 1 Results from synthetic data example
Full size table
Fig. 3
figure 3

The first row exhibits \(A_5\) in its arbitrary coordinate system, which needs to be rotated while also identifying which portion of the signal contains inliers and outliers. The second row exhibits the results of the methodology presented here by correctly identifying the inliers and outliers while robustly and optimally solving for the optimal rotation matrix

Full size image

5.2 Shock data

To further illustrate the effectiveness and utility of the methodology, a real data set from a series of shock experiments are used. Shock data is particularly challenging for traditional frequency-domain assessments of orientations that rely on signal stationarity. The experiment consisted of a test body instrumented with eleven triaxial accelerometers, many of which are located within the test body. Only one of the eleven accelerometers was aligned with the coordinate system of the test body, known as the global coordinate system, while the remaining ten accelerometers were not. Physical impediments such as complex internal geometry can inhibit an accelerometer in aligning with the test body thereby resulting in a local coordinate system that differs from the global coordinate system. In the example provided, each channel number corresponds to the same accelerometer number. Thus, channel number 1 refers to accelerometer/object 1.

The test body was ejected from an ejection unit 30 times. The shock imposed onto the test body from the ejection unit was recorded before it reached the ground using a sample rate of 32 kHz. All the ejection shock events from a single channel number and spatial direction were then concatenated into one time series. Post-processing of the data included resampling the data down to 167 Hz followed by 40 Hz low pass filter. Resampling the data to a lower sample rate was performed in order to reduce the size of the data set. The final low pass filter step was designed to isolate rigid body responses from the test body. Figure 4 provides an example of the final preprocessed data from accelerometer number two.

Fig. 4
figure 4

Concatenated shock data from triaxial accelerometer 2. The rows of the figure denote the data collected from each of the three spatial directions: X, Y, and Z, respectively. Each spike corresponds to a single ejection event. The local orientation of accelerometer 2 is the only accelerometer that is also in the orientation of the test body

Full size image

Figure 5 provides the inlier results from the MLE architecture and RANSAC framework described above. All channels were estimated to have an inlier fraction of greater than 0.85; therefore, the MLE mixture model does an adequate job of selecting inliers from a real data set. The authors were not aware of any significant outliers from the data set. Thus, the outliers selected from the model must be noise or responses found at either tail of the fitted t-distribution.

Fig. 5
figure 5

Estimated inlier fraction for all 11 triaxial accelerometers using the MLE mixture model and RANSAC framework

Full size image

One way to compare how the expected rotation matrices, \(\check{Q_i}\), listed in the part drawings, compares to the estimated rotation matrices, \(\hat{Q_i}\), provided by the methodology above, is to calculate the angle, \(\vartheta \), between each row of these matrices for every accelerometer. Calculating this vector angular deviation, \(\vartheta \), is shown below:

$$\begin{aligned} \vartheta _{(i, ii)}= & {} \textrm{atan2}\left( ||( \check{\varvec{q}}_{(i, ii)} \times \hat{\varvec{q}}_{(i, ii)} )||^2, \check{\varvec{q}}_{(i, ii)} \cdot \hat{\varvec{q}}_{(i, ii)} \right) \nonumber \\ {}{} & {} : i \in \{1,\ldots , n\}, \quad ii \in \{1,2,3\}. \end{aligned}$$
(24)

The vector, \( \check{\varvec{q}}\), denotes a row vector from an expected rotation matrix, \(\check{Q_i}\), and \(\hat{\varvec{q}}\) denotes a row vector from an estimated rotation matrix, \(\hat{Q_i}\). The first subscript denotes the \(i^\textrm{th}\) accelerometer and the second subscript denotes using the \(ii^\textrm{th}\) row from either the the expected or estimated rotation matrices. The first, second, and third row from the rotation matrices can be related to the X, Y, and Z spatial directions, respectively. The Euclidean norm is denoted as \(||\bullet ||^2\) and \(\textrm{atan2}(\bullet )\) refers to the 2-argument arctangent operator.

Figure 6 provides a bar plot of \(\vartheta \) for every channel number and their respective spatial/channel direction. For the majority of the channels, the vector angular deviation between the rotation matrices are very low, usually just a few degrees. However, channel number 11 shows a significant deviation. Channel 11, denoting accelerometer 11, suggests that there are significant alignment issues with channel directions X and Z due to nearly a 90\(^{\circ }\) deviation. The issue becomes apparent when visually inspecting the expected and estimated rotation matrices for channel 11. The estimated rotation can be approximately achieved from a series of linear transformations to the original expected rotation matrix. One, multiplying the first row of the expected rotation matrix by a negative one. Two, swapping the newly modified first row with the third row. These transformations suggest that the methodology has found two issues during the data acquisition test setup. Firstly, a polarity issue with the X channel direction requiring a sign change. Secondly, it appears that the X and Z channel directions were swapped during acquisition. The work presented here has identified both issues automatically allowing the analyst to easily make a posttest correction.

Fig. 6
figure 6

Estimated angular deviations, \(\vartheta \), using the row vectors from the expected and estimated rotation matrices

Full size image

Each triaxial accelerometer has three cables, one for each spatial direction. In the example provided here, a total of 33 cables, three from each of the eleven accelerometers must be wired correctly into the data acquisition (DAQ) system. It is common for highly instrumented test bodies to contain dozens of accelerometers. Human error can often creep in with the most common example being channel swaps. For example, the DAQ is configured such that a particular accelerometer is in their local X, Y, and Z spatial directions. However, the test engineering has miswired the DAQ such that the spatial directions are now Z, Y, and X. Consequently, the data from the X and Z spatial directions are swapped, which was the very problem that was identified above.

Another way to compare how \(\check{Q_i}\) compares to \(\hat{Q_i}\) is to calculate the rotation required to align \(\check{Q_i}\) to \(\hat{Q_i}\). The methodology to perform this rotation is actually OPA. Decomposition of this meta rotation matrix provided by OPA into its individual Euler angles (yaw, pitch, and roll) allows for a different interpretation. Calculating the Euler angles on the resulting matrix from matrix subtraction, \(\check{Q_i} - \hat{Q_i}\), often does not work because the resulting matrix may have a rank less than 3. The absolute value of the Euler angles for each accelerometer is provided in Fig. 7. The Euler interpretation provides a very similar result compared to the vector interpretation with channels numbers 1 through 10 having angular deviations within few degrees with channel 11 also having a high angular deviation. However, with the Euler interpretation, it is less clear how the X and Z channels are swapped.

Fig. 7
figure 7

Estimated angular deviations between expected and estimated orientations using Euler angles

Full size image

Ideally, the estimated group average utilizing various statistical architectures within RANSAC frameworks would be similar, provided that all the assumptions in each architecture were met. The group average estimated from a MLE mixture architecture will be denoted as \(G_{\textrm{MLE}}\) and the group average from a nonparametric architecture will be denoted as \(G_{\textrm{NonPara}}\). Calculating the alignment between the two group averages is performed using OPA, the meta rotation matrix provided by OPA is once again decomposed into Euler angles. The notation \(G_{\textrm{NonPara}} \xrightarrow {} G_{\textrm{MLE}}\) denotes that object on the right hand side of the arrow is the target object, \(G_{\textrm{MLE}}\) in this example. The Euler angles shown in Fig. 8 demonstrate that the two group averages from different statistical architectures align incredibly close to each other. Irrespective of which group average is considered the target object, the angular discrepancies are less than a degree. A salient result is how the angular discrepancies for the X and Y spatial directions are an order of magnitude larger than the angular discrepancies for the Z spatial direction.

Fig. 8
figure 8

Uncertainty in the alignment of the group average, G, from two different RANSAC frameworks: MLE mixture model, \(G_\textrm{MLE}\), and a nonparametric order-based statistics model, \(G_\textrm{NonPara}\). Calculating the alignment between the two group averages is performed using OPA. The notation \(G_{\textrm{NonPara}} \xrightarrow {} G_{\textrm{MLE}}\) denotes that the object on the right hand side of the arrow is the target object, \(G_{\textrm{MLE}}\). Comparing the alignment of the two group averages provides two choices as to which group average is considered the target object when performing OPA. Regardless of which group average is the target, the rotation matrix, provided by OPA, is then decomposed into Euler angles. The resulting rotation matrix when swapping which group average is considered the target object can be trivially calculated by taking the inverse of the original rotation matrix. Although the rotation matrices are linked by a linear transformation, decomposing the matrices results in asymmetrical Euler angles

Full size image

A hypothesis for why there exists a magnitude difference in the angular discrepancies for the Z spatial direction is due to the signal content of the data set. The shock data set has significantly more excitation in the Z spatial direction in the coordinate system of the test body due to the ejection motion directed along this spatial direction. This is evident in Fig. 4 with the amplitude of the acceleration content in the Z spatial direction being roughly an order of magnitude larger than that of the X and Y spatial directions. Channel 2 is a convenient triaxial accelerometer to reference because it is the only accelerometer that is supposed to be aligned with the test body, i.e., its rotation matrix to align with the test body is simply the identity matrix.

To further illustrate the concept above, a signal-to-noise ratio (SNR) metric, \(\varvec{z}\), will be defined uniquely for this problem space. The SNR metric for each accelerometer, \(A_i\), is defined as a row vector representing the SNR ratio for each of the three spatial directions, \(\varvec{z}_i \in \mathbb {R}^{(1 \textrm{x} 3)}\). The data from each accelerometer can be represented as three column vectors denoted as \(\varvec{a}_{(i,k)}: k=\{x, y, z\}\) and shown below:

$$\begin{aligned} A_i= & {} \left[ \varvec{a}_{(i,x)}, \ \varvec{a}_{(i, y)}, \ \varvec{a}_{(i, z)} \right] \end{aligned}$$
(25)
$$\begin{aligned} \varvec{z}_i= & {} \left[ \frac{\textrm{RMS}(\varvec{a}_{(i,x)})}{\textrm{RMS}(\varvec{\epsilon }_{i, x})}, \frac{\textrm{RMS}(\varvec{a}_{(i,y)})}{\textrm{RMS}(\varvec{\epsilon }_{i, y})}, \frac{\textrm{RMS}(\varvec{a}_{(i,z)})}{\textrm{RMS}(\varvec{\epsilon }_{i, z})} \right] \nonumber \\{} & {} : i \in \{1,\ldots , n\}. \end{aligned}$$
(26)

The SNR metric shown in (26) utilizes the RMS of the residuals defined in Sect. 4 as the noise component. Figure 9 provides the SNR metric for all of the channels and spatial directions; the figure also provides supplementary evidence that the underlying group average is dependent on the signal content of the underlying data. The SNR metric for the Z spatial direction is roughly eight times the SNR metric for the remaining spatial directions. The imbalance in the SNR metric between spatial directions explains why the uncertainty in the group average along the Z spatial direction is an order of magnitude less than the other spatial directions. This result aligns with one’s intuition that the underlying rotation estimates are dependent on the quality and signal content of the data set. The authors have noticed that data sets with roughly an equal SNR metric between all spatial directions provide a similar magnitude of uncertainties across all the spatial directions for the group average. Such data sets occur during single-axis, sinusoidal, vibration testing. This is when a test body is subjected to a single-axis excitation and then is rotated and re-mounted to test the subsequent orthogonal axes. Therefore, the accelerometers record roughly equal signal content from all the spatial directions over the course of the entire test series.

Fig. 9
figure 9

SNR of the channel numbers and their spatial directions. The SNR for the Z spatial direction is considerably larger than the remaining spatial directions due to the shock event occurring in the Z direction of the test body’s coordinate system. See Fig. 4 for an example of shock data collected from channel/accelerometer 2 which shares the same coordinate system as the test body’s

Full size image

Uncertainties in the group average will propagate to uncertainties in the final rotation matrices for each of the individual channel numbers. Figure 10 compares how the absolute Euler angular differs between the various architectures. For most of the channel numbers, the angular differences are only a few degrees. The angular differences between the various architectures for the Z spatial direction are typically much smaller than the other spatial directions, most likely due to having a vastly higher SNR metric along this spatial direction.

Fig. 10
figure 10

Absolute values of the Euler angles between the estimated rotation matrices utilizing two different RANSAC frameworks: MLE mixture model and a nonparametric order-based statistics model. Notice how the uncertainties in the estimated rotation matrices in the Z direction are much lower than the other spatial directions for most of the channels. These results are likely due to the higher SNR in the Z direction, see Fig. 9

Full size image

Finally, the SNR metric also provides a method in assessing the validity of the anisotropic scaling estimates. Tables 2 and 3 provide tabular results of estimated anisotropic scaling values for each channel number and their spatial direction. From analyzing the time series data, the authors expect that the anisotropic scalings for all the channels should be approximately one for unity scaling. However, both architectures estimated a scaling factor of 0.37 for channel 6 along the Y spatial direction. The nonparametric architecture estimated a scaling value of 0.633 for channel 4 and scaling value of 0.542 for channel 11 both along the Y spatial directions. The values are shown in bold in Tables 2 and 3. The scaling values for the Z spatial direction exhibit less variance which is hypothesized to be attributed to the higher SNR metric. In general, the anisotropic scaling estimates exhibit more variability than the rotational estimates. The authors recommend that the scaling estimates be used to help guide an analyst for further analysis.

Table 2 Results from shock data using the MLE architecture with a RANSAC framework
Full size table
Table 3 Results from shock data using the nonparametric architecture with a RANSAC framework
Full size table

One of the assumptions made for the MLE architecture was that the residuals are independent among the spatial directions. The inlier fraction for each channel number in Table 2 is less than the assumed 95% joint value. This could imply that the residuals are correlated along their spatial direction; although it appears that the effects on the final rotations and scalings are benign. The inlier fraction for each spatial direction in Table 3 are all 98.3% with the expected joint inlier fractions for each channel number to be around 95%. The actual joint inlier fraction was between 96 and 97%. The difference in the estimated inlier percentages is attributed to the different statistical architectures. Both statistical architectures provide similar rotation estimates sharing the same magnitude on the Frobenius norm. The rotational error associated with channel 11 is consistent between both of the statistical architectures with a error that is 2–4 times greater in magnitude compared to the error from all of the other channel numbers.

6 Conclusion

We have presented how to implement various statistical architectures with a RANSAC framework in the context of Procrustes-type problems. The methodology presented here suggests how to incorporate robust techniques of RANSAC and LO-RANSAC, while using the spatial median, within various Procrustes-type problems. Utilizing a GOPA algorithm followed by a OAPA algorithm allows for the group average to be robustly calculated while the final algorithm provides optimal rotation and scalings matrices. The efficacy of MLE architecture as a method for characterizing outliers when the noise is either normally or multivariate normally distributed has been demonstrated. The inclusion of robust parametric models within the RANSAC framework using the t-distribution offers another layer of robustness over the classical Gaussian distribution that has been previously used while allowing the method to identify outliers. A nonparametric architecture using order-based statistics has also been provided when the underlying noise does not follow any elementary mixture type distribution.

A challenging synthetic case study has been provided to elucidate the effectiveness of the methodology. The synthetic case study correctly identified outliers and inliers among the various accelerometers along with correct rotations and scalings. A real data set from a series of shock experiments was also provided. The MLE and nonparametric architectures provided similar rotation and scaling estimates. Minor differences between the architectures were exhibited in the form of their estimated inlier fractions among the accelerometers. A vector and an Eulerian method were provided in analyzing the angular deviations between the expected and estimated rotation matrices. Both architectures found that estimated rotation matrix for accelerometer 11 differed significantly from its expected rotation matrix, suggesting an installation error occurred. Uncertainty in the orientation of the group average from the various architectures yielded minimal discrepancies. A SNR metric was provided as a method for assessing validity of scalings and rotations. Channel directions with a high SNR metric provided consistency in their estimated rotations and scalings. The application provided was in the domain of data analysis for structural dynamics; however, the methodology can be applied to other domains, particularly, digital image processing for point cloud data. Additional work is required to further understand how changes in noise resulting in different SNR levels affect the rotational and anisotropic scaling estimates herein. A more intricate synthetic study could be utilized to elucidate these nuances.