Deep Multiple Auto-Encoder-Based Multi-view Clustering

Abstract

Multi-view clustering (MVC), which aims to explore the underlying structure of data by leveraging heterogeneous information of different views, has brought along a growth of attention. Multi-view clustering algorithms based on different theories have been proposed and extended in various applications. However, most existing MVC algorithms are shallow models, which learn structure information of multi-view data by mapping multi-view data to low-dimensional representation space directly, ignoring the nonlinear structure information hidden in each view, and thus, the performance of multi-view clustering is weakened to a certain extent. In this paper, we propose a deep multi-view clustering algorithm based on multiple auto-encoder, termed MVC-MAE, to cluster multi-view data. MVC-MAE adopts auto-encoder to capture the nonlinear structure information of each view in a layer-wise manner and incorporate the local invariance within each view and consistent as well as complementary information between any two views together. Besides, we integrate the representation learning and clustering into a unified framework, such that two tasks can be jointly optimized. Extensive experiments on six real-world datasets demonstrate the promising performance of our algorithm compared with 15 baseline algorithms in terms of two evaluation metrics.

1 Introduction

Multi-view data, collected from different information sources or with distinct feature extraction approaches, is ubiquitous in many real-world applications. For instance, an image can be described by color, texture, edges and so on; a piece of news may be simultaneously reported by languages of different countries. Since different views may describe distinct perspectives of data, only using the information of a single view is usually not sufficient for multi-view learning tasks. Therefore, it is reasonable and critical to synthesize heterogeneous information from multiple views.

As there are a lot of unlabeled multi-view data in real life, unsupervised learning, especially multi-view clustering, has attracted widespread interest from researchers. To exploit the heterogeneous information contained in different views, various MVC algorithms have been investigated from different theory aspects, such as graph-based clustering algorithms [1], spectral clustering-based algorithms [2], subspace clustering-based algorithms [3], nonnegative matrix factorization-based algorithm [4, 5] and canonical correlation analysis-based algorithms [6, 7]. Although these existing multi-view clustering algorithms have achieved reasonable performance, most of them are not capable of modeling the nonlinear nature of complex data, because they use shallow and linear embedding models to reveal the underlying clustering structure in multi-view data.

To overcome this drawback, one effective way is to integrate deep learning into clustering algorithms to comprehensively utilize the feature learning ability of neural networks. Recently, several works have been devoted to developing deep multi-view clustering algorithms, e.g., deep canonical correlation analysis (DCCA) [6] and multi-view deep matrix factorization (DMF-MVC) [9]. DCCA learns the data of each view, fuses information of different views into a common consensus representation and then conducts some clustering approaches (such as k-means) on the learned representation; DMF-MVC uses a deep semi-NMF structure to capture the nonlinear structure and generated a valid consensus at the last level. However, these two algorithms do not simultaneously model consistent and complementary information among multiple views. Similar to DCCA and DMF-MVC, [4, 5] just focus on exploring consistent information with different formulations, while [3, 11] concentrate on exploring complementary information. In fact, exploring consistent or complementary information among multiple views is an important research direction [10]. Recently, [12, 13] have also shown that simultaneously discerning these two kinds of information can achieve better representation learning, but they belong to semi-supervised learning-based methods, i.e., partial label information of multi-view data must be provided. Therefore, it is still worth researching how to learn a low-dimensional representation with consistent and complementary information across multiple views via neural networks for multi-view clustering.

In addition, most existing multi-view clustering methods cluster data in two separate steps: They first extract the low-dimensional representation of multi-view data and then use traditional clustering methods (such as k-means and spectral clustering) to process the obtained representation. This two-step learning strategy may lead to unsatisfactory clustering performance, because the learned low-dimensional representation is not necessarily suitable for subsequent clustering tasks and the correlation between these two steps is not fully explored. DEC [8] designs a clustering embedding layer to integrate representation learning and clustering tasks into a unified framework, which realizes the mutual benefit of these two steps by co-training the clustering together with representation learning, i.e., minimizing the KL (Kullback–Leibler) divergence between the predicted cluster label distribution with the predefined one. Nevertheless, DEC is just suitable for dealing with single-view data, without consideration of the complementary information between multi-view data; therefore, the clustering performance in multi-view data is unsatisfactory.

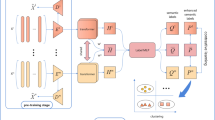
In this paper, we propose a multi-view clustering algorithm based on multiple auto-encoder, named MVC-MAE (see Fig. 1). Specially, MVC-MAE first employs multiple auto-encoders to capture the nonlinear structure information in multi-view data and derive the low-dimensional representations of data in different views. Then, MVC-MAE designs a novel cross-entropy-based regularization to guarantee the obtained low-dimensional representations between any two views more consistent as well as complimentary. Meanwhile, a local regularization is also incorporated to protect the local invariance within each view. In addition, MVC-MAE integrates the representation learning and clustering into a unified framework, such that two tasks can be jointly optimized, which can achieve mutual benefit for the clustering step and representation learning, avoiding the shortcomings resulted from performing a post-processing step (e.g., k-means) after obtaining the low-dimensional representation, because in this way the learned representation may not be best suited for clustering.

Fig. 1

The architecture of MVC-MAE. $L_{2CC}^{{(s_{1} ,s_{2} )}}$ denotes the regularization loss of consistent and complementary information between views $X^{{(s_{1} )}}$ and $X^{{(s_{2} )}}$, $L_{CC}^{{}}$ denotes the sum of losses between any two views, and $Z$ denotes the concatenation of learned low-dimensional representations (i.e., $\{ H^{(s)} \}_{s = 1}^{S}$) from different views. At the clustering step, the clustering embedding layer performs clustering based on $Z$ and in return, adjusting $Z$ according to the current clustering result

The contributions of this paper are summarized as follows:

• We propose a novel deep multi-view clustering algorithm (MVC-MAE), which learns a low-dimensional representation with consistent and complementary information across multiple views via multiple auto-encoder and identifies clusters in a unified framework. The deep model captures the hierarchical and nonlinear nature of multi-view data, and the joint optimization of representation learning and clustering can achieve mutual benefit for each other, such that improving the clustering performance.

• A novel cross-entropy-based regularization and an affinity graph-based local regularization are designed and incorporated into the objective function. The former is used to force the low-dimensional representations of the same samples in different views to be as consistent and complementary as possible, while the latter is used to protect the local geometrical information within each view.

• We conduct extensive experiments on six real multi-view datasets and compare the results of our MVC-MAE with that of fifteen baseline algorithms to evaluate the performance of the proposed approach. The experimental results demonstrate that the MVC-MAE outperforms baseline algorithms in terms of two evaluation metrics.

The rest of this paper is arranged as follows. Section 2 describes some related work. Section 3 introduces MVC-MAE algorithm in detail. Extensive experiments are conducted in Sect. 4. Finally, we give conclusions in Sect. 5.

2 Related Work

2.1 Shallow Multi-view Clustering Algorithms

Shallow multi-view clustering algorithms use shallow and linear embedding models to reveal the underlying clustering structure in multi-view data. For example, Liu et al. [4] and Wang et al. [5] adopted nonnegative matrix factorization (NMF) techniques, aiming to obtain a consensus indicator factorization among multi-view data; Cao et al. [3] extended subspace clustering into the multi-view domain and utilized the Hilbert–Schmidt independence criterion (HSIC) as a diversity term to preserve the complementary of multi-view representations; Wang et al. [31] proposed a position-aware exclusivity regularizer to enforce the affinity matrices of different views to be as complementary as possible and employed a consistent indicator matrix to support the label consistency among these representations; Kumar et al. [14] developed a spectral clustering and kernel learning-based co-training style; Li et al. [30] learnt the optimal label matrix by capturing the diversity and consistency between data space and label space and designed a self-weight strategy to weight each view in data space; Kamalika et al. [15] projected the data in each view to a lower-dimensional subspace based on canonical correlation analysis (CCA); and Nie et al. [16] tried to find a fusion graph across all views and then use graph-cut algorithms or spectral clustering on the fused graph to produce the clustering results.

Although these shallow multi-view clustering algorithms have achieved reasonable performance, they cannot fully capture hierarchical and nonlinear structure information in each view. Meanwhile, because the optimization ways of these algorithms are either based on eigenvalue decomposition or matrix decomposition, such that a lot of memory space and running time must be consumed, this makes these algorithms cannot be applied to large-scale multi-view datasets.

2.2 Deep Multi-view Clustering Algorithms

Complex data are usually composed of various hierarchical attributes, each of which is helpful to understand the sample at different abstract levels. In recent years, deep multi-view clustering algorithms have been proposed, because deep learning can effectively and efficiently learn the hierarchical information embedded in data. Zhao et al. [9] extended deep matrix factorization to multi-view case to enforce the last layer nonnegative representation of each view in deep matrix factorization to be the same, so as to maximize the consensus information among views; the model proposed by Huang et al. [32] revealed the hierarchical information of data in a layer-wise way and automatically learned the weight of each view without introducing extra parameters; Li et al. [34] combined local manifold learning and nonnegative matrix factorization to propose a deep graph regularized NMF model, which extracts more discriminative representations through hierarchical graph regularization; and Andrew et al. [6] adopted two deep networks to extract the nonlinear features of each view and then maximized the correlation between the extracted low-dimensional representations at the top layer by utilizing the CCA.

Although these deep multi-view clustering algorithms have captured the nonlinear structure, they did not simultaneously model consistent and complementary information among multiple views. Our MVC-MAE is also a deep multi-view clustering algorithm, but it captures consistent and complementary information across different views as well as the local geometrical information in a unified framework. Meanwhile, it incorporates a clustering embedding layer into the deep structure to co-train the clustering step together with representation learning.

3 The Proposed Algorithm

In this section, we present our MVC-MAE algorithm in detail.

3.1 Notations

Let $X = \{ X^{(s)} \in \Re_{{}}^{{m \times n^{s} }} \}_{s = 1}^{S}$ represent the original data of all views, where $S$ denotes the number of views, $n^{s}$ is the feature dimension of $s{\text{-th}}$ view, $m$ is the number of samples, and $X_{{}}^{(s)}$,$X_{i}^{(s)}$,$X_{i,j}^{(s)}$ represent the $s{\text{-th}}$ view multi-view data, the $i{\text{-th}}$ sample of the $s{\text{-th}}$ view and the $(i,j){\text{-th}}$ element in the $s{\text{-th}}$ view data, respectively.

Given $X = \{ X^{(s)} \in \Re_{{}}^{{m \times n^{s} }} \}_{s = 1}^{S}$, MVC-MAE aims to group samples into $C_{Cluster}$ clusters by integrating the hierarchical and heterogeneous information of $X$, such that data samples within the same cluster are more similar than those in different clusters. The similarity $sim(X_{i}^{(s)} ,X_{j}^{(s)} )$ between the sample $X_{i}^{(s)}$ and $X_{j}^{(s)}$ can be measured by some function, such as Euclidean distance or Pearson correlation based on $X^{(s)}$.

3.2 The Architecture of MVC-MAE

The critical issue for multi-view clustering is to reasonably fuse intra-view information and inter-view information to derive more high-quality results. To this end, MVC-MAE first uses multiple auto-encoders to capture the hierarchical and nonlinear information and then constructs affinity graphs with respect to different views to respect the local geometrical information, as well as exerts regularizations to preserve the consistent and complementary information among different views. To jointly optimize the representation learning and clustering, MVC-MAE develops a clustering embedding layer after the auto-encoders. The architecture of MVC-MAE is shown in Fig. 1. Based on this architecture, we try to capture four kinds of information, i.e., hierarchical and nonlinear structure information, local geometrical information, consistent and complementary information and clustering structure information of data samples.

3.2.1 Hierarchical and Nonlinear Structure Information

The hierarchical and nonlinear structure information of multi-view data is captured by multiple deep auto-encoder. As an excellent framework to capture hierarchical and nonlinear structure information between the low-dimensional representation and the input data, auto-encoder [17] has been popularly practiced in various areas. Deep auto-encoder is composed of two components, i.e., the encoder component mapping the input data to the low-dimensional space and the decoder component mapping the representations in low-dimensional space to reconstruction space. Both of them consist of multiple nonlinear functions. Generally speaking, the decoder component can be regarded as the mirror image of the encoder component and they have the same number of network layers and share a middle-hidden layer.

MVC-MAE contains multiple encoder components and multiple decoder components, where $E^{(s)}$ and $D^{(s)}$ correspond to the encoder and decoder component of $s{\text{-th}}$ view, respectively. Let $E^{(s)}$ and $D^{(s)}$ be composed of $L$ layers nonlinear functions and $H_{i}^{(s,l)}$ be the low-dimensional representation of $i{\text{-th}}$ sample at $l{\text{-th}}$ layer of $E^{(s)}$. Then, the encoder component $E^{(s)}$ of the s-th view can be formulated as follows:

$$\begin{gathered} H_{i}^{{(s,1)}} = \sigma \left( {W^{{(s,1)}} X_{i}^{{(s)}} + b^{{(s,1)}} } \right) \hfill \\ \qquad\ldots \hfill \\ H_{i}^{{(s,l)}} = \sigma \left( {W^{{(s,l)}} H_{i}^{{(s,l - 1)}} + b^{{(s,l)}} } \right) \hfill \\ \qquad \ldots \hfill \\ H_{i}^{{(s,L)}} = \sigma \left( {W^{{(s,L)}} H_{i}^{{(s,L)}} + b^{{(s,L)}} } \right) \hfill \\ \end{gathered}$$

(1)

where $\sigma ( \cdot )$ represents the nonlinear activation function, and $W_{{}}^{(s,l)}$ and $b_{{}}^{(s,l)}$ denote the weight matrix and bias vector of l-th layer of the encoder component in the s-th view. The decoder components are dedicated to reconstructing multi-view data as $\{ \tilde{X}^{(s)} \}_{s = 1}^{S}$ from the low-dimensional representation $\{ H^{(s,L)} \}_{s = 1}^{S}$. Thus, the decoder component $D^{(s)}$ of the s-th view can be formulated as follows:

$$\begin{gathered} H_{i}^{{(s,L + 1)}} = \sigma \left( {W^{{(s,L + 1)}} H_{i}^{{(s,L)}} + b^{{(s,L + 1)}} } \right) \hfill \\ \qquad \ldots \hfill \\ H_{i}^{{(s,2*L - 1)}} = \sigma \left( {W^{{(s,2*L - 1)}} H_{i}^{{(s,2*L - 2)}} + b^{{(s,2*L - 1)}} } \right) \hfill \\ \end{gathered}$$

(2)

Finally, the loss function of multiple auto-encoders is defined as follows:

$${\mathcal{L}}_{AE} = \sum\limits_{s = 1}^{S} {\sum\limits_{i = 1}^{m} {\left\| {(\tilde{X}_{i}^{(s)} - X_{i}^{(s)} ) \odot B_{i}^{(s)} } \right\|} } = \sum\limits_{s = 1}^{S} {\left\| {(\tilde{X}_{i}^{(s)} - X_{{}}^{(s)} ) \odot B^{(s)} } \right\|}$$

(3)

where $\odot$ means the Hadamard product and $B_{{}}^{(s)} = \{ B_{i}^{(s)} \}_{i = 1}^{m}$ denotes the weight of $s{\text{-th}}$ view, which is used to impose more penalty on the reconstruction error of the nonzero elements than that of zero elements [18]. In this way, ${\mathcal{L}}_{AE}$ can alleviate the instability caused by sparse data reconstruction to a certain extent and distinguish some more important features. $B_{{}}^{(s)} = \{ B_{i}^{(s)} \}_{i = 1}^{n}$ is defined as:

$$B_{i,j}^{(s)} = \left\{ {\begin{array}{*{20}l} \beta \hfill & {X_{i,j}^{(s)} \ne 0} \hfill \\ 0 \hfill & {X_{i,j}^{(s)} = 0} \hfill \\ \end{array} } \right.$$

(4)

where β≥0. By minimizing ${\mathcal{L}}_{AE}$, auto-encoders not only smoothly capture the data manifolds but also preserve the similarity among samples [19].

3.2.2 Local Geometrical Information

The local geometrical information [20] is captured by affinity graphs $\{ W^{(s)} \}_{i = 1}^{S}$ that are constructed from multi-view data $X = \{ X^{(s)} \in \Re_{{}}^{{m \times n^{s} }} \}_{s = 1}^{S}$. Firstly, Euclidean distance is adopted to measure the similarities between samples, and then, each sample is represented as a node, which is connected to its k most similar nodes (k-NN). The process is repeated $S$ times, each dealing with a view. The procedure for constructing affinity graphs with respect to different views is shown in Algorithm 1, where $N_{k} (X_{i}^{(s)} )$ is the set of $k$ nearest neighbors of sample $X_{i}^{(s)}$, and $j_{k}$ is the $k{\text{-th}}$ neighbor of sample $X_{i}^{(s)}$.

Let $P_{i,j}^{(s)} = P_{i,j}^{(s,s)}$ be the joint probability between sample $X_{i}^{(s)}$ and $X_{j}^{(s)}$ in the $s{\text{-th}}$ view, which is defined as:

$$P_{i,j}^{(s,s)} = \frac{1}{{1 + \exp ( - H_{i}^{(s)} (H_{j}^{(s)} )^{T} )}}$$

(5)

where $(H_{j}^{(s)} )^{T}$ means the transpose of the matrix $H_{j}^{(s)}$. Then, the local geometrical information within each view can be respected by maximizing the following likelihood estimation:

$${\mathcal{L}}_{Local} = \sum\limits_{s = 1}^{S} {\mathop {\mathop \prod \limits^{{}} }\limits_{{W_{i,j}^{(s)} > 0}} (P_{i,j}^{(s)} )}$$

(6)

With the negative log-likelihood, maximizing Eq. (6) is equivalent to minimizing Eq. (7):

$${\mathcal{L}}_{Local} = \sum\limits_{s = 1}^{S} {( - \sum\limits_{{W_{i,j}^{(s)} > 0}} {\log P_{i,j}^{(s)} } )}$$

(7)

3.2.3 Consistent and Complementary Information

The consistent of multi-view data means that there is some common knowledge across different views, while the complementary principle of multi-view data refers to some unique knowledge contained in each view that is not available in other views. Since different views describe the same sample from different perspectives, the consistent and complementary information contained in multi-view data should be preserved as much as possible. Therefore, how to capture consistent and complementary low-dimensional representation across different views is a key issue of MVC. A straightforward method is to concatenate these representations $\left\{ {H^{(s,L)} } \right\}_{s = 1}^{S}$ directly as the final representation, but it cannot guarantee consistent information among multiple views. Another widely used method is to enforce multi-view data to share the same highest encoder layer (i.e., $H^{(s,L)}$). However, this way will lead to the loss of a lot of complementary information from multi-view data, because all low-dimensional representations are enforced to be in a unified latent space.

In this study, we design a novel regularization strategy inspired by the cross-entropy loss function of binary classification. In the binary classification problem, let $Y_{i}^{t} \in \{ 0,1\}$ be the true label of $i{\text{-th}}$ sample and $Y_{i}^{p}$ be the prediction probability of $i{\text{-th}}$ sample, then the loss function of the cross-entropy is defined as:

$$\begin{gathered} {\mathcal{L}}_{B} (Y^{t} |Y^{p} ) = - \sum\limits_{i = 1}^{m} {(Y_{i}^{t} \log (Y_{i}^{p} ) + (1 - Y_{i}^{t} )\log (1 - Y_{i}^{p} ))} \hfill \\ = - \sum\limits_{i = 1}^{m} {(\log (Y_{i}^{p} )^{{Y_{i}^{t} }} + \log (1 - Y_{i}^{p} )^{{(1 - Y_{i}^{t} )}} )} \hfill \\ = - \sum\limits_{i = 1}^{m} {\log \left( {(Y_{i}^{p} )^{{Y_{i}^{t} }} \cdot (1 - Y_{i}^{p} )^{{(1 - Y_{i}^{t} )}} } \right)} \hfill \\ = - \mathop \Pi \limits_{i}^{m} \left( {(Y_{i}^{p} )^{{Y_{i}^{t} }} \cdot (1 - Y_{i}^{p} )^{{(1 - Y_{i}^{t} )}} } \right) \hfill \\ \end{gathered}$$

(8)

If $Y_{i}^{t} = 1$, i.e., the true label of $i{\text{-th}}$ sample is 1, ${\mathcal{L}}_{B} (Y^{t} |Y^{p} ) = - \sum\nolimits_{i = 1}^{m} {\log \left( {(Y_{i}^{p} )^{{Y_{i}^{t} }} } \right)}$; otherwise, ${\mathcal{L}}_{B} (Y^{t} |Y^{p} ) = - \log \left( {(1 - Y_{i}^{p} )^{{(1 - Y_{i}^{t} )}} } \right)$.

However, no label information can be available in MVC. So, we use $C_{i,j}^{{(s_{1} ,s_{2} )}}$ to indicate whether two representations $H_{i}^{{(s_{1} )}}$ and $H_{j}^{{(s_{2} )}}$ from two views describe the same sample, if it is true, $C_{i,j}^{{(s_{1} ,s_{2} )}} { = }1$; otherwise, $C_{i,j}^{{(s_{1} ,s_{2} )}} { = 0}$. In other words, $C_{i,j}^{{(s_{1} ,s_{2} )}} { = }1$, if $i = j$; otherwise, $C_{i,j}^{{(s_{1} ,s_{2} )}}$ = 0. Based on $C_{i,j}^{{(s_{1} ,s_{2} )}}$, we propose a novel cross-entropy loss function for MVC.

In order to improve clustering quality, we hope the differences between low-dimensional representations ($H_{i}^{{(s_{1} )}}$ and $H_{j}^{{(s_{2} )}}$) of the same sample ($i = j$) from different views are as small as possible, while the differences between those representations ($H_{i}^{{(s_{1} )}}$ and $H_{j}^{{(s_{2} )}}$) of different samples ($i \ne j$) from different views are as large as possible. Therefore, ${\mathcal{L}}_{2CC}^{{(s_{1} ,s_{2} )}}$ with respect to view $s_{1}$ and $s_{2}$ is defined as:

$$\begin{gathered} L_{2CC}^{{(s_{1} ,s_{2} )}} \hfill \\ = \prod\limits_{i,j}^{m} {\left( {(P_{i,j}^{{(s_{1} ,s_{2} )}} )^{{{C_{i,j}{(s_{1} ,s_{2} )}} }} (1 - P_{i,j}^{{(s_{1} ,s_{2} )}} )^{{{1 - C_{i,j}{(s_{1} ,s_{2} )}} }} } \right)} \hfill \\ = \sum\limits_{i,j = 1}^{m} {\log \left( {(P_{i,j}^{{(s_{1} ,s_{2} )}} )^{{{C_{i,j}{(s_{1} ,s_{2} )}} }} (1 - P_{i,j}^{{(s_{1} ,s_{2} )}} )^{{{1 - C_{i,j}{(s_{1} ,s_{2} )}} }} } \right)} \hfill \\ = \sum\limits_{i,j = 1}^{m} {\log \left( {(P_{i,j}^{{(s_{1} ,s_{2} )}} )^{{{C_{i,j}{(s_{1} ,s_{2} )}} }} (1 - P_{i,j}^{{(s_{1} ,s_{2} )}} )^{{{1 - C_{i,j}{(s_{1} ,s_{2} )}} }} } \right)} \hfill \\ = \sum\limits_{i,j = 1}^{m} {(C_{i,j}^{{(s_{1} ,s_{2} )}} \log (P_{i,j}^{{(s_{1} ,s_{2} )}} ) + (1 - C_{i,j}^{{(s_{1} ,s_{2} )}} )\log (1 - P_{i,j}^{{(s_{1} ,s_{2} )}} ))} \hfill \\ \end{gathered}$$

(9)

where $P_{i,j}^{{(s_{1} ,s_{2} )}}$ is the joint distribution between $X^{{(s_{1} )}}$ and $X^{{(s_{2} )}}$ views, which is defined as follows:

$$P_{i,j}^{{(s_{1} ,s_{2} )}} = \frac{1}{{1 + \exp ( - H_{i}^{{(s_{1} )}} (H_{j}^{{(s_{2} )}} )^{T} )}}$$

(10)

when $C_{i,j}^{{(s_{1} ,s_{2} )}} { = }1$, ${\mathcal{L}}_{2CC}^{{(s_{1} ,s_{2} )}} = \sum\nolimits_{i,j = 1}^{m} {\left( {C_{i,j}^{{(s_{1} ,s_{2} )}} \log (P_{i,j}^{{(s_{1} ,s_{2} )}} )} \right)}$, thus maximizing ${\mathcal{L}}_{2CC}^{{(s_{1} ,s_{2} )}}$ means to enforce the two representations close to each other; if $C_{i,j}^{{(s_{1} ,s_{2} )}} { = 0}$, ${\mathcal{L}}_{2CC}^{{(s_{1} ,s_{2} )}} = \sum\nolimits_{i,j = 1}^{m} {\left( {(1 - C_{i,j}^{{(s_{1} ,s_{2} )}} )\log (1 - P_{i,j}^{{(s_{1} ,s_{2} )}} )} \right)}$, maximizing $L_{2CC}^{{(s_{1} ,s_{2} )}}$ means to push them away.

In the case that two samples $X_{i}^{(s)}$ and $X_{j}^{(s)}$ are not the same sample ($i \ne j$), but they are similar according to the local geometrical information, the representations $H_{i}^{(s)}$ and $H_{j}^{(s)}$ should also be similar, and they should not be pushed away. Therefore, Eq. (9) is relaxed as follows:

$${\mathcal{L}}_{2CC}^{{(s_{1} ,s_{2} )}} = \sum\limits_{i,j = 1}^{m} {\left( {C_{i,j}^{{(s_{1} ,s_{2} )}} \log (P_{i,j}^{{(s_{1} ,s_{2} )}} )} \right)} + \sum\limits_{{i,j = 1,W_{i,j}^{{s_{1} }} = 0,W_{i,j}^{{s_{2} }} = 0}}^{m} {\left( {(1 - C_{i,j}^{{(s_{1} ,s_{2} )}} )\log (1 - P_{i,j}^{{(s_{1} ,s_{2} )}} )} \right)}$$

(11)

The loss function with respect to the case that $S > 2$ is extended in formula (12):

$${\mathcal{L}}_{CC} = \sum\limits_{{s_{1} = 1}}^{S} {\sum\limits_{{s_{2} = s1 + 1}}^{S} {{\mathcal{L}}_{2CC}^{{(s_{1} ,s_{2} )}} } }$$

(12)

3.2.4 Clustering Structure Information

To preserve the clustering structure in low-dimensional representation, a clustering embedding loss (CEL [8]) is adopted, which is measured by KL-divergence in MVC-MAE. Specifically, based on the learned representations of different views, we concatenate them as $Z = \mathop {||}\limits_{s = 1}^{S} H^{(s)}$, where $||$ represents concatenation operation, which can also preserve the complementary information in each view to some extent. Given the initial cluster centroids $\{ \mu_{j} \}_{j = 1}^{{C{}_{Cluster}}}$, according to [8], we use the Student’s t distribution as a kernel to measure the similarity between the representation $Z_{i}$ and centroid $\mu_{j}$:

$$Q_{i,j} = \frac{{(1 + \left\| {Z_{i} - \mu_{j} } \right\|^{2} )^{ - 1} }}{{\sum\nolimits_{j^{\prime}} {(1 + \left\| {Z_{i} - \mu_{j^{\prime}} } \right\|^{2} )^{ - 1} } }}$$

(13)

where $Q_{i,j}$ is interpreted as the probability of assigning the sample $i$ to cluster $j$. Let $E_{i,j}$ be the auxiliary distribution of $Q_{i,j}$, it is computed by raising $Q_{i,j}$ to its second power and normalized with the frequency per cluster, i.e.:

$$E_{i,j} = \frac{{{{Q_{i,j}^{2} } \mathord{\left/ {\vphantom {{Q_{i,j}^{2} } {f_{i} }}} \right. \kern-\nulldelimiterspace} {f_{i} }}}}{{\sum\nolimits_{j^{\prime}} {{{Q_{i,j^{\prime}}^{2} } \mathord{\left/ {\vphantom {{Q_{i,j^{\prime}}^{2} } {f_{j^{\prime}} }}} \right. \kern-\nulldelimiterspace} {f_{j^{\prime}} }}} }}$$

(14)

where $f_{j} = \sum\nolimits_{i} {Q_{i,j} }$ is the soft cluster frequencies of the cluster $j$.

Then, the KL divergence loss between the soft assignment $Q_{i,j}$ and the auxiliary distribution $E_{i,j}$ is defined as follows:

$${\mathcal{L}}_{CLU} = \sum\limits_{i}^{{}} {\sum\limits_{j}^{{}} {E_{i,j} \log \frac{{E_{i,j} }}{{Q_{i,j} }}} }$$

(15)

During the training procedure, we optimize the clustering loss according to Eq. (15) for helping auto-encoder to adjust the representation $Z$ and to obtain the final clustering results, such that the representation learning and clustering can be jointly optimized.

3.2.5 Total Loss

By integrating the above loss functions, the total loss function is defined as:

$${\mathcal{L}} = {\mathcal{L}}_{AE} + \alpha {\mathcal{L}}_{Local} + \gamma {\mathcal{L}}_{CC} + \theta {\mathcal{L}}_{CLU}$$

(16)

where $\alpha$,$\gamma$ and $\theta > 0$ are hyper-parameters. By minimizing the total loss function, we obtain the final clustering results directly from the last optimized $Q$ by $\mathop {\arg }\limits_{i} \max (Q_{i} )$, which is the most likely assignment.

3.3 Model Optimization

To optimize the proposed algorithm, we apply the Adam optimizer to minimize the objective in Eq. (16). In specific, the optimization process of the proposed algorithm is mainly divided into two stages: the pre-training stage and the fine-tuning stage.

3.3.1 Pre-training stage

In order to avoid falling into the local optimal solution, we first pre-train the auto-encoding of each view layer by layer under the learning rate of 1e-3 through the minimization formula (3). The representation $\left\{ {H^{(s)} } \right\}_{s = 1}^{S}$ is obtained through forwarding propagation, and then, they are concatenated as $Z$. Before the first training, the cluster centers $\{ \mu_{j} \}_{j = 1}^{{C{}_{Cluster}}}$, the auxiliary distribution $E$ and the soft assignment distribution $Q$ need to be initialized. Here, we use k-means cluster Z to initialize $\{ \mu_{j} \}_{j = 1}^{{C{}_{Cluster}}}$ and calculate $E$ and $Q$ through Eqs. (14) and (13), respectively. Moreover, we calculate the affinity matrices of different views by calling ConsAG.

3.3.2 Fine-tuning stage

In this training stage, the cluster centers $\{ \mu_{j} \}_{j = 1}^{{C{}_{Cluster}}}$ are updated together with the embedding $Z$ using the Adam optimizer based on the gradients of ${\mathcal{L}}_{CLU}$ with respect to $\{ \mu_{j} \}_{j = 1}^{{C{}_{Cluster}}}$ and $Z$. We first calculate $E$ and $Q$ with the updated $\{ \mu_{j} \}_{j = 1}^{{C{}_{Cluster}}}$ and $Z$ by Eq. (14) and (13). It is worth noting that to avoid instability in the training process, we update $E$ every 10 iterations in the optimization process. We calculate clustering loss ${\mathcal{L}}_{CLU}$ according to Eq. (15) and update the whole framework of our proposed algorithm by minimizing Eq. (16). Finally, we compute final $Q$ by Eq. (13) and infer clustering labels based on $Q$. The algorithm step is shown in Algorithm 2. The corresponding source codes are available at https://github.com/***********.

3.4 Complexity Analysis

The MVC-MAE consists of four components: $S$ auto-encoders, the consistent and complementary regularizer, the local geometrical information, the CEL. We analyze the time complexity of each part in turn. The time complexity of a single auto-encoder is $O\left( {m*n*L} \right)$, where $n$ denotes the maximum dimension of all layers. Thus, the total time complexity of $m$ auto-encoders is $O\left( {S*m*n*L} \right)$. The time complexity of the consistent and complementary regularizer is $O\left( {S^{2} *m^{2} } \right)$. The time complexity of the local geometrical component is $O\left( {m^{2} *k} \right)$. The time complexity of the CEL component is $O\left( {m*n_{z} *C_{cluster} } \right)$, where $n_{Z}$ denotes the dimension of the embedding $Z$. Finally, the total time complexity of MVC-MAE is $O\left( {S*m*n*L + S^{2} *m^{2} + m^{2} *k} \right)$.

4 Experiments

4.1 Experiments Setting

4.1.1 Datasets

We carry out extensive experiments on six real-world datasets, including one text dataset (BBCSport¹), five image datasets (HW2source,² 100leaves³, ALOI,⁴ Caltech101,⁵ and NUSWIDEOBJ [33]). Their statistics are summarized in Table 1, where #sample, #view, #cluster and #n^s denote the number of samples, the number of views, the number of clusters and the feature dimension of the s-th view in the corresponding dataset, respectively. We also present the detailed descriptions of each dataset below.

Table 1 Statistics of six datasets

4.1.2 BBCSport

A text dataset contains 544 sports news and 5 topical areas. Each piece of news is divided into two parts, corresponding to two views.

4.1.3 HW2source

A handwritten numerals (0–9) dataset contains 2000 samples and 10 digits. Two types of features, i.e., Fourier coefficients of the character shapes and the pixel, are selected as two views.

4.1.4 100leaves

An image dataset contains 1600 samples and 100 plant species. Three types of features, i.e., texture histogram, fine-scale margin and shape descriptor, are generated to represent three views.

4.1.4.1 ALOI

An image dataset contains 100 subjects and 110,250 samples. We select 108 samples for each subject, a total of 10,800 samples for experimental evaluation. For each image, four types of features, i.e., RGB color histograms, HSV color histograms, color similarity, Haralick features, are generated to represent four views.

4.1.5 Caltech101

An image dataset contains 102 subjects and 9144 samples. For each image, six types of features, i.e., GABOR feature, wavelet moments (WM), Centrist feature (CENT), HOG feature, GIST feature and LBP feature, are generated to represent six views.

4.1.5.1 NUSWIDEOBJ

An image dataset for object recognition contains 31 classes and 30,000 images. For each image, six types of features, i.e., color histogram, CM, CORR, edge direction histogram and wavelet texture, are generated to represent six views.

4.1.6 Compared Algorithms

We compare the proposed MVC-MAE with the following clustering algorithms:

• 1. NMF [21] (Single view): a standard nonnegative matrix factorization (NMF) method, which is executed on data of each view and results from all views are reported.

• 2. AE [22] (Single view): a single-view clustering algorithm, which is executed on data of each view and results from all views are reported. The number of each layer of AE is the same as that of MVC-MAE.

• 3. AE-C: a single-view clustering algorithm, which concatenates the features of multiple views as its input. The number of each layer of AE-C is the same as that of MVC-MAE.

• 4. AE-CS: a shallow version of AE-C, only one nonlinear function layer is contained in the encoder and decoder component of AE-CS, respectively.

• 5. CoregSC [14]: an approach with centroid-based co-regularization, which enforces the clustering results of different views to be consistent with each other.

• 6. MultiNMF [4]: an NMF-based method, which searches for a factorization that gives a consensus clustering scheme across all views.

• 7. MultiGNMF [5]: an improved version of MultiNNMF, which integrates manifold learning into MultiNMF, such that the local geometrical information of each view can be considered.

• 8. DiMSC [3]: a subspace clustering method, which uses the Hilbert–Schmidt independence criterion (HSIC) as the diversity term to explore complementary information across different views.

• 9. RMSC [23]: a spectral clustering-based robust method, which employs Markov chain to solve the latent transition probability matrix from the similarity matrices of different views with the low-rank and sparse constraints.

• 10. MVCF [24]: a concept factorization-based method, which makes full use of data correlation between views.

• 11. MVGL [25]: a multi-view graph clustering method, which optimizes a global graph with an exact number of the connected components from a different single-view graph and then obtains the clustering indicators, without post-process or any graph techniques.

• 12. SwML [26]. a self-weighted multi-view graph clustering method, which optimizes a unified similarity graph by introducing a self-weighted learning strategy.

• 13. AMGL [16]. a parameter-free multi-view graph clustering method, which can automatically assign suitable weights to all graphs without introducing any parameters.

• 14. DCCA [6]. a deep CCA-based method, which captures nonlinear structure information by adopting two deep networks and employs CCA to maximize the consistent information between two deep networks.

• 15. DMF-MVC [9]. a deep MF-based method, which learns the hierarchical information in multi-view data by designing a deep semi-nonnegative matrix factorization framework and maximizes the consensus information from each view by enforcing the final representation of each view to be similar.

Among these MVC algorithms, NMF, AE, AE-C, AE-CS, CoregSC, MultiNMF, MultiGNMF, DiMSC, MVCF, RMSC, DCCA and DMF-MVC require an additional clustering step to assign cluster label for each sample based on the learned representation or affinity graph. In this study, we use k-means or spectral clustering to assign cluster labels according to the original papers.

4.1.7 Evaluation Metrics

The quality of clustering results is evaluated by comparing the obtained cluster labels with the original labels provided by the datasets. Two commonly used metrics, i.e., the accuracy (ACC) and the normalized mutual information metric (NMI) [28], are selected to measure the effectiveness of the proposed algorithm. ACC is used to compute the percentage of agreements between the true labels and the clustering labels, which is defined as:

$${\text{ACC}} = \frac{{\sum\nolimits_{i = 1}^{m} {{\mathbf{1}}\left\{ {\overline{{C_{i} }} = C_{i} } \right\}} }}{m}$$

(17)

where $m$ is the total number of samples; $C_{i}$ and $\overline{{C_{i} }}$ are the true label and the clustering label of $i{\text{ - th}}$ sample, respectively. ${\mathbf{1}}\{ x\}$ is the indicator equation, when the result is assigned to be 1 if the predicted result is the same as the true result and 0, otherwise.

The normalized mutual information is employed to measure the similarity of two clusters, which is defined as:

$${\text{NMI}} = \frac{{\sum\nolimits_{j,y} {\frac{{m_{j,y} }}{m}\log \frac{{mm_{j,y} }}{{m_{j} \hat{m}_{y} }}} }}{{\sqrt {\left( {\sum\nolimits_{j} {m_{j} \log \frac{{m_{j} }}{m}} } \right)\left( {\sum\nolimits_{y} {\hat{m}_{y} \log \frac{{\hat{m}_{y} }}{m}} } \right)} }}$$

(18)

where $m_{j}$ denotes the number of samples contained in cluster $C_{j} (1 \le j \le C_{Cluster} )$, $\hat{m}_{y}$ denotes the number of samples belonging to the class ${\mathcal{Y}}_{y} (1 \le y \le C_{Cluster} ),$ and $m_{j,y}$ denotes the number of samples that are in the intersection between cluster $C_{j}$ and ${\mathcal{Y}}_{y}$.

For these two metrics (ACC and NMI), the larger value indicates better clustering performance.

4.1.8 Implementation Details

We implement MVC-MAE, AE, AE-C and AE-CS by using Python language and TensorFlow framework, adopt Adam optimizer to train our model and employ LeakyReLU [27] as the activation function of all internal layers except for the input layer, output layer and clustering embedding layer. For baseline algorithms, we adopt the same network layer configuration on each dataset as MVC-MAE, as shown in Table 2. For MVC-MAE, $\alpha$,$\gamma$ and $\theta$ are set to 10, 0.1 and 0.1, respectively, in the experiment. Besides, we run each algorithm 20 times on each dataset on the platform of Ubuntu Linux 18.04 with NVIDIA 1080ti Graphics Processing Units (GPUs) and 64 GB memory size and then record the average results as well as the standard deviations. All codes of compared algorithms are downloaded from the authors’ home pages, and they are carried out by comprehensively tuning the corresponding hyper-parameters.

Table 2 The configurations of MVC-MAE on different datasets. We only show the architecture of the encoder (the second column). The decoder reverses the encoder. The number of neurons in the cluster embedding layer is set to the number of clusters in the corresponding dataset (the third column)

Besides, DCCA can only deal with the dataset with two views, so we run DCCA on subdatasets composed of two views and report the best results.

4.2 Clustering Performance

Table 3 shows ACC and NMI of the proposed algorithm and 15 comparison algorithms on three datasets (HW2sources, BBCSport and 100leaves), and Table 4 shows ACC and NMI of the proposed algorithm and 7 compared algorithms (AE, AE-C, AE-CS, CoregSC, MVCF, RMSC and DCCA) on the other three datasets (ALOI, Caltech101and NUSWIDEOBJ). In Table 4, the results of some algorithms, such as MultiNMF, MultiGNMF and DMF-MVC, are not provided, because the scale of datasets ALOI, Caltech101 and NUSWIDEOBJ, i.e., the number of samples, the number of views and the feature dimension of each view, is relatively large, and these algorithms are very time-consuming. In Tables 3 and 4, the best results are highlighted in bold, where the value 0.00 in brackets indicates that the value is close to zero, 0 indicates zero, and “-” denotes that the dataset does not have the corresponding view. OOM denotes “out of memory.”

Table 3 Cluster performance on three small datasets (HW2sources, BBCSport and 100leaves)

Table 4 Cluster performance on three big datasets (ALOI, Caltech101 and NUSWIDEOBJ)

From Tables 3 and 4, we make the following observations:

• 1. MVC-MAE is superior to all the compared algorithms in two evaluation metrics on most datasets. These results clearly show that the proposed algorithm can achieve the promising clustering performance. Although both DCCA and DMF-MVC are deep MVC algorithms, they cannot achieve the desired performance, where DCCA does not capture complementary information, while DMF-MVC does not fully capture hierarchical information in each view and complementary information across views, because the nonlinear activation function is not added between layers of deep neural network. DiMSC does not achieve a good result on all datasets because it is just a shallow model and requires an extra clustering step. MultiNMF and MultiGNMF show relatively good results, but both are inferior to MVC-MAE.

• 2. We also can find from Table 4 that MVC-MAE not only obtains better clustering results but also is easily applied to large-scale data through mini-batch training. Although CoregSC, MVCF and RMSC can perform clustering tasks on the ALOI and Caltech101 datasets, OOM occurs when these three algorithms deal with a larger dataset (NUSWIDEOBJ).

• 3. The clustering performance of AE and NMF varies across different views, and the clustering results of AE are better than those of NMF, AE-C superior to AE and AE-CS. It indicates that the deep learning algorithm is superior to NMF in single-view clustering algorithms, because the deep learning algorithm captures the complex hierarchical information of data; integrating information from multiple views can improve the performance of MVC; and directly concatenating all views does not distinguish the importance of each view.

• 4. RMSC also obtains good experimental results due to the suppression of noise. In addition, the results of MVCF, MVGL and SwML are also good, second only to MVC-MAE. This demonstrates that it is important to distinguish the weight of consistent information about different views.

4.3 Ablation Study of the Proposed Algorithm

In this subsection, we carry out some ablation studies of MVC-MAE, aiming to explore the contributions of consistent and complementary, local geometric regularization and the fusion of low-dimensional representations from different views on the clustering results. To this end, we define the following three variants of MVC-MAE: 1) MVC-MAE_-No-CC, which optimizes Eq. (16) with $\gamma$ = 0, represents that MVC-MAE does not consider the consistency and complementary information; 2) MVC-MAE_-No-Local, which optimizes Eq. (16) with $\alpha$ = 0, represents that MVC-MAE does not consider the local geometrical information; and 3) MVC-MAE_-Meansums all the representations $\left\{ {H^{(s)} } \right\}_{s = 1}^{S}$ of different views and averages them to get the representations $Z$ as to the input of CEL. The clustering results of these algorithms are reported in Table 5. From Table 5, we can observe that the clustering results of MVC-MAE on six datasets are significantly better than those of three variants, which proves that consistent and complementary, local geometric regularization and the concatenation of low-dimensional representations of different views are helpful to improve the performance of clustering, and all of them are indispensable.

Table 5 Cluster performance on ablation study

4.4 Parameter Sensitivity

To explore how the clustering performance of MVC-MAE varies with the hyper-parameters $\alpha$, $\gamma$ and $\theta$, we run MVC-MAE under different parameter configurations. In the experiments, we vary the value of $\alpha$ from [0.001,0.01,0.1,1,10,100] and set $\gamma { = }0.1$, $\theta { = }0.1$; or vary the value of $\theta$ from [0.001,0.01,0.1,1,10,100] and set $\alpha { = }10$,$\gamma { = }0.1$; or vary the value of $\gamma$ from [0.001,0.01,0.1,1,10,100] and set $\alpha { = }10$,$\theta { = }0.1$. The ACC and NMI of MVC-MAE under different parameter configurations are shown in Fig. 2. It can be seen from Fig. 2 that the clustering performance of MVC-MAE is relatively stable under $0 < \alpha < 1$, $0 < \theta < 1$,$0 < \gamma < 0.1$. It indicates that MVC-MAE is robust and setting parameters is not a complex task.

Fig. 2

The clustering performance of MVC-MAE on six datasets under various $\alpha$,$\gamma$,$\theta$

4.5 Visualization

In this study, the visualization tool T-SNE [29] is employed to map low-dimensional representations obtained by the proposed MVC-MAE and matrix factorization-based algorithms into a two-dimensional (2D) space for exploring the co-relationship between samples. Taking HW2sources as an example, the visualization results are plotted in Fig. 3, where different clusters are identified by different colors and symbols.

Fig. 3

Visualization on HW2sources dataset. Each point indicates one sample

From Fig. 3, we can see that points with the same color are grouped except for Fig. 3e. The layout of points in Fig. 3b and f has clearer boundary than that of other subgraphs; meanwhile, the points within each cluster in Fig. 3b are more compact than in Fig. 3f, but the gaps among clusters in Fig. 3b are narrower than in Fig. 3f.

4.6 Consumed Time

In this section, we compare the running time of MVC-MAE and some representative algorithms on HW2sources, BBCSport, 100leaves and NUSWIDEOBJ. The corresponding results are shown in Fig. 4. It can be seen from Fig. 4 that single-view clustering algorithms are generally more efficient than multi-view clustering because the multi-view clustering methods need to process multi-view data. Among multi-view clustering methods, DiMSC and MVGL have the longest running time, and our method MVC-MAE runs much faster than DiMSC and MVGL. Moreover, MVC-MAE can also process large-scale multi-view data quickly. In Fig. 4d, we do not provide the running time of MultiNMF, CorgSC and DiMSC, because they are very slow on NUSWIDEOBJ. These results indicate that the MVC-MAE algorithm has higher efficiency.

Fig. 4

Running time of different algorithms on four datasets

5 Conclusion

In this paper, we proposed a deep multi-view clustering algorithm based on auto-encoder, termed MVC-MAE, which adopts auto-encoder to capture the nonlinear structure information of each view in a layer-wise manner and incorporates the local invariance within each view and consistent as well as complementary information between any two views together. To preserve consistent and complementary information among views, the affinity graphs are constructed and the cross-entropy-based regularizer is developed. Besides, representation learning and clustering are integrated into a unified framework for jointly optimizing. Extensive experiments are carried out on six real-world datasets, including three small-scale and three large-scale datasets, and the experimental results are compared with fifteen baseline algorithms. The experimental results demonstrate that MVC-MAE outperforms other compared algorithms.

As the next step, we plan to simultaneously consider the clustering results obtained by clustering different hierarchical representations of each auto-encoder, instead of just utilizing the output of the last layer of encoder components to perform clustering tasks, aiming to comprehensively learn knowledge from multi-view data. Another research direction is to capture discriminative features from multiple views by utilizing mutual information maximization theory.