Skip to main content

Advertisement

SpringerLink
Log in

Effects of Size, Surface Energy and Casimir Force on the Superharmonic Resonance Characteristics of a Double-Layered Viscoelastic NEMS Device Under Piezoelectric Actuations

  • Research Paper
  • Published:
Iranian Journal of Science and Technology, Transactions of Mechanical Engineering Aims and scope Submit manuscript

Abstract

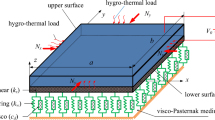
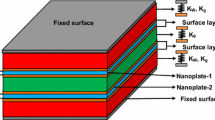
This paper investigates the nonlinear characteristics of a double-layered viscoelastic nanoelectromechanical system (NEMS) in the vicinity of superharmonic resonance. Two nanobeams are made of piezoelectric material and coupled through a visco-Pasternak medium in between. Modified couple-stress theory together with Gurtin–Murdoch surface elasticity theory is utilized to take into account the effects of size-dependency and surface energy for the nanosized structure. Kelvin–Voigt model is also implemented to consider the impact of viscoelasticity. The differential equations of motion are established based on Hamilton’s principle and decomposed to a set of nonlinear ordinary differential equations via Galerkin discretization method. Arclength continuation technique is schemed to capture the frequency–response curves near superharmonic resonance of the system. The influence of the couple-stress parameter, surface strain energy and dispersion force on the nonlinear behavior of the system near superharmonic resonance has been studied. It is observed, that the hardening and softening behaviors of the system are remarkably affected by the size and surface parameters, and interatomic Casimir force. Finally, considering all the mentioned effects, the influence of the DC and AC voltage loads on the dynamic pull-in behavior of the NEMS device is investigated. For these cases, some frequency ranges are addressed as the pull-in band in which the lower nanobeam collapses.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  • Abdel-Rahman EM, Nayfeh AH (2003) Secondary resonances of electrically actuated resonant microsensors. J Micromech Microeng 13:491

    Article  Google Scholar 

  • Alsaleem FM, Younis MI, Ouakad HM (2009) On the nonlinear resonances and dynamic pull-in of electrostatically actuated resonators. J Micromech Microeng 19:045013

    Article  Google Scholar 

  • Arani AG, Kolahchi R, Mortazavi S (2014) Nonlocal piezoelasticity based wave propagation of bonded double-piezoelectric nanobeam-systems. Int J Mech Mater Des 10:179–191

    Article  Google Scholar 

  • Arani AG, Abdollahian M, Kolahchi R (2015a) Nonlinear vibration of embedded smart composite microtube conveying fluid based on modified couple stress theory. Polym Compos 36:1314–1324

    Article  Google Scholar 

  • Arani AG, Kolahchi R, Zarei MS (2015b) Visco-surface-nonlocal piezoelasticity effects on nonlinear dynamic stability of graphene sheets integrated with ZnO sensors and actuators using refined zigzag theory. Compos Struct 132:506–526

    Article  Google Scholar 

  • Arefi M, Zenkour AM (2017) Nonlocal electro-thermo-mechanical analysis of a sandwich nanoplate containing a Kelvin–Voigt viscoelastic nanoplate and two piezoelectric layers. Acta Mech 228:475–493

    Article  MathSciNet  MATH  Google Scholar 

  • Askari AR, Tahani M (2017) Size-dependent dynamic pull-in analysis of geometric non-linear micro-plates based on the modified couple stress theory. Physica E 86:262–274

    Article  Google Scholar 

  • Azizi S, Ghazavi MR, Rezazadeh G, Ahmadian I, Cetinkaya C (2014) Tuning the primary resonances of a micro resonator, using piezoelectric actuation. Nonlinear Dyn 76:839–852

    Article  MATH  Google Scholar 

  • Dai H, Wang L (2017) Size-dependent pull-in voltage and nonlinear dynamics of electrically actuated microcantilever-based MEMS: a full nonlinear analysis. Commun Nonlinear Sci Numer Simul 46:116–125

    Article  MathSciNet  Google Scholar 

  • Fakhrabadi MMS, Yang J (2015) Comprehensive nonlinear electromechanical analysis of nanobeams under DC/AC voltages based on consistent couple-stress theory. Compos Struct 132:1206–1218

    Article  Google Scholar 

  • Farokhi H, Ghayesh MH (2017) Viscoelasticity effects on resonant response of a shear deformable extensible microbeam. Nonlinear Dyn 87:391–406

    Article  MATH  Google Scholar 

  • Fu Y, Zhang J (2011) Size-dependent pull-in phenomena in electrically actuated nanobeams incorporating surface energies. Appl Math Model 35:941–951

    Article  MathSciNet  Google Scholar 

  • Ghorbanpour Arani A, BabaAkbar Zarei H, Eskandari M, Pourmousa P (2017) Vibration behavior of visco-elastically coupled sandwich beams with magnetorheological core and three-phase carbon nanotubes/fiber/polymer composite facesheets subjected to external magnetic field. J Sandw Struct Mater. https://doi.org/10.1177/1099636217743177

    Google Scholar 

  • Guo J-G, Zhao Y-P (2004) Influence of van der Waals and Casimir forces on electrostatic torsional actuators. J Microelectromech Syst 13:1027–1035

    Article  Google Scholar 

  • Gupta RK (1997) Electrostatic pull-in test structure design for in situ mechanical property measurements of microelectromechanical systems (MEMS). Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology

  • Gurtin ME, Murdoch AI (1975) A continuum theory of elastic material surfaces. Arch Ration Mech Anal 57:291–323

    Article  MathSciNet  MATH  Google Scholar 

  • Hajnayeb A, Khadem S (2011) Nonlinear vibrations of a carbon nanotube resonator under electrical and van der Waals forces. J Comput Theor Nanosci 8:1527–1534

    Article  Google Scholar 

  • Huang J-M, Liew K, Wong C, Rajendran S, Tan M, Liu A (2001) Mechanical design and optimization of capacitive micromachined switch. Sens Actuators A 93:273–285

    Article  Google Scholar 

  • Kacem N, Hentz S, Pinto D, Reig B, Nguyen V (2009) Nonlinear dynamics of nanomechanical beam resonators: improving the performance of NEMS-based sensors. Nanotechnology 20:275501

    Article  Google Scholar 

  • Kacem N, Baguet S, Hentz S, Dufour R (2012) Pull-in retarding in nonlinear nanoelectromechanical resonators under superharmonic excitation. J Comput Nonlinear Dyn 7:021011

    Article  Google Scholar 

  • Lamoreaux SK (2004) The Casimir force: background, experiments, and applications. Rep Prog Phys 68:201

    Article  Google Scholar 

  • Li Q, Fan S, Tang Z, Xing W (2012) Non-linear dynamics of an electrothermally excited resonant pressure sensor. Sens Actuators A 188:19–28

    Article  Google Scholar 

  • Lin W-H, Zhao Y-P (2005a) Casimir effect on the pull-in parameters of nanometer switches. Microsyst Technol 11:80–85

    Article  Google Scholar 

  • Lin W-H, Zhao Y-P (2005b) Nonlinear behavior for nanoscale electrostatic actuators with Casimir force Chaos. Solitons Fractals 23:1777–1785

    Article  MATH  Google Scholar 

  • Lu P, He L, Lee H, Lu C (2006) Thin plate theory including surface effects. Int J Solids Struct 43:4631–4647

    Article  MATH  Google Scholar 

  • Mehrdad Pourkiaee S, Khadem SE, Shahgholi M (2015) Nonlinear vibration and stability analysis of an electrically actuated piezoelectric nanobeam considering surface effects and intermolecular interactions. J Vib Control 23(12):1873–1889. https://doi.org/10.1177/1077546315603270

    Article  MathSciNet  MATH  Google Scholar 

  • Miandoab EM, Pishkenari HN, Meghdari A, Fathi M (2017) A general closed-form solution for the static pull-in voltages of electrostatically actuated MEMS/NEMS. Physica E 90:7–12

    Article  Google Scholar 

  • Mirkalantari SA, Hashemian M, Eftekhari SA, Toghraie D (2017) Pull-in instability analysis of rectangular nanoplate based on strain gradient theory considering surface stress effects. Physica B 519:1–14

    Article  Google Scholar 

  • Najar F, Nayfeh A, Abdel-Rahman E, Choura S, El-Borgi S (2010a) Nonlinear analysis of MEMS electrostatic microactuators: primary and secondary resonances of the first mode. J Vib Control 16:1321–1349

    Article  MathSciNet  MATH  Google Scholar 

  • Najar F, Nayfeh AH, Abdel-Rahman EM, Choura S, El-Borgi S (2010b) Dynamics and global stability of beam-based electrostatic microactuators. J Vib Control 16:721–748

    Article  MATH  Google Scholar 

  • Oskouie MF, Ansari R, Sadeghi F (2017) Nonlinear vibration analysis of fractional viscoelastic Euler-Bernoulli nanobeams based on the surface stress theory. Acta Mech Solida Sin 30(4):416–424

    Article  Google Scholar 

  • Ouakad HM, Younis MI (2010) Nonlinear dynamics of electrically actuated carbon nanotube resonators. J Comput Nonlinear Dyn 5:011009

    Article  Google Scholar 

  • Pourkiaee SM, Khadem SE, Shahgholi M (2016) Parametric resonances of an electrically actuated piezoelectric nanobeam resonator considering surface effects and intermolecular interactions. Nonlinear Dyn 84:1943–1960

    Article  MATH  Google Scholar 

  • Pourkiaee SM, Khadem SE, Shahgholi M, Bab S (2017) Nonlinear modal interactions and bifurcations of a piezoelectric nanoresonator with three-to-one internal resonances incorporating surface effects and van der Waals dissipation forces Nonlinear Dyn 1-32

  • Rokni H, Seethaler RJ, Milani AS, Hosseini-Hashemi S, Li X-F (2013) Analytical closed-form solutions for size-dependent static pull-in behavior in electrostatic micro-actuators via Fredholm integral equation. Sens Actuators A 190:32–43

    Article  Google Scholar 

  • Ru C (2010) Simple geometrical explanation of Gurtin-Murdoch model of surface elasticity with clarification of its related versions. Sci China Phys Mech Astron 53:536–544

    Article  Google Scholar 

  • Shaat M, Mohamed S (2014) Nonlinear-electrostatic analysis of micro-actuated beams based on couple stress and surface elasticity theories. Int J Mech Sci 84:208–217

    Article  Google Scholar 

  • SoltanRezaee M, Afrashi M (2016) Modeling the nonlinear pull-in behavior of tunable nano-switches. Int J Eng Sci 109:73–87

    Article  MathSciNet  MATH  Google Scholar 

  • SoltanRezaee M, Farrokhabadi A, Ghazavi MR (2016) The influence of dispersion forces on the size-dependent pull-in instability of general cantilever nano-beams containing geometrical non-linearity. Int J Mech Sci 119:114–124

    Article  Google Scholar 

  • Wang G-F, Feng X-Q (2009) Surface effects on buckling of nanowires under uniaxial compression. Appl Phys Lett 94:141913

    Article  Google Scholar 

  • Wang Z-Q, Zhao Y-P, Huang Z-P (2010) The effects of surface tension on the elastic properties of nano structures. Int J Eng Sci 48:140–150

    Article  Google Scholar 

  • Wen-Hui L, Ya-Pu Z (2003) Dynamic behaviour of nanoscale electrostatic actuators. Chin Phys Lett 20:2070

    Article  Google Scholar 

  • Xu T, Younis MI (2016) Nonlinear dynamics of carbon nanotubes under large electrostatic force. J Comput Nonlinear Dyn 11:021009

    Article  Google Scholar 

  • Yan Z, Jiang L (2012) Surface effects on the vibration and buckling of piezoelectric nanoplates. EPL (Europhys Lett) 99:27007

    Article  Google Scholar 

  • Yang F, Chong A, Lam DCC, Tong P (2002) Couple stress based strain gradient theory for elasticity. Int J Solids Struct 39:2731–2743

    Article  MATH  Google Scholar 

  • Younis MI (2011) MEMS linear and nonlinear statics and dynamics, vol 20. Springer, Berlin

    Book  Google Scholar 

  • Zhang J, Wang C (2012) Vibrating piezoelectric nanofilms as sandwich nanoplates. J Appl Phys 111:094303

    Article  Google Scholar 

  • Zhang L, Liu J, Fang X, Nie G (2014) Effects of surface piezoelectricity and nonlocal scale on wave propagation in piezoelectric nanoplates. Eur J Mech A Solids 46:22–29

    Article  Google Scholar 

  • Zhao Y-P, Wang L, Yu T (2003) Mechanics of adhesion in MEMS—a review. J Adhes Sci Technol 17:519–546

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanics Engineering, Iran University of Science and Technology, Narmak, Tehran, 16846-13114, Iran

    Sasan Rahmanian & Shahrokh Hosseini-Hashemi

  2. Mechanical Engineering Department, School of Engineering, Tarbiat Modares University, Tehran, Iran

    Mohammad-Reza Ghazavi

  3. Center of Excellence in Railway Transportation, Iran University of Science and Technology, Narmak, Tehran, 16846-13114, Iran

    Shahrokh Hosseini-Hashemi

Authors
  1. Sasan Rahmanian
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mohammad-Reza Ghazavi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shahrokh Hosseini-Hashemi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shahrokh Hosseini-Hashemi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rahmanian, S., Ghazavi, MR. & Hosseini-Hashemi, S. Effects of Size, Surface Energy and Casimir Force on the Superharmonic Resonance Characteristics of a Double-Layered Viscoelastic NEMS Device Under Piezoelectric Actuations. Iran J Sci Technol Trans Mech Eng 43 (Suppl 1), 343–355 (2019). https://doi.org/10.1007/s40997-018-0161-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40997-018-0161-1

Keywords

Search

Navigation