Polynomization of the Chern–Fu–Tang conjecture

Abstract

Bessenrodt and Ono’s work on additive and multiplicative properties of the partition function and DeSalvo and Pak’s paper on the log-concavity of the partition function have generated many beautiful theorems and conjectures. In January 2020, the first author gave a lecture at the MPIM in Bonn on a conjecture of Chern–Fu–Tang, and presented an extension (joint work with Neuhauser) involving polynomials. Partial results have been announced. Bringmann, Kane, Rolen, and Tripp provided complete proof of the Chern–Fu–Tang conjecture, following advice from Ono to utilize a recently provided exact formula for the fractional partition functions. They also proved a large proportion of Heim–Neuhauser’s conjecture, which is the polynomization of Chern–Fu–Tang’s conjecture. We prove several cases, not covered by Bringmann et. al. Finally, we lay out a general approach for proving the conjecture.

1 Introduction and main results

Chern et al. [5] conjectured an inequality for k-colored partition functions. A partition of n is called k-colored if each part can appear in k colors and the number of these partitions has been denoted by $p_{-k}(n)$.

Conjecture 1

([5]) Let $n > m \ge 1$ and $k \ge 2$, except for $(k,n,m) = (2,6,4)$, then

$$\begin{aligned} p_{-k} (n-1) \, p_{-k} (m+1) \ge \, p_{-k} (n) \, p_{-k} (m). \end{aligned}$$

(1.1)

The conjecture has been motivated by two results. The first was the work of Nicolas [18] and DeSalvo and Pak [7] on the log-concavity of the partition function $p(n)= p_{-1}(n)$, $n >25$. The second was the work of Bessenrodt and Ono [3] and Alanazi et al. [1] on an inequality involving additive and multiplicative properties of the partition function. The conjecture is based on numerical evidence [5, Table 1]. For $b=a-2$, the conjecture implies the log-concavity for $p_{-k}(n)$ with respect to n for $n \ge 3$ , $k \ge 2$. One has to exclude the case $k=2$ and $n=5$, since $\left( p_{-2}(5)\right) ^2 < p_{-2}(4) \, p_{-2}(6)$.

In [11] we proposed a polynomization of the Bessenrodt–Ono inequality. We also refer to recent work by Beckwith and Bessenrodt [2], Dawsey and Masri [6], and Hou and Jagadeesan [14]. We transferred the inequality of the discrete k-colored partition function to an inequality between values of polynomials $P_n(x)$, defined as the coefficients of the q-expansion of all powers of the Euler product [19]:

$$\begin{aligned} \sum _{n=0}^{\infty } P_{n}\left( x\right) \, q^n := \prod _{n=1}^{\infty } \left( 1 - q^n \right) ^{-x}, \qquad ( q,x \in \mathbb {C}, \, \vert q \vert < 1). \end{aligned}$$

(1.2)

The polynomials can easily be recorded, for example $P_0(x)=1, P_{1}(x)=x, P_2(x)=(x+3)x/2$. They have interesting properties. The k-colored partition function $p_{-k}(n)$ is equal to $P_n(k)$. Further, let for example, the root $x=-3$ of $P_2(x)$ be given. Then the 2nd coefficient of the 3rd power of $\prod _n (1-q^n)$ vanishes. Let $a,b \in \mathbb {N}$ with $a+b >2$ and $x \in \mathbb {R}$ with $x>2$. Then the inequality states:

$$\begin{aligned} P_a(x) \, \cdot \, P_b(x) > P_{a+b}(x). \end{aligned}$$

(1.3)

The proof was provided in [12].

Building on Chern–Fu–Tang’s result for $k=2$ and the positivity of the derivative of $P_{a,b}(x):= P_a(x) \, \cdot \, P_b(x) - P_{a+b}(x)$ for $x >2$, we proposed an extension of the Chern–Fu–Tang conjecture [8].

Conjecture 2

(Heim, Neuhauser) Let $a > b \ge 0$ be integers. Then for all $x \ge 2$:

$$\begin{aligned} \Delta _{a,b}(x) := P_{a-1}(x) P_{b+1}(x) - P_{a}(x) P_{b}(x) \ge 0, \end{aligned}$$

(1.4)

except for $b=0$ and $(a,b) = (6,4)$. The inequality (1.4) is still true for $x \ge 3$ for $b=0$ and for $x \ge x_{6,4}$ for $(a,b)=(6,4)$. Here $x_{a,b}$ is the largest real root of $\Delta _{a,b}(x)$.

Remarks

• (1) Conjecture 2 implies Conjecture 1.

• (2) We have $\Delta _{a,b}(0)=0$ and $\Delta _{a,a-1}(x)= 0$. The leading coefficient of the polynomial $\Delta _{a,b}(x)$ is equal to $\frac{a-b-1}{a! \, (b+1)!}$ for $a > b+1$. Thus, we have

  $$\begin{aligned} \lim _{x \rightarrow \infty } \Delta _{a,b}(x) = \infty . \end{aligned}$$

• (3) We have $\Delta _{a,0}(2)> 0$ and $\Delta _{a,1}(2)> 0$ for $a > 4$. This follows from [12].

• (4) The case $b=0$ follows from (1.3) using properties of $P_{a-1,1}(x)$ [12].

• (5) In [8] the case $b=1$ was already announced (proof is given in the present paper).

• (6) The conjecture as stated in [8] for $(a,b)=(6,4)$ is refined. Note that $\Delta _{6,4}(2)<0$, which does not allow $\Delta _{6,4}\left( x\right) \ge 0$ for all $x >2$. This was also observed during the presentation (see also [4], remark related to Conjecture 2).

Table 1 Polynomials $\Delta _{a,0}\left( x\right)$, their sets of roots, and largest real roots

Expanding on an exact formula for the fractional partition function (in terms of Kloosterman sums and Bessel functions) by Iskander et al. [15], recently, Bringmann et al. [4] proved that for all positive real numbers $x_1,x_2,x_3,x_4$ and $n_1,n_2,n_3,n_4 \in \mathbb {N}$:

$$\begin{aligned} P_{n_{1}}(x_{1}) \, P_{n_{2}}(x_{2}) \ge P_{n_{3}}(x_{3}) \, P_{n_{4}}(x_{4}), \end{aligned}$$

(1.5)

with respect to some general assumptions. They also obtained an explicit version. We recall their result. Let $f(x) = O_{\le }\left( g(x)\right)$ mean that $\vert f(x) \vert \le g(x)$ in the relevant domain.

Theorem 1.1

([4]) Fix $x \in \mathbb {R}$ with $x \ge 2$, and let $a, b \in \mathbb {N}_{\ge 2}$ with $a > b+1$. Set $A:= a-1 - ({x}/{24})$ and $B:= b - ({x}/{24})$, we suppose $B \ge \max \, \left\{ 2 \, x^{11}, ({100}/({x -24})) \right\}$. Then

$$\begin{aligned} \Delta _{a,b}(x)= & {} P_{a-1}(x) \, P_{b+1}(x) - P_{a}(x) \, P_{b}(x)\\= & {} \pi \, \left( \frac{x}{24}\right) ^{\frac{x}{2} + 1} (A B)^{-\frac{x}{4} - \frac{5}{4}} \, e^{\pi \sqrt{\frac{2 x}{3}} \left( \sqrt{A} + \sqrt{B} \right) } \left( \sqrt{A} - \sqrt{B} \right) \left( 1 + O_{\le }\left( \frac{2}{3} \right) \right) . \end{aligned}$$

This leads to proof of the Chern–Fu–Tang conjecture and to a large proportion of the Heim–Neuhauser conjecture. We provide more details in the final section of this paper.

Corollary 1.2

([4]) For any real number $x \ge 2$ and positive integers

$$\begin{aligned} b \ge B_0:= \max \, \left\{ 2 \, x^{11} + \frac{x}{24}, \frac{100}{x - 24} + \frac{x}{24} \right\} , \end{aligned}$$

(1.6)

Conjecture 2 is true.

Corollary 1.3

([4]) The conjecture of Chern–Fu–Tang (Conjecture 1) is true. In particular $p_{-2}(n)$ is log-concave for $n \ge 6$, and $p_{-k}(n)$ is log-concave for all n and $k \in \mathbb {N}_{\ge 3}$.

In this paper we show that Conjecture 1 and Conjecture 2 are closely related to the Bessenrodt–Ono inequality: $x \, P_{a-1}(x) \ge P_{a}(x)$. The appearing rational function $({P_{b+1}(x)}/{P_b(x)})$ will be approximated by a linear factor, depending on b.

We prove Conjecture 2 for $b \in \{0,1,2,3\}$, and all integers $a >b$ and all real numbers $x \ge x_0=2$. Further, in the odd cases $b=1$ and $b=3$, Conjecture 2 is already true for $x \ge 1$. To prove that $\Delta _{a,b}(x) \ge 0$, we study $\Delta _{a,b}(x_0) \ge 0$ and prove that $\Delta _{a,b}'(x)>0$ for all $x > x_0$. We believe that this approach is the most direct method to prove Conjecture 2.

The positivity of the derivative is expected, since $\Delta _{a,b}(x) >0$ for $x \ge x_0$ is a statement on the largest real root $x_{a,b}$ of $\Delta _{a,b}(x)$ and the observed property, that the real parts of the complex roots seem to be smaller than $x_{a,b}$ (see Fig. 1).

Fig. 1

Roots of $\Delta _{a,2}(x)$ with a positive real part. Blue = real root, red = complex root

As already mentioned, the case $b=0$ has been almost proved in [12]. The complete statement and proof is given in Section 2. In Section 3 we prove the following results.

Theorem 1.4

Let $a \in \mathbb {N}$, $b \in \{1,2,3\}$ and $x \in \mathbb {R}$. For b odd we put $x_0:=1$ and for b even we put $x_0:=2$. Let $a_0= a_0(b):= b+2$. Then

$$\begin{aligned} \Delta _{a,b}(x) = P_{a-1}(x) \, P_{b+1}(x) - P_a(x) P_b(x) > 0 \end{aligned}$$

(1.7)

for all $a \ge a_0$ and $x > x_0$.

The cases $x=x_{0}$ will be stated in Proposition 2.4 and Corollary 3.2. There the strict inequality does not hold in general. It fails for example for $(a,b,x_0) =( 4,2,2)$. Further, we obtain:

Corollary 1.5

Let $b \in \{1,2,3\}$ be given. Then $\Delta _{a,b}'(x) >0$ for all $a \ge a_0$ and $x > x_0$.

In Sect. 4 we provide the proofs of our theorems and in Sect. 5 we outline a program to attack all cases of Conjecture 2. We recommend to read these two sections simultaneously.

Finally, in Sect. 6, we provide some numerical data. All computations have been done using PARI/GP or Julia.

2 The polynomials $\Delta _{a,b}(x)$ and $P_{a,b}(x)$

We first recall from [9] some basic properties of the polynomials $P_n(x)$ introduced (1.2) in the introduction.

These polynomials are unique solutions of the recursion formula $P_n(x) = ({x}/{n}) \sum _{k=1}^n \sigma (k) \, P_{n-k}(x)$ with $P_0(x):=1$. Here $\sigma (n)= \sum _{d \vert n} d$. Then $P_n(x) = ({x}/{n!}) \sum _{k=0}^{n-1} a_{n,k} \, x^k$ for all $n \in \mathbb {N}$ with $a_{n,k} \in \mathbb {N}_0$. We have

$$\begin{aligned} a_{n,n-1}=1 \text { and }a_{n,0} = (n-1)! \, \sigma (n). \end{aligned}$$

(2.1)

There is a direct connection between the polynomialized Chern–Fu–Tang inequality (1.4) and the Bessenrodt–Ono inequality (1.3). Let $a \ge 1$, then

$$\begin{aligned} \Delta _{a,0}(x) = P_{a-1}(x) P_1(x) - P_a(x) P_{0}(x) = P_{a-1,1}(x). \end{aligned}$$

(2.2)

In the following we assume that $a \ge 2$, since $\Delta _{1,0}(x)$ = 0. From Remark (2) after Conjecture 2 we have that $\Delta _{a,0}(0) =0$ and that $\lim _{x \rightarrow \infty } \Delta _{a,0}(x) = \infty$. Deriving (2.2) we obtain $\Delta _{a,0}'(0) =P_{a-1}^{\prime }\left( 0\right) P_{1}\left( 0\right) +P_{a-1}\left( 0\right) P_{1}^{\prime }\left( 0\right) -P_{a}^{\prime }\left( 0\right) P_{0}\left( 0\right) =-P_{a}^{\prime }\left( 0\right) =-({\sigma \left( a\right) }/{a})<0$. Let us record the first polynomials and several properties in Table 1 where we let $Z_n$ be the set of roots of $\Delta _{a,0}$ and $x_{a,0}$ be the largest real root.

Theorem 2.1

([12]) Let $a >2$. Then for all $x>2$ we have the property

$$\begin{aligned} \Delta _{a,0}(x) = P_{a-1,1}(x) >0. \end{aligned}$$

(2.3)

Let $a=2$. Then $\Delta _{2,0}(3)=0$ and for all $x >3$ we have the strict inequality $\Delta _{2,0}(x) >0$. We further have $\Delta _{3,0}(2) = \Delta _{4,0}(2)=0$. Let $a >4$ and $x \ge 2$, then we have $\Delta _{a,0}(x)>0$.

We deduce from ([12], proof of Proposition 5.1) the following result.

Corollary 2.2

Let $a\ge 2$ and $x \ge 2$. Then $\Delta _{a,0}'(x)>0$.

We have that $\Delta _{a,0}\left( x\right) > 0$ for all $a \ge 5$ and $x \ge 2$. Since $\Delta _{a,0}(1) = p\left( a-1\right) - p\left( a\right)$ we obtain with Theorem 2.1:

Lemma 2.3

Let $a \ge 5$. Then there exists a real number $\alpha$, $1< \alpha <2$, such that $\Delta _{a,0}(\alpha )=0$. Let $x_{a,0}$ be the largest real root of $\Delta _{a,0}(x)$. Then $1< x_{a,0} < 2$ and $\Delta _{a,0}(x) >0$ for all $x > x_{a,0}$.

For $b \in \{ 0,1,2 \}$ we have the following useful property.

Proposition 2.4

Let $x_0 =2$ and let $b \in \{ 0,1,2 \}$. Then $\Delta _{a,b}(x_0)>0$ for $a \ge 5$. Let $b=1$, then this is already true for $a \ge 3$. The bounds for $b=0$ and $b=2$ are sharp.

Proof

The following quotients are all larger or equal to $x_0$. Let $b \in \{0,1,2\}$. Then $({P_{b+1}(x_0)}/{P_{b}(x_0)}) \ge x_0$:

$$\begin{aligned} \frac{P_1(x_0)}{P_0(x_0)} = x_0, \quad \frac{P_2(x_0)}{P_1(x_0)} = \frac{5}{2} > x_0, \,\, \text { and } \,\, \frac{P_3(x_0)}{P_2(x_0)} = 2 = x_0. \end{aligned}$$

Thus, $\Delta _{a,b}(x_0) \ge P_{b}(x_0) \Delta _{a,0}(x_0)$ and $\Delta _{a,b}(x_0) > 0$ for $a \ge 5$. The explicit shape and values of the involved polynomials for $a \le 4$ complete the proof:

$$\begin{aligned} \Delta _{3,1}(x)= & {} \frac{ x^2}{12} \left( x^2 +11 \right) , \\ \Delta _{4,1} (x)= & {} \frac{x^2}{24} \left( x^3 + 6x^2 + 11 x + 6 \right) . \end{aligned}$$

We have $\Delta _{3,0}(x_0) = \Delta _{4,0}(x_0) = 0$ and $\Delta _{4,2}(x_0)=0$. $\square$

3 Log-concavity of partition numbers

Nicolas [18] and DeSalvo and Pak [7] proved the log-concavity of the partition function p(n) for $n \ge 26$:

$$\begin{aligned} p(n)^2 - p(n-1) p(n+1) \ge 0. \end{aligned}$$

(3.1)

Note that (3.1) fails for all $1 \le n \le 25$ odd, but is still true for n even. Explicit study of the small cases (Table 2) leads to the following refined result:

Proposition 3.1

Let $q(n):= p(n)/p(n-1)$. Then $q(n+2) \le q(n)$ for all $n \ge 2$ and $q(27) \ge q(n)$ for all $n \ge 27$. For $n \le 27$ we have the following chain:

$$\begin{aligned} q(2)> & {} q(4)> q(6)> q(3)> q(8)> q(5)=q(10)> q(12)> q(7)=q(9)\\> & {} q(14)>q(11)> q(16)> q(13)>q(15)> q(18)> q(17)> q(20) \\> & {} q(19)>q(22)> q(21)> q(24)> q(23)> q(26)> q(25) > q(27). \end{aligned}$$

Table 2 Approximate values of $q\left( n \right)$ for $1\le n \le 30$

Corollary 3.2

Let a and b be positive integers. Let $a > b+1$. Then

$$\begin{aligned} \Delta _{a,b}(1) \ge 0 \end{aligned}$$

(3.2)

is true for all b odd and for all $b \ge 26$. For $1 < b \le 26$ even we have the following result. Inequality (3.2) is satisfied for $a\in A_{0}\left( b\right) \cup \left\{ a\in \mathbb {N}:a\ge a_{1}\left( b\right) \right\}$ from Table 3.

Table 3 Data when inequality (3.2) is satisfied

Proof

The proof follows from Proposition 3.1 and

$$\begin{aligned} \Delta _{a,b}(1) \ge 0 \Longleftrightarrow q(a) \le q(b+1). \end{aligned}$$

(3.3)

$\square$

4 Proof of Theorem 1.4

Let us first recall a formula [17] for the coefficients of $P_n(x)$. Let $P_n(x) = \sum _{m=1}^n A_{n,m} \, x^m$. Then

$$\begin{aligned} A_{n,m} = \frac{1}{m!} \sum _{\begin{array}{c} k_1, \ldots , k_m \in \mathbb {N} \\ k_1+ \ldots + k_m=n \end{array}} \, \prod _{i=1}^{m} \frac{\sigma (k_i)}{k_i}. \end{aligned}$$

(4.1)

4.1 Case $b=1$ and Theorem 1.4 for $x_0=1$.

We prove here that $\Delta _{a,1}(x)>0$ for all $a \ge 3$ and $x >x_0=1$.

Proof

Corollary 3.2 implies $\Delta _{a,1}(x_0) \ge 0$ for all $a \ge 3$. Note that $\Delta _{a,1}(x)$ has degree $a+1$ and has non-negative coefficients for $2< a < 6$. This implies that the theorem is already true for $x >0$. We have $\Delta _{6,1}\left( x\right) >0$ for $x\ge x_{0}$. Let $F_{a}\left( x\right) =P_{a-1}\left( x\right) ((x+3)/{2}) -P_{a}\left( x\right)$. Then $\Delta _{a,1}\left( x\right) =xF_{a}\left( x\right)$. Therefore to show that $\Delta _{a,1}\left( x\right) > 0$ it is sufficient to show that $F_{a}\left( x\right) >0$.

This we prove by induction on $a\ge 3$ for $x >x_0$. Note that $F_{a}\left( x\right) >0$ for $x>x_{0}$ and $3\le a \le 6$. Therefore in the induction step we assume $a \ge 7$ and that $F_{m} \left( x\right) >0$ is true for all $3 \le m < a$ and $x > x_0$. Now we will show $F_{a}^{\prime }\left( x\right) >0$ for all $x > x_0$. The derivative $F_{a}^{\prime }\left( x\right)$ is equal to

$$\begin{aligned}&P_{a-1}'(x) \, \frac{x+3}{2} + P_{a-1}(x) \, \frac{1}{2} - P_{a}'(x) \\&\qquad =\,\sum _{k=1}^{a-1} \frac{\sigma (k)}{k} P_{a-1-k}(x) \, \frac{x+3}{2} - \sum _{k=1}^{a} \frac{\sigma (k)}{k} P_{a-k}(x) + P_{a-1}(x) \, \frac{1}{2}. \end{aligned}$$

This follows from [9]:

$$\begin{aligned} P_n'(x) = \sum _{k=1}^n \frac{\sigma (k)}{k} \, P_{n-k}(x). \end{aligned}$$

(4.2)

By the induction hypothesis we obtain

$$\begin{aligned} \sum _{k=1}^{a-1} \frac{\sigma (k)}{k} P_{a-1-k}(x) \, \frac{x+3}{2} > \frac{\sigma (a-1)}{a-1} \frac{x+3}{2} + \sum _{k=1}^{a-2} \frac{\sigma (k)}{k} P_{a-k}(x) \end{aligned}$$

and

$$\begin{aligned} F_{a}^{\prime }\left( x\right)> & {} \frac{\sigma (a-1)}{a-1} \frac{x+3}{2} - \sum _{k=a-1}^{a} \frac{\sigma (k)}{k} P_{a-k}(x) + P_{a-1}(x) \, \frac{1}{2} \\= & {} \frac{1}{2} \, P_{a-1}(x) - \frac{\sigma (a-1)}{a-1} \frac{x}{2} + \frac{3\sigma (a-1)}{2\, (a-1)} - \frac{ \sigma (a)}{a}. \end{aligned}$$

In the last step we utilize the property $a< \sigma (a) < a \left( 1 + \ln (a) \right)$ and obtain

$$\begin{aligned} F_{a}^{\prime }\left( x\right) > \frac{1}{2} \, P_{a-1}(x) - \frac{\sigma \left( a-1\right) x}{2\left( a-1\right) } +\frac{3}{2}-\left( 1 + \ln (a) \right) . \end{aligned}$$

The coefficients of the polynomial $P_{a-1}\left( x\right)$ are provided by (4.1) and it implies that the coefficients of $P_{a-1}\left( x\right) -(({\sigma \left( a-1\right) })/({a-1}))x$ are not negative. Therefore we obtain $P_{a-1}\left( x\right) -(({\sigma \left( a-1\right) })/({a-1}))x\ge P_{a-1}\left( 1\right) -(({\sigma \left( a-1\right) })/({a-1}))$ for $x\ge 1$. Since $P_{a-1}\left( 1\right)$ is the partition number of $a-1$ we have $P_{a-1}\left( 1\right) \ge a-1$. Finally $F_{a}^{\prime }\left( x\right)>((a-1)/2)-(({1+ \ln \left( a-1\right) })/2)+(3/2)-1-\ln \left( a\right) >0$ for $a\ge 7$. Since $F_{a}\left( 1\right) =2P_{a-1}\left( 1\right) -P_{a}\left( 1\right) \ge 0$ we obtain $F_{a}\left( x\right) >0$. $\square$

Proof of Corollary 1.5 for the case $b=1$

We have shown in the previous proof that $F_{a}\left( x\right) >0$ and $F_{a}^{\prime }\left( x\right) >0$ for $x>x_{0}$ and $a\ge 7$. Therefore also $\Delta _{a,1}^{\prime }\left( x\right) =xF_{a}^{\prime }\left( x\right) +F_{a}\left( x\right) >0$ for $x>x_{0}$. We also mentioned in the previous proof that the coefficients of $\Delta _{a,1}\left( x\right)$ are not negative for $2<a<6$. For $a=6$ it can be checked directly that $\Delta _{6,1}^{\prime }\left( x\right) >0$ for $x\ge x_{0}$. This proves Corollary 1.5 for $b=1$. $\square$

4.2 Case $b=2$ and Theorem 1.4 for $x_0=2$.

Proof

Let $x_0=2$. We have $P_{2}\left( x\right) =\left( x+3\right) ({x}/{2})$ and $P_{3}\left( x\right) =\left( x+8\right) \left( x+1\right) ({x}/{6})$. Let $F_{a}\left( x\right) = (({x+4})/{3})P_{a-1}\left( x\right) -P_{a}\left( x\right)$. Since $\left( x+8\right) \left( x+1\right) \ge \left( x+4\right) \left( x+3\right)$ for $x\ge 2$ we obtain

$$\begin{aligned} \Delta _{a,2}\left( x\right) \ge \left( x+3\right) \frac{x}{2}\left( \frac{x+4}{3}P_{a-1}\left( x\right) -P_{a}\left( x\right) \right) =\left( x+3\right) \frac{x}{2}F_{a}\left( x\right) . \end{aligned}$$

For $x=x_{0}$ we have equality.

We will show $F_{a}\left( x\right) > 0$ by induction on a. It holds for $a=4$ as $F_{4}\left( x\right) =\left( x+1\right) \left( x-1\right) \left( x-2\right) ({x}/{72})>0$ for $x>2$. Similarly, we can show that $F_{a}\left( x\right) >0$ for $x>2$ for $5\le a\le 13$. The following proposition shows that $F_{a}^{\prime }\left( x\right) >0$ for $x>x_{0}$ if we assume $F_{m}\left( x\right) >0$ for $x>x_{0}$ for $4\le m<a$.

The last step in the induction is the following. In Proposition 2.4 we showed that $\Delta _{a,2}\left( x_{0}\right) \ge 0$ for $a\ge 5$ and $\Delta _{4,2}\left( x_{0}\right) =0$ can be checked easily. Additionally, $F_{a}\left( x_{0}\right) =({\Delta _{a,2}\left( x_{0}\right) })/({\left( x_{0}+3\right) ({x_{0}}/{2}))}\ge 0$. Using $F_{a}^{\prime }\left( x\right) >0$ for $x>x_{0}$ we can conclude that $\Delta _{a,2}\left( x\right) \ge \left( x+3\right) ({x}/{2})F_{a}\left( x\right) >0$ for $x>x_{0}$. $\square$

Proposition 4.1

Let $a\ge 14$ and assume that $F_{m}\left( x\right) =(({x+4})/3)P_{m-1}\left( x\right) -P_{m}\left( x\right) >0$ for $x>x_{0}=2$ and $4\le m<a$. Then $F_{a}^{\prime }\left( x\right) >0$.

Proof

For $F_{a}^{\prime }\left( x\right)$ we obtain

$$\begin{aligned} \frac{1}{3}P_{a-1}\left( x\right) +\frac{x+4}{3}\sum _{k=1}^{a-1}\frac{\sigma \left( k\right) }{k}P_{a-1-k}\left( x\right) -\sum _{k=1}^{a}\frac{\sigma \left( k\right) }{k}P_{a-k}\left( x\right) . \end{aligned}$$

We apply the assumptions and obtain

$$\begin{aligned} F_{a}^{\prime }\left( x\right)> & {} \frac{1}{3}P_{a-1}\left( x\right) +\frac{x+4}{3}\sum _{k=a-3}^{a-1}\frac{\sigma \left( k\right) }{k}P_{a-1-k}\left( x\right) -\sum _{k=a-3}^{a}\frac{\sigma \left( k\right) }{k}P_{a-k}\left( x\right) \\= & {} \frac{1}{3}P_{a-1}\left( x\right) +\frac{x+4}{3}\left( \frac{\sigma \left( a-3\right) }{a-3}\left( x+3\right) \frac{x}{2}+\frac{\sigma \left( a-2\right) }{a-2}x+\frac{\sigma \left( a-1\right) }{a-1}\right) \\&{}-\frac{\sigma \left( a-3\right) }{a-3}\left( x+8\right) \left( x+1\right) \frac{x}{6}-\frac{\sigma \left( a-2\right) }{a-2}\left( x+3\right) \frac{x}{2}-\frac{\sigma \left( a-1\right) }{a-1}x-\frac{\sigma \left( a\right) }{a}\\= & {} \frac{1}{3}P_{a-1}\left( x\right) \\&{}-\frac{\sigma \left( a-3\right) }{a-3}\left( x-2\right) \frac{x}{3}-\frac{\sigma \left( a-2\right) }{a-2}\left( x+1\right) \frac{x}{6}-\frac{\sigma \left( a-1\right) }{a-1}\frac{2x-4}{3}-\frac{\sigma \left( a\right) }{a}\\\ge & {} \frac{1}{3}P_{a-1}\left( x\right) -\frac{1+\ln \left( a\right) }{6}\left( x+1\right) \left( 3x-2\right) .\\ \end{aligned}$$

We apply now (4.1) to be able to use that

$$\begin{aligned} P_{a-1}\left( x\right)= & {} \frac{\sigma \left( a-1\right) }{a-1}x+\sum _{k=1}^{a-2}\frac{\sigma \left( a-1-k\right) \sigma \left( k\right) }{2\left( a-1-k\right) k}x^2+\sum _{m=3}^{a-1}A_{a-1,m}x^{m}\\\ge & {} x+\frac{a-2}{2}x^{2}+\sum _{m=3}^{a-1}A_{a-1,m}x^{m} \end{aligned}$$

for $x\ge 0$. Therefore

$$\begin{aligned} F_{a}^{\prime }\left( x\right)> & {} \frac{x}{3}+\frac{a-2}{6}x^{2}+\frac{1}{3}\sum _{m=3}^{a-1}A_{a-1,m}x^{m}-\frac{1+\ln \left( a\right) }{6}\left( x+1\right) \left( 3x-2\right) \\= & {} \frac{1+\ln \left( a\right) }{3}+\frac{1-\ln \left( a\right) }{6}x+\frac{a-5-3\ln \left( a\right) }{6}x^{2}+\frac{1}{3}\sum _{m=3}^{a-1}A_{a-1,m}x^{m}\\= & {} \frac{4a-16-12\ln \left( a\right) }{6}+\frac{4a-19-13\ln \left( a\right) }{6}\left( x-2\right) \\&{}+\frac{a-5-3\ln \left( a\right) }{6}\left( x-2\right) ^{2}+\frac{1}{3}\sum _{m=3}^{a-1}A_{a-1,m}x^{m}>0 \end{aligned}$$

for $a\ge 14$ and $x>x_{0}=2$. $\square$

Proof of Corollary 1.5 for the case $b=2$

From the proof of Theorem 1.4 for the case $b=2$ we see that $F_{a}\left( x\right) >0$ for $x>x_{0}=2$. The previous proposition showed that $F_{a}^{\prime }\left( x\right) >0$ for $a\ge 14$. Therefore $\Delta _{a,2}^{\prime }\left( x\right) =\left( x+({3}/{2})\right) F_{a}\left( x\right) +\left( x+3\right) ({x}/{2})F_{a}^{\prime }\left( x\right) >0$ for $a\ge 14$. The remaining cases for $4\le a\le 13$ can be checked directly.$\square$

4.3 Case $b=3$ and Theorem 1.4 for $x_{0}=1$

Proof

We have $P_{3}\left( x\right) =({x}/{6})\left( x+1\right) \left( x+8\right)$ and $P_{4}\left( x\right) =({x}/{24})\left( x+1\right) \left( x+3\right) \left( x+14\right)$. As $\left( x+3\right) \left( x+14\right) \ge ({1}/{3})\left( x+8\right) \left( 3x+17\right)$ for $x\ge 1$ we obtain

$$\begin{aligned} P_{4}\left( x\right) \ge \frac{x}{72}\left( x+1\right) \left( x+8\right) \left( 3x+17\right) . \end{aligned}$$

Let $F_{a}\left( x\right) =\frac{3x+17}{12}P_{a-1}\left( x\right) -P_{a}\left( x\right)$. Then

$$\begin{aligned} \Delta _{a,3}\left( x\right) =P_{a-1}\left( x\right) P_{4}\left( x\right) - P_{a}\left( x\right) P_{3}\left( x\right) \ge \frac{x}{6}\left( x+1\right) \left( x+8\right) F_{a}\left( x\right) \end{aligned}$$

(4.3)

for $x\ge 1$. Note that for $x=x_{0}=1$ we have equality. We also have $F_{a}\left( x\right) >0$ for $x>1$ and $5\le a\le 14$.

The proof will be by induction on a. The following proposition shows that $F_{a}^{\prime }\left( x\right) >0$ for $x>x_{0}$ and $a\ge 15$, if we assume that $F_{m}\left( x\right) >0$ for $x>x_{0}$ and $5\le m<a$.

By Corollary 3.2$\Delta _{a,3}\left( x_{0}\right) \ge 0$ for $a\ge 5$. Additionally,

$F_{a}\left( x_{0}\right) =({\Delta _{a,3}\left( x_{0}\right) })/(({x_{0}}/{6})(x_{0}+1) \left( x_{0}+8\right) )\ge 0$. Using $F_{a}^{\prime }\left( x\right) >0$ for $x>x_{0}$ and (4.3) we can conclude that $\Delta _{a,3}\left( x\right) \ge ({x}/{6})\left( x+1\right) \left( x+8\right) F_{a}\left( x\right) >0$. $\square$

Proposition 4.2

Let $a\ge 15$. If $F_{m}\left( x\right) =(({3x+17})/{12})P_{m-1}\left( x\right) -P_{m}\left( x\right) >0$ for $x>x_{0}$ and for all $5\le m<a$ then $F_{a}^{\prime }\left( x\right) >0$.

Proof

The derivative $F_{a}^{\prime }\left( x\right)$ is equal to

$$\begin{aligned} \frac{1}{4}P_{a-1}\left( x\right) +\frac{3x+17}{12}\sum _{k=1}^{a-1}\frac{\sigma \left( k\right) }{k}P_{a-1-k}\left( x\right) -\sum _{k=1}^{a}\frac{\sigma \left( k\right) }{k}P_{a-k}\left( x\right) . \end{aligned}$$

Applying the assumptions leads to

$$\begin{aligned} F_{a}^{\prime }\left( x\right)> & {} \frac{1}{4}P_{a-1}\left( x\right) +\frac{3x+17}{12}\sum _{k=a-4}^{a-1}\frac{\sigma \left( k\right) }{k}P_{a-1-k}\left( x\right) -\sum _{k=a-4}^{a}\frac{\sigma \left( k\right) }{k}P_{a-k}\left( x\right) \\= & {} \frac{1}{4}P_{a-1}\left( x\right) +\frac{3x+17}{12} \bigg ( \frac{\sigma \left( a-4\right) }{a-4}P_{3}\left( x\right) +\frac{\sigma \left( a-3\right) }{a-3}P_{2}\left( x\right) +\frac{\sigma \left( a-2\right) }{a-2}x\\&{}+\frac{\sigma \left( a-1\right) }{a-1} \bigg ) -\frac{\sigma \left( a-4\right) }{a-4}P_{4}\left( x\right) -\frac{\sigma \left( a-3\right) }{a-3}P_{3}\left( x\right) -\frac{\sigma \left( a-2\right) }{a-2}P_{2}\left( x\right) \\&{}-\frac{\sigma \left( a-1\right) }{a-1}x-\frac{\sigma \left( a\right) }{a} \\= & {} \frac{1}{4}P_{a-1}\left( x\right) -\frac{\sigma \left( a-4\right) }{a-4}\frac{5x}{36}\left( x+1\right) \left( x-1\right) -\frac{\sigma \left( a-3\right) }{a-3}\frac{x}{24}\left( x^{2}+10x-19\right) \\&{}-\frac{\sigma \left( a-2\right) }{a-2}\frac{x}{12}\left( 3x+1\right) -\frac{\sigma \left( a-1\right) }{a-1}\frac{9x-17}{12}-\frac{\sigma \left( a\right) }{a}. \end{aligned}$$

Now, $x^{2}+10x-19\le x^{2}+10x-11=\left( x+11\right) \left( x-1\right)$ and $9x-17\le 9x-9$. As $-x<0$ we obtain

$$\begin{aligned} F_{a}^{\prime }\left( x\right)> & {} \frac{1}{4}P_{a-1}\left( x\right) -\frac{\sigma \left( a-4\right) }{a-4}\frac{5x}{36}\left( x+1\right) \left( x-1\right) -\frac{\sigma \left( a-3\right) }{a-3}\frac{x}{24}\left( x-1\right) \left( x+11\right) \\&{}-\frac{\sigma \left( a-2\right) }{a-2}\frac{x}{12}\left( 3x+1\right) -\frac{\sigma \left( a-1\right) }{a-1}\frac{3x-3}{4}-\frac{\sigma \left( a\right) }{a}\\\ge & {} \frac{1}{4}P_{a-1}\left( x\right) -\frac{1+\ln \left( a\right) }{72}\left( 13x^{3}+48x^{2}+17x+18\right) . \end{aligned}$$

Now

$$\begin{aligned} P_{a-1}\left( x\right)= & {} \frac{\sigma \left( a-1\right) }{a-1}x+\sum _{k=1}^{a-2}\frac{\sigma \left( a-1-k\right) \sigma \left( k\right) }{2\left( a-1-k\right) k}x^{2}\\&{}+\sum _{j=1}^{a-3}\sum _{k=1}^{a-j-2}\frac{\sigma \left( a-1-j-k\right) \sigma \left( k\right) \sigma \left( j\right) }{6\left( a-1-j-k\right) jk}x^{3}+\sum _{m=4}^{a-1}A_{a-1,m}x^{m} \\\ge & {} x+\frac{a-2}{2}x^{2}+\sum _{j=1}^{a-3}\frac{a-j-2}{6}x^{3}+\sum _{m=4}^{a-1}A_{a-1,m}x^{m} \\= & {} x+\frac{a-2}{2}x^{2}+\left( {\begin{array}{c}a-2\\ 2\end{array}}\right) \frac{x^{3}}{6}+\sum _{m=4}^{a-1}A_{a-1,m}x^{m}. \end{aligned}$$

Then

$$\begin{aligned} F_{a}^{\prime }\left( x\right)> & {} \frac{1}{4}x+\frac{a-2}{8}x^{2}+\left( {\begin{array}{c}a-2\\ 2\end{array}}\right) \frac{x^{3}}{24}+\frac{1}{4}\sum _{m=4}^{a-1}A_{a-1,m}x^{m}\\&{}-\frac{1+\ln \left( a\right) }{72}\left( 13x^{3}+48x^{2}+17x+18\right) \\= & {} -\frac{1+\ln \left( a\right) }{4}+\frac{1-17\ln \left( a\right) }{72}x+\frac{3a-22-16\ln \left( a\right) }{24}x^{2}\\&{}+\frac{3\left( a-2\right) \left( a-3\right) -26-26\ln \left( a\right) }{144}x^{3}+\frac{1}{4}\sum _{m=4}^{a-1}A_{a-1,m}x^{m}\\= & {} \frac{a^{2}+a-58-64\ln \left( a\right) }{48}+\frac{9a^{2}-9a-286-304\ln \left( a\right) }{144}\left( x-1\right) \\&{}+\frac{3a^{2}-9a-52-58\ln \left( a\right) }{48}\left( x-1\right) ^{2}\\&{}+\frac{3\left( a-2\right) \left( a-3\right) -26-26\ln \left( a\right) }{144}\left( x-1\right) ^{3}+\frac{1}{4}\sum _{m=4}^{a-1}A_{a-1,m}x^{m} >0 \end{aligned}$$

for $a\ge 15$ and $x>x_{0}=1$. $\square$

Proof of Corollary 1.5 for the case $b=3$

From the proof of Theorem 1.4 for the case $b=3$ we observe that $F_{a}\left( x\right) >0$ for $x>x_{0}=1$. The previous proposition shows that $F_{a}^{\prime }\left( x\right) >0$ for $a\ge 15$ and $x>x_{0}$. Therefore $\Delta _{a,3}^{\prime }\left( x\right) =({1}/{6})\left( 3x^{2}+18x+8\right) F_{a}\left( x\right) +({x}/{6})\left( x+1\right) \left( x+8\right) F_{a}^{\prime }\left( x\right) >0$. For the remaining cases $5\le a\le 14$ it can be checked directly that $\Delta _{a,3}^{\prime }\left( x\right) >0$. $\square$

5 Conjecture 2: approach for general b

We offer a general approach to Conjecture 2, based on four assumptions. Let $x_0>0$ and $a > b+1$. We define

$$\begin{aligned} H_{b}(x):= & {} \frac{P_{b+1}(x)}{P_{b}(x)} - \frac{x}{b+1}, \end{aligned}$$

(5.1)

$$\begin{aligned} G_{b}(x):= & {} \frac{x}{b+1}+H_{b}\left( x_{0}\right) =\frac{x-x_{0}}{b+1}+ \frac{P_{b+1}\left( x_{0}\right) }{P_{b}\left( x_{0}\right) }, \end{aligned}$$

(5.2)

$$\begin{aligned} F_{a,b}(x):= & {} G_{b}\left( x\right) P_{a-1}\left( x\right) -P_{a}\left( x\right) . \end{aligned}$$

(5.3)

5.1 Four assumptions

In this subsection let $a>b+1$ and $x_{0}>0$ be fixed.

Assumption 5.1

$\Delta _{a,b}\left( x_{0}\right) \ge 0$.

Assumption 5.2

$H_b(x) \ge H_b(x_0)$ for all $x\ge x_{0}$.

Assumption 5.3

For all $x>x_{0}$ and $a-1-b\le k\le a-1$ let

$$\begin{aligned} G_b(x) P_{a-1-k}\left( x\right) -P_{a-k}\left( x\right) \le 0. \end{aligned}$$

(5.4)

Assumption 5.4

(Induction hypothesis) $F_{m,b}\left( x\right) >0$ for $x>x_{0}$ and $b+2\le m<a$.

Remarks

• (1) If $H_b(x)$ is monotonically increasing for $x\ge x_{0}$, then Assumption 5.2 is valid.

• (2) Assumption 5.2 implies

  $$\begin{aligned} \Delta _{a,b}\left( x\right) \ge P_{b}\left( x\right) F_{a,b}\left( x\right) . \end{aligned}$$

  (5.5)

  For $x=x_0$ we have equality by (5.2) and (5.3).

The idea is to generalize the induction step approach on $a>b+1$ from the previous section to arbitrary b and show as the main intermediate step

$$\begin{aligned} F_{a,b}^{\prime }\left( x\right) \ge 0. \end{aligned}$$

(5.6)

Then from part 2 of the previous remarks we obtain $F_{a,b}\left( x_{0}\right) ={\Delta _{a,b}\left( x_{0}\right) }/{P_{b}\left( x_{0}\right) }$. Assumption 5.1 implies $F_{a,b}\left( x\right) \ge 0$ and together with (5.5) we obtain also $\Delta _{a,b}\left( x\right) \ge 0$ for $x\ge x_{0}$.

Using the assumptions is not sufficient to complete the induction step. The estimate (5.7) below on $F_{a,b}^{\prime }\left( x\right)$ can in general yet only be bounded asymptotically for large a, see next subsection.

For now we are going to explain how we can use the assumptions from the beginning of this subsection for a lower bound on $F_{a,b}\left( x\right)$. If we derive (5.3) we obtain

$$\begin{aligned} F_{a,b}^{\prime }\left( x\right)= & {} \frac{1}{b+1}P_{a-1}\left( x\right) + G_b(x) P_{a-1}^{\prime }\left( x\right) -P_{a}^{\prime }\left( x\right) \\= & {} \frac{1}{b+1}P_{a-1}\left( x\right) + G_b(x) \sum _{k=1}^{a-1}\frac{\sigma \left( k\right) }{k}P_{a-1-k}\left( x\right) -\sum _{k=1}^{a}\frac{\sigma \left( k\right) }{k}P_{a-k}\left( x\right) . \end{aligned}$$

Using now Assumption 5.4 we obtain

$$\begin{aligned} F_{a,b}^{\prime }\left( x\right)> & {} \frac{1}{b+1}P_{a-1}\left( x\right) + G_b(x) \sum _{k=a-1-b}^{a-1}\frac{\sigma \left( k\right) }{k}P_{a-1-k}\left( x\right) {}-\sum _{k=a-1-b}^{a}\frac{\sigma \left( k\right) }{k}P_{a-k}\left( x\right) \\= & {} \frac{1}{b+1}P_{a-1}\left( x\right) +\sum _{k=a-1-b}^{a-1}\frac{\sigma \left( k\right) }{k} \left( G_b(x) P_{a-1-k}\left( x\right) -P_{a-k}\left( x\right) \right) -\frac{\sigma \left( a\right) }{a} \end{aligned}$$

and with Assumption 5.3 we can continue

$$\begin{aligned} \begin{array}{rcl} F_{a,b}^{\prime }\left( x\right) &{}>&{}\displaystyle \frac{1}{b+1}P_{a-1}\left( x\right) \\ &{}&{}\displaystyle {} -\left( 1+\ln \left( a\right) \right) \left( 1+\sum _{k=a-1-b}^{a-1}\left( P_{a-k}\left( x\right) - G_b(x) P_{a-1-k}\left( x\right) \right) \right) . \end{array} \end{aligned}$$

(5.7)

5.2 An estimate using associated Laguerre polynomials

Here we will explain an idea how to show the positivity of right hand side of (5.7). We want to bound the coefficients of $P_{a-1}\left( x\right)$ from below in such a way that they dominate the coefficients of the subtracted polynomial. Unfortunately this approach here in the end only works asymptotically and only for most coefficients.

Let $L_{n}^{\left( 1\right) }\left( x\right) =\sum _{k=0}^{n}\left( {\begin{array}{c}n+1\\ n-k\end{array}}\right) ({\left( -x\right) ^{k}}/{k!})$ be the associated Laguerre polynomial of degree n with parameter $\alpha =1$. Then $P_{n}\left( x\right) \ge ({x}/{n})L_{n-1}^{\left( 1\right) }\left( -x\right) =\sum _{k=1}^{n}\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) ({x^{k}}/{k!})$ for $x>0$. This follows from [10] or directly from Kostant’s formula (4.1) as it implies $A_{n,m}\ge ({1}/{m!})\sum _{\begin{array}{c} k_{1},\ldots ,k_{m}\in \mathbb {N} \\ k_{1}+\ldots +k_{m}=n \end{array}}1=({1}/{m!})\left( {\begin{array}{c}n-1\\ m-1\end{array}}\right)$. From (5.7) we obtain

$$\begin{aligned} F_{a,b}^{\prime }\left( x\right)> & {} \frac{1}{b+1}\sum _{k=1}^{a-1}\left( {\begin{array}{c}a-2\\ k-1\end{array}}\right) \frac{x^{k}}{k!}\end{aligned}$$

(5.8)

$$\begin{aligned}&{}-\left( 1+\ln \left( a\right) \right) \cdot \left( 1+\sum _{k=a-1-b}^{a-1}\left( P_{a-k}\left( x\right) - G_b(x) P_{a-1-k}\left( x\right) \right) \right) . \end{aligned}$$

(5.9)

This is positive if we can bound the coefficients of (5.9) by the coefficients $({1}/({b+1}))\left( {\begin{array}{c}a-2\\ k-1\end{array}}\right)$. This is always possible for $2\le k\le a-2$ for large $a\ge a_{0}$.

Then for example for $x_{0}=2$ we could deduce from Corollary 1.3 that $\Delta _{a,b}\left( x_{0}\right) \ge 0$. As explained shortly before then we also have $F_{a,b}\left( x_{0}\right) =({\Delta _{a,b}\left( x_{0}\right) }/{P_{b}\left( x_{0}\right) })\ge 0$. Therefore, $F_{a,b}\left( x\right) >0$ for $x>x_{0}$. Then (5.5) implies $\Delta _{a,b}\left( x\right) \ge P_{b}\left( x\right) F_{a,b}\left( x\right) >0$ for $x>x_{0}$.

5.3 Proof of Assumptions 5.2 and 5.3 for $b\in \left\{ 0,1,2,3,4,5,6\right\}$

Our approach to prove Assumption 5.3 again uses induction. For $b=5$ the smallest initial point we can choose is $x_{0}\ge 2.0554$. This means that for $b>5$ we can also only choose $x_{0}\ge 2.0554$. For values of $b<5$ we could also have chosen $x_{0}=2$ for example, compare Table 6.

Having proven Assumptions 5.2 and 5.3 for the cases $b\in \left\{ 4,5,6\right\}$ carries out the induction step up to inequality (5.7). What is left to do is to prove that the right hand side of (5.7) is really positive (and to check that $\Delta _{a,b}\left( x_{0}\right) \ge 0$ for $x_{0}=2.0554$). The positivity can probably be shown using the method proposed in the last subsection. So the analysis of bounding the coefficients of (5.9) has to be carried out in the cases $b\in \left\{ 4,5,6\right\}$ in order to complete the proof of Theorem 1.4 in these cases.

Proposition 5.5

For $b\in \left\{ 0,1,2,3,4,5,6\right\}$ the functions $x\mapsto (({P_{b+1}\left( x\right) })/{P_{b}\left( x\right) })-({x}/({b+1}))$ are monotonically increasing for $x\ge x_{0}\ge 0.776$ which implies Assumption 5.2.

Remark 5.6

Actually the proof will show that the functions are monotonically increasing for all $x> 0$ for $b\in \left\{ 0,1,2,3,4,6\right\}$ with the exception of $b=5$ where we need the restriction on $x_{0}$.

Proof

The derivative is

$$\begin{aligned} \frac{P_{b+1}^{\prime }\left( x \right) P_{b}\left( x\right) -P_{b+1}\left( x\right) P_{b}^{\prime }\left( x\right) }{\left( P_{b}\left( x\right) \right) ^{2}}-\frac{1}{b+1}. \end{aligned}$$

(5.10)

Let

$$\begin{aligned} N_{b}\left( x\right) =P_{b+1}^{\prime }\left( x\right) P_{b}\left( x\right) -P_{b+1}\left( x\right) P_{b}^{\prime }\left( x\right) . \end{aligned}$$

(5.11)

Then (5.10) is not negative if and only if $N_{b}\left( x\right) -({1}/({b+1}))\left( P_{b}\left( x \right) \right) ^{2}\ge 0$. By Table 4 all are not negative for $x\ge x_{0}$.

Table 4 Polynomials $N_{b}\left( x\right) -({1}/({b+1}))\left( P_{b}\left( x\right) \right) ^{2}$ for $b\in \left\{ 0,1,2,3,4,5,6\right\}$

Proposition 5.7

Let $b\in \left\{ 1,2,3,4,5,6\right\}$ then $x\mapsto ({P_{k+1}\left( x\right) }/{P_{k}\left( x\right) })-({x}/({b+1}))$ is monotonically increasing for $x>x_{0}=2.0554$ and $0\le k\le b$ and

$$\begin{aligned} \frac{P_{b+1}\left( x_{0}\right) }{P_{b}\left( x_{0}\right) } \le \frac{P_{k+1}\left( x_{0}\right) }{P_{k}\left( x_{0}\right) } \end{aligned}$$

(5.12)

for $0\le k\le b$. This implies Assumption 5.3 for $x_{0}=2.0554$.

Proof

Deriving the functions $x\mapsto ({P_{k+1}\left( x\right) }/{P_{k}\left( x\right) })-({x}/({b+1}))$ for $0\le k\le b$ we obtain using similarly $N_{k}\left( x\right)$ from (5.11) $(({N_{k}\left( x\right) -({1}/({b+1}))\left( P_{k}\left( x\right) \right) ^{2}})/{\left( P_{k}\left( x\right) \right) ^{2}})$. This is not negative if and only if the numerator is not negative. Obviously this is larger than $N_{k}\left( x\right) -(1/({k+1}))\left( P_{k}\left( x\right) \right) ^{2}$ which we have seen to be not negative in the proof of the previous proposition. What remains to check is that $({P_{b+1}\left( x_{0}\right) }/{P_{b}\left( x_{0}\right) }) \le ({P_{k+1}\left( x_{0}\right) }/{P_{k}\left( x_{0}\right) })$ for $0\le k\le b-1$, compare Table 5.

Table 5 Approximate values of $\frac{P_{b+1}\left( x_{0}\right) }{P_{b}\left( x_{0}\right) }$ for $b\in \left\{ 1,2,3,4,5,6\right\}$

For fixed b we can also determine the smallest $x_{0}$ for which (5.12) holds (Table 6).

Table 6 Approximate smallest $x_{0}$ for which (5.12) holds

5.4 Partial result

Unfortunately we cannot show Assumption 5.2 for all b yet, but we can show the following weaker version.

Lemma 5.8

If we assume that $\Delta _{b+1,B}\left( x\right) >0$ for all $x>x_{0}>0$ and $0\le B\le b-1$ then $({P_{b+1}\left( x\right) }/{P_{b}\left( x\right) })$ is monotonically increasing for $x>x_{0}$.

Proof

If we consider its derivative we obtain $(({P_{b+1}^{\prime }\left( x\right) P_{b}\left( x\right) -P_{b+1}\left( x\right) P_{b}^{\prime }\left( x\right) })/{\left( P_{b}\left( x\right) \right) ^{2}})$. The numerator is

$$\begin{aligned}&\sum _{k=1}^{b+1}\frac{\sigma \left( k\right) }{k}P_{b+1-k}\left( x\right) P_{b}\left( x\right) -P_{b+1}\left( x\right) \sum _{k=1}^{b}\frac{\sigma \left( k\right) }{k}P_{b-k}\left( x\right) \\&\qquad =\, \frac{\sigma \left( b+1\right) }{b+1}P_{b}\left( x\right) +\sum _{k=1}^{b}\frac{\sigma \left( k\right) }{k}\left( P_{b+1-k}\left( x\right) P_{b}\left( x\right) -P_{b+1}\left( x\right) P_{b-k}\left( x\right) \right) . \end{aligned}$$

Now for $A=b+1$ and $B=b-k\le b-1=A-2$ we can apply the assumption and obtain that all $P_{b+1-k}\left( x\right) P_{b}\left( x\right) -P_{b+1}\left( x\right) P_{b-k}\left( x\right) =\Delta _{A,B}\left( x\right) >0$ for $x>x_{0}$. $\square$

6 Concluding remarks

We consider sequences $\{a_n\}_{n=0}^{\infty }$ with non-negative elements. A sequence is log-concave if $a_n^2 - a_{n-1} \, a_{n+1} \ge 0$ for all $n \in \mathbb {N}$, and strongly log-concave if the inequalities are strictly positive. Let $c_{n}:= \sum _{i+j =n} a_i \, b_j$ be the convolution of two sequences. Hoggar [13] proved that the convolution of two finite positive log-concave sequences is again log-concave. This result was extended by Johnson and Goldschmidt [16] to infinite sequences. Let $x_1$ and $x_2$ be complex numbers, then the convolution of the two sequences $\left\{ P_n(x_1)\right\} _{n}$ and $\left\{ P_n(x_{2})\right\} _{n}$ is equal to $\left\{ P_n(x_1 + x_2)\right\} _{n}$. Note that $P_n(x)>0$ for $x>0$.

The link between $\Delta _{a,b} \ge 0$ and log-concavity is given by the following observation. Let $x>0$ and $a,b \in \mathbb {N}$ with $a> b+1$:

$$\begin{aligned} \Delta _{a,b}(x) \ge 0 \Longleftrightarrow \frac{P_{b+1}(x)}{P_b(x)} \ge \frac{P_{a}(x)}{P_{a-1}(x)}. \end{aligned}$$

(6.1)

Remarks

Let $x>0$ be given.

• (a) Let $\Delta _{b+2,b}(x) \ge 0$ for all $b \in \mathbb {N}_0$. Then $\{P_n(x)\}$ is log-concave.

• (b) Let $\{P_n(x)\}$ be log-concave, then $\Delta _{a,b}(x) \ge 0$ for all $a >b+1$ and $b \in \mathbb {N}_0$.

Bringmann et al. [4] proved (see also introduction), that there exists a constant $B_0 = B_0(x) := \max \left\{ 2x^{11}+({x}/{24}), ({100}/({x-24}))+({x}/{24})\right\}$ for $x \ge 2$ such that $\Delta _{a,b}(x) \ge 0$ for all $b \ge B_0(x)$ and $a \ge b+1$ (Table 7).

Table 7 Approximate values of $\max \left\{ 2x^{11}+({x}/{24}), ({100}/({x-24}))+({x}/{24})\right\}$

Let $x=k \in \mathbb {N}_{\ge 2}$, then $B_0(k) =2k^{11}+({k}/{24})$. Thus, $\Delta _{a,b}(x) \ge 0$ for fixed $x>0$ and all pairs (a, b) with $a \ge b+1$ and $b \in \mathbb {N}_{0}$ is equivalent to $\{P_n(x)\}$ log-concave. Now, by [4] it is sufficient to show that the quotients $({P_{n}(x)}/{P_{n-1}(x)})$ are decreasing when n is increasing for all $1 \le n \le B_0(x)$. In [4] this last step had been executed successfully for $k=2$ and $n \ge 6$ and $k=3$ and all n. The authors also invented some sophisticated computer calculations for $k=4$ and $k=5$. Although, they still needed a 5 day and a 71 day long computer calculation for these cases. It follows that $\{P_n(2)\}$ is log-concave for $n \ge 6$ and $\{P_n(k)\}$ is log-concave for $k=3,4$ and 5. Applying the result of Johnson and Goldschmidt finally proves the Chern–Fu–Tang conjecture. Note that $\lim _{x \rightarrow \infty } B_0(x) = \infty$, which makes this method difficult to prove Conjecture 2, for general $x\ge 2$. For $0< x <3$, the sequence $\{P_n(x)\}$ is never log-concave (for small n) since $\Delta _{2,0}(x)<0$, which causes technical problems (see also $k=1$ and $k=2$, where finitely many exceptions appear). In this paper we offer an approach which takes care of $x \ge x_0$ bounded from below. We fix b and determine $a_0 \in \mathbb {N}$ and $x_0 \in \mathbb {R}_{>0}$ such that $\Delta _{a,b}\left( x\right) \ge 0$ for all $a \ge a_0$ and $x \ge x_0$. This takes into account that exceptions may exist and allows for example to vary $a_0$ and $x_0$. Let $b \in \{0,1,2,3\}$. We have determined $a_0$ and $x_0$ dependent on b, such that $\Delta _{a,b}(x) \ge 0$ and $\Delta _{a,b}'(x) \ge 0$ for $a \ge a_0$ and $x \ge x_0$.

Fig. 2

Roots of $\Delta _{a,27}(x)$ and $\Delta _{a,28}(x)$ with a positive real part blue = real root, red = complex root

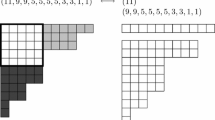
We expect for $b \ge 27$ and $x_0=1$ that $a_0$ can be chosen as $b+2$. This can be considered as the generic case (see Fig. 2 which illustrates this expectation). If we assume $0< x_0 < 1$, then it is an interesting but challenging task to determine $a_0 = a_0(b,x_0)$.