1 Introduction

Conventional composite materials present the dispersed phase topologically isolated within the matrix [1]. In contrast, interpenetrating phase composites (IPCs) consist of two or more continuous and topologically interconnected phases throughout the microstructure [2]. Due to their continuous morphology, each phase can directly contribute to the final properties of the composite, allowing a combination of distinct properties [3, 4]. Multiple combinations of materials to fabricate IPCs have already been studied in the literature [5,6,7,8,9,10,11,12]. Metal-ceramic IPCs have been studied for multiple applications such as orthopaedic applications [9], high-temperature environments, high cyclic fatigue scenarios, and braking systems [5, 7].

The spatial arrangement of the constituent phases within the IPCs significantly affects their overall properties [4, 5, 7, 10]. IPCs with the phases randomly distributed across the composite provide uncertainties and lower control over the composite properties, inducing undesired anisotropy [10]. In contrast, architected IPCs with a periodic phase distribution across the composite can provide great control over the desired properties through the modification of the different parameters that define the 3D topology.

Typically, metal-ceramic IPCs are produced resorting to infiltration-based techniques wherein preexisting interconnected porous ceramic preforms are infiltrated with a metallic phase [2, 13]. Additive manufacturing (AM) enables the fabrication of porous controllable ceramic structures that can be used for the manufacture of metal-ceramic IPCs. Among the AM classes that allows the fabrication of complex ceramic materials, vat photopolymerization technologies, namely Digital Light Processing (DLP), excels in terms of dimensional resolution, thin walls fabrication, low surface roughness, and shape fidelity [14, 15]. The operating principle consists in the photopolymerization of a ceramic loaded resin through a light source that reticulates the polymeric material present in the composition, shaping a solid part [16, 17]. Between each layer, the substrate moves upwards or downwards allowing new layers to be hardened by the light source.

Lattice structures are periodic porous structures composed of one or more repeating unit cells, being divided into several categories [18]. Among these structures, a class of shell-based 3D lattice structures has gained attention from the scientific community mainly due to the development of AM technologies that enabled their fabrication: Triply Periodic Minimal Surface (TPMS) structures [3, 19]. TPMS structures are defined by mathematical functions that provide a periodic surface with zero mean curvature, delivering a continuous and smooth geometry that allows high surface/volume fractions, high pore interconnectivity, and an even distribution of stress [3, 18,19,20]. Multiple studies that compared TPMS structures with more traditional lattice structures concluded that the continuous and smooth geometry empowers the first to have better mechanical properties, especially those related to energy absorption [18, 21]. The properties of the TPMS structures were found to be dependent on their geometry and basic indexes in several studies [21,22,23,24]. Albeit the use of DLP technology to 3D print TPMS structures, there are relatively few studies that utilize ceramic materials in this process [19, 25, 26].

In this work, TPMS-based aluminium–alumina IPCs were designed, manufactured, and characterized. AM Digital Light Processing (DLP) technology was used to produce multiple alumina TPMS structures, and investment casting was used to infiltrate aluminium into the alumina structures. The influence of the TPMS structure’s geometry, along with the number of unit cells and the volume fraction of the two phases, was evaluated. For both, the IPCs and the ceramic structures, a morphological characterization was performed, and their mechanical properties were assessed during uniaxial compression.

2 Materials and methods

The porous alumina structures were designed using nTopology software and manufactured using the AM DLP technology. These structures were then infiltrated with a casting aluminium alloy by investment casting. Several steps were taken to produce the proposed IPCs, including design of the structures, printing, debinding and sintering, and investment casting.

2.1 Design and manufacture of alumina structures

Multiple TPMS structures were designed using nTopology CAD software. Three TPMS (Primitive, Diamond, and Gyroid) having different numbers of unit cells and distinct volume fractions were studied, giving rise to 24 structures with overall dimensions of 15 × 15 × 15 mm3. Preliminary printability tests were conducted to determine a reproducible printable range that ensures open macro-porosity for subsequent infiltration. These tests established that a volume fraction range of 12.5% to 20% was optimal for the TPMS selected.

Figure 1 presents the design methodology for Gyroid structures. Table 1 presents the equations, the number of unit cells, structure models, and geometry types. Table 2 presents the experimental groups in analysis.

Fig. 1
figure 1

Design methodology for gyroid structures

Full size image
Table 1 Equations, unit cells, structure models, and geometry type of the TPMS structures modelled
Full size table
Table 2 Experimental groups according to their geometry and volume fraction
Full size table

The modelled structures were printed using the Bison 1000 DLP Printer and the Bison High alumina resin both from Tethon 3D (USA). A layer resolution of 100 µm was used with an exposure time of 180 s in a heated chamber at 45 °C. The light intensity used was 2 mW/cm2. After printing, the structures were immersed in isopropyl alcohol for 20 min while undergoing ultrasonic cleaning.

The green samples were then subjected to a simultaneous debinding and sintering process in an air atmosphere furnace. This thermal cycle is divided into 3 stages: debinding up to 500 °C at 1 °C/min heating rate, followed by a 5 °C/min heating rate to a 2-h plateau at 1600 °C for sintering, ending with a cooling stage at 5 °C/min cooling rate.

2.2 Manufacture of IPCs’ specimens

To manufacture the envisioned metal-ceramic IPCs, a near eutectic aluminium alloy (EN_AB-44300, also known as AlSi12(Fe)) was infiltrated in the alumina specimens previously produced through investment casting.

Initially, the alumina structures were encased in an assembly tree, which was further covered with a commercial investment powder enclosure (Eurovest jewellery investment powder from SRS). After a 2-h rest, the ceramic moulding underwent a thermal cycle in a furnace with extraction to dewax and consolidate the ceramic enclosure. The investment casting process takes place in a semi-automatic investment casting equipment, the VC400F from Indutherm (Germany). In this equipment, the aluminium is melted at 650 °C within an argon atmosphere. The casting process is executed under the influence of a vacuum system that creates a pressure differential of 1 bar. After pouring and cooling, the ceramic enclosure is dissolved in water through agitation, resulting in the assembly tree with all the structures infiltrated with aluminium. Subsequently, several post-processing steps are required, including cutting of all the feeding channels, as well as grinding and polishing to unveil the IPCs.

2.3 Characterization

2.3.1 Morphological analysis

The morphological characterization of the alumina structures and IPCs was performed using Scanning Electron Microscopy (SEM) and Micro Computed Tomography (Micro-CT). SEM was used to evaluate the ceramic samples regarding their layer size, microstructure before and after sintering, and possible manufacturing defects. In the case of the IPCs, SEM was used to access the aluminium–alumina interface and identify possible defects. In both cases, the samples were coated with a carbon layer and the analysis was performed on an SEM Hitachi SU-70 (Japan) with an electron accelerating voltage of 15 kV. Micro-CT was used to obtain a virtual 3D model and detect possible defects, through the analysis of multiple cross sections in each sample. The analysis was performed on a Bruker Skyscan 1275 (Germany) X-ray microtomography equipment with an aluminium filter and scanning parameter set between 65 and 70 kV at a resolution of 13 m\(\mu\), depending on the sample.

2.3.2 Crystalline and physical characterization

X-Ray Diffraction (XRD) was used to characterize the crystalline phases of both materials in the IPCs. This analysis was completed on a Panalytical X´Pert PRO3 (The Netherlands) equipment using steps of 0.026° 2θ s−1 on a 2θ° range from 20° to 90°.

The bulk and relative density of the ceramic structures was assessed following the ASTM C20-00 standard [27]. Additionally, the geometrical density of both the ceramic structures and IPCs was determined for each experimental group. Shrinkage and mass loss were evaluated for the ceramic structures before and after sintering, and the solids’ content was estimated.

2.3.3 Compression testing

In the absence of a recognized standard to test the proposed components under uniaxial compression, the analysis followed ISO 13314:2011 that “specifies a test method for compressive properties of porous and cellular metals” [28]. The tests were conducted on a universal testing machine Shimadzu AG-25TA (Japan) with a displacement speed of 0.2 mm/min, using a 20 kN load cell for the alumina structures and a 250 kN cell for the IPCs. The samples were tested in the perpendicular direction to the printed layers. Every experimental group of ceramic structures was subjected to a minimum of seven tests, while each experimental group of IPCs underwent at least five tests.

3 Results and discussion

3.1 Physical properties

After printing, a dimensional deviation from the CAD model was detected. In the X–Y-direction (perpendicular to the printing direction), the samples measured 15.16 ± 0.05 mm and in the Z-direction (printing direction), the samples exhibited 14.86 ± 0.07 mm. This implies that, to obtain model-accurate parts after printing, adjustments of −1.07% in X–Y-direction and 0.93% in Z-direction would be needed. After sintering (see Fig. 2), in the X–Y-direction, the samples measured 13.50 ± 0.04 mm and in the Z-direction, the samples measured 12.73 ± 0.07 mm. The values obtained for linear shrinkage, volumetric shrinkage, and mass loss after sintering are presented in Table 3. Shrinkage in the Z-direction was higher than in the X–Y-direction. This anisotropic shrinkage behaviour is well documented in the literature and is a result of the layer-by-layer fabrication characteristic of the printing technology [29, 30]. Also, the values achieved for shrinkage are similar with those presented in the literature [31, 32], with discrepancies attributable to distinct factors, including solids’ content, particle size, particle-size distribution, and the sintering cycle. The mass loss of the samples after sintering was determined to be 21.43%. This implies that 78.57 wt% of the resin content is alumina, while 21.43 wt% consists of organic material. Given that the density of alumina is 3.98 g/cm3 and the density of methacrylate monomers used in ceramic vat photopolymerization resins ranges between 1.00 and 1.12 g/cm3 [33], the volume percentage of solids in the samples was determined to be from 47.95 vol.% to 50.78 vol.%, typical of a high-loaded ceramic resin.

Fig. 2
figure 2

Sintered ceramic structures where the columns present the different geometries (P2, P3, D2, D3, G2, and G3, respectively) at different volume ratios (12.5%, 15.0%, 17.5%, and 20.0%, respectively)

Full size image
Table 3 Linear shrinkage, volumetric shrinkage, and mass loss after sintering
Full size table

The determined bulk density was 3.04 ± 0.07 g/cm3, resulting in a relative density of 76.27 ± 1.71%, indicating that the ceramic presented around 23.73% of porosity. In the study conducted by Wu et al. [34], the impact of different particle-size distributions and debinding processes on alumina ceramics printed by SLA was studied. Samples with a bimodal particle-size distribution, subjected to thermal debinding and sintering at 1750 °C for 4 h exhibited an 83.2% relative density. In contrast, samples with the same distribution and sintering cycle subjected to vacuum debinding improved the value of relative density to 91.2%. Hsiang et al. [35] compared two different photosensitive resin systems to fabricate alumina ceramics using DLP and found that depending on the system and post-printing treatments, the relative density varied between 84 and 94%. Regarding this work, the porosity attained might have positive effects on the behaviour of the IPCs, as it could improve the mechanical interlocking between both materials.

Table 4 displays the volume fraction of the parts at three stages: CAD design, after printing, and after sintering. The volume fraction after printing was determined considering the average mass of the samples, their volume, and an average density of 2.5 g/cm3 for the post-printed material. Likewise, the volume fraction after sintering was determined using the same methodology but considering the previously determined density for alumina (3.04 g/cm3).

Table 4 Volume fraction of alumina parts from CAD design, after debinding and after sintering
Full size table

The post-printing volume fraction presented a deviation from the CAD models. The processing of photosensitive ceramic resins often results in overexposure not only due to light scattering effects caused by the interaction between light and particles in a liquid medium [36] but also due to the energy transmitted from the light source to the resin through the printing parameters, such as exposure time and light intensity [37]. Consequently, variations in the thickness of the printed parts' walls occur, significantly impacting the post-printing volume fraction, as previously reported in a number of studies using DLP [38, 39].

The geometric density of the IPCs was determined for each experimental group, with Table 5 presenting the average values obtained as a function of the volume fraction. Additionally, the predicted density of the IPCs was determined using the bulk density of alumina (3.04 g/cm3, obtained using Archimedes method), the theoretical density of the alloy (2.68 g/cm3), and considering the aluminium–alumina volume fraction after sintering. Since the density of alumina is higher than that of the alloy, the predicted density demonstrated an increase as the volume fraction increased. In comparison to the geometrical density of the IPCs, which remained consistent across all experimental groups, higher values were observed. This discrepancy can be attributed to the presence of manufacturing defects such as porosity, which will be further analysed in the following section.

Table 5 Geometrical density and predicted density for each IPC volume fraction
Full size table

3.2 Samples’ morphology

Figure 3 presents the microstructure of the printed parts in both green and sintered conditions. In Fig. 3a, it is visible that the ceramic particles are surrounded by the organic binder of the resin. In Fig. 3b, after sintering, the micrograph reveals, as expected, the absence of this organic phase, and while some level of porosity is still observed, the densification of the alumina becomes evident due to the presence of necks and changes in the particle geometry. Additionally, it can be inferred that the resin used in this work possesses a bimodal particle distribution due to the presence of two distinct sets of particles with different sizes.

Fig. 3
figure 3

SEM micrographs of samples on a Green and b Sintered conditions

Full size image

SEM was used to measure the thickness of the layers in both green and sintered conditions. Green samples presented a layer thickness of 98.95 ± 0.51 mm, while sintered samples exhibited a layer thickness of 84.67 ± 0.41 mm, which represents a linear shrinkage in Z-direction of 14.43%. Furthermore, small printing defects characteristic of DLP technique, such as step effect and pores derived from the light scattering effect [40, 41], were found on both sintered and green samples. SEM analysis of the IPCs (see Fig. 4a, b) has proven that while aluminium can successfully fill the complex geometries of the ceramic structures, the aluminium–alumina interface presents some irregularities. This is attributed to shrinkage during solidification and the low wettability of alumina by the melted aluminium [42].

Fig. 4
figure 4

SEM micrographs of an IPC: a G2_15; b magnification along the interface of G2_15

Full size image

Micro-CT analysis revealed that DLP manufacturing of TPMS ceramic structures is effective, as it replicates the complex geometries specified in the CAD model. Concerning IPCs (see Fig. 5), Micro-CT analysis proven that investment casting can successfully infiltrate the alumina structures, albeit residual porosity. When comparing experimental groups, it was found that Diamond IPCs showed a higher prevalence of this pores due to their narrower channels for the aluminium to flow. Santos et al. [43] studied the permeability to water of polymeric TPMS structures with different levels of total porosity produced by material jetting. Their findings revealed that Diamond is the less permeable and more tortuous TPMS. Furthermore, it is known from the literature that turbulent flow during casting can lead to internal defects, including porosity, which can be formed due to a phenomenon known as gas engulfing [44].

Fig. 5
figure 5

Micro-CT of a P2_15 IPC

Full size image

3.3 Crystalline characterization

The diffractogram of the sintered alumina (see Fig. 6) reveals the presence of α-Al2O3 as the main phase with trace amounts of a MgAl2O4 spinel phase. In the literature, Magnesium Oxide (MgO) is acknowledged as a sintering aid for alumina ceramics as it lowers the densification temperature, inhibits grain growth, enhances flexural strength, and increases bulk density [45, 46]. Spinel is formed at temperatures above 1300 °C, through the reaction between α-Al2O3 and MgO [47]. The diffractogram of the aluminium alloy reveals the presence of two phases: silicon and aluminium.

Fig. 6
figure 6

Diffractograms of used sintered alumina and aluminium alloy

Full size image

3.4 Compression tests

3.4.1 Ceramic structures

A typical stress–strain curve for each IPC of the P2 geometry is presented in Fig. 7a. The samples do not exhibit the typical brittle fracture behaviour characterized by a linear region followed by a sudden stress drop. Instead, the alumina structures demonstrated a pseudo-ductile layer-by-layer failure behaviour, where local cracks and fractures initiate at relatively small compressive loads, leading to stress fluctuations throughout the stress–strain response of the samples. Zhang et al. [25] studied alumina TPMS samples manufactured by SLA, and with respect to mechanical properties, it was found that the samples experience brittle fracture at moderate volume fractions and pseudo-ductile layer-by-layer fracture at low-volume fractions (the volume fraction at which the failure mode shifts was estimated to be between 21 and 25%).

Fig. 7
figure 7

Compression of ceramic structures: a typical stress–strain curve for each IPC of the P2 geometry; b compressive strength (σmax)

Full size image

The compressive strength (σmax) values determined for each experimental group are presented in Fig. 7b. It is evident that both the sample geometry and their volume fraction significantly influence the compressive strength. When comparing samples with the same geometry, a linear increase in the structures´ compressive strength is observed as the volume fraction increases (R-square > 0.93055). This linear relation is expected, as the addition of more material (thicker walls) contributes to reinforcing the porous structure. When comparing geometries, it is noticeable that D3 withstands the highest load before experiencing failure. The intricate geometry of this structure seems to mitigate the occurrence of local cracks and fractures that typically lead to failure. Additionally, the increase in the number of unit cells positively influences the compressive strength of the samples, resulting in an average improvement of 18.65 ± 7.14%. As demonstrated in several studies, this improvement is mostly related to the mitigation of localized fractures [21, 23, 24]. This can be achieved with tortuous structures with thin features that hinder the progression of the crack.

3.4.2 IPCs

The stress–strain curves of the IPCs exhibited a very distinct behaviour from those of the ceramic structures (see Fig. 8a, b, c). Instead of a pseudo-ductile layer-by-layer failure behaviour, they demonstrate an energy absorption behaviour characterized by an initial elastic region, a middle plateau region, and a final densification region. The addition of the secondary aluminium phase modified the mechanical behaviour of the initial parts. Bartolomeu et al. [48] demonstrated that the introduction of PEEK in a Ti6Al4V cellular structure manufactured by selective laser melting enhanced the stiffness of the composite obtained. Similarly, Song et al. [3] investigated the constituent phases of polymeric IPCs (Polypropylene and VeroBalckPlus) and found noteworthy differences in the mechanical behaviour between the sum of two independent phases and a whole IPC.

Fig. 8
figure 8

IPC´s compression tests: stress–strain curve of a P3_15, b D3_15, and c G3_15; d deformation behaviour of presented IPCs on a given strain, where each dot in the stress–strain curve has a corresponding deformation image

Full size image

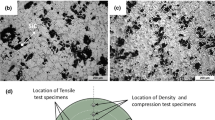
For a more in-depth analysis of the behaviour of the manufactured IPCs, images were captured during the compression tests (see Fig. 8d). Since the behaviour is identical between similar experimental groups (each TPMS geometry has an analogous deformation behaviour, inherent to the geometry), only samples with 3 × 3 × 3 unit cells and 15% volume fraction were presented. Figure 8a presents the typical response of a P3_15 IPC to compressive loading, revealing several distinct stages of deformation. Initially, the sample undergoes elastic deformation, maintaining its original shape. Once the elastic stage ends, barrelling occurs throughout the compression process, and cracks predominantly start between the aluminium–alumina interface. Afterwards, during the plateau region, major fractures appear in the IPC due to the compressive stresses exceeding the material´s strength. Notably, the stress–strain curve indicates a reduction in tension during the plateau region. Upon analysing the corresponding image in this region, it reveals material detachment from the sample due to the substantial fractures and deformation occurring within the IPC. As the IPC enters the densification stage, it undergoes crushing, resulting in increased tension. Figure 8b presents the typical response of a D3_15 IPC to compressive loading. In the initial stages of the compression test, the sample undergoes elastic deformation, maintaining its original shape. Once the elastic stage ends, barrelling occurs throughout the compression process, and cracks start to form in the outer regions of the sample. Subsequently, during the plateau region, small fractures appear in the IPC due to the compressive stresses exceeding the material´s strength. As the IPC enters the densification stage, it undergoes crushing, resulting in increased tension. Figure 8c presents the typical response of a G3_15 IPC to compressive loading. The stages of deformation identified exhibited an identical behaviour to the D3_15 IPC, with the main difference being that the cracks form mostly on the aluminium–alumina interface, leading to several fractures as the sample deforms.

According to the international standard ISO 13314:2011 [28], the following mechanical properties have been determined for the produced IPCs: compressive offset stress (σ0.2%), plateau stress (σplateau), absorbed energy up to an extension of 0.5 (W0.5), and Specific Energy Absorption (SEA) (see Fig. 9).

Fig. 9
figure 9

Mechanical properties of IPCs: a Compressive offset stress (σ0.2%); b Plateau stress (σplateau); c Absorbed energy up to an extension of 0.5 (W0.5); d Specific Energy Absorption (SEA)

Full size image

Regarding the compressive offset stress (see Fig. 9a), relatively similar results were observed, with no discernible relationship between this property and the geometries or volume fractions. To obtain a rightful comparison, compression tests on the aluminium alloy after casting were performed, showing a compressive offset stress of 171.52 ± 4.04 MPa, below IPCs average value, found to be 182.42 ± 5.49 MPa when considering all the experimental groups.

Regarding the plateau stress, it is clear that both the geometry of the IPC and their volume fraction influence the results (see Fig. 9b). The increase in the alumina phase resulted in a linear reduction (R-square > 0.94368) in stress during the plateau stage. During this plateau, the aluminium phase predominantly supports the IPC. Despite the alumina phase being already fractured, it continues to contribute to the structural integrity of the IPC by acting as an obstacle to plastic deformation. Consequently, the increase in the plateau stress is attributed to the increase in the volume of the aluminium phase. Additionally, comparing distinct geometries, Diamond and Gyroid IPCs exhibit similar plateau stress levels, which are on average 10.31 ± 1.02% higher than those observed in Primitive IPCs. This difference can be attributed to the material detachment identified in the visual analysis of their compressive behaviour. The more intricate topologies of Diamond and Gyroid seem to prevent the occurrence of major fractures that leads to material detachment. Also, there is no noticeable influence on the plateau stress of the samples with an increase in the number of unit cells.

Concerning the energy absorbed during compression for each IPC, Fig. 9c displays the values obtained for absorbed energy up to an extension of 0.5 (W0.5), while Fig. 9d presents the Specific Energy Absorption (SEA) up to 0.5 strain. SEA is defined as the energy absorbed per unit mass of material, calculated by dividing W0.5 by the geometrical density of the IPCs. In Fig. 9c, it is perceived that an increase in volume fraction leads to a linear reduction (R-square > 0.9136) in the absorbed energy. Comparing geometries, Diamond and Gyroid IPCs have, on average, 6.79 ± 3.10% higher energy absorption than Primitive IPCs, as will be further discussed. Also, as the experimental geometric density for all the IPCs is identical, SEA of the IPCs demonstrates the same exact tendency as W0.5, having Diamond and Gyroid IPCs, on average, 6.79 ± 3.10% higher SEA than Primitive IPCs.

To understand the inferior performance of Primitive IPCs when compared to Diamond and Gyroid IPCs, nTopology was used to analyse and deconstruct the morphology of the IPCs. To simplify and enhance visual clarity, only samples with 2 × 2x2 unit cells and 20% volume fraction were used in this analysis: P2_20, G2_20, and D2_20 (see Fig. 10). Based on the CAD render of the IPCs, it is evident that Primitive IPCs exhibit distinct characteristics compared to Gyroid and Diamond IPCs. The closed cell nature of Primitive TPMS results in the IPC having three spatially independent phases: the alumina structure, aluminium enclosed in the structure, and aluminium surrounding the structure. This suggests that the two distinct aluminium phases will mechanically behave independently due to the absence of a chemical or even physical connection. In contrast, although Gyroid and Diamond also have three spatially independent phases, the mechanical interlocking between them will enhance their mechanical properties, as reflected in the plateau stress and energy absorption of the structures.

Fig. 10
figure 10

CAD render of decomposed IPCs with 20% volume fraction and 2 × 2x2 unit cells

Full size image

4 Conclusions

In this study, aluminium–alumina IPCs based on TPMS were effectively designed, manufactured, and characterized. The designs included distinct TPMS structures (Diamond, Gyroid, and Primitive), distinct volume fractions, and different number of unit cells. The effect of the alumina TPMS on the mechanical properties of the IPCs was studied through uniaxial compression tests. The main conclusions are summarized as follows:

  1. 1.

    SEM and Micro-CT analysis revealed that DLP technology can replicate the complex geometries specified in the CAD model, providing good surface quality, despite the existence of some defects inherent to the manufacturing process.

  2. 2.

    The alumina TPMS structures presented a pseudo-ductile layer-by-layer behaviour under uniaxial compression.

  3. 3.

    The compressive strength of the ceramic structures is influenced by the ceramic volume fraction, the number of unit cells, and the type of TPMS structure. An increase in the ceramic volume fraction led to a linear increase in the compressive strength. Increasing the number of unit cells from 2 × 2 × 2 to 3 × 3 × 3 results in an 18.65% improvement in compressive strength. Regarding TPMS structures, the compressive strengths follow the order: Diamond > Gyroid > Primitive.

  4. 4.

    The manufactured IPCs presented a typical energy absorption behaviour under uniaxial compression, with an initial elastic region, a middle plateau region, followed by a densification stage.

  5. 5.

    The combination of aluminium alloy and the alumina TPMS structures resulted in an improvement of approximately 6% in compressive offset stress compared to the aluminium alloy alone. Diamond and Gyroid IPCs exhibit similar plateau stress, approximately 10.31% higher than that of Primitive IPCs. Energy absorption up to 0.5 strain and the SEA presented identical behaviour across all IPCs due to their indistinguishable geometrical density. Both metrics revealed that Diamond and Gyroid IPCs have similar values, which are on average 6.79% higher than that of Primitive IPCs.