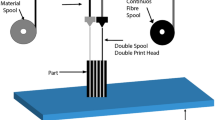
Abstract
This paper presents an experimental and numerical study on the mechanical properties of continuous glass fibre-reinforced composites fabricated using the material extrusion technique. Specimens with varying numbers of reinforcement layers are 3D printed using a MarkForged Mark Two printer. Both flexural and tensile tests are conducted to evaluate the performance of these specimens. In addition, a numerical modelling approach based on finite-element analysis (FEA) is developed to simulate the flexural and tensile properties of the composites. A comparison between the model predictions and experimental results reveals a reasonable agreement. The findings of this research provide valuable insights into the emerging field of continuous fibre-reinforced 3D printing technology, enabling users to design and fabricate parts that meet the specific requirements of their applications with a high level of confidence.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Composite materials have emerged as a promising solution for lightweight structures with excellent mechanical properties. However, the high cost of tooling, particularly for complex geometries and small batches, has limited their widespread adoption. Additive manufacturing (AM), also known as 3D printing, offers a potential solution to overcome these obstacles and promote the application of composite materials [1].
AM enables the production of a wide range of parts with complex geometries and exceptional design flexibility. Material extrusion is a widely utilized AM method for composite materials, which involves depositing molten material in layer-by-layer filaments [2]. It offers numerous advantages, including process flexibility, robustness, reliability, minimal material wastage, and affordable printers and consumables. An example of material extrusion is fused filament fabrication (FFF) [or fused deposition modelling (FDM)].
Although short fibres and particles have been used as reinforcing phases for thermoplastic composites, they provide limited (up to 20%) improvements in mechanical performance due to their weak reinforcement effect [3]. The innovation of 3D printing continuous fibre-reinforced composites (CFRCs) has ushered in a new era for the design and fabrication of complex composite structures with high performance at a reduced cost [4]. Markforged’s Mark One and Mark Two printers, for instance, enable the printing of continuous carbon fibre-reinforced nylon, yielding mechanical properties an order of magnitude higher than those of common 3D printers [5]. Kabir et al. [6] have provided a critical review of 3D printed continuous fibre-reinforced composites, showing studies have been done on tensile [7,8,9,10] and flexural properties [7, 8] of composites reinforced with continuous carbon fibre (CCF). These studies have also investigated the effects of fibre orientations [7,8,9] and the number of fibre-reinforced layers [10].
However, there is a scarcity of studies on 3D printed composites reinforced with other types of continuous fibre. Dickson et al. [11] explored additive manufacturing of continuous fibre-reinforced composites using FDM and evaluated three types of reinforcements: carbon, Kevlar, and glass fibre. Both flexural and tensile tests were conducted, revealing that the “Isotropic” pattern exhibited higher strength and modulus than the “Concentric” pattern for both flexural and tensile loadings. The printed composites demonstrated up to a 6.3-fold enhancement in tensile strength and a fivefold enhancement in flexural strength compared to the nylon control samples. The study also observed that the strength of the nylon composite followed the order: carbon fibre > glass fibre > Kevlar fibre. However, the increase in mechanical strength was somewhat limited with a continued increase in fibre content, primarily due to weak bonding between the fibre/nylon layers and the presence of increased air voids, which intensified with higher fibre content. Chacón et al. [12] investigated 3D printed continuous fibre-reinforced composites reinforced with carbon, glass, and Kevlar fibres. The study demonstrated that carbon fibre-reinforced composites exhibited the best mechanical performance, with stiffness and strength increasing with fibre volume content. However, a moderate increase was observed with further increases in fibre volume content, particularly in the case of Kevlar and glass fibres, due to weak bonding between the fibre/nylon layers and the presence of defects. Furthermore, it was found that flat samples exhibited higher strength and stiffness values than on-edge samples. Khosravani et al. [13] studied the fracture behaviour of 3D printed FFF glass fibre-reinforced nylon composites under tensile and semi-circular bending tests. They found the fracture load under tension increased with fibre volume fraction up to 45%, and the structural integrity under semi-circular bending increased with fibre volume fraction. Chen et al. [14] printed continuous glass fibre-reinforced polylactic acid composites and showed the printed composites reached fibre content 45 wt% and flexural strength 313 MPa. Caminero et al. [15] found glass fibre-reinforced composites exhibited the best impact performance, while carbon fibre resulted in the lowest ones and similar to nylon performance, leading to a more brittle behaviour. Saidane et al. [16] studied the tensile, flexural and short beam bending properties of 3D printed continuous glass fibre-reinforced polyamide composites. It was shown that the Young’s modulus followed the rule of mixtures (RoM); the tensile strength increased proportionally with the glass fibre content up to 10.8%; and the calculated flexural stiffness overestimates the experimental results by about 15%. Alarifi [17] evaluated the flexural performance of 3D printed nylon/glass fibre and nylon/carbon fibre composite materials, and found that fibre loading and orientation significantly influenced mechanical properties of composite. The maximum modulus and flexural strength were found in nylon composites loaded with glass fibre at 0° fibre raster orientation.
It is shown from the literature that the research on 3D printed continuous glass fibre-reinforced composites is limited, especially for the flexural properties. No modelling approach exists for predicting the flexural strength of 3D printed continuous glass fibre-reinforced composites. Thus, this study aims to address this technical gap by investigating the mechanical properties of continuous glass fibre-reinforced FFF composites. The tensile and flexural properties of FFF composites containing varying numbers of fibreglass layers are studied both experimentally and numerically. The results provide a more comprehensive understanding about the failure mechanisms and answer the question whether continuous glass fibre can effectively replace CCF in the design of 3D printed structural components. In addition, it is shown that the FEA-based simulation tool can help practical design of 3D printed continuous fibre-reinforced composites.
2 Methodology
2.1 Test specimens
In this study, Onyx and HSHT (High Strength High Temperature) fibreglass filaments from Markforged were chosen. The material properties supplied by Markforged are given in Table 1.
The test specimens in this study were printed on a Markforged Mark Two printer. The printing parameters were: matrix raster angle: ± 45°; printing speed: 14 mm/min; nozzle temperature: 265–270 °C; layer thickness: 0.1 mm.
The specimens for tensile testing were prepared in accordance with ASTM D3039/D3039M-17. The dimensions are given in Fig. 1a. The gauge section had a thickness of 2 mm and was composed of 20 layers, with each layer being 0.1 mm thick. The top and bottom of each specimen consisted of a four-layer Onyx wall. The remaining layers were either Onyx or HSHT fibreglass. The layups of the tensile specimens are presented in Table 2, where O and G stand for Onyx and HSHT fibreglass, respectively, the numbers indicate the number of layers for Onyx or HSHT fibreglass, and the subscript S denotes symmetry, e.g., [O4/G/O5]S means [O4/G/O10/G/O4]. Following ASTM D3039/D3039M-17, five specimens were tested for each layup.
For flexural testing, the specimens were prepared following ASTM D7264/D7264M-15. The gauge section had a thickness of 4 mm and comprised 40 layers, with each layer being 0.1 mm thick. Similar to the tensile specimens, the top and bottom of each flexural specimen featured a four-layer Onyx wall. The layups of the flexural specimens are provided in Table 3.
For both the tensile and flexural specimens, the isotropic pattern is chosen for the HSHT layers, and the fibre orientation is shown in Fig. 2.
2.2 Tensile test
The tensile test was conducted in accordance with ASTM D3039/D3039M-17 using a Lloyds EZ50 Advanced Materials Testing Machine equipped with a 50 kN load cell, as depicted in Fig. 3. To ensure accurate displacement measurement, an extensometer (Epsilon 3542-025M-025-ST) with a gauge length of 25 mm and a maximum travel of 6.25 mm was employed. Prior to each test, measurements of the length, width, and height of the gauge section were taken at three distinct locations using a Vernier calliper. These measurements were recorded, and the averages were determined. In addition, the specimens were visually inspected, and any noticeable defects, unusual features, or quality issues were noted.
The test machine was controlled through a laptop interface program, which facilitated adjustments of displacement rate, preload, preload rate, and extension/load limits. Following the recommendations in ASTM D3039/D3039M-17, a fixed displacement rate of 2 mm/min was employed for all specimens reinforced with fibre. However, for pure Onyx specimens that exhibited substantial plastic deformation, the displacement rate was increased to 5 mm/min. The tests were continued until failure occurred, and load and displacement data were exported at a minimum of 1 data point per second.
2.3 Flexural test
The flexural properties were determined using the three-point bending test, in accordance with ASTM D7264/D7264M-15, performed on a Lloyds EZ50 Advanced Materials Testing Machine. The three-point bending test involves placing a rectangular flexural specimen on two supports, separated by a specified span length. A compression force is then applied at the midspan of the beam until failure occurs. The recommended span-to-thickness ratio of 32:1 was selected for the test specimens.
A 10 kN load cell was utilized for all specimens during the three-point bending test. The test was controlled by setting the displacement rate of the loading nose at the recommended rate of 2 mm/min, as specified in ASTM D7264/D7264M-15. Load and displacement data were recorded and exported at a resolution of 1 data point per second. Figure 4 illustrates a representative test specimen used in the flexural test.
2.4 Finite-element analysis
The tensile and flexural tests are simulated using finite-element analysis (FEA) conducted in Ansys Workbench [18]. The longitudinal modulus E11 and the shear moduli G12, G13 and G23 of the HSHT composite are derived using Hashin’s model [19], and the transverse moduli E22 and E33 are derived using the stress–strain relationship [20]. The strength values are defined based on the supplied material datasheet from MarkForged. Material degradation factors are also introduced to simulate progressive failure [21]. These composite material properties are then used to define glass/Onyx and Onyx fabrics in Ansys ACP Pre (Ansys Composite Pre-processor). Composite specimens are defined using these fabrics. The resulting composite model is exported as a shell to Ansys Mechanical for static structural analysis.
In the case of tensile properties, the composite specimen includes two tabs on each end, as depicted in Fig. 5. One tab is subjected to fixed support, while the other tab undergoes a prescribed displacement. Linear analysis is conducted, and the force–displacement curve is obtained upon completion of the simulation.
According to ASTM D3039/D3039M-17 [22], the tensile strength (ST) is determined using the following equation:
The tensile modulus (ET) is calculated as
where b and h are the width and thickness of the specimen, respectively, Pmax is the maximum load encountered before failure, σT is the tensile stress, and εT is the tensile strain.
For the flexural properties, the composite specimen is supported by two rollers at a span length of L and loaded at its mid-span. The span-to-thickness ratio is chosen to be 32. The hybrid composite is modelled as a shell structure, while the supporting and loading rollers are represented as cylindrical solids, as shown in Fig. 6. The supporting rollers are subjected to fixed support, and a prescribed displacement is applied to the loading roller. Frictional contact is defined between the rollers and the composite specimen. Nonlinear analysis is conducted, and the force–displacement curve is obtained upon completion of the simulation.
The failure load is determined from the peak value of the load–displacement curve. Since the stress distribution is uniform in compression but non-uniform in bending, according to Weibull statistical theory [23], the flexural strength is approximately 30% higher than the compressive strength. Consequently, the maximum bending load was increased by approximately 30%. As per procedure A of ASTM D7264/D7264M-15 [24], the flexural strength (SF) is given by
The flexural modulus (EF) is calculated as
where L, b and h are the span, width and depth of the specimen, D is the maximum deflection before failure, Pmax is the maximum load encountered before failure, σF is the flexural stress, and εF is the flexural strain.
3 Results and discussion
3.1 Tensile test
The dimensions are quite consistent with errors ± 0.05 mm. No visible defects could be seen for all specimens. The T2G specimens, which contain two HSHT fibreglass layers, exhibit an average recorded failure load and extension of 4285 N and 6.6 mm, respectively. Figure 7 presents the stress–strain curves obtained from both the experiments and FEA. As shown, the stress–strain relationship is predominantly linear until brittle failure occurred, indicating minimal plastic deformation. The T2G specimens display an average elastic modulus of 2.63 GPa and an ultimate tensile strength of 85.41 MPa.
Figure 8 shows a failed T2G specimen alongside an untested one. The failed specimen exhibits a fracture along a 45° angle following the path of the Onyx filaments, which is likely the path of least resistance once the fibre layers failed. According to Ekoi et al. [25], this is the typical failure mode for Onyx. It can be deduced that at low reinforcement content, the tensile failure mode is dominated by Onyx.
The T4G specimens show increased strength and stiffness compared to the T2G specimens, with an average maximum load of 8850 N and an average extension to failure of 6.8 mm. Further enhancement in strength and stiffness is observed in the T6G specimens, with an average maximum recorded load of 12,209 N and an average extension to failure of 6.8 mm.
Figure 9 depicts the T4G (left) and T6G (right) specimens. On the left, three failed T4G specimens are shown next to an untested specimen, exhibiting three distinct failure modes. The bottom specimen displays a similar failure mode to the T2G specimens, while the other two specimens failed in a more destructive manner. The second specimen from the bottom exhibits a mixed mode of 45° angle fracture and filament splitting. The second specimen from the top displays a failure along the length of the specimen, occurring at the interface between two fibreglass filaments. According to Ekoi et al. [25], this long splitting failure is the typical failure mode for the unidirectional fibre composite. It is likely to be caused by insufficient bonding between filaments.
The right side of Fig. 9 illustrates two failed T6G tensile specimens alongside an untested specimen, showcasing two types of failure. The bottom specimen displays a fracture that roughly follows a 45° angle, with fibre fracture sites influencing the crack path. The middle specimen exhibits multiple fracture sites along its length, with the crack propagating between different fibre fracture sites, connecting them along the filament interface.
It is seen that the T4G and T6G specimens failed in two different modes, either dominated by Onyx or fibre. Thus, as fibre reinforcement increases, failure is shifting from 45° angle fracture to long splitting failure.
The T8G specimens, which contain eight HSHT fibreglass layers, exhibit a linear increase in strength compared to specimens with lower reinforcement fibre content. The average recorded failure load and extension are 17,145 N and 7.1 mm, respectively. The stress–strain curves from both the experiments and FEA are presented in Fig. 10. Once again, the behaviour remains linearly elastic until brittle failure occurred. The T8G specimens display an average elastic modulus of 9.70 GPa and an ultimate tensile strength of 345.39 MPa.
Figure 11 illustrates two failed T8G specimens alongside an untested specimen. Both failed specimens experienced catastrophic failure, exhibiting multiple fracture sites along the gauge section. This suggests that failure was entirely dictated by the fracture of the reinforcement fibres, which is in agreement with Ekoi et al. [25] for the unidirectional fibre composite.
The T10G specimens, which have the highest reinforcement fibre content among all tested specimens, exhibit higher stiffness compared to other specimens. However, the average ultimate tensile strength is lower than that of the T8G specimens, with a recorded average maximum load of 15,845 N and an average extension to failure of 5.4 mm. Figure 12 presents three failed T10G specimens alongside an untested specimen. These specimens display visible fibre failure; however, failure does not propagate throughout the specimen, possibly due to insufficient interlayer adhesion. While reinforcement is increased, the insufficient interlayer adhesion leads to premature failure and reduced tensile strengths.
The tensile strengths and moduli of all composite specimens, with varying numbers of HSHT layers, are depicted in Fig. 13, with complete data given in Table 4. The FEA simulation demonstrates that both tensile strength and modulus increase with the number of HSHT layers. The experimental results indicate an increase in tensile strength with the number of HSHT layers up to 8 HSHT layers, followed by a decrease. A similar trend was also found by Khosravani et al. [13]. Dickson et al. [11] found the tensile strength was 194 MPa when the composite contained 25% continuous glass fibre, and this is in good agreement with the results in Table 4. Furthermore, the experimental tensile strengths are consistently higher than those obtained from the FEA simulation. Notably, the T8G specimens exhibit the largest difference, with the experimental tensile strength being 40% higher than the FEA prediction. The experimental tensile moduli align well with the FEA results. These differences in tensile strengths are due to the mechanical properties of an HSHT fibre-reinforced composite being preserved at significantly higher strains than the typical failure strains of the HSHT fibres alone. This preservation is attributed to Onyx’s ability to inhibit the propagation of cracks originating from clusters of failed HSHT fibres [26]. However, it should be noted that this effect diminishes once the number of HSHT layers reaches more than eight, i.e., 40%.
3.2 Flexural test
The flexural properties of the composite specimens are evaluated through the three-point bending test configuration. The F6G specimens, containing six HSHT fibreglass layers, are characterised by the presence of three HSHT fibreglass layers just below the top wall and just above the bottom wall. The recorded average maximum load for the F6G specimens is 77.30 N.
Figure 14 displays the stress–strain curves obtained from both the experiments and FEA for the F6G specimens. The specimens exhibited linear elastic behaviour until reaching the maximum load, followed by a gradual stress decrease with increasing strain due to the development of cracks along the direction of fibres [12]. The average flexural modulus and strength of the F6G specimens are found to be 5.91 GPa and 71.35 MPa, respectively. However, it should be noted that the FEA model overestimates the flexural strength.
Upon completion of the tests, slight wrinkling is observed on the top compressive face of the specimens, indicating the failure of the reinforcement fibreglass layers. Microscopy analysis of the flexural specimens, as shown in Fig. 15, confirms the buckling and subsequent fracture of the fibreglass layer. In addition, noticeable repeating voids are observed above the HSHT fibreglass layers, suggesting a possible adhesion issue during the printing process of Onyx filament onto the HSHT fibreglass layer. This insufficient adhesion may contribute to the discrepancy between the experimental and FEA results. The repeating nature of the voids is likely due to their location between neighbouring printed Onyx filaments, which become prominent sites of buckling.
With an increased number of HSHT fibreglass layers (12 layers), the F12G specimens exhibit a significant increase in failure load compared to the F6G specimens, with an average of 151.91 N. The failure mode remains similar to that of the F6G specimens, characterised by compressive face buckling. The average flexural modulus and strength of the F12G specimens are determined to be 9.07 GPa and 140.23 MPa, respectively.
For the F18G specimens, containing 18 HSHT fibreglass layers, the recorded average maximum load was 162.45 N. The stress–strain curves, shown in Fig. 16, exhibit similar flexural behaviour to the previous specimens. The average flexural modulus and strength of the F18G specimens are measured as 10.37 GPa and 149.95 MPa, respectively.
Figure 15 provides microscopic images of a failed F18G specimen, revealing compressive face buckling. In contrast to F6G specimens, the presence of fewer voids is evident, providing an explanation for the good flexural strength observed, which aligns well the FEA prediction.
Contrary to expectations, the F24G specimens, with the highest number of HSHT fibreglass layers, does not exhibit the highest strength among all the specimens, similar to the behaviour observed in the T10G tensile specimens. The recorded average maximum load for the F24G specimens is 157.58 N. The average flexural modulus and strength of the F24G specimens are determined as 11.56 GPa and 145.46 MPa, respectively.
The behaviour of the F24G specimens follows a similar trend to that of the F18G specimens, with an increase in stiffness but a decrease in flexural strength. Microscopy analysis reveals the presence of shear bands near the ends of the specimen, as shown in Fig. 17, which may contribute to the decreased flexural strength.
The flexural strengths and moduli of all composite specimens with varying numbers of HSHT layers are presented in Fig. 18, with complete data given in Table 5. The FEA simulation demonstrates that both flexural strength and modulus increase with an increasing number of HSHT layers. However, experimental results indicate that the flexural strength increases up to 18 HSHT layers, after which it starts to decrease. Notably, the experimental flexural moduli align well with the FEA predictions. Similar to tensile loading, when the number of reinforcement layers is increased, the insufficient interlayer adhesion leads to delamination and premature failure. Therefore, the flexural strength decreases.
4 Conclusions
This paper presents an experimental and numerical study on the mechanical properties of continuous glass fibre-reinforced FFF composites. The main objective is to enhance our understanding of this novel material and investigate its stiffness, strength, and failure mechanisms under both tensile and bending loadings, considering varying amounts of HSHT fibreglass reinforcement. FEA models are also developed to simulate the tensile and flexural behaviours.
The experimental findings demonstrate that the addition of HSHT fibreglass into the Onyx matrix significantly increases the stiffness and strength of the 3D printed parts. This improvement continues until the reinforcement volume fraction reaches approximately 40%. However, further increases in the reinforcement volume fraction lead to a reduction in strength while maintaining increased stiffness. Based on failure analysis and microscopy observations of the specimens, it is hypothesised that the decrease in strength is attributed to interlaminar bonding failure between the HSHT fibreglass and the Onyx matrix.
It is shown the FEA-based model is useful for predicting the stiffness and strength of most specimens in both tension and bending, although some discrepancies exist. It is observed that the predicted tensile properties tend to be conservative compared to the experimental results, while the FEA-based model over-estimates some flexural strengths.
In conclusion, this study provides valuable insights into the mechanical properties of 3D printed parts reinforced with HSHT fibreglass. The relationships between the amount of HSHT fibreglass reinforcement and the mechanical properties have been established. These findings contribute to the broader understanding of continuous fibre-reinforced composites and facilitate the design and optimization of 3D printed structural components using this technology. Further research is recommended to address the challenges associated with interlaminar bonding and explore methods to improve the overall strength and durability of these composites.
Data availability
All data generated or analysed during this study are included in this published article.
References
Ngo TD et al (2018) Additive manufacturing (3D printing): a review of materials, methods, applications and challenges. Compos B Eng 143:172–196
Wang Y et al (2020) Overview of 3D additive manufacturing (AM) and corresponding AM composites. Compos A Appl Sci Manuf 139:106114
Ning F et al (2015) Additive manufacturing of carbon fiber reinforced thermoplastic composites using fused deposition modeling. Compos B Eng 80:369–378
Tian X et al (2022) 3D printing of continuous fiber reinforced polymer composites: development, application, and prospective. Chin J Mech Eng Addit Manuf Front 1(1):100016
Blok LG et al (2018) An investigation into 3D printing of fibre reinforced thermoplastic composites. Addit Manuf 22:176–186
Kabir SMF, Mathur K, Seyam A-FM (2020) A critical review on 3D printed continuous fiber-reinforced composites: history, mechanism, materials and properties. Compos Struct 232:111476
Parmiggiani A, Prato M, Pizzorni M (2021) Effect of the fiber orientation on the tensile and flexural behavior of continuous carbon fiber composites made via fused filament fabrication. Int J Adv Manuf Technol 114(7):2085–2101
Lupone F et al (2022) Experimental characterization and modeling of 3D printed continuous carbon fibers composites with different fiber orientation produced by FFF process. Polymers 14(3):426
Mei H et al (2019) Influence of mixed isotropic fiber angles and hot press on the mechanical properties of 3D printed composites. Addit Manuf 27:150–158
Chabaud G et al (2019) Hygromechanical properties of 3D printed continuous carbon and glass fibre reinforced polyamide composite for outdoor structural applications. Addit Manuf 26:94–105
Dickson AN et al (2017) Fabrication of continuous carbon, glass and Kevlar fibre reinforced polymer composites using additive manufacturing. Addit Manuf 16:146–152
Chacón JM et al (2019) Additive manufacturing of continuous fibre reinforced thermoplastic composites using fused deposition modelling: effect of process parameters on mechanical properties. Compos Sci Technol 181:107688
Khosravani MR et al (2022) Fracture studies of 3D-printed continuous glass fiber reinforced composites. Theoret Appl Fract Mech 119:103317
Chen K et al (2021) Optimization of printing parameters of 3D-printed continuous glass fiber reinforced polylactic acid composites. Thin-Walled Structures 164:107717
Caminero MA et al (2018) Impact damage resistance of 3D printed continuous fibre reinforced thermoplastic composites using fused deposition modelling. Compos B Eng 148:93–103
Saidane EH et al (2022) 3D printed continuous glass fibre-reinforced polyamide composites: fabrication and mechanical characterisation. J Reinf Plast Compos 41(7–8):284–295
Alarifi IM (2022) A performance evaluation study of 3d printed nylon/glass fiber and nylon/carbon fiber composite materials. J Market Res 21:884–892
Dong C (2023) Finite element analysis of additively manufactured continuous carbon fiber-reinforced composites. JOM 75(10):4150–4157
Chou T-W (1992) Microstructural design of fiber composites. Cambridge University Press, Cambridge
Hashin Z (1983) Analysis of composite materials—a survey. J Appl Mech 50(3):481–505
Garnich MR, Akula VMK (2008) Review of degradation models for progressive failure analysis of fiber reinforced polymer composites. Appl Mech Rev 62(1):010801
ASTM International (2017) Standard test method for tensile properties of polymer matrix composite materials, in ASTM D3039/D3039M-17. ASTM International, West Conshohocken
Bullock RE (1974) Strength ratios of composite materials in flexure and in tension. J Compos Mater 8:200–206
ASTM International (2015) Standard test method for flexural properties of polymer matrix composite materials, in ASTM D7264/D7264M-15. ASTM International, West Conshohocken
Ekoi EJ, Dickson AN, Dowling DP (2021) Investigating the fatigue and mechanical behaviour of 3D printed woven and nonwoven continuous carbon fibre reinforced polymer (CFRP) composites. Compos B Eng 212:108704
Aveston J, Sillwood JM (1976) Synergistic fibre strengthening in hybrid composites. J Mater Sci 11(10):1877–1883
Acknowledgements
The authors thank WesTrac for providing the MarkForged Mark Two 3D printer and materials for making the test specimens.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions. The authors did not receive support from any organisation for the submitted work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dong, C., Davies, I.J. Mechanical properties of continuous glass fibre-reinforced composites made by material extrusion. Prog Addit Manuf (2024). https://doi.org/10.1007/s40964-024-00566-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40964-024-00566-4