Influence of Graphite-Phase Parameters on the Mechanical Properties of High-Silicon Ductile Iron

Abstract

High silicon solid solution-strengthened ductile iron exhibits advantageous combinations of static strength and ductility due to elevated silicon contents. However, the Charpy impact toughness decreases rapidly with increasing silicon content. In particular, the transition temperature between ductile and brittle fracture behaviour is shifted significantly to higher temperatures. Therefore, the optimum adjustment of the graphite phase is of major importance in order to achieve sufficient toughness properties. So far, little is known about the influence of the graphite phase on the toughness properties of high-silicon ductile iron. In the present study, the graphite particle distribution was therefore systematically varied for ductile iron grade EN-GJS-500-14. The effect of the graphite nodule count in the range from 77 to 273 1/mm², and the influence of the average particle size and particle distance on the Charpy impact energy and the characteristics of the resulting transition curves were investigated by means of statistical analyses. The results that were obtained indicate that the ductile-to-brittle transition temperature in Charpy impact tests can be reduced by about 22 °C by increasing the average nodule count by 100 1/mm². Additionally, both the lower and upper shelf energies are raised by increasing the nodule count by 100 1/mm². Based on these results, it becomes apparent to producers that the inoculation technology for toughness-stressed components needs to be specifically considered and adapted.

Introduction

Toughness describes the resistance of a material to crack propagation and is generally expressed by determining the absorbed mechanical energy during plastic deformation.¹ Toughness properties are usually determined in the Charpy impact test according to DIN EN ISO 148-1, which is usually used as a qualification method for numerous technical applications.² The impact strength measured at room temperature in conventional steel grades can vary between 10 and 350 J depending on the chemical composition. For example, high carbon steels have a toughness of usually 10–40 J, while pipeline steels can show an impact toughness of up to 350 J. In their studies, Cao et al. also report of a ferritic-martensitic 5Mn3Al steel with a Charpy impact energy of up to 450 J.³

Ductile iron (DI) alloys exhibit significantly lower toughness properties compared to conventional steel alloys, which is due to the notch effect of the graphite phase on the metallic matrix.⁴ However, compared to cast iron with lamellar (LGI) and compacted graphite (CGI), DI shows higher toughness properties due to the spherical formation of the graphite phase resulting in a reduced notch effect of the graphite nodules on the surrounding matrix.

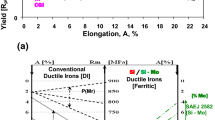
From the literature, it is generally known that graphite-phase parameters such as the nodularity and the nodule count have a significant effect on the toughness properties and the transition behaviour of the material. The effect of the nodularity on the toughness properties of conventional ductile iron can be observed from Figures 1 and 2. As Figure 1 shows, the Charpy impact energy of a ferritic–pearlitic DI increases significantly by about 13 J at constant temperature by raising the average nodularity from 20 to 95%. Figure 2 shows that the upper shelf energy (USE) increases by 7 J due to increasing the nodularity from 50 to 100% for a ferritic–pearlitic ductile iron with 2.2 wt%. However, high silicon DI shows a higher tolerance towards a lower graphite nodularity.^5,6

Figure 1

Influence of the nodularity on the impact strength of a ferritic–pearlitic ductile iron according to Al-Ghonamy et al.⁷

Figure 2

Transition curves based on Charpy impact tests on ductile irons with varying nodularity according to Hasse.⁶

Besides the influence of the nodularity of the graphite phase, the nodule distribution has to be considered, too. The effect of the average graphite nodule diameter on the USE and the ductile-to-brittle transition temperature (DBTT), determined in fracture mechanic tests, is shown in Figure 3.⁸ Both the lowest temperature in the upper shelf and the DBTT increase significantly with rising graphite nodule diameter. In particular, an increase of the nodule diameter in the range between 20 and approx. 50 μm causes a significant increase. The transition curve is thus clearly shifted to higher temperatures. The authors attribute this observation to several metallurgical causes. On the one hand, a finer matrix structure ensures that microcracks can propagate more quickly through the microstructure, but on the other hand, larger graphite precipitates cause a higher stress concentration at the graphite–ferrite interface, further promoting crack propagation.

Figure 3

Effect of the average graphite nodule diameter on lowest temperature of the upper shelf energy and the transition temperature of a ferritic ductile iron in fracture mechanics tests.⁸

A larger nodule size usually correlates directly with a lower nodule count at constant volumetric graphite content. Labrecque et al. report in their paper of a patent of Rio Tinto presenting the influence of the average graphite nodule count on the transition behaviour of DI, Figure 4.^9,10 It was demonstrated that the transition temperature decreases significantly with increasing nodule count, with concomitant reduction of USE. This effect is attributed to the fact that crack initiation requires more energy at higher nodule count and that grain boundary segregation occurs independently of the nodule shape, since the severity of prior austenite grain boundary segregation is reduced as a result of the increased nodule count. The decrease in USE, on the other hand, is attributed to the shorter nodule distance. The authors conclude from their investigations that an increased nodule count (here: 300 1/mm²) should be achieved in order to obtain sufficient toughness properties at both low and room temperatures. Consistent results were obtained in a study by Unkic et al., who performed Charpy impact tests on DI samples with a carbon content of 3.6 wt% and a silicon content of approx. 2.1 wt%.¹¹ The two series of tests that were studied differ mainly in their graphite nodule counts (100 and 300 1/mm²). The authors observed a tendency towards higher USE at higher temperatures as a result of lower nodule counts, Figure 5. However, a clear effect of the nodule count of graphite on the DBTT cannot be identified.

Figure 4

Transition curves of Charpy impact tests on ferritic ductile iron with varying nodule counts according to Ref. 10.

Figure 5

Transition curves of Charpy impact tests on ductile iron with varying nodule counts according to Ref. 11.

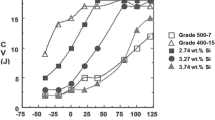
Solid solution-strengthened high silicon DI that were incorporated in the European standard DIN EN 1563 in 2012 exhibits very good combinations of static strength and ductility^12,13 and is therefore ideally qualified for the use in lightweight applications.¹⁴ The current standard revision is DIN EN 1563:2019, which lists high silicon DI grades in group 2. The advantageous static properties of these alloys enable their use in many applications that could not be considered yet due to lower mechanical properties, such as in the automotive industry, the shipbuilding industry, in the wind energy or mechanical engineering sector.^15,16,17 It is very well known that due to the increased silicon (Si) content, however, the toughness properties of solid solution-strengthened DI are significantly reduced compared to conventional ferritic–pearlitic-strengthened DI grades.¹⁸ In particular, the DBTT is significantly raised by increasing the Si content, as can be seen in Figure 6.¹⁹ This phenomenon is generally attributed to the formation of FeSi long-range orderings of B2- and DO₃ phase formations in the ferritic matrix as the silicon content increases.^20,21 As the Charpy impact test is the common testing method for the characterization of toughness properties for DI alloys, minimum impact energy values at certain temperatures cannot be met for many applications. In these cases, an individual qualification of these materials can be carried out on the basis of fracture mechanical strength certificates, such as described in the FKM guidelines.^22,23 For both foundrymen and designers, the aspects mentioned above lead to an increased uncertainty regarding the use of castings made of high-silicon ductile iron in dynamically loaded components.

Figure 6

Transition curves obtained in Charpy impact tests for different ductile iron grades¹⁹ (CV: Charpy impact energy).

Therefore, ductile iron grades with lower silicon contents are typically used for casting applications at low temperatures, such as in the wind energy.²⁴ However, it must be noted that such castings must then be dimensioned larger due to their lower static properties, which can result in a significant increase of the component weight. Therefore, increasing the silicon content while maintaining the same toughness properties can be a suitable metallurgical tool to significantly reduce the design weight of DI components.

Therefore, an optimal adjustment of the graphite phase is of major importance, particularly for high silicon DI alloys. It is known from the literature that the addition of silicon leads to a significant reduction of the nodularity of the graphite.^25,26 The negative effect on the toughness properties caused by silicon must therefore be encountered by an optimized adjustment of the graphite nodule count, nodule size and average distance. However, the current state of research only shows the influence of the graphite phase in conventional DI alloys. Data on the effect of the graphite-phase parameters are not yet available for modern materials of high silicon DI. In particular, no critical values for graphite-phase parameters are known for ductile iron alloys with elevated silicon contents. In order to fill this current research gap, the present study aims at investigating the influence of specific graphite-phase parameters on the impact strength of high silicon DI.

Design of Experiments

In the present study, a total of four DI alloys, referred to as LLNC, LNC, MNC and HNC (very low, low, medium and high nodule count), was investigated on the basis of a predominantly constant chemical composition. The base alloy was set with a Si content of 3.8 wt% and a near-eutectic composition according to DI grade EN-GJS-500-14. Therefore, the investigated alloys differ mainly in their graphite phase formation, in particular the graphite nodule count. After production of the samples, the alloys were studied with regard to their microstructural characteristics, static strength and Charpy impact energy.

Experimental Procedure

Samples of alloy LLNC were produced externally in a foundry in Germany. For casting of the alloys LNC, MNC and HNC, raw materials consisting of remelt material (DI grade EN-GJS-400-15), high purity iron and ferrosilicon (FeSi75) were prepared and melted in a medium-frequency induction furnace with a maximum capacity of 250 kg. The intended chemical composition was a ductile iron grade 500-14 with 3.8 wt% Si and a near-eutectic composition. The melt was superheated to 1500 °C and held for five minutes in order to remove impurities. After deslagging and casting samples for spectrometric analysis, the magnesium (Mg) treatment was performed by using the pour-over method. Thus, 1.3 wt% of a cerium-free Mg pre-alloy (45 wt% Si, 6.25 wt% Mg, 1.9 wt% Ca) and a cerium-containing inoculant (64–70 wt% Si, max. 1.2 wt% Al, 1.8–2.4 wt% Ca, 0.8–1.2 wt% Bi, 0.8–1.2 wt% Ce) with a grain size of 0.6–2 mm was placed onto the bottom of a pouring ladle and was covered with 2.75 wt% of a low-alloyed steel scrap. After the Mg treatment, the melt was deslagged. For alloy LNC, the melt was inoculated with 0.1 wt% and for alloy MNC with 0.2 wt% inoculant in the pouring ladle just before casting. For alloy HNC, a two-step inoculation consisting of 0.3 wt% ladle inoculation and 0.1 wt% mould inoculation was conducted by placing an additional mould inoculant onto the pouring filter. After the inoculation, samples for both thermal analysis and spectrometric analysis were produced, and the melt was poured at about 1350 °C. For alloys LNC, MNC and HNC, two furan-bonded sand moulds, each containing Y-shaped standard test blocks according to DIN EN 1563 (2 Y_II and 2 Y_IV standard test blocks per mould), were produced, as shown in Figure 7. For each alloy, a total of 5 tensile test specimens, 2 metallographic specimens and up to 24 Charpy V-notch specimens were machined from the test blocks. For alloy LLNC, casting geometries with a wall thickness of 30 mm were analyzed. Samples for spectrometric examinations were produced by pouring the melt in a copper die directly after inoculation and prior to casting. They were then ground with grinding paper (80-SiC) and tested using a spark emission spectrometer.

Figure 7

Casting geometry and position of samples for metallographic and mechanical analysis.

Specimen Analysis

For quasi-static tensile tests, cylindrical samples with a diameter of 18 mm were machined from the standard test blocks using a water-cooled core drill. The positions of the samples in the Y_II test block geometry correspond to the positions “a” and positions “a” and “d” for Y_IV standard test blocks according to the standard DIN EN 1563, respectively.¹² Tensile test specimens of shape A according to DIN EN 50125 were machined with a testing diameter of d₀=8 mm and an overall length of 115 mm.²⁷ After machining of the specimens, tensile tests were conducted using a main cross-speed of 0.6 mm/min.

Charpy V-notch specimens were machined from two Y_II standard test blocks. For each temperature, three to four specimens were tested on a Zwick/Roell HIT50P pendulum impact tester with a maximum impact energy of 50 J per temperature in the range of -60 °C to +120 °C, according to DIN EN ISO 148-1.²

Metallographic samples were taken from the direct vicinity of the tensile and Charpy test specimens. After cold-embedding and grinding (180, 320, 500 and 1000 SiC grinding paper), metallographic samples were polished (9, 3 and 0.25 μm) using a diamond suspension. Microstructural analyses of both polished and nital-etched (0.3% HNO₃) specimens were carried out using an optical up-light microscope and automated image analysis. Per specimen, a total of five images was taken across the specimen’s surface and analyzed regarding the nodularity, the nodule count, particle size particle distance and the pearlite fraction by converting the images into binarized micrographs and applying automated images analysis using the software AxioVision. According to ISO 945-4, the roundness of each particle was determined and the nodularity is calculated as shown in Eqn. 1.²⁸ According to ISO 945-4, the nodule count was determined by adding up the number of particles of with a minimum roundness of 0.6. For the evaluation of the graphite parameters, a lower threshold for the nodule area of ~25 square microns was considered. A perfect circle nodule with a roundness of 1.0 would have a diameter of 5.64 microns, which is significantly smaller than the minimum size of 10 microns Maximum Feret Diameter specified by ISO 945-4.

Based on the raw data of the image analysis, the average particle distance was measured by calculating its distance to the closest particle. For this purpose, the k-Nearest-Neighbours (kNN) algorithm was used with Minkowski Distance as distance metric. The average distance of five images per sample was used for further comparison to minimize variance per sample.

$$ p_{{{\text{Nod}}}} = \frac{{A_{{{\text{VI}}}} + A_{{\text{V}}} }}{{A_{{{\text{all}}}} }} $$

(1)

with: P_Nod: Nodularity in %; A_VI and A_V: total area of graphite particles with roundness ≥ 0.6 to ≤ 1.0; A_all: total area of all graphite particles.

In order to evaluate the statistical significance of the results, additional regression analyses were performed for the presented correlations. In each case, R − Sq_adj. along with the corresponding p value was determined for a confidence interval of 95%. A p value $\le$ 0.05 thus indicates statistical significance of the respective results.

After solidification, samples for spectrometric analysis were prepared by grinding the casting skin with 80 SiC paper. For each sample, at least three measurements were performed on a Hitachi model OE750 spectrometer. According to Eqn. 2, the carbon equivalent (CE) was then calculated. Table 1 summarizes the chemical compositions of all the investigated alloys.

$$ {\text{CE}} = \% C + \frac{1}{3}\left( {\% Si + \% P} \right) $$

(2)

Table 1 Chemical Compositions of the Investigated Alloys (Contents in wt%, Carbon Content Determined via Thermal Analysis)

Results

Microstructural Analysis

As can be seen in Figure 8, it was possible to see a significantly different distributions of the graphite phase on the basis of an alloy with 3.8 wt% Si by varying the inoculation. Table 2 shows that the minimum average nodule count of 76.9 1/mm² was observed in alloy LLNC. An inoculation with 0.1 wt% of inoculant in alloy LNC results in an average nodule count of 175.3 1/mm², which increases to 248.7 1/mm² by raising the inoculant amount to 0.3 wt%. A two-step inoculation consisting of a ladle inoculation with 0.3 wt% and an additional mould inoculation with 0.1 wt% mould inoculant results in a further increase of the nodule count to 272.7 1/mm² in Y_II standard test blocks. The total particle number, which corresponds to the number of all graphite precipitates according to Form I–VI, increases simultaneously from 177.1 to 448.0 1/mm². Corresponding to the increase in the nodule count, it can be observed that the nodularity of alloy LLNC to HNC, determined according to ISO 945-4,²⁸ decreases steadily from 81.7 to 65.0%. In accordance with what was expected, the increase in graphite nodule and particle count is accompanied by a decrease in graphite particle size, as shown in Figure 9. These correlations can be regarded as statistical significant with a p value of 0.0006 and 0.002, respectively. It is noticeable that a significantly higher degree of correlation is achieved when considering the average graphite particle count than when considering the graphite nodule count. Additionally, it is shown that a statistical significant correlation between the average particle and nodule count and the nodularity can be determined, shown in Figure 10. The particle size increases rapidly with increasing nodularity, which was not expected according to the literature. The average pearlite content is below 3% in all alloys that were studied.

Figure 8

Overview of micrographs of alloys (a) LLNC, (b) LNC, (c) MNC and (d) HNC at 100x magnification (obtained from Y_II-standard test blocks, nital-etched).

Table 2 Microstructural Results of the Investigated Analysis via Automated Image Analysis

Figure 9

Left: Correlation between the average particle and nodule count and the average particle size; right: Correlation between average nodule count and average particle distance.

Figure 10

Correlation between the average particle size and the average nodularity.

Mechanical Properties

Figure 11 shows the effect of the average particle count on the static mechanical properties of all alloys that were studied. It can be observed that both the tensile strength (UTS) and the yield strength (YS) increase with higher graphite particle count. The UTS increases from 476 in alloy LLNC to 544 MPa in alloy HNC, while the YS increases from 363 to 419 MPa. This linear trend is evident in specimens of both lower (Y_II/30 mm) and higher wall thickness (Y_IV). Both the effects of the particle count on the UTS and on the YS show a statistical significance with p value of 0.005 and 0.001, respectively. The elongation at fracture (A) increases significantly, particularly when the particle count is increased from 177 to 282 1/mm². The uniform elongation (A_g) in alloys LNC, MNC and HNC is only slightly higher than in alloy LLNC, but also shows a plateau above a particle count of 252 1/mm². However, these correlations have to be considered as not statistical significant according to p values of 0.179 and 0.220, respectively.

Figure 11

Influence of the average particle count (including grade LLNC) on the static mechanical properties of the investigated alloys.

The results in Figure 12 show that the influence of the graphite nodule count on both strength and elongation corresponds to the observations from Figure 11. Overall, correlations for UTS and YS show higher R − Sq_adj.-values when the graphite particle count is used, whereas they are lower for correlations of A and A_g compared to correlations using graphite nodule count.

Figure 12

Influence of the average nodule count (including grade LLNC) on the static mechanical properties of the investigated alloys.

Figures 13 and 14 show the results of the correlations with respect to the static mechanical properties excluding the data of alloy LLNC analogous to those in Figures 11 and 12 in order to compare the quality of the correlations. It can be observed that the correlations of the graphite particle count show an overall better correlation with respect to the mechanical properties. Except for the elongation at fracture the nodule count shows a higher correlation compared to the graphite particle count.

Figure 13

Influence of the average particle count (excluding grade LLNC) on the static mechanical properties of the investigated alloys.

Figure 14

Influence of the average nodule count (excluding grade LLNC) on the static mechanical properties of the investigated alloys.

As indicated in Figures 15 and 16, static strength is decreasing with increasing particle size and nodularity. However, the latter effect, which is contrary to the literature, could be attributed to higher particle sizes in alloys LLNC and LNC, as shown in Figure 10. It can be seen that both UTS and YS decrease statistically significant with increasing particle size. The elongation at fracture and uniform elongation initially increase slightly between 300 and 500 μm², reach their maximum at a nodule size of 479 μm² at 21.1% and drop to 11.1% when the graphite particle size is further increased. An analogous effect of the average particle distance can be observed from Figure 17, showing a statistical significance with p values below 0.05.

Figure 15

Influence of the average particle size on the static mechanical properties of the investigated alloys.

Figure 16

Influence of the average nodularity on the static mechanical properties of the investigated alloys.

Figure 17

Influence of the average particle distance in Y_II standard test blocks on the static mechanical properties

The transition curves of the investigated alloys determined on specimens from lower wall thickness in Charpy impact tests are shown in Figure 18. In all alloys, a wide transition range between ductile fracture behaviour in the upper shelf and brittle fracture behaviour in the lower shelf can be observed. With increasing nodule count, the transition range gets wider. The lower shelf energy (LSE) of alloys MNC and HNC is about 2.5 J, while it is about 1 J in alloys LLNC and LNC. The USE of alloys MNC and HNC is correspondingly 11.5 J, whereas the USE of the LLNC and LNC alloys is between 7 and 8 J. The transition temperature DBTT was obtained by determining the impact energy at half the USE. In alloy LLNC, it is 85 °C. By increasing the nodule count in alloy LNC to 475 1/mm² , the DBTT decreases to 60 °C. In alloy MNC, it is 35 °C, in series HNC 30 °C.

Figure 18

Transition curves from Charpy V-notch impact energy, obtained in low wall thickness (25–30 mm).

The single main effects of the average graphite particle and nodule count on both the upper and lower shelf energy (LSE, USE) as well as on the DBTT can be observed from Figure 19. It can be summarized that the correlations of LSE, USE and DBTT show a higher correlation coefficient of as well as a higher statistical significance when the graphite particle count is considered. Except for the results of the USE, a significant correlation of the average particle count and toughness values could be obtained from the analysis. Figure 20 shows the effect of the average particle size on the Charpy impact energy and transition temperature. Both LSE and USE decrease when the average particle size of the alloy is increased. The DBTT is raised at increasing particle sizes. However, results of the regressions analysis show that only the correlations for DBTT do show a statistical significance. Figure 21 shows analogous correlations for the average particle distance and the characteristic values of the Charpy impact test. However, no statistical significance was determined for these.

Figure 19

Effect of the average graphite particle/ nodule count on the Charpy impact energy and DBTT, obtained in low wall thickness (25–30 mm).

Figure 20

Effect of average particle size on the Charpy impact energy and DBTT, obtained in low wall thickness (25–30 mm).

Figure 21

Effect of the average particle distance on the Charpy impact energy and DBTT, obtained in low wall thickness (25–30 mm).

Discussion

From the spectrometer analyses, it appears that the chemical compositions were analyzed sufficient accuracy. In particular, the Si content could be controlled within a limited range of ± 0.12 wt%. Given the large effect of Si on the mechanical properties, this has to be considered a basic requirement for further comparative analyses. The resulting microstructures are found to be fully ferritic (pearlite content < 3% in low wall thickness) and differ significantly in graphite-phase parameters such as graphite nodule count, in their graphite particle size and the mean particle distance. According to the literature, the single graphite parameters are coupled to each other, as is shown in Figure 9.

In agreement with data from the literature, a clear effect of the graphite phase on the static mechanical properties is shown.^7,29 The effect of the particle count (pc) on the UTS and YS can be described in a simplified way using the following regression functions.

$$ {\text{UTS }}\left[ {{\text{MPa}}} \right] = 0.21{ } \cdot {\text{pc }}\left[ {\frac{1}{{{\text{mm}}^{2} }}} \right] + 452.7\,\,\left( {R - {\text{Sq}}_{{{\text{adj}}.}} = { 78}.{3} \% , \, p \, = \, 0.00{5}} \right) $$

(3)

$$ {\text{YS}}[{\text{MPa}}] = 0.19 \cdot {\text{pc}}\left[ {\frac{1}{{({\text{mm}}^{2} )}}} \right] + 336.8\,\,\left( {R - {\text{Sq}}_{{{\text{adj}}.}} = { 18}.{2} \% , \, p \, = \, 0.00{1}} \right) $$

(4)

Thus, the increase in UTS in Y_II standard test blocks is approximately 21 MPa per 100 1/mm². The YS is raised by about 19 MPa per 100 1/mm², respectively. However, the increase in UTS and YS by an average of 21 and 19 MPa per increase in nodule count by 100 1/mm² is about 40 MPa less compared to data from Orlowicz et al. who studied the effect of the particle count on the UTS in ductile iron with a Si content of 2.5–2.8 wt%.³⁰ Therefore, the effect of the nodule count for high silicon DI on the strength is a factor of 3 times lower, which is attributed to the predominant solution strengthening effect of Si.

$$ {\text{UTS }}\left[ {{\text{MPa}}} \right] = 0.27{ } \cdot {\text{nc }}\left[ {\frac{1}{{{\text{mm}}^{2} }}} \right] + 464.0\,\,\left( {R - {\text{Sq}}_{{{\text{adj}}.}} = { 78}.{1} \% , \, p \, = \, 0.00{5}} \right) $$

(5)

$$ {\text{YS }}\left[ {{\text{MPa}}} \right] = 0.23 \cdot {\text{ nc }}\left[ {\frac{1}{{{\text{mm}}^{2} }}} \right] + 349.4\,\,\left( {R - {\text{Sq}}_{{{\text{adj}}.}} = { 79}.{2} \% , \, p \, = \, 0.00{5}} \right) $$

(6)

$$ {\text{UTS }}\left[ {{\text{MPa}}} \right] = - 2.70{ } \cdot {\text{ p}}_{{{\text{Nod}}.}} \left[ {\text{\% }} \right] + 722.7\,\,\left( {R - {\text{Sq}}_{{{\text{adj}}.}} = { 55}.{1} \% , \, p \, = \, 0.0{34}} \right) $$

(7)

$$ {\text{ YS}}\left[ {{\text{MPa}}} \right] = - 2.55{ } \cdot {\text{p}}_{{{\text{Nod}}.}} \left[ {\text{\% }} \right] + 587.8\,\,\left( {R - {\text{Sq}}_{{{\text{adj}}.}} = { 73}.{6} \% , \, p \, = \, 0.00{8}} \right) $$

(8)

$$ {\text{UTS }}\left[ {{\text{MPa}}} \right] = - 3.10{ } \cdot {\text{pd }}\left[ {{\mu m}} \right] + 635.4\,\,\left( {R - {\text{Sq}}_{{{\text{adj}}.}} = { 96}.{7} \% , \, p \, = { 4}.{3}*{1}0^{{ - {5}}} } \right) $$

(9)

$$ {\text{YS }}\left[ {{\text{MPa}}} \right] = - 2.57{ } \cdot {\text{pd }}\left[ {{\mu m}} \right] + 492.5\,\,\left( {R - {\text{Sq}}_{{{\text{adj}}.}} = { 91}.{6} \% , \, p \, = { 5}.0*{1}0^{{ - {4}}} } \right) $$

(10)

The investigations show a considerable influence of the graphite phase on the toughness properties. The effect of the average particle size (ps) can be described by the logarithmic regression functions Eqns. 11–13.

$$ {\text{DBTT }}\left[ {^\circ {\text{C}}} \right] = 0.10{ } \cdot {\text{ps }}\left[ {{\mu m}^{2} } \right] + 3.5\,\,\left( {R - {\text{Sq}}_{{{\text{adj}}.}} = { 9}0.{5} \% , \, p \, = \, 0.0{32}} \right) $$

(11)

$$ {\text{LSE }}\left[ {\text{J}} \right] = - 0.003{ } \cdot {\text{ps }}\left[ {{\mu m}^{2} } \right] + 3.4\,\,\left( {R - {\text{Sq}}_{{{\text{adj}}.}} = { 62}.{8} \% , \, p \, = \, 0.{133}} \right) $$

(12)

$$ {\text{USE }}\left[ {\text{J}} \right] = - 0.004{ } \cdot {\text{ps }}\left[ {{\mu m}^{2} } \right] + 12.8\,\,\left( {R - {\text{Sq}}_{{{\text{adj}}.}} = { 46}.{3} \% , \, p \, = \, 0.{199}} \right) $$

(13)

Analogous to the effect of the particle size, Eqns. 14–16 illustrate the quantitative impact of the average particle distance (pd).

$$ {\text{DBTT }}\left[ {^\circ {\text{C}}} \right] = 2.47 \cdot {\text{pd }}\left[ {{\mu m}} \right] - 39.6\,\,\left( {R - {\text{Sq}}_{{{\text{adj}}.}} = { 8}0.{1} \% , \, p \, = \, 0.0{69}} \right) $$

(14)

$$ {\text{LSE }}\left[ {\text{J}} \right] = - 0.08{ } \cdot {\text{pd }}\left[ {{\mu m}} \right] + 4.6\,\,\left( {R - {\text{Sq}}_{{{\text{adj}}.}} = { 45}.{2} \% , \, p \, = \, 0.{2}0{3}} \right) $$

(15)

$$ {\text{USE }}\left[ {\text{J}} \right] = - 0.09{ } \cdot {\text{pd }}\left[ {{\mu m}} \right] + 14.2\,\,\left( {R - {\text{Sq}}_{{{\text{adj}}.}} = { 26}.{3} \% , \, p \, = \, 0.{289}} \right) $$

(16)

As shown in Figure 19, the characteristic values of Charpy impact toughness show a higher correlation when considering the graphite particle count. These results are confirmed by studies by Cree et al. The authors demonstrate that the graphite particle count is more correlative compared to the graphite nodule count.³¹ This quantitative influence can be described in a simplified way by the regression equations shown in Eqns. 17–19. The equations indicate that the LSE and USE increase by nearly 1J per 100 1/mm². Therefore, these results are in contrast with studies from Unkic et al. who observed a decrease of the USE at elevated nodule counts.¹¹ However, it must be noted that the influence on the USE is not statistically significant. Furthermore, the DBTT increases by 22 °C per 100 1/mm². These results thus show a good agreement with the data presented in⁹ , where an increase in nodule count of 100 1/mm² leads to a decrease of the DBTT of about 30 °C. However, compared to results from Komatsu et al.⁸, the decrease in DBTT due to nodule count is greater by about 40 °C. However, it should be considered that toughness testing in these studies was carried out on an alloy with 2.4 wt% Si in fracture mechanics tests rather than Charpy impact tests.

$$ {\text{DBTT }}\left[ {^\circ {\text{C}}} \right] = - 0.22 \cdot {\text{pc }}\left[ {\frac{1}{{{\text{mm}}^{2} }}} \right] + 123.6\,\,\left( {R - {\text{Sq}}_{{{\text{adj}}.}} = { 99}.{9} \% , \, p \, = { 5}.0*{1}0^{{ - {4}}} } \right) $$

(17)

$$ {\text{LSE }}\left[ {\text{J}} \right] = 0.008{ } \cdot {\text{pc }}\left[ {\frac{1}{{{\text{mm}}^{2} }}} \right] - 0.6\,\,\left( {R - {\text{Sq}}_{{{\text{adj}}.}} = { 9}0.{8} \% , \, p \, = \, 0.0{31}} \right) $$

(18)

$$ {\text{USE }}\left[ {\text{J}} \right] = 0.009{ } \cdot {\text{pc }}\left[ {\frac{1}{{{\text{mm}}^{2} }}} \right] + 8.0\,\,\left( {R - {\text{Sq}}_{{{\text{adj}}.}} = { 78}.{1} \% , \, p \, = \, 0.0{76}} \right) $$

(19)

The results presented can support manufacturers and customers in evaluating the influence of the graphite phase on the toughness properties of high silicon DI compared to conventional DI alloys. In this way, it enables optimal toughness properties to be utilized for component applications by adjusting the graphite phase in a sufficient way.

Conclusions

In the present study, the graphite phase with focus on the adjusted nodule count of high-silicon DI was systematically varied, and its influence on the toughness properties in the Charpy impact test was determined. Based on these investigations, the results can be summarized as follows:

• 1) The graphite parameters that were studied are closely related to each other. In accordance with expectations, a higher nodule count is accompanied by a lower average nodule distance.

• 2) A critical nodule count of approximately 175 1/mm² could be observed. Below this value, the elongation at fracture decreases rapidly till down to 10% in specimens from Y_II standard test blocks. A side effect due to a different chemical compositions could be excluded. A decreasing nodule count leads to a steadily reducing effect on the strength. A reduction of the nodule count of 100 nodules per mm² results in a decrease of the UTS by approx. 27 MPa and the YS by approx. 23 MPa.

• 3) Related to this, the UTS and YS decrease by an average of 31 and 26 MPa when the particle distance is increased by 10 μm, respectively. For the effect on the elongation at fracture, it can be observed that an average particle distance of 35 μm results in the highest elongation at fracture of 21%. At higher particle distances, the elongation at fracture decreases to about 10%.

• 4) The characteristic values of Charpy impact toughness show a higher and statistical significant correlation when considering the graphite particle count instead of graphite nodule count. Based on the regression analyses, it could be determined that in particular, the transition temperature shows significant correlations with the investigated microstructural parameters.

• 5) It was shown that both the LSE and USE increase with increasing average particle counts. Additionally, the DBTT in Charpy impact tests decreases significantly with higher particle counts. Raising the particle count by about 100 nodules/mm² leads to reduction of the DBTT by about 22 °C. In particular, particle counts below about 400/mm² are considered to be critical for sufficient toughness properties.

Appendix

See Tables

Table 3 Raw Data of Static Mechanical Testing

3,

Table 4 Raw Data of Charpy Impact Tests

4 and

Table 5 Raw Data of Automated Image Analysis (Average Per Image)

5.