1 Introduction

China is the largest coal producer worldwide. The depths of most coal mines in Eastern, Northern, and Northeastern China exceed 600 m (Mazaira et al. 2015; Zhang et al. 2024a). During different periods of geological history, hard and thick rock layers with high strength, thickness, and good integrity were inevitably formed in the strata; they are distributed in Shanxi, Ordos, Shandong, and other mining areas in China (Fig. 1) (Bai et al. 2022). Hard and thick rock strata usually have a thickness exceeding 10 m and a compressive strength of exceeding 60 MPa. Once hard and thick rock strata are broken, a large amount of strain energy is immediately released, inducing strong dynamic disasters such as coal bumps and strong mining-induced earthquakes, which seriously threaten the safety of people’s lives and property (Zhang et al. 2023, 2024b; Xiao et al. 2022, 2023).

Fig. 1
figure 1

Schematic diagram of the strata structure of typical deep coal mine of Ordos mining areas

Full size image

Researchers have proposed various hypotheses and theories aimed at the characteristics of rock stratum movement, including the cantilever beam hypothesis, key stratum theory, masonry beam theory, and thin-plate theory. Among them, the key stratum theory proposed by Qian et al., which unifies the movement of rock strata from the coal seam to the key strata, provides a theoretical basis for studying the formation and destabilisation of the overburden structure (Qian et al. 2010).

Based on key stratum theory, Pang et al. (2021) used numerical simulations to analyse the stress evolution characteristics of the overlying rock strata breakage instability process and revealed the mechanism of rock strata breakage instability. Combining the key stratum theory and plate theory, Song et al. 2011) investigated the distribution characteristics of overlying rock strata breakage during coal mining. Jiang et al. (2014) established a hard and thick rock strata thin-plate mechanical model, deduced the expression formula of the rock strata breaking span, and verified the theoretically deduced rock strata breaking span with that of the actual rock strata with good results. Xu et al. (2019) concluded that the breakage of hard and thick rock strata was the primary reason for strong mining-induced earthquakes and discussed the stress and energy evolution characteristics of the breakage process of hard and thick rock strata.

The focal mechanism of rock mass ruptures has been investigated by numerous researchers. As a method to obtain the information of rock/rock mass rupture moment magnitude, focal mechanism, and stress state, moment tensor inversion is widely used in earthquake, coal mining, hydraulic fracturing, and other fields (Anikiev et al. 2014). Cao et al. (2008) established the equivalent point source model of hard and thick roof fracture vibration to reveal the focal mechanism of hard and thick roof fracture. Chen et al. 2019) used the P-wave inversion method to reconstruct the focal mechanism of mining-induced earthquakes in the Qianqiu coal mine. Rock mass fracture types include shear, shear-tension, and shear compression failures. Using the moment tensor theory, Li et al. (2019) analysed the focal mechanism of a typical huge mountain slip and obtained the failure type and fault plane parameters of the rock mass.

Previous studies have shown that the physical and mechanical properties of hard and thick rock strata of different layers significantly affect the breakage law of hard and thick rock strata. However, these studies primarily used the thin-plate theory to investigate the fracture law of low-position hard and thick rock strata. Moreover, there have been no reports on the fracture mechanisms and laws of high-position hard and thick rock strata. With an increase in coal mining depth, rock mass ruptures are becoming increasingly complicated. Therefore, the source parameters of rock mass rupture must be analysed and the focal mechanism of rock mass rupture during coal mining, which is important for the monitoring and early warning of disasters, must be investigated.

Based on the Volasov’s thick plate and moment tensor inversion theories, this study investigated the characteristics of high-position overburden fracture migration and the law of the focal mechanism of rock mass rupture. This study aimed to provide a reference for safe and efficient coal mining under similar hard and thick rock strata conditions.

2 Engineering background

The Dongtan coal mine is located in Shandong Province, China. The current main coal seam is the 3upper coal seam, with a buried depth of approximately 670 m in No. 6 mining area. The thickness of the 3upper coal seam ranges as 4.12–6.70 m, with an average of 5.41 m. The 63upper 06 panel has a length of 1456.3 m, width of 260 m, and elevation of − 604.5– − 670.3 m, with an average of − 637.4 m (Fig. 2). A full-seam longwall mining method was used. The mining sequence of the panels was as follows: 63upper 04⇒63upper 05⇒63upper 03⇒63upper 06, as shown in Fig. 2. As of March 2023, the 63upper 06 working face had advanced 1050 m.

Fig. 2
figure 2

Location and division of panels of the No.6 mining area in Dongtan coal mine

Full size image

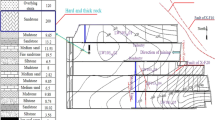
According to key strata theory, three hard and thick rock strata exist above the coal seam and can be divided into three strata: (a) hard stratum 1: Medium sandstone stratum 5.73 m above the 3upper coal seam with a thickness of 30.9 m; (b) hard stratum 2: Fine sandstone stratum 68.46 m above the 3upper coal seam with a thickness of 51.29 m; (c) hard stratum 3: Fine sandstone stratum 119.75 m above the 3upper coal seam with a thickness of 219.22 m (Fig. 3).

Fig. 3
figure 3

Stratigraphic diagram of the lithology of the No. 6 mining area in the Dongtan coal mine (Drilling #170)

Full size image

3 Mechanical behaviours of high position hard and thick rock strata

3.1 Mechanical model

Research shows that the breakage of the main key strata is caused by multiple panel mining (Wang et al. 2016). The primary reason for this is that the panel incline width (b) of panel 63upper 05 panel is considerably smaller than the limit span of the rock beam breakage, and the main key strata generally do not break during the mining of a single panel. Meanwhile, the panel length (a) is greater than the limit span of the rock beam (l1) breakage during the mining process of the panel. The main key strata are generally capable of spanning two or more panels, and the ratio of rock strata thickness to panel length generally does not satisfy the thin-plate requirements. The breaking of the main key strata, both sides of which must be greater than the limit span of the rock beam breakage, is shown in Fig. 4.

Fig. 4
figure 4

Movement of multi panels schematic of hard and thick rock strata

Full size image

During the mining of 63upper 05 panel, the rock strata below the main key strata gradually broke and collapsed. Owing to the overlying rock load, the main key strata were damaged in the roadway position of the panel and remained in a stable state. In the mining process of the 63upper 06 panel, the stress concentration phenomenon occurred at the damage site in the roadway position of the 63upper 05 and 63upper 06 panels. Simultaneously, the overhanging roof length of the main key strata increased, the damage of the main key strata was aggravated, and the state of “simply supported—plastic hinge” was gradually formed (Fig. 5).

Fig. 5
figure 5

Damage schematic of hard and thick rock strata

Full size image

The main key strata were in a sub-equilibrium state after mining the 63upper 05 panel. With the continuous mining of the working face, the main key strata in the state of simply supported edge plastic hinges were gradually transformed into a four-sided simply supported state (Fig. 6).

Fig. 6
figure 6

Formation process of four-sided simply supported edges thick plate

Full size image

According to the plate theory, when the ratio of rock strata thickness to the panel incline width is between 1/100–1/80 and 1/8–1/5, it can be solved using the thin plate theory, as shown in Eq. (1). In contrast, it should be solved using thick plate theory. Calculations showed that the main key strata above the coal seam of 63upper 06 panel satisfied the requirements of the thick-plate theory. Figure 7 shows the mechanical model of hard and thick rock strata.

$$\left( {\frac{1}{100} \sim \frac{1}{80}} \right){ \le }\frac{{h_{1} }}{b}{ \le }\left( {\frac{1}{8} \sim \frac{1}{5}} \right)$$
(1)

where b is the single-panel inclination width (m) (b = 260 m) and h1 is the thickness of the rock stratum (m).

Fig. 7
figure 7

Geometry shape and coordinate of thick plate

Full size image

3.2 Damage evolution characteristics

Based on Volasov’s thick-plate theory, the basic equations for the mechanical model of thick plates with hard and thick rock strata can be obtained as (Eq. 2) (He et al. 2009):

$$\left\{ {\begin{array}{*{20}l} {\frac{2}{5}D\left[ {\left( {1 - \mu } \right)\nabla ^{2} \varphi _{x} + \left( {1 + \mu } \right)\frac{{\partial f}}{{\partial x}} + \frac{1}{2}\frac{\partial }{{\partial x}}\left( {\nabla ^{2} w} \right)} \right] + \frac{2}{3}Gh\left( {\frac{{\partial w}}{{\partial x}} - \varphi _{x} } \right) = 0} \hfill \\ {\frac{2}{5}D\left[ {\left( {1 - \mu } \right)\nabla ^{2} \varphi _{y} + \left( {1 + \mu } \right)\frac{{\partial f}}{{\partial y}} + \frac{1}{2}\frac{\partial }{{\partial y}}\left( {\nabla ^{2} w} \right)} \right] + \frac{2}{3}Gh\left( {\frac{{\partial w}}{{\partial y}} - \varphi _{y} } \right) = 0} \hfill \\ {\frac{2}{3}Gh\left[ {\nabla ^{2} w - f} \right] + q\left( {x,y} \right) = 0} \hfill \\ \end{array} } \right.$$
(2)

where \(E\) is the elastic modulus of rock strata (GPa), μ is Poisson’s ratio, h is the thickness of the rock stratum (m), D is bending stiffness (\(D = Eh^{3} /12\left( {1 - \mu^{2} } \right)\)), G is shear modulus (\(G = E/2\left( {1 + \mu } \right)\)), q is the overburden load (MPa), f is the transverse shear strain (\(f = \partial \varphi_{x} /\partial x + \partial \varphi_{y} /\partial y\)), and w is the deflection of the plate.

Based on the boundary conditions before the initial fracture of the hard and thick strata, the bending moments of the hard and thick rock strata at x = a/2 and y = b′/2 reached their maximum values Mmax (Eqs. 3, 4):

$$\left\{ \begin{gathered} \left. w \right|_{(x = 0,a)} = 0,\left. {\varphi_{y} } \right|_{(x = 0,a)} = 0,\left. {M_{x} } \right|_{(x = 0,a)} = 0 \hfill \\ \left. w \right|_{{(y = 0,b^{\prime})}} = 0,\left. {\varphi_{x} } \right|_{{(y = 0,b^{\prime})}} = 0,\left. {M_{y} } \right|_{{(y = 0,b^{\prime})}} = 0 \hfill \\ \end{gathered} \right.$$
(3)
$$\left\{ \begin{gathered} M_{x} = \frac{D}{5}\sin \frac{{\uppi x}}{a}\sin \frac{{\uppi y}}{{b^{\prime}}} \cdot \left[ {\frac{{q_{11} ({5 \mathord{\left/ {\vphantom {5 {a^{2} + {{4\mu } \mathord{\left/ {\vphantom {{4\mu } {ab^{\prime}}}} \right. \kern-0pt} {ab^{\prime}}}}}} \right. \kern-0pt} {a^{2} + {{4\mu } \mathord{\left/ {\vphantom {{4\mu } {ab^{\prime}}}} \right. \kern-0pt} {ab^{\prime}}}}} + {\mu \mathord{\left/ {\vphantom {\mu {b^{\prime}}}} \right. \kern-0pt} {b^{\prime}}}^{2} )}}{{D\uppi ^{2} \left( {{1 \mathord{\left/ {\vphantom {1 {a^{2} + {1 \mathord{\left/ {\vphantom {1 {b^{{\prime}{2}} }}} \right. \kern-0pt} {b^{{\prime}{2}} }}}}} \right. \kern-0pt} {a^{2} + {1 \mathord{\left/ {\vphantom {1 {b^{{\prime}{2}} }}} \right. \kern-0pt} {b^{{\prime}{2}} }}}}} \right)^{2} }} + \frac{{6q_{11} \mu ({1 \mathord{\left/ {\vphantom {1 {b^{\prime}}}} \right. \kern-0pt} {b^{\prime}}}^{2} - {1 \mathord{\left/ {\vphantom {1 {ab^{\prime}}}} \right. \kern-0pt} {ab^{\prime}}})}}{{5Gh\left( {{1 \mathord{\left/ {\vphantom {1 {a^{2} + {1 \mathord{\left/ {\vphantom {1 {b^{{\prime}{2}} }}} \right. \kern-0pt} {b^{{\prime}{2}} }}}}} \right. \kern-0pt} {a^{2} + {1 \mathord{\left/ {\vphantom {1 {b^{{\prime}{2}} }}} \right. \kern-0pt} {b^{{\prime}{2}} }}}}} \right)}}} \right] \hfill \\ M_{y} = \frac{D}{5}\sin \frac{{\uppi x}}{a}\sin \frac{{\uppi y}}{{b^{\prime}}} \cdot \left[ {\frac{{q_{11} ({5 \mathord{\left/ {\vphantom {5 {a^{2} + {{4\mu } \mathord{\left/ {\vphantom {{4\mu } {ab^{\prime}}}} \right. \kern-0pt} {ab^{\prime}}}}}} \right. \kern-0pt} {a^{2} + {{4\mu } \mathord{\left/ {\vphantom {{4\mu } {ab^{\prime}}}} \right. \kern-0pt} {ab^{\prime}}}}} + {\mu \mathord{\left/ {\vphantom {\mu {b^{\prime}}}} \right. \kern-0pt} {b^{\prime}}}^{2} )}}{{D\uppi ^{2} \left( {{1 \mathord{\left/ {\vphantom {1 {a^{2} + {1 \mathord{\left/ {\vphantom {1 {b^{{\prime}{2}} }}} \right. \kern-0pt} {b^{{\prime}{2}} }}}}} \right. \kern-0pt} {a^{2} + {1 \mathord{\left/ {\vphantom {1 {b^{{\prime}{2}} }}} \right. \kern-0pt} {b^{{\prime}{2}} }}}}} \right)^{2} }} + \frac{{6q_{11} \mu ({1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0pt} a}^{2} - {1 \mathord{\left/ {\vphantom {1 {ab^{\prime}}}} \right. \kern-0pt} {ab^{\prime}}})}}{{5Gh\left( {{1 \mathord{\left/ {\vphantom {1 {a^{2} + {1 \mathord{\left/ {\vphantom {1 {b^{{\prime}{2}} }}} \right. \kern-0pt} {b^{{\prime}{2}} }}}}} \right. \kern-0pt} {a^{2} + {1 \mathord{\left/ {\vphantom {1 {b^{{\prime}{2}} }}} \right. \kern-0pt} {b^{{\prime}{2}} }}}}} \right)}}} \right] \hfill \\ \end{gathered} \right.$$
(4)

where a is the panel length (m) and b′ is the multipanel incline width (m).

The maximum tensile stress σmax existed on the lower surface of the hard and thick rock strata (Eq. (5)):

$$\sigma_{max} = \frac{{6M_{max} }}{{h^{2} }}$$
(5)

As mining activities advance, the relationship between the suspended roof span of the main key strata and the multipanel inclination width, as shown in Eq. (6).

$$b_{1} = b^{\prime } { - 2}\sum H \cot \alpha$$
(6)

where b′ is the multi panel incline width (m) (b′ = 520 m), b1 is the ultimate suspended roof span of main key strata (m), h is the thickness of the rock stratum (m), ΣH is the distance between hard and thick rock strata and coal seam (m), and α is angle of rupture of the overburden (°), where the value of α is generally 70°.

The calculation results indicate that the ultimate suspended roof span (b1) of the main key strata was 432.8 m.

When the maximum tensile stress σmax reached the ultimate tensile stress σt of rock strata, bending tensile failure occurred in the hard and thick rock strata, that is (Eq. (7)):

$$\sigma_{max} = \sigma_{t} = \frac{{6q_{11} (5/a^{2} + {{4\mu } \mathord{\left/ {\vphantom {{4\mu } {ab^{\prime } }}} \right. \kern-0pt} {ab^{\prime } }} + \mu /b^{\prime 2} )}}{{5\uppi ^{2} h^{2} \left( {1/a^{2} + {1 \mathord{\left/ {\vphantom {1 {b^{\prime 2} }}} \right. \kern-0pt} {b^{\prime 2} }}} \right)^{2} }} + \frac{{6q_{11} \mu (1/b^{\prime 2} - 1/ab^{\prime } ))}}{{25\left( {1 - \mu } \right)\left( {1/a^{2} + {1 \mathord{\left/ {\vphantom {1 {b^{\prime 2} }}} \right. \kern-0pt} {b^{\prime 2} }}} \right)}}$$
(7)

where h is the thickness of the main key strata (h = 219.22 m), q is the overburden load (the overburden load is calculated according to the equivalent load of the buried depth of 338.63 m, i.e., q = 8.72 MPa), μ is the Poisson's ratio of rock strata (μ = 0.26), b′ is the ultimate suspended roof span of hard and thick rock strata (m) (b′ = 432.8 m), and σt is the tensile strength (σt = 5.41 MPa).

By substituting these parameters into Eq. (7), the ultimate rupture length (a) of the main key strata was obtained as 314 m.

When the thick plate a = b′, a square “O-X” fracture type occurs in the high position hard and thick strata (Eq. 8):

$$a =\uppi h\sqrt {\frac{{2\sigma_{t} }}{3q(1 + \mu )}}$$
(8)

As evident, when a = b′ = 394.5 m, the overburden fracture form was square O-X fracture type. With an increase in the mining distance, the overburden fracture formed a vertical O-X fracture type (Fig. 8).

Fig. 8
figure 8

Evolution diagram of overburden fracture type

Full size image

3.3 Energy release and migration

According to the principle of energy conservation, the deformation process of the key layer before breaking involved the gradual accumulation of strain energy. The total energy (\(E\)) released by the fracture of the key stratum is shown in Eq. (9) (Zhou et al. 2019). The breeding and occurrence of mining-induced earthquakes are processes of gradual accumulation and sudden release of energy. The specific process is as follows. Before coal mining, under the influence of the primary rock stress, the overlying strata have a certain elastic strain energy. ⇒ In the process of coal mining, the direct roof collapses, the overlying strata overhanging roof and the elastic energy of the overlying strata continues to be accumulated and becomes larger. ⇒ The coal face is further advanced, the overlying strata overhanging roof length increase continuously, and the overlying strata continues to accumulate energy. ⇒ When the overlying strata overhanging the roof length reaches its limit, the energy released from the overlying strata fracture spreads to the surroundings.

$$\left\{ \begin{gathered} E = \sum\limits_{i}^{n} {(E_{Gi} + E_{Vi} + E_{Wi} + E_{Zi} )} \hfill \\ E_{Gi} = m_{i} gH_{i} = \rho abh_{1} gH_{i} \hfill \\ E_{Vi} = \frac{{(1 - 2\mu_{i} )(1 + 2\lambda_{i} )^{2} \gamma_{i}^{2} h_{i}^{2} }}{{6E_{i} }} \hfill \\ E_{Wi} = \frac{{(1 - 2\mu_{i} )^{2} \gamma_{i}^{2} h_{i}^{2} }}{{6G_{i} (1 - \mu_{i} )^{2} }} \hfill \\ E_{Zi} = \xi E_{V(i - 1)} \hfill \\ \end{gathered} \right.$$
(9)

where \(E\) is the total energy released by the rupture of the key stratum (J), \(E_{Gi}\) is the gravitational potential energy (J), \(E_{Vi}\) is the volumetric strain energy stored in each rock stratum (J), \(E_{Wi}\) is the bending deformation energy of each rock stratum (J), \(E_{Zi}\) is the strain energy generated by the horizontal stress transferred from the fractured rock strata below the key stratum (MPa), \(g\) is the gravitational acceleration (m s−2), \(\lambda_{i}\) is the ratio of the average horizontal principal stress to the vertical principal stress, \(m_{i}\) is the mass of each rock stratum (kg), \(H_{i}\) is the descending height of each rock stratum (m), \(\mu_{i}\) is the Poisson’s ratio of each rock stratum; \(\gamma_{i}\) is the bulk density of each rock stratum (N m−3); \(h_{i}\) is the thickness of each rock stratum (m), \(G_{i}\) is the shear modulus of each rock stratum (MPa), \(\rho\) is the rock strata density (kg/m3), a is the panel length (m), b is the panel incline width (m), \(E_{V(i - 1)}\) is the strain energy transferred from the i-1st key stratum (J), and \(\xi\) is the strain energy transfer coefficient.

Most of the elastic energy released by rock strata fractures is in the form of heat or acoustic emissions (Zhang et al. 2023). The energy that reaches the working face \(E^{\prime }\) can be calculated using Eq. (10):

$$E^{\prime } = (0.01 - 0.001)El^{ - \beta }$$
(10)

where \(l\) is the distance from the epicentre to the working face (m) and \(\beta\) is the energy attenuation coefficient (\(\beta { \ge }1\)), which is related to the energy of the epicentre and the properties of the rock strata.

Figure 9 shows the law of energy propagation for different attenuation coefficients. Based on a previous study, E = 109 J generated by the instantaneous breakage of the main key strata was considered as an example. When the energy attenuation coefficient β was 1, the energy transmission distance reached 110 m, and the energy attenuation arriving at the coal face was 9.1 × 104 J (E < 105 J). When the energy attenuation coefficient β was 1.5, the energy propagation distance reached 30 m, and the energy attenuation arriving at the coal face was 6.1 × 104 J. When the energy attenuation coefficient β was 2, the energy propagation distance reached 20 m, and the energy attenuation arriving at the coal face was 2.5 × 104 J. When the energy attenuation coefficient β was 2.5, the energy attenuation arriving at the coal face was less than 105 J, which did not satisfy the minimum energy required for microseismic occurrence (E = 105 J). With an increase in the energy attenuation coefficient, the propagation distance required for the energy to reach the coal face to decrease to less than 105 J gradually decreased. After the instantaneous breakage of the main key strata, its range of influence was approximately 110 m. This is consistent with a previous conclusion based on field data that strong mining-induced earthquakes are mainly concentrated in hard and thick rock strata 100–290 m above the coal seam (Liang et al. 2021).

Fig. 9
figure 9

The law of energy propagation under different attenuation coefficients

Full size image

4 Focal mechanisms of strong mining-induced earthquakes

4.1 Mining-induced earthquakes distribution

A total of 488 large-energy (E ≥ 105 J) mining-induced earthquakes occurred during mining in the No. 6 mining area of the Dongtan coal mine (Fig. 10). Among these, 64 large-energy mining-induced earthquakes occurred in the 63upper 03 panel, whereas 131 and 158 occurred in the 63upper 04 and 63upper 05 panels, respectively (Table 1). Since February 2020, more than 135 large-energy mining-induced earthquakes have occurred in panel 63upper 06. Large energy mining-induced earthquakes seriously threaten and restrict safe and efficient coal production.

Fig. 10
figure 10

Mining-induced earthquakes distribution with energy of 105J and above during the mining period of the mined panels in No.6 mining area: a 63upper04 panel; b 63upper05 panel; c 63upper06 panel

Full size image
Table 1 Mining-induced earthquakes statistics for 63upper 03–06 panels in No. 6 mining area
Full size table

As shown in Fig. 11, a large amount of strain energy was also gradually concentrated in the high-position rock strata, which were mainly distributed in the areas of the sub-key and main key strata. However, when the coal seam in the 63upper 06 panel was exploited, minor earthquakes occurred both in the overlying rock of the panel and the adjacent goaf (Fig. 10). Most of the strong-mining-induced earthquakes had energies greater than 6 × 105 J, which were related to the synergistic rupture of multiple key strata.

Fig. 11
figure 11

Distribution of strong mining-induced earthquakes during mining. a 2020.4; b 2020.6; c 2020.11; d 2021.1; e 2021.2; f 2021.5

Full size image

Previous research has demonstrated a correlation between the synergistic fracture movement of multiple key strata and underground mining spaces (Zhang et al. 2023). During the mining process of the 63upper 06 panel, the movement of the rock strata above the coal seam was inevitably affected by the neighbouring working face that was mined in the previous period (i.e., 63upper 03, 63upper 04, and 63upper 05 panels) and formed a certain scale of the overhanging roof structure. Continuous mining of the 63upper 06 panel will inevitably lead to fracture and damage to the overlying strata of the coal seam and further development of the overhanging roof, resulting in a gradual increase in underground mining space.

The primary reason for this is that the existing spatial equilibrium structure in the adjacent goaf was broken because of the influence of the mining disturbance on the working face. The existing spatial equilibrium structure in the adjacent goaf was broken because of the influence of mining disturbances on the working face (He et al. 2021). Research has shown that the connection between adjacent panels depends on the coal pillar width between them. A coal pillar width exceeding 20 m can effectively isolate the overburden movement of the two panels (Yu 2016).

Only a 3.5 m narrow coal pillar was reserved between the 63upper05 and 63upper06 panels. Therefore, changes in the overburden structure and rock mass stress state of the goaf carry a risk of inducing mine earthquakes. The change in the overburden structure in the goaf cause relative movement between rock blocks with insufficient collapse. However, the scope of the suspended rock strata gradually increases, and the overlying rock strata are broken with the continuous advancement of the working face (Mu et al. 2013; Zhang et al. 2019).

4.2 Criterion of focal mechanisms of strong mining-induced earthquakes

The focal mechanism is a physical quantity that describes the mechanical process of a source during a mining-induced earthquake (Drzewiecki et al. 2008). Through an analysis of the focal mechanism of mining-induced earthquakes, the mechanism of mining-induced earthquakes can be explained (Liu et al. 2023).

Because the moment tensor cannot directly reflect the source rupture type, the moment tensor M was decomposed into a double-couple component (MDC), an isotropic component (MISO), and a compensated linear vector dipole component (MCLVD). The magnitudes of the MISO, MDC, and MCLVD components can be expressed using the eigenvalues of the moment tensors M, M1, M2, and M3 (M1 ≥ M2 ≥ M3), respectively (Eq. 11) (Young et al. 1992).

$$\left\{ {\begin{array}{*{20}l} {M_{{{\text{ISO}}}} = \frac{{M_{1} + M_{2} + M_{3} }}{3}} \\ {M_{{{\text{DC}}}} = \frac{{M_{1} - M_{3} - \left| {M_{1} + M_{3} - 2M_{2} } \right|}}{2}} \\ {M_{{{\text{CLVD}}}} = \frac{{2(M_{1} + M_{3} - 2M_{2} )}}{3}} \\ \end{array} } \right.$$
(11)

Based on the moment tensor theory, the source rupture type criterion was combined while considering the tensile and compressive cases, and the proportions of MDC, MISO, and MCLVD components were calculated. The proportions are represented by PDC, PISO, and PCLVD, respectively (see Eq. (12)).

$$\left\{ {\begin{array}{*{20}l} {P_{{{\text{ISO}}}} = \frac{{M_{{{\text{ISO}}}} }}{{\left| M \right|}} \times 100\% } \hfill \\ {P_{{{\text{DC}}}} = \frac{{M_{{{\text{DC}}}} }}{{\left| M \right|}} \times 100\% } \hfill \\ {P_{{{\text{CLVD}}}} = \frac{{M_{{{\text{CLVD}}}} }}{{\left| M \right|}} \times 100\% } \hfill \\ {\left| M \right| = \left| {M_{{{\text{ISO}}}} } \right| + M_{{{\text{DC}}}} + \left| {M_{{{\text{CLVD}}}} } \right|} \hfill \\ \end{array} } \right.$$
(12)

where |M|, |MISO|, and|MISO|are the absolute values of M, MISO, and MCLVD, respectively.

Accordingly, the source rupture types were categorised into five types: pure shear failure type (PDC ≥ 60%), pure tensile failure type (PDC ≤ 40% and PISO > 0), pure compression failure type (PDC ≤ 40% and PISO < 0), shear-tensile failure type (40% < PDC < 60% and PISO > 0), and shear-compression failure type (40% < PDC < 60% and PISO < 0) (Fig. 12).

Fig. 12
figure 12

Criterion of focal mechanisms of mining-induced earthquakes (normal vector n and slip vector v of focal plane) (Yang et al. 2023)

Full size image

4.3 Source rupture types of mining-induced earthquakes

As this study analysed the focal mechanism of mining-induced earthquakes, only the results of the source parameters and moment tensor inversion calculation parameters of strong mining-induced earthquakes are described briefly. The process of obtaining the source and moment tensor inversion calculation parameters for strong mining-induced earthquakes can be found in Reference Wu et al. (2023).

Statistical results of corner frequency f0, seismic moment M0, moment magnitude MW, focal radius R, stress drop ∆σ, apparent stress σa, and local magnitude ML of certain strong mining-induced earthquakes on the 63upper 06 panel are presented in Table 2. The calculation parameters for the moment tensor inversion are listed in Table 3.

Table 2 Statistics of source parameters and moment magnitude
Full size table
Table 3 Calculation parameters of the moment tensor
Full size table

Six components (M11, M12, M13, M22, M23, M33) and three eigenvalues (M1, M2, M3) of the moment tensor were computed using MATLAB. Table 4 lists the results of the moment tensor calculations for the 12 strong-mining-induced earthquakes.

Table 4 Calculation results of the moment tensor
Full size table

Using Eq. (12), the proportions of MISO, MDC, and MCLVD components of the 12 mining-induced earthquakes were calculated (Fig. 13). The focal mechanism of the mining-induced earthquake was determined and expressed in the form of a beach ball, as presented in Table 5.

Fig. 13
figure 13

Moment tensor proportions of each component

Full size image
Table 5 Focal mechanisms of strong mining-induced earthquakes in 63upper06 panel
Full size table

As shown in Table 5, there were four mining-induced earthquake source rupture types: pure compression, pure shear, tension-shear, and shear-compression ruptures. The results showed that the pure shear rupture type of mining-induced earthquakes had the highest percentage. This indicates that the rock strata slid along the fracture joint surface under mining disturbance and released a large amount of strain energy to induce a strong mining-induced earthquake. This is consistent with the conclusion of Cao (2009) based on microseismic monitoring data of the Baodian coal mine; that is, the strain energy released from the shear fracture of the rock strata during mining is located above 106 J. The occurrence of the fracture surface of mining-induced earthquakes, including strike angle φ, dip angle δ, and rake angle θ, as shown in Table 6. As shown in Fig. 14, the rupture plane dip angle δ of shear rupture was generally within 15°, while the rupture plane dip angle δ of compression rupture was larger, and the largest rupture plane dip angle δ was 75.42°.

Table 6 The occurrence of the fracture surface of strong mining-induced earthquakes in 63upper 06 panel
Full size table
Fig. 14
figure 14

Occurrence and distribution of fracture surface

Full size image

Figure 15 shows the source rupture type and the distribution of mining-induced earthquakes occurring at the 63upper 06 panel. The source rupture types of the mining-induced earthquakes were primarily pure shear and shear-compression failure types, which were mainly distributed in the goaf behind the working face. This is owing to the bearing effect of the coal pillar, which prevents certain of the rock strata from collapsing in time. As the face continued to advance, the overhanging roof area of the unbroken rock strata above the coal seam gradually increased, resulting in an increase in the load on the unbroken rock strata below. Simultaneously, combined with the epicentre location of the strong mining-induced earthquake and the coal mining distance, the “2020.07.12 mining-induced earthquake (E = 8.38 × 105 J)” was induced by the initial fracture of the main key strata (i.e., mining distance 315 m and the source rupture type was shear-compression). Therefore, the mutual misalignment and slippage of the rock strata induced several pure shear and shear- compression failure-type events.

Fig. 15
figure 15

Distribution and source rupture type of mining-induced earthquakes

Full size image

5 Conclusions

Based on microseismic monitoring technology combined with the theory of moment tensor inversion, the characteristics of overburden fractures and the focal mechanism of earthquakes induced during coal mining were investigated. The main conclusions are as follows:

  1. (1)

    Hard and thick rock strata are difficult to break under single-panel mining conditions because of their high thickness and strength of the rock strata. The breakage of hard and thick rock strata is caused by multi-panel mining, which releases a large amount of strain energy.

  2. (2)

    Based on Volasov's thick-plate theory, the theoretical calculation showed that the initial fracture span of the main key strata was 314 m, which is consistent with the actual mining distance of the working face. This verified that strong mining-induced earthquakes were induced by the initial fracture of the main key strata.

  3. (3)

    Based on the moment tensor inversion theory, the source rupture types of strong mining-induced earthquakes during mining were inverted. Most of the source rupture types of strong mining-induced earthquakes were dominated by the shear failure type, the dip angle of the focal fracture surface of the shear failure type is generally distributed within 15°.