1 Introduction

The compressive strength is defined as the resistance to failure under the action of compressive forces. It is an essential geomechanical parameter in many areas such as the exploration and development of minerals and fossil fuels, the evaluation of engineering disasters, the geotechnical investigation, as well as the civil infrastructures such as urban underground spaces, nuclear facilities, tunnels, high-rise buildings, and underground gas storage sites (Escartín et al. 2008; Yagiz 2009; Huang et al. 2012; Gullu and Hazirbaba 2010; Haimson 2011; Kapang et al. 2013; Rabah et al. 2014; Rohmer et al. 2016; Wang et al. 2020). Although the laboratory uniaxial or triaxial point load measurements can provide reliable compression strength data (Tsiambaos and Sabatakakis 2004), are time consuming and expensive (Negara et al. 2017). Therefore, it is imperative to finding an economic and convenient method to predict the compressive strength at the in-situ condition. The prediction is difficult since they are too many influential factors to be considered due to the fact that the rock is basically a poroelastic material, including mineralogical compositions, diagenetic process, bedding inclination, sedimentary environments, and pore fluids (Meng et al. 2006; Forquin et al. 2010; Zhao et al. 2012; Maleki and Bayat 2012; Pan et al. 2013; Luo et al. 2014; Zhong et al. 2014; Lisabeth and Zhu 2015; Ündül 2016; Dessouki et al. 2016; Peng et al. 2017; Fakir et al. 2017; Lou et al. 2018; Tang 2018; Yin and Yang 2018; Wang et al. 2019; Gharechelou et al. 2020). Pseudo-triaxial compression test is an experimental method that simulates the axisymmetric stress state by applying radial and circumferential stresses to replicate the stress conditions of underground materials.This experimental method is highly valuable for investigating the mechanical properties of rocks.

The well logging data provides a reliable way to reach the aim with respect to the drillability of a well (Tokle et al. 1986; Onyia 1988; Khaksar et al. 2009; Kumar and Rao 2012). Previous studies showed that petrophysical properties such as electrical, acoustic, and radioactive parameters measured by downhole well logging tools are related with the rock’s compressive strength, and can be used to obtain the compressive strength. These methods can be classified as: (1) Direct regressions with acoustic velocity, resistivity, density, as well as radioactive intensity (Chang 2004; Chang et al. 2006; Olea et al. 2008; Sharma et al. 2010; Najibi et al. 2015; Xu et al. 2016; Abbas et al. 2018); (2) Indirect regressions with some geological and formation parameters interpreted from well logging data such as porosity, shale content, water saturation, surface area, grain size, and elastic modulus (Talesnick et al. 2001; Agustawijaya 2007; Nadah et al. 2013; Dewhurst et al. 2015; Silva et al. 2015; Kitamura and Hirose 2017; Yang et al. 2017; Farrokhrouz and Asef 2017; Hashiba et al. 2019); (3) Statistical or machine learning techniques such as support vector regression, grey forecasting model, genetic algorithm, artificial neural network, and gene expression programming (Rafiai and Jafari 2011; Rabbani et al. 2012; Cabalar et al. 2012; Liu et al. 2015; Zingg et al. 2016; Babanajad et al. 2017; Asadi 2017; Hassanvand et al. 2018; Vapnik et al. 2018; Kandiri et al. 2020). However, these methods mentioned above have obvious deficiencies: (1) The empirical equations are developed in terms of specific study and rock type, which are strongly lithological dependent; (2) The precise petrophysical parameters such as porosity, mineral content, and surface area are very difficult to obtain in unconventional formations such as gas shale and tight sand; (3) The influence of the grain size, microstructure, pore geometry, and pore size distribution on the compress strength is still not completed investigated (Forquin et al. 2008; Heap et al. 2014; Baud et al. 2014; Shen and Shao 2016; Bubeck et al. 2017; Griffiths et al. 2017; Farid et al. 2017).

NMR measurement uses the established CPMG pulse sequence to obtain the transverse T2 relaxation time distribution. Provide sensitivity to pore geometry or fluid phase (i.e. oil, brine and gas) when hydrogen-containing liquid is present.The low field nuclear magnetic resonance (NMR) technique is featured as lithology-independent and non-invasive, which provides formation properties such as porosity, permeability, fluid saturation, and pore size distribution. The low field NMR measurement can be performed both in laboratory analysis and in field exploration. It is more convenient for the core-log calibration compared with other pore geometry characterization methods such as scanning electron microscopy (SEM) and X-ray computed tomography (X-CT) (Lou et al. 2018; Heap et al. 2014; Farid et al. 2017; Yang et al. 2019). This method has been applied to study rock’s elastic properties, geomechanical behaviors, as well as the strength and deformation characteristics (Zhai et al. 2017; Yang et al. 2018; Li et al. 2019; Ge et al. 2020). The aim of the research is to investigate the relationship between the pore size distribution and the compressive strength of the tight reservoir using the NMR measurement, to recognize the contribution of different pore ranges on the rock’s strength characteristics. In additional, the conventional parameters such as porosity, mineral content, static and dynamic elastic modulus, as well as acoustic velocity are also measured during the experiment. We hope the research finding can provide more comprehensive recognitions on the impact of the compressive strength besides the rock matrix.

2 Materials and experiments

2.1 Geological background and pretreatment

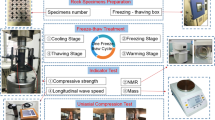
Mahuangshan area is belonged to the Yanchi County, Ningxia Hui autonomous region of China, as seen in Fig. 1. It is located in the central Tianhuan Depression of Ordos basin. Chang 6 Formation is the main oil production reservoir with the thickness ranges from 80 to 110 m. It is a typical delta deposit, developed mainly with grey-green fine grain sandstone, siltstone, and dark mudstone. 12 samples from two wells are collected for our experiments. These samples are reshaped and polished to cylindrical plungers with the diameter of approximate 2.5 cm and the length of 4.5–5 cm. They are put in to an oil-cleaning instrument at the temperature of 90 centigrade for 10 days to remove the remnants of the original fluids and the invaded drilling mud. Then, they are moved to an oven with the temperature and time of 95 centigrade and 24 h, respectively, to ensure that there is no fluid in the pore space. We measure the density, gas filled porosity, and gas permeability for these dried samples. They are performed by XP205 analytical balance, UltraPoreTM-300 helium pycnometer system (Corelab Incorporation), and UltraPeamTM-400 helium permeability system (Corelab Incorporation). Next, they are saturated with sodium chloride solution with the salinity of 90 g/L, which is equivalent with the formation water. It is performed by an auto-saturating container, with the saturating duration and confining pressure of 48 h and 20 MPa, to ensure the completely saturation state. The water saturated porosity is obtained using the Archimedes' principle. Acoustic velocities, NMR relaxation spectrums are conducted for fully saturated samples. NMR spectrums of irreducible water saturated samples are also collected. They are saturated again to conduct the pseudo-triaxial compression test. Lastly, they are crushed into powders for X-ray diffraction (XRD) analysis by AXS D8 advance X-Ray diffractometer (Bruker Incorporation). Types and contents of minerals and clays can be extracted easily.

Fig. 1
figure 1

Location, tectonic division and stratigraphic sequence division of the Triassic Yanchang Formation of Mahuangshan area in the Ordos Basin

Full size image

2.2 Low field NMR measurement

We use MARAN-II ultra-rock spectrometer (Oxford Instrument Incorporation) with an approximate main frequency of 2 MHz, to perform NMR measurements. The experiments are conducted in CNPC key well logging laboratory. To ensure the maximal acquisition of all hydrogen-related signals and the data quality, the acquisition parameters are as follows: the waiting time is 6 s, the echo spacing is 0.2 ms, the of scan number is 256, the receiving gain is 80%, and the echo number is 8192. The pulse sequence used is the conventional Carr-Purcell-Meiboom-Gill (CPMG) pulse sequence. The measured decaying signals are then inverted into the transversal relaxation (T2) spectrums with the WinDXP software package.

As is known, the low field NMR measures the transversal relaxation of the spins in porous rocks, where the total signal intensity or the spectrum amplitude can be calibrated to the porosity of the sample. Details on the workflow of the calibration were addressed in many articles (Ge et al. 2023; Xu et al. 2015; Xiao et al. 2012). In our measurement, we used the standard samples with known porosity values to establish the calibration equation between the porosity and the normalized initial echo amplitude. Then, the porosity of the real core samples can be obtained conveniently. The linear calibration equation is expressed as,

$$\phi_{NMR} = m \times S + n$$
(1)

where ϕNMR is the porosity calibrated by the NMR measurement; S is the normalized initial echo amplitude by the CPMG pulse sequence; m and n are calibration constants.

Besides the porosity, the cutoff value of the transversal relaxation time (T2c) is also a very important parameter obtained by the low field NMR measurement. It is generally used to divide the entire T2 spectrum into two categories. The fluids in pores with T2 value higher than T2c are movable and vice versa. The parameter is often obtained by the comparison between the fully saturated T2 spectrum and the irreducible saturated T2 spectrum. details on the cutoff value were addressed by many authors (Ge et al. 2015; Chen et al. 2023; Testamanti and Rezaee 2017).The bound water saturation in core samples refers to the percentage of water in the rock that is immobilized because it is trapped by the particles or mineral surfaces of the rock. This portion of water cannot flow freely and constitutes the non-mobile water within the total porosity. The movable water in the core can be separated and only bound water can be left in the core by centrifugal experiment at a certain speed on the completely saturated water sample.Therefore, the bound water saturation can be calculated by the nuclear magnetic experiment data after completely saturated water and centrifugation.

2.3 The pseudo-triaxial compression and the acoustic measurement

The pseudo-triaxial compression tests were performed by Autolab 1500 (New England Research Incorporation) in CNPC key well logging laboratory. The confining pressure is 39 MPa, and the temperature is 30 degrees Celsius. The axial stress, axial strain and radial strain are recorded during the pressure loading process. Therefore, the static elastic parameters such as Young’s modulus, the shear modulus, the bulk modulus, the Poisson’s ratio, as well as the compressive strength can be computed by Chinese National Standard ‘Methods for determining the physical and mechanical properties of coal and rock-Part 9: Methods for determining the triaxial strength and deformation parameters of coal and rock (GB/T 23561.9–2009).

The dynamic elastic parameters such as the Young’s modulus, shear modulus, bulk modulus, Poisson’s ratio are computed by the acoustic velocities and the density. There are expressed as follows,

$$E_{d} = \frac{{\rho V_{s}^{2} \left( {3V_{p}^{2} - 4V_{s}^{2} } \right)}}{{V_{p}^{2} - V_{s}^{2} }}$$
(2)
$$S_{d} = \rho V_{s}^{2}$$
(3)
$$V_{d} = \rho \left( {V_{p}^{2} - \frac{{3V_{s}^{2} }}{4}} \right)$$
(4)
$$P_{d} = \frac{{V_{p}^{2} - 2V_{s}^{2} }}{{2\left[ {(V_{p}^{2} - V_{s}^{2} )} \right]}}$$
(5)

where Vp and Vs are compressive velocity and shear velocity, respectively; ρ is the density of the rock.

3 Results and discussion

3.1 Basic petrophysical properties

The basic petrophysical parameters are shown in Table 1 and Fig. 2. It is seen that the gas filled porosity ranges from 4% to 15.55%, and the gas permeability ranges from 0.04mD to 0.96mD, lower than conventional reservoirs. The permeability is generally increased with the porosity, but simple regression is difficult to fitting the permeability. The brine saturated porosity, NMR calibrated porosity is generally in accordance with the gas filled porosity, indicating that the pores are fully saturated with water and good performance of NMR measurements. In additional, the compressive wave (P wave) velocity, the shear wave (P wave) velocity, and the bulk density show favorable linear relationships with the porosity, indicating that the velocity and density for the rock matrix is stable.

Table 1 Basic petrophysical parameters for these samples
Full size table
Fig. 2
figure 2

Porosity comparisons and their relationships with permeability, acoustic velocity, and density

Full size image

Figure 3 gives the absolute content of minerals and clays observed by XRD analysis. It is seen that the rock matrix is mainly composed by quartz, K-feldspar, plagioclase, and clay, but their contents vary broadly. Moreover, the clay is mainly composed by illite–smectite mixed layer and chlorite. Due to the heterogeneous development of these minerals, it is difficult to obtain their contents and spatial distribution via conventional well logging data. The detailed experiment results of the mineralogical and clay distributions are shown in Tables 2 and 3, respectively.

Fig. 3
figure 3

Distribution of minerals and clays observed by XRD analysis (Q quartz, F K-feldspar, P plagioclase, C calcite, D dolomite, Py pyrite, Cl clay, I/S illite–smectite mixed layer, I illite, K kaolinite, Ch chlorite)

Full size image
Table 2 Mineralogical composition for these samples
Full size table
Table 3 Absolute clay composition for these samples
Full size table

3.2 NMR T2 spectrums

Figure 4 show NMR spectrums for samples at different saturating states. It is seen that most spectrums for fully water saturated samples are mono-modal distributed but the peak position ranges from 4 to 100 ms. The shape of spectrums for irreducible water saturated samples is similar to fully water saturated samples and the left part remains unaltered, whereas the right part is decreased. It is easy to interpret since the low relaxation time is corresponded to the small pore radius. Table 4 summarized the geometric mean (T2gm) and the arithmetic mean (T2am) of fully water saturated and irreducible water saturated samples, the cutoff value (T2c), the movable water saturation (Swm), as well as the irreducible water saturation (Swi). We can conclude that T2am is positively correlated with T2gm for samples under the fully saturated state. However, there is no obvious correlation between T2am and T2gm for samples under the irreducible water saturated state. T2c is generally lower than 13 ms and ranges from 3 to 13 ms, revealing that a dynamic value is more reasonable.

Fig. 4
figure 4figure 4

NMR T2 spectrums for samples under the fully water saturated state and the irreducible water saturated state

Full size image
Table 4 NMR parameters for these rock samples
Full size table

It is should be noted that both the geometric mean (T2gm) and the arithmetic mean (T2am) are expressed as,

$$T_{2gm} = \sqrt[{\sum\limits_{i = 1}^{p} {f_{i} } }]{{\prod\limits_{i = 1}^{p} {T_{2i}^{{f_{i} }} } }}$$
(6)
$$T_{2am} = \frac{{\sum\nolimits_{i = 1}^{p} {T_{2i} f_{i} } }}{{\sum\nolimits_{i = 1}^{p} {f_{i} } }}$$
(7)

where fi is the amplitude for the corresponding T2i; p is the total number of the T2 spectrum.

Physically, the geometric mean is used to describe the concentration degree of the T2 spectrum and the arithmetic mean is used to describe the average position of the T2 spectrum (Xiao et al. 2018).

3.3 Geomechanical behaviors

Figure 5 show the time-dependent axial stress, the axial strain, the radial strain, and the volumetric strain of samples during the pressure loading stage. It is seen that the stress–strain response is complicated. Some samples with similar petrohysical properties and mineralogical compositions behave significant differences in geomechanical properties. Table 3 and Fig. 6 summarizes the static and dynamic geomechanical parameters and their interrelationships for these samples obtained from stress–strain relationships and acoustic measurements. It is observed that the static Young’s modulus and static shear modulus are generally higher, and are positively correlated with their dynamic values. However, the static volumetric modulus and Poisson's ratio are generally lower than dynamic values and show no clear correlations (Table 5).

Fig. 5
figure 5figure 5

Time-dependent axial stress, axial strain, as well as radial strain for fully water saturated samples

Full size image
Fig. 6
figure 6

Relationship between static and dynamic geomechanical parameters

Full size image
Table 5 Static and dynamic geomechanical parameters for fully water saturated samples
Full size table

3.4 Pore size and component control on the compressive strength

Figure 7 gives the correlations of the compressive strength (CS) and NMR parameters including T2gm, T2am, Swi, Swm, T2c, and NMR porosity. It is seen that the compressive strength is decreased with the increase of T2gm and T2am for core samples under the fully water saturated state. This phenomenon indicates that rock’s strength is controlled by the pore size. Rock samples with larger pore radius are easier to reach the failure state. It seems that there is no clear relationship between the compressive strength and the T2gm and T2am for samples under the irreducible water saturated state. It is easy to be interpreted since the NMR response of irreducible water saturated rock sample is mainly contributed by clay bound water and capillary bound water, which cannot be used to characterize the pore size distribution of all ranges. Moreover, it is observed that the compressive strength is positively correlated with the irreducible water saturation, whereas negatively correlated with the movable water saturation, suggesting that the compressive strength is mainly controlled by the pore distribution. The rock is easier to be fractured for higher percentage of movable fluids, which are often resided in larger pores. We also exam the influence of T2 cutoff values and NMR porosity on the compressive strength, as is shown in Fig. 7e, f. It is seen that the compressive strength is weakly decreased with the increase of the cutoff value, although the physical explanation is not understood. In additional, the compressive strength is negatively correlated with the NMR obtained porosity, which is similar to most of previous publications.

Fig. 7
figure 7

Relationship between the compressive strength and NMR parameters

Full size image

Based on the discussion, it is practical for us to establish the model to predict the compressive strength using the NMR obtained parameters, which can be expressed as,

$$CS = a \times T_{2gm} + b \times \phi_{NMR} + c$$
(8)

where a, b, c are fitting parameters, which may vary in different regions. In this study, they are − 1.583, − 12.292, 320, respectively. The correlation coefficient is as high as 0.92. We did not recommend to use the irreducible water saturation and the movable water saturation for the regression since both are difficult to obtain by fully saturated spectrums.

We re-exam the relationship between the compressive strength and mineral compositions, as shown in Fig. 8. It seems that there are no clear correlations between the compressive strength and the mineral contents expect for the plagioclase. The result indicates that plagioclase may be the brittle mineral in the studied region. The empirical equation can be expressed as,

$$CS = d \times V_{plagioclase} + e$$
(9)

where d and e are fitting parameters. In this study, they are − 2.942 and 290.58. The correlation coefficient for this fitting is as low as 0.39.

Fig. 8
figure 8

Relationship between the compressive strength and the mineral composition

Full size image

Figure 9 gives the comparison between two different methods. It is seen that the precision obtained from the direct regression between the compressive strength and the plagioclase content is relative lower than the result obtained by the NMR parameters. Moreover, it is very difficult to obtain the plagioclase content because they are no direct well logging measurements to detect the minerals’ compositions and their contents, expect the elemental capture spectroscopy (ECS) logging.

Fig. 9
figure 9

Comparison between the experimented and predicted compressive strength

Full size image

4 Conclusions

We investigated the relationship between the pore size and the compress strength for tight sandstone based on laboratory NMR measurements and pseudo-triaxial compression tests, aiming to develop an effective way to predict the compressive strength using the NMR data. The main conclusions are as follows:

  1. 1.

    The rock’s strength is controlled by the pore size distribution for tight sandstone with similar minerals’ compositions. The rock is easier to easier to reach the failure state for larger average pore radius, supported by the observation between the compressive strength and the geometric, as well as the arithmetic mean of the transversal relaxation time.

  2. 2.

    The rock’s strength is influenced by the fluid distribution state. The compressive strength is positively correlated with the irreducible water saturation, but negatively correlated with the movable water saturation. The rock is easier to be fractured with the increase of the percentage of larger pores and movable fluids. The rock is easier to be fractured for higher percentage of movable fluids, which are often resided in larger pores.

  3. 3.

    There are weak correlations between the compressive strength and the mineral contents, indicating that the rock’s strength estimated by brittle minerals may be invalid.

  4. 4.

    The compressive strength for water saturated samples can be predicted precisely through multiple regressions with NMR parameters such as T2gm and porosity. The empirical equation can be potentially used for geophysical prospecting with NMR logging data.

It is noted that our observations are limited to laboratory studies of tight sandstone, much work should be done to further investigate their relationships. Moreover, the fluid phases and their distributions under the reservoir condition should be considered since the pore is not only wetted by the single water phase.