1 Introduction

With the rapid development of rock mass engineering technology, both the scales and depths associated with rock mass engineering are increasing and the problem of multi-field coupling is becoming more and more prominent (Damirchi et al. 2022; Zhang et al. 2023a, b). The fluid flow characteristics of fractured rocks are one of the important factors used to evaluate the safety of underground engineering. In addition, natural rock mass exhibits various defects, including micro-cracks and the macroscopic discontinuous surfaces such as pores and joint fissures (Eberhardt et al. 2004; Cappa et al. 2005; Zhang et al. 2023a, b). These defects act as underground water storage and as paths for water migration which lead to the heterogeneity and anisotropy of rock infiltration which increases the complexity of fracture media problems (Leung and Zimmerman 2012; Zhu and Tang 2006; Tang et al. 2002). The study of the mechanical and seepage characteristics of non-uniform rock possesses both theoretical research value and practical significance for engineering.

The seepage–stress coupling of rock mass has become a hot research topic in the field of rock mechanics which has been a major concern of scholars and studied both at home and abroad. Several methods exist for the study of the permeability characteristics of rock joints, such as field measurements, laboratory triaxial seepage experiments, and numerical simulations. Rock permeability measured by field measurements is usually reliable but has not been widely used due to the complex geological environments, repeated mining disturbances, and high costs (Johnson 2006; Baptiste and Chapuis 2014). Permeability tests of most rock samples are carried out in the laboratory. The evolution of the permeability law in the stress–strain processes of rocks have been extensively discussed through servo permeability tests (Adhikary and Guo 2015; Zhang et al. 2021, 2015). However, seepage experiment systems are airtight, and hence do not allow the monitoring of the hydraulic aperture changes of microscopic and macroscopic cracks during the experiments. Therefore, it is impossible to quantitatively analyse the pore connectivity, fluid seepage paths, and other factors.

With the rapid development of computer performance in recent years, increasing efforts have been invested in numerical simulations for the determination of rock permeability. The most commonly used numerical simulation methods include finite element, discrete element, and finite-discrete hybrid models (Lisjak and Grasselli 2014; Hudson 2002). Compared with the finite element method, the DEM and the mixing method can simulate the movements and separation of blocks. In DEM, the rock mass is considered to have discontinuous surfaces between the separated rock blocks. In addition, the blocks (polygon blocks) cannot be damaged and the fissures are generated along the edges of the polygon blocks (Liu et al. 2014). By using this method, the geometrical characteristics (inclination, length, opening degree, etc.) of rock mass fissures can be described with a relatively high accuracy and the germination, expansion, and closure of joints between polygon blocks can simulate the formation process of cracks in rocks and the response process of microscopic and macroscopic cracks under stress loads (Ghazvinian et al. 2014). Therefore, DEM has been widely used to evaluate the hydraulic characteristics of rock mass fractures (Yao et al. 2015a; Zhang et al. 2018).

Based on the “web of science core collection” database, the author enters the keyword “Universal Distinct Element Code” in the “Topic” subject, the 237 papers with a year of 2000–2023 were analyzed, as shown in the Fig. 1 (the colors in the figure represent different years, that is, the red color is 2020–2023, and the size of the circle in the figure represents the number of publications, and the larger the size of the circle, the larger the number of publications), The author information of some statistics is shown as "ANONYMOUS", The top 10 authors are "ANONYMOUS", GAO FQ, CUNDALL PA, ITASCA, ITASCA CONSULTINGGROUPINC, HOEK E, KAZERANI T, BARTON N, ZHAO XB, ZHAO J, Among them, "ANONYMOUS" published a large number of related articles, with 103 articles, which clearly shows that the number of articles published from 2020 to 2023 has increased significantly, which is closely related to the improvement of computer performance.

Fig. 1
figure 1

The number of authors' publications and citations relationships on the theme of UDEC

Full size image

The “Keyword” of related articles is organized and analyzed, as shown in the Fig. 2 (the colors in the figure represent different years, that is, the red color is 2020–2023, and the size of the square in the figure represents the number of publications, and the larger the square size, the larger the number of publications). The top 10 keywords were behavior, numerical simulation, failure, model, strength, deformation, rock, stress, stability, and damage, among which, there are a large number of articles related to “behavior” as a keyword, with 103 articles. The results show that the relevant research results of scholars are more concentrated in the study of the mechanical properties of rock samples and engineering scales(He et al. 2021; Wasantha et al. 2017; Wasantha and Konietzky 2017), and there are relatively few studies on the modeling methods and seepage characteristics of heterogeneous rocks, and rock, as a typical heterogeneous material, is an important basis for solving the hydraulic engineering problems of geotechnical and mining systems (Guglielmi et al. 2008).

Fig. 2
figure 2

Keyword characteristics and citation relationships with UDEC as the theme

Full size image

Based on previous research results, this paper mainly studies the influence of the block homogeneity and the heterogeneity of block and joint parameters on the seepage characteristics of rock mass fracture networks. The work considers not only the constant elastic modulus and the initial joint hydraulic aperture but also the form of the elastic model and the initial joint hydraulic aperture heterogeneity described by a Weibull distribution (which describes the heterogeneity of rock more accurately). Based on the Fish program embedded in the DEM for secondary development, a new method for parameter assignment of blocks and joints is proposed. The Weibull distribution is adopted to consider the heterogeneity of the block and joint hydraulic parameters. The influence of block homogeneity, hydraulic aperture homogeneity, and stress on the seepage characteristics of the model is analysed in detail, the relationship between the EHA and pressure, confining pressure, and shape parameters are further discussed.

2 Modelling method of heterogeneous systems

2.1 Contact constitutive model

Several studies have shown that the UDEC 2D polygon is a common DEM that can reliably simulate the mechanical behaviour of rocks under both laboratory and field conditions (Damjanac and Fairhurst 2010; Kazerani et al. 2012). Two polygon block types are generated in UDEC: deformable and rigid. The blocks are connected by joints. The blocks cannot be destroyed and the mechanical behaviour of joints between the multiple deformations can effectively reproduce the initiation, expansion, and closing processes of fractures in rocks. There are two modes of failure for each joint: tensile and shear damage (Yao et al. 2015b). Contact Constitutive Model is shown in Fig. 3.

Fig. 3
figure 3

Fluid–structure interaction calculations of joints in UDEC. a Joint constitutive relationship, b joint flow, c Hydraulic opening of joint under hydraulic coupling (Lisjak and Grasselli 2014), d Principle of hole pressure update, e The law of joint opening change

Full size image

Udec can simulate the fluid flow of a jointed rock under static load. The block in the model is non-seepage. The fluid can only flow in the joints of the rock (Itasca 2011) (Fig. 2). The flow of joints between two block planes is as follows:

$$q = \frac{{kba^{x} \Delta p}}{{\text{l}}},$$
(1)
$$k = \frac{1}{{12\upmu l}}$$
(2)

K is the permeability coefficient of the joints, a is the width of the crack, b is the empirical coefficient, μ is the fluid viscosity, x is the crack aperture index, l is the length of the joint fracture, and \(\Delta p\) is the pressure between the domains. The cubic law is now widely used: x = 3 and b = 1. During the simulation process, the mechanical deformation of joints will affect the hydraulic aperture of joints, as shown in Fig. 3. The hydraulic aperture of joints is calculated by the following formula:

$$a = a_{0} + \Delta a,$$
(3)
$$\Delta a = \frac{\sigma n}{{kn}}$$
(4)

where a0 is the joint hydraulic aperture in the absence of stress, бn is the normal stress on the joint, kn is the stiffness of the joints, and ares is the residual hydraulic aperture of the joints.

2.2 Construction and parameterization of heterogeneous model

In this paper, a method for the interaction between MATLAB and UDEC data is proposed, which can realize the construction and parameter assignment of heterogeneous models, as shown in Fig. 4.

Fig. 4
figure 4

Heterogeneous model construction and parameter assignment process

Full size image

In order to simulate the material properties of joint fractures obeying a certain distribution (Fisher distribution, normal index, negative exponential distribution, logarithmic distribution, etc.) to the computational unit and joint, this paper proposes a method for interacting MATLAB with UDEC data, which is detailed in Chapter 4 (Modelling method of heterogeneous rock). Based on this data interaction method, the non-uniform quantitative control of modeling and parameter assignment can be realized. furthermore, the influence characteristics of constant fracture opening, fracture opening, and length-opening correlation distribution on the hydraulic properties of rock mass were studied.

Using the method of interaction between MATLAB and UDEC data, it is also possible to assign material properties that obey any distribution (Fisher distribution, normal index, negative exponential distribution, logarithmic distribution, etc.) to the calculation unit and joint, which is not only applicable in UDEC software, but also in 3DEC and FLAC3D software. Table 1 shows the uniaxial compression (UCS) and uniaxial tensile (TEN) calculation models of specimen size constructed by 3DEC and FLAC3D numerical simulation software, respectively, and the heterogeneity of bulk modulus, shear modulus and joint stiffness is described by using weibull probability distribution function. The evolution characteristics of flow rate and equivalent hydraulic gap width with stress and water pressure of the heterogeneous model were analyzed.

Table 1 Heterogeneous numerical calculation model
Full size table

UDEC's built-in joint generator can generate joint groups with occurrence rules, and polygon joints can also be generated using the Thiessen polygon method. Based on the method of interaction between MATLAB and UDEC data proposed in this paper, the modeling method based on the experimental fracture model can be realized, as shown in Fig. 5, see ref Fan et al. (2019). Numerical calculation models of type III., type II., type I, and type Y fractures were constructed, and the stress sensitivity and flow evolution characteristics of different fracture modes were analyzed, and the detailed analysis data are detailed in documen, see ref Fan et al. (2019). It is also possible to construct a feature model in which the geometric parameters (length, tendency, opening, etc.) of joint fissures are randomly distributed according to some mathematical statistical method, as detailed at the end of the discussion section.

Fig. 5
figure 5

Experimental fractured samples and reconstruction models (Fan et al. 2019)

Full size image

3 Numerical simulation model

3.1 Numerical model parameter validation

During the numerical simulation, the selection of reasonable physical and mechanical parameters can allow the effective reproduction of the rock’s mechanical behaviour. An established method was used to fit the mechanical parameters (Gao and Stead 2014; Gao 2013; Bai et al. 2016; Baptiste and Chapuis 2014). The numerical simulation results were fitted with the uniaxial compressive and tensile data obtained by laboratory experiments. Subsequently, the parameters of the block and joints in the computational model were determined. In the simulation, the block was an elastomer. The mechanical strength of the model was controlled by the joint failure process between the blocks and the joints between the blocks could be broken by tensile and shear forces. The failure criteria are shown by formulas (1) and (2). A ‘FISH’ program was used to determine whether the joint was broken when the joints exhibited tensile damage. In this case, the broken joints were classified into the “tensile damage” group. When the joints suffered shear damage, they were allocated to the “shear damage” group. The number of broken joints in each group was recorded separately.

The experimental results of the uniaxial compression test and the numerical simulation are shown in Fig. 6. An “X”-shaped form of destruction is present on the specimen (Fig. 6a). The same failure mode is also obtained by the numerical simulation, as shown in Fig. 6b. Figure 6c is the stress–strain curve of the uniaxial compression test of the model. The stress peak of the specimen’s uniaxial compression is 75.03 MPa. Before reaching the peak stress, the stress increases slowly at first with the increasing strain, followed by an approximately linear increase. When the peak stress is reached, the stress values fluctuate in a small range, followed by a sharp drop of the stress value. The results of the numerical simulation show good consistency with the experimental data. In the simulation process, the number of joints with tensile failure and shear failure were recorded. The damage percentage is the number of damaged joints divided by the total number of joints before reaching the peak stress of 65%. The joints mainly showed tensile failure beyond peak stress value. The joints start to suffer shear damage and the amount of destruction rapidly increases when the peak stress is reached. The percentage of joints damaged due to shear and tensile were 20% and 15%, respectively, after reaching the peak stress. The shear failure was stable at 42%. The tensile failure was stable at 17%. Nearly 59% percent of the joints in the model were destroyed. The rate of shear damage was about 2.5 times the rate of tensile failure.

Fig. 6
figure 6

Calibration of the numerical model by the uniaxial compression tests: a failure pattern of the laboratory sample; b failure pattern of the numerical model; and c stress–strain curve of the numerical model

Full size image

The tensile fractures in the numerical simulation are presented as straight lines throughout the specimen, as shown in Fig. 7a, which is consistent with the damage pattern obtained by the laboratory test shown in Fig. 7b. Figure 7c shows the stress–strain curve of the tensile test of the model. Before reaching the peak stress, the stress increases linearly with the increasing strain. A “cliff-type” drop of the stress values occurs after reaching the stress peaks. The numerical simulation results and laboratory results show a satisfactory correlation. According to the curve, tensile failure is prevalent during tension experiments. When the stress reaches the peak stress level of 25%, tensile damage gradually starts to form. Beyond the peak stress, the number of joints with tensile damage stabilises at about 16.7% following a sharp increase. Nearly 17.5% of the joints in the model are damaged, while only a small number of joints exhibit shear damage.

Fig. 7
figure 7

Calibration of the numerical model to the Brazilian tests: a failure pattern of the laboratory sample; b failure pattern of the numerical model; and c stress–strain curve of the numerical model

Full size image

The physical and mechanical parameters of the block and joints applied in the numerical model are shown in Table 2. The fitting results of the uniaxial compression and tensile experiments show that the physical and mechanical parameters selected in Table 2 are reasonable.

Table 2 Mechanical parameters obtained by sample fitting with the numerical model
Full size table

4 Modelling method of heterogeneous rock

Rocks are heterogeneous materials and there are randomly distributed pores in the fractured rock mass. In addition, the distribution of the hydraulic parameters is further complicated by the variance in the environmental stresses. Laboratory results show that Weibull distribution plays a significant role in the study of the rock-size effect and strength theory (Tang 1997; Wong et al. 2006; Zhu et al. 2018). Therefore, this paper applies the Weibull distribution function to describe the rock block and joint hydraulic parameters.

The statistical distribution of rock mechanical parameters can be described as:

$$\varphi \left( a \right) = \frac{m}{{a_{0} }}\left( {\frac{a}{{a_{0} }}} \right)^{m - 1} e^{{ - \left( {\frac{a}{{a_{0} }}} \right)^{m} }}$$
(5)

where the scale parameter a is relative to all mechanical parameters of the rock (block and joint). a0 is the average value of the corresponding rock mechanical parameters, the parameter m defines the shape of the Weibull function and defines the degree of the block and joint homogeneities.

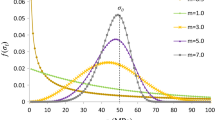
The non-uniform distribution of the microscopic mechanical properties of the rock is described by (7). The parameter distribution of rock media with various homogenization coefficients is shown in Fig. 8a. With the increase of the uniformity coefficient m, the mechanical properties of rock blocks and joints are concentrated in a narrow range, indicating that a higher degree of rock homogeneity. When the uniformity coefficient m value decreases, the distribution of the rock blocks and joint mechanical properties widens. The results show that the properties of rock media tend to be non-uniform. In this work, m = 1, 2, 3, 5, and 10 were considered, as shown in Fig. 8b.

Fig. 8
figure 8

Distribution of rock mechanics parameters

Full size image

The material property number n was assigned to designated contacts. Every contact initially defaulted to jmat = 1. The maximum value of n was 50 which corresponded to isotropic linear elastomers, elastoplastic bodies, and so on. This limits the grouping of materials to no more than 50 groups when describing their heterogeneity. The built-in parameter assignment function of the software performed poorly when describing the heterogeneity of the block and joint materials.

For this reason, the Fish program was developed to assign the hydraulic parameters of rock blocks and joints while conforming to the Weibull distribution while describing the heterogeneity of the calculation models. The assignment process is shown in Fig. 9. The following process was used:

  1. (1)

    The basic model is established to record the number of calculation zones and contacts (N1 and N2, respectively).

  2. (2)

    The rock parameters fitted above and the hydraulic aperture value of joints in a zero-stress state obtained by scanning electron microscopy are taken as the average value (a0) of the block and joint hydraulic parameters. The shape parameter m is determined to generate the mechanical parameters of zones and joints in accordance with the Weibull distribution using the MATLAB software. The number of parameters of zone and joint is N1 and N2, respectively.

  3. (3)

    Two arrays (array N1 and array N2) are created in UDEC. The parameters generated in step 2 are loaded into the arrays. The zone and contact cells in the model are then traversed for parameter assignment.

Fig. 9
figure 9

Flowchart of the heterogeneous parameter assignment method

Full size image

Finally, the heterogeneous calculation model which obeys the Weibull distribution parameters is obtained. The heterogeneous anisotropic materials established by the introduced method are greatly improved.

Taking the volume modulus of the rock mass and the hydraulic aperture of the joints as an example, Fig. 10 shows the distribution characteristics and frequency statistics of the elastic modulus subject to the Weibull distribution.

  1. (1)

    Here, a in (7) represents the volume modulus of the rock. The shape parameter (m) is selected as 5 and the mean value of the elastic modulus is a0 = 5.09 GPa.

  2. (2)

    The number of zones in the model is 3806. The elastic modulus of 3806 is in accordance with the Weibull distribution generated by MATLAB, while the Poisson ratio is 0.28. The volume modulus and shear modulus of the rock mass are calculated according to (8) and (9).

  3. (3)

    The model is assigned by traversing the zone calculation unit in the model.

Fig. 10
figure 10

Distribution characteristics and frequency statistics of the elastic modulus

Full size image

Figure 11 shows the distribution characteristic diagram of the volume modulus of the rock mass. Figure 12 shows the distribution characteristics and frequency statistics of the hydraulic aperture subject to the Weibull distribution. At this point, a in (7) represents the initial hydraulic aperture of the joint. The shape parameter (m) is selected as 2. The mean value of the initial hydraulic aperture is a0 = 7.02 μm. The number of contacts in the model is 3854 which is in accordance with the Weibull distribution generated by MATLAB. The model is assigned by traversing the contact calculation unit in the model.

Fig. 11
figure 11

Distribution characteristic diagram of the volume modulus of the rock mass

Full size image
Fig. 12
figure 12

Distribution characteristics and frequency statistics of the hydraulic aperture

Full size image

Figure 13 shows the distribution characteristic diagram of the initial hydraulic aperture of the joints.

$$K = \frac{E}{{3\left( {1 - 2\mu } \right)}}$$
(6)
$$G = \frac{E}{{2\left( {1 + \mu } \right)}}$$
(7)

where K is the volume modulus, G is the shear modulus, E is the elastic modulus, μ is the Poisson ratio.

Fig. 13
figure 13

Distribution characteristic diagram of the initial hydraulic aperture of the joints

Full size image

5 Numerical simulation scheme determination

Based on the non-uniform rock mass modelling method, a total of 50 seepage calculation models were established in this work and the influence of block homogeneity, hydraulic aperture homogeneity, and stress on the seepage characteristics of the model was studied in detail. The models were divided into three categories: in category I, the applied average edge length was 1, 3, 5, 7, and 9 mm and 5, 10, 50, 100, and 500 iterations were carried out, totalling 25 established numerical models. Subsequently, the impact of block homogeneity on the seepage characteristics was studied by category II which included models with average edge lengths of 1, 3, 5, 7, and 9 mm with a number of iterations of 5. In category II of the models, M = 1, 2, 3, 5, and 10 were selected to describe the heterogeneity of the initial hydraulic aperture of the calculation model. Category II was used to analyse the influence of hydraulic aperture homogeneity on the seepage characteristics. Category III focused on the exploration of the seepage characteristics of rock samples in various stress environments. Two experimental stress paths were designed, as shown in Fig. 14. Scheme 1: the confining pressure was 5 MPa and axial pressure was 5–30 MPa; Scheme 2: the confining pressure was 5–30 MPa and axial pressure was 5 MPa. The osmotic pressure difference between the upper and lower ends of the model was 1 MPa and the two sides of the model were separated by a non-seepage boundary. The method introduced above was used to determine whether the joint seepage is balanced or not. When the model is balanced, the “print max” command was input in the command window to record the seepage flow rate. To reduce the influence of accidental factors, every model was calculated at least five times.

Fig. 14
figure 14

Stress Path of Seepage Experiments. a Confining pressure of 5 MPa, and axial pressure of 5–30 MPa; b Confining pressure of 5–30 MPa, and axial pressure of 5 Mpa

Full size image

5.1 Various degrees of homogeneity of the blocks

The response of rock under uniaxial compression is simulated by the establishment of two-dimensional numerical models using UDEC. Using the command Voronoi tessellation generator, the blocks were divided into polygonal blocks and joints. Different iterations created different homogeneous blocks. A total of 25 numerical models with average side lengths of 1, 3, 5, 7, and 9 mm and iterations of 5, 10, 50, 100, and 500 were established. Using these models, the effects of the homogeneity of different blocks on the seepage characteristics were analysed. The simulation results are shown in Fig. 15. The higher number of iterations corresponded to a better size distributed.

Fig. 15
figure 15

Seepage results of models using various degrees of block homogeneity

Full size image

The seepage simulation results of the various block homogeneity models (Fig. 15) show that different homogeneity models, with the average block size larger than 3 mm in the model, the total flow after 500 iterations is slightly larger than that with any other number of iterations. When the average block size of the model is less than or equal to 3 mm, the total flow at 500 iterations is slightly smaller than that achieved by any other number of iterations. According to the various curves shown in Fig. 14, the total flow positively correlates with N0.5 and shows a strong linear relationship described by a correlation coefficient greater than 0.9996. Note that N here is half the number of blocks in the model. When the number of iterations is 5, the relationship between the number of meshes and the total traffic is:

$$Q = (0.2827\sqrt N - 0.4495) \times 10^{ - 5}$$
(8)

The parameters of the linear fitting obtained by other number of iterations are shown in Fig. 15. The smallest slope was obtained (0.2801) when the number of iterations was 500. The corresponding intercept of the straight line, however, was the largest (− 0.3645).

5.2 Various degrees of homogeneity of the joint hydraulic aperture

The default number of iterations was 5 when using the command Voronoi tessellation generator to divide the blocks into polygonal blocks and joints. In this case, the initial hydraulic parameters of the joints obeying the Weibull distribution are assigned to the model with average side lengths of 1, 3, 5, 7, and 9 mm by using the Fish program introduced in the previous paper. The obtained distribution describes the heterogeneity of the initial hydraulic aperture of the model.

By observing the rock samples from Laosangou coal mine with scanning electron microscopy, the fracture widths under zero stress in Fig. 16 can be obtained: 6.81, 7.42, 7.74, and 6.77 µm, respectively. This method is based on coal petrology and tectonic geology. The pore, fracture morphology, and size of the rocks are observed by scanning electron microscopy throughout the characterization of residual traces of rock mass during the chemical and physical analysis stages. In our model, the hydraulic aperture under zero stress takes the average value of the above four values, namely a0 = 7.02 μm. Taking a0 as the average value for the initial joint hydraulic aperture and m as the shape parameter of the Weibull distribution function, in the present work m = 1, 2, 3, 5, and 10 were considered. Figure 17 shows the joint hydraulic aperture distribution of various average block size calculation models with the shape parameter set to m = 10.

Fig. 16
figure 16

Microscopic crack structure of a rock sample

Full size image
Fig. 17
figure 17

Hydraulic aperture distribution of joints in different average block size models

Full size image

Figure 18 shows the simulation results of a hydraulic aperture model consisting of initial joints with various homogeneities. The total discharge is still positively correlated with N0.5. Firstly, a linear function was used to fit the data. The correlation of the shape parameter m = 1 was 0.9801, which is the lowest value achieved. When the shape parameter was m = 1, the linear relationship between the total flow and N0.5 is weaker than that obtained by other shape parameters. When a polynomial function is used to fit the shape parameters, the correlation reaches 0.9999, as shown on the right side of Fig. 18. The increase of the shape parameter m corresponds to the increase of R2 which indicates that the linear relationship between the total flow and N0.5 increases with the increase of the shape parameter. In addition, the slope of the fitting linear model also increases gradually. The maximum slope value was 1.6433 for m = 10.

$$Q = a^{*} \ln (x) + b$$
(9)

where Q is the total flow, x is the shape parameter, and a and b are parameters related to the average size of the blocks.

$$a = {44}.{9}0{\text{1n}}^{{ - {1}.0{14}}}$$
(10)
$$b = 0.0{234}n^{{4}} - 0.{57}0{2}n^{{3}} + {5}.{1559}n^{{2}} - {2}0.{896}n + {32}.0{39}$$
(11)
Fig. 18
figure 18

Seepage results of various hydraulic aperture homogeneity models

Full size image

where n is the average size of the blocks.

The relationship between the total flow rate and the shape parameter m is further analysed below. The relationship between the total flow rate and the shape parameter m is shown in Fig. 19a for various block sizes. There is a logarithmic relationship between the total seepage flow rate and the shape parameter. As shown by (11), the correlation coefficient is greater than 0.9654. a and b are parameters related to the average size of the blocks. The relationship between the parameters a and b and the average size of the blocks was also investigated, as shown in Fig. 19b, c. There is a power exponential relationship between the parameter a and the average size of the blocks, as shown by (12) (a correlation coefficient of 0.9954). The relationship between the parameter b and the average block size is fitted by a quadratic polynomial obtaining a correlation coefficient of 1, as shown by (13). The results show that the average block size and shape parameter m of the model have a great influence on the initial total flow of the model. When the average size and shape parameter m of the model are known, the initial flow of the model can be quantitatively analysed by (11)–(12). The flow chart is as follows: by substituting the average block size n of the model into (12)–(13), the specific values of parameters a and b can be obtained. By substituting the obtained parameters and shape parameter m into (11), the initial total flow value Q of the model can be estimated.

Fig. 19
figure 19

Variation curve of Flow rate and parameters. a Variation of the flow rate as a function of the shape parameters; b and c is the relationship between the parameters a and b and the average size of the blocks

Full size image

5.3 Various stress environments

It should be noted that in the case of setting the shape parameter m = 1, the model calculates 1,000,000 steps without reaching a steady state. Therefore, the seepage data at m = 1 is not included in the following analysis.

Figure 20 shows the variation of the flow rate with the increasing axial stress and shape parameters. In Fig. 20a, uniform refers to a constant hydraulic aperture of the joints of the model, namely a0 = 7.02 μm. With the increase of the axial stress, the seepage flow decreases gradually, reaching a minimum of 30 MPa. It is found that the relationship between the flow rate and the axial pressure is a two-time polynomial with a correlation of more than 99.72%. According to Fig. 20b, under identical stress conditions, the seepage flow increases gradually with the increase of the shape parameters. With further analysis, there is a logarithmic relationship between the total seepage flow and the shape parameters, exhibiting a correlation coefficient greater than 0.9654.

Fig. 20
figure 20

Flow variation curves. a Variation of the flow rate with the axial pressure; b Variation of the flow rate with the shape parameters

Full size image

Figure 21 shows the variation of the flow rate as a function of the radial stress. In Fig. 21a, with the increase of the radial stress, the seepage flow rate decreases gradually. The decrease of the flow rate is significantly greater than that observed with the increase of the axial pressure. The main cause is that the seepage direction of the model is vertical and the seepage passage is mainly composed of vertical joints. The hydraulic aperture of vertical joints is less sensitive to the axial stress, while the vertical hydraulic apertures are more sensitive to confining pressure. This is consistent with the observation found in the scientific literature (Zhang et al. 2018). According to Fig. 21a, the relationship between the flow rate and the confining pressure is cubic polynomial, with a correlation of more than 99.98%. According to Fig. 21b, under identical stress conditions, the increase of the shape parameters corresponds to a gradual increase of the seepage flow rate. In addition, the relationship between the flow rate and shape parameters under identical stress conditions is further analysed. There is a logarithmic relationship between the total flow rate and the shape parameters, with a correlation of more than 96.64%.

Fig. 21
figure 21

Flow variation curves. a Variation of the flow rate as a function of the confining pressure; b Variation of the flow rate as a function of the shape parameters

Full size image

6 Discussion

In this paper, the seepage characteristics of heterogeneous rocks are studied by establishing a DEM model. By fitting the mechanical parameters obtained by numerical simulations with the mechanical properties of sandstone, it is reasonable and feasible to incorporate the physical and mechanical parameters of the ore body and joint into the model. Because the fracture characteristics in rocks not only determine the seepage characteristics of rocks but also affect the mechanical properties of rocks, the obtained fracture development characteristics are applied to the numerical model by using scanning electron microscopy on rock samples. The hydraulic parameters determined above are taken as the average values of the corresponding parameters. Subsequently, the calculation models based on the Weibull distribution with various shape parameters are established.

Firstly, the relationship between the total flow rate and the model block was analysed while the initial hydraulic aperture was constant. It was found that the total flow is positively correlated with N0.5 under various conditions and they show a strong linear relationship. The correlation coefficient was greater than 0.9996 which is consistent with previous findings (Yao et al. 2015a). Hence, a parameter assignment method for heterogeneity of model joints was proposed and the seepage characteristics of joints were described by the Weibull distribution, where the shape parameters (m) of 1, 2, 3, 5, and 10 were investigated. It was found that the total flow rate shows a strong linear relationship with N0.5, and the R2 increases gradually with the increase of the shape parameter m. This shows that with the increase of the shape parameters, the linear relationship between the total flow rate and N0.5 increases and the slope value of the fitting linear model increases gradually. Based on the above findings, this paper proposed a method for estimating the initial total flow value Q of the model.

Because people are accustomed to and adopt the cubic law to describe the flow law of actual cracks, in some cases (such as considering the roughness and degree of the crookedness of joints) the meaning of the gap width of joints is no longer geometric. Subsequently, the concept of the equivalent hydraulic aperture is proposed which combines the actual characteristics of the cracks with the cubic law (Yuan 2002; Liu et al. 2016), i.e., the obtained flow of cracks is substituted for the cubic law to obtain the fracture width.

$$Q/\ddot{A}H = Cb_{{^{n} }}^{3}$$
(12)
$$\ddot{A}H = \Delta p/l$$
(13)

where Q is the total flow, \(\ddot{A}H\) is the head difference of the fracture surface, C is a constant related to the gravitational acceleration, the viscosity coefficient of the water, and the shape and size of the fracture surface. For the ease of analysis, the value of C was chosen as 1/12μ. bn is the EHA, △p is the differential pressure between the upper and lower pressure in our models (1 MPa), and l is the length of the numerical direction model (0.1 m).

In formulas (14), (15), the EHA bn is obtained as follows:

$$b_{{^{n} }}^{{}} = \sqrt[3]{12\mu Ql/\Delta p} = \sqrt[3]{{1.2 \times 10^{ - 9} \times Q}}$$
(14)

According to the above formula, we analysed the relationship between the EHA and the confining pressure, axial pressure, and shape parameters in various stress environments. Figures 22 and 23 show the variation of the EHA under various confining pressures and various axial pressures, respectively.

Fig. 22
figure 22

Variation curves of the EHA. a Variation of the EHA as a function of the confining pressure; b Variation of the EHA as a function of the shape parameters

Full size image
Fig. 23
figure 23

Variation curves of the EHA. a, b Variation of the EHA as a function of the axial pressure; c Variation of the EHA as a function of the shape parameters

Full size image

The variation of the EHA for various confining pressures is shown in Fig. 22. Under the same stress conditions, the EHA is the smallest when the shape parameter m is 2. With the increase of the shape parameter, the EHA increases gradually, while the EHA decreases gradually with the increase of the confining pressure. The relationship between the EHA and the confining pressure is linear, with a correlation coefficient greater than 0.9796, as shown in Fig. 22a. The relationship between the EHA and the shape parameters is logarithmic, with a correlation coefficient greater than 0.9642, as shown in Fig. 22b.

The variation of the EHA for various axial compression values is shown in Fig. 23. Under the same stress conditions, the EHA is the smallest when the shape parameter m is 2. With the increase of the shape parameter, the EHA increases gradually and decreases gradually with the increase of the axial pressure. Referring to the fitting results of the EHA under various confining pressures, the relationship between the equivalent hydraulic clearance width and the axial pressure is fitted preliminarily by using linear formulas. As shown in Fig. 23a, the correlation coefficient is greater than 0.9436. According to the variation characteristics of the EHA under various axial pressures, when a quadratic polynomial is used to fit the relationship between the EHA and the axial pressures, as shown in Fig. 23b, the correlation coefficient is greater than 0.9924. The relationship between the EHA and the shape parameters is still logarithmic with a correlation coefficient greater than 0.9688, as shown in Fig. 23c.


In this paper, Weibull distribution is used to consider the non-uniformity of the mechanical parameters of coal and rock. Although the mechanical parameters of some coal-rock units may not exhibit different distribution laws or the simulation data may be only consistent with the actual coal-rock mechanical parameters in the statistical sense, at the current research level, the method presented in this paper is a reasonable, feasible, and effective. From another point of view, the macro-mechanical behaviour of coal and rock is essentially the collective effect of a large number of units in both the coal and rock mass, while the individual mechanical behaviour of each unit has a limited influence on the macro-mechanical properties of the system. Therefore, if enough units are used, the randomness of this assignment method has a negligible effect on the macro-mechanical behaviour of coal and rock.

$$f\left( x \right) = \frac{1}{{\sqrt {2\pi } \sigma }}\exp \left( {\frac{{ - \left( {x - \mu } \right)^{2} }}{{2\sigma^{2} }}} \right)$$

UDEC's built-in joint generator can generate joints with regular occurrence rules, and polygonal joints can also be generated using the Thiessen polygon program. Some scholars have pointed out that these two types of joints cannot truly reflect the characteristics of structural planes, and cannot truly simulate the characteristics of the random distribution of geometric parameters (length, tendency, opening, etc.) of joint cracks in rock mass according to some mathematical statistical method (Darcel et al. 2017; Long and Billaux 2010). Using the method of interaction between MATLAB and UDEC data, Based on the two-dimensional stochastic fracture modeling idea of Monte Carlo method, assuming that the number of different fracture inclination angles obeys the positive Pacific distribution function in the two intervals of 0–90 and 90–180 degrees, and the fracture length varies in the range of 0.15–0.35, the numerical calculation model with 300 fractures that meets the above conditions is shown in the Fig. 24. Furthermore, the two-dimensional discrete element degree udec was developed to study the influence characteristics of constant fracture opening, fracture opening obeying weibull distribution and length-opening correlation distribution on the hydraulic properties of rock mass.

Fig. 24
figure 24

Diagram of the stochastic fracture network model

Full size image

7 Conclusion

  1. 1.

    In this paper, a parametric method for heterogeneous rocks is proposed. A Weibull distribution model is introduced to describe the distribution characteristics of the heterogeneity of blocks and joints. The mechanical parameters of both rocks and joints are inverted by establishing uniaxial compression and Brazilian splitting models of sandstone. Moreover, the initial hydraulic opening of joints is obtained by scanning electron microscopy. Taking the hydraulic parameters obtained as the average value of the corresponding parameters and combining them with the Weibull distribution coefficient to generate lithologic parameters under different shape parameters m, the Fish program is developed to obtain the random distribution of rock mass element and joint calculation parameters. This program also overcomes the limited number of parameters in UDEC which cannot exceed 50.

  2. 2.

    Based on the established heterogeneous model, the effects of block homogeneity and joint hydraulic aperture degree of homogeneity on the seepage characteristics are analysed in a zero stress environment. The results show that the total flow is positively correlated with N0.5 and shows a strong linear relationship. With the increase of the value of the shape parameter, the linear relationship between the total flow and N0.5 is also enhanced. In addition, a method for estimating the initial total flow value Q of heterogeneous models is proposed.

  3. 3.

    It is found that the relationship between the flow rate and the axial pressure is a quadratic polynomial, characterised by a correlation of more than 99.72%. At the same time, the relationship between the flow rate and the confining pressure is a cubic polynomial with a correlation of more than 99.98%. In identical stress environments, the increase of the shape parameters corresponds to a gradual increase in the seepage flow rate. It is found that there is a logarithmic relationship between the total seepage flow rate and the shape parameters. The EHA linearly depends on the confining pressure and the EHA has a quadratic polynomial relationship with the axial pressure. In identical stress environments, the EHA has a logarithmic relationship with the shape parameters.