1 Introduction

Increasing attention has been paid on the issue of slope failure in open pit mining. In recent years, more than 30 open-pit coal mines in Chinese Baiyinhua coalfield, Shengli coalfield, Baorixile coalfield and Huolinhe coalfield have encountered large deformation and landslide disasters. It is extremely difficult to prevent and control landslides, the number and scale of which are usually large and the loss caused by which is extremely severe. For instance, at Baorixile Open-pit Coal Mine (Ju and Li 2009), a total of 8 large-scale soft rock landslides were recorded as of the end of 2016. Among them, the landslide occurred at the western end of the stope in October 2008 had a volume of about 3.5 million m3 and the direct economic loss was nearly 100 million yuan. Another case is Datang Shengli East II Open-pit Coal Mine (Jiang 2022) whose non-working end slopes suffered two huge landslides in July 2012 and August 2013, and it is as yet unable to conduct the coal production normally. Such landslide accidents have seriously impeded the safe production, economic and social sustainable development of open-pit coal mines in China. Therefore, the analysis and assessment of slope stability is the primary problem to be solved in open pit mining and also the premise and foundation of slope engineering projects (Zou and Wei 2006). Scientific evaluation of slope stability is able to provide guidance on reasonable control measures in mining engineering.

At present, scholars have proposed a variety of methods to evaluate the slope stability. These methods can be divided into two types, i.e., deterministic and non-deterministic methods. The former ones mainly consist of the limit equilibrium method, the numerical analysis method, the probabilistic method, the graphic method, the engineering analogy method, the natural history analysis method, etc. (Deng and Li 2012; Chang et al. 2016; Sun et al. 2019; Pan et al. 2019; Zhang et al. 2020). However, traditional methods on slope stability assessment have some limitations. No matter the limit equilibrium method or the numerical analysis method, it requires a large amount of geological investigation in the early stage, resulting in a great amount of workload and high economic cost (Zhang 2008; Hong et al. 2019). Non-deterministic methods relate to a number of basic theories in different disciplines, including the Chaos theory, the Fuzzy theory, the Stochastic theory, the Mutation theory, the Artificial Neural Network theory, the Grey System theory, etc. (He et al. 2019; Li et al. 2011; Yang et al. 2020; Nabila et al. 2021; Yuan and Li 2021). With the deepening study of slope stability, modern mathematical theories and methods are introduced into the slope stability evaluation, such as the Fuzzy Comprehensive Evaluation method, the TOPSIS evaluation method, the Grey Relational analysis, the Principal Component analysis, the Reliability analysis, the Measurement Uncertainty theory, the Least Square Support Vector Machine method, the Matter-element Extension theory, the Game theory-Cloud model, and so on (Chen et al. 2008; Yuan et al. 2013; He et al. 2014; Tian et al. 2016; Chen et al. 2019; Jena et al. 2020; Huang et al. 2020; Wang et al. 2021; Zhang et al. 2022). Hence, the evaluation system is greatly enriched. Zhou et al. (1995) applied a fuzzy evaluation model to the slope stability evaluation and considered it as an applicable model suitable for promotion. Chen and Yang (2005) built a new intelligent model for slope stability evaluation by introducing the genetic algorithm into the artificial neural network (ANN) and constructing a T-S type reasoning system. Li et al. (2011) established a landslide database based on 31 typical landslide cases in history and compared the slope to be evaluated with the database to achieve the evaluation results. Ren (2017) employed the ideal point method to assess the slope stability, used an improved entropy weight method to determine the weight coefficient of each index, and established an early warning system of slope landslides. Wang and Xu (2011) developed an evaluation model of slope stability based on the projection pursuit optimized by the particle swarm (PSO-PP). The evaluation model was proved to have good feasibility and high accuracy. Qin et al. (2022) proposed an single-valued neutrosophic number-based adaptive neuro fuzzy inference system (SVNN-ANFIS) approach to evaluate the slope stability of an open-pit mine. Traditional deterministic methods have the following deficiencies: (1) the evaluation method has strong randomness. For example, the limit equilibrium method is difficult to determine the position of the sliding surface for the rock and soil slope with complex structure. The numerical analysis method is greatly influenced by the selection of physical parameters. (2) The evaluation method is dependent on experience. For instance, both the graphic method and the engineering analogy method require a certain degree of experience. (3) The evaluation method has a small scope of application. For example, the natural history analysis method needs to trace the evolution process of the slope and is mainly used to assess natural slopes. Non-deterministic methods also have some shortcomings. (1) There is an imbalance between subjective and objective factors. For example, the fuzzy comprehensive evaluation method is more subjective while the support vector machine method is more objective. (2) Specific weight values are needed for calculation in the evaluation process. Yue et al. (2018) and Zhao (2022) used Game theory to solve the weight of the same evaluation index system, but the obtained weight values of each index were not only numerically different, but even the weight orders of some indices were different, indicating that the use of specific weight values for risk assessment is unstable. (3) The evaluation method is dependent on the number of samples. For example, the reliability analysis method requires a large number of samples to obtain the distribution and statistical parameters of random variables, but the actual number of samples is limited.

To overcome the above shortcomings and evaluate slope stability effectively and economically, the Poset decision-making theory is applied in this work to establish a multi-factor risk assessment system based on an open-pit slope of Yuanbaoshan Open-pit Coal Mine. The importance degree and data information contained in the index itself is fully considered. The weights are embedded into the evaluation method by means of implicit weighting, without requiring specific weight values to participate in the calculation. This avoids the controversy about the weight assignment. The Poset evaluation model is constructed to evaluate the slope stability and its accuracy and rationality are verified with the actual situation, which provides a new feasible method for slope stability evaluation.

2 Partially ordered set (Poset) theory

A partially ordered set (A, ≤) refers to the set A equipped with the partial order relation ≤ , where the partial order relation ≤ is a binary relation satisfying reflexivity, antisymmetry and transitivity on the nonempty set A. When this binary relation is used for decision making, it should be noted that the evaluation value and the evaluation relation are essentially different. Yue et al. (2018) provided their conversion relation. For ∀x,y ∈ A, then

$$x \le y \Leftrightarrow c_{j} \left( x \right) \le c_{j} \left( y \right),\quad j = 1,2, \ldots ,n$$
(1)

where x and y are evaluation objects, cj represents the jth evaluation index, cj(x) is the normalized value of x on the index cj, and cj(y) is the normalized value of y on the index cj.

Under the premise that the weights of the indices meet ω11 ≥ ω12 ≥ ··· ≥ ω1n, Chen et al. (2019) realized the implicit weighting in the form of a matrix for decision making with multiple objects and indices.

$$D = \left( {d_{ij} } \right)_{m \times n} = XE = \left( {\begin{array}{*{20}c} {x_{11} } & {x_{11} + x_{12} } & \cdots & {x_{11} + x_{12} + \cdots + x_{1n} } \\ {x_{21} } & {x_{21} + x_{22} } & \cdots & {x_{21} + x_{22} + \cdots + x_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {x_{m1} } & {x_{m1} + x_{m2} } & \cdots & {x_{m1} + x_{m2} + \cdots + x_{mn} } \\ \end{array} } \right)$$
(2)

where D is the cumulative transformation matrix, X is the evaluation matrix, and E is the upper triangular matrix, \(E = \left( {\begin{array}{*{20}c} 1 & 1 & \cdots & 1 \\ 0 & 1 & \cdots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\ \end{array} } \right)\).

In the matrix D, if each value in the row m − 1 is greater than or equal to the value in the corresponding position of the row m, the evaluation object m− 1 is better than or equal to the evaluation object m. For a given poset (A, ≤), ∀x,y ∈ A, if x is better than or equal to y, sxy = 1. Otherwise, sxy = 0, and S = (sxy)m×m is called the comparison relation matrix of (A, ≤).

However, when the index weight does not satisfy the ranking of ω11 ≥ ω12 ≥ ··· ≥ ω1n, the above calculation cannot be carried out. Aiming at the situation that the weight order of some evaluation indices cannot be determined, Gao et al. expressed the weight relation among the indices in terms of weight sets, namely, ω11 ≥ ··· ≥ ω1i−1 ≥ {ω1i, ω1i+1, ···ω1j} ≥ ω1j+1 ≥ ··· > ω1n. Among them, the weight values of any two indices in the set {ω1i, ω1i+1, ···ω1j} cannot be ascertained, and ω1i−1 ≥ max{ω1i, ω1i+1,···ω1j} ≥ min{ω1i, ω1i+1, ···ω1j} ≥ ω1j+1. In other words, if the weight order of some evaluation indices cannot be determined, the corresponding indices are added as a new index, and then its weight is ranked with other index weights. In this way, the Poset theory can be reapplied.

The comparison relation matrix cannot visually reflect the partial order relation, so it is necessary to depict a relation diagram. A Hasse matrix can be obtained by the conversion calculation of the comparison relation matrix, and then a Hasse diagram can be plotted. The Hasse diagram is a special directed graph, visually showing the partial order results of the evaluation objects. It is a powerful tool to exhibit the transitive and structural relations among the evaluation objects. Fan (2003) illustrated the conversion relation between the comparison relation matrix S and the Hasse matrix by the following expression,

$$H_{s} = \left( {S - I} \right) - \left( {S - I} \right)^{2}$$
(3)

where S is the comparison relation matrix, Hs is the Hasse matrix, I is the unit matrix, and (S − I)2 indicates the Boolean operation (i.e. 1 + 1 = 1, 1 + 0 = 1, 0 + 0 = 0, 1 × 1 = 1, 1 × 0 = 0, 0 × 0 = 0).

For any poset (A, ≤), the set F(x) = {y ∈ A|x ≤ y} is the upper set of A, the set O(x) = {y ∈ A|x ≥ y} is the lower set of A, and the set U(x) is the incomparable set of A. For any x ∈ A, the average height (Brüggemann and Patil 2011) of the evaluation object on the poset (A, ≤) is

$$hav\left( x \right) = \frac{{\left| {F\left( x \right)} \right|}}{{\left| {F\left( x \right)} \right| + \left| {O\left( x \right)} \right|}}\left| {O\left( x \right)} \right| + \frac{{\left| {O\left( x \right)} \right|}}{{\left| {F\left( x \right)} \right| + \left| {O\left( x \right)} \right|}}\left( {\left| {O\left( x \right)} \right| + \left| {U\left( x \right)} \right|} \right)$$
(4)

In the equation of U(x) = A-O(x)-F(x), |F(x)|, |O(x)|, and |U(x)| is the number of elements in the set of F(x), O(x), and U(x), respectively.

The entire scheme sets can be ordered according to hav(x).

3 Evaluation process

3.1 Establishment of the poset evaluation model

To construct the poset evaluation model, firstly, each index and grade interval of the target samples are determined, then the values of left and right endpoints of the grade intervals are used as the index values to construct grade samples, and the risk degree is determined by the comparison and ranking of the sample to be evaluated and the grade samples on each index (Zhang et al. 2022). If a target sample is sandwiched between the left endpoint and the right endpoint of the grade interval, this sample belongs to the risk level.

Based on the actual data of the engineering background, combined with field experience and related research results, the evaluation indices of the slope stability are comprehensively selected. The risk classification criteria and the influence degrees of the selected indices on the slope stability are determined. The classification criteria are constructed as the grade samples to insert into the sample group and participate in the overall ranking to reflect the risk degree of the target sample. The evaluation indices are ordered according to the importance of their weights, and the most important index is put at the first place, then second and then again. The new index data is obtained by adding the processed index data by column. This accumulative process is a way of implicit weighting. Each scheme is compared on each index one by one and the comparison relation matrix is obtained through calculation. According to Eq. (3), the Hasse matrix is converted and is used to draw a Hasse diagram. The clustering among the samples is visually illustrated in the graph. By using Eq. (4) to calculate the average height, the better and worse relation within the layer set can be clarified. The Hasse diagram can be interpreted structurally, and the risk grade of the target sample can be finally determined. The flow chart of the poset evaluation model is shown in Fig. 1.

Fig. 1
figure 1

Flow chart of the poset evaluation model

Full size image

3.2 Quantitative processing of qualitative indices

Not all evaluation indices of slope stability are quantitative and some qualitative indices cannot be calculated in the evaluation matrix. Therefore, qualitative indices are quantitatively processed in a hierarchical way according to the research results of Zhang et al. (2022). That is, the qualitative indices are divided into four grades according to the risk grade classification criteria of slope stability: stable (0.2), generally stable (0.4), slightly stable (0.6) and unstable (0.8). The processing results are shown in Table 1.

Table 1 Risk grade classification criteria of the slope
Full size table

4 Poset evaluation model of slope stability

4.1 Evaluation indices and grade classification criteria of slope stability

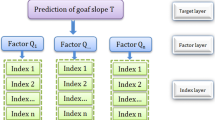
Slope failure is often caused by multiple factors, so the evaluation index of slope stability is not unique. The evaluation indices alter with different situations, and the weights of the evaluation indices and the risk grades are also different. By analyzing the factors influencing slope stability (Wang and Xu 2011) and combining with practical situations of open-pit slopes, from the four perspectives of rock mass structural characteristics, slope morphology, environment conditions and engineering conditions, 24 evaluation objects are selected in the present study as the evaluation indices of slope stability, i.e., cohesion (weak layer), internal friction angle (weak layer), elastic modulus, Poisson’s ratio, dip angle of the down-dip weak layer, joint length, joint condition, filling condition, cohesion (fault), internal friction angle (fault), relative distance to the free face, included angle between strata strike and slope strike, dip angle of the down-dip fault, transmissivity, slope angle, slope height, slope contour, slope section, maximum rainfall, in-slope groundwater or confined water head, seismic intensity, weathering degree, blasting particle vibration velocity and vehicle vibration intensity. Based on the above analysis, the index system of slope stability evaluation is established, as shown in Fig. 2. Four risk grades of slope stability are determined by linear distribution, i.e., stable (Grade I), generally stable (Grade II), slightly stable (Grade III) and unstable (Grade IV). The risk grade classification criteria are given in Table 1.

Fig. 2
figure 2

Hierarchy structure of the slope stability evaluation index system

Full size image

4.2 Normalization processing of index data

Dimensional difference often exists in the data of different indices. To eliminate the dimensional influence and make the data comparable, it is necessary to normalize the data. Normalization processing of index data includes the benefit type and the cost type:

$$y_{ij} = \frac{{x_{ij} - x_{\min } }}{{x_{\max } - x_{\min } }}$$
(5)
$$y_{ij} = \frac{{x_{\max } - x_{ij} }}{{x_{\max } - x_{\min } }}$$
(6)

The index’s influence on the results determines the choice of the processing method. For the classification criteria of slope stability risk grades in this paper, cohesion, internal friction angle, elastic modulus, relative distance to the free face and dip angle of the down-dip fault are positive indicators. Larger values indicate lower risk of a slope landslide. Hence, Eq. (5) is used for processing these indices. The other evaluation indices are inverse indicators. Larger values imply higher risk of a slope landslide, so the Eq. (6) is applied for data processing.

4.3 Ranking the weights of the evaluation indices

Index weights are crucial for any weight-based evaluation model. In the poset evaluation model, there is no need to calculate specific weights, but accurate prediction of samples can be achieved by ranking the weights (Jia et al. 2021). According to practical engineering experience and the methods of solving the weights of the influencing factors and evaluation indices in the literatures (Zhu et al. 2018; Wei et al. 2019; Wang et al. 2021; Zhao 2022), after comparative analysis, the weight ranking of the evaluation indices is carried out by using the improved CRITIC-G2 weighting method.

(1) Determine the weights of the objective indices of the improved CRITIC method

The improved CRITIC weighting method is a difference-driven objective weighting method that can reflect both the variation degree of each evaluation index and the influence degree between the evaluation indices (Zhu et al. 2018). Firstly, the improved CRITIC information is employed to reflect the real information of the data and the mean deviation of the evaluation indices is introduced. Secondly, instead of the decision-makers’ subjective conclusion, the ratio of the improved CRITIC information of each evaluation index and the least important evaluation index is used to determine the importance degree. The main steps of weight calculation are as follows.

① Calculate the information contained in each index by

$$C_{k} = \frac{{\sigma_{k} }}{{u_{k} }}\sum\limits_{i = 1}^{m} {\left( {1 - \left| {t_{ik} } \right|} \right)} ,\quad k = 1,2, \ldots ,m$$
(7)

where Ck is the improved CRITIC information amount of the kth evaluation index, σk is the standard deviation of the kth evaluation index, uk is the mean value of the kth index, \(\sum\nolimits_{i = 1}^{m} {(1 - \left| {t_{ik} } \right|)}\) is the quantified value of the influence degree between the kth index and the other indices, and tik is the correlation coefficient of the evaluation indices i and k.

② Determine the weight of each index by

$$W_{k} = \frac{{C_{k} }}{{\sum\nolimits_{i = 1}^{m} {C_{i} } }},\quad i = 1,2, \ldots ,m$$
(8)

where Wk is the weight of the kth index.

(2) Determine the weights of the subjective indices in the G2 method

The G2 weighting method is a function-driven subjective weighting method that assigns a score range to an evaluation index according to the relative importance of each evaluation index under the condition of uncertain information and risk. It calculates the weight of each evaluation index in the group decision-making process through quantitative calculation (Yan et al. 2010). The weight calculation of the G2 weighting method is as follows.

Based on the experts’ experience and their preferred coefficients, the m indices in the original index set {ui} are reordered as {ui1, ui2, … uik, …, uim} according to the importance degree. ui1 is the most important index while uim is the least important index. The experts make a rational judgment on the ratio (rkm) of the importance degree of uik to uim.

$$r_{km} = a_{k} ,\quad k = 1,2, \ldots ,m - 1$$
(9)

However, in certain cases, due to the lack of some information, the experts cannot give an exact value of ak, so they have to assign it a range of values [d1k, d2k]. The bounded, closed, real number is considered as an interval number consisting of d1 and d2, and is denoted as Dk, where Dk = [d1k, d2k].

$$e(D_{k} ) = d_{2k - d1k}$$
(10)
$$n(D_{k} ) = (d_{2k} + d_{1k} )/2$$
(11)
$$\varphi (D_{k} ) = n(D_{k} ) + \varepsilon e(D_{k} )$$
(12)
$$r_{km} = a_{k} \in [d_{1k} ,d_{2k} ],\quad k = 1,2, \ldots ,m - 1$$
(13)

In the above equations, e(Dk) is the interval length, n(Dk) is the midpoint of the interval, φ(Dk) is the interval mapping function of the experts’ risk attitude, and ε is risk attitude factor (ε ≤ 0.5). − 0.5 ≤ ε ≤ 0 means a conservative attitude. When ε = 0, it is neutral. 0 ≤ ε ≤ 0.5 indicates a risk. For a specified expert, ε is a definite number.

If the assignment of {Dk} is accurate, the weight of the k-th index in the G2 method (WG) is calculated by the following equation,

$$W_{G} = \varphi (D_{k} )/\sum\limits_{i = 1}^{m} {\varphi (D_{i} )} ,\quad k = 1,2, \ldots ,m.$$
(14)

(3) Determine the comprehensive weights in the improved CRITIC-G2 method

To take into account the decision-makers’ intuitive understanding of the evaluation indices and the objective survey data that truly reflect the slope instability characteristics, the confidence interval of the observed values of Ck is denoted as [C1k, C2k], where k = 1, 2, …, m. Based on the ratio of the upper bounds to the lower bounds of the confidence interval of the improved CRITIC information, the interval of the ratio of the importance degrees of the two indices is calculated and then substituted into the rational judgement interval artificially given in the G2 method, namely

$$R_{km} = \left\{ {\begin{array}{*{20}l} {[d_{1k} ,d_{2k} ] = \left[ {\min \left( {\frac{{C_{1k} }}{{C_{1m} }},\frac{{C_{2k} }}{{C_{2m} }}} \right),\max \left( {\frac{{C_{1k} }}{{C_{1m} }},\frac{{C_{2k} }}{{C_{2m} }}} \right)} \right],\quad C_{k} > C_{m} ,} \hfill & {k = 1,2, \ldots ,m} \hfill \\ {[1,1],\quad C_{k} \le C_{m} ,} \hfill & {k = 1,2, \ldots ,m} \hfill \\ \end{array} } \right..$$
(15)

The assigned weight (WZ) of the kth evaluation index in the improved CRITIC-G2 interval is obtained by

$$W_{Z} = \frac{{0.5 \times (d_{1k} + d_{2k} ) + \varepsilon (d_{2k} - d_{1k} )}}{{\sum\nolimits_{i = 1}^{m} {0.5 \times (d_{1i} + d_{2i} ) + \sum\nolimits_{i = 1}^{m} {\varepsilon (d_{2i} - d_{1i} )} } }},\quad k = 1,2, \ldots ,m.$$
(16)

The CRITIC method is adopted to reorder the evaluation indices of slope stability. After the reordering, relevant experts are invited to score the factor layer and the index layer with the score range of [0, 1]. Considering the experts’ inability to give an exact number, the probability of slope instability caused by each index is replaced by an interval number. According to the experts’ scoring interval, the improved G2 method based on the improved CRITIC is used to calculate the weight of each evaluation index. The risk attitude factor (ε) of the experts is known to be 0.25. The scores of each index at factor level and index level are substituted into Eq. (16). The results are shown in Tables 2 and 3, and the weight values of each evaluation index are obtained.

Table 2 Expert scores and improved weight values at factor level
Full size table
Table 3 Expert scores and improved weight values at criterion level
Full size table

The weight order at the factor layer is ω1 > ω2 > ω3 > ω4. At the index layer, the weight orders are ω11 > ω12 > ω13 > ω14 > ω15 > ω19 > ω110 > ω111 > ω113 > ω112 > ω114 > ω16 > ω17 > ω18 for the indices of rock mass stractural characteristics, ω22 > ω21 > ω23 > ω24 for the indices of slope morphnolgy, ω32 > ω33 > ω34 > ω31 for the indices of environment conditions, and ω41 > ω42 for the inices of engineering conditions. Figure 3 shows the distributions of the index weights.

Fig. 3
figure 3

Factor and index weight distributions

Full size image

4.4 Application example

To verify the feasibility of the comprehensive evaluation model based on the Poset theory for the stability evaluation of the open-pit slope, the east end slope at Yuanbaoshan Open-pit Coal Mine is taken as the research background. The slope height is 200 m. The slope angle is 20°. There is a weak bedding layer with a dip angle of about 12° in the slope. The cohesion is 21.5 kPa and the internal friction angle is 16.86°. There is a large normal fault at the east side, which is 35° away from the slope strike. The dip angle of the fault is 50°. The relative distance to the free face is 108 m. The rock mass has loose structure and poor integrity, which is considered as broken loose rock masses. The specific parameters are listed in Table 4.

Table 4 Slope engineering parameters
Full size table

4.5 Comparison relation matrix

Risk grade samples of slope stability are constructed. A1, A2, A3 and A4 are grade sets constructed according to the endpoint values of the risk grade interval, that is, A1 = (25, 25, 10, 0.25, 5, 1, 0.2, 0.2, 500, 25, 200, 30, 65, 0.2, 15, 100, 0.2, 0.2, 0.2, 20, 20, 3, 5 0.2), A2 = (25, 20, 10, 0.3, 10, 3, 0.4, 0.4, 500, 25, 200, 45, 55, 0.4, 30, 250, 0.4, 0.4, 0.4, 50, 40, 5, 15, 0.4), A3 = (10, 10, 5, 0.35, 15, 20, 0.6, 0.6, 300, 15, 140, 60, 45, 0.6, 45, 400, 0.6, 0.6, 0.6, 100, 100, 8, 25, 0.6), and A4 = (4, 5, 1, 0.5, 15, 20, 0.8, 0.8, 100, 10, 30, 90, 30, 0.8, 45, 400, 0.8, 0.8, 0.8, 100, 100, 12, 25, 0.8). The cohesion (weak layer), internal friction angle (weak layer), elastic modulus, Poisson’s ratio, dip angle of the down-dip weak layer, joint length, joint condition, filling condition, cohesion (fault), internal friction angle (fault), relative distance to the free face, included angle between strata strike and slope strike, dip angle of the down-dip fault, water transmissivity, slope angle, slope height, slope contour and slope section, maximum rainfall, in-slope groundwater or confined water head, seismic intensity, weathering degree, blasting particle vibration velocity and vehicle vibration intensity are used to constructed the sample to be evaluated (A5), and are inserted into the sample group of empirical data to participate in the ranking, as shown in Table 5. By integrating the experts’ experience, this method is able to improve subjectivity, balance subjective factors and objective factors, and reflect the importance of indices themselves and the data information of the indices (Lebanon and Lafferty 2002; Silan et al. 2021).

Table 5 Evaluation set data
Full size table

The evaluation index data is normalized based on Eqs. (5) and (6), hence, the sample data are all in the interval of [0, 1]. After data processing, the evaluation matrices of the four factors are adjusted in the order of index weights as follows:

$$\begin{aligned} & X_{1} = \left[ {\begin{array}{*{20}l} {1.000} \hfill & {1.000} \hfill & {0.474} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill \\ {1.000} \hfill & {1.000} \hfill & {0.474} \hfill & {0.800} \hfill & {0.500} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {0.714} \hfill & {0.750} \hfill & {0.667} \hfill & {0.667} \hfill & {0.667} \hfill & {0.895} \hfill \\ {0.286} \hfill & {0.333} \hfill & {0.250} \hfill & {0.600} \hfill & {0.000} \hfill & {0.500} \hfill & {0.333} \hfill & {0.647} \hfill & {0.429} \hfill & {0.500} \hfill & {0.333} \hfill & {0.333} \hfill & {0.333} \hfill & {0.000} \hfill \\ {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill \\ {0.833} \hfill & {0.791} \hfill & {1.000} \hfill & {0.200} \hfill & {0.300} \hfill & {0.625} \hfill & {0.667} \hfill & {0.812} \hfill & {0.571} \hfill & {0.917} \hfill & {0.833} \hfill & {0.667} \hfill & {0.750} \hfill & {0.526} \hfill \\ \end{array} } \right] \\ & X_{2} = \left[ {\begin{array}{*{20}l} {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill \\ {0.500} \hfill & {0.500} \hfill & {0.667} \hfill & {0.667} \hfill \\ {0.000} \hfill & {0.000} \hfill & {0.333} \hfill & {0.333} \hfill \\ {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill \\ {0.667} \hfill & {0.833} \hfill & {0.500} \hfill & {0.333} \hfill \\ \end{array} } \right],\quad X_{3} = \left[ {\begin{array}{*{20}l} {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill \\ {0.625} \hfill & {0.750} \hfill & {0.778} \hfill & {0.667} \hfill \\ {0.000} \hfill & {0.000} \hfill & {0.444} \hfill & {0.333} \hfill \\ {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill \\ {0.375} \hfill & {0.625} \hfill & {0.667} \hfill & {0.750} \hfill \\ \end{array} } \right],\quad X_{4} = \left[ {\begin{array}{*{20}l} {1.000} \hfill & {1.000} \hfill \\ {0.500} \hfill & {0.667} \hfill \\ {0.000} \hfill & {0.333} \hfill \\ {0.000} \hfill & {0.000} \hfill \\ {0.415} \hfill & {0.500} \hfill \\ \end{array} } \right] \\ \end{aligned}$$

Then, according to Eq. (2), the evaluation matrix of the evaluation index set of various factors is accumulated, and the cumulative transformation matrices containing the weights are obtained as follows,

$$\begin{aligned} & D_{1} = \left[ {\begin{array}{*{20}l} {1.000} \hfill & {2.000} \hfill & {3.000} \hfill & {4.000} \hfill & {5.000} \hfill & {6.000} \hfill & {7.000} \hfill & {8.000} \hfill & {9.000} \hfill & {10.000} \hfill & {11.000} \hfill & {12.000} \hfill & {13.000} \hfill & {14.000} \hfill \\ {1.000} \hfill & {2.000} \hfill & {3.000} \hfill & {3.800} \hfill & {4.300} \hfill & {5.300} \hfill & {6.300} \hfill & {7.300} \hfill & {8.014} \hfill & {8.764} \hfill & {9.431} \hfill & {10.098} \hfill & {10.765} \hfill & {11.660} \hfill \\ {0.286} \hfill & {0.619} \hfill & {1.118} \hfill & {1.718} \hfill & {1.718} \hfill & {2.218} \hfill & {2.551} \hfill & {3.198} \hfill & {3.627} \hfill & {4.127} \hfill & {4.460} \hfill & {4.793} \hfill & {5.126} \hfill & {5.126} \hfill \\ {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill \\ {0.833} \hfill & {1.624} \hfill & {1.624} \hfill & {1.824} \hfill & {2.124} \hfill & {2.749} \hfill & {3.416} \hfill & {4.228} \hfill & {4.799} \hfill & {5.716} \hfill & {6.549} \hfill & {7.216} \hfill & {7.966} \hfill & {8.492} \hfill \\ \end{array} } \right] \\ & D_{2} = \left[ {\begin{array}{*{20}l} {1.000} \hfill & {2.000} \hfill & {3.000} \hfill & {4.000} \hfill \\ {0.500} \hfill & {1.000} \hfill & {1.667} \hfill & {2.334} \hfill \\ {0.000} \hfill & {0.000} \hfill & {0.333} \hfill & {0.666} \hfill \\ {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill \\ {0.667} \hfill & {1.500} \hfill & {2.000} \hfill & {2.333} \hfill \\ \end{array} } \right],\quad D_{3} = \left[ {\begin{array}{*{20}l} {1.000} \hfill & {2.000} \hfill & {3.000} \hfill & {4.000} \hfill \\ {0.625} \hfill & {1.375} \hfill & {2.153} \hfill & {2.820} \hfill \\ {0.000} \hfill & {0.000} \hfill & {0.444} \hfill & {0.777} \hfill \\ {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill \\ {0.375} \hfill & {1.000} \hfill & {1.667} \hfill & {2.417} \hfill \\ \end{array} } \right],\quad D_{4} = \left[ {\begin{array}{*{20}l} {1.000} \hfill & {2.000} \hfill \\ {0.500} \hfill & {1.167} \hfill \\ {0.000} \hfill & {0.333} \hfill \\ {0.000} \hfill & {0.000} \hfill \\ {0.415} \hfill & {0.915} \hfill \\ \end{array} } \right] \\ \end{aligned}$$

If each value in the row of m − 1 is greater than or equal to the value at the corresponding position of the mth row, sxy = 1 is recorded; otherwise, sxy = 0 is recorded. As a result, the comparison relation matrices of the evaluation index sets of various factors are obtained, i.e.

$$\begin{aligned} & S_{1} = \left[ {\begin{array}{*{20}l} 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ 0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ \end{array} } \right],\quad S_{2} = \left[ {\begin{array}{*{20}l} 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ 0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ \end{array} } \right] \\ & S_{3} = \left[ {\begin{array}{*{20}l} 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ 0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ \end{array} } \right],\quad S_{4} = \left[ {\begin{array}{*{20}l} 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ 0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ \end{array} } \right] \\ \end{aligned}$$

The evaluation matrixes of the above 4 types of evaluation index sets are arranged in a descending order of weights and integrated into the evaluation matrix with comprehensive factors and indices as

$$\begin{aligned} & X = \left[ {\begin{array}{*{20}l} {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill \\ {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {0.800} \hfill & {0.500} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {0.714} \hfill & {0.750} \hfill & {0.667} \hfill & {0.667} \hfill \\ {0.286} \hfill & {0.333} \hfill & {0.499} \hfill & {0.600} \hfill & {0.000} \hfill & {0.500} \hfill & {0.333} \hfill & {0.647} \hfill & {0.429} \hfill & {0.500} \hfill & {0.333} \hfill & {0.333} \hfill \\ {0.000} \hfill & {0.000} \hfill & {0.098} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill \\ {0.833} \hfill & {0.791} \hfill & {0.000} \hfill & {0.200} \hfill & {0.300} \hfill & {0.625} \hfill & {0.667} \hfill & {0.812} \hfill & {0.571} \hfill & {0.917} \hfill & {0.833} \hfill & {0.667} \hfill \\ \end{array} } \right. \\ & \quad \left. {\begin{array}{*{20}l} {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill & {1.000} \hfill \\ {0.667} \hfill & {0.895} \hfill & {0.500} \hfill & {0.500} \hfill & {0.667} \hfill & {0.667} \hfill & {0.625} \hfill & {0.750} \hfill & {0.778} \hfill & {0.667} \hfill & {0.500} \hfill & {0.667} \hfill \\ {0.333} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.333} \hfill & {0.333} \hfill & {0.000} \hfill & {0.000} \hfill & {0.444} \hfill & {0.333} \hfill & {0.000} \hfill & {0.333} \hfill \\ {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill \\ {0.750} \hfill & {0.526} \hfill & {0.667} \hfill & {0.833} \hfill & {0.500} \hfill & {0.333} \hfill & {0.375} \hfill & {0.625} \hfill & {0.667} \hfill & {0.750} \hfill & {0.415} \hfill & {0.500} \hfill \\ \end{array} } \right] \\ \end{aligned}$$

The cumulative transformation matrix and comparison relation matrix containing weight information under comprehensive factors and indices can be obtained by repeating the operation steps under single factor,

$$\begin{aligned} & D = \left[ {\begin{array}{*{20}l} {1.000} \hfill & {2.000} \hfill & {3.000} \hfill & {4.000} \hfill & {5.000} \hfill & {6.000} \hfill & {7.000} \hfill & {8.000} \hfill & {9.000} \hfill & {10.000} \hfill & {11.000} \hfill & {12.000} \hfill \\ {1.000} \hfill & {2.000} \hfill & {3.000} \hfill & {3.800} \hfill & {4.300} \hfill & {5.300} \hfill & {6.300} \hfill & {7.300} \hfill & {8.014} \hfill & {8.764} \hfill & {9.431} \hfill & {10.098} \hfill \\ {0.286} \hfill & {0.619} \hfill & {1.118} \hfill & {1.718} \hfill & {1.718} \hfill & {2.218} \hfill & {2.551} \hfill & {3.198} \hfill & {3.627} \hfill & {4.127} \hfill & {4.460} \hfill & {4.793} \hfill \\ {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill \\ {0.833} \hfill & {1.624} \hfill & {1.624} \hfill & {1.824} \hfill & {2.124} \hfill & {2.749} \hfill & {3.416} \hfill & {4.228} \hfill & {4.799} \hfill & {5.716} \hfill & {6.549} \hfill & {7.216} \hfill \\ \end{array} } \right. \\ & \quad \left. {\begin{array}{*{20}l} {13.000} \hfill & {14.000} \hfill & {15.000} \hfill & {16.000} \hfill & {17.000} \hfill & {18.000} \hfill & {19.000} \hfill & {20.000} \hfill & {21.000} \hfill & {22.000} \hfill & {23.000} \hfill & {24.000} \hfill \\ {10.765} \hfill & {11.66} \hfill & {12.16} \hfill & {12.66} \hfill & {13.327} \hfill & {13.994} \hfill & {14.619} \hfill & {15.369} \hfill & {16.147} \hfill & {16.814} \hfill & {17.314} \hfill & {17.981} \hfill \\ {5.126} \hfill & {5.126} \hfill & {5.126} \hfill & {5.126} \hfill & {5.459} \hfill & {5.792} \hfill & {5.792} \hfill & {5.792} \hfill & {6.236} \hfill & {6.569} \hfill & {6.569} \hfill & {6.902} \hfill \\ {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill & {0.000} \hfill \\ {7.966} \hfill & {8.492} \hfill & {9.159} \hfill & {9.992} \hfill & {10.492} \hfill & {10.825} \hfill & {11.200} \hfill & {11.825} \hfill & {12.492} \hfill & {13.242} \hfill & {13.657} \hfill & {14.157} \hfill \\ \end{array} } \right] \\ & S = \left[ {\begin{array}{*{20}l} 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ 0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 1 \hfill & 1 \hfill \\ \end{array} } \right] \\ \end{aligned}$$

4.6 Hasse matrix and Hasse diagram

There is a conversion relationship between the comparison relation matrix and the Hasse matrix. Equation (3) is adopted to convert the comparison relation matrix into the Hasse matrix:

$$\begin{aligned} & H_{{R_{1} }} = \left[ {\begin{array}{*{20}l} 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right],\quad H_{{R_{2} }} = \left[ {\begin{array}{*{20}l} 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right],\quad H_{{R_{3} }} = \left[ {\begin{array}{*{20}l} 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right] \\ & H_{{R_{4} }} = \left[ {\begin{array}{*{20}l} 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right],\quad H_{R} = \left[ {\begin{array}{*{20}l} 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right] \\ \end{aligned}$$

According to the method in the literature (Yue et al. 2018), the Hasse matrix is used to draw the Hasse diagram of the poset, as shown in Fig. 4. The Hasse diagram can directly exhibit the ranking relationship among the samples. It is divided into different layer sets. Samples in the same layer set have their advantages and disadvantages, and it is difficult to tell them apart. As illustrated in Fig. 5, the samples inside the layer set can be sorted again by comparing the average height. Equation (5) is employed to calculate the average height (Carlsen and Bruggemann 2008; Li et al. 2018). Poset ranking involves the concept of linear expansion (Bruggemann and Annoni 2014). For a poset, if all possible linear extensions are found, it is possible to calculate the average height of the individual element. Comparison and order ranking are carried out according to the obtained height (Winkler 1982).

Fig. 4
figure 4

Hasse diagrams

Full size image
Fig. 5
figure 5

Distributions of average height values

Full size image

Through calculation, it is found that, as shown in Fig. 4a, the risk grade of A5 is laid between the samples A2 and A3 under the condition of rock mass structural characteristics. The ranking order is A1 > A2 > A5 > A3 > A4 and the average height values can be seen in Fig. 5a. Thus, the risk grade of A5 belongs to Grade II (generally stable). From Fig. 4b, under the condition of slope contour, the risk grade of A5 is worse than that of the sample A1 and better than that of the sample A3. The height values are presented in Fig. 5b, and the ranking order is A1 > A2 = A5 > A3 > A4, so the risk grade of A5 is Grade II (generally stable). The risk grade of A5 under the factor of environment conditions is between A2 and A3 (seen Fig. 4c), and the height values are shown in Fig. 5c. The ranking order is A1 > A2 > A5 > A3 > A4. Hence, the risk grade of A5 is Grade II (generally stable). As can be seen in Fig. 4d, the risk grade of A5 under the factor of engineering conditions is between A2 and A3 as well. The height values are presented in Fig. 5d. The ranking order is A1 > A2 > A5 > A3 > A4, so the risk grade of A5 is Grade II (generally stable). Under comprehensive factors, as illustrated in Fig. 4e, the risk grade of A5 lies between the samples A2 and A3. The height values are provided in Fig. 5e. The ranking order is A1 > A2 > A5 > A3 > A4, therefore, the risk grade of A5 is Grade II (generally stable).

To sum up, the risk grade of A5 is Grade II (generally stable) in the evaluation sets of various factors, and the structural characteristics of rock masses have the greatest impact on the slope stability, and the slope under the evaluation of comprehensive factors is generally stable (Grade II). As a result, considering the weight orders of all indices and the evaluation results of comprehensive factors, the slope is generally stable (Grade II). The evaluation result obtained by the poset evaluation method is consistent with the actual situation, indicating that the Poset theory is applicable to the evaluation of slope stability in open pit mines.

5 Conclusions

  1. (1)

    The poset evaluation method is applied to judge the stability of an open-pit slope. It is able to eliminate the influence of the variation of index weights on the judgment. The evaluation results show that after normalized processing of the evaluation index data under various factors, the importance of rock mass structural characteristics is in the first place. The grade samples A1, A2, A3 and A4 are constructed according to the endpoint values of the risk grade intervals. The comparison relation matrix is established with the evaluation index set A5. By using the conversion relation between the comparison relation matrix and the Hasse matrix, it is concluded that the risk grade of A5 lies between the samples A2 and A3, and the slope is in a generally stable state (Grade II) under the comprehensive evaluation of various factors, which is consistent with the actual situation of the engineering project and verifies the rationality and feasibility of the Poset theory.

  2. (2)

    The poset evaluation method can be used to classify and cluster the risk degree of an open-pit slope, which can accurately assess the slope stability and facilitate a rational slope design. Moreover, prevention and control measures can be determined according to the main factors affecting the slope stability so as to avoid landslides.

  3. (3)

    For the evaluation of the open-pit slope stability, 24 influencing factors are selected as the evaluation indices from four aspects, namely rock mass structural characteristics, slope contour, environment conditions and engineering conditions. However, owing to the fact that a great number of factors influence the slope stability, the integrity of the evaluation system needs to be further improved.