1 Introduction

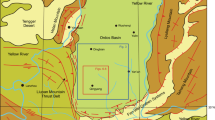
The Ordos Basin generates more than 50 million tons of oil and gas annually, serving as China's most enormous petroleum production basin (Hou et al. 2022). The Mesozoic Triassic Chang 7 Member shale oil reservoir plays a significant role during this process, which is distributed widely in the basin and contains numerous high expulsion oils in the tight play zone, see (Fig. 1Yang et al. 2016). Driven by the North American shale oil revolution, the Chang 7 Member organic-rich shale oil was mainly exploited by hydraulic fracturing (Niu et al. 2022). Due to the strong vertical anisotropic caused by the lacustrine sedimentary genesis, the hydraulic fracture height usually encounters a significant impediment from in-situ stress difference and interface between stratus (Li et al. 2017; Huang et al. 2019; Pang et al. 2022). Thus in-situ stress evaluation from the scale of the basin becomes necessary for the exploitation and development of shale oil in the Ordos Basin.

Fig. 1
figure 1

Sedimentary facies and sand body distribution in Chang 7 Member, Ordos Basin

Full size image

In-situ stress evaluation of deep formation is an essential branch of reservoir geomechanics and the key to solving problems such as hydraulic fracturing stimulation and wellbore stability (Abou-Sayed et al. 1978; Ito and Zoback 2000; Bing et al. 2014). The deep in-situ stress evaluation is divided into single-well ground stress evaluation and regional ground stress evaluation. The single-well ground stress evaluation focuses on the ground stress evaluation of the target section. In contrast, the regional ground stress evaluation focuses more on the planar distribution of the structural-scale ground stress. The evaluation methods of single well ground stress include the hydraulic fracturing method, Kaiser effect method, differential strain method, multipole logging method, and so on (Stephansson and Zang 2012). Among them, the first three belong to the experimental evaluation, and the multipole logging method belongs to the geophysical evaluation. Jin Yan (Yan et al. 2006) believed that it is difficult to obtain the ground stress of complex shale formations individually, and it is necessary to combine multiple testing methods to evaluate the ground stress of the reservoir accurately. In addition to field tectonic phenomenon observation, the mainstream method since the 1980s has been the finite element method for regional ground stress evaluation at the tectonic scale (Huiskes and Chao 1983; Rietbergen and Bert 1995; Fahey and Carter 1993). That is, the three-dimensional geological modeling of basins, faults, and other structures is carried out, the grid is divided, combined with the loading stress of previous tectonic movements, the numerical calculation is carried out, and the current regional ground stress field is obtained (Brown and Shie 1991).

The regional stress field evaluation based on the finite element method belongs to the forward modeling method, which could quickly calculate the ground stress distribution in thousands of square kilometers to ensure robustness. However, affected by the grid size, this method has no precision advantage in evaluating the stress field in shale oil reservoirs. Although the ground stress evaluation of a single well has a small error, there are problems such as difficulty in downhole coring and limited multipole logging data. Therefore, this method has not been widely used in regional ground stress evaluation at the tectonic scale.

In the field of reservoir geomechanics, various methods have been employed to assess ground stress and tectonic stress coefficients. However, the method presented in this study, which involves conducting ground stress Kaiser tests on a large number of wells and analyzing the horizontal stress difference and tectonic stress coefficients, is relatively novel. One of the primary reasons for the limited application of this method in previous studies is the sheer volume of data required. Conducting Kaiser tests on a large number of wells and analyzing the results necessitates the collection and processing of a vast amount of data, which can be time-consuming and resource-intensive. Additionally, the availability of suitable wells for downhole coring and testing may be limited in some regions, further restricting the application of this method. Despite these challenges, our study demonstrates the potential of this method to provide valuable insights into the ground stress characteristics and tectonic stress regime of the Chang 7 Member in northern Shaanxi.

In this study, based on mastering a large number of experimental and logging data, the inversion method was used to evaluate the regional distribution of ground stress in the Chang 7 Member in northern Shaanxi. First, combined with the Kaiser effect method and the Sn ground stress calculation model, the ground stress of the target layers of 600 wells in the region was evaluated separately. Then, the plane distribution map of regional horizontal stress and horizontal stress difference is drawn by interpolation method, and the refined and regionalized evaluation of the in situ stress of Chang 7 member shale oil reservoirs in northern Shaanxi was realized from the basin scale.

2 Calculation of ground stress of a single well in the shale oil reservoir

2.1 Transverse isotropy with a vertical axis of symmetry (TIV) formation ground stress calculation model

At present, the widely used ground stress calculation models include the Eaton model (Alvarez and Lucas 2007), Anderson model (Barnes 1976), and Newberry model (Barnes 1976), as well as the Sixth Five model and Seventh Five model proposed by Huang Rongzun (Deng and Huang 1997). In 2008, S.M.Higgins (Higgins et al. 2008) established a horizontal ground stress calculation model (Sn model) for TIV formation, which takes into account the anisotropy of rocks. Therefore, in this study, we used the Sn model to calculate the ground stress of a single well.

$${\sigma }_{v}^{i}={\rho }_{0}g{H}_{0}+{\sum }_{i} {\rho }_{i}gd{h}_{i}$$
(1)
$${\sigma }_{\mathrm{h}}=\frac{v}{1-v}\left({\sigma }_{\mathrm{V}}-a{\sigma }_{\mathrm{pp}}\right)+\frac{E}{1-{v}^{2}}{\varepsilon }_{\mathrm{h}}+\frac{Ev}{1-{v}^{2}}{\varepsilon }_{H}+a{\sigma }_{\mathrm{PP}}$$
(2)
$${\sigma }_{\mathrm{H}}=\frac{v}{1-v}\left({\sigma }_{\mathrm{V}}-a{\sigma }_{\mathrm{pp}}\right)+\frac{E}{1-{v}^{2}}{\varepsilon }_{\mathrm{H}}+\frac{Ev}{1-{v}^{2}}{\varepsilon }_{h}+a{\sigma }_{\mathrm{PP}}$$
(3)

In which, \({\sigma }_{v}^{i}\) is overlying ground stress, MPa, \({\sigma }_{\mathrm{H}}\)、\({\sigma }_{\mathrm{h}}\) is maximum and minimum horizontal principal ground stress, MPa, \({\sigma }_{\mathrm{PP}}\) is formation pore pressure, MPa, \(a\) is fffective stress factor, \(E\) is Young's modulus, \(v\) is Poisson's ratio, \({\varepsilon }_{\mathrm{h}}\)、\({\varepsilon }_{H}\) is maximum and minimum horizontal tectonic stress coefficient, g is gravitational acceleration, \(\rho\) is density, g/cm3.

2.2 Dynamic and static elastic parameter conversion

The dynamic Young's modulus of rock refers to the mechanical property parameter exhibited by rock under various dynamic or cyclically varying loads (such as sound waves, shocks, vibrations, etc.) (Eissa and Kazi 1988; Wolfenden et al. 1989). Sound velocity measurements could give it well logging or seismic data. The static Young's modulus is the mechanical parameter the rock exhibits under static load, which needs to be measured in the laboratory. The deformation and failure of the wellbore are relatively slow stationary processes. Therefore, the modulus's dynamic and static conversion must be calculated using logging data for rock mechanics evaluation (Lacy 1997). The dynamic and static transformation relationship of Young's modulus in the vertical direction of this study area is shown in Fig. 2, and its fitting relationship is formula (4); the dynamic and static transformation relationship of Poisson's ratio is shown in Fig. 3, and its fitting relationship is formula (5).

$${E}_{S}=0.76*{E}_{d}-4.34$$
(4)
$$\mu_{s} = - 105.97*\mu_{{\text{d}}} + 32.{1}0{5}$$
(5)
Fig. 2
figure 2

Conversion of dynamic and static Young's modulus of reservoir rock in Chang 7 Member in northern Shaanxi

Full size image
Fig.3
figure 3

Dynamic and static Poisson's ratio transformation of reservoir rocks in Chang 7 Member in northern Shaanxi

Full size image

In which, \(Es\) is dynamic Young's modulus, GPa, \({E}_{d}\) is static Young's modulus, GPa, \({\mu }_{s}\) is dynamic Poisson's ratio, \({\mu }_{\mathrm{d}}\) is static Poisson's ratio.

3 Regional ground stress interpretation results

3.1 Geology background

The Triassic Yanchang Formation in the Northern Shaanxi Area is characterized by a complex stratigraphy and diverse lithology. The formation is primarily composed of mudstone, siltstone, and sandstone, with occasional interbeds of shale and coal. The depth of the Yanchang Formation varies across the region, with typical depths ranging from approximately 2,000 to 3,500 m below the surface. The overburden lithology of the Yanchang Formation is dominated by mudstone and siltstone, which contribute to the formation's low permeability and high sealing capacity. These characteristics make the Yanchang Formation a suitable target for shale oil and gas exploration. The formation's depth and overburden lithology play a crucial role in the assessment of reservoir geomechanics, as they influence the in-situ stress distribution, rock mechanical properties, and fracture behavior.

Since the Mesozoic, the in-situ stress field in the Ordos Basin has been affected by the three-phase tectonic activities of Indo-China, Yanshan, and Xishan(Shixiang et al. 2013). As shown in Fig. 4, during the Indo-China period, the Ordos Basin was affected by the collision between the Qiangtang-South China plate and the Eurasian plate, resulting in a tectonic stress field of north–south compression and east–west extension (Zhang et al. 2015). The maximum principal stress trace is approximately SN trending. During the Yanshanian period, it was affected by the collision between the paleo-Pacific plate and the Eurasian plate, resulting in the effect of extrusion from the periphery of the basin to the inside of the bay. The maximum principal stress trace is rotated counterclockwise to the NW–SE direction. Affected by the collision of the Pacific Plate and the Indian Ocean Plate during the Himalayan period, the maximum principal stress trace rotates clockwise in the NNE-SSW direction (Liu et al. 2017).

Fig. 4
figure 4

Schematic diagram of tectonic movements in the Ordos Basin and its surroundings

Full size image

3.2 Calculation of stress tectonic coefficient in Northern Shaanxi

In this study, we conducted ground stress Kaiser tests on 60 critical wells in the Chang 7 member in northern Shaanxi to assess the in-situ reservoir stress characteristics. Downhole coring was performed on each well, and the cores were subjected to Kaiser tests to determine the horizontal ground stress characteristics. The results of these tests are presented in Fig. 5, which shows the distribution of horizontal ground stress in the Chang 7 member. SH ranged from 20.3 to 38.1 MPa, while Sh varied between 25.7 and 47.3 MPa. The horizontal stress difference was found to be between 1.0 and 12.0 MPa, with an average value of 5.8 MPa (Fig. 6). Based on the experimental results of the in-situ reservoir stress in the Chang 7 member from the 60 groups, we calculated the maximum and minimum tectonic stress coefficients. The average values of the experimental results were used to determine the applicable tectonic stress coefficients for the Chang 7 member in northern Shaanxi. As shown in Fig. 7, the maximum horizontal tectonic stress coefficient was found to be 0.232, while the minimum horizontal tectonic stress coefficient was 0.215.

Fig. 5
figure 5

Ground stress test results of Kaiser test in Chang 7 section in northern Shaanxi

Full size image
Fig.6
figure 6

Test results of horizontal stress difference in Chang 7 Member in northern Shaanxi

Full size image
Fig.7
figure 7

Horizontal maximum and minimum tectonic stress coefficients of Chang 7 Member in northern Shaanxi

Full size image

As shown in Fig. 8, The D181 well was used as an example to investigate the longitudinal distribution pattern of ground stress in the Chang 7 section reservoir and to verify the accuracy of the ground stress logging interpretation model. The accuracy of the logging interpretation of the ground stress parameters in the Chang 7 section was in good agreement with the ground stress values measured by the Kaiser experiment, with the error controlled to within 14%.

Fig. 8
figure 8

Dan-181 well logging curve and in-situ stress interpretation results

Full size image

3.3 Regional ground stress distribution

3.3.1 Drawing process

In this study, we selected 600 wells in key blocks in northern Shaanxi to calculate the ground stress of the Chang 7 section of a single well in batches. The calculation was performed using Python code, which was compiled to automate the process according to formulas 1–3. The mean value of the ground stress for each well was then calculated and used as input data for the plane distribution map.

We used the sand body distribution maps of the Chang 71, Chang 72, and Chang 73 sublayers in northern Shaanxi as a base to create the plane distribution map. The mean ground stress values for each well were plotted on the sand body distribution maps at the corresponding well locations. The values were represented as points on the map, with each point corresponding to a single well.

Next, we manually connected the contour areas according to the ground stress values to form the plane distribution map of the horizontal maximum ground stress and the horizontal stress difference. The contour lines were drawn to represent areas with similar ground stress values, and the areas between the contour lines were shaded to indicate the range of ground stress values in each area. The resulting plane distribution maps are shown in Figs. 9, 10, 11, 12, 13, 14 and 15.

Fig.9
figure 9

Distribution of the horizontal maximum principal stress in the Chang 71section in northern Shaanxi

Full size image
Fig.10
figure 10

Distribution of the horizontal maximum principal stress at the Chang 72 section in northern Shaanxi

Full size image
Fig.11
figure 11

Distribution of the horizontal maximum principal stress at the Chang 73 level in northern Shaanxi

Full size image
Fig.12
figure 12

Distribution of horizontal stress difference in Chang 71 in northern Shaanxi

Full size image
Fig.13
figure 13

Distribution of horizontal stress difference in Chang 72 in northern Shaanxi

Full size image
Fig.14
figure 14

Plane distribution of horizontal stress difference in Chang 73 in northern Shaanxi3

Full size image
Fig. 15
figure 15

Schematic illustration showing the types of in situ stress regimes based on Anderson’s classification (after Brooke-Barnett et al., 2015 (Brooke-Barnett et al. 2015)). a thrust-faulting stress regime, b strike-slip faulting stress regime and c normal faulting stress regime. The pink plane indicates the orientation of a propagated hydraulic fracture in the associated stress regime

Full size image

The plane distribution maps provide a visual representation of the spatial distribution of ground stress in the Chang 7 section in northern Shaanxi. These maps can be used to identify areas with high or low ground stress, which can have important implications for reservoir geomechanics and shale oil and gas exploration. The maps also provide valuable information for the design of hydraulic fracturing treatments and the optimization of well placement.

3.3.2 Distribution law of ground stress in Chang 71, Chang 72, and Chang 73

As shown in Figs. 9, 10 and 11, the SH of Chang 71, Chang 72, and Chang 73 increased layer by layer, and the high value of SH was distributed near Jiyuan, Dingbian, and Zhoujiawan. The SH range of the Chang 71 section was concentrated in the range of 20 to 62 MPa. Among them, the ground stress above 50 MPa was mainly distributed in the northwest area north of Jiyuan. Overall, there was a gradual downward trend from west to east. The SH range of the Chang 72 section was concentrated in 18 to 62 MPa. Among them, the ground stress above 50 MPa was mainly distributed in Jiyuan, Youfangzhuang, Dingbian, and west of Yanchi. On the whole, there was a downward trend from northwest to southeast. The SH range of the Chang 73 section was concentrated in the range of 20 to 62 MPa.Ground stress above 50 MPa was mainly distributed in the north Wucangbao, Jiyuan, and Dingbian areas.

As shown in Figs. 12, 13 and14, the horizontal stress difference of Chang 7 member shale oil reservoirs in northern Shaanxi showed the distribution characteristics of high in the west and low in the east. And the horizontal stress difference of Chang 71, Chang 72, and Chang 73 sections increases sequentially. The horizontal stress difference range of the Chang 71 section was concentrated in the 2.6 to 8.4 MPa, and the overall value changed little. The horizontal stress difference above 6.5 MPa was mainly distributed in Yanchi, Dingbian, Youfangzhuang, and the west of Yuancheng. Overall, there was a downward trend from west to east. The horizontal stress difference range of the Chong 72 section was concentrated in the field of 2.6 to 8.8 MPa. The horizontal stress difference above 6.5 MPa was mainly distributed in the western region, and the maximum value in the west of Yanchi and Jiyuan area was above 8 MPa.Overall, there was a downward trend from west to east. The horizontal stress difference range of the Chong 73 sections was concentrated in the 3.2 to 8.6 MPa. The overall value didn't change much but changed more frequently. The horizontal stress difference above 6.5 MPa was mainly distributed south of Yanchi, Dingbian, west of Gengwan, and the Ansai area. On the whole, it first decreased and then increased from northwest to southeast.

4 Discussion and analysis

In the finite element simulation method, solving the regional stress field, tectonic movement, fault, etc., as boundary conditions are essential in solving the partial differential equilibrium equation (Guo et al. 2015). The general process of the method is: discrete 3D model, assemble stiffness matrix, consider boundary conditions, construct equilibrium equation, solve displacement field, and solve stress field (Advani and Lee 1982). The main types of in situ stress regimes based on Anderson’s classification are shown in Fig. 15. From Fig. 16, we can get a rough distribution of faults in the Ordos Basin, which shows the center of Ordos Basin is inactive as the edge of the basin has a bunch of faults. In 2020, Ju (Ju et al. 2020) used the finite element method to calculate the current ground stress field of the Yanchang Formation in the Ordos Basin, using the Indo-China, Yanshan, and Himalayan stress fields and faults as boundary conditions, and found that the NF stress regime is dominant in the Yanchang Formation reservoir, so the Sv > SHmax > Shmax, differential stress between the magnitudes of Sv and Shmin is relatively large (Fig. 17).

Fig. 16
figure 16

Types of faults in the Ordos Basin and surrounding areas (.Heidbach et al. 2016)

Full size image
Fig.17
figure 17

Planar distribution of horizontal stress difference in Chang 6 in Ordos Basin simulated by FEM (Liu et al. 2020)

Full size image

Liu (Liu et al. 2020) established a reservoir heterogeneity model and a geomechanically heterogeneity model and with the finite element method, and predicted the 3D distribution of in situ stress. They found that Δσ is between 5 and 12.5 MPa, and the stress difference in west is bigger than in east, see Fig. 18. Chang 6 formation is adjacent to Chang 7 formation, so we take the result from Liu as a reference.

Fig. 18
figure 18

Geological overview map of Yanchang Formation in Ordos Basin (Zhi et al. 2017)

Full size image

In Liu's study, the three-dimensional distribution of in-situ stress in the Ordos Basin of China was determined through finite element numerical simulation. The study focused on the effects of reservoir and petrophysical characteristics on the distribution of in-situ stress. By establishing reservoir heterogeneity and geomechanical heterogeneity models, the study predicted the 3D distribution of reservoir physical parameters and in-situ stress. The study found that clay content negatively correlated with horizontal stress difference (Δσ) and horizontal principal stress difference coefficient (Kh). Rock density, porosity, and permeability had little effect on Δσ and Kh. Fluid properties affected the in-situ stress magnitude, with water saturation greater than 60% negatively correlated with Δσ and Kh. Poisson's ratio had a weak effect on Δσ but a significant negative correlation with Kh.

In contrast, our study proposed a new method based on the Kaiser effect method and the Sn Model to evaluate regional ground stress in shale oil reservoirs from point to point. Kaiser tests were used to obtain regional tectonic stress coefficients. Combined with the dynamic and static transformation of elastic parameters, the Sn ground stress calculation model suitable for the Northern Shaanxi Area was constructed. The plane distribution maps of SH and the difference between SH and Sh were drawn. The study found that the SH in this area was between 20 and 60 MPa, and the So was between 2.6 MPa and 8.8 MPa. The forward modeling results coincided well with the inversion results in this research. The research results indicated that the movement of plate and shell and deposition were critical factors of regional ground stress distribution.

Comparing the two studies, it is evident that both studies aimed to predict the in-situ stress distribution in reservoirs. However, the methods used were different. Liu's study used finite element numerical simulation and focused on the effects of reservoir and petrophysical characteristics on the distribution of in-situ stress. Our study proposed a new method based on the Kaiser effect method and the Sn Model to evaluate regional ground stress from point to point. The results of both studies provide valuable insights into the factors affecting the distribution of in-situ stress in reservoirs. However, our study offers a novel approach to evaluating regional ground stress in shale oil reservoirs, which can be a valuable reference for further integration of geologic and engineering in evaluating shale oil reservoirs.

The current structural form of the Ordos Basin is generally an asymmetric, north–south rectangular basin with a broad and gentle east wing and a steep and narrow west wing (Yin et al. 2019). The faults and folds on the basin's edge are relatively developed, the internal structure is relatively simple, and the stratum is gentle. The bottom boundary of the Chang 7 section is a broad and soft slope dipping from east to west (Qu et al. 2020). The current stratum is buried at about 700–2600 m, as shown in Fig. 18.

It could be seen from the formula (1), that the change of gravity with the buried depth not only affects the magnitude of the principal vertical stress but also derives the stress component in the horizontal direction, thereby affecting the magnitude of the horizontal stress. The principal vertical stress was related to the density of the rock and its burial depth. Horizontal stress was mainly influenced by rock mechanics parameters, horizontal stress components of principal vertical stress, pore pressure, and tectonic stress. Assuming that the target layer was located in a closed system, it could be considered that the pore pressure and its horizontal stress components were constant. The current ground stress is mainly affected by the burial depth and rock mechanical parameters, and the burial depth is proportional to the horizontal maximum principal stress.

5 Conclusion

We devised a novel method to evaluate the regional in-situ stress in the shale oil reservoir, aiming to solve the challenges of vertical anisotropy and analyze the main influencing factors of regional in-situ stress. Completing 60 groups of Kaiser in-situ stress tests in which samples were from 60 critical wells, we calculated the regional tectonic stress factor of SH and Sh in the northern Shanbei area, which are 2.232 and 2.125, respectively. Based on the logging data, we used the Sn model to calculate the ground stress in Chang 7 Member of 600 wells and drew the ground stress distribution map of each sublayer in Chang 71, Chang 72, and Chang 73 in northern Shaanxi. The SH was between 20 and 60 MPa, and the high-stress value is mainly distributed in the west and north. The horizontal stress difference was between 2.6  and 8.8 MPa, and the high-stress weight is distributed primarily in the northwest.

By comparison, it was found that this method's regional ground stress field inverted is consistent with the results simulated by the finite element method. Combined with the analysis of geological factors, the tectonic activities such as plate collision and the paleo topography related to the burial depth of the strata were the main controlling factors of the regional stress field distribution of the Chang 7 Member in northern Shaanxi. This study proposed a new idea for analyzing the regional stress field in deep strata by combining reservoir geomechanics and structural geology. The research results provided a reference for the integrated layout of geology and engineering for shale oil explorers.