1 Introduction

In situ stresses are very critical parameters for geomechanics analyses and rock engineering design. It is commonly assumed that in situ stresses are consisted of three principal stresses: the minimum horizontal stress, the maximum horizontal stress, and vertical stress. The vertical stress, or overburden stress is easier to obtain. However, determinations of the minimum and maximum horizontal stresses are not so straight forward. Some field tests can be used to measure horizontal stresses (e.g., Hudson et al. 2003; Haimson and Cornet 2003; Ljunggren et al. 2003; Schmitt et al. 2012), particularly the minimum horizontal stress (e.g., mini-frac test; leak-off test; diagnostic fracture injection test or DFIT). However, field test results may not be available in the interested depth. Various theoretical and empirical methods have been proposed to estimate horizontal stresses in isotropic rocks (e.g., Warpinski et al. 1985; Thiercelin and Plumb 1994; Zajac and Stock 1997; Okabe et al. 1998; Zoback et al. 2003; Li and Purdy 2010; Meng et al. 2011; Zhang and Zhang 2017; Zhang et al. 2018). However, many geologic formations are naturally fractured rocks (e.g., Zhang and Roegiers 2005; Peng and Zhang 2007; Lv et al. 2020). For these rocks, the isotropic model presents a large uncertainty in the horizontal stress determination.

We recently examined in situ stresses and pore pressures in the Xujiahe tight gas reservoirs using the isotropic model. The studied Xujiahe reservoirs are the Triassic sandstones located in the Xinchang and Xiaoquan gas fields in the western Sichuan basin, as described in Zhang et al. (2020). Comparing to the field measurements of in situ stresses, the calculated result from the isotropic model has a certain difference with the measured result. This may be caused by naturally fractured rocks in the reservoirs, which induces formation anisotropy (Fig. 1). Figure 1a shows a group of high dip-angle or vertical natural fractures existed in the outcrops of the reservoir rocks. The downhole image logging results also verify that high dip-angle fractures (dark parts in Fig. 1c) exist in the reservoir. However, low dip-angle fractures and bedding planes are also prevalent in other reservoir rocks, as shown in Fig. 1b, d.

Fig. 1
figure 1

Naturally fractured Xu2 sandstones in the Triassic Xujiahe reservoirs: a a group of vertical fractures in the outcrop; b low dip-angle fractures and bedding planes in the outcrop; c high dip-angle fractures from the image log in Well Lian150, d low dip-angle fractures from the image log in Well Chuanxiao150

Full size image

Measured results indicate that the high dip-angle fractures cause an obvious reduction of the minimum horizontal stress in the rocks. This stress reduction also causes a decrease in the formation breakdown pressure for hydraulic fracturing operations. Therefore, it is critically important to predict in situ stresses in the anisotropic rocks for optimizing hydraulic fracturing design and operations. In the following sections the isotropic model and measured in situ stresses in the Xujiahe reservoirs are firstly introduced, then the anisotropic models are studied to examine the impacts of natural fractures on the minimum and maximum horizontal stresses.

The minimum and maximum horizontal stresses in the isotropic rocks are usually calculated from the following equations (e.g. Daines 1982; Thiercelin and Plumb 1994):

$$\sigma_{h} = \frac{\nu }{1 - \nu }\left( {\sigma_{V} - \alpha p_{p} } \right) + \alpha p_{p} + \frac{E}{{1 - \nu^{2} }}\left( {\varepsilon_{h} + \nu \varepsilon_{H} } \right) + \frac{{E\alpha_{T} }}{1 - \nu }\Delta T$$
(1)
$$\sigma_{H} = \frac{\nu }{1 - \nu }\left( {\sigma_{V} - \alpha p_{p} } \right) + \alpha p_{p} + \frac{E}{{1 - \nu^{2} }}\left( {\varepsilon_{H} + \nu \varepsilon_{h} } \right) + \frac{{E\alpha_{T} }}{1 - \nu }\Delta T$$
(2)

where σh is the minimum horizontal stress; σH is the maximum horizontal stress; σV is the vertical stress; pp is the pore pressure; α is Biot’s poroelastic coefficient; E is Young’s modulus of the rock; ν is Poisson’s ratio of the rock; εh is the tectonic strain in the minimum horizontal stress direction; εH is the tectonic strain in the maximum horizontal stress direction; αT is the thermal expansion coefficient; ΔT is the increase in temperature of the formation. In the following study, the thermal effect is not considered.

From Eqs. (1) and (2), if the vertical stress, pore pressure and tectonic strains are available, the minimum and maximum horizontal stresses in the isotropic rock can be calculated. Pore pressure is a very important parameter for determining horizontal stresses. The pore pressures in deep reservoirs, particularly in oil and gas reservoirs, are usually overpressured, and this will significantly increase horizontal stresses. However, horizontal stresses will be reduced in a depleted reservoir (Dohmen et al. 2013, 2017). Pore pressures can be measured from well tests or predicted from well logging data (e.g., Zhang 2011; Zhang 2013a, b). However, tectonic strains in Eqs. (1) and (2) are difficult to be obtained, and this may cause large uncertainty in horizontal stress calculation. Therefore, in-situ stress measurements are recommended for back calculating tectonic strains and calibrating horizontal stress calculations.

2 Measured in situ stresses and simplified isotropic horizontal stress model

By integrating bulk density well logging data in the western Sichuan basin, the following empirical equation is obtained for estimating vertical stress in the studied area (Zhang et al. 2020):

$$\sigma_{V} = 0.0246Z$$
(3)

where Z is the depth in m; σV is in MPa.

In order to obtain horizontal stresses, pore pressure needs to be determined first. Based on pore pressure measurements, pressure kicks, well influxes while drilling and well tests, the pore pressure profile in the studied area is obtained as shown in Fig. 2. The annotations in Fig. 2a, b are the approximate depths of the major formation tops. In the figure, J2s represents the Jurassic gas reservoir. The Xu2, Xu3, Xu4, Xu5 are different rock groups of the Xujiahe rocks in the upper Triassic formations. The Xu2 and Xu4 are the gas reservoirs (primarily tight sandstones, i.e., Xujiahe reservoirs), and the Xu3 and Xu5 are the source rocks (mainly mudstones).

Fig. 2
figure 2

Pore pressures and in situ stresses from field measurements in the Jurassic and Triassic Xujiahe formations. a Pressures and stresses, b pressure and stress gradients. In the figure, Pp, Sh, SH, Sv represent pore pressure, the minimum horizontal, maximum horizontal and vertical stresses, respectively

Full size image

Hydraulic fracturing injection tests (mini-frac tests and the DFIT) were performed in the studied area and used for in-situ stress determination. In a normal or strike-slip faulting stress regime, the closure pressure in the hydraulic fracturing injection test is equal to the minimum horizontal stress. Based on this principle, the minimum horizontal stress is obtained in the Xujiahe formations (mainly Xu2 and Xu4 sandstones) and shallower formations, as shown in Fig. 2. The maximum horizontal stress is then calculated using the formation breakdown pressures and closure pressures measured from the injection tests. Image log data and in situ stress polygon method using borehole breakouts and drilling-induced tensile failures (Zhang 2019; Zhang et al. 2020) are also applied to analyze the maximum horizontal stress. Based on these results (Fig. 2) the maximum horizontal stress can be approximately described by the following equation:

$$\sigma_{H} = 1.42\sigma_{h}$$
(4)

From Fig. 2, the measured pore pressure and in situ stresses in the Xujiahe sandstones in the studied area have the following behaviors:

  1. (1)

    Pore pressures are highly overpressured and much higher than the hydrostatic pressure.

  2. (2)

    Pore pressure gradient in the Xu4 formation is very high, causing a much higher minimum horizontal stress. However, from the bottom of the Xu4 formation to the Xu2 formation, pore pressure gradient reduces markedly. For instance, the Xu2 has a much smaller pore pressure gradient (15.6 MPa/km) than the Xu4 (20 MPa/km), which causes a smaller minimum horizontal stress gradient in the Xu2.

  3. (3)

    From the Jurassic formations to the Xu5 and Xu4 formations, the minimum horizontal stress is very close to the vertical stress (σh ≈ σV < σH). The in situ stress state is in the strike-slip faulting regime but close to the reverse faulting stress regime.

  4. (4)

    The minimum horizontal stress gradient in the Xu2 reservoir is smaller than the vertical stress gradient and σh < σV < σH, because it has a lower pore pressure gradient. This is favorable for hydraulic fracturing in the Xu2 reservoir, because the formation with a smaller minimum horizontal stress has a much lower formation breakdown pressure and hence needs a much smaller treatment pressure. Comparing with the Xu4 reservoir, the Xu2 has a favorite stress regime although it is still in the strike-slip faulting stress regime, and it can generate vertical fractures by hydraulic fracturing.

The following empirical equation of the minimum horizontal stress is obtained from the measured data in Fig. 2:

$$\sigma_{{\text{h}}} = k_{0} \left( {\sigma_{{\text{V}}} - p_{{\text{p}}} } \right) + p_{{\text{p}}}$$
(5)

where k0 is a parameter dependent on rock lithology and tectonic stress, and in the studied area k0 = 0.7, as shown in Fig. 2a.

Comparing Eq. (5) with Eq. (1), the following empirical relation can be obtained for estimating the minimum horizontal stress in the isotropic rock in the studied area, assuming \(k_{0} = \frac{{\nu}}{1 - \nu} + c\) in Eq. (5):

$$\sigma_{{\text{h}}} = \frac{\nu }{1 - \nu }\left( {\sigma_{{\text{V}}} - p_{{\text{p}}} } \right) + p_{{\text{p}}} + c\left( {\sigma_{{\text{V}}} - p_{{\text{p}}} } \right)$$
(6)

where c is the minimum stress coefficient. By comparing Eq. (5) with Eq. (6) and assuming an average Poisson’s ratio νa, c value can be obtained: \(c = 0.7 - \frac{{\nu_{{\text{a}}} }}{{1 - \nu_{{\text{a}}} }}\). If νa = 0.25 is assumed, then c = 0.367.

Equations (5) or (6) can be applied to estimate the minimum horizontal stress for the isotropic rocks in the studied area. However, it can be seen from Fig. 2 that the measured data of the minimum horizontal stress is scattered, particularly in the Xu2 formation. The reason could be that the rocks contain natural fractures, causing it to behave anisotropically. Therefore, it is necessary to study in situ stress behaviors in the anisotropic rocks. As shown in Fig. 1a, c, vertical or high dip-angle natural fractures are present in the Xu2 formation, and production data confirmed that this type of reservoir is the best reservoir in this area. This formation can be simplified as the rock containing a set of mutually parallel vertical fractures, and in situ stresses in this rock can be modeled by the HTI model. However, some rocks in the Xu2 reservoir contain low dip-angle or horizontal fractures (Fig. 1b, d), and this reservoir is the second best producing reservoir compared to the reservoir shown in Fig. 1c. In situ stresses in this type of reservoir can be modeled by the VTI model.

3 Horizontal stresses in the transversely isotropic rocks

3.1 VTI model of the horizontal stresses

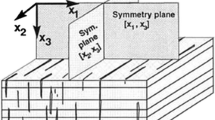
Sedimentary rocks are normally composed of strata containing interfaces or bedding planes. This causes anisotropy in rock properties, particularly when the interfaces or bedding planes are weaker than the rock matrix (e.g., Lang et al. 2011; Shoemaker et al. 2019). For example, most shales are anisotropic rocks because clay minerals of the shale are oriented in the bedding direction. This causes the shale stiffer if it is loaded parallel to the bedding direction than perpendicular to the bedding direction (e.g. Crawford et al. 2020). Many uniaxial compression tests have been conducted in shale core samples with weak bedding planes orientated different angles to the loading direction. The test results show that rock properties are very dependent on loading directions. If rock properties are uniform horizontally within a layer (Fig. 3) but vary vertically from layer to layer (e.g. a shale), then the formation can be treated as the vertical transverse isotropy (VTI). In the VTI rock the vertical axis is the axis of symmetry, while the horizontal plane is the plane of transverse isotropy, as shown in Fig. 3a.

Fig. 3
figure 3

The VTI in-situ stress model. a VTI model, b mechanical parameters that can be obtained from compression tests loading in vertical direction, c loading in horizontal direction

Full size image

Horizontal stress solutions for the VTI rock without considering thermal effect have been presented (e.g., Amadai and Pan 1992; Thiercelin and Plumb 1994; Zhang 2013a, b). The minimum and maximum horizontal stresses (σh_VTI, σH_VTI) with thermal effects in the VTI rock can be written as follows:

$$\sigma_{{{\text{h}}\_{\text{VTI}}}} = \frac{{E_{{\text{h}}} \nu_{{\text{V}}} }}{{E_{{\text{V}}} \left( {1 - \nu_{{\text{h}}} } \right)}}\left( {\sigma_{{\text{V}}} - \alpha_{{\text{V}}} p_{{\text{p}}} } \right) + \alpha_{{\text{h}}} p_{{\text{p}}} + \frac{{E_{{\text{h}}} }}{{1 - \nu_{{\text{h}}}^{2} }}(\varepsilon_{{\text{h}}} + \nu_{{\text{h}}} \varepsilon_{{\text{H}}} ) + \frac{{E_{{\text{h}}} \alpha_{{{\text{Th}}}} }}{{1 - \nu_{{\text{h}}} }}\Delta T$$
(7)
$$\sigma_{{{\text{H}}\_{\text{VTI}}}} = \frac{{E_{{\text{h}}} \nu_{{\text{V}}} }}{{E_{{\text{V}}} \left( {1 - \nu_{{\text{h}}} } \right)}}\left( {\sigma_{{\text{V}}} - \alpha_{{\text{V}}} p_{{\text{p}}} } \right) + \alpha_{{\text{h}}} p_{{\text{p}}} + \frac{{E_{{\text{h}}} }}{{1 - \nu_{{\text{h}}}^{2} }}\left( {\varepsilon_{{\text{H}}} + \nu_{{\text{h}}} \varepsilon_{{\text{h}}} } \right){ } + \frac{{E_{{\text{h}}} \alpha_{{{\text{Th}}}} }}{{1 - \nu_{{\text{h}}} }}\Delta T$$
(8)

where EV and νV are Young’s modulus and Poisson’s ratio in the vertical direction, respectively; Eh and νh are Young’s modulus and Poisson’s ratio in the horizontal direction, respectively; αh and αV are Biot’s coefficients in the horizontal and vertical directions, respectively; αTh is the thermal expansion coefficient in the horizontal direction.

If the thermal effect is neglectable, Eqs. (7) and (8) can be simplified as:

$$\sigma_{{{\text{h}}\_{\text{VTI}}}} = \frac{{E_{{\text{h}}} \nu_{{\text{V}}} }}{{E_{{\text{V}}} \left( {1 - \nu_{{\text{h}}} } \right)}}\left( {\sigma_{{\text{V}}} - \alpha_{{\text{V}}} p_{{\text{p}}} } \right) + \alpha_{{\text{h}}} p_{{\text{p}}} + \frac{{E_{{\text{h}}} }}{{1 - \nu_{{\text{h}}}^{2} }}(\varepsilon_{{\text{h}}} + \nu_{{\text{h}}} \varepsilon_{{\text{H}}} )$$
(9)
$$\sigma_{{{\text{H}}\_{\text{VTI}}}} = \frac{{E_{{\text{h}}} \nu_{{\text{V}}} }}{{E_{{\text{V}}} \left( {1 - \nu_{{\text{h}}} } \right)}}\left( {\sigma_{{\text{V}}} - \alpha_{{\text{V}}} p_{{\text{p}}} } \right) + \alpha_{{\text{h}}} p_{{\text{p}}} + \frac{{E_{{\text{h}}} }}{{1 - \nu_{{\text{h}}}^{2} }}\left( {\varepsilon_{{\text{H}}} + \nu_{{\text{h}}} \varepsilon_{{\text{h}}} } \right)$$
(10)

where EV < Eh = E and E is Young’s modulus for the isotropic rock;νV < νh = ν and ν is Poisson’s ratio for the isotropic rock.

Substituting Eh = E andνh = ν into Eqs. (9) and (10), the horizontal stresses in the VTI rock becomes:

$$\sigma_{{{\text{h}}\_{\text{VTI}}}} = \frac{{E\nu_{{\text{V}}} }}{{E_{{\text{V}}} \left( {1 - \nu} \right)}}\left( {\sigma_{{\text{V}}} - \alpha_{{\text{V}}} p_{{\text{p}}} } \right) + \alpha_{{\text{h}}} p_{{\text{p}}} + \frac{E}{{1 - \nu^{2} }}(\varepsilon_{{\text{h}}} + \nu\varepsilon_{{\text{H}}} )$$
(11)
$$\sigma_{{{\text{H}}\_{\text{VTI}}}} = \frac{{E\nu_{{\text{V}}} }}{{E_{{\text{V}}} \left( {1 - \nu } \right)}}\left( {\sigma_{{\text{V}}} - \alpha_{{\text{V}}} p_{{\text{p}}} } \right) + \alpha_{{\text{h}}} p_{{\text{p}}} + \frac{E}{{1 - \nu^{2} }}\left( {\varepsilon_{{\text{H}}} + \nu\varepsilon_{{\text{h}}} } \right)$$
(12)

The above equations show that more rock property parameters (EV, νV, αh and αV) are needed to model horizontal stresses in the VTI rock than those in the isotropic rock. The dynamic rock properties of the VTI rock can be calculated from the acoustic velocities from well logging measurements through cross dipole sonic method (Mavko et al. 2009). However, the dynamic properties need to be converted to static properties in order to apply Eqs. (9) and (10). The static rock properties of the VTI rock (e.g. EV, Eh, νV,νh) can also be directly obtained from laboratory tests for loading in horizontal and vertical directions (Fig. 3b, c).

Laboratory compression tests in shale gas formations indicate that vertical and horizontal Young’s moduli are very different and EV < Eh (Fig. 4). Analyzing test data in the Haynesville shale formation indicate that vertical and horizontal Young’s moduli have the following relation:

$$E_{\text{h}} /E_{\text{V}} = 10.06E_{\text{V}}^{ - 0.594}$$
(13)

where Young’s moduli are in GPa. Using all data shown in Fig. 4 for regression analysis the following relation can be obtained:   Eh/E V = 11.55E −0.629V .

Fig. 4
figure 4

Compression test data of vertical and horizontal Young’s moduli in several shale formations. a Eh/EV versus EV, b Eh and EV plots

Full size image

For easier application of the VTI model, the ratio of the two moduli can be approximately expressed as a simplified form: Eh/EV = 1.438 (Fig. 4b). The test data in more than 10 worldwide shale oil and gas formations are plotted in Fig. 4, including the Cretaceous Travis Peak shales from Thiercelin and Plumb (1994), the Baxter shale from Higgins et al. (2008), the Haynesville shales from Buller et al. (2010), Sone (2012), and Zhang (2019), the Eagle Ford shale outcrop cores from Knorr (2016), the Marcellus shale from Jin et al. (2018) and Wang et al. (2020), shale gas, tight oil formations and cap rocks from Crawford et al. 2020, the Longmaxi shale in China, and the Boryeong shale in Korea (Cho et al. 2012). The EV and Eh from these tests (as plotted in Fig. 4) have a similar trend as the one obtained from the Haynesville shale.

For anisotropy in Poisson’s ratio, laboratory test results reported in Zhang (2019) have the following relation, νh = 1.37νV. If Eh = 1.438EV and νh = ν = 1.37νV are used to describe the anisotropic mechanical parameters of the shale, then the rock property term in Eqs. (9) and (10) becomes \(\frac{{E_{{\text{h}}} \nu_{{\text{V}}} }}{{E_{{\text{V}}} \left( {1 - \nu_{{\text{h}}} } \right)}} = 1.05\frac{\nu }{1 - \nu }\). However, laboratory test results from Crawford et al. (2020) show that no systematic relationship between \(\frac{{\nu_{{\text{V}}} }}{{1 - \nu_{{\text{h}}} }}\) and νV, and measured Poisson’s ratios scatter evenly around the isotropic line (Crawford et al. 2020); therefore, it might be reasonable to assume νh ≈νV, and then \(\frac{{E_{{\text{h}}} \nu_{{\text{V}}} }}{{E_{{\text{V}}} \left( {1 - \nu_{{\text{h}}} } \right)}} \approx 1.438\frac{\nu }{1 - \nu }\), which has a much higher magnitude than \(\frac{\nu }{1 - \nu }\). If αh = αV = α is assumed, then the second and third terms of the right side of Eq. (9) or (10) are the same to the ones in the isotropic case. Consequently, the VTI rock has a higher minimum or maximum horizontal stress than the isotropic rock.

The other method to relate EV and Eh is using the relationship of Young’s moduli in rock mass and rock matrix. For the VTI rock, Young’s modulus (EV) of the rock mass and Young’s modulus (Eh or E) of the rock matrix are dependent on the properties of the natural fractures in the rock mass, and it has the following relationship for a set of mutually parallel fractures (Duncan and Goodman 1968):

$$\frac{{E_{{\text{h}}} }}{{E_{{\text{V}}} }} = 1 + \frac{E}{{k_{{\text{n}}} s}}$$
(14)

where kn is the fracture normal stiffness; s is the fracture spacing. If n is the fracture density (numbers of fractures per unit length), then it can be related to fracture spacing, i.e., \(n = \frac{1}{s + b}\), and b is the fracture aperture. If fracture spacing is very large compared to the fracture aperture, then \(n \approx \frac{1}{s}\). Equation (14) indicates that Eh/EV increases as the fracture density increases, and Eh/EV > 1.

We can use a parameter (A) to describe the anisotropy of Young’s modulus and assume \(A = 1 + \frac{E}{{k_{{\text{n}}} s}}\). From Eq. (14) for the VTI rock, \(\frac{{E_{{\text{h}}} }}{{E_{{\text{V}}} }} = A\). Therefore, the minimum horizontal stress of the VTI rock (Eq. 9) can be rewritten as the following equation:

$$\sigma_{{{\text{h}}\_{\text{VTI}}}} = \frac{A\nu}{{C_{{\text{V}}} \left( {1 -\nu } \right)}}\left( {\sigma_{{\text{V}}} - \alpha_{{\text{V}}} p_{{\text{p}}} } \right) + \alpha_{{\text{h}}} p_{{\text{p}}} + \frac{E}{{1 - \nu^{2} }}(\varepsilon_{{\text{h}}} +\nu \varepsilon_{{\text{H}}} )$$
(15)

where parameter A increases as the fracture density increases and as the fracture stiffness decreases, and A > 1; CV = ν/νV and normally CV ≥ 1 for the VTI rock. Parameter CV increases as the fracture density increases and as the fracture stiffness decreases. Comparing Eq. (15) with Eq. (1), it shows that A and CV are two important parameters to control the minimum horizontal stress in the VTI rock, and the same is for the maximum horizontal stress.

Based on Eq. (6), for the VTI rocks in the Xujiahe formations Eq. (15) can be simplified as the following empirical equation to predict the minimum horizontal stress:

$$\sigma_{{{\text{h}}\_{\text{VTI}}}} = \frac{A\nu}{{C_{{\text{V}}} \left( {1 -\nu } \right)}}\left( {\sigma_{{\text{V}}} - p_{{\text{p}}} } \right) + p_{{\text{p}}} + c\left( {\sigma_{{\text{V}}} - p_{{\text{p}}} } \right)$$
(16)

3.2 HTI model of the horizontal stresses

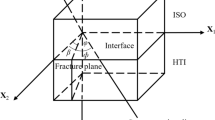
The model of horizontal transverse isotropy (HTI) can be used to model the rock that is isotropic along the vertical direction but anisotropic in one horizontal direction. For example, a rock containing a set of mutually parallel vertical fractures is a HTI medium (Fig. 5). Applying the stress and strain governing equation of the transversely isotropic (TI) model, the following equations for the minimum and maximum horizontal stresses in the HTI rock can be derived (derivations and equations with thermal effect can be found in “Appendix 1”):

$$\sigma_{{{\text{h}}\_{\text{HTI}}}} = \frac{{E_{{\text{h}}} \nu_{{{\text{Vh}}}} \left( {1 + \nu_{{{\text{VH}}}} } \right)}}{{E_{V} \left( {1 - \nu_{{{\text{Vh}}}} \nu_{{{\text{hV}}}} } \right)}}\left( {\sigma_{{\text{V}}} - \alpha_{{\text{V}}} p_{{\text{p}}} } \right) + \alpha_{{\text{h}}} p_{{\text{p}}} + \frac{{E_{{\text{h}}} (\varepsilon_{{\text{h}}} + \nu_{{{\text{Vh}}}} \varepsilon_{{\text{H}}} )}}{{1 - \nu_{{{\text{Vh}}}} \nu_{{{\text{hV}}}} }}$$
(17)
$$\sigma_{{{\text{H}}\_{\text{HTI}}}} = \frac{{\nu_{{{\text{VH}}}} + \nu_{{{\text{Vh}}}} \nu_{{{\text{hV}}}} }}{{1 - \nu_{{{\text{Vh}}}} \nu_{{{\text{hV}}}} }}\left( {\sigma_{{\text{V}}} - \alpha_{{\text{V}}} p_{{\text{p}}} } \right) + \alpha_{{\text{V}}} p_{{\text{p}}} + \frac{{\left. {E_{{\text{V}}} \left( \varepsilon \right._{{\text{H}}} + \nu_{{{\text{hV}}}} \varepsilon_{{\text{h}}} } \right)}}{{1 - \nu_{{{\text{Vh}}}} \nu_{{{\text{hV}}}} }}$$
(18)

where the meanings of anisotropic Young’s moduli and Poisson’s ratios are shown in Fig. 5b–d, andνhV/Eh = νVh/EV (see “Appendix 1” for details). Therefore, there are six independent parameters of Young’s moduli, Poisson’s ratios, and Biot’s coefficients.

Fig. 5
figure 5

The HTI rock with a set of vertical fractures and the compression tests for obtaining Young’s moduli and Poisson’s ratios in the HTI rock. a HTI model, b loading in vertical direction, c loading in the minimum horizontal stress direction, d loading in the maximum horizontal stress direction

Full size image

In the HTI rock, νVH = ν and νVh > νVH > νhV; EV = E. Hence, it can be assumed that νVhνhV ≈ ν2, and Eqs. (17) and (18) can be approximately written as follows:

$$\sigma_{{{\text{h}}\_{\text{HTI}}}} \approx\frac{{E_{{\text{h}}} \nu_{{{\text{Vh}}}} }}{{E\left( {1 -\nu } \right)}}\left( {\sigma_{{\text{V}}} - \alpha_{{\text{V}}} p_{{\text{p}}} } \right) + \alpha_{{\text{h}}} p_{{\text{p}}} + \frac{{E_{{\text{h}}} (\varepsilon_{{\text{h}}} + \nu_{{{\text{Vh}}}} \varepsilon_{{\text{H}}} )}}{{1 - \nu^{2} }}$$
(19)
$$\sigma_{{{\text{H}}\_{\text{HTI}}}}\approx \frac{{\nu}}{1 -\nu }\left( {\sigma_{{\text{V}}} - \alpha_{{\text{V}}} p_{{\text{p}}} } \right) + \alpha_{{\text{V}}} p_{{\text{p}}} + \frac{{E\left. {\left( \varepsilon \right._{{\text{H}}} + \nu_{{{\text{hV}}}} \varepsilon_{{\text{h}}} } \right)}}{{1 - \nu^{2} }}$$
(20)

It should be noted that the minimum horizontal stress is perpendicular to the direction of the fracture strike and the maximum horizontal stress is in the direction of the fracture strike (Fig. 5a). In contrast to the VTI model, Young’s moduli in the HTI rock have the following relation: Eh < EV = E; therefore, Young’s modulus of the rock mass (Eh) and Young’s modulus of the rock matrix (EV or E) in the HTI rock can be related by the following equation:

$$\frac{1}{{E_{{\text{h}}} }} = \frac{1}{{E_{{\text{V}}} }} + \frac{1}{{k_{{\text{n}}} s}}$$
(21)

Hence, we have the following relationship for the HTI rock:

$$\frac{{E_{{\text{h}}} }}{{E_{{\text{V}}} }} = \frac{1}{{1 + \frac{E}{{k_{{\text{n}}} s}}}} = \frac{1}{A}$$
(22)

Based on Eq. (22), Eq. (19) can be written in the following form:

$$\sigma_{{{\text{h}}\_{\text{HTI}}}}\approx \frac{{C_{{\text{H}}}\nu }}{{A\left( {1 -\nu } \right)}}\left( {\sigma_{{\text{V}}} - \alpha_{{\text{V}}} p_{{\text{p}}} } \right) + \alpha_{{\text{h}}} p_{{\text{p}}} + \frac{{E(\varepsilon_{{\text{h}}} + C_{{\text{H}}}\nu \varepsilon_{{\text{H}}} )}}{{A\left( {1 - \nu^{2} } \right)}}$$
(23)

where parameter \(A = 1 + \frac{E}{{k_{{\text{n}}} s}} > 1\); parameter CH = νVh/ν > 1 and CH increases as the fracture density increases and as the fracture stiffness decreases. The two parameters CH and A have opposite impacts on the minimum horizontal stress.

Comparing Eq. (23) with Eq. (1) (without thermal effect), the difference of the minimum horizontal stresses in the HTI model and in the isotropic model is the two parameters of A and CH. Normally, A > CH; therefore, the minimum horizontal stress calculated from the HTI model is smaller than that calculated from the VTI model or the isotropic model. This implies that the rock containing vertical fractures has a smaller minimum horizontal stress than the one containing horizontal fractures (VTI) or without fractures (isotropic rock).

Similarly, the maximum horizontal stress in the HTI model in Eq. (20) can be expressed as the following form:

$$\sigma_{{{\text{H}}\_{\text{HTI}}}}\approx \frac{{\nu}}{{\left( {1 -\nu } \right)}}\left( {\sigma_{{\text{V}}} - \alpha_{{\text{V}}} p_{{\text{p}}} } \right) + \alpha_{{\text{V}}} p_{{\text{p}}} + \frac{{E(\varepsilon_{{\text{H}}} + C_{{\text{H}}} \nu\varepsilon_{{\text{h}}} /A)}}{{\left( {1 - \nu^{2} } \right)}}$$
(24)

Comparing Eq. (24) with Eq. (2), the HTI rock and isotropic rock have a very similar maximum horizontal stress.

Based on Eq. (6), the minimum horizontal stress in Eq. (23) can be simplified as the following equation for the HTI model in the Xujiahe formation:

$$\sigma_{{{\text{h}}\_{\text{HTI}}}}\approx \frac{{C_{{\text{H}}}\nu }}{{A\left( {1 -\nu } \right)}}\left( {\sigma_{{\text{V}}} - p_{{\text{p}}} } \right) + p_{{\text{p}}} + \frac{c}{A}\left( {\sigma_{{\text{V}}} - p_{{\text{p}}} } \right)$$
(25)

where c is the same parameter as defined in Eq. (6).

3.3 A simplified model for the minimum horizontal stress estimate in naturally fractured rocks

For the rock containing a set of inclined fractures, the VTI or HTI model for horizontal stress calculation cannot be applied directly. To solve this issue, an approximate method is proposed to estimate the minimum horizontal stress. When the dip angle of the fractures varies from 0 to 90 degrees, we assume that the minimum horizontal stress changes gradually from the VTI model to the HTI model. Additionally, we use a linear interpolation to consider this change from the VTI model to the HTI model. That is, if the dip angle of the fractures is 0, the VTI model is used; if the dip angle of the fractures is 90 degrees, the HTI model is used; if the dip angle of the fractures is in between of 0 to 90 degrees, a linear interpolation method is used to calculate the minimum stress. According to this approach and assuming αh = αV = α, the minimum horizontal stress in the anisotropic case can be approximately obtained by combining Eqs. (15) and (23):

$$\sigma_{{{\text{h}}\_{\text{TI}}}}\approx \frac{{\beta+ \left( {90 - \beta } \right)B^{2} }}{90B}\frac{\nu }{1 - \nu }\left( {\sigma_{{\text{V}}} - \alpha p_{{\text{p}}} } \right) +\alpha p_{{\text{p}}} + \frac{{\beta + \left( {90 - \beta } \right)A}}{90A}\frac{{E(\varepsilon_{{\text{h}}} + C_{{\text{B}}} \nu \varepsilon_{{\text{H}}} )}}{{\left( {1 - \nu^{2} } \right)}}$$
(26)

where β is the dip angle of the inclined fractures (degree), and for the horizontal fracture β = 0, for the vertical fracture β = 90°;\(B = \frac{A}{{C_{{\text{A}}} }}\), \(C_{{\text{A}}} = C_{{\text{V}}} + \frac{{C_{{\text{H}}} - C_{{\text{V}}} }}{90}\beta\), and \(C_{{\text{B}}} = \frac{{90 + (C_{{\text{H}}} - 1)}\beta}{90}\).

Similarly, based on Eq. (6) and simplified VTI and HTI models, Eqs. (16) and (25), the empirical minimum horizontal stress in the studied Xujiahe reservoirs can be written in the following form for different β:

$$\sigma_{{{\text{h}}\_{\text{TI}}}}\approx \frac{{\beta+ \left( {90 - \beta } \right)B^{2} }}{90B}\frac{\nu }{1 - \nu }\left( {\sigma_{{\text{V}}} - p_{{\text{p}}} } \right) + p_{{\text{p}}} + \frac{{\beta + \left( {90 - \beta } \right)A}}{90A}c\left( {\sigma_{{\text{V}}} - p_{{\text{p}}} } \right)$$
(27)

3.4 Discussions

The minimum and maximum horizontal stresses for the VTI an HTI models are obtained in the above sections. The VTI model (Eqs. 9 and 10) can be used for the formation with a set of horizontal fractures or bedding planes, such as shale formations. The HTI model (Eqs. 17 and 18) can be used for the formation with a set of vertical fractures. For the applications using the simplified or approximate equations proposed in this paper (e.g. Equations 26 and 27), calibrations by the measured data are recommended to verify the applicability. The following section illustrates a case application for using the proposed equations.

4 A case application in a naturally fractured gas reservoir

4.1 Measured minimum horizontal stresses and formation breakdown pressures

Image logging results in more than dozen wells in the Xujiahe gas reservoirs in the studied area show that the Xu 2 sandstone reservoir contains many natural fractures with different dip angles. The density of the natural fractures increases as the fracture dip angle increases, and most natural fractures are fractures with high dip angles. Figures 6 and 7 present the natural fracture impacts on the minimum horizontal stresses and breakdown pressures in 10 wells, which have both natural fracture data, measured results of the minimum horizontal stresses and formation breakdown pressures. Figure 6a shows that the trend of the measured minimum horizontal stress gradient decreases as the fracture density increases. Figure 6b indicates that the trend of the measured formation breakdown pressure gradient also decreases as the fracture density increases. Figure 7 shows that the fracture dip angles have noticeable impacts on the minimum horizontal stress gradient and formation breakdown pressure gradient. The minimum horizontal stress gradient and formation breakdown pressure gradient decrease as the fracture dip angle increases (Fig. 7). Figures 6a and 7a indicate that natural fractures can result in a decrease of the minimum horizontal stress by up to 3 MPa/km. This is consistent to the HTI model, because when the fracture dip angle increases, the naturally fractured rock approaches the HTI rock which has a smaller horizontal stress. The fitting results in Figs. 6 and 7 are not very good, and this may be caused by the data quality. The natural fractures in these figures were interpreted from image logs, and the minimum horizontal stress data were interpreted from DFIT tests. Uncertainties existed in the interpretations which might affect data quality.

Fig. 6
figure 6

Measured data in 10 wells in the Xu2 formation in the Xinchang gas field: a fracture density versus the minimum horizontal stress gradient, b fracture density versus formation breakdown pressure gradient

Full size image
Fig. 7
figure 7

Measured data in 13 wells in the Xu2 formation in the Xinchang, Xinsheng and Gaomiao gas fields: a fracture dip angle versus the minimum horizontal stress gradient, b fracture dip angle versus formation breakdown pressure gradient

Full size image

Figures 6b and 7b also indicate that formation breakdown pressure decreases as the fracture density and dip angle increase, and natural fractures can cause a decrease of the breakdown pressure by up to 10 MPa/km (or 50 MPa at depth of 5000 m), a much larger decrease than the minimum horizontal stress decrease. Therefore, the naturally fractured formation is much easier to be hydraulically fractured than the intact rock.

4.2 The minimum horizontal stress estimate in the naturally fractured rock

Dynamic Young’s moduli, Poisson's ratios, and bulk modulus in the transversely isotropic rock can be obtained from the acoustic velocities. The dynamic data then need to be converted to the static data to apply the transversely isotropic models (VTI and HTI) in Eqs. (9) and (17) or the combined anisotropic model Eq. (26) or Eq. (27) to calculate the minimum horizontal stresses. The conversion from dynamic to static rock properties using empirical equations has certain uncertainty. Another method is to use static rock properties obtained from laboratory tests. If these rock properties are difficult to obtain, then empirical equations can be used to estimate horizontal stresses in the anisotropic rocks. Based on the measured data of natural fractures and the minimum horizontal stresses in the studied area, empirical equations of the minimum horizontal stress can be obtained from Figs. 6a and 7a:

$$\sigma_{{{\text{h}}, {\text{f}}}} = e^{ - 0.037n} \sigma_{{\text{h}}}$$
(28)
$$\sigma_{{{\text{h}}, {\text{f}}}} = e^{ - 0.002\beta} \sigma_{{\text{h}}}$$
(29)

where σh,f is the minimum horizontal stress in the naturally fractured rock (MPa); n is the density of the fractures (1/m); σh is the minimum horizontal stress in the isotropic rock (MPa), which can be obtained from either Eq. (1) or Eq. (6).

Similarly, empirical equations of the formation breakdown pressure can be obtained from Figs. 6b and 7b:

$$p_{{{\text{b}}, {\text{f}}}} = e^{ - 0.088n} p_{{\text{b}}}$$
(30)
$$p_{{{\text{b}}, {\text{f}}}} = e^{ - 0.006\beta} p_{{\text{b}}}$$
(31)

where pb,f is the formation breakdown pressure in the naturally fractured rock (MPa); pb is the formation breakdown pressure in the isotropic rock and can be obtained from Kang et al. (2020).

If measured fracture data are available, Eqs. (28)–(31) can be used to estimate the minimum horizontal stress and formation breakdown pressure in the studied area. Figure 8 shows an example of the application in Well Xin-10 in the studied area, and Fig. 8c illustrates the comparisons of the minimum horizontal stress estimations from empirical equation (Eq. 29), the proposed anisotropic method (Eq. 27) and the isotropic model (Eq. 6). Gamma ray log data in this well (Fig. 8a) show that the Xu2 sandstone reservoir located at depth of 4877 to 4887 m is a naturally fractured gas-bearing formation. The dip angles of the natural fractures in the reservoir are interpreted from well log data and ploted in Fig. 8b, and the natural fractures have different dip angles varying from 24° to 63°. The minimum horizontal stresses are estimated from the fracture dip angle correlation (Eq. 29), the proposed anisotropic model (Eq. 27), and the isotropic method, (Eq. 6), which are plotted in Fig. 8c for comparison. In the proposed anisotropic model of Eq. (27), vertical stress (σV) is calculated from Eq. (3), pore pressure (pp) is obtained from the measured results in Fig. 2. Poisson’s ratio (ν) is calculated from Vp and Vs from sonic log data, and parameters A = 1.438, CH = CV = 1.37, c = 0.45, α = 1 are used for calculations. It can be seen from Fig. 8c that the proposed anisotropic model estimates a smaller minimum horizontal stress than the isotropic model because of presence of inclined natural fractures. The minimum horizontal stress reduction caused by high dip-angle fractures can reach 6% (Fig. 8c). This stress reduction is beneficial for hydraulic fracturing operations, because it causes formation breakdown pressure to decrease. Therefore, rock anisotropic effects need to be considered for in-situ stress estimate. Figure 8c also shows that the calculated result from proposed anisotropic model of Eq. (27) is consistent to the one from the empirical equation (Eq. 29). This implies that the proposed anisotropic model is applicable. The same conclusion is obtained from other wells in the studied area.

Fig. 8
figure 8

The minimum horizontal stresses calculated from different methods. a well logging data (Gamma ray), b fracture dip angles interpreted from well logs, c the minimum horizontal stresses (Sh) estimated from the empirical equation of Eq. (29), the proposed anisotropic model of Eq. (27), and the isotropic model of Eq. (6)

Full size image

It should be noted that empirical equations, Eqs. (28)–(31), are obtained from the measured data in the Xujiahe reservoirs and may only be applicable in the studied area, and for applications to other areas, calibrations may be needed.

5 Conclusions

The following conclusions and recommendations are given based on this study:

  1. (1)

    Field measured data indicate that horizontal stresses in naturally fractured rocks have anisotropic behaviors.

  2. (2)

    For naturally fractured rocks, anisotropic models should be used for estimating in situ stresses. The VTI and HTI horizontal stress models are obtained. Comparing with the isotropic model, the VTI model gives a higher prediction of the minimum or maximum horizontal stress than the isotropic model. In contrast, the HTI model produces a lower minimum horizontal stress; however, the HTI model and isotropic model give a very similar maximum horizontal stress.

  3. (3)

    Case study shows that the naturally fractured formation with high dip-angle or vertical fractures has a lower minimum horizontal stress, and in this case the HTI model is more suitable. However, for the formation with horizontal fractures or bedding planes, it has a higher minimum horizontal stress, and the VTI model is more suitable.

  4. (4)

    Measured data in the studied area indicate that the minimum horizontal stress and formation breakdown pressure decrease as the dip angles of the natural fractures increase.

  5. (5)

    A combined model (Eqs. 26 and 27) of the VTI and HTI is proposed and can be used for estimating the minimum horizontal stress for the rock containing natural fractures with different dip angles. Comparing with measured minimum horizontal stresses in the Xujiahe reservoirs, the proposed model gives a very good estimation. Since the combined model is a simplified solution, calibrations by measured data are recommended prior to practical applications.

  6. (6)

    Natural fractures with high dip-angles cause anisotropy in rocks and reduce formation breakdown pressure. This can increase hydraulic fracturing efficiency. If this anisotropy in the oil or gas reservoir can be detected from seismic or other geophysical methods, it may be possible to find the engineering sweet spots of the reservoir.