1 Introduction

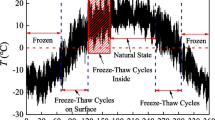
In underground geotechnical construction, such as nuclear waste storage, hot dry rock mining, shale gas, and petroleum gas drilling (Ranjith et al. 2012; Ma et al. 2020; Manatunga et al. 2021; Zhang et al. 2021; Xu et al. 2022), the physical and mechanical properties of the surrounding rock mass are significantly altered by the drastic temperature changes (Homand-Etienne and Houpert 1989; Ping et al. 2022). At the same time, as shown in Fig. 1, the surrounding rock masses near the free surface area are subjected to a combination of compressive and tensile stresses, i.e., in a coupled compressive-tensile state (Heuze 1983). To ensure the safety of geotechnical engineering under complex environmental conditions, it is essential to investigate the changes in mechanical properties of rocks under the coupled compression-tension mechanical state after different temperature treatments.

Fig. 1
figure 1

Typical triaxial extension failure of rock engineering cases(Huang et al. 2022): a the rock slope caused by underground mining(Tang et al. 2019); b numerical results of surrounding rock after excavation(Liang et al. 2020); c triaxial extension stress state

Full size image

So far, the research on rock's physical and mechanical properties at high temperatures has been extensive. For example, Sha et al. (2019) studied the effect of heating a rock specimen for 3 h using charcoal fire on the P-wave velocity(Vp), Brazilian tensile strength, and its microstructural evolution on the mechanical properties of the specimens of granite. Dwivedi et al. (2008) found that granite specimens’ permeability, thermal conductivity, and diffusivity decreased with increasing temperature in the range of 30–160 °C, and the specific heat increased, the tensile strength decreased with the increase of temperature. Vishal et al. (2011) studied the effect of temperature on the tensile strength of khondalite and provided valuable information on the variation of the tensile strength of rock with heat treatment methods. It was found that different mineral fractions have different thermal responses, and the strength of the rock increases first and then decreases with increasing temperature. The rock does not follow a homogeneous pattern due to changes in its chemical composition and response to heat. Zhang et al. (2016) reported the differences in physical and mechanical properties such as mass, density, porosity, P-wave velocity, strength, and strain of many rocks between 25 and 500 °C. It was found that the loss of water at high temperatures has a considerable effect on the physical and mechanical properties of rocks, such as the increase and enlargement of microcracks and new cracks. The process of thermal property change was divided into three stages, and the cut-off points of 100 °C and 300 °C are used to explain the evolution of the mechanical properties of rock at each stage. Sirdesai et al. (2017) analyzed the effect of high temperature on the internal structure of sandstone. The results showed that the increase in temperature caused the evolution of pores and fissures, and the ratio of connected pores and unconnected pores changed, which increased the effective porosity and total porosity of the rocks; In addition, the plasticity of the specimens started to form after 500 °C and gradually increased with the increase of temperature. Li et al. (2019) used chevron cracked notched Brazilian discs (CCNBD) to obtain a power-of-three relationship between temperature and fracture toughness values of granite specimens in the range of 100–800 °C and found that water-cooled conditions corroded the specimens more than air-cooled conditions. The specimens fractured more at 300 °C with transgranular fracture and cracked more at 400–800 °C with intergranular fracture. In addition, Yin et al. (2020a) conducted a three-point bending test on notched semi-circular bending (NSCB) granite specimens treated at 25–800 °C, and found that the damage behaviour of the specimens changed from brittle to ductile first at 300–500 °C, which would lead to the crack initiation fracture toughness and the unstable fracture toughness of the specimens were reduced. It was concluded that the leading cause of this phenomenon might be microcracks and holes caused by thermal damage.

Moreover, many scholars have conducted a detailed analysis of microscopic damage and destruction caused by high temperatures (Ping et al. 2020). Kumari et al. (2019) used ARAMIS Photogrammetry and acoustic emission, SEM to investigate the crack sprouting and cracking of granite specimens subjected to different cooling treatments (constant high temperature, slow cooling, and fast cooling) within 1000 °C. The development processes showed that as the temperature increased, the specimens changed from brittle to quasi-brittle failure, with trans-granular cracks appearing at 200 °C and intragranular fractures at 600 °C. Both crack closure and unstable crack propagation regions increased significantly above 500 °C. The crack closure process resulted in the compression of the original thermally induced intergranular cracks, while the unstable crack propagation process shows the process of crack recombination, which was caused by the recrystallization of the grains after melting and confirmed by SEM results. Yao et al. (2016) measured the 3D damage of heat-treated sandstone specimens by CT, and found that the change of CT mean value decreased with the increase of temperature, as did the mean density and P-wave velocity. While the dynamic tensile strength of the specimens increased with the increase of loading rate, according to the split Hopkinson pressure bar (SHPB) test. The tensile strength decreases with increasing heat treatment temperature at the same loading rate except for 450 °C. And an empirical model of LS tensile strength based on the loading rate and heat treatment conditions was established. In addition to the above tests, as shown in Table 1, uniaxial compression tests, theoretical analysis and numerical simulation studies have been carried out by many scholars.

Table 1 References for the study of high-temperature properties of some typical rock materials
Full size table

After that, the physical and mechanical properties of rocks with different moisture contents in geotechnical engineering have also received wide attention from scholars due to the presence of surface water and groundwater (Vásárhelyi 2005; Vasarhelyi and Van 2006; Bohloli and Hoven 2007; Huang et al. 2018; Chen et al. 2019), and relevant studies are shown in Table 1. For example, Vasarhelyi and Van (2006) stated that a minimal water content of even 1% can have a significant effect on the strength of the rock in some cases, and therefore suggested that the wet strength of the rock, and preferably the water sensitivity must be established to assess its potential strength variability and deformability. Subsequently, Scholars have come to the common conclusion that high moisture content corresponds to a small elastic modulus and a low strength, and the high water content reduces the brittle properties of the rock and enhances its plastic deformation properties (Chen et al. 2019). In particular, the effect of water content on mud-bearing rocks is more significant than that of hard rocks (Erguler and Ulusay 2009). Hu et al. (2014) reported that the elastic modulus and strength decrease with increasing clay and water contents in Callovo-Oxfordian (Cox) argillite. Furthermore, Some scholars Huang et al. (2018) have also considered freeze–thaw damage at low temperatures caused by water content. Therefore, it is essential to consider the water content's effect on the rock's mechanical properties.

On the other hand, different unloading paths of rock masses have also become one of the leading research hotspots for many scholars in recent decades. One of the most common ways is to conduct triaxial unloading experiments in the laboratory to restore underground excavation conditions (Yang et al. 2017). However, most experiments still use the loading path that keeps the axial stress and unloads the confining pressure (Liu and Yi 2022), that is, the compression-compression coupled loading method. There are a few tests to keep the confining pressure and unload the axial stress, that is, the compression-tensile coupling loading method, which can also be called the confined direct tension test or the triaxial extension, as shown in Fig. 1.

Ramsey and Chester (2004) first realized the triaxial extension. They found that with the increasing confining pressure, the damage mode of the rock specimen would change from pure tensile fracture to mixed tensile-shear fracture and finally to pure shear fracture, which made up for the gap in the transition from tensile fracture to shear fracture of the rock. Since then, many scholars McCormick and Rutter (2022) have continued to conduct relevant experimental and numerical studies. For example, Liu et al. (2019) developed a new device for triaxial tensile testing of sandstone and further compared the results with the results of triaxial compression testing. Zeng et al. (2019) designed a simple device used in the MTS815 triaxial cell to perform triaxial tensile tests of sandstone under different confining pressures from 0 to 60 MPa, and gave a more accurate confining pressure boundary point of fracture mode than Ramsey’s result. Liu et al. (2021a) further revealed granite's tensile strength and fracture surface morphology within 12 MPa confining pressure. In addition, Liu et al. (2022c) developed a compression-tension conversion device applied to the MTS815 experimental machine and then proposed a newly shaped specimen to realize triaxial tensile tests within 0–140 MPa confining pressure.

Although many scholars have studied the mechanical properties of rocks after high-temperature treatment, there are still few reports on the triaxial tensile mechanical properties of rocks after high-temperature treatment, especially soft rocks. In this study, triaxial extensions were carried out on sandstones with different moisture contents after different thermal treatments. The changes in the physical composition of the specimens after treatment were analyzed, the influence of temperature on the microstructure of the specimens was discussed by SEM results, and the mechanism of thermal treatment and moisture content on the mechanical properties of rocks were explained. The results can provide some reference for the construction of projects such as deep nuclear waste disposal.

2 Test preparation

2.1 Specimen preparation

As shown in Fig. 2, the sandstone used for testing was obtained from a quarry in Wuding County, Yunnan Province, China, about 128 km from Kunming, the capital of Yunnan Province. All specimens were drilled from a rock block in the same direction to ensure minimal variation between specimens. The specimens were machined to a standard cylindrical shape of size φ50 mm × h100 mm, then carefully smoothed to meet the ISRM (1978) requirements. Then, the specimens were machined into the I-shape shown in Fig. 2 using a CNC engraving and milling machine (Liu et al. 2022b). Here, the left and right sides of the specimens were elliptically cut to ensure a uniform variation in the cross-sectional area. As shown in Fig. 2, the XRD results showed that the mineral composition of the natural specimens was Quartz (69.97%), Anorthite (10.66%), Chlorite (9.98%), Dolomite (5.79%), Muscovite (1.42%), Illite (0.82%), Hematite (0.98%) and Albite (0.38%). The specimen's microstructure is dense, and the particle size is 0.05–0.6 mm. The basic mechanical parameters of the specimens in the natural state are: uniaxial compressive strength 8.47 MPa, direct tensile strength 0.97 MPa, indirect tensile strength 1.90 MPa, cohesion 7.73 MPa, and internal friction angle 32.99°. The average density is 2036 kg/m3, and the average P-wave velocity is 1829 m/s.

Fig. 2
figure 2

Introduction of specimens: a geographical location of the specimen; b SEM image; c mineral composition; d polarized photographs of thin sections (The letters Qtz., Ab., Hem., and Cal. represent Quartz, albite, montmorillonite, Hematite, and calcite, respectively)

Full size image

In this study, the heating furnace was heated to the target temperatures of 100, 200, 300, 500, and 800 °C at a heating rate of 5 °C/min, and maintained at a constant temperature for 2 h to ensure the specimens were thoroughly heat treated and avoid thermal shock (Shu et al. 2022). After the constant temperature is over, the heating furnace will be cooled naturally and opened when the temperature reaches room temperature, which can effectively avoid thermal damage caused by a sharp drop in ambient temperature around the rock specimen.

At the end of natural cooling, part of the specimen undergoes a process of water absorption saturation-natural dehydration, making the saturation of the specimen reach 0, 0.2, 0.5, 0.8, 1, where the water saturation coefficient (Kt) of the rock specimen at different moments is calculated by Eq. 1. (Kazak and Kazak 2019)

$$K_{t} = \frac{{m_{t} - m_{d} }}{{m_{s} - m_{d} }}$$
(1)

where mt is the mass of the specimen at time t, ms is the mass of the specimen in the water-saturated state, and md is the mass of the specimen in the dry state.

2.2 Testing scheme

As shown in Figs. 3 and 4, to perform the triaxial tensile test, we machined the compression-tension conversion device, which can be equipped with the MTS815 test machine (Liu et al. 2022c). In detail, the compression-tension conversion device is installed in the triaxial chamber of the MTS815 test machine to achieve axial tension of the specimen by axial compression of the tester. At the same time, the confining pressure is provided by the confining pressure system of the tester, thus realizing triaxial extension.

Fig. 3
figure 3

Compression-tension conversion device(Liu et al. 2022c) and stress conversion of a specimen under triaxial extension

Full size image
Fig. 4
figure 4

Test procedure of the test: a specimen processing; b P-wave velocity and mass test; c heating; d P-wave velocity and mass test; e moisture content control and specimen adhesion; f test and g SEM scan

Full size image

The experiment steps are as follows: firstly, apply a contact load of 0.3kN to the specimen according to the force control method; secondly, the confining pressure is loaded to 20 MPa at a constant rate of 0.2 MPa/s. Thirdly, the compressive stress is applied to the compression-tension conversion device at a steady rate of 0.15 mm/min. In this case, the axial deviatoric stress of the specimen is tensile stress, and the confining pressure is compressive stress. Thus, the triaxial extension is formed; Finally, the specimen is continuously loaded along the axial direction until it breaks. Here, displacement control is chosen over force control because force control usually causes the specimen to break suddenly near the peak load. An axial displacement extensometer is adopted to monitor the axial strain within 50 mm in the middle of the specimen.

3 Results and discussion

3.1 Evolution of physical properties after thermal treatment

3.1.1 Evolution of specimen mass and P-wave velocity

After the specimens experienced different thermal treatments and cooling, the color of the specimen at T = 100 °C is a little darker than that at room temperature, while the surface of the specimen at T = 200 °C is darker; and then became brighter and redder at T = 500 °C, and finally turned to orange at T = 800 °C. When struck with a finger, it emits a ceramic-like sound that is unusually crisp. In addition, macroscopic cracks appeared on individual specimens after T = 800 °C treatment.

As shown in Fig. 5 and Table 2, sandstone specimens’ P-wave velocity (Vp) increases first and then decreases with the temperature increase. The Vp variation law is not a simple linear relationship with temperature. The medium and low-temperature treatment (T = 25–200 °C) enhanced the Vp; this reflects that the mechanical properties of sandstone specimens are improved to a certain extent after being subjected to before T = 200 °C and deteriorated after T = 200 °C. Then it decreased to 1785.71 m/s after T = 400 °C and further reduced to 758.66 m/s after T = 800 °C. From the viewpoint of Vp change, the damage of sandstone specimens is more significant at T > 200 °C, especially after T = 300 °C.

Fig. 5
figure 5

Variation of P-wave velocity (Vp) and mass change with temperature

Full size image
Table 2 References for the study of high-temperature properties of some typical rock materials
Full size table

Vp is a response of internal pores and interstitial materials in rock, which is another perspective of the mechanical properties of the rock. The change of Vp with temperature shows that the inner pores of the rock become smaller first and then more extensive as the temperature increases. At the same time, the variations of thermal expansion and cooling contraction of different mineral particles are different. When T is small, the thermal expansion of mineral particles enables the internal fissures of the rock to smaller and thus increase Vp; with T rises to a critical threshold, the internal fissures are squeezed to a minimum value, and the continued heating leads to the continuous expansion of mineral particles, new cracks are created and Vp is reduced. Therefore, the overall mechanical properties of the rock show a trend of first strengthening and then weakening with the temperature change.

Moreover, the mass of the sandstone specimens also decreases with increasing temperature, showing a significant negative linear correlation. More specifically, the curve of the specimen mass resembles a logarithmic function curve within T = 25–500 °C, while the mass decreases substantially at 800 °C. The main reason for this phenomenon is the evaporation of water from the pores and microfractures inside the specimen.

3.1.2 Evolution of the mineral composition

As shown in Fig. 6, the composition of the sandstone specimens changed significantly after different temperature treatments. Among them, Quartz increased with increasing T but decreased sharply at T = 800 °C. Mica and Hematite decreased with the T increase, showing a negative linear correlation. Sodium feldspar gradually increased with increasing T, indicating a positive linear correlation. Chlorite was detected in two groups of specimens at room temperature and 200 °C but disappeared at T > 500 °C, while Calcium hydroxide did not exist at T = 25 °C- 500 °C, and occurred at T = 800 °C. The main reason for its production is that dolomite underwent thermal decomposition after T > 750 °C to produce CaO. Subsequently, CaO absorbed water from the air, thus transforming Calcium hydroxide. This change will increase the overall porosity of the rock and may also lead to spalling or even destruction of the rock surface.

Fig. 6
figure 6

Variations of mineral composition with temperature

Full size image

3.2 Mechanical properties after thermal treatment

Figure 7 showed axial stress-axial strain curves and the relationship between axial deviatoric stress, ultimate strain εa, and elastic modulus E with T under triaxial extension. In the axial stress-axial strain curves, the axial stress is the value of the confining pressure minus the axial tensile stress, where the axial tensile stress is the ratio of the axial load applied to the specimen by the testing machine to the area of the specimen section. All curves exhibit a complete and smooth downward convex shape. Take T = 200 °C as an example, the stress–strain curve can be divided into three stages, the elastic stage(O-A), the plastic stage(A-B), and the fracture stage(B-C). In fact, after reaching the peak load, the specimen breaks down immediately, and the B-C stage can be said t nonexistent. A-B is called the plastic segment because no acoustic emission signal is monitored before the peak load (Liu et al. 2021b), i.e., no new cracks appear, so this stage is the deformation stage of the grain and matrix inside the specimen.

Fig. 7
figure 7

Stress–strain curves and the evolution of elastic modulus, ultimate strain, and axial deviatoric stress of specimens

Full size image

In addition, Table 3 shows that the absolute value of axial stress shows a trend of decreasing and then increasing with the increase of T under the triaxial extension with constant confining pressure. On the one hand, when T ≤ 200 °C, the axial stress is tensile stress, and the failure mode of the specimen is a tensile-shear failure, the increase in T will enhance the strength of the specimen at this time. When T ≥ 300 °C, the axial stress is compressive stress, the failure mode of the specimen is a pure shear failure, and the increase of T will reduce the strength of the specimen. Besides, at the same temperature change range, the weakening effect of high temperature on the specimen is significantly greater than its strengthening effect. The ultimate strain εamax of the other specimens varied from − 34.25 × 10–4 to 30.69 × 10–4 with slight fluctuation, except that the εa of the specimens increased suddenly when T = 200 °C. In addition, the elastic modulus of the specimens showed a good negative correlation with the T on the whole.

Table 3 Parameters of sandstone specimens under triaxial extension
Full size table

The triaxial extension damage evolution characteristics of the specimen after thermal treatment are shown in Fig. 8. DTM is the damage variable under the action of thermal–mechanical coupling. After thermal treatment, the specimen generated thermal damage DT, which can be calculated by Eq. 2 (Pan et al. 2022), where ET is the fitted value of the quadratic function of the elastic modulus after thermal treatment, and E0 is the fitted value of the elastic modulus at room temperature. According to the strain equivalence principle, the constitutive relation and DTM expression of thermal–mechanical coupling damage of specimens are shown in Eqs. 3–5, and the results are shown in Table 3.

$$D_{T} = 1 - E_{T} /E_{0}$$
(2)
$$\sigma^{*} = E_{T} \varepsilon \left( {1 - D_{M} } \right)$$
(3)
$$\sigma^{*} = E_{0} \varepsilon \left( {1 - D_{T} } \right)\left( {1 - D_{M} } \right) = E_{0} \varepsilon \left( {1 - D_{TM} } \right)$$
(4)
$$D_{TM} = D_{T} + D_{M1} - D_{T} D_{M}$$
(5)
Fig. 8
figure 8

Evolution characteristics of the damage variables of sandstone specimens after thermal treatment during triaxial tension

Full size image

In triaxial extension, based on the strain equivalence assumption (Lemaitre 1985), the damaged intrinsic relationship of Eq. 6 can be obtained, which leads to the derivation of the expression of DTM in Eq. 7.

$$\sigma_{3} = E_{T} \varepsilon_{3} \left( {1 - D_{TM} } \right) + 2v\sigma_{1}$$
(6)
$$D_{TM} = 1 - \frac{{\sigma_{3} - 2v\sigma_{1} }}{{E_{T} \varepsilon_{3} }}$$
(7)

The relationship between DTM and ε3 is shown in Fig. 8. In the elastic stage, DTM is equal to DT and remains constant; then, with the increase of strain ε3, DTM increases rapidly and is related to ε3 as a two-phase exponential function. It is found that DTM quickly reaches a great damage value under the action of axial tensile stress, which is highly different from the damage evolution under uniaxial/triaxial compression. This is mainly because the specimen is subjected to axial tensile stress after the elastic stage and enters the plastic stage to begin yielding. The axial stress in the specimen is more about the deformation and elongation of the grains inside the specimen in the direction of the tensile stress, so most damage occurs near the elastic stage. In the uniaxial/triaxial compression test (Wang et al. 2021), more extrusion and friction occur between the grains of the specimen, and only a small amount of strain is required to complete the shear damage after the elastic stage. Hence, the damage occurs mainly near the ultimate strain εmax. Significantly, the initial DTM is larger at T = 500 °C than at T = 800 °C because E is larger at T = 500 °C; therefore, ET will be smaller, resulting in a larger DTM.

3.3 Failure modes after thermal treatment

The failure morphology and fracture modes of the specimens are related to T. As shown in Fig. 9, the failure surface of all specimens is approximately a flat or slightly inclined line. It is not difficult to find that the failure surface is smoother and presents a straight line overall at T = 500 °C and 800 °C, despite the latter having a slight depression on the left side. Correspondingly, the mechanical behavior of the two groups of specimens is similar. The axial deviatoric stress and axial ultimate strain are smaller than other specimens. The failure mode at this time is a pure shear failure; the fracture surface is perpendicular to σ3 because the high temperature accelerated the expansion of microcracks in the specimens, and the effective length of the original horizontal microcracks increased. Under axial tensile stress, the horizontal microcracks in the specimen that the high temperature has extended are more likely to penetrate between them.

Fig. 9
figure 9

Macroscopic failure patterns of post-heated specimens under triaxial extension tests

Full size image

In contrast, the fracture of sandstone specimens at T = 25 °C, 100 °C, 200 °C, and 300 °C is somewhat uneven. Especially at T = 200 °C, the specimens' axial ultimate strain and axial deviatoric stress are also slightly larger than others. This is mainly because the heating causes some of the micro-cracks inside the rock to close, rather than the microstructure damage caused by structural thermal stress, which the P-wave velocity of the specimen can also prove. At this time, the failure mode of the specimens is a combined tensile-shear failure, so there will be a certain amount of undulation in the section. At T = 300 °C, the failure mode of the specimen transitions from tensile-shear failure to pure shear failure, so the section is relatively smooth. Therefore, in the triaxial extension, different heating temperatures will change the failure mode of the specimens; the specimen will be a combined tensile-shear failure at T < 300 °C and a pure shear failure at T ≥ 300 °C.

3.4 Microstructural characteristics after thermal treatment

To understand the effect of thermal treatment on the microstructure of the rock and the microscopic characteristics of the fracture surfaces of the specimens, we performed SEM tests on S25, S200, S500, and S800 specimens and obtained the SEM images shown in Fig. 10. On the whole, T increases the grain size in different degrees. With the increase of T, the microstructure fracture mode changes from inter-granular fracture to a mixture of inter- and trans-granular fracture. The microcracks and micropores in the specimen changed from gradually closing to expanding, adding, and grain melting. The specific analysis is as follows.

Fig. 10
figure 10

SEM images of post-heated specimens under triaxial tensile test

Full size image

When T = 25  °C, the distribution of grains and pores of the specimen section is more uniform, the mineral particles are closely arranged, and most of the larger mineral particles are filled with flocculent clay material; most specimen sections are intergranular fractures. An inter-granular fracture will consume less energy than a trans-granular fracture, which also verifies the reasonableness of the tensile stress of σ3 for specimen S25-0 in Table 3. At T = 200 °C, mineral grain boundaries are evident in the × 30 picture; there are fewer pores, and the grain size is slightly expanded than T = 25 °C. The × 200 picture shows a more pronounced expansion of mineral grains, and even bulging of the matrix between mineral grains by development and extrusion can be observed in the × 1000 picture, and intergranular fracture dominated the section.

At T = 500 °C, most grains have obvious grain boundaries and penetrate cracks in some areas, presumably due to the different expansion coefficients of varying mineral grains at this temperature. The images of × 200 and × 1000 reveal sprouting new microcracks. The specimen's cross-section is dominated by intergranular fracture and small transgranular fracture areas. However, the specimen are purely shear fractured at this time, the number of transgranular fractures would theoretically increase (Liu et al. 2022a), perhaps due to the peculiarities of the loading paths that lead to this anomaly. At T = 800 °C, the obvious melting of mineral grains or matrix, results in the blurred boundary of mineral grains. × 200 picture show that the entire section has been melted into a sticky mass, which should be formed by the liquid phase material flowing between the grains and within the pores after cooling in the molten state; At this time, the fracture between matrix and transgranular is more dominant in the specimen.

3.5 Mechanical characteristics of specimens with different moisture contents

3.5.1 Stress–strain curves

As shown in Fig. 11, the stress–strain curves have the same trend as Fig. 7, while the curve will be more curved with the moisture contents increasing. It indicated that the existence of moisture reduced the brittle properties of the rock and enhanced its plastic deformation properties under triaxial extension; this is consistent with the reference(Chen et al. 2019). Figure 12 illustrates the relationship between axial deviatoric stress, axial ultimate strain, elastic modulus, and moisture content. It is found that when T < 500 °C, the axial deviatoric stress decreases with the moisture content increases, and decreases obviously at T = 500 °C and Kt = 0–20%. Then the axial deviatoric stress is little affected by moisture content, and the influence of temperature becomes significant. As shown in Fig. 12b, c, the axial ultimate strain increases nearly linearly with the increase in moisture content, and the elastic modulus shows a decreased trend with the increase in moisture content.

Fig. 11
figure 11

Stress–strain curves of specimens after thermal treatment and with different moisture content under triaxial extension

Full size image
Fig. 12
figure 12

Mechanical characteristics of specimens with different moisture contents after high-temperature treatment and water immersion under triaxial extension: a axial deviatoric stress versus moisture content; b axial ultimate strain versus moisture content; c elastic modulus versus moisture content

Full size image

3.5.2 Failure characteristics

The macroscopic and microscopic characteristics of sandstone specimens with different moisture contents are shown in Figs. 13 and 14. It is found that the visible fractures of the specimens are all horizontal cracks, which is determined by the axial tensile stress, although the temperature and moisture content have changed somewhat.

Fig. 13
figure 13

Failure modes of specimens with different moisture content after temperature and water immersion treatment under triaxial tension

Full size image
Fig. 14
figure 14

SEM images of specimens with different moisture contents subjected to temperature and immersion treatment under triaxial tension at T = 25 °C

Full size image

Figure 14 shows the microstructure of the specimens at different moisture contents at T = 25 °C. At Kt = 0, the microstructure of the specimens is intact and continuous wave-like. At Kt = 20%, some water erosion caused small particles can be seen. Compared with Kt = 0, the specimen's microstructure is no longer complete. At Kt = 50%, the specimen showed water erosion traces and produced obvious micro cracks. At Kt = 80%, a partial dry zone appears in the middle of the grain, the matrix inside the specimen falls off obviously, and microcracks appear in the grain. At Kt = 100%, the matrix in the vicinity of the grains inside the specimen widely falls off, showing an apparent fine-grained structure.

3.5.3 Energy evolution characteristics

After the specimens were heat treated and then treated with different moisture contents, assuming that the energy at the beginning of axial unloading was equal to zero, the energy consumed in the axial direction from the time of unloading to the time of failure was calculated separately for each specimen, and the results are shown in Table 4 and Fig. 15. It is found that the overall energy consumption is T = 200 °C > T = 25 °C > T = 500 °C > T = 800 °C, and with the increase of moisture content, the greater the energy consumed by the specimen, which is because the increase of moisture content reduces its bearing capacity, but increases its plastic deformation capacity, which makes the specimen damage consume more energy under the combination. Moreover, assuming that the axial energy at Kt = 0 is 1, the relative axial energy is shown in Fig. 15b. When Kt ≤ 20%, the axial energy consumption changes greatly when T = 25 °C, indicating that the water sensitivity of the specimen at room temperature is higher than that of the specimen after high-temperature treatment. When Kt > 20%, the energy consumption of the specimen after high-temperature treatment changes greatly, and the water sensitivity is significant.

Table 4 Parameters of sandstone specimens under triaxial extension after thermal treatment and after soaking and air-drying with a certain moisture content
Full size table
Fig. 15
figure 15

Axial energy consumption of specimens with different moisture contents under triaxial tension: a axial energy versus moisture content and b relative axial energy versus moisture content

Full size image

4 Discussions

The main reasons for the change in mechanical properties of the specimens that were heat treated with different moisture contents are as follows:

  1. 1.

    The deformation of mineral grains and the matrix itself. From the mechanical performance of the specimens after different temperature treatments, it is found that the mechanical properties of sandstone are enhanced at T ≤ 200 °C. At this time, all grains are thermally expanded, there is sufficient compressible space around them for expansion and deformation, and there is adequate cooling deformation space between the grains and the matrix during the cooling process so that no new microcracks are generated. As shown in Fig. 16, the thermal expansion of the grains brought by the temperature does not fully return to their original shape after cooling, so the grains get a certain degree of filling between them, thus enhancing their mechanical properties. And when T ≥ 300 °C, the grains expand further, but there is no sufficient compressible space around them, and the grains squeeze each other, while during the cooling process, different mineral particles shrink to different degrees, and microcracks naturally appear between the particles that shrink fast and those that shrink slowly. Although the thermal stress enables the grains to expand to a certain extent, the microcracks triggered by the damage to the specimen are more remarkable, especially the high temperature and the melting of the matrix and grains, but also substantially reduce the overall mechanical properties of the specimen.

  2. 2.

    Changes in mineral composition. XRD results show that Chlorite disappears with increasing temperature, Enstatite and Calcium hydroxide appear with increasing temperature, Hematite decreases rapidly with increasing temperature, etc. In addition, Kumari et al. (2019) pointed out that around 573 °C is the phase change point of Quartz grains, at which the Quartz will change from α-phase to β-phase. This change will cause the volume expansion of Quartz, leading to gaps and cracks in and around the quartz grains, which in turn will destroy the integrity of the sandstone and lead to its mechanical property deterioration.

  3. 3.

    Loss of moisture in the specimen. High temperatures are often accompanied by water evaporation. Scholars (Zhang et al. 2016) showed that different temperatures correspond to other states of water loss; from Fig. 5, the specimen quality decreases with the rise in temperature to verify this fact.

  4. 4.

    The existence of water causes the disintegration of the grains or matrix of the specimen, which is the main reason for the change in the mechanical properties of the specimen. The physical and mechanical parameters of the specimens in the triaxial extension decreased to a different extent with the change in water content, which is consistent with the results of previous tests such as UCT, BT and SHPB.

Fig. 16
figure 16

Schematic diagram of the damage evolution process of the specimen

Full size image

5 Conclusions

  1. a.

    The stress–strain curve of soft sandstone under triaxial tensile test after high heating temperature treatment and natural cooling with certain moisture content is a smooth and complete concave curve before the peak load, which can be divided into three stages: elastic stage, yield stage, and damage stage. The E and m of the specimen decrease with the increase of T, and the εamax increases first and then decreases with the increase of T. A higher moisture content corresponds to a lower strength, a lower elastic modulus, and a greater plastic deformability. The triaxial extension strength of sandstone is strengthened until 200 °C and then gradually decreases with the heating temperature, during which the tensile strength corresponds well with the P-wave velocity.

  2. b.

    The damage of all specimens in triaxial extension exhibited distinct brittle failure, rather than the high temperature that would cause the specimens to change their failure mode from brittle failure to quasi-brittle failure as in the compression test. With Kt = 0, T ≤ 300 °C and T = 200 °C, Kt ≤ 80% as the inflection points, the specimens achieved the transition from tensile-shear fracture to pure shear fracture in triaxial extension.

  3. c.

    The microstructure fracture mode changed from intergranular fracture to a mixture of intergranular fracture and trans-granular fracture with the increase of T, and the increase in moisture content Kt increased the degree of disintegration of the grains or matrix inside the specimen.

  4. d.

    The mechanism of thermal treatment influences the triaxial tensile mechanical properties of soft sandstone, mainly the loss of water inside the specimen, the reduction of the overall mass, the expansion and melting of mineral particles, the development of microcracks and micropores and the spontaneous chemical reaction of mineral grains, and the combined effect of these factors will lead to the enhancement or deterioration of the mechanical properties of the specimen under triaxial extension.