1 Introduction

As an associated product in the coal formation process, coalbed methane is not only an important factor that affects the safe and efficient production of mines but is also a high-quality clean energy source. Many countries, including China, are rich in coal bed methane reserves and regard it as a significant energy source (Zhang et al. 2022; Liu et al. 2009; Zhou et al. 2020; Li et al. 2021a, b). However, the dense nature of coal reservoirs makes the extraction of coalbed methane very restricted, and effective permeability enhancement technology measures are needed to increase the permeability of coal reservoirs. After nearly 70 years of development since the first hydraulic fracturing in the United States, hydraulic fracturing has become an effective technical measure to increase the production of oil, shale gas, natural gas, and coal bed methane (Yu et al. 2013; Jiang et al. 2017; Wasantha et al. 2017; Li et al. 2021a, b).

Many factors influence hydraulic fracturing, and most scholars have conducted research on the fracture initiation and expansion law of fracturing around the physical strength of coal, ground stress, pore pressure, coal structure, and inhomogeneity of the reservoir. (Hubbert and Willis 1972; Fan et al. 2014) proposed a tensile damage initiation theory when the stress concentration in the hole wall due to hydraulic fracturing is considered. By analyzing the annular tensile stress in the well wall, they concluded that the fracture initiation began when the annular tensile stress exceeded the tensile strength of the borehole wall rock. Subsequently, (Dunlap 1962; Kehle and Ralph, 1964) investigated the relationship between hydraulic fracture borehole and ground stress and concluded that fractures extended along the direction perpendicular to the minimum principal stress, and the results laid the foundation for subsequent studies on hydraulic fracturing. Detournay et al. (1989) established fracture initiation guidelines for rock fracturing based on the consideration of the effects of physical differences and pore structure on fracture initiation pressure. Hanson et al. (1981) found that placing natural fractures at different boundaries of the rock samples caused changes in local ground stress, which in turn affected the expansion of hydraulic fractures. (Haimson and Fairhurst 1967) investigated the effects of natural cracks and stress fields on the morphological characteristics of hydraulic cracks by theory and experiments. Daneshy (1978) investigated the expansion law of hydraulic cracks in laminated formations by theory and experiment and found that strong interfaces had minimal effects on the expansion of hydraulic cracks, whereas the hindering effect of weak interfaces on crack expansion does not change with the interface properties on both sides. Li et al. (2014) conducted a physical simulation of horizontal well fracturing from tuff penetration to coal seam by a true triaxial test rig and found that many long fractures were formed when the elastic modulus of the rock and coal seams had huge difference. Zhang et al. (2017) compared the extension of fractures within water and supercritical CO2 fractured sandstones and shales by micro-CT and found that hydraulic fracturing did not present a reticulated fracture structure similar to that seen after supercritical CO2 fracturing. Tan et al. (2017a, b) comparatively studied the law of hydraulic fracture initiation from the top and bottom plates of the coal rock seams and cross-interface extension through layers under different combinations of coal rock, sandstone, and shale; analyzed the effects of structural surface cementation strength on hydraulic fracture extension through layers; and grasped the characteristics of hydraulic fracture vertical asymmetric extension. Xing et al. (2018) investigated the vertical expansion behavior of cracks and constructed a control model with multi-parameter effects by considering the effects of interlayer stress difference, interfacial cementation strength, net pressure within the seam, and vertical stress difference. Liu et al. (2016) investigated the fracture initiation and extension pattern of hydraulic fracturing considering azimuth, different well slope angles, and injection parameters in stratified media.

The aforementioned studies mainly investigated the expansion mechanism of hydraulic fracture by theory and experiment, and several research in the numerical simulation of hydraulic fracturing had been conducted by relevant scholars. Yan et al. (2016, 2018), Yan and Jiao (2018) established a numerical solution method for fluid–solid coupling based on a combined finite-element-discrete-element approach to analyze the formation mechanism of complex hydraulic seam networks in fractured reservoirs, considering the characteristics of coal rock matrix and intra-seam seepage properties, as well as fluid filtration loss. Wang et al. (2018) conducted a hydraulic fracturing simulation study on the simultaneous extension of multiple fractures by combining the extended finite element method and the cohesive unit method. They found that fracture spacing and ground stress difference have a huge effect on the fracture length and width when multiple fractures are extended simultaneously. Gordeliy and Peirce (2013a, b) developed a coupled stress-percolation model for calculating the fracture tip singularities by considering the fracture intermittent fluid pressure singularities and hysteresis phenomena. Shi et al. (2016) used a multi-point constraint approach to limit the fracture width and calculated the problem of proppant interference with the fracture and its transport pattern within the fracture numerically. Zeng et al. (2018) conducted a numerical simulation study of multi-crack extension by setting different physical rock parameters (e.g., material properties, Young's modulus, and fracture toughness) and found that the non-homogeneity of the rock had a significant effect on the hydraulic crack extension. Dahi-Taleghani and Olson (2011) investigated the relationship among fracture intersections during hydraulic fracturing in impermeable media blocked by natural fractures based on a node-rich numerical model. Li et al. (2019) improved the intrinsic relationship of the bilinear cohesive unit by considering the Moore–Coulomb criterion for natural cracks and developed a two-dimensional flat surface pore pressure cohesive unit model. The aforementioned studies indicate that hydraulic fracturing studies mainly focus on the effects of stress fields, natural fractures, and different lithologies on hydraulic fracturing and on shales and sandstones. The laminated coal aspects of hydraulic fracturing are much less studied.

As such, this paper investigates the effect of laminar dip angle on the hydraulic fracture extension in coal by real triaxial hydraulic fracture test and numerical simulation. A hydraulic fracture extension study method based on finite element mesh embedded with zero-thickness cohesive cells was established using Python language incorporated into ABAQUS numerical simulation and analysis software to study the hydraulic fracture extension law of laminated coal under different fracturing conditions to systematically and accurately describe the fracture extension behavior during the hydraulic fracturing of laminated coal and provide theoretical and design guidance for the research on hydraulic fracturing of coal rock reservoirs.

2 Hydraulic fracturing physical simulation test design

2.1 Test equipment and systems

The test was conducted with a true triaxial gas-bearing coal sample fracturing and seepage test system from the State Key Laboratory of Gas Geology and Gas Control of Henan Polytechnic University. The hydraulic fracturing test device consists of three major parts, namely, triaxial stress loading system, fracturing fluid injection system, and monitoring and control acquisition system (Fig. 1).

Fig. 1
figure 1

Schematic of the true triaxial hydraulic fracturing test system

Full size image

2.2 Sample preparation

Considering the maximum allowable specimen size of the true triaxial testing machine, the test specimen was prepared by means of the coal–rock combination. The coal blocks used in the test were taken from the No. II-1 coal seam in Zhaogu No. 2 Coal Mine, Xinxiang, China. After transporting the fresh large pieces of raw coal specimens with obvious laminar structure from the underground to the laboratory, the raw coal samples were processed into rectangular coal samples with dimensions of 200 mm × 180 mm × 95 (± 5) mm by using a laboratory wire cutter. Due to the limitation of the coal sample size, this test specimen was prepared by the coal–rock assemblage method, and concrete simulation was used to replace the rock in the coal–rock assemblage during specimen preparation.

2.3 Test method and procedure

To study the influence of laminar characteristics on the expansion of hydraulic fractures in coal, a real triaxial hydraulic fracturing test of the combined body with different coal laminar orientations was conducted to study the characteristics of laminar characteristics on the expansion behavior of hydraulic fractures, and the specific test protocol is presented in Table 1. The true triaxial physical simulation hydraulic fracturing test system uses multiple sets of equipment to work together, and the specific test steps are given as follows.

  1. (1)

    Specimen maintenance. After the preparing the specimens, they were maintained for one month to obtain the final coal–rock composite specimens for the hydraulic fracturing test of the coal.

  2. (2)

    Fracture hole drilling. The specimen is placed, loaded, and fixed into the true triaxial loading chamber, and the magnetic drill is fixed and magnetized on the true triaxial equipment. The hole is precisely positioned at the center of the specimen with a central drilling length of 100 mm and a drilling diameter of 10 mm.

  3. (3)

    Fracture tube assembly. After the specimen drilling is completed and removed, the fracture pipe (6 mm diameter) is placed inside the borehole and sealed with WD type AB glue, and the strength of this type of glue can reach more than 30 MPa to meet the test conditions.

  4. (4)

    Three-way stress loading. After the glue reaches strength, the specimen is placed in the true triaxial loading chamber, and the three-way stress is applied to simulate the ground stress environment of the reservoir by the true triaxial testing machine using the step-by-step synchronous loading method by first loading the three-way stress synchronously to the low stress level and then loading it synchronously step-by-step to the set stress level.

  5. (5)

    Hydraulic fracturing. Start the fracturing fluid injection system; inject fracturing fluid evenly into the specimen according to the set displacement; record the change curve of the injection pressure and injection volume through the monitoring and control acquisition system, and continue to inject for 1 min to allow the specimen to fully extend the hydraulic fracture and complete the hydraulic fracturing test of the specimen when the fracturing fluid overflows around the specimen and the injection pressure curve starts to decrease continuously.

  6. (6)

    Disassembly of the specimen. Stop each test monitoring and acquisition system, unload the three-way stress of the specimen in the true triaxial loading chamber smoothly to 0 MPa, observe the cracks on the surface of the specimen, and then follow the main seam that extends to the surface of the sample.

  7. (7)

    Manual splitting. The specimens were dissected to grasp the expansion path, morphology, and extent of hydraulic fractures inside the specimens by the expansion of fracturing fluid. The overall flow of hydraulic fracturing test is detailed in Fig. 2.

Table 1 Hydraulic fracturing scheme
Full size table
Fig. 2
figure 2

Schematic of the overall flow of hydraulic fracturing test

Full size image

3 Analysis of hydraulic fracturing test results

3.1 Characterization of hydraulic fracture morphology

After the hydraulic fracturing test, the morphological characteristics of hydraulic fracturing crack initiation are observed through layer propagation. The crack characteristics of the fracturing samples under different bedding conditions are illustrated in Fig. 3.

Fig. 3
figure 3

Propagation pattern of hydraulic crack

Full size image

As presented in Fig. 3a, with a laminar inclination angle of 0° and injection displacement of 20 mL/min, two main cracks were produced during hydraulic fracturing, one first expanded along the laminar surface and then penetrated the coal sample in the direction of the maximum principal stress to reach the upper coal-rock interface, and the other directly penetrated the coal sample in the direction of the maximum principal stress and reached the coal-rock interface. Finally, the two main cracks reunited at the intersection and penetrated the whole coal–rock intersection. As depicted in Fig. 3b, under the conditions of laminar inclination angle of 90° and variable displacement injection (20 mL/min changed to 40 mL/min), a main fracture was produced in the coal sample during hydraulic fracturing, and the main fracture penetrated the whole sample along the laminar direction. Furthermore, the main fracture formed a penetration fracture after reaching the upper coal–rock intersection and continued to extend through the intersection directly after reaching the lower coal–rock junction and along the direction of the maximum principal stress to the lower bottom surface of the whole sample. As illustrated in Fig. 3c, when the laminar dip angle is 60° and injection displacement is 20 mL/min, the hydraulic fracture was extended mainly along the laminar surface after the fracture started to occur at the injection point of the coal sample (the area shown by blue dotted lines in Fig. 3c). Subsequently, it reached the coal–rock intersection and penetrated the whole intersection in the laminar direction.

When the laminar dip angle is perpendicular to the direction of the maximum principal stress, the hydraulic crack that encounters the weak surface of the laminar structure mainly shows two evolutions of penetration closure and obedience followed by turning. Through closure means that the hydraulic crack passes directly through the natural structural weak surface, and the extension and expansion of the hydraulic seam network are not affected. First obedient and then turning means that the crack first extends along the natural structural weak surface for a while and then turns and expands. As displayed in Fig. 3a, in the crack propagation process, the bedding plane first propagates along this direction. However, under the influence of ground stress, the crack will turn again and expand along the maximum principal stress direction. When the laminar dip is parallel to the maximum principal stress direction, the hydraulic cracks are confined to the weak surface of the laminar structure, and the hydraulic seam network shows a submissive evolution. As exhibited in Fig. 3b, the hydraulic crack begins along the maximum principal stress direction and then continues to expand through the bedding plane along the maximum principal stress direction, thereby forming a relatively single crack structure. When the laminar dip angle is 30° from the maximum principal stress direction (acute angle), the hydraulic crack encounters the weak surface of the laminar structure mainly in a submissive evolutionary manner, but a large open slip crack is formed between the laminar surfaces. As displayed in Fig. 3c, the hydraulic crack starts along the maximum principal stress direction and then continues to expand through the bedding plane along the maximum principal stress direction, thereby forming a relatively single crack structure.

3.2 Characteristic analysis of the whole change curve of injection pressure

The injection pressure variation curve is a full record of the fracturing fluid pressure changes during the processes of fracture initiation and expansion, which can be used to dynamically characterize the fracture initiation and expansion. The injection pressure variation curves for the hydraulic fracturing of specimens under different stratigraphic conditions are shown in Fig. 4.

Fig. 4
figure 4

Injection pressure–time curve during fracturing

Full size image

By observing the injection pressure variation curves, the pressures for the initial fracture of the coal under the conditions of 0°, 90°, and 60° of the lamina dip angle are 13.58, 11.27, and 13.43 MPa, respectively, and the three are relatively close to one another. The relationship between the pressure and the dip angle of the seam is not evident.

As exhibited in Fig. 4a, the injection pressure curve can be divided into three stages under the conditions of 0° laminar dip angle and injection displacement of 20 mL/min: In Stage 1, which refers to the fracture initiation period, the water pressure in the injection borehole continues to rise with the constant injection of fracturing fluid, and when the damage strength of the coal is exceeded, the initial rupture occurs, and the injection pressure reaches 13.58 MPa and then rapidly drops to 7.04 The second stage refers to the fracture extension period, where the injection pressure fluctuates between 7 and 9 MPa, and the fracture continues to expand through the laminated surface with the continuous injection of fracturing fluid, with a relatively long period. In the third stage, the specimen is destroyed, the macroscopic fracture inside the coal sample expands to the coal–rock interface and forms a large fracture through it, the fracturing fluid overflows greatly, and the specimen is completely destroyed.

As presented in Fig. 4b, under the conditions of 90° laminar dip angle and variable displacement injection (20 mL/min becomes 40 mL/min), the injection pressure curve can be divided into four stages: the first stage is the fracture initiation period, the initial stage (displacement of 20 mL/min) encounters the natural weak face of the coal at the injection pressure of 11.27 MPa when the initial fracture occurs and then rapidly drops to 4.85 MPa with a large initial fracture scale. The second stage is the fracture expansion period, the injection pressure curve is undulating with the continuous injection of fracturing fluid, the highest injection pressure is 12.69 MPa, the fracture expands along the laminar surface, and the injection pressure decreases to approximately 8.50 MPa and maintains a stable period. In the third stage, the fracture penetration period is a variable displacement. After the fracturing fluid displacement rises to 40 mL/min, the injection pressure climbs sharply and undulatively, and the injection pressure falls down less, indicating that the fracture penetration process generates less new fractures. The fourth stage is the specimen destruction period, where the internal main hydraulic fracture extends to the surface of the specimen, the fracturing fluid overflows in large quantities, and the specimen is completely destroyed.

As illustrated in Fig. 4c, the injection pressure curve can be divided into two stages at a laminar dip angle of 60° and an injection displacement of 20 mL/min: the first stage is the fracture initiation–extension stage, in which the initial fracture occurs when the injection pressure reaches 13.43 MPa as the water pressure in the injection borehole continues to rise, and then the injection pressure rapidly extends along the laminar surface, and the injection pressure then falls to 9.43 MPa. In the second stage, the specimen is destroyed when the fracture fluid is injected continuously and the internal macroscopic fracture is extended along the laminar surface to the intersection, and the fracture fluid gradually overflows from the intersection and the specimen is destroyed.

4 Numerical simulation method for hydraulic fracturing of coal

4.1 Simulation of coal hydraulic fracturing cohesive unit method

Compared with solid elements, cohesive elements can accurately model structures with large aspect ratios and withstand tensile and shear strains without any stresses; also, such elements are zero-thickness (Hu et al. 2003; Liu et al. 2018). The sprouting and extension of cracks during the hydraulic fracturing of coal can be simulated well by using this zero-thickness cohesive unit.

4.1.1 Fluid flow model within the fracture

The fracturing fluid flow in the fracture consists of tangential and normal flows. Assuming that the fracturing fluid in the fracture is selected as an incompressible Newtonian fluid, it conforms to Newton’s law of viscosity:

$$\tau = \mu \frac{{{\text{d}}u}}{{{\text{d}}y}},$$
(1)

where: τ is the shear stress, du/dy is the shear deformation rate, and μ is the fracturing fluid viscosity.

The tangential flow equation of fluid in the fracture is:

$$q_{t} w = - \frac{{w^{3} }}{12\mu }\nabla p_{w} ,$$
(2)

where qt is the flow rate of fracturing fluid per unit area, w is the fracture width, \(\nabla p_{w}\) is the pressure gradient in the direction of the fracture, and \(\frac{{w^{3} }}{12\mu }\) can be understood as permeability or flow resistance.

The normal flow of the filtration behavior of the coal–rock porous matrix in the fracture is defined as follows:

$$\left\{ {\begin{array}{*{20}l} {q_{{\text{a}}} = c_{{\text{a}}} \left( {p_{{\text{m}}} - p_{{\text{a}}} } \right)} \hfill \\ {q_{{\text{b}}} = c_{{\text{b}}} \left( {p_{{\text{m}}} - p_{{\text{b}}} } \right)} \hfill \\ \end{array} } \right.,$$
(3)

where \(q_{{\text{a}}}\) and \(q_{{\text{b}}}\) are the normal fluid loss flow rates at the top and bottom surfaces of the unit, respectively; \(c_{{\text{a}}}\) and \(c_{{\text{b}}}\) are the fluid loss coefficients on the top and bottom surfaces, respectively; \(p_{{\text{m}}}\) is the fracture flow pressure at the midplane of the unit; and \(p_{{\text{a}}}\) and \(p_{{\text{b}}}\) are the pore pressures at the top and bottom surfaces of the unit, respectively.

4.1.2 Intrafracture fluid flow model

In cohesive unit failure theory, the crack propagation process demonstrates that the crack tip overcomes, separates, and fractures the cohesive force, and the crack initiation and propagation are controlled by the traction–separation criterion.

  1. (1)

    Initial damage

The tensile component of the crack traction force is mainly caused by the crack fluid pressure, and its shear component is induced by the ground stress difference and the local shear stress site caused by the presence of natural cracks. For cracks with mixed tensile-shear damage mode, the initial damage displacement is not a constant value but is related to the tension–shear mixing mode and mixing ratio under specific loading conditions. The initial damage is predicted using the second-order stress criterion of the mixed tension–shear mode, as shown in Eq. (4) (Wang et al. 2020):

$$\left( {\frac{{t_{n} }}{{\sigma_{t} }}} \right)^{2} + \left( {\frac{{t_{s} }}{{\sigma_{s} }}} \right)^{2} = 1,$$
(4)

where σt and σs are the tensile and shear strengths, respectively; and tn and ts are the normal and tangential tractions, respectively.

  1. (2)

    Damage evolution

The damage degree of the cohesion unit is characterized by introducing the damage factor D, which increases monotonically from 0 to 1 after the initial damage occurs. Then, the stress change caused by the damage can be expressed as:

$$\left\{ {\begin{array}{*{20}l} {t_{n} = \left( {1 - D} \right)\overline{t}_{n} ,\;{\text{Tensile state}}} \hfill \\ {t_{n} = \overline{t}_{n} ,\;{\text{Compression state}}} \hfill \\ {t_{n} = \left( {1 - D} \right)\overline{t}_{s} } \hfill \\ \end{array} } \right.$$
(5)

where \(\overline{t}_{n}\) and \(\overline{t}_{s}\) are the stress components of the current separation displacement under the linear elastic law.

4.2 Cohesive element embedding process

Cohesive element cells are embedded between entity elements by writing an ABAQUS plug-in in Python programming language. After embedding, a cohesive element exists between any two adjacent entity cells. The solid cells and their adjacent cohesive cells are connected by two shared nodes, and any two adjacent cohesive elements are connected by sharing a node. Figure 5 depicts a schematic of the process of embedding the cohesive force-containing pore–pressure cells into the original finite cell mesh. To simulate the flow over the cohesive unit driven by the fracturing fluid, two additional pore pressure nodes are required on each cohesive unit to calculate the fluid pressure gradients in the tangential and normal directions. The nodes in the dashed circles in Fig. 5 have the same coordinates, and the cohesion cells have zero thickness. All adjacent cohesion cells need to share an identical pore pressure node to ensure that fluid pressure can be transferred between them. Therefore, pore pressure nodes with the same coordinates should be combined.

Fig. 5
figure 5

Schematic of the process of embedding a cohesion-containing pore-pressure cell into a finite cell mesh

Full size image

4.3 Validation of numerical model validity for hydraulic fracturing of coal

To verify the correctness of the cohesive cell embedding method, the validity of the model, and the accuracy of the model grid, the numerical model is compared and verified by the classical KGD theoretical model and the laboratory test in this paper.

4.3.1 Numerical validation of computational models

This validation model is a two-dimensional planar model (Fig. 6). The model is divided into fracture and non-fracture zones. The size of the fracture zone is 300 mm × 200 mm in line with the laboratory test size, whereas that of the whole model is 1500 mm × 1000 mm considering the boundary effect. The model is divided into 32,448 units, of which 16,263 are pore fluid–stress coupled plane strain units (type CPE4P), and 16,185 are cohesive pore pressure units (type COH2D4P) with an overall size to fracture zone size ratio of 5:1.

Fig. 6
figure 6

Numerical model for model validation

Full size image

The initial ground stress is applied using predefined, the minimum principal stress is applied in the x-direction, the maximum principal stress is applied in the y direction, and the z-direction is the coal seam thickness direction (the direction is shown in the Fig. 6). The x and y directional degrees of freedom of the nodes of the model edges perpendicular to the x and y directions are constrained, the pore pressure at the boundary around the model is set to 0 (net pore pressure), and the initial pore ratio is defined as 0.0554.

4.3.2 Numerical calculation model mechanics parameter determination

The triaxial compression failure test of the coal was carried out with the help of the laboratory coal rock triaxial creep–seepage test system. The confining pressure was set to 5 MPa, the size of the coal sample was Φ 50 mm × 100 mm, and the bedding inclination was 0° (perpendicular to the loading direction). The parallel tests have two groups (Samples A and B), and the coal–rock triaxial creep–seepage test system is displayed in Fig. 7a.

Fig. 7
figure 7

Triaxial creep seepage test system and test results

Full size image

The stress–strain curves of the coal samples with a confining pressure of 5 MPa are demonstrated in Fig. 7a. The compressive strengths of the two groups of test coal samples are 41.81 MPa and 36.26 MPa; and the elastic moduli are 4.08 GPa and 4.13 GPa. Therefore, the elastic modulus of the coal in this numerical model is set to 4.00 GPa according to the triaxial compression test, and the tensile strength is set to 1.16 MPa according to the Brazilian splitting test. The basic physical and mechanical parameters of the numerical model (unit system is mm) are displayed in Table 2.

Table 2 Physical and mechanical parameters of the validated numerical model
Full size table

4.3.3 Validation of numerical models

  1. (1)

    KGD model validation

The numerical model calculation results are compared with the classical KGD theoretical model, which is a two-dimensional plane strain model in this paper, and assumes the same conditions as the KGD model. The equation for calculating the injection point seam width in the KGD theoretical model is expressed in Eq. (6) (Yew and Weng 2015):

$$w_{{\text{o}}} = 1.32\left[ {\frac{{8\left( {1 - v} \right)Q^{3} \mu }}{G}} \right]^{1/6} t^{1/3} ,$$
(6)

where \(w_{{\text{o}}}\) is the injection point fracture width, m; \(G\) is the coal rock shear modulus, Pa; \(v\) is the coal rock Poisson’s ratio; \(\mu\) is the fracturing fluid viscosity, Pa·s; \(Q\) is the fracturing fluid discharge volume injected into a single flank fracture, m3/s; and \(t\) is the fracturing fluid injection time, s.

The basic physicomechanical parameters in Table 2 were subjected to KGD theoretical model and numerical simulation calculations. The variation of crack width at the injection point with time is analyzed statistically, and the results of the injection point crack width comparison are revealed in Fig. 8. In the early stage of hydraulic fracture expansion, the calculated injection point seam width of the KGD model is larger than the numerical simulation results, but the difference in the injection point seam width gradually decreases with the increase in fracture duration. The two seam width data basically match in the late stage of fracture, which proves the correctness of the cohesive cell embedding, the validity of the model, and the accuracy of the model grid from the perspective of injection point seam width change.

  1. (2)

    Hydraulic fracturing test verification

Fig. 8
figure 8

Numerical simulation results compared with KGD model

Full size image

To further verify the accuracy of the simulation results, the numerical simulation injection point pressure variation and crack propagation were compared with the laboratory real triaxial stress conditions of the coal (laminar dip angle 0°) hydraulic fracturing test, the numerical model boundary conditions and laboratory test conditions remain the same, the fracturing fluid injection displacement are 20 mL/min, and the injection pressure variation curves and crack propagation throughout the whole process is presented in Fig. 9.

Fig. 9
figure 9

Comparison of injection pressure change and crack propagation

Full size image

The initial fracture pressure of the coal in the laboratory hydraulic fracturing test is 13.58 MPa, the initial fracture pressure of the coal in the numerical simulation is 14.02 MPa, and the initial fracture pressure of the coal is basically the same between the two. After the first rupture, the test injection pressure is maintained between 6 and 9 MPa until its complete destruction, the injection pressure calculated by the numerical simulation is maintained between 7 and 9 MPa after the initial rupture, and the injection pressure during the fracture stabilization period is basically the same between the two (i.e., the penetration damage of the laboratory test specimen will lead to a sudden drop in injection pressure, but the numerical model does not exhibit coal penetration damage because of the boundary effect). The comparison of the fracturing fluid injection pressure variation curves of the laboratory test and the numerical simulation test shows that the numerical simulation and the laboratory hydraulic fracturing test are basically the same throughout the injection pressure variation (i.e., the reliability of the present numerical model is verified from the perspective of the fracturing fluid injection pressure variation).

As exhibited in Fig. 9c and d, the comparison between the crack propagation morphology of the hydraulic fracturing test in the laboratory and the numerical simulation of the hydraulic fracturing crack morphology results suggest that two main cracks appeared in the hydraulic fracturing test in the laboratory, mainly due to the existence of natural fractures and other weak surface structures in real coal, which caused a main crack to deflect but eventually spread along the direction of the maximum principal stress through the bedding plane, and the two cracks finally revealed the same growth law. Given that the boundary effect is considered in the numerical simulation, no fracturing failure of the sample is tested in the laboratory during the fracturing process. Therefore, the crack growth of the numerical simulation water pressure is only compared with the crack depicted in the red solid line in Fig. 9c. The comparison of the two indicates that the propagation of hydraulic cracks extends through the bedding plane along the direction of the maximum principal stress, thereby showing roughly the same propagation law, that is, the reliability of this numerical model is verified from the perspective of the propagation morphology of hydraulic cracks.

In summary, the results of this numerical model are compared and analyzed from the perspectives of injection point slit width variation, fracturing fluid injection pressure variation, and crack propagation morphology through classical theoretical models and laboratory fracturing tests to verify the validity of the cohesive unit method and the numerical model of hydraulic fracturing.

5 Numerical simulation of hydraulic fracturing of bedding coal

5.1 Numerical model of hydraulic fracturing of bedding coal

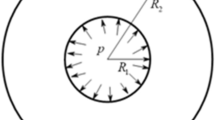
The numerical calculation model of the hydraulic fracturing of coal with bedding (taking the bedding dip angle of 30° as an example) is demonstrated in Fig. 10. The radius of the fracturing area is 2.5 m, and the radius of the whole model is 12.5 m. The size of the whole model is consistent with that of the fracturing area and the numerical model for effectiveness verification. The ratio of the whole model to the size of the fracturing area is set to 5:1. The numerical model is divided into 57,271 elements, including 34,586 pore fluid stress coupled plane strain elements (type CPE4P) and 22,685 cohesive pore pressure elements (type COH2D4P). The degree of freedom of the boundary nodes of the model adopts fixed support constraints, that is, the degrees of freedom in the x and y directions are constrained, and the rotational degrees of freedom in the xy plane are not constrained. In order to improve the accuracy of numerical simulation calculation, the grid is densified in the square area in the center of the hydraulic fracturing numerical calculation model, and hydraulic fracturing calculation is only carried out in the square area.

Fig. 10
figure 10

Numerical calculation model of hydraulic fracturing of bedding coal

Full size image

5.2 Simulation test scheme

The bedding dip angle, stress field, and fracturing fluid displacement are taken as single factor control variables to analyze the hydraulic crack propagation law under different conditions. The bedding dip angle (bedding and x horizontal direction) of coal is set to 0°, 30°, and 60°. Four groups of stress fields are set as (5 MPa, 2.5 MPa), (5 MPa, 5 MPa), (5 MPa, 7.5 MPa), and (5 MPa, 10 MPa). At the same time, to reflect the relationship between displacement and injection pressure, the fracturing fluid injection is loaded in the form of variable displacement and variable displacement waveform loading form, and the peak displacement of fracturing fluid is set to 0.006 m3/s. The numerical simulation test scheme is displayed in Table 3.

Table 3 Numerical simulation test scheme
Full size table

5.3 Numerical simulation results analysis

5.3.1 Effect of bedding dip angle on hydraulic crack propagation

The comparison of the pore pressure nephogram (Figs. 11a, 16a and 17a) suggests that a low pore pressure area is formed in a certain range in front of the main fracture, whereas a high pore pressure area is formed on both sides of the main fracture. Based on this, the development direction of the main fracture can be judged by the location of the low pore pressure area, whereas no obvious low pore pressure area is observed in front of the branch fracture. The formation of low pore pressure in the fracturing process is related to the tensile stress relief in front of the fracture.

Fig. 11
figure 11

Cloud plot of hydraulic fracturing simulation results for a laminar dip angle of 0°

Full size image

The comparison of the x-direction stress (S11) distribution nephogram (Figs. 11b, 12b and 13b) indicates that an elliptical compressive stress concentration area is formed on both sides of the main fracture when the bedding dip angle is 0°. When the bedding dip angle is 30°, the regional compressive stress concentration area cannot be formed on both sides of the main crack, and only compressive stress concentration is observed in a small area near the intersection of the bedding and the main crack. The failure to form compressive stress concentration may be caused by the stress release caused by the shear slip failure of the bedding. When the bedding dip angle is 60°, a x-shaped compressive stress concentration zone is formed, in which one wing is distributed along both sides of the main fracture, and the other wing is roughly perpendicular to the bedding and is gradually rotating.

Fig. 12
figure 12

Cloud plot of hydraulic fracturing simulation results for a laminar dip angle of 30°

Full size image
Fig. 13
figure 13

Cloud plot of hydraulic fracturing simulation results for a laminar dip angle of 60°

Full size image

The comparison of the nephogram of the fracture opening shape (Figs. 11c, 12c and 13c) shows that under the condition of bedding inclination of 0° and 30°, the main fractures pass through the bedding plane and open the fractures at the bedding, and the expansion of the bedding plane becomes more obvious when the bedding inclination is 30°. When the bedding dip angle is 60°, the hydraulic crack is limited between the bedding planes, but obvious open slip cracks are observed on the bedding plane.

The comparison of the expansion and evolution nephogram of the hydraulic fracture network during hydraulic fracturing indicates that under the fracturing test conditions of stress field (5 MPa, 10 MPa) and fracturing fluid displacement of 0.006 m3/s, the hydraulic crack can pass through the bedding surface, and the main crack approximately expands toward the maximum principal stress (i.e., y direction) when the bedding dip angle is 0° and 30°. As demonstrated in Fig. 14a, at the initial stage of hydraulic fracturing under the condition of bedding dip angle of 0°, the hydraulic crack extends to the bedding plane and directly passes through the bedding plane, thereby forming a small-scale crack network structure only at the bedding plane. As exhibited in Fig. 14b, at the initial stage of hydraulic fracturing under the condition of bedding inclination of 30°, when the hydraulic crack extends to the bedding plane, it also passes through the bedding plane, but it will crack at the bedding and form a branch fracture structure with large range of hydraulic shear. After extending to a certain range, the crack turns and continues to expand in the direction of the maximum principal stress. As revealed in Fig. 14c, when the bedding dip angle is 60°, the hydraulic fracture fails to pass through the bedding, the fracturing scale is limited to the coal seam within two adjacent beddings, and the main fracture extends along the bedding direction, indicating that the control effect on the fracture propagation direction under this bedding condition is stronger than the in-situ stress.

Fig. 14
figure 14

Cloud diagram of expansion and evolution processes of hydraulic fracture network

Full size image

As presented in Fig. 15, the initial fracture pressures of coal hydraulic fracturing under the conditions of bedding dip angle of 0°, 30° and 60° are 16.38, 16.08, and 17.06 MPa respectively, which are relatively close, indicating that the relationship between the initial fracture pressure and bedding dip angle is not obvious. In the later stage of fracturing, the injection pressure of the three groups of tests is stable between 7.98 MPa and 10.37 MPa, which is higher than the sum of the minimum principal stress (5 MPa) and the tensile strength of coal seam (1.13 MPa) (6.13 MPa), indicating that the increase rate of fracturing fluid is higher than the increase rate of fracture propagation volume, thereby driving the expansion of fracture morphology. According to the change curve of injection pressure and displacement, a correlation between injection pressure and displacement was observed, and the pressure changes synchronously with the displacement. It also shows that the large displacement fracturing method is helpful in driving the dynamic expansion of fractures. When the bedding dip angle is 60°, the injection pressure in the stable period is significantly smaller than that under the conditions of 0° and 30°, which is due to the formation of large slip cracks at the bedding plane under the condition of 60° and the continuous expansion along this direction, and the slip cracks disperse the injection pressure.

Fig. 15
figure 15

Injection pressure variation curve throughout

Full size image

5.3.2 Effect of stress field on crack propagation in water pressure

The numerical model of hydraulic fracturing with coal bedding inclination of 30° is used for the simulation test to analyze the influence of change in stress field on the crack propagation law of hydraulic fracturing of coal with bedding. In this numerical calculation model, the stresses in the x and y directions are set as 5 MPa and 2.5–10 MPa, respectively, with an increase in 2.5 MPa, and other basic mechanical parameters remain unchanged. Through numerical simulation calculation, the nephogram of the hydraulic fracturing test results of bedding coal under different stress conditions, which is limited to space, is obtained. Here, only the nephogram of the hydraulic fracture opening results is compared and analyzed (Fig. 16).

Fig. 16
figure 16

Crack tension cloud under different stress conditions

Full size image

As demonstrated in Fig. 16a, hydraulic crack propagation expands along the maximum principal stress direction at the initial stage. When the crack gradually approaches the bedding plane, it begins to expand in a direction parallel to the bedding plane. This phenomenon shows that under the condition of bedding and stress, the control effect of bedding on hydraulic crack propagation is stronger than that of stress field. As presented in Fig. 16b and c, under this stress condition, the hydraulic cracks all pass through the bedding surface, but the control effect of the bedding surface on the hydraulic cracks only causes them to expand in the direction with a certain included angle with the maximum principal stress. Among them, under the stress condition of (5 MPa, 7.5 Mpa), the hydraulic cracks have multiple branch cracks, but the expansion at the bedding is not evident. This finding suggests that under the condition of bedding and stress, the bedding and stress field can control the expansion of hydraulic crack, but the control effect of stress field on hydraulic crack is stronger than bedding. As exhibited in Fig. 16d, under this stress condition, the hydraulic crack runs through the whole bedding plane and expands along the direction of the maximum principal stress, and a branch crack structure is formed on each bedding plane. A complex hydraulic crack network structure dominated by tensile hydraulic cracks and accompanied by bedding shear cracks is formed under the combined action of this stress and bedding. When the difference between the maximum principal stress and the minimum principal stress is low, the stress field cannot control the crack growth direction, and the hydraulic crack growth direction is mainly affected by the bedding. When the difference between the maximum principal stress and the minimum principal stress is large, the control of the stress field on the crack propagation direction is enhanced, and the hydraulic crack propagation direction is mainly along the maximum principal stress direction, but branch cracks exist in the bedding direction.

Figure 17 illustrates the comparison curve of injection pressure changes in the whole process of hydraulic fracturing under different stress conditions. The initial fracture pressure of coal in the four groups of hydraulic fracturing simulation tests is 13.77, 14.21, 15.40, and 16.08 MPa. With the continuous change in the maximum principal stress, the initial fracture pressure increases with the maximum principal stress, but this increase is not apparent. In the stable period of injection pressure, the injection pressure under the stress condition of (5 MPa, 2.5 MPa) is significantly lower than that under other stress conditions, because the hydraulic fracture under this fracturing condition is limited to the range of two beddings, and a large open slip fracture is formed at the bedding, thereby dispersing the injection pressure.

Fig. 17
figure 17

Injection pressure variation curve under different stress conditions

Full size image

6 Conclusion

Coal hydraulic fracturing and antireflection are the premises of large-scale development and utilization of coalbed methane resources. In this paper, the hydraulic crack propagation law of layered coal under different fracturing conditions is investigated by combining laboratory test and numerical simulation. The main conclusions are drawn as follows.

  1. (1)

    On the one hand, the hydraulic crack in the physical simulation experiment propagates along the direction of the maximum principal stress when the bedding dip angle is 0° (perpendicular to the maximum principal stress). On the other hand, the range in the bedding direction is small, that is, the control effect of the maximum principal stress on the hydraulic crack propagation is stronger than that of bedding. Under a bedding inclination of 60°, the hydraulic crack expands in the bedding direction after the injection point extends to the bedding structural plane, that is, the control effect of this bedding condition on the hydraulic crack propagation is stronger than the maximum principal stress. When the bedding dip angle is 90° (parallel to the maximum principal stress), the hydraulic crack only propagates along the bedding direction.

  2. (2)

    The bedding dip angle has minimal effect on the initial fracture pressure of coal in the hydraulic fracturing process, and the fluctuation times of the whole injection pressure change curve are high, indicating that the hydraulic crack propagation is completed in multiple stages. The reasonable setting of fracturing fluid displacement is conducive to the formation of complex hydraulic fracture network structures. The variable displacement test reveals that small displacement is conducive to the opening of primary natural fractures whereas the large displacement is conducive to the passage of hydraulic cracks through structural planes and coal rock interfaces.

  3. (3)

    The fluid flow equation and mechanical damage criterion of cohesive element are analyzed. A global and local method of finite element mesh embedding zero-thickness cohesive element and a pore pressure node merging method for simulating fracturing are established using Python language and ABAQUS numerical analysis platform, respectively.

  4. (4)

    In (σx, σy) = (5 MPa, 10 MPa) under the stress condition, the main fracture is formed along the main stress direction while the secondary branch fracture is formed along the bedding direction under the condition of the coal bedding dip angle of 30°, indicating that the comprehensive action of the stress condition and bedding can form a more complex hydraulic fracture network structure. Under the condition of coal bedding dip angle of 0°, a relatively single crack grid is formed, and the crack extends along the direction of the maximum principal stress through the bedding. Under the condition of coal bedding dip angle of 60°, the control effect of this stress field on hydraulic crack is weaker than that of bedding.

  5. (5)

    Under different stress field conditions, the control effect of coal bedding on the hydraulic crack changes with the stress field. Therefore, the control effect of stress field and bedding inclination on hydraulic crack can be effectively combined to form a complex crack network structure.