Energy dissipation mechanisms in fluid driven fracturing of porous media

Abstract

We present a novel approach for calculating the energy dissipated during fluid driven fracturing in saturated porous media. Analytical functions describing both of the solid and fluid energy dissipation modes are derived based on a thermodynamic formulation for Non Local Damage and Transport (NLDT) in porous media. The thermodynamically consistent NLDT model derivation leads to a system of non-linear equations which are solved numerically in a mixed finite element framework. The proposed model is used to simulate hydraulic fracturing in a benchmark example and the aspects of energy dissipation are investigated. In this formulation, hydraulic fracture is presented as a disturbance of two continuum fields: (1) damage which describes the degraded stiffness of the solid material, and (2) non-liner permeability which evolves in the fracture zone to describe the elevated fluid flow velocity. A parametric study is performed to investigate the various mechanisms in different cases of loading and material properties. The model provides physics-based grounds for hydraulic fracturing optimization based on improved understanding of energy dissipation mechanisms

Article Highlights

• A detailed study of hydraulic fracturing energy budget is presented

• The underlying model is a continuum Non Local Damage Transport (NLDT) model

• Energy supplied through fluid injection can be either stored as elastic energy, or dissipated through fluid viscous flow and solid damage mechanisms

• Energy storage and dissipation functions are analytically derived and computed quantitatively based on a mixed FEM model

• Quantitative calculations of energy storage and dissipation are in agreement with available experimental and field data

• The study of energy budget can lead to advances in the hydraulic fracturing optimization

Appendices

Appendix A: Constitutive relationships

1.1 Appendix A.1: Poroelastic damage relationships

Based on the the fluid pressure definition in Eq. (24), the fluid content increment $\zeta$ can be rewritten as:

$$\begin{aligned} \zeta =\frac{P}{M(D)}+\alpha (D)\varepsilon _{kk} \end{aligned}$$

(A.1)

Equation (A.1) instates that the increment in the fluid content $\zeta$ is calculated as a function of the addition of the ratio of fluid pressure to Biot’s Modulus M and the solid volumetric strain scaled by th Biot’s coefficient $\alpha$. Substituting Eq. (A.1) in Eq. (23) leads to the redefinition of the stress tensor as:

$$\begin{aligned} \begin{aligned} \sigma _{ij}&=C_{ijkl}^u(D)\varepsilon _{kl}-\left[ \frac{P}{M(D)}+\alpha (D)\varepsilon _{kk}\right] M(D) \alpha (D)\delta _{ij}\\&=\left[ C_{ijkl}^u(D)-M(D)\alpha ^2(D)\delta _{ij}\delta _{kl}\right] \varepsilon _{kl}-\alpha (D)\delta _{ij}P\\&=C_{ijkl}(D)\varepsilon _{kl}-\alpha (D)\delta _{ij}P \end{aligned} \end{aligned}$$

(A.2)

Thus, the relationship between the undrarined stiffness tensor $C_{ijkl}^u(D)$ and the drained stiffness tensor $C_{ijkl}(D)$ can be defined as Shao (1998):

$$\begin{aligned} C_{ijkl}^u(D)=C_{ijkl}(D)+M(D)\alpha ^2(D)\delta _{ij}\delta _{kl} \end{aligned}$$

(A.3)

where the drained stiffness tensor that is function of isotropic damage can be expressed as Lemaitre (2012):

$$\begin{aligned} C_{ijkl}(D)=(1-D)\left[ \lambda \delta _{ij}\delta _{kl}+\mu \left[ \delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}\right] \right] \end{aligned}$$

(A.4)

where the elastic Lame constant is $\lambda$ and $\mu$ is the shear modulus.

During the evolution of damage in poroelastic materials, the opening up of microvoids within the solid skeleton leads to variations in the ratios of compressibility between the solid and fluid constituents. Several studies have illustrated the role of compressibility in hydraulic fracturing predictions (Aguilera 2008; Nagel et al. 2011). Unlike LEFM-based models, the presented NLDT continuum model can accommodate for non-linear variations of compressibility ratios. In this study, following (Cheng 1997; Shao 1998; Cheng 2016; Mobasher and Waisman 2021a), compressibility variations are expressed through the variations of Biot’s modulus and coefficient that are described by:

$$\begin{aligned} \alpha (D)=1-\frac{K(D)}{K_s} \end{aligned}$$

(A.5)

and

$$\begin{aligned} M(D)=\frac{K^u-K(D)}{\alpha (D)^2} \end{aligned}$$

(A.6)

In the above, $K(D)=(1-D)K$ is the damaged bulk modulus and $K=\lambda +\frac{2\mu }{3}$ is the elastic bulk modulus. The solid grain bulk modulus is denoted as $K_s$. Following the above definitions and the derivations in Cheng (1997); Shao (1998), the undrained bulk modulus is defined as:

$$\begin{aligned} K^u=\frac{2\mu (1+\nu ^u)}{3(1-2\nu ^u)} \end{aligned}$$

(A.7)

where $\nu ^u$ denotes the undrained Poisson’s ratio. Based on the above definitons, it follows that a positive energy dissipation requires the satisfaction of the following (Rice and Cleary 1976):

$$\begin{aligned} \mu >0;~~-1<\nu<\nu ^u<0.5 \end{aligned}$$

(A.8)

1.2 Appendix A.2: Equivalent stress

Several experimental studies have related damage growth to material point parameters e.g. strains and stresses. In the context of damage mechanics, damage at a material point can be related to the effective solid stress ${\bar{\sigma }}_{ij}$, which is defined as Lemaitre (2012); Selvadurai and Shirazi (2004); Mobasher and Waisman (2021a):

$$\begin{aligned} {\bar{\sigma }}_{ij}=\frac{\sigma _{ij}+\alpha (D)P\delta _{ij}}{1-D} \end{aligned}$$

(A.9)

The expression of ${\bar{\sigma }}_{ij}$ in Eq. (A.9) provides an evaluation of the stresses experienced by the solid skeleton component of the poroelastic mixture, which is believed to drive the damage evolution. Several experimental (Makurat et al. 1991; Olsson and Barton 2001) and numerical (Zhang and Sanderson 1996; Min et al. 2004) studies investigated the damage growth mechanisms in porous geomaterials. These studies have concluded the following major void development mechanisms; the first is micorvoid width opening which resembles Mode I fracture and void volumetric dilation, and the second is shear dilation at material points experiencing large shear stresses beyond shear strength. In this study, we follow the Hayhurst type equivalent stress measure that accounts for both mechanisms. The local equivalent stress measure used in this study is defined as:

$$\begin{aligned}&{\bar{\sigma }}^{eq}= {\left\{ \begin{array}{ll} \chi &{} \text {if }\chi \ge 0 \\ 0 &{} \text {otherwise }\\ \end{array}\right. } \end{aligned}$$

(A.10)

$$\begin{aligned}&\chi = a_1{\bar{\sigma }}^{(1)}+a_2\bar{\tau }^e-(1-a_1-a_2){\bar{\sigma }}_{kk}-\sigma ^{th} \end{aligned}$$

(A.11)

Equation (A.10) imposes that only positive values of $\chi$ will contribute to the evolution of the equivalent stress measure that will dictate the growth of damage and permeability. This condition is required in order to satisfy the irreversible damage growth that is required to maintain positive energy dissipation as mentioned earlier and discussed in detail in Lemaitre (2012, 2001); Kachanov (2013); Mobasher et al. (2018). The evolution of the parameter $\chi$ is driven by three components which are a) ${\bar{\sigma }}^{(1)}$, the highest eigen-value of the effective stress which controls Mode-I like microvoid aperture width increase, b) ${{\bar{\tau }}}_e=\sqrt{\frac{3}{2}{\bar{\sigma }}_{ij}^{dev}{\bar{\sigma }}_{ij}^{dev}}$ which is the invariant that describes the shear stress intensity based on the effective deviatoric stress ${\bar{\sigma }}_{ij}^{dev}={\bar{\sigma }}_{ij}-\frac{1}{3}{\bar{\sigma }}_{kk}\delta _{kl}$, and c) ${\bar{\sigma }}_{kk}$ which is the volumetric stress controlling pressure dilation. The parameter $\sigma ^{th}$ is the threshold stress below which the equivalent stress should remain zero ${\bar{\sigma }}^{eq}=0$. The threshold stress can be used to account for in-situ stresses (Mobasher and Waisman 2021a). The material parameters $a_1$ and $a_2$ can be used to define the competition between the different terms contributing to $\chi$ provided that $0\le a_1, a_2\le 1$ and $a_1+a_2\le 1$.

As defined in Eqs. (25)–(27), and following (Mobasher and Waisman 2021a), two versions of the local equivalent strain ${\bar{\sigma }}^{eq}$ will be used in the following sections. The first is ${\bar{\sigma }}^{eq,\kappa }$ which is used to derive permeability growth and the second is ${\bar{\sigma }}^{eq,D}$ which is used to derive damage growth. In this model, independent values of $a_1$ and $a_2$ can be used for each of the two versions of the local equivalent stress ${\bar{\sigma }}^{eq,\kappa }$ and ${\bar{\sigma }}^{eq,D}$.

1.3 Appendix A.3: Anisotropic Darcy law

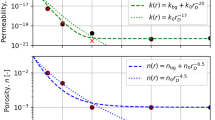
Based on the empirical definitions of the non-linear permeability defined in earlier experimental and numerical studies (Shiping et al. 1994; Kiyama et al. 1996; Gobran et al. 1987; Selvadurai and Shirazi 2004; Mikelic et al. 2015; Tang et al. 2002; Mobasher and Waisman 2021a; Mobasher et al. 2018), the local permeability which is the driving term on the right hand side of Eq. (26) can be defined as:

$$\begin{aligned} {\bar{\kappa }}({\bar{\sigma }}^{eq,\kappa })=\left[ 1+b_1({\bar{\sigma }}^{eq,\kappa })^{b_2}\right] \kappa _0 \end{aligned}$$

(A.12)

The initial permeability $\kappa _0$ is defined as $\kappa _0= k_0 /\mu _f$ where $k_0$ is the solid skeleton hydraulic conductivity and $\mu _f$ is the fluid dynamic viscosity. The parameters $b_1$ and $b_2$ are material constants (Selvadurai 2004; Selvadurai and Shirazi 2004). Following the solution of Eq. (26), as detailed in Sect. 4, the anisotropic permeability ${\tilde{\kappa }}_{ij}$ can be calculated from the isotropic permeability using the following decomposition:

$$\begin{aligned} {\tilde{\kappa }}_{ij}({\bar{\sigma }}^{eq,\kappa })=\left[ \begin{array}{*2{c}} \kappa _0+ \left( {\tilde{\kappa }}-\kappa _0\right) \cos \theta &{} 0 \\ 0 &{} \kappa _0+ \left( {\tilde{\kappa }}-\kappa _0\right) \sin \theta \end{array}\right] \end{aligned}$$

(A.13)

where the decomposition angle $\theta =\frac{1}{2}\tan ^{-1}\left( \frac{2 {{\bar{\sigma }}}_{12}}{{{\bar{\sigma }}}_{11}-{{\bar{\sigma }}}_{22}}\right)$ is defined based on the effective stress components.

1.4 Appendix A.4: Damage evolution law

Following the damage model used in Mobasher et al. (2018); Mobasher and Waisman (2021a), damage evolution law is defined as:

$$\begin{aligned}&D({\tilde{\sigma }}^{eq,D})= {\left\{ \begin{array}{ll} 0 &{} \text {if }{\tilde{\sigma }}^{eq,D} \le S^i \\ \frac{S^f\left( {\tilde{\sigma }}^{eq,D}-S^i\right) }{{\tilde{\sigma }}^{eq,D}\left( S^f-S^i\right) }&{} \text {if }S^i \le {\tilde{\sigma }}^{eq,D} \le S^{th} \\ D^{max} &{} \text {if }S^{th} \le {\tilde{\sigma }}^{eq,D} \end{array}\right. } \end{aligned}$$

(A.14)

$$\begin{aligned}&S^{th}=-\frac{S^fS^i}{\left( S^f-S^i\right) }\left[ D^{max}-\frac{S^f}{\left( S^f-S^i\right) }\right] ^{-1} \end{aligned}$$

(A.15)

It is important to note the the damage growth is driven by the non-local equivalent stress measure ${\tilde{\sigma }}^{eq,D}$ calculated from Eq. (27), which is in turn driven by the local equivalent stress discussed ${\bar{\sigma }}^{eq,D}$ in Section Appendix A.2. The parameters $S^i$ and $S^f$ indicate damage initiation ($D=0$) and failure ($D=1$) stresses. In order to avoid singular matrices and mesh deletion algorithms, we define a maximum damage $D^{max}\approx 1$ which corresponds to a stress value of $S^th$. Additional information about the damage law and the $D^{max}$ condition can be found in Londono et al. (2016); Lyakhovsky et al. (1997); Mobasher and Waisman (2021a).

1.5 Appendix A.5: Variable non-local length scale

Non-local damage models assuming a constant length scale exhibit several drawbacks such as excessive damage widening and spurious oscillations at large values of damage, which are discussed in details in Geers et al. (1998); de Borst and Verhoosel (2016); Poh and Sun (2017). Therefore, in this model we employ a variable length scale definition g which is used to control the size of the non-local zone in the calculation of the damage driving non-local equivalent stress ${\bar{\sigma }}^{eq,D}$ calculated in Eq. (27). Following the definition used in Mobasher et al. (2017), we define $g(\sigma ^{eq})$ as:

$$\begin{aligned}&g({\bar{\sigma }}^{eq,D})=\nonumber \\&\quad {\left\{ \begin{array}{ll} k_1(l^d)^2 &{} \text {if }{\bar{\sigma }}^{eq,D} \le g^i \\ \left[ 1-\left( 1-k_1\right) \frac{g^f-{\bar{\sigma }}^{eq,D}}{g^f-g^i}\right] (l^d)^2 &{} \text {if }g^i \le {\bar{\sigma }}^{eq,D} \le g^f \\ (l^d)^2 &{} \text {if }{\bar{\sigma }}^{eq,D} \ge g^f \end{array}\right. } \end{aligned}$$

(A.16)

The scaling parameter $k_1$ varies between $k_1=0$ which represents a local model and $k_1=1$ which represents $g=(l^d)^2$, and where $k_1$ is a scaling parameter, $0<k_1<1$. The length scale is varying linearly between effective local equivalent stress values of ${\bar{\sigma }}^{eq,D}=g^i$ and ${\bar{\sigma }}^{eq,D}=g^f$. A detailed discussion in Mobasher and Waisman (2021a) on the choice of the variable non-local length scale model, conditions for thermodynamic consistency, and its numerical implementation.

Appendix B: Properties and parameters used in the hydraulic fracturing simulation

See Table 1.

Table 1 Modeling parameters of rock material used in the hydraulic fracturing model