Constant-curvature bending response of thin glass: Analytical, numerical and experimental study of “clamp-bending” tests

Abstract

New generation thin, lightweight and damage-resistant glass, having impressively impact resistance and ability to be bent up to small radii, appears to be the optimal material for extremely deformable structural elements. Its structural use and design require an accurate evaluation of its mechanical properties. However, standard methods to test the glass strength, as the Four-Point Bending and the Coaxial Double Ring test, cannot be used for thin glass, due to its high deformability. Here, an innovative test is proposed, consisting into deforming a thin element into a costant-curvature shape, by prescribing a rotation on two opposite edges of a rectangular plate, while allowing the adjustment of the distance between the supporting hinges. This produces a deformation into an arch of a circle and to a constant stress distribution, allowing to determine the thin glass strength with very simple formulas. An innovative experimental setup, recently proposed for twisting tests on thin glass, has been adapted for constant-curvature bending tests, based on the results of both analytical modelling and numerical analyses. This has been used to perform an experimental campaign, comprising 15 destructive tests on chemically tempered thin glass.

1 Introduction

In the last decades, architecture has developed new ways to respond to the flow of energy that affects building performance and the people’s comfort, changing to transformable and dynamic objects (Linn et al. 2014). In particular, kinetic and adaptive façades proved to be an effective approach to provide natural lighting and fresh air and to increase the building energy efficiency (GhaffarianHoseini et al. 2013; Omrany et al. 2016).

In recent years, several authors (Silveira 2016; Ganatra 2016; Louter et al. 2018) have proposed the pioneering use in the built environment of thin glass, with thickness lower than 2 mm, originally conceived for electronic screens. Indeed, due to its low weight, high impact and scratching resistance, excellent optical quality and ability to be bent up to small radii, it is proving to be the optimal material for extremely deformable structural elements for façades and building skins. First examples of its structural use are the FIFA World Cup 2014 players’ bench, and the lightweight retractable canopy developed by Neugebauer (2015). The use of thin glass have been proposed for the construction of kinetic and adaptive elements (Topçu 2017; Silveira et al. 2018), where its flexibility allows to obtain the large deformations and movements (Bedon et al. 2018) required to maintain a dynamic optimum in performances with regard to energy and comfort-related aspects. More recently, its use in composites for structural purposes, as for example sandwich panels consisting of two thin glass panes with an inner polymer core, has been studied (Kothe et al. 2021; Hänig and Weller 2021).

The design with thin glass causes a totally new kind of thinking. One of its main feature is that, due to its thinness, it deforms into developable surfaces (Neugebauer et al. 2018), without stretching or compressing of the mid-surface of the glass, allowing to maintain a low stress-level. There are a lot of developable surfaces that can be explored (Neugebauer et al. 2018), for example cylindrically or conically shaped geometries, developable orbs, etc. A paradigmatic case is that of the hyperbolic paraboloid, a ruled double curved anticlastic shape commonly used for cold-bent thick glass (Galuppi et al. 2014; Nehring and Siebert 2018), obtained by twisting the plate through four opposite concentrated forces at its corners. This undergoes a buckling phenomenon (Datsiou and Overend 2016; Spagnoli et al. 2019; Quaglini et al. 2020) causing a shape modification to a cylindrical surface where bending is essentially unidirectional along one of the diagonals. In (Galuppi 2018), it has been demonstrated that, for thin glass, this instability phenomenon arises for very low distortions, and it may be exploited to obtain shape modifications with high level of distortion. Current research has not yet explored all forms and shape modifications that can be obtained with thin glass, whose majority entail single curvature bending.

The use of thin glass in the built environment makes the determination of its bending strength a very actual research field, currently at a pioneering stage. Consider that the material is still in a process of development: there are different products, and production companies are continuously improving the obtainable thickness, the production process and the thermal/chemical treatments, strongly influencing the material strength.

An innovative test for the assessment of the performance of thin glass, consisting into deform a rectangular glass sheet into an arch of a circle, was suggested, from a qualitative point of view, in (Neugebauer 2016). In (Zaccaria et al. 2022), three different setup for this “clamp bending” test were developed. The main adavantage of this kind of test is that it allows achieve a constant bending moment and a consequent constant stress distribution on nearly the whole surface. A possible way to deform the thin glass plate into a constant-curvature shape is to prescribe a rotation on two straight opposite edges of the plate, while allowing an accurate adjustment of the distance between the supporting hinges. This allows to determine not only the thin glass strength, but also its peculiar characteristics as the minimum radius of curvature, that may be regarded as a “measure” of its bendability (Peng et al. 2021).

In the present paper, first the large deformation constant-curvature bending of rectangular thin glass panes is analytically studied in Sect. 2, based on the inextensional theory of thin plates. The analytical results are validated by means of comparison with preliminary numerical analyses. The obtained result are used to design the experimental setup, presented in Sect. 3. This has been used to perform experimental “clamp bending” tests on chemically tempered thin glass, whose results are detailed recorded in Sect. 4. This kind of test can be performed by using the same experimental apparatus adopted in (Galuppi and Riva 2022) to perform large deformation twisting tests on thin glass plates. Indeed, the developed test bench, that can be used to test specimens with different size and thickness, was conceived so that it can be modified, by making some slight modification in position of constraints and actuators, to perform large-deflection bending tests. Finally, the major outcomes from this research and the concluding remarks are presented in Sect. 5.

2 Large-deflection bending of thin glass, with constant curvature

2.1 The analytical model

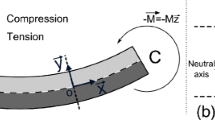
Consider the rectangular plate of size $L \times b$ and thickness h shown in Fig. 2, and the reference frame with the x, y and z axes parallel to the sides of length b, L and h, respectively, and the origin in the plate center. The plate is subjected to a bending moment M about the x axis, provoking its deformation on the y, z plane, as shown in Fig. 1b.

Fig. 1

(a) Considered geometry for the thin glass plate and (b) loading conditions on the y, z plane

Fig. 2

Qualitative deformed shape of (a) a thick plate and (b) a thin plate, subjected to a pure bending moment

The easiest way to study this bending problem is to consider the plate as a beam of length L and width b. In this case, the elementary (small deflection) theory of bending of beam predicts that the cross-section in the (y, z) plane distorts into a circular arc of radius $\rho _x$, related to the bending moment by

$$\begin{aligned} \frac{1}{\rho _y}=\frac{M}{EI_x}, \end{aligned}$$

(2.1)

where E is the Young’s modulus of glass, and $I_x=bh^3/12$ is the moment of inertia with respect to the x axis. Due to the Poisson’s effect, a beam with standard thickness will deform also on the x, z plane, with radius $\rho _x=- \rho _y/\nu$, where $\nu$ is the Poisson’s ratio and the minus sign indicates that the centres of curvature are located on opposing sides of the surface. The resulting anticlastic deformed shape is qualitatively shown in Fig. 2a.

However, according to the inextensional theory for thin flat plates proposed by Mansfield (1955, 1964), that perfectly describes the response of thin glass plates (Galuppi 2018), a thin plate tends to resist to the applied loads primarily by its flexural stiffness, with null strains of the middle surface of the plate. Consequently, the mode of deformation is a developable surface, with zero Gaussian curvature, allowing to maintain a low stress level (Galuppi et al. 2014; Neugebauer et al. 2018). In the present case, the deformation into an anticlastic surface predicted by the beam theory would entail strong membrane stress, associated with noticeable middle surface strains, leading to a noteworthy increase in elastic energy. Hence, in order to reduce the membrane stresses, the plate tends to find an alternative form of deformation, with single curvature, where its midplane remains unstretched (Ottens 2018; Nehring and Siebert 2018; Galuppi and Riva 2022), as qualitatively shown in Fig. 2b. Hence, as observed by Ashwell (1957), the plate deflects into a single curvature shape, with radius given by

$$\begin{aligned} \frac{1}{\rho _y}=\frac{M}{E^*I_x}, \ \ \ \ \ \ \text {where} \ \ \ \ \ E^*=\frac{E}{1-\nu ^2}, \end{aligned}$$

(2.2)

where $E^*$ is sometimes called plane strain Young’s modulus.

Fig. 3

Deformed shape of the plate on the y, z plane

As shown in Fig. 3, the deformed shape of the plate in the y, z plane is an arc of circle of radius $\rho _y$, covering an angle $2\varphi$, that may be evaluated as

$$\begin{aligned} \varphi =\frac{L}{2\rho _y}=\frac{L}{2}\frac{M}{E^*I_x}. \end{aligned}$$

(2.3)

The maximum deflection $v_{max}$, the length $L'$ (correspondent to the final distance between the beam’s ends and the variation of length $\delta =L-L'$ in y direction, may be evaluated as a function of $\varphi$ as

$$\begin{aligned}&v_{max}=\frac{L}{2}\ \frac{1-\cos \varphi }{\varphi }\,, \end{aligned}$$

(2.4a)

$$\begin{aligned}&L'=L\ \frac{\sin \varphi }{\varphi }\,, \end{aligned}$$

(2.4b)

$$\begin{aligned}&\delta =L \ \left( 1-\frac{\sin \varphi }{\varphi }\right) \,. \end{aligned}$$

(2.4c)

The maximum strain is recorded at the extrados panel surface, i.e., at $z=h/2$, and reads

$$\begin{aligned} \varepsilon _{y,max}=\frac{1}{\rho _y}\frac{h}{2}=\frac{\varphi h}{L}. \end{aligned}$$

(2.5)

By accounting for (2.2), (2.3) and (2.5), direct relationships may be found between the maximum axial stress acting in the glass plate, i.e., $\sigma _{y,max}=\frac{M}{I_z}\frac{h}{2}$, the radius of curvature, and the angle $\varphi$

$$\begin{aligned} \sigma _{y,max}=\frac{M}{I_x}\ \frac{h}{2}=\frac{E^* }{\rho _y}\ \frac{h}{2}=\frac{\varphi E^* h}{L}. \end{aligned}$$

(2.6)

Notice that the relation of $\varphi$ with both the bending moment and the maximum stress is linear. Formula (2.6) will be used in the sequel to evaluate the maximum bending angle, or alternatively the minimum bending radius, that is supposed to be achieved in experimental tests performed up to the glass breakage.

Graphs in Fig. 4 show the analytical dependence of radius of curvature $\rho$ and angle $\varphi$ on the plate thickness, considered to be in the range $[0.5 \div 2.5]$ mm and on the maximum stress (from 20 MPa to 200 MPa), evaluated as per eq. (2.6), for a plate of length $L=1$ m, made of glass with Young’s modulus $E= 70000$ MPa and Poisson’s ratio $\nu =0.22$.

Fig. 4

(a) Radius of curvature $\rho _x$ and (b) angle $\varphi$ covered by the arc, as a function of the plate thickness and of the maximum stress

The bending angle and the bending radius correspondent to the glass breakage may be estimated by means of formula (2.6), by considering as $\sigma _{y;max}$ the ultimate strength of thin glass. The European Norm EN 12337-1:2000 (2000) provides a typical/general used value of 150 MPa for chemical prestressed glass, while literature data suggested values between 150 MPa (Neugebauer 2015) and 200 MPa (Ganatra 2016). More recent contrubutions (Zaccaria et al. 2022) provide evidence that 1.1 mm Falcon glass with laser cut edges and chemically strengthened for 8 h, produced by ACG, can have a characteristic bending strength equal to 230 MPa. However, the actual strength strongly depends on the chemical prestressing processes, that depends on the producer. Here, a value of 150 MPa is considered.

Once the bending angle correspondent to this value is known, the related maximum deflection, the final distance between supports and the length reduction may be evaluated as per eq. (2.4). Table 1 records the results obtained for the thin glass plates that have been experimentally tested, of length $L=1$ m, width $b=0.5$ m, and thickness $h=1.1$ mm and $h=2.1$ mm.

Table 1 Relevant geometric parameters and bending moment correspondent to a maximum stress of 150 MPa

2.2 Preliminary numerical analyses

To validate the proposed approach, and to evaluate its accuracy in modelling the response of thin panes, the analytical findings have been compared with the results of numerical analyses performed with the software Abaqus. The considered geometry is, again, a plate of length $L=1000$ mm and width $b=500$ mm, while two different values are considered for the thickness, i.e., $h=1.1$ mm and $h= 2.1$ mm.

FEM analyses have been performed by modelling the glass panel as a 3D geometry, discretized by using quadratic 20 nodes solid elements with reduced integration (C3D20R in the code library). The structured mesh has been obtained by dividing the plate length in 100, the width in 20, and the thickness in 3 elements. Glass has been modelled with linear elastic material response, with E=70000 MPa and $\nu$= 0.22.

Denote by $\overline{\varphi }$ the end rotation correspondent to a maximum stress of 150 MPa, recorded in Table 1. The bending process has been numerically modelled by prescribing a rotation of $\overline{\varphi }$ at the end at $y=0$, and of $-\overline{\varphi }$ at the other end, i.e., $y=L$. The axial displacement is prevented at $y=0$, while it is left free at $y=L$. Displacements in x and z directions have been isostatically fixed, so to prevent rigid body motion. Non-linear geometric analyses have been run.

Figure 5a and b show the numerically evaluated out-of-plane displacement, plotted on the deformed shape, for the 1.1 mm and 2.1 mm thick glass panes, respectively. It is easy to verify that the deformed shape perfectly corresponds to an arc of circle, i.e., it is a single-curvature surface, rather than a anticlastic surface as predicted by the beam theory.

Fig. 5

Contour plot of the out-of-plane (z) displacement, evaluated numerically, for (a) 1.1 mm and (b) 2.1 mm thick glass panes

Figure 6 shows the numerically evaluated distribution of the maximum principal stress, oriented in tangential direction, for the two considered geometries. It may be noticed that, apart for some small stress localization in proximity of the constrained ends of the plate, the maximum tensile stress is constant along the plate length, and of the order of 150 MPa.

Fig. 6

Results of the numerical analysis in terms of maximum tensile stress, for (a) 1.1 mm and (b) 2.1 mm thick glass panes

Figure 7a and b show the analytical relation between the prescribed rotation $\varphi$ and the axial stress $\sigma$ and the bending moment $M_b$, evaluated as per Eqs (2.6) and (2.3), respectively. Obviously, both the relationship are linear. The comparison with the FEM data, also plotted in the same graphs, show a perfect agreement between analytics and FEM.

Fig. 7

Comparison between analytical results (lines) and numerical data (markers), in terms of (a) rotation-stress and (b) rotation-bending moment relation

Table 2 summarizes the comparison between analytical and numerical results, in terms of maximum deflection $v_{max}$ and total axial displacement $\delta$, for both 1 mm and 2.1 mm thick plates. The same Table compares the numerically obtained bending moment, evaluated by considering the moment reaction at the beam’s ends, and the maximum principal stress at the center of the plate. These are compared with the analytical values obtained by means of eq. (2.4).

Table 2 Comparison between analytical and numerical results

The perfect correspondence between analytical an numerical results (Table 2 and Fig. 7) confirms that (2.2) is the correct formula to interpret the large deformation constant-curvature bending (clamp bending) of thin glass.

3 Experimental

3.1 Concept design of the experimental setup

The main advantage of the constant-curvature bending configuration shown in Fig. 1b is that it allows to evaluate the bending stress as a function of the prescribed rotation, by means of the simple relation (2.6). However, to realize an experimental setup allowing to obtain this configuration for a 1 m long plate is a challenge, from the practical point of view, since this requires high values of the rotation angle, as per (2.3).

A first possibility is to constrain one plate’s edge with a articulated parallelogram, i.e., a constrain preventing both the axial displacement and the rotation at the left end of the plate, while leaving it free to move in the out-of-plane direction, as illustrated in Fig. 8a. The other short edge is constrained with a roller, allowing rotation and axial displacement. The rotation should be prescribed at the right end of the plate, by means of a rotary motor coupled to a gearmotor and a torque meter, while measuring the rotation angle with a transducer. On the other hand, the constrain at the left end side is much more complicated to be constructed. In this way, the qualitative plate deformation, on the y, z plane, is that shown in Fig. 8a. This setup would allow to obtain the results illustrated in Sect. 2, for a plate of length L, by using a specimen of length L/2. For example, if a plate one meter long is used, the obtained deformation would coincide with half of the deformation of a 2 m long plate.

Fig. 8

Possible configurations for the experimental setup

Fig. 9

Geometry of the steel rollers: (a) cross sectional view and (b) practical realization

However, the preliminary study presented in Sect. 2 has highlighted that this setup could not be used, since the deformation obtained for the 1.1 mm thick plate would be excessively high, causing the specimen to interpenetrate with the test bench, as schematically shown in Fig. 8b. This situation would be very difficult to manage from an experimental point of view.

This is why an alternative geometrical setup has been chosen for the experimental tests. In particular, as shown in Fig. 8c, the two shorter ends of the plate are constrained by a roller, allowing the axial displacement, and a hinge, respectively. This static scheme allows the two edges to get closer one to each other, as schematically shown also in Fig. 3. This axial movement could also be controlled, by means of an actuator. Indeed, the distance between the supports can be easily evaluated, as a function of the radius of curvature, by means of relation (2.4). This configuration presents some similarity with the “clamp bender” recently presented by Zaccaria et al. (2022).

Since the glass strength is significantly affected by the panel size (Bonati et al. 2020; Pisano et al. 2021), we found of particular interest to develop an experimental setup able to test thin glass panel with size of the same order of magnitude of the structural elements used in the practice. Notice that, since the rotation angle necessary to achieve a datum curvature is strongly dependent by the element length, according to eq. (2.3), to test longer plates requires higher rotations. Furthermore, from the practical point of view, to increase the specimens size will consistently increase the force necessary to overcome the friction and to move the support according to the analytical law (2.4). Henceforth, the scale factor consistently affects the design and the movements of the testing equipment, and hence the required actuators.

3.2 Specimens geometry

The tested samples are 1000 mm and 500 mm wide panes, made of chemically tempered Falcon glass, produced by ACG Europe. As discussed in the previous Section, two different values of thickness, i.e., 1.1 mm and 2.1 mm, have been considered. The short edges of the glass specimens are inserted in cylindrical steel rollers 600 mm wide, with 50 mm of radius, containing a 500 mm long, 27 mm deep and 6 mm wide slit. An EVA foil is introduced in the slit, as shown in Fig. 9, to prevent stress concentration, by avoiding direct contact between glass and metal.

The experimental campaign will be carried out on 5 specimens 1.1 mm thick, and 15 specimens 2.1 mm thick. The glass thickness have been measured in different points of the 1.1 mm thick and specimens 2.1 mm thick specimens. The recorded minimum mean thickness is of approximatively 1.07 mm and 2.06 mm, respectively.

3.3 Experimental setup and instrumentation

In (Galuppi and Riva 2022), an experimental setup to perform large deformation twisting test on thin glass sheets, with the same size considered here, has been proposed. The test bench had a particular design, allowing to use it for both twisting and constant-curvature bending (clamp bending) tests, by making some slightly modification in constraints and actuators, so to have different constraints and allowable movements. The objective is to employ an equipment that can prescribe an equal-and-opposite rotation at thin sheet edges, while paying attention to consequently adjust the distance between hinges, so to induce a constant bending moment. More in detail, the equipment originally designed to test thin glass specimens subjected to twisting was predisposed to be easily changed in a pure bending test equipment, as shown in Fig. 10. The idea was to allow a rapid switch between torsion and ”clamp bending” tests, by using the same components of the test bench. In the practise, this was realised by substituting all the elements placed on one of the two supports, without changing anything else.

Fig. 10

Schematic representation of the equipment for ”clamp bending” of thin glass

The equipment, extensively described in (Galuppi and Riva 2022), is constituted by a base frame, a movable support free to slide along y-direction (on the right in Fig. 10) and a fixed support (on the left), welded to the base frame. On the movable support, the setup is exactly the same of that shown in (Galuppi and Riva 2022), i.e., constituted by: (1) a roller, in which glass short-edge could be accommodated, held in position by two cylindrical bearings; (2) an elastic joint, to allow small misalignments but, at the same time, ensuring high torsional stiffness and (3) a gear motor, designed to produce enough torque moment at the desired rotational speed.

Fig. 11

Test bench for ”clamp bending” of thin glass

Fig. 12

Geometric relationship among out-of-plane and axial displacement, and measured transducer elongation

The fixed support is conceptually the same as the movable one, except for the introduction of a torque meter between the elastic joint and the gear box: the objective is to measure the bending moment applied to the thin glass specimen. It is important to underline that the two gear motors are actuated at the same rotational speed and, being the inertia moment of the thin sheet constant along its length, equal-and-opposite moments results to be applied at sheet edges: this justifies the measurement of bending moment at only one edge. Note that the gear motor placed on the fixed support is the same employed to apply the twisting moment in (Galuppi and Riva 2022).

In spite of very low friction forces at linear guides, in order to be totally confident that pure moment is applied to the thin sheets, a controlled displacement is externally applied at the basis of the movable support, according to eq. (2.4)c. Such a displacement is applied from a servo-hydraulic testing machine (MTS810) through a metallic rope wrapped up on a pulley. To overcome the resisting effect of friction, which initially opposes the translation of the movable support, an axial pre-load (of about 250 N) was initially applied. The maximum allowable displacement of the moving support is of about 625 mm, a value much lower than the expected ones, recorded in Table 1. Figure 11 shows the test bench in the laboratory of the University of Parma (Italy).

Similarly to previous torsional tests, angular position transducer is placed directly on the shaft of one of the gear motors, that is rigidly linked to the roller, whereas a linear rod transducer is placed at the plate center, to measure the maximum plate deflection $v_{max}$. In order to correctly compare the results in terms of out-of-plane displacement with the analytical and numerical results, it is necessary to consider that the value of displacement measured by the transducer does not correspond to the out-of-plane displacement, since it is affected by the axial displacement of the plate center, as schematically shown in Fig. 12.

In the initial undeformed configuration,¹ the transducer is located at a distance $d_1 = 415$ mm from the plate center, and $d_2 = 88$ mm below the glass pane, and its initial length is $l_0=\sqrt{d_1^2+d_2^2}$. Due to both the out-of-plane and the (axial) in-plane displacement, the initial angle $\alpha _0$ decreases as the pane deformation increases. The transducer elongation $\Delta l$ is related to the maximum deflection $v_{max}$ by

$$\begin{aligned}{} & {} \Delta l=l-l_0=\frac{d_1-\delta /2}{\cos (\alpha )}-l_0, \nonumber \\{} & {} \text {where} \ \ \alpha =\arctan \frac{v_{max}+d_2}{d_1-\delta /2}. \end{aligned}$$

(3.1)

4 Results and comparisons

As previously stated, 5 specimens 1.1 mm thick, and 15 specimens 2.1 mm thick have been tested, in the laboratory of the University of Parma (Italy). The test velocity has been chosen so to obtain a mean stress rate of 2 MPa/s, according to EN ISO 1288:2016 (2016) specification. This corresponds to a prescribed angular velocity of 0.0247 rad/s for the 1.1 mm thick specimens, and 0.0129 rad/s for the 2.1 mm thick specimens.

Remarkably, all the tested specimens were able to reach angles much higher than those expected (recorded in Table 1). Figure 13a show the impressive deformation of a 2.1 mm thick glass specimens, for $\varphi \simeq 120^{\circ }$. By comparing this Figure with the numerically evaluated deformed shape (Fig. 5b), it can be noticed that the deformation of the thin glass plates is much higher than expected.

Fig. 13

(a) ”Clamp bending” of a 2.1 mm thick glass specimen and (b) glass shards obtained after breakage of a 2.1 mm thick glass specimen

Due to their extreme deformability, it was not possible to test up to breakage the thinner ($h=$ 1.1 mm) specimens. This is why, in the sequel, only results obtained for 2.1 mm thick specimens are presented. Obviously, the higher values of rotation angle (correspondent to very low value of the radius of curvature) correspond to values of strength much higher than those recorded by literature (Neugebauer 2015; Ganatra 2016) (i.e., 150$\div$200 MPa), according to (2.6).

The enormous amount of strain energy stored in the glass is confirmed by the low size of fragments,² shown in Fig. 13b: shards have length of less than 1 cm, and thickness of a few millimeters.

4.1 Experimental results

Two 2.1 mm thick sample experienced premature failure due to handling and mounting on the experimental test bench. For the remaining 13 specimens, Fig. 14 shows the relation between the prescribed rotation angle, and the bending moment. Crosses indicate the glass breakage.

Fig. 14

Results of ”clamp bending” test on 2.1 mm thick specimens: bending moment as a function of the prescribed rotation angle

It can be noticed that the specimens break for values of rotation angle and bending moment much higher than those expected, recorded in Table 1. Only two samples experienced early failure: the first at about $\varphi =101.9^{\circ }$, $M=82.71$ Nm, the second at about $\varphi =117.7^{\circ }$, $M=98.08$ Nm. For the remaining 13 specimens, the mean value for the maximum bending moment is of 135.5 Nm, consistently higher than the analytically predicted maximum bending moment recorded in Table 1, i.e., 55.125 Nm. Obviously, also the rotation angle and the roller horizontal displacement at the breakage are much higher that the theoretically predicted values, recorded in the same Table.

Unfortunately, the experimental setup was not able to accommodate the required value for $\delta$ for such high values of the rotation angle, because the maximum allowable displacement of the moving roller was of about 625 mm, correspondent to a rotation of about $125^{\circ }$. To evaluate the bending strength, the experimental tests were prosecuted, by increasing $\varphi$ while keeping fixed $\delta$. This correspond to the change of slope of the rotation-moment curves plotted in Fig. 14, at $\varphi \simeq 125^{\circ }$.

Figure 15 shows the results of the experimental tests, in terms of relation between the prescribed rotation angle and the axial displacement $\delta$ (Fig. 15a) and the maximum deflection $v_{max}$ (Fig. 15b). It can be seen from Fig. 15a that the left-hand-side graphs is truncated in correspondence of $\delta \simeq 625$ mm, while the rotation angle continue to increase.

Fig. 15

Results of ”clamp bending” test on 2.1 mm thick specimens: (a) maximum deflection and (b) axial displacement of the moving roller, as a function of the prescribed rotation angle

Generally speaking, the experimental data, in particular for what concerns the maximum deflection, show a very low dispersion.

It can be noticed from Fig. 15a that $\delta$ is approximatively null for rotation angles lower than, approximatively, 5$^{\circ }$. This because, due to the static friction of the linear guides, and to the deformability of the metallic rope driving the roller movement, the movable roller starts to move after the beginning of the rotation.³ Consequently, also the out-of-plane deflection is $v_{max}\simeq 0$ for $\varphi < 5^{\circ }$.

4.2 Refined numerical analyses

In order to interpret in a more accurate way the results of the experimental tests, refined numerical analyses have been performed, by considering the actual constrain conditions and loads. In particular, the assembly composed by the glass (1 m $\times$ 0.5 m $\times$ 2.06 mm) pane, the steel rollers (having the cross-section geometry shown in Fig. 9a), and the EVA foil are modelled, as shown in Fig. 16a.

Fig. 16

(a) Solid model, with position of the reference points, and (b) adopted mesh

The mesh used in the FE analyses is shown in Fig. 16b. Again, quadratic 20 nodes solid elements with reduced integration are used, and the glass plate thickness is divided into 3 elements. The values for the relevant material properties used in the FEM simulations are recorded in Table 3.

The internal surface of the slit of the steel elements has been coupled with reference points RP1 and RP2, shown in Fig. 16a. The former, at $y = 0$, corresponds to the fixed steel element, while the latter is at $y = L$, in correspondence of the movable steel element. Null displacement along x and z directions have been prescribed at the reference points, as well as null rotation about y and z axes, so to avoid rigid body displacement and rotations. Furthermore, null y displacement have been prescribed to RP1, while it is left free⁴ at RP2.

To account for the influence of the elastic joints connecting the gear motor and the movable steel roller on the bending response, these has been modelled, following (Galuppi and Riva 2022), as nonlinear connectors, with uncoupled behavior, connecting the rotational degree of freedom (about the x axis) of the reference points RP1 and RP2 with auxiliary reference points at the same locations. The load has been applied as two equal concentrated moment, with opposite sign, at these points.

To correctly simulate the real deformation process, the numerical analyses have been divided in two steps, considering the approximate values of bending moment recorded in the experimental tests. First, two equal and opposite concentrated moments of 118 Nm are applied at the auxiliary reference points located at the two beam’s ends. At the end of the load step, the axial displacement $\delta$ of the moving roller (i.e., of RP2) is measured. In the second load step, the applied moment is increased to 155 Nm, while keeping fixed $\delta$.

Table 3 Considered values for the relevant material properties

Figure 17a and b show the out-of-plane displacement and the maximum principal stress, respectively, at the end of the first load step, plotted on the deformed geometry. It may be noticed that, since the deformed shape is and arc of circle, i.e., the curvature is constant along the plate axis, the maximum principal stress is constant, too.

Fig. 17

Contour plot of (a) out-of-plane displacement and (b) maximum principal stress at the end of the first load step

Contour plot in Fig. 18 shows the out-of-plane displacement and the maximum principal stress at the end of the second load step. It may be noticed that, since the axial displacement is now kept constant, the deformed shape is not anymore with constant curvature. Consequently, the maximum deflection slightly decreases (from 361.5 mm to 348.8 mm), and the maximum principal stress now varies along the plate axes, being maximum in proximity of the roller constraints.

Fig. 18

Contour plot of (a) out-of-plane displacement and (b) maximum principal stress at the end of the second load step

Notice from Fig. 18b that the maximum stress is recorded in proximity of the short edges of the plate, so allowing to evaluate the maximum stress as a function of the applied bending moment, according to Eq. (2.6).

To emphasize the change in the deformed shape, Fig. 19a shows the lateral view of the deformed shape of the plate, during the first load step, for different values of the rotation angle, i.e., for $\varphi =$ $30^{\circ }$, $60 ^{\circ }$, $90^{\circ }$, and $120 ^{\circ }$. It is evident that the plates deform into an arc of a circle. Figure 19b shows the comparison between the deformed shape at the end of the first load step (i.e., for $\varphi \simeq 126 ^{\circ }$), and at the end of the second step. In the latter case, due to the fixed axial displacement, the deformed shape of the glass element is not anymore circular, i.e., the curvature is not uniform, and the maximum deflection slightly decreases.

Fig. 19

Deformed shape of the glass pane (a) during the first load step, for different values of $\varphi$, and (b) at the end of the two load steps

4.3 Comparison of experimental, analytical and numerical results

It this Section, the experimental results are compared with the outcomes of the refined numerical analysis, as well as to the analytical model presented in Sect. 2.1. To account for the initial slip, the experimental curves have been shifted of $5^{\circ }$.

Figure 20 shows the comparison in terms of the bending moment-rotation angle curve.

Fig. 20

Comparison of analytically, numerically and experimentally evaluated bending moment, as a function of the prescribed rotation angle

Fig. 21

Comparison of analytically, numerically and experimentally evaluated (a) maximum deflection and (b) axial displacement of the moving roller, as a function of the prescribed rotation angle

With respect to the analytical solution, the FEM analysis accounts for the presence, in the experimental apparatus, of the neoprene sheet and of the elastic joint connecting the gear motor and the movable steel roller. These reduce the stiffness of the assembly, with respect to the analytical prediction. On the other hand, the numerical model considers the presence of the steel rollers, that reduce the “free length” of the plate of 50 mm, so increasing its stiffness. As a results of these two contrasting effects, the overall stiffness evaluated numerically is very similar to the analytically estimated one. The analytical and numerical curves present a good agreement with the experimental results. This confirms that the performed experimental tests may be easily modelled by means of the simple formulae proposed in Sect. 2.1. In particular, the actual stress for a given value of the rotation angle may be simply evaluated by means of relation (2.6).

Figure 21 shows the comparison in terms of the axial displacement $\delta$, and of the maximum deflection $v_{max}$, whose value has been calculated, from the experimentally measured transducer elongation, according to (3.1).

Again, there is a very good agreement between the analytical and the experimental findings, confirming that the plate deforms with constant curvature. The radius of curvature at the glass breakage is of about 1 m.

The good agreement between numerical and experimental results allows to estimate the thin glass strength. It may be observed that, since the sample breakage occurs for $\varphi$ comprised approximatively between 125$^{\circ }$ and 138$^{\circ }$, corresponding to values of the bending moment between 105 Nm and 156 Nm, the sample strength may be evaluated to be in the range [300, 440] MPa.

5 Conclusions

The paper presents an innovative experimental procedure to evaluate the response of thin glass undergoing large deflection bending. The considered element is a rectangular plate with two opposite edges inserted in steel rollers, with interposed EVA foil, that constrain edges themselves to remain straight. The plate is bent by rotating the rollers about their axis, while one of them is axially translated, so to impart the specimen a constant-curvature deformation, similarly to the “clamp bender” recently presented by Zaccaria et al. (2022). If the test is performed until the glass breakage, the proposed test methodology allows to determine not only the thin glass strength, but also its peculiar characteristics as the minimum radius of curvature. The proposed experimental setup is designed to be albe to test large panes, of length of the order of the meter, so to correctly capture the glass strength of structural elements with standard size. Remarkably, this may be done by using the same test bench adopted in (Galuppi and Riva 2022) to perform large deformation twisting tests on thin glass plates, here adapted for bending test by making some slight modification in position of constraints and actuators.

The results of an experimental campaign conduced on 13 glass panes, 1 m long and 2.1 mm thick, have shown a very good agreement between the experimental findings and the simple analytical model, based on the inextensional theory for thin flat panes by Mansfield (1955, 1964). This confirms that the proposed test bench is able to bent the thin plate into a constant-curvature shape, allowing to use very simple formulas to evaluate the stress state.

The 2.1 mm thick AGC Falcon glasses have exhibited an impressive flexibility, and a very high strength, and they have been bent up to a radius of curvature of the order of 1 m. Unfortunately, the experimental setup was not able to accommodate the required axial displacement for such high values of curvature, for specimens 1 m long. To evaluate the bending strength, the experimental tests were prosecuted up to breakage, by increasing the rotation angle while keeping fixed the distance between the supports. After the stop of the movable roller, the deformed shape of the glass element is not anymore circular, and hence the stress state cannot be evaluated with simple analytical relations. The comparison with the results of refined FEM analyses, accounting for this phenomenon, have allowed to estimate the bending strength, that turns out to be in the range [300, 440] MPa.

However, the current proposed experimental setup can be used to test up to breakage, with a constant-curvature shape, thin glass specimens with lower length, and/or lower strength, that depends on the chemical tempering process, and hence on the manufacturing Company. Alternatively, slight modifications in the base frame and in the linear guides supporting the movable support would allow to bend, with constant curvature, 1 m long thin glass specimens.

Furthermore, the developed test bench, allowing to perform both bending and twisting test with large deformation, appears to be suitable to be used to assess the performance not only of thin glass but, more generally, of highly deformable structural elements, as for example carbon fiber composite shells (Schlothauer et al. 2020), or materials to be used for healthcare, robotics, and electronics applications, requiring high flexibility and bendability (Heremans et al. 2016; Peng et al. 2021).