The strength of aged glass

Abstract

Glass is known for its excellent durability, but the strength of glass is very sensitive to the characteristics of its surface, which is known to accumulate damage during its service life. There is however, a lack of strength data on weathered or aged glass, particularly on thermally or chemically treated glass. In this study a carefully calibrated sand trickling test is used to produce surface damage equivalent to erosive action of 20 years of natural weathering on different types of glass: soda-lime-silica annealed, soda-lime-silica fully toughened and aluminosilicate chemically toughened. The soda-lime-silica glass specimens are tested destructively in their as-received and artificially aged form in a conventional coaxial double ring set-up, while the alumino-silicate chemically toughened specimens are tested in an improved coaxial double ring set-up. Fractography is subsequently used to identify and measure the critical flaw size on each specimen. The strength data are analysed statistically and the design strengths for each glass type are obtained. It is found that all glasses suffer a loss in strength after artificial ageing, with fully toughened glass providing the best post-aged performance. It was also found that the degree of toughening in the glass affects the erosion resistance, with chemically toughened glass outperforming the other glasses in this respect.

1 Introduction

Contemporary architectural trends frequently require glass to bear higher loads than those typically imposed on a traditional infill panel. This need is currently addressed with the use of high strength glass in the form of heat treated or chemically toughened glass. High strength glass is produced with toughening procedures that introduce an advantageous residual stress profile through the thickness of the glass, which is characterized by tensile stress in the core and compressive stress at the surfaces (as shown in Fig. 1).

Fig. 1

Residual stress profile through the glass thickness for: a heat treated and; b chemically toughened glass

Fig. 2

Flaw in fully toughened glass: a $\upalpha \le \hbox {d}_{\mathrm{c}}:{\vert }\upsigma _{\mathrm{r}}(\upalpha ){\vert }< {\vert }\upsigma _{\mathrm{r}}\hbox {(t)}{\vert }$ and; b $\upalpha>\hbox {d}_{\mathrm{c}}{:} \upsigma _{\mathrm{r}}(\upalpha )>0$

The ability of toughened glass to retain a safe level of its beneficial residual stress profile during its service life is essential. However, flaws that accumulate on the surface of toughened glass have a twofold detrimental effect: (i) they act as stress-concentration points similarly to annealed glass and; (ii) they impose the stress concentration at a depth, $\alpha$, from the surface, where the compressive residual stress is smaller than that found on the surface for flaw depths $\alpha \le d_{c} ({\vert }\sigma _{\mathrm{r}}(\alpha ){\vert }< {\vert }\sigma _{\mathrm{r}}\hbox {(t)}{\vert }$, Fig. 2a). The residual compressive stress is ineffective when the flaw depth exceeds the case depth ($\sigma _{\mathrm{r}}(\alpha )>0$, Fig. 2b). In this case, the flaw is expected to grow under the influence of the residual tensile stress $\sigma _{\mathrm{r}}(\alpha )$ at the flaw tip and the stress arising from the external loads until the stress intensity factor at the flaw tip reaches a critical value and fracture occurs.

The mechanical performance of toughened glass can be divided into scratch and erosive resistance. Realistic linear scratches similar to those found in chemically toughened glass can be reproduced with indenters of $90{^{\circ }}$, $120{^{\circ }}$ or $136{^{\circ }}$ tip angles (Glaesemann et al. 2012; Schneider et al. 2012). Similar values of vertical deformation at a micro-scale level were found for scratches in annealed and fully toughened glass indicating that their hardness does not differ (Schneider et al. 2012). However, differences were noticed at a nanoscale level indicating that chemically toughened glass exhibits the highest hardness (Schula 2014). Chip formation along the direction of the scratch, occurs at lower loads for fully toughened glass but not in annealed glass, indicating the superior scratch resistance of annealed glass (Schneider et al. 2012). The pattern of crack formation during scratching of chemically toughened glass was found to differ from heat treated (fully toughened or heat strengthened) glass in that lateral cracks preceded the formation of radial/median cracks in the former (Gross 2012). Unsurprisingly, strength reductions were reported for heat treated and annealed glass after scratching; scratched heat treated glass was stronger than scratched annealed glass indicating that the depth of the flaws induced were smaller than the case depth (Swab et al. 2013).

Erosive resistance tests were also proposed for assessing the mechanical performance of chemically toughened glass in Glaesemann et al. (2012) and Nordberg et al. (1964). Its erosive resistance was found to be a function of the abrasion mass and the time and temperature used in the toughening process (Butaev and Vygorka 1987). Chemical toughening was found to offer a slight improvement over the performance of annealed glass when exposed to erosive action for small masses of abrasive medium, in terms of glass mass loss, roughness and optical transmission but the strength of glass was assessed (Bousbaa et al. 2003). Additionally, the erosive damage in the above studies was chosen arbitrarily with no apparent correlation to natural damage.

Fig. 3

Artificial ageing of glass with falling abrasive method: a whole set-up and; b glass specimen abrasion

The mechanical performance of aged toughened glass can be evaluated by testing naturally aged specimens. However, sourcing of naturally aged toughened glass is difficult, due to the relatively recent use of toughened glass in the building industry. In fact, only one study appears to exist on the weathering action on fully toughened glass (Afolabi et al. 2016) wherein, weathered fully toughened glass was found to meet the strength requirements set in ASTM E1300-12A (2012) after 20 years of exposure. However, a comprehensive statistical analysis of strength data is not available. No such study on chemically toughened glass could be found.

Artificial ageing methods can be used to expedite the process of natural ageing. DIN 52348 (1985) is currently the only standard on the artificial ageing of glass, proposing a falling abrasive method. Recent research showed that DIN52348 significantly overestimates strength at low probabilities of failure compared to the naturally aged annealed glass tested in that study (Datsiou and Overend 2017). However, it was found that by changing the parameters set in DIN 52348, it was possible to produce similar levels of damage to those found in naturally aged annealed glass (Datsiou and Overend 2017). However, no forms of toughened glass were investigated in this study.

The present paper addresses the paucity of data on aged toughened glass by evaluating the decrease in strength of toughened glass caused by erosion of 20-year equivalent natural ageing. Section 2 uses the authors’ previous results in Datsiou and Overend (2017) to select suitable parameters for the artificial ageing of annealed, fully toughened and chemically toughened glass performed in the subsequent part of this study. Section 3 describes the materials used in this study and Sect. 4 explains the experimental methods: artificial ageing and evaluation tests. Finally, Sects. 5 and 6 present salient results and conclusions, respectively.

2 Assessment procedure for the strength of aged glass

A falling abrasive method (Fig. 3) is used in this study for the artificial ageing of glass. The method involves dropping of abrasive medium (of specific mass, M, grain size range, GSR) from a controlled drop height, H, on a single glass specimen that is fixed on an inclined rotating base ($45{^{\circ }}$ to the floor). After abrasion and prior to their destructive testing, the glass specimens are stored for a specific amount of time, $t_{\mathrm{c}}$ in specific conditions (temperature, T and humidity, RH). Further details on the method are available in DIN 52348 (1985) and Datsiou and Overend (2017).

Fig. 4

Procedure for the evaluation of durability of novel glass

Fig. 5

Artificially aged annealed glass: a strengths at $\hbox {P}_{\mathrm{f}}=0.008$ and $\hbox {P}_{\mathrm{f}}=0.50$ probabilities of failure and; b shape factor of the Weibull distribution (Table 1)

Table 1 Ageing parameters and fracture strength data of artificially aged annealed glass (Datsiou and Overend 2017)

Table 2 Toughened glass specimens

The authors’ previous research in Datsiou and Overend (2017) showed that artificial ageing of glass with the falling abrasive method has the potential to produce similar Weibull parameters and therefore, similar levels of damage to those found in naturally aged glass. These results are condensed in this section into a procedure for the assessment of the strength of aged glass (Fig. 4):

Step 1 :

Destructive testing of as-received glass: Perform coaxial double ring (CDR) tests to obtain fracture strength data of the as-received glass. Fit a 2-parameter Weibull distribution to the data (as shown in Datsiou and Overend 2017) to obtain strength results at low $P_{\mathrm{f}}=0.008$ complying with the recommendations of ASTM E1300-12A (2012) or mean $P_{\mathrm{f}}=0.50$ probabilities of failure.

Step 2 :

Establish the target level of erosion to which the glass will be exposed during its intended application. Damage accumulation varies and is a function of the level of exposure (location and type of application).

(2a):

Known erosion level: If reliable CDR data on naturally aged glass exposed to the target erosion level, are available proceed to step 3. If not, source, test destructively and obtain and the design strength, mean strength and the Weibull shape factor for such naturally aged glass.

(2b):

Unknown erosion level: Assume a general erosion level e.g. the erosion level of $\hbox {NA-AN}_{\mathrm{a-b}}$ which corresponds to 20 years of exposure to erosive action in a low rise façade (Datsiou and Overend 2017) (design strength of $10.0\le \sigma _{\mathrm{f},0.008}\le 18.36\hbox { MPa}$ and mean strength of $37.41 \le \sigma _{\mathrm{f},0.50}\le 52.76\hbox { MPa}$ and shape factor of $3.4 \le \beta \le 4.2$).

Step 3 :

Selection of artificial ageing parameters: Select artificial ageing parameters of the falling abrasive method for the target level of erosion.

(3a):

Known erosion level: Refer to Fig. 5a–b to match the design or mean strength of naturally aged glass and the shape factor of the Weibull distribution obtained in step 2 with the strength of one of the artificially aged series in Datsiou and Overend (2017). Subsequently, refer to Table 1 to obtain the ageing parameters that were used for the selected artificially aged series.

(3b):

Unknown erosion level: Select $H=3.1\hbox { m}$, $M=3.0\hbox { kg}$, $0.5 \le { GSR} \le 9.5\hbox { mm}$ (99.9% of 0.5–0.7mm and 0.1% of 8.0–9.5 mm), ${ RR}=250\hbox { rpm}$ and $t_{\mathrm{c}}=7$ days to replicate damage of $\hbox {NA}_{\mathrm{a-b}}$ in Datsiou and Overend (2017).

Step 4 :

Artificial ageing: Artificially age the as-received glass with the ageing parameters selected in step 3.

Step 5 :

Destructive testing of artificially aged glass: Perform CDR tests on the artificially aged glass.

Step 6 :

Evaluation of aged strength: Compare strength of artificially aged with that of as-received glass to assess strength degradation.

3 Specimens

The strength of chemically toughened glass (CT), fully toughened glass (FT) and annealed glass (AN) are evaluated in the subsequent sections of this paper after exposure to erosive action using the procedure described in Sect. 2. Fifteen specimens were used per series (Table 2). Annealed glass and fully toughened glass were soda-lime-silica glass whilst chemically toughened glass was aluminosilicate glass. The residual surface compression (measured perpendicular to the edges at the centre of each specimen with a scattered light polariscope, SCALP-05, Glasstress Ltd.) and is given in Table 2.

4 Experimental methods and data processing

Annealed, fully toughened glass and chemically toughened glass were observed under an optical microscope to obtain qualitative images of their surface damage and tested to destruction in their as-received and artificially aged state to evaluate their aged strength. For consistency, artificial ageing and destructive tests were always performed on the tin side for the annealed and fully toughened glass specimens. The tin side was identified with a UV light. No such distinction was possible or deemed necessary between the two surfaces of chemically toughened glass because the surface quality of both surfaces is expected to be identical as a result of the Fusion Downdraw production process (Dockerty 1967).

4.1 Artificial ageing

The artificial ageing parameters were selected using the procedure described in Sect. 2. The damage found in the naturally aged glass of Datsiou and Overend (2017) was used as the target level of damage to be introduced in the fully toughened and chemically toughened glass specimens. The strength and shape factor of this naturally aged annealed glass ($10.0 \le \sigma _{\mathrm{f},0.008} \le 18.36\hbox { MPa}$ and $3.4 \le \beta \le 4.2$) was mapped onto Fig. 5 to identify the artificial ageing parameters to be used in the sand abrasion to induce the target level of erosion. Series SA,21 provides the best correlation to the damage of the naturally aged glass in terms of strength at low probabilities of failure, $\sigma _{\mathrm{f}0.008}$ and shape factor, $\beta$ of the Weibull distribution. Therefore, the artificial ageing parameters for this series obtained from Table 1 are: $H=3.1\hbox { m}$, $M=3.0\hbox { kg}$, $0.5 \le { GSR} \le 9.5\hbox { mm}$ (99.9% of 0.5–0.7 mm and 0.1% of 8.0–9.5 mm), ${ RR}=250\hbox { rpm}$ and $t_{\mathrm{c}}=7$ days. The abraded specimens are deemed to be equivalent to the 20 years of erosive action to which the naturally aged glass of Datsiou and Overend (2017) was exposed. These artificial ageing parameters were used for all the sand abraded AN, FT and CT glass in this study. After abrasion the specimens were stored for 7 days at ambient laboratory conditions ($T=22\,{\pm }\,3\,{^{\circ }}\hbox {C}$ and ${ RH}=42\,{\pm }\,8\%$), prior to destructive testing.

4.2 Destructive testing

The suitability of a coaxial double ring (CDR) set-up and its alternatives are investigated in this section for annealed, fully toughened and chemically toughened glass.

4.2.1 Coaxial double ring set-up

Fig. 6

Set-up and max. principal stress along section A-A$^{\prime }$ for: a, b conventional CDR; c, d Set-up A: rubber plunger; e, f Set-up B: 6082T6 aluminium plate and; g, h Set-up B: 7075T6 aluminium plate

Annealed and fully toughened glass A coaxial double ring set-up (Fig. 6a) with a diameter of $D_{\mathrm{L}}=51\hbox { mm}$ for the loading and $D_{\mathrm{S}}=127\hbox {mm}$ for the support ring was used for the annealed and fully toughened glass. Fast stress rates of 20 MPa/s (13.6 mm/min) and 70 MPa/s (20 mm/min) were chosen for annealed and fully toughened glass respectively to induce fracture rapidly and thus, minimize the effect of sub-critical crack growth. The failure stress is given by Eqs. (1) and  (2) for annealed and fully toughened glass respectively are obtained from the numerical model in Datsiou and Overend (2017) which was also modified to suit:

$$\begin{aligned} \sigma =0.0674\cdot P \end{aligned}$$

(1)

and

$$\begin{aligned} \sigma =0.0173\cdot P \end{aligned}$$

(2)

Chemically toughened glass The CDR numerical model in Datsiou and Overend (2017) was also modified to suit the dimensions of $180 \times 180 \times 2$ mm of the chemically toughened glass and an applied displacement of $\delta _{\mathrm{applied}}=5.5\,\hbox { mm}$. Experimental strain gauge data showed good agreement with the numerical model (Fig. 7a). However, deviations from the linear analytical formulas in Timoshenko and Krieger (1987) are noticed as a result of the significant non-linear / membrane effects that develop due to the small thickness of the glass plate and the high displacements required to induce fracture.

A corollary of this non-linearity is that the expected uniform equibiaxial stress within the loading ring is no longer achieved and high radial stress concentrations (EN 1288 2000; Adler and Mihora 1992), that increase with increasing load, appear beneath the loading ring (Fig. 6b). Stress concentrations and the non-biaxial stress state in the loading ring make this set-up unreliable for thin high strength glass as the fracture strength obtained from the test is sensitive to the location and orientation of flaws within the loading ring (Beason and Morgan 1984; Overend 2007).

4.2.2 Improvements to the coaxial double ring set-up

It is therefore necessary to modify the coaxial double ring set-up to destructively test thin, high-strength glass in a reliable and reproducible manner. EN 1288 (2000) proposes the application of gas pressure within the volume confined by the loading ring which increases as a function of the applied ring load to create a uniform stress state within the loading ring area. However, this method is complicated to control experimentally because the gas pressure needs to be varied in real time during the test as a function of the applied load / displacement, to normalise the excessive development of radial stresses at the boundaries of the loading ring. This method is therefore, disregarded.

Set-up  A—silicone rubber plunger: Previous research suggests that application of a uniformly distributed load with a silicon rubber plunger over the loading ring area (Fig. 6c), can be used to create a uniform equibiaxial stress field for the destructive testing of thin photovoltaic panels (Blaumeiser and Schneider 2016). However, further numerical investigation of this set-up by the authors (details available in Datsiou 2017) for a Shore Hardness $60{^{\circ }}$, silicon rubber, shows that an almost uniform surface stress is only achieved for relatively low applied displacements, $\delta _{\mathrm{applied}} < 0.75\hbox { mm}$ (corresponding to $\sigma _{\mathrm{f}} < 100\hbox { MPa}$, Fig. 6d) and a glass thickness of 2 mm. Other limitations of this set-up are: (i) excessive distortion of the rubber elements causing numerical convergence problems which require a computationally inefficient high density mesh; (ii) defining the rubber material properties is not trivial and requires very careful material characterization and; (iii) uncertainties associated with fitting a material model (Ogden, Yeoh, Mooney Rivlin etc) to describe the rubber stress - strain data.

Set-up B—use of spreader plates: An alternative variation of a CDR set-up is investigated here. This involves introducing an additional plate above the glass specimen in the CDR set-up (Fig. 6e, g). The additional plate increases the bending stiffness of the un-bonded unit and reduces the ratio of applied displacement over the specimen’s thickness, $\delta _{\mathrm{applied}}/{t}$. This is expected to reduce excessive development of radial stress concentrations below the boundaries of the loading ring.

Aluminium ($E_{\mathrm{A}}=70\hbox { GPa}$ and $v_{\mathrm{A}}=0.30$) was chosen for the additional plate to suit the material properties of glass ($E_{\mathrm{G}}=70\hbox { GPa}$ and $v_{\mathrm{G}}=0.23$) and in particular, a medium strength and a high strength alloy conforming to Grades 6082T6 and 7075T6 respectively (BS EN 485-2:2013 2013 and BS EN 573-3:2013 2013). This set-up was investigated numerically (details available in Datsiou 2017) for an additional $180 \times 180 \times 4.75$ mm aluminium plate (stress and plastic strain data available in Boller and Seeger (1987) for Grades 6082T6 and 7075T6). The model was validated with experimental strain gauge data for a 4.75 mm thick, 6082T6 Grade aluminium plate and a 2 mm thick glass plate (Fig. 7b).

Fig. 7

Max principal stress for chemically toughened glass at points E and D for: a conventional CDR and; b Set-up B

The experimental and numerical results validate the initial assumption that an equibiaxial stress field can be created within the area of the loading ring up to an applied total of $P=36$ kN (Figs. 7b, 6f) for the 6082T6 alloy. However, as the applied load/displacement exceeds $P=36\hbox { kN}$ / $\delta _{\mathrm{applied,D}}\approx 2.2\hbox { mm}$, the 6082T6 alloy plate reaches its ultimate tensile strength. This increases the load sharing factor of glass and results in stress concentrations underneath the loading ring. The Grade 7075T6 aluminium plate reaches its maximum tensile capacity at a higher applied displacement, $\delta _{\mathrm{applied}}\approx 3.1\hbox { mm}$ and thereby, suppresses significant stress concentrations ($\left( {\sigma _{max} -\sigma _E} \right) /\sigma _{E} >10\%$) up to an applied displacement of $\delta _{\mathrm{applied}}=3.5\hbox { mm}$ (Fig. 6h).

The above investigation indicates that the introduction of a Grade of 6082T6 aluminium plate with a thickness of 4.75 mm is able to suppress the development of significant radial stress concentrations $\left( {\sigma _{max} -\sigma _E } \right) /\sigma _{E} >10\%$) and produce an almost equibiaxial stress field up to an applied displacement of $\delta _{\mathrm{applied}}=2.6\hbox { mm}$ / load of $P=41\hbox { kN}$. Whereas when a Grade 7075T6 aluminium is used instead these limits are pushed to $\delta _{\mathrm{applied}}=3.5\hbox { mm}$/$P=80\hbox { kN}$. The above show that 4.75 mm thick aluminium plates of Grade 6082T6 and 7075T6 are respectively sufficient for the destructive testing of the sand abraded chemically toughened glass (CT-SA) and the as-received chemically toughened glass (CT-AR) of this study (failure loads below $P < 20\,\hbox {kN}$ and $P < 60\,\hbox {kN}$ are expected respectively for the former and the latter). The high stress rate chosen to induce fracture is 50 MPa/s (30 mm/min) for CT-SA and 90 MPa/s (45 mm/min) for CT-AR. The mean failure stress within the loading ring is given by Eq. (3) for CT-SA up to $P\approx 20\,\hbox { kN}$ / $\delta _{\mathrm{applied}}\approx 1.4\,\hbox { mm}$, and Eq. (4) for CT-AR up to $P\approx 60\,\hbox { kN}$ and $\delta _{\mathrm{applied}}\approx 3\,\hbox { mm}$:

$$\begin{aligned} \sigma =0.0075\cdot P \end{aligned}$$

(3)

and

$$\begin{aligned} \sigma =0.0068\cdot P \end{aligned}$$

(4)

4.3 Data processing methods

The experimental failure load was converted to failure stress using Eqs. (1–4) depending on the type of glass. High stress rates induce fracture within a few seconds, thereby minimizing the influence of sub-critical crack growth. Nevertheless, sub-critical crack growth occurs. This can be normalised as follows to a 6 s (mean failure time for all specimens of this study) equivalent stress:

$$\begin{aligned}&\int \limits _0^{t_f -t_r } {\left[ {\sigma _f (t)+\sigma _r } \right] ^{n}} dt=\int \limits _0^{t_{ref} -t_r } {\left[ {\sigma _{f,6} +\sigma _r } \right] ^{n}dt} \Rightarrow \nonumber \\&\sigma _{f,6}=-\sigma _r +\left( {\sigma _f +\sigma _r } \right) \cdot \left[ {\frac{t_f -t_r }{\left( {t_{ref} -t_r } \right) \cdot \left( {n+1} \right) }} \right] ^{1/n}\nonumber \\ \end{aligned}$$

(5)

where: $\sigma _{\mathrm{f}}$: the failure stress, $\sigma _{\mathrm{r}}$: the residual surface compression, $\sigma _{\mathrm{f},6:}$ the equivalent stress for the reference time period of 6 s, $t_{\mathrm{f}}$: the time to failure, $t_{\mathrm{r}}$: the time when tensile stresses exceeds the residual surface compression, $t_{\mathrm{ref}}$: the equivalent time of 6 s and n: the static fatigue constant.

However, it is not possible to apply Eq. (5) to chemically toughened glass because its residual surface stress is unknown. There are also some uncertainties in applying Eq. (5) to sand abraded fully toughened glass because the residual stress at the flaw tips (induced by the sand abrasion) is not known. The latter applies even for known fractographic analysis data as the critical flaw depth is expected to have grown under the influence of sub-critical crack growth.

Therefore, the failure stress data for all specimens in this study is not converted to an equivalent stress (more information shown in Datsiou 2017). This removes the above mentioned uncertainties and permits comparison across different types of glass. This therefore, means that sub-critical crack growth has been neglected but, this is not expected to cause any significant changes in the results; the difference in failure strength after accounting for sub-critical crack growth, was $1.2\% \le {\left( {\sigma _f -\sigma _{f,6} } \right) }/{\sigma _f }\le 3.7\%$ for the annealed as-received glass (Fig. 8). Errors incurred by neglecting sub-critical crack growth in the other test series in this study are expected to be no larger than that in annealed as-received glass and are therefore, considered negligible. However, when lower stress rates are used during the destructive tests these errors are expected to increase and therefore, this approach would no longer be valid.

Fig. 8

Experimental and 6s equivalent failure stress for annealed as-received glass

Fig. 9

Micrographs of as-received, sand abraded-sand impacts and sand abraded-gravel impact of: a–c annealed; d–f fully toughened and g–i chemically toughened glass

The fracture stress data were subsequently fitted to a two-parameter Weibull distribution with a weighted least squares regression method (details available in Datsiou and Overend 2017, 2016). The goodness-of-fit was evaluated with the Anderson Darling method for a confidence level of 95%.

5 Results and discussion

5.1 Microscopy

Micrographs of the surface were obtained prior and after the artificial ageing for the three types of glass (Fig. 9). The surface of as-received annealed (Fig. 9a) and chemically toughened glass (Fig. 9g) are almost defect free at a magnification level of 100$\times$ whilst as-received fully toughened glass has multiple digs on its surface (Fig. 9d) which were potentially introduced during manufacture and/or transportation of the glass.

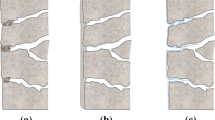
Artificial ageing with sand abrasion results in digs and some lateral cracks in annealed, fully toughened and chemically toughened glass (Fig. 9b, e, h respectively). Flaws induced by impact of sand grains are similar in all types of glass (Fig. 9b, e, h). However, the flaws induced by the larger gravel particularly on the annealed and fully toughened glass differ from those in the chemically toughened glass as follows: (a) digs surrounded by lateral cracks that intersect with the glass surface are found in fully toughened and annealed glass. However, these flaws are larger in annealed (Fig. 9c) than fully toughened glass (Fig. 9f) and; (b) gravel impacts do not form digs in chemically toughened glass but result in abrasive damage (Fig. 9i).

Table 3 Salient results of the Weibull statistics analysis for fracture strength data of all series

5.2 Fracture strength

Table 3 shows the fracture strength statistics for annealed, fully toughened and chemically toughened glass in as-received and artificially aged form. All series showed acceptable goodness-of-fit and therefore, the Weibull distribution is successful in describing the strength data. Unsurprisingly, as-received chemically toughened glass is the strongest, followed by fully toughened glass and subsequently annealed glass; The strength of as-received fully toughened glass (FT-AR) and chemically toughened glass is 191 and 321% respectively larger than annealed glass (AN-AR) at mean probabilities of failure ($P_{\mathrm{f}}=0.50$, Table 3). This is because of the combined effect of the residual surface compression and the thermal healing of flaws during the toughening process of toughened glasses (Zaccaria and Overend 2015).

Fig. 10

Cumulative distribution functions of strength for a annealed glass (as-received and artificially aged); b fully toughened glass (as-received and artificially aged) and; c chemically toughened glass (as-received and artificially aged)

Fig. 11

Fragmentation of sand abraded: a fully toughened and; b chemically toughened glass

Fig. 12

Critical flaws (of max, average and min depths) in sand abraded: a–c annealed; d–f fully toughened and; g–i chemically toughened glass

Strength reduction is evident in all types of glass after sand abrasion. In particular, annealed glass suffers a 61 and 68% reduction in strength for $P_{\mathrm{f}}=0.008$ and $P_{\mathrm{f}}=0.50$ respectively after artificial ageing (Fig. 10a). Fully toughened glass had a better response than annealed glass after artificial ageing showing a reduction of 19 and 40% in as-received strength for $P_{\mathrm{f}}=0.008$ and $P_{\mathrm{f}}=0.50$ respectively (FT-SA, Fig. 10b). This better performance is a result of the residual surface stress and the relatively large case depth of fully toughened glass. Whereas, chemically toughened glass had the worst performance among all types of glass despite its high degree of toughening. In particular, it suffered a 98 and 83% reduction in as-received strength for $P_{\mathrm{f}}=0.008$ and $P_{\mathrm{f}}=0.50$ respectively (CT-SA, Fig. 10c). Additionally, the strength of sand abraded chemically toughened glass (CT-SA) at low probabilities of failure ($P_{\mathrm{f}}=0.008$) is even lower than that of annealed sand abraded glass (AN-AR).

5.3 Post fracture optical microscopy

Post-fracture optical microscopy was successfully performed for all of the annealed and fully toughened glass artificially aged specimens but only on a small percentage of the sand abraded chemically toughened glass. In general, chemically toughened glass is expected to fail in fairly large fragments, typically larger than fully toughened glass (Fig. 11a). However, the high loads, that were required for the thin chemically toughened glass in this study, to overcome the residual surface compression, increase the elastic energy that is stored within the specimen. This energy is released upon fracture and is dissipated in opening new crack surfaces, resulting in a very dense fragmentation pattern (Fig. 11b). Therefore, post-fracture microscopy was only possible for the few chemically toughened glass specimens that failed at the “lower” stress tail of the Weibull distribution and thereby resulted in “larger” fragments. Specimens that fail at the lower stresses do so because they have relatively deeper flaws on their surface and therefore, post-fracture microscopy in those specimens is biased because it will only reveal the upper range (maximum depth) of critical flaws.

Optical microscopy reveals average critical flaw depths after sand abrasion of $472\, \upmu \hbox {m}$ ($132 \le \alpha \le 1370\, \upmu \hbox {m}$) in annealed glass, $127\, \upmu \hbox {m}$ ($72 \le \alpha \le 218\, \upmu \hbox {m}$) for fully toughened glass and $96\, \upmu \hbox {m}$ ($71 \le \alpha \le 132\, \upmu \hbox {m}$) for chemically toughened. Typical micrographs of the critical flaws are shown in Fig. 12a–i, representing the largest, average and smallest flaw for each type of glass revealed with the optical microscope.

Statistical analysis of the flaw depths followed by fitting the data to a 2–parameter Weibull distribution (Fig. 13) producing acceptable goodness-of-fit. Larger critical flaws were therefore, found for annealed, followed by fully toughened and then chemically toughened glass. This implies that the degree of toughening/amount of residual surface stress has an effect on the critical flaw depth for the same artificial ageing procedure and thereby, the abrasive resistance of glass. In particular, higher residual surface stress results in smaller flaw depths under the same ageing conditions.

Fig. 13

CDFs for critical flaw depths for annealed, fully toughened and chemically toughened, sand abraded glass

Critical flaws of $95 \,\upmu \hbox {m}$ ($P_{\mathrm{o}}=0.50$), are expected to entirely remove (100% reduction) the beneficial effects of the surface compression for chemically toughened glasses whose case depths typically range between 40–$90\, \upmu \hbox {m}$ (Gy 2008; Varshneya and Kreski 2012; Zijlstra and Burggraaf 1968). However, the statistical analysis for chemically toughened glass involved only the largest critical flaws (because the fragmentation pattern in the specimens that failed at higher loads was too dense to permit fractographic analysis) and is therefore, conservative. Therefore, flaws could, but are not always expected to, completely remove the favourable effect of the residual surface stress. Fully toughened glass showed a better response than chemically toughened glass; its residual surface stress was only reduced by 11% (** in Table 2) at the flaw tip for the mean flaw depth of $z=0.128\hbox { mm}$ ($P_{\mathrm{o}}=0.50$). This smaller reduction in residual stress is a result of the larger case depth of the fully toughened glass (1.22 mm in this study).

6 Conclusions

The aim of this paper was to investigate the strength of aged annealed, fully toughened and chemically toughened glass exposed to erosive action. To this end, the authors’ previous results (Datsiou and Overend 2017) on the sand abrasion of glass with a falling abrasive set-up were reformatted into in a user-friendly procedure that permits the selection of artificial ageing parameters to represent different levels of exposure.

This procedure was then implemented on glasses with different treatments (annealed, fully toughened and chemically toughened). The investigation involved pre- and post-fracture optical microscopy and destructive testing with coaxial double ring (CDR) tests. However, the small thickness of chemically toughened glass (2 mm) in combination with its high strength lead to undesirable stress concentrations when using the conventional coaxial double ring test set-up. This means that the uniform equibiaxial stress state within the loading ring is not maintained and the conventional Coaxial Double Ring test is no longer appropriate. Therefore, the first step in this investigation was to propose an alternative test set-up that generates a uniform equibiaxial stress within the loading ring area. Of the alternative set-ups investigated, the best results were obtained with an additional 4.75 mm thick, Grade7075T6, aluminium plate between the top of the glass specimen and the loading ring in the CDR set-up.

Unsurprisingly, the evaluation of the 3 types of glass in their as-received form showed that chemically toughened glass is the strongest followed by fully toughened glass and annealed glass. However, the favourable effect of the residual surface compression of toughened glass was diminished after abrasion, equivalent to erosive action of 20 years. In particular, the beneficial surface compression can be completely eliminated in chemically toughened glass as the flaws that are introduced by the artificial ageing, can be significantly deeper than its case depth. In fact, chemically toughened glass suffered a 98% reduction in as-received strength at low probabilities of failure ($P_{\mathrm{f}}=0.008$). Additionally, a 61% reduction in as–received strength was reported for annealed glass ($P_{\mathrm{f}}=0.008$) whilst fully toughened glass had the best post-aged strength as it only suffered a 19% reduction in as-received strength at low probabilities of failure ($P_{\mathrm{f}}=0.008$). This is due to the larger case depth that is available in fully toughened glass which in this study was an order of magnitude larger than the depth of the surface flaws.

However, despite its very high reduction in strength, chemically toughened glass showed the largest resistance to surface abrasion during the artificial ageing; flaws introduced by gravel (8.0–9.5 mm) resulted in deeper flaws in annealed glass, followed by fully toughened glass and finally, chemically toughened glass. This suggests that the level of residual surface compression affects the depth of critical flaws introduced by erosive ageing and therefore the erosive resistance of the glass.

The findings of this research indicate that fully (thermally) toughened glass could be safely used for load bearing applications even when exposed to ageing. However, the reduction in strength after ageing should be carefully considered during the design process. On the other hand, the significant reduction in strength in chemically toughened glass suggests that it should be used with caution in load bearing applications. The limitations of chemically toughened glass could be potentially addressed with bi-tempered glass (Zaccaria 2016) whose enhanced properties of high residual surface compression and large case depth could potentially outperform other toughened glasses. Further investigations are however, needed to verify the performance of bi-toughened glass and to identify safe service life duration limits for all types of glass exposed to different ageing conditions.