Introduction

The edge-seal provides long-term resistance against permeation of moisture and gases from the inter-pane spaces of insulating glass units (IGU). It is of high importance for the compliance of facade glazing with today’s strict energy saving regulations, e.g. German Standards (EnEV 2009). In order to meet these standards, it is essential for manufacturers to accurately describe the complex mechanical and thermochemical degradation processes within the edge-seal in the long-term. It is equally important to comprehend the physical transport processes within the edge-seal. This provides a solid understanding of the aging behavior of IGUs in terms of design rules as well as quality assurance and improved finite element simulations. With these tools at hand, the factors are revealed which limit the service-life of IGUs. Moreover, this enhances life time prediction and lowers the risks of premature failure in use. Both lead to significant economic benefits for the manufacturers. Thus, the theoretically estimated life time of more than 25 years could be reached through a better prediction of the material behavior.

Fig. 1
figure 1

Schematic representation of an IGU with occurring loads, influencing parameters and deformations during service-life (Lichtenberger 2005)

Full size image

Fogging within the inter-pane space of IGU is the main cause of failure in service (Wolf 2003). This is caused by different failure mechanisms, depending on the time of occurrence. In the last 30 years two major studies observed and analyzed the changing of the micro-climate within the inter-pane space due to the permeation of water through the edge-seal over a period of several years (Feldmeier et al. 1984; Gravin and Wilson 1998). The influence of higher temperatures within the edge-seal on the moisture permeability has been described by Wolf (1992). Other parameters that influence long-term durability of the edge-seal are UV exposure or mechanical loads in operation. These were compiled and elaborated by Lichtenberger (1995, 2005) as seen in Fig. 1.

Fig. 2
figure 2

Schematic representation of an increased gas loss through the edge-seal due to mechanical stresses

Full size image

While fogging within the inter-pane space is the main failure of an IGU, its thermal insulation determines the energy saving. Here, the loss of the filling gas drastically increases the thermal conductivity. This is described by permeability coefficients for Argon of each seal (Wolf 2002). Both the diffusion resistance and its dependency on temperature of elastomers and polyisobutene (PIB) have been widely studied by Schuck (1980), Beckmann (1991) and others. However, only a few studies consider the influence of stresses on the permeation behavior within the edge-seal. In order to overcome this drawback, the scope of this paper is analyzing the gas loss through the edge-seal coupled to the stress-strain behavior. Both are heavily influenced by climate loads within an IGU which are considered by a novel testing method. Climate loads are usually defined as the pressure and temperature differences inside and outside the inter-pane cavity (Feldmeier 2003).

This work focuses on transport processes within dual-sealed IGUs. Their edge-seal typically consists of a primary and a secondary seal and a metallic spacer. For the primary seal, thermoplastic PIB is most commonly used due to its low permeability of water and gases (Massoth 1987). The secondary seal consists of the elastomeric sealants polysulfide, polyurethane or silicone. They are individually selected for different using conditions (Wolf 2002). Here, polysulfide has the lowest permeation of typical filling gases (e.g. Argon) and water. Silicone excels due to its exceptional wetting properties, i.e. superior adhesion to glass and repelling of water. Whereas polyurethane’s main feature is its low price combined with intermediate mechanical and permeation properties.

Basics

Behavior of insulating glass units under load

Climate loads on IGUs directly affect permeation within the edge-seal in various ways. It is generally amplified by temperature and the pressure gradient (Crank and Park 1968). In his work, Wolf (2002) mentions additional factors, i.e. UV exposure, which results in a chemical aging of secondary and primary sealants. Furthermore, a degradation of the secondary sealant’s mechanical properties due to Mullin’s effect, wind loads and processing defects, enhances the gas loss rate through the edge-seal. Due to the fact that the diffusion process is the rate-limiting step regarding permeation (Müller-Plathe 1994), most theoretical durability calculations of the edge-seal are only based on the diffusion through the edge-seal. They are not covering changes of the transport mechanism due to the degradation of the edge-seal.

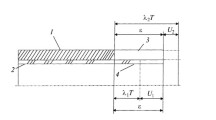
Permeation is not only altered by chemical and physical factors. In addition, it is assumed, that the gas loss increases with mechanical loads, but the exact dependency of permeation on the stress-strain behavior has not been adequately experimentally investigated. It is unclear, whether this is an anisotropic effect due to chain orientation or a macroscopic effect of geometrical changes of the seal. Assuming that the sealant’s length l is constant, when the primary seal is expanded and its height \(h_{0}\) is increased to \(h_{1}\) due to a widening of the seal, the resulting projected area \(A_{1}\) doubles for \(h_{1 }= 2 \cdot h_{0 }\) (see Fig. 2).

On the other hand, it appears that besides the influence of geometrical changes, the gas loss is also altered by the stress-strain state of the sealant. It is assumed, that due to deformation of a polymer, the resulting orientation of the polymer chains lead to an anisotropy in the free volume. Vrentas and Vrentas (1992) describe a model that correlates the diffusion coefficient and the free volume. The free volume changes with previous plastic deformations, the orientation of polymer chains and the application of tensile stresses. A similar conclusion has been drawn by Boersma et al. (2003). In their study the effects of tensile stresses induced into plastic films on their oxygen permeation properties has been analyzed and an increase in permeation rate with stresses has been reported. A clear correlation between stresses one the one hand and oxygen permeability on the other hand has been found. Geertz et al. (2009) has also observed a similar phenomenon within long-term tested polyethylene pipes. The diffusion of stabilizers enhances due to an inhomogeneous local distribution of tangential stress throughout the pipe wall. As mentioned previously, most studies analyze the permeation resistance of sealants without external loads. Although climate loading lead to internal stresses within the edge-seal it is unquantified at present. For the IGU it is still difficult to draw reliable conclusions out of the experiments in literature due to large uncertainties in the diffusion coefficient values as in Crocombe et al. (1996) and Duncan et al. (2005). Additionally, the permeation behavior of thermoplastics and thermosets has been studied mostly. Nonetheless, it appears that the gas loss is increased due to mechanical stresses-strain (see Fig. 2). Thus, this study aims at identifying the influence of the stress state on permeation processes, studying each parameter decoupled from the others.

Permeation process through the edge-seal

In this work, we consider the polymeric sealants as homogenous isotropic materials at room temperature well above their glass transition. The most important quantity to describe the barrier properties of a sealant is the permeability P (Pauly 1989). Permeation of a gas through polymer membranes occurs due to a pressure differential at opposite membrane interfaces. This transport process is typically described in terms of a solution-diffusion mechanism as a proportional relationship between the solubility S and the diffusion D (Stern and Fried 2007; Crank and Park 1968; Vieth 1991; Müller-Plathe 1994):

$$\begin{aligned} P=S\cdot D \end{aligned}$$
(1)

Here, the molecular diffusion is the rate-determining step in the permeation process. The diffusion of permanent gases through polymer membranes can normally be described by Fick’s two laws. Miscellaneous techniques of solving Fick’s equations exist for different boundary conditions and membrane geometries (Crank 1975). Stern and Fried (2007) derives the following equation from Fick’s first law to describe the substance flux density J:

$$\begin{aligned} J=\overline{P} \frac{(p_h -p_i )}{\delta }, \end{aligned}$$
(2)

where is the mean permeability coefficient, \(p_{h}\) and \(p_{i}\) the pressure of two opposing membrane interfaces and \(\delta \) the effective thickness. Since a proportional relation between substance flux density J and the projected area A exists, the gas loss increases due to mechanical loads on the sealants and the resulting deformations. Müller-Plathe (1994) describes the permeability P as a mass flow of a specific gas at standard temperature and pressure (STP) conditions through a sealant with the thickness \(\Delta x\) and the effective plane A due to a certain pressure gradient \(\Delta p\), with the following equation:

$$\begin{aligned} P=\frac{\dot{m}\cdot \Delta x}{A\cdot \Delta p} \end{aligned}$$
(3)

The substance flux density J can be derived by a comparison of the permeation equations from Müller-Plathe (1994) and Stern and Fried (2007) assuming, that \(\Delta p=(p_h -p_i )\) and \(\Delta {\mathop x\limits ^ =\delta }\):

$$\begin{aligned} J=\frac{\dot{m}}{A}\Leftrightarrow \dot{m}=J\cdot A \end{aligned}$$
(4)

The mass flow—also referred to as the gas loss—can be easily and cost-effectively measured. Thus, the experimental results from standards, e.g. the German Standard DIN EN 1279-3, are widely used to quantify and calculate the durability of an IGU (see chapter 3). By solving Eq. (3) towards the gas loss it appears that is inversely proportionally to the effective thickness \(\Delta \, x\) of the sealant. Assuming, that the effective thickness of the primary seal decreases over time due to necking, the gas loss is additionally enhanced. The temperature dependence of a permeation process can be described by the Arrhenius-type equation, which is defined by

$$\begin{aligned} P=P_0 \cdot e^{\frac{-E_p }{RT}}, \end{aligned}$$
(5)

where \(E_{p}\) is the apparent activation energy of the permeation process, R is the universal gas constant, T the absolute temperature and \(P_{0}\) is a constant.

Standard measurement of the gas loss rate of insulating glass units

In order to guarantee both, high thermal and noise insulating performances of an IGU across the system’s entire service life, it is necessary for manufacturers to measure additional quantities, e.g. the gas loss rate \(L_{i}\). Thus, it is possible to ensure high quality standards within the production of IGUs and understand the failure behavior of such a system due to only a few cost-effective experimental tests. For that purpose, the European standard DIN EN 1279-3 (2003) defines a measurement of the gas loss rate through the edge-seal on a standardized specimen. The gas loss rate is defined within the standard DIN EN 1279-3 (2003) by

$$\begin{aligned} L_i =87.6\cdot 10^{6}\frac{\dot{m}}{c_i \cdot V_{int} \cdot \rho _{o,i} }\cdot \frac{T}{T_o }\cdot \frac{P_o }{P}. \end{aligned}$$
(6)

It describes the loss of the filling gas with the initial concentration \(c_{i}\), the internal volume \(V_{int}\) and the density measured at \(T_{o}\) and \(P_{o}\) at an atmospheric pressure P and specific temperature T during the sealing of the IGU in percentage per year. The test sample has a length of \(502\,\pm \,2\) and \(352\,\pm \,2\) mm width. It consists of two 4 mm thick glasses and an edge-seal with a height of 12 mm. However, structure of the IGU, type and quantity of the desiccant and insulating gas strongly depend on the manufacturer. The thickness of the primary sealant, for instance, varies between 0.3 and 0.6 mm and its width is between 3 and 5 mm, depending on the amount of PIB, pressure and holding time during manufacturing. Furthermore, it is proposed to subject the specimens to the climate test according to the preliminary European standard prEN 1279-2 (1993) before proceeding with the experiment.

Afterwards, the specimen is enclosed within a gas-tight ring cassette as shown in Fig. 3. Then Helium is induced to the ring gap and circulates for a while in order to measure at a stationary state. The specimen should be free of internal stresses and the gas loss is measured at \(20 \pm 1\,^{\circ }\)C by a gas chromatograph with a thermal conductivity or electron capture detector over 30 min. Generally the gas loss is measured in \(\upmu \)g per hour with the equation

$$\begin{aligned} \dot{m}=2\cdot A_{PM} \cdot \frac{C_{Ar} }{A_{PE} }\cdot \frac{\rho _{Ar} \cdot T_0 }{P_0 }\cdot \frac{P_m }{T_m }, \end{aligned}$$
(7)

where \(A_\mathrm{{PM}}\) is the integral of the measured Argon peak, \(A_\mathrm{{PE} }\) the integral of the calibration measurement’s peak. \(P_{m}\) and \(T_{m}\) describe the atmospheric pressure and temperature of the Argon during the gas loss measurement, while \(T_{0}\) and \(P_{0}\) describe atmospheric pressure and temperature during the measurement. \(C_{Ar }\)is a measurement factor and has, in this work, a value of 5.03 ml.

Fig. 3
figure 3

Typical structure of the ring cassette from DIN EN 1279-3, Appendix C (2003): 1 lower mask, 2 frame, 3 upper mask, 4 specimen 5 flushing gas: in- and out-let

Full size image

To ensure that the gas loss is stationary, several measurements are conducted. During the measurement, the temperature of the separation column needs to be constant. In addition, it is important to ensure a column free of any contamination, which could lower the sensitivity of the sensor and lead to non-reproducible results. Furthermore, the test is not able to measure the gas loss at other test conditions. Thus, it is not possible to determine, e.g. the effect of climate loads and deformations on the edge-seal’s gas loss.

Fig. 4
figure 4

Concept 1: Mechanical displacement control of the edge-seal

Full size image

Concepts for inducing long-term mechanical stresses into the edge-seal

With the test standard of DIN EN 1279-3, Appendix C (2003) one can only measure the gas loss for a stress free state. In complementation to the existing German and European standard, this paper introduces three concepts for a measurement of the gas loss under mechanical stresses hereafter. These concepts allow to independently identifying the influence of stresses within the edge-seal—resulting from climate loads—on transport processes. Thus, one should be able to consider influencing parameters in design rules for insulating glass units. A major challenge of these concepts is the realistic reproduction of a stress state similar to climate loads without introducing parasitic loads within the edge-seal, the glass and the aluminum frame of the cassette. Furthermore, if the IGU is placed within a temperature chamber, one might deal with a restricted setup dimensions. Also, the concepts should precisely control the stress-stain state of the edge-seal on a long-term scale, because the equilibrium saturation for the specimen may takes some time. Last but not least, the test method should be economically and physically feasible, since it can be significantly expensive to conduct tests that usually require sophisticated test setups and a considerable test time. Thus, a suitable concept must be easily implemented within existing test rigs and low processing costs. In the following, three concepts are explained in detail. Advantages and disadvantages of each will be discussed, then the concepts will be compared to each other in terms of stress state reproduction accuracy, needed installation space, expansion control and manufacturing complexity.

Fig. 5
figure 5

Concept 2: Displacement of the edge-seal via pneumatic cylinders within the inter-pane space

Full size image
Fig. 6
figure 6

Concept 3A: Displacement of the edge-seal by injecting Argon via a pressure controlled inlet

Full size image

The first concept is a straightforward one. As shown in Fig. 4, the deformation of the edge-seal is realized by a mechanical widening of the seal with screws that are bonded to the glass. The strain-state is caused by a uniform tightening of each screw. As a major advantage, the edge-seal can be steadily and precisely deformed and thus, a homogeneous stress state is induced. In contrast, this concepts lacks in reproducing climate loadings realistically. The widening of the edge-seal may cause a distortion of the PIB, because the pressure within the inter-pane space drops below the atmospheric pressure. However, the deformation of the frame can be adjusted individually for each side. Additionally, the rather large dimensions make it difficult to implement the concept within existing experimental setups and the displacement of the edge-seal might damage the aluminum foil of the ring cassette at a certain displacement. In contrast, this concept does not locally weaken the edge-seal. Moreover, the displacement elements must be bonded with the glass panes. In this study, eight displacement elements are planned. In a next processing step, the displacement elements must be joined with the aluminum frame. Thus, the concept also leads to an increased manufacturing complexity.

The second concept induces the mechanical load by a pneumatic cylinder, which is placed within the inter-pane space as shown in Fig. 5. This results in rather small dimensions of the test setup on the one hand. On the other hand it leads in terms of possible leakage to new challenges. Air that leaks into the inter-pane space increases its mass fraction and decreases the partial pressures of Argon, thus resulting in a change of the Argon’s gas loss. The pneumatic connection needs to be brought out of the inter-pane space, which also weakens the edge-seal in terms of gas leakage. However, this concept can precisely and robustly control the expansion of the edge-seal. Another negative aspect of this concept is the introduction of different stress states resulting from the different contact areas of the pneumatic cylinder. This could lead to inconsistent deformations of the lower PIB layer. Therefore, the concept does not accurately reproduce climate loads within the edge-seal. Besides, the insertion of the cylinder into the inter-pane space leads to an additional step within the manufacturing process and the pneumatic connection needs to be sealed.

Fig. 7
figure 7

Concept 3B: Displacement of the edge-seal by injecting Argon through the edge-seal

Full size image
Table 1 A comparison of the three concepts for inducing long-term mechanical stresses into the edge-seal
Full size table

Furthermore, a deformation of the edge-seal can be applied by injecting Argon within the inter-pane space and thus, creating an internal overpressure similar to climate loads. The Argon is injected through one of the glasses by a precision pressure regulator (see Fig. 6). In contrast to the previously introduced concepts, this concept is able to reproduce climate loads precisely. Another striking advantage is the rather small construction dimensions. On the other hand, the resulting stress concentration from the drilling process might lead to a premature failure of the IGU. Thus, an analytically evidence of the structural strength must be given. If the drill hole is not completely sealed it could lead to additional leakage of Argon. Though this might lead to an increased need for Argon, the measurement and displacement control are not significantly affected. In order to avoid a destruction of the specimen due to high pressures, Argon could be induced through the edge-seal as shown in Fig. 7. However, this complicates the manufacturing of the edge-seal due to the additional sealing at the inlet. One must ensure on the one hand that no Argon leaks out of the inter-pane space into the ring gap. On the other hand, the inlet needs to be brought out of the ring cassette, which must be redesigned. Furthermore, a displacement transducer is used, which, supports and simplifies the displacement control and ensures a realistic displacement of the edge-seal concerning climate loads.

However, it would be possible to induce the relative overpressure by changing the outside temperature as specified by the standard DIN EN 1279-2 (2003). In contrast to the injection of Argon this concept would also change the sealant’s mechanical behavior. Thus, it is not possible to investigate the permeation behavior within the edge-seal resulting solely from mechanical stresses by this way.

The advantages and disadvantages of each concept were discussed above. In order to objectively evaluate the introduced concepts, an evaluation scale is defined for each criterion after VDI guide line 2225 (1964). The comparison of the three concepts is displayed below (see Table 1).

The internal pressure controlled permeation test setup

After evaluating possible concepts to induce a long-term strain on the edge-seal, concept 3A appears to be the most feasible and suited solution. It is hereafter referred to as the internal pressure controlled permeation test (IPCPT). By adding an additional inlet pipe, the gas loss measurement can be easily expanded in order to measure at climate loads (see Fig. 8). The Argon is induced within the inter-pane space and the Helium, which serves as the flushing gas, is let into the annular gap between IGU and ring cassette. As stated before, the Helium is let into a cooling trap, which concentrates the Argon before the measurement with a gas chromatograph.

Fig. 8
figure 8

The experimental setup of the extended measurement of standard DIN EN 1279-3, Appendix C (2003). 1 helium; 2 argon; 3 IGU; 4 cooling trap; 5 gas chromatograph

Full size image
Fig. 9
figure 9

Results of the finite element analysis—the calculated maximum principal stresses at the edge of the hole

Full size image

As discussed before, some challenges regarding this concept exist and influenced the construction. In the following, the solutions regarding these problems are explained. First, it is necessary to ensure that the glass does not fail as a result of the applied internal overpressure. For the specimen, a glass pane with a drilled hole of a diameter of 15 mm in the middle of the panes is used, because of a higher breakage risk of the glass during the tempering procedure if the hole is close to one of the edges. Therefore, a finite element analysis (FEA) of the stress concentration and the applied internal pressure was conducted. The FEA-model is built in ANSYS 16.0 using a shell181-element for the glass pane (see Fig. 9). The model itself consists only of a quarter of a glass pane of the IGU taking advantage of the symmetric conditions. The edge support is simulated flexible by using linear spring elements at the edges (combin14) due to higher stress on the edge of the drilling hole considering a flexible support. There are only few values for effective spring stiffnesses of the edge seal in literature. Ensslen and Becker (2014) for example give a stiffness of about 2.75 N/mm per millimeter edge length at \(23~^{\circ }\)C with a tension velocity of 1 mm/min. Considering creep of the edge seal during the permeation test, a value of 1 N/mm per millimeter edge length should be suitable. The rotational stiffness is assumed as zero since it has an advantageous effect on the stress at the edge of the drilling hole. The internal pressure is applied as a surface load on the glass pane. In Fig. 9, the maximum principal stress of the glass pane is shown for an internal pressure of 100 hPa. The results of the stresses converge with a mesh of 1 mm and a refinement of the mesh at the edge of the drilling hole of 0.3 mm.

The calculated maximum principal stress at the edges of the hole would be about 82 MPa with a load of 100 hPa. Due to production, only heat strengthened glass with a characteristic bending strength of 70 MPa (5 % fractile) can be used for the specimens. This means that the surface pressure due to the tempering will be exceeded and a sub critical crack growth will take effect, which reduces the bending strength of the glass. In order to be able to use the specimens in a relevant inner pressure level and to reach high widening values of the edge seal, the maximum load is limited to 80 hPa with a slight risk of a failure of the glass. It is supposed that the edges of the drilled hole in the middle of the glass pane have the same strength as the bending strength of the glass.

Fig. 10
figure 10

Redesigned ring cassette to realize a displacement measurement of the edge-seal: 1 lower mask, 2 frame, 3 upper mask, 4 specimen, 5 flushing gas: in- and out-let, 6 pocket for displacement sensor, 7 drilling hole

Full size image

Moreover, it must be guaranteed that the Argon loss at the drill hole is minimized. Therefore, an insert is constructed, which minimized the connection’s effective area and thus, the gas loss through the connection. An even deformation of the edge-seal is realized by a R300 precision pressure regulator from AirCom Pneumatic GmbH. This pressure regulator has a regulation range from 0.001 to 0.014 bars with an adjustment accuracy smaller than 0.002 bar. A displacement transducer, which has been internally developed by the State Materials Testing Institute Darmstadt (MPA) and Institute for Material Science (IFW) in additionally assists the deformation control. It is a half bridge based on strain gauges and has an accuracy of 20 \(\mu \)m. Unlike other displacement sensors the C-shaped displacement transducer is easily manufactured and it is easy to install on the IGU’s surface. The clamping forces for adjusting the sensor are at 7.5. N. However, slightly changes of the ring cassette’s construction are unavoidable (see Fig. 10). Moreover, it should be secured, that the bonding of the cover, as well as the cover may not lead to a stiffening of the IGU. The toleration of the slight deformations increases the accuracy of the reproduced climate loads.

The test setup is implemented on a test rig at the MPA and IFW Darmstadt. First experiments are conducted in order to analyze the test setup’s feasibility and performance. The system’s function in terms of the impermeability of the insert could be shown during the performed test measurements. Futher tests are conducted at the moment and another test setup is built at Kömmerling Chemische Fabrik GmbH in Germany. We gladly share the test results of the IPCPT measurement in a publication at a later time.

Conclusion

In this work, a novel test method for measuring the gas loss rate of an IGU is introduced. Thereby, the existing standard test is extended to cover the influence of climate loads on the gas loss. Three concepts are evaluated in terms of possible challenges and advantages to obtain the most suitable and feasible solution. Main criteria are the reproducibility of the climate load, the displacement of the edge-seal and the manufacturing complexity of the concept. Additionally the concept must be adaptable to the existing test according to the European Standard DIN EN 1279-3, Appendix C (2003). The Internal Pressure Controlled Permeation Test is chosen. A prototype test setup is implemented at the MPA and IFW in Darmstadt. The feasibility of the test setup has been shown. During this study, several details have been optimized. To this day, experiments are conducted to proof the assumption that the gas loss is enhanced depending on the stress-strain state within the edge-seal.