Adaptive Space-Vector Hysteresis-Based Control with Constant Switching-Frequency for Three-Level Shunt Active Power Filters

Abstract

This paper proposes a new constant-frequency space-vector hysteresis current control (CF-SVHCC) technique for three-level neutral-point diode-clamped (TL-NPC) inverters in shunt active power filter applications when applied to three-phase isolated neutral point (INP) systems. The proposed techniques is developed based on two recognized modulation methods, space-vector pulsewidth modulation and adaptive hysteresis-band current control. The proposed technique consists of two alternating adaptive hysteresis-band strategies around the error-current vector in the $\alpha \beta$ stationary reference frame (SRF). The first strategy is designed with the purpose of utilizing the medium- and large-voltage vectors of the TL-NPC inverter to keep the error-current vector within the adaptive hysteresis boundary, while the second one is designed according to the small-voltage vectors of the TL-NPC inverter to balance its neutral point voltage. The main part of this proposed technique is a supervisory controller that operates in SRF to effectively avoid inter-phase dependency. This smart controller systematically uses the zero-voltage vectors and the nonzero-voltage vectors associated with the alternating adaptive hysteresis-band strategies in order to prevent high switching frequency and maintain the switching frequency constant in INP systems, respectively. The proposed CF-SVHCC performance is validated by extensive simulation studies for both steady-state and transient conditions.

Introduction

The multilevel inverter technology is anticipated to become an established resource for maturing the newly established and rapidly growing high-power applications that require considerable rise of both voltage and current amplitudes [1]. The main benefits of these types of inverters have been distinguished since the first neutral-point-clamped (NPC) inverter was introduced in 1981 by Nabae et al. [2]. This special configuration enhances the inverter power rating because the voltage stress of each semiconductor device is reduced to one-half of the DC-side voltage for a typical three-level inverter compared to a two-level inverter and will be even lower for higher level inverters. Moreover, their voltage harmonic content is by far lower than that of two-level inverters with the same condition owing to the inverter modulated-voltage improvements [3].

The existing SAPF technologies typically use a two-level-type voltage source inverter (VSI) structure [4]; however, for high-power applications, three-level-type VSI structures have been verified to operate more efficient [3]. A three-level NPC (TL-NPC) inverter can be engaged in a variety of systems (three-wire and four-wire power systems) [5]. In a TL-NPC inverter, the splitting DC-side-capacitor voltage has to be maintained half of the DC-side voltage. The key benefits of three-level VSIs are lower harmonic content, reduced voltage stress on the semiconductor switches, and improved switching losses.

Numerous control approaches for multilevel inverters have been introduced to control either voltage [6] or current [6]. They can be principally categorized into two classes: indirect current control (ICC) and direct current control (DCC) techniques. Carrier-based modulation and space-vector modulation (SVM) belong to the first category and have been considered as among the most popular modulation strategies for multilevel inverters because of their operation at a constant modulation frequency. An alternative approach to control current through multilevel inverters is to use a DCC-type technique. Hysteresis current control (HCC), which is a DCC-type modulation, is a popular approach due to its various advantages, i.e., simplicity, fast-response, and inherent peak current-limiting capability without requiring system parameter information. However, a fixed-band HCC technique introduces a number of disadvantages including variation of modulation frequency, excess load current harmonic distortions, and difficulties with vector conversion. The problems associated with these current control techniques are due to their complexity in implementation, demanding extensive system information, stability issues, and limitations in transient response [7].

The application of DCC to multilevel inverters is more rewarding but also more challenging. The popular control options are multi-band, multi-offset, time-based and space-vector strategies, and one-cycle control [8,9,10,11]. The first two methods use $n-1$ hysteresis-bands for an $n-$level inverter to identify an out-of-band current-error; however, there are difficulties associated with DC tracking errors and maintaining a constant switching frequency by changing the band magnitude. Time-based strategies overcome this flaw by utilizing solely one group of hysteresis-bands while also switching between voltage series when an out-of-band error is discovered; however, they are sensitive to noise at current zero crossings and have defective dynamic responses [12]. Space-vector strategies overcome these problems by directly correcting the current phasor error using the best voltage vector, which is selected according to current-error derivatives, per-phase leg comparators and a switching table [13]. However, inaccurate load back-electromotive force (EMF) estimation may result in wrong voltage vector selection and more harmonic distortions compared with the open-loop phase disposition modulation.

There are various strategies to solve the issues connected to the limitations of hysteresis controls [14,15,16,17]. One approach to keep a fixed modulation frequency is to compensate the influence of inaccurate load back-EMF by varying the hysteresis-band using the derivative of the output current-error and the inverter switching state [18]; however, the current-error derivative is vulnerable to high frequency noise specifically at higher switching frequencies. An alternative method to maintain a constant switching frequency is to compute the demanded hysteresis-band variation that synchronizes the current-error zero crossings to an external clock [19]; however, the regulators performance can be degraded due to computation issues [14]. In addition, both of the above-mentioned strategies can cause phase-leg interactions since they demand three separate current controls for a three-phase system while an INP system is only a two-degree-of-freedom problem [20].

This paper proposes a new and relatively simple modulation technique for TL-NPC inverters. It is designed based on the combination of the three-level SRF-type SVM technique from the ICC category and the three-level AHCC technique from the DCC category in order to provide the advantages of interphases independency and constant switching frequency, as well as neutral point voltage balancing, especially when applied to three-phase INP power systems. The proposed method consists of six different units; (1) a measurement unit for measuring the required signals, (2) an error computation unit for calculating the current-error vector in SRF, (3) an area and sector detection unit for detecting the sector and area of the current-error vector in alternating hysteresis strategies when the neutral point voltage is either balanced using the first strategy including 12 sectors associated with 12 medium- and large-voltage vectors or unbalanced using the second strategy including 6 sectors associated with six small-voltage vectors, (4) a voltage vector selection unit for selecting an appropriate voltage vector among the small-, medium- and large-voltage vectors of the TL-NPC inverter, (5) an adaptive hysteresis-band calculation unit for obtaining the hysteresis boundary in SRF, and (6) a supervisory control unit for defining which voltage vector should be applied to bring the current error back towards the hysteresis boundary, maintain the switching frequency constant, and balance the neutral point voltage. Simulation studies are performed using the MATLAB software to verify the steady state and transient performances of the proposed three-level CF-SVHCC technique in different scenarios.

Fig. 1

Three-level SAPF configuration; a basic compensation principle, b detailed TL-NPC inverter structure

Fig. 2

DCC-type SAPF control strategy with the proposed three-level CF-SVHCC

System Structure and Operation

Shunt Active Power Filter

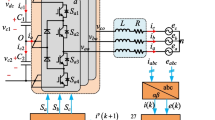
The operation principle of a TL-NPC-based SAPF topology is shown in Fig. 1a. It is a voltage-type inverter controlled as a current source and is attached in parallel with a group of nonlinear loads. Harmonic current compensation is attained by injecting the load current harmonic components equal in magnitude but opposite in phase to PCC. The SAPF block diagram, shown in Fig. 1a, consists of four different parts; (1) a measurement circuit, (2) a reference current circuit, (3) a modulation circuit, and (4) a TL-NPC inverter. The control technique to produce the reference current is a basic condition that controls the performance of SAPF [21]. The diagram of the control technique, used in this paper, is shown in Fig. 2.

In this study, it is assumed that the power system supplies the fundamental active power of the nonlinear loads and active power losses of SAPF, while SAPF compensates the current harmonics of the nonlinear loads. The regulation of the DC-side voltage guarantees an effective current control for SAPFs, as shown in Fig. 2. As can be realized from this figure, the measured DC-side voltage is primarily compared to its reference counterpart $0.5V_{dc}^*$. The error is then fed to a PI controller. The output of the PI controller is measured as the amplitude of the source current, and this is denoted by $I_{sm}^*$. This current takes care of the load active power demand and the SAPF losses. It also contains the component of the source current responsible for regulation of the SAPF DC-side voltage at a set value of $V_{dc}^*$. The peak value of the power system voltage is attained from the three-phase measured PCC voltages. Multiplying the source current amplitude $I_{sm}^*$ by the three-phase unit voltage vectors results in the three-phase reference source currents. Because the DCC method is used, the three-phase load currents are measured and subtracted from the reference currents resulting in the three-phase reference currents of SAPF.

Neutral-Point-Clamped Inverter

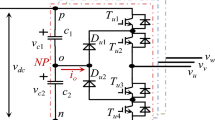
Figure 1b illustrates the configuration of a TL-NPC inverter. It is considered that the capacitor voltages are identical and equal to $0.5V_{dc}^*$ (shown in Fig. 2). In this case, the phase-to-neutral voltage of each phase according to Fig. 1b can be written as:

$$\begin{aligned} u_{\textit{xn}}=m_x\times \frac{V_{\textit{dc}}}{2} \end{aligned}$$

(1)

where,

$$\begin{aligned} m_x\in \left\{ -1,\ 0,\ +1\right\} \end{aligned}$$

and,

$$\begin{aligned} x\in \left\{ a,\ b,\ c\right\} \end{aligned}$$

Then, the per-phase phase-to-neutral voltage of the inverter will be:

$$\begin{aligned} u_{\textit{an}}= & {} \frac{V_{dc}}{3}\bigg (m_a-0.5 \times m_b- 0.5 \times m_c\bigg ) \end{aligned}$$

(2)

$$\begin{aligned} u_{\textit{bn}}= & {} \frac{V_{dc}}{3}\bigg (m_b-0.5 \times m_a-0.5 \times m_b\bigg ) \end{aligned}$$

(3)

$$\begin{aligned} u_{\textit{cn}}= & {} \frac{V_{dc}}{3}\bigg (m_c-0.5 \times m_a-0.5 \times m_b\bigg ) \end{aligned}$$

(4)

The inverter voltages can be transformed to a vector represented in SRF ($\mathbf {U}=u_{\alpha }+ju_{\beta }$) by the following equation:

$$\begin{aligned} \begin{bmatrix} u_\alpha \\ u_\beta \\ u_0 \end{bmatrix} =\frac{2}{3} \begin{bmatrix} 1&-1/2&-1/2\\ 0&3/2&-\sqrt{3}/2\\ 1/2&1/2&1/2 \end{bmatrix} \quad \begin{bmatrix} u_{\textit{an}}\\ u_{\textit{bn}}\\ u_{\textit{cn}} \end{bmatrix} \end{aligned}$$

(5)

The converted inverter voltages of the TL-NPC inverter are illustrated in Fig. 1a.

Fig. 3

Proposed three-level CF-SVHCC hysteresis-based modulation technique

Fig. 4

Alternative hysteresis strategies; a voltage vectors, b balanced capacitor voltages, c unbalanced capacitor voltages

Proposed Vector-Based Current Control

Figure 3 briefly describes the proposed vector-based modulation technique. As mentioned earlier, this technique consists of six different units; (1) the measurement unit, (2) the error computation unit, (3) the area and sector detection unit, (4) the voltage-vector selection unit, (5) the adaptive hysteresis-band calculation unit, and (6) the supervisory control unit. As can be observed in Fig. 2, initially, the capacitor voltages, the SAPF currents and the PCC voltages need to be measured. Then, the SAPF currents along with the reference currents provided by the reference current circuit are transferred to SRF. Here, the error currents can be calculated simply by subtracting the reference currents from the measured currents. By defining the current-error vector magnitude and angle, the area and sector detection unit can define the sector where it lies for the either balanced or unbalanced neutral point. However, in order to find the area, it needs the datum associated with the outer hysteresis-band, which is provided by the hysteresis-band calculation unit. After defining the area and the sector, the voltage vector is selected by the voltage vector selection unit among the three voltage vector categories, i.e., small, medium and large vectors (shown in Fig. 4a). The selected voltage vector is not the one that determines the switching signals. This information along with all other data are fed into the supervisory control unit to decide which voltage vector should be applied in order to bring the current-error vector within the adaptive hysteresis boundary to reach the reference current vector, maintain the switching frequency constant, and balance the neutral point voltage, simultaneously. To balance the neutral point voltage, this paper proposes a new simple technique. As shown in Fig. 4a, there are three voltage vector categories according to their magnitudes. The only voltage vector category that directly controls the neutral point voltage is the small vectors (small hexagon) because it includes two switching patterns associated with the capacitor $C_1$: charging ($\mathrm {U}_1-\mathrm {U}_6$) and discharging ($\mathrm {U}_{21}-\mathrm {U}_{26}$). The charging pattern charges the capacitor $C_1$ and discharges the capacitor $C_2$, but the discharging pattern does the opposite. Therefore, two look-up tables (explained in Tables 1, 2) and two alternating hysteresis strategies (shown in Fig. 4b, c) are considered here. The first look-up table and hysteresis strategy are used when the neutral point voltage is balanced and the second ones are used when the neutral point voltage is unbalanced.

Table 1 Definition of sectors for balanced neutral point voltage

Table 2 Definition of sectors for unbalanced neutral point voltage

Area and Sector Detection Unit

As shown in Figs. 4b, c, the tip of the reference current vector ($i_{APF}^*$) moves on a circle around the origin of the coordinate system. The analysis is performed in SRF; hence the transformation of the three hysteresis-bands into this frame results in two circular hysteresis-bands and three areas in total. These areas are adopted in order to use the zero-, medium- and large-voltage vectors for Fig. 4b when the neutral point voltage is balanced and the zero and small-voltage vectors for Fig. 4c when the neutral point voltage is unbalanced. In the mentioned figures, the values of $r_2$ (constant) and $r'_2$ (variable) are defined by the hysteresis-band calculation unit. The reference and actual currents can be expressed in a complex form as follows [22]:

$$\begin{aligned} \vec {i}^*_{\textit{APF}}= & {} i^*_{\textit{APF}\alpha }+ji^*_{\textit{APF}\beta } \end{aligned}$$

(6)

$$\begin{aligned} \vec {i}_{\textit{APF}}= & {} i_{\textit{APF}\alpha }+ji_{\textit{APF}\beta } \end{aligned}$$

(7)

Similarly, the current-error vector is expressed in SRF as [22]:

$$\begin{aligned} \Delta \vec {i}_{\textit{APF}}=\vec {i}_{\textit{APF}}-\vec {i}^*_{\textit{APF}}=\Delta i_{\textit{APF}\alpha }+j\Delta i_{\textit{APF}\beta } \end{aligned}$$

(8)

The current-error vector tip can be located in one of the three areas of Fig. 4b (A$\mathrm {_I}$, A$\mathrm {_{II}}$, or A$\mathrm {_{III}}$) or Fig. 4c (A$\mathrm {'_I}$, A$\mathrm {'_{II}}$, or A$\mathrm {'_{III}}$). The areas A$\mathrm {_I}$ and A$\mathrm {'_I}$ characterize one sector, i.e., $S_0$ and $S'_0$, respectively. The area A$\mathrm {_{II}}$ is subdivided into twelve sectors: $S_1-S_{12}$ associated with the zero-, medium- and large-voltage vectors and the area A$\mathrm {'_{II}}$ is subdivided into six sectors: $S'_1-S'_6$ associated with the zero- and small-voltage vectors. The angle between any two consecutive sectors is $30^\circ$ for Fig. 4b because there are twelve distinct medium- and large-voltage vectors and $60^\circ$ for Fig. 4b because there are six distinct small-voltage vectors. The tip of the current-error vector lies in a sector that is detected according to its area and angle $\gamma$ with respect to the $\alpha$-axis. Tables 1 and 2 give the conditions that must be satisfied for the current-error vector to reside in each particular sector regardless the neutral point is balanced or unbalanced.

Fig. 5

HCC for a TL-NPC inverter according to the ideal voltage value; a ideal voltage, b switchings of areas

Voltage Vector Selection Unit for Balanced Neutral Point

Considering Fig. 4b and Table 1, when the error-vector tip is located in area A$\mathrm {_I}$ (sector $S_0$), the error-vector magnitude is small and measured satisfactorily within the required accuracy for tracking the reference current. Then, one of the three zero-voltage vectors (U$_0$, U$_7$ or U$_{14}$) closest to the previous switching is applied, and no connection is made. For the second area A$\mathrm {_{II}}$, if the error-vector tip is located in any of the even numbered sectors, i.e., $S_2$, $S_4$, $S_6$, $S_8$, $S_{10}$ or $S_{12}$, one of the medium-hexagon-voltage vectors (U$_8$, U$_9$, U$_{10}$, U$_{11}$, U$_{12}$, or U$_{13}$) will be selected (shown in Fig. 2a). Otherwise, one of the large-hexagon-voltage vectors (U$_{15}$, U$_{16}$, U$_{17}$, U$_{18}$, U$_{19}$, or U$_{20}$) will be applied when the error-vector tip is located in one of the odd numbered sectors, i.e., $S_1$, $S_3$, $S_5$, $S_7$, $S_9$ or $S_{11}$.

Voltage Vector Selection Unit for Unbalanced Neutral Point

Considering Fig. 4c and Table 2, when the error-vector tip is located in the area A$\mathrm {'_I}$ (sector $S'_0$), the error vector magnitude is small and measured satisfactorily within the required accuracy for tracking the reference current. Then, one of the three zero-voltage vectors (U$_0$, U$_7$ or U$_{14}$) closest to the previous switching is applied, and no connection is made. But for the second area A$\mathrm {'_{II}}$, if the capacitor $C_1$ needs to be charged, one of the charging pattern, i.e. U$_1$, U$_2$, U$_3$, U$_4$, U$_5$ or U$_6$ will be selected. Otherwise, one of the discharging pattern, i.e. U$_{21}$, U$_{22}$, U$_{23}$, U$_{24}$, U$_{25}$ or U$_{26}$, will be selected.

Fig. 6

Ideal voltage calculation using switching signals

Hysteresis-Band Calculation Unit

According to the hysteresis current control principle, the switching frequency can be kept constant at a selected value by varying the hysteresis-band according to the system parameters, i.e., the filter inductance, the PCC voltage, and the DC-side voltage [23]. Therefore, here, the aim is to calculate the outer hysteresis-band in SRF for the TL-NPC inverter of Fig. 1b and include it in the proposed three-level CF-SVHCC technique to create a three-phase current signal with a constant modulation frequency. Fig. 1b shows the topology of a three-phase TL-NPC inverter, which is connected to PCC through a first-order low-pass filter. In this case, it can be considered that the grounded neutral point of the system is connected to the midpoint of the inverter DC-side because the analysis is performed in SRF. Therefore, each phase, which is supplied by a half bridge inverter leg, can be analyzed independently to derive the following phase-a leg voltage and current relationship:

$$\begin{aligned} \frac{di_{\textit{APFa}}}{dt}=\frac{1}{L_f}\Big (u_{\textit{an}}-R_fi_{\textit{APFa}}-v_a\Big ) \end{aligned}$$

(9)

where $u_{\textit{an}}$ and $i_{\textit{APFa}}$ are the phase-a inverter output voltage and current, respectively, $R_f$ and $L_f$ are the filter resistance and inductance, respectively, and $v_a$ is the phase-a PCC phase voltage. Fig. 5 shows the three-level hysteresis switching process over one fundamental cycle of the ideal voltage. Based on this figure, the SAPF current $i_{\textit{APFa}}$ contains two components, i.e., the fundamental component ($i_{\textit{Fa}}$) and the ripple component ($i_{\textit{Ra}}$). Therefore, the SAPF current can be written as [24]:

$$\begin{aligned} i_{\textit{APFa}}=i_{\textit{Fa}}+i_{\textit{Ra}} \end{aligned}$$

(10)

By substituting (10) into (9), the following equation can be obtained by neglecting the voltage drop across the series resistance:

$$\begin{aligned} \frac{di_{\textit{Ra}}}{\textit{dt}}=\frac{1}{L_f}\Big (u_{\textit{an}}-v_{\textit{ideala}}\Big ) \end{aligned}$$

(11)

where,

$$\begin{aligned} v_{\textit{ideala}}=v_a+L_f\frac{di_{\textit{Fa}}}{\textit{dt}} \end{aligned}$$

According to Fig. 6, when the ideal voltage is positive and the output current error exceeds the upper/lower hysteresis-band, the switching signal ($S_a$) becomes zero/one and the inverter voltage ($u_{\textit{an}}$) switches to zero/upper DC-side voltage. On the other hand, when the ideal voltage is negative, and the output current error exceeds the upper/lower hysteresis-band, $S_a$ becomes zero/one and $u_{\textit{an}}$ switches to the lower DC-side voltage/zero. Therefore, the switching periods for Areas 1 and 2 can be expressed as (considering that the capacitor voltages are fixed during the analysis, i.e., $V_{dc}/2$) [24]:

$$\begin{aligned} T_{a1}= & {} [f_{swa1}]^{-1}=\frac{L_f h_{a1} V_{dc}}{v_{\textit{ideala}} \big (0.5V_{dc}-v_{\textit{ideala}}\big )} \end{aligned}$$

(12)

$$\begin{aligned} T_{a2}= & {} [f_{swa2}]^{-1}=\frac{L_f h_{a2} V_{dc}}{-v_{\textit{ideala}} \big (0.5V_{dc}+v_{\textit{ideala}}\big )} \end{aligned}$$

(13)

Equations (12) and (13) can be rearranged into essentially identical expressions for the switching frequency during situations where the ideal inverter output voltage is either positive or negative, as [24]:

$$\begin{aligned} h_{a1}= & {} \frac{v_{\textit{ideala}} \big (0.5V_{\textit{dc}}-v_{\textit{ideala}}\big )}{L_f f_{swa1} V_{\textit{dc}}}\ \ \ v_{\textit{ideala}}\ge 0 \end{aligned}$$

(14)

$$\begin{aligned} h_{a2}= & {} \frac{v_{\textit{ideala}} \big (0.5V_{\textit{dc}}-v_{\textit{ideala}}\big )}{L_f f_{swa2} V_{\textit{dc}}}\ \ \ v_{\textit{ideala}}<0 \end{aligned}$$

(15)

where $h_{a1}$ and $h_{a2}$ show how the hysteresis-bands vary during the positive and negative ideal inverter voltages, respectively. Since the switching frequency during the positive and the negative half fundamental cycles are remained constant (i.e., $f_{swa1}=f_{swa2}=f_{sw}$), the three-level variable hysteresis-band expressions can now be combined as:

$$\begin{aligned} h_a=h_{\textit{max}}\Bigg [\bigg (\frac{\left| v_{\textit{ideala}} \right| }{V_{\textit{dc}}}\bigg )\bigg (0.5-\frac{\left| v_{\textit{ideala}} \right| }{V_{\textit{dc}}} \bigg )\Bigg ] \end{aligned}$$

(16)

where $h_{\textit{max}}=V_{dc}/(L_ff_{\textit{sw}})$. Subsequently for the other phases, the hysteresis-band will be obtained as bellow:

$$\begin{aligned} h_b= & {} h_{\textit{max}}\Bigg [\bigg (\frac{\left| v_{\textit{idealb}} \right| }{V_{\textit{dc}}}\bigg )\bigg (0.5-\frac{\left| v_{\textit{idealb}} \right| }{V_{\textit{dc}}} \bigg )\Bigg ] \end{aligned}$$

(17)

$$\begin{aligned} h_c= & {} h_{\textit{max}}\Bigg [\bigg (\frac{\left| v_{\textit{idealc}} \right| }{V_{\textit{dc}}}\bigg )\bigg (0.5-\frac{\left| v_{\textit{idealc}} \right| }{V_{\textit{dc}}} \bigg )\Bigg ] \end{aligned}$$

(18)

Because the proposed three-level CF-SVHCC works in SRF, therefore the aforementioned adaptive hysteresis-bands must be transformed to this frame. Hence, the new hysteresis-band can be expressed in SRF using the inverse transformation matrix of (5) as follows:

$$\begin{aligned} h_{\textit{new}}=\sqrt{h_\alpha ^2+h_\beta ^2} \end{aligned}$$

(19)

The important issue in calculating the above adaptive hysteresis bands is the calculation of the absolute value of the ideal voltage ($\left| v_{\textit{ideal}} \right|$) for each phase. To do this, an artificial-neural-network-based algorithm called adaptive linear combiner (ADALINE) is used to estimate these voltages using the switching signals belonged to each phase. There are a number of harmonic estimation techniques reported in the literature [25,26,27], among which discrete Fourier transform (DFT), Kalman filter (KF) and ADALINE are the most popular ones. ADALINE has been proven to be superior to the KF and DFT techniques in finding the magnitudes and phases of the harmonics [28]. Therefore, in this paper, this algorithm is employed. The estimation procedure proposed by this method over one fundamental power cycle for phase-a is shown in Fig. 6. The phase-a inverter output voltage along with its fundamental component, which aims to be extracted from the total switching signal, are shown in Fig. 5. This switching signal, which is denoted by $S_{tot.}$, is revealed in Fig. 6. To produce this switching signal, $S_{a1}$ and $\bar{S}_{a2}$ are employed. The absolute value of the phase-a inverter voltage for estimating the absolute value of the ideal voltage can be calculated as:

$$\begin{aligned} \left| u_{\textit{an}} \right| =\frac{V_{dc}}{2}\times S_{\textit{tot}.} \end{aligned}$$

(20)

Considering that this voltage, which has been obtained by the phase-a switching signals of the TL-NPC inverter of Fig. 1b, with the fundamental angular frequency of $\omega =2\pi f$ includes an unknown fundamental component, a finite number of harmonic components with a maximum order N, and a decaying DC offset component ($U_{\textit{dca}}$), at any sample instant k, it can be written by the Fourier series as:

$$\begin{aligned} \begin{aligned} u_{a}[k]&=\sum _{n=1}^{N}U_{\textit{na}}\sin \big (\omega knT_s+\varphi _{\textit{na}}\big )+U_{\textit{dca}}e^{-kT_s/\tau _a}\\ {}&=\sum _{n=1}^{N}\Big [G_{\textit{na}}\sin \big (n\theta _a\big )+H_{\textit{na}}\cos \big (n\theta _a\big )\Big ]\\ {}&\quad +\,U_{\textit{dca}}-\frac{\theta _aU_{\textit{dca}}}{\omega \tau _a} \end{aligned} \end{aligned}$$

(21)

Fig. 7

Zero-voltage vector selection; a balanced neutral point, b unbalanced neutral point

where,

$$\begin{aligned} G_{na}=U_{\textit{na}}\cos \varphi _{\textit{na}} \quad \text {\textit{and}} \quad H_{\textit{na}}=U_{\textit{na}}\sin \varphi _{\textit{na}} \end{aligned}$$

In this equation, $U_{\textit{na}}$, $\varphi _{\textit{na}}$, $\tau _a$, $N_s$, and $T_s$ are the amplitude of the nth harmonic, the phase angle of the nth harmonic, the time constant of the decaying DC offset, the sampling rate, and the sampling period, respectively. Rearrangement of this equation in order to represent it as a matrix form yields:

$$\begin{aligned} \begin{aligned} u_{fa}[k]=\big (\mathbf {W}_a[k]\big )^T\mathbf {X}_a[k] \end{aligned} \end{aligned}$$

(22)

Fig. 8

Steady-state response of CF-SVHCC with a 5 kHz switching frequency in grid-connected TL-NPC application

where,

$$\begin{aligned} \mathbf {W}_a[k]= & {} \Big [G_{1a}, H_{1a},..., G_{Na}, H_{Na}, U_{dca}, -\frac{U_{dca}}{\tau _a}\Big ]^T\\ \mathbf {X}_a[k]= & {} \Big [\sin \theta _{a}, \sin \theta _{a},..., \sin \theta _{a}, \sin \theta _{a}, 1, -\frac{\theta _a}{\omega }\Big ]^T \end{aligned}$$

where T, $\mathbf {W}_a [k]$, and $\mathbf {X}_a [k]$ represent the transpose symbol, the known input vector, and the adjustable weight vector. The algorithm tries to estimate the actual signal ($u_{a} [k]$) by changing the adjustable weight vector using a weight-updating rule. Therefore, it is assumed that the weight vector is unknown. The estimated signal ($\hat{u}_{a} [k]$) can be calculated by multiplying the estimated adjustable weight vector $\hat{\mathbf {W}}_a [k]$ by the known vector $\mathbf {X}_a [k]$. The adjustable weight vector is:

$$\begin{aligned} \begin{aligned} \hat{\mathbf {W}}_a[k]=\Big [\hat{G}_{1a}, \hat{H}_{1a},..., \hat{G}_{Na}, \hat{H}_{Na}, \hat{U}_{dca}, -\frac{\hat{U}_{dca}}{\tau _a}\Big ]^T \end{aligned} \end{aligned}$$

(23)

The error signal $e_a [k]$ is the difference between the desired and estimated signals, and can be calculated as $e_a [k]=u_{a} [k]-\hat{u}_{a} [k]$. The weight vector is updated with the Widrow-Hoff updating rule and is specified as follows:

$$\begin{aligned} \begin{aligned} \hat{\mathbf {W}}_a[k+1]=\hat{\mathbf {W}}_a[k]+\alpha _{ada}\frac{\mathbf {X}_a[k]e_a[k]}{\mathbf {X}_a[k]^T\mathbf {X}_a[k]} \end{aligned} \end{aligned}$$

(24)

Fig. 9

Dynamic response of CF-SVHCC with a 5 kHz switching frequency in grid-connected TL-NPC application

where $\alpha _{ada}$ is the reduction factor with a practical range of 0.01–1. The amplitude of the nth harmonic (here the fundamental component is required) is estimated using the in-phase and quadrature-phase components as:

$$\begin{aligned} \hat{U}_{na}[k]= & {} \sqrt{\Big (\hat{\mathbf {W}}_{(2n-1)a}[k]\Big )^2+\Big (\hat{\mathbf {W}}_{(2n)a}[k]\Big )^2} \end{aligned}$$

(25)

$$\begin{aligned} \hat{\varphi }_{na}[k]= & {} {\left\{ \begin{array}{ll} \arctan \Big (\frac{\hat{\mathbf {W}}_{(2n)a}[k]}{\hat{\mathbf {W}}_{(2n-1)a}[k]}\Big ), &{} {\hat{\mathbf {W}}_{(2n-1)a}[k]\ge 0} \\ \pi +\arctan \Big (\frac{\hat{\mathbf {W}}_{(2n)a}[k]}{\hat{\mathbf {W}}_{(2n-1)a}[k]}\Big ), &{} {\hat{\mathbf {W}}_{(2n-1)a}[k]< 0} \end{array}\right. }\nonumber \\ \end{aligned}$$

(26)

Supervisory Control Unit

The supervisory control unit attempts to select a proper voltage vector such that the current-error vector is maintained within the hysteresis-band and ramps up and down with a constant modulation frequency and, at the same time, balance the neutral point voltage. This unit tracks the direction of the current-error vector by calculating its derivative. If it is ramping up from the inner hysteresis-band ($r_1=r'_1$) towards the outer hysteresis-band ($r_2=r'_2=h_{new}$), then one of the zero-voltage vectors closest to the previous switching state will be applied (shown in Fig. 7a for balanced neutral point voltage and Fig. 7b for unbalanced neutral point voltage) until the current-error reaches the outer hysteresis-band. Once it hits the outer hysteresis-band, one of the nonzero-voltage vectors of Table 1 for balanced neutral point voltage or Table 2 for unbalanced neutral point voltage depending on where the current-error vector tip in the sectors lies is applied. The same procedure is repeated when the current-error vector is ramping down. The procedure for selecting the zero-voltage vectors is illustrated in Figs. 7a ,b. As can be realized from these figures, U$_0$, U$_7$ or U$_{14}$ is selected when the previous non-zero voltage vector that moves the current-error vector towards $S_0$ has two zero-switching (Z) states, two positive-switching (P) states or two negative-switching (N) states, respectively.

Fig. 10

Dynamic response of CF-SVHCC with a 10 kHz switching frequency in SAPF application

Fig. 11

Performance investigation of the proposed three-level CF-SVHCC compared to the AHCC technique in both grounded and isolated systems; a–d C-AHCC in GNP system, e–h C-AHCC in INP system, g–l proposed modulation technique in INP system

Simulation Results

To validate the performance of the proposed three-level CF-SVHCC technique, three case studies are simulated for steady-state and dynamic conditions. Moreover, a comparison is undertaken to expose the superiority of this technique over the conventional AHCC method [24].

Steady-State Performance for TL-NPC Application

To evaluate the steady-state performance, it is initially considered that the TL-NPC inverter of Fig. 1b is connected to PCC in the absence of the nonlinear loads (grid-connected). The inverter is assigned to produce the following reference currents:

$$\begin{aligned} {\left\{ \begin{array}{ll} I^*_{APFa}=10 \times \sin (\omega t-\pi /2) \\ I^*_{APFb}=10 \times \sin (\omega t-2\pi /3-\pi /2) \\ I^*_{APFc}=10 \times \sin (\omega t+2\pi /3-\pi /2) \\ \end{array}\right. } \end{aligned}$$

(27)

The system performance is evaluated for a 5 [kHz] switching frequency. Fig. 8 shows the simulation results. In these figures, sections (a), (b), (c), (d), (e), (f), (g), (h), and (i) show the fundamental component of the TL-NPC output voltages called ideal voltages estimated by the ADALINE algorithm using the total switching signal ($S_{tot.}$), the adaptive hysteresis-bands [calculated using (16–18)] and the new band [calculated using (19)], the angle of the current-error vector ($\gamma$) with respect to the $\alpha$-axis to detect the sector and area in the alternating hysteresis strategies (shown in Figs. 4b, c), the changing trend in sectors demonstrating how the current-error vector moves inside the outer hysteresis band in order to obtain the predefined switching frequency, the generated inverter currents, the capacitor voltages confirming that the proposed technique has managed to balance the neutral point voltage by regulating the capacitor voltages using the zero-voltage vectors, the current vector in SRF, the current-error vector in SRF, and the harmonic spectrum of the phase-a generated current showing that the maximum harmonic component value roughly occurs at 5 kHz verifying that the switching frequency is maintained almost constant, respectively. These results confirm that the proposed technique produces the reference currents with a nearly constant switching frequency in the INP system of Fig. 1a and balance the capacitor voltages.

Dynamic Performance for TL-NPC Application

Here, as in the previous section, the structure of Fig. 1b is considered when the neutral point is isolated. However, the performance of the proposed modulation technique is investigated for a transient change (a sudden reference change happening at 0.01 s for a 50% magnitude increase). The inverter is assigned to produce the following reference currents at a 5 kHz modulation frequency:

$$\begin{aligned} {\left\{ \begin{array}{ll} I^*_{\textit{APFa}}=(10\xrightarrow {\textit{After}}15) \times \sin (\omega t-\pi /2)\\ I^*_{\textit{APFb}}=(10\xrightarrow {\textit{After}}15) \times \sin (\omega t-2\pi /3-\pi /2)\\ I^*_{\textit{APFc}}=(10\xrightarrow {\textit{After}}15) \times \sin (\omega t+2\pi /3-\pi /2)\\ \end{array}\right. } \end{aligned}$$

(28)

Figure 9 reveals the simulation waveforms. The results verify that the proposed scheme works very well under a sudden reference change, and, at the same time, keeps the switching frequency constant.

Dynamic Performance for SAPF Application

In this case, the aim is to apply the proposed approach for the SAPF application in the INP system of Fig. 1a for a 10 kHz switching frequency. In this system, two nonlinear loads are considered. It is assumed that Load 2 is switched on at 0.14 s. The SAPF control system is shown in Fig. 2. The simulation results for this case study are shown in Fig. 10. In this figure, sections (a), (b), (c), (d), (e), (f), (g), (h), and (i) show the estimated ideal voltages, the current-error vector ramping up and down within $r_1=r'_1$ and $r_1+r_2 (=h_{new})=r'_1+r'_2 (=h_{new})$ with a constant modulation frequency, the angle of the current-error vector ($\gamma$) with respect to the $\alpha$-axis, the changing trend in sectors, the load currents, the SAPF currents, the source currents, the SAPF current vector trajectory in SRF, and the harmonic spectrum of the phase-a source current before and after load change, respectively. These results expose that SAPF properly compensates the nonlinear loads (THD% = 27.39%) in the INP system of Fig. 1a that makes the source current almost sinusoidal before (THD% = 3.46%) and after (THD% = 2.48%) the sudden load change using the proposed modulation technique.

Comparison Study

Multilevel SAPFs are progressively being used in high-power applications due to their high voltage and high current handling capability. In most high-performance SAPF applications, HCC is commonly used because of its simplicity of implementation, fast current control response and inherent peak current limiting capability; however, the modulation frequency varies within a fixed band producing non-optimum current ripples. To overcome this drawback, the AHCC modulation has been proposed in the literature [24]. However, when AHCC is employed in INP systems, interphases dependency breeds very high-switching frequencies. To overcome these drawbacks, this paper proposed the vector-based modulation technique in SRF that eliminates the switching frequency variation of HCC and the interphases dependency of AHCC. Fig. 11 shows the comparison study. As can be realized from Figs. 11a, d, g, when the AHCC is applied in the three-phase grounded neutral point system of Fig. 1b, it can properly complete its task in maintaining the switching frequency nearly constant by varying the hysteresis-band, but when it is used in the INP system of the same system, because of the presence of the interacting common mode current in the system, as shown in Fig. 11b, e, h, AHCC does not work appropriately. However, the proposed technique overcomes the interphase dependency by gathering the three current-error vectors in one vector in SRF and, at the same time, maintains the switching frequency nearly constant with a lower harmonic content, as shown in Fig. 11c, f, i.

Conclusion

In this paper, a new vector-based CF-SVHCC technique for three-level NPC-based SAPFs has been presented. The proposed technique is developed in SRF based on two recognized strategies, SVPWM and AHCC. The procedure has been done in SRF based on SVPWM strategy by converting the three error-currents to a single vector that can be located in 12 sectors of the first hysteresis strategy associated with the zero-, medium- and large-voltage vectors and 6 sectors of the second hysteresis strategy associated with the zero- and small-voltage vectors for unbalanced and unbalanced neutral point voltages, respectively. As a result, the interphases dependency, which causes high switching frequencies in three-phase INP systems, is prevented. The adaptive hysteresis-bands obtained from the AHCC strategy are transferred into SRF to determine the outer hysteresis-band. The number and the position of the error-current sectors, in which the error-current vector moves, have been chosen in order to ensure the switching between two adjacent voltage levels of the inverter. In fact, the supervisory control unit systematically selects the zero-voltage vectors based on the data provided from the other units and the nonzero-voltage vectors in order to prevent high switching frequency caused by the phase interaction leading to maintaining the switching frequency constant and balance the neutral point voltage. The proposed technique retains all benefits of the conventional HCC including fast dynamic reaction, implementation simplicity, adjacent voltage vector switching, etc. The further introduced advantages are constant switching frequency, interphases independency and neutral point voltage balancing. The superior performance of the proposed method has been exposed through extensive steady-state and transient simulation investigations in the three-phase isolated neutral-point power system for both grid-connected TL-NPC inverter and SAPF applications.