Introduction

Dyes are considered to be one of the oldest man-made chemicals (Yusuf et al. 2017). They are extensively consumed in cosmetic and food industries and their global annual production is about 700,000 tons (Yusuf et al. 2017). Of this amount, approximately 10%–15% are released into the environment during manufacturing and usage (Padamavathy et al. 2003). Some dyes are hazardous; they may cause skin irritation, sneezing, and sore eyes, and sometimes can affect a person’s immune system (Svedman et al. 2019). Therefore, these pollutants should be treated before their discharge into the environment.

Remediation can be done using several techniques, such as coagulation–flocculation, reverse osmosis membranes, adsorption on the activated carbon and ion exchange method ultrafiltration. Though these methods are moderately effective in detoxification, however, there is production of secondary waste which sometimes are toxic and these cannot be treated again (Ferreira et al. 2001). Hence, an efficient method to eliminate toxic dyes from the industrial effluents has to be developed.

Advanced oxidation processes (AOPs) are powerful methods which can be used for wastewater treatment, particularly in cases where contaminant species appear especially recalcitrant to biological processes (Anotai et al. 2011). These processes, based on the generation of powerful oxidizing agents especially hydroxyl radicals (·OH), include photocatalysis (Nasuhoglu et al. 2012), H2O2/ozonation processes (Shu and Chang 2005), Fenton process (Li et al. 2012) and electro-Fenton process (Mansour et al. 2015a).

Electro-Fenton is considered to be an indirect oxidation process in which a mixture of H2O2 and Fe2+ is generated electrochemically throughout the process and (·OH) is produced (Mansour et al. 2014; Puga et al. 2021). Indeed, in this process, the added O2 is reduced at the cathode to form H2O2. This later reacts with the added Fe2+ ions, in an acidic medium, to produce ·OH (Mansour et al. 2012, 2015b). Generated ·OH are able to rapidly react with organic pollutants and to oxidize them into harmless compounds, such as inorganic ions, carbon dioxide (CO2) and water (Oturan 2021; García-Espinoza et al. 2021).

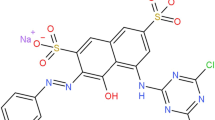
Congo red (CR) is an anionic dye that has two azo bonds as chromophore and is widely used in paper, plastic, rubber, and textile industries (Do et al. 2022). Due to its high toxicity, mutagenicity and carcinogenicity cause serious health problems (Wakelyn 2007; Paba et al. 2021). Several researchers used several treatment for Congo red dye removal, such as Fenton reaction, catalytic wet air oxidation, photocatalytic and photo-Fenton oxidation (Shaban et al. 2017; Setyaningtyas et al. 2019; Chowdhury and Bhattacharyya 2019).

In this study, the degradation of Congo red dye will be performed using the electro-Fenton process. This is an environmentally friendly technique as there is no involvement of harmful chemical reagents for wastewater treatment and is efficient for the purification of polluted water by persistent and/or toxic organic micropollutants (Mansour et al. 2012). On the other side, carbon is widely used as a cathode material for H2O2 generation since it exhibits high overpotential for hydrogen evolution and low catalytic activity for H2O2 decomposition (Mansour et al. 2012).

The present work aims to perform three objectives. The first one is to investigate the effect of operating parameters, including pH, Fe2+ concentration, current intensity and electrolyte support concentration, on the degradation of Congo red dye by the electro-Fenton process. The second aim is the use of Doehlert methodology design combined with response surfaces to optimize the electro-Fenton operating conditions for the removal of Congo red dye from aquatic solutions. The Doehlert design is a second-degree polynomial model which allows the study of multiple factors, each at different levels, simultaneously. This quadratic model is a convenient and effective approach for the application of a reduced number of experiments while still capturing the important information and optimizing the variables of interest (El Faroudi et al. 2023). By employing this mathematical model, it becomes possible to simultaneously vary multiple factors, revealing the actual impact and interaction among them, instead of the traditional approach of altering one factor at a time (El Faroudi et al. 2023). In order to achieve this objective, the evolution of Congo red concentrations was monitored by Ultraviolet/visible spectrophotometer. The third aim is the mineralization of Congo red dye monitored by the removal of total organic carbon (TOC) and the suggestion of a plausible degradation pathway. The outcome of these objectives would provide a sustainable and efficient wastewater management practice, which are crucial for reducing organic pollutant emissions in the environment.

Materials and methods

Chemicals

Congo red (≥ 75%) was purchased from Sigma Aldrich. FeSO4 7H2O (purity 99%) and Na2SO4 (purity 99%) respectively used as a reactant and electrolyte support were obtained from Acros organics. The initial pH of the Congo red solutions was adjusted with Acros analytical grade hydrochloric acid. All solutions were prepared in deionized water and all other chemicals used in the analysis were acquired from Acros organics and Sigma Aldrich.

Analytical determinations

The solutions were filtered on Sartorius Minisart® 0.45 μm GF prefilters (Goettingen, Germany).

The evolution of Congo red concentrations was monitored by ultraviolet/visible spectrophotometer (LABOMED, INC., UV-2950, USA) at a wavelength of 498 nm. The total organic carbon (TOC) of the initial and electrolyzed samples was measured with a Total Organic Shimadzu TOC-VCPH/CPN analyzer. Organic carbon compounds were burned and converted to CO2, which was detected and measured using a non-dispersive infrared sensor (NDIR). Reproducible TOC values were achieved by the standard non-purgeable organic carbon (NPOC). Every sample was triple-metered.

Experimental procedure

The degradation of the Congo red dye by the electro-Fenton process was performed in an indivisible glass cylindrical cell of 300 ml equipped with two electrodes. The cathode was a carbon felt electrode (Le Carbone Lorraine RVG 4000—Mersen, Paris La Défense, France) placed on the internal wall of the cell. Its dimensions were 90 mm × 75 mm, specific area was 0.7 m2 g−1, thickness was 12 mm, density was 0.088 g cm−3 and carbon yield was 99.9%.

The anode was a double platinum wire electrode (Metrohm, 6.0338.100) placed at the center of the cell to provide a good distribution of potential. The pH of the Congo red solutions was regulated to 3 using hydrochloric acid (HCl). A catalytic amount of FeSO4 7H2O was added to the cell just prior to the start of electrolysis. The electrodes were connected to a direct current power supply (Metrix, model AX 322) operating in galvanostatic mode to monitor the amperage. The ionic strength was kept constant by adding Na2SO4 as a supporting electrolyte. The initial Congo red concentration was 0.1 mM and its degradation was evaluated after 30 min reaction time in most cases.

Doehlert experimental design

The experimental design of Doehlert was applied to determine the optimum conditions for the Congo red degradation. The influence of three factors: initial Fe2+ concentration (U1), electrolysis time (U2) and current intensity (U3) were examined. The removal rate of Congo red was the considered response (Y). The Doehlert matrix is composed of N experiments where N = K2 + K + 1, with K is the number of variables. For K = 3, the matrix included 13 experiences distributed uniformly across the space of the coded variables (Xi). The number of repetitions in the center point of the plane was set to 3 (experiments 13–15) in order to get an estimate of the experimental error. The conversion of natural variables (Ui) into coded variables (Xi) was carried out using the following equation (Hammami et al. 2009):

$${X}_{\mathrm{i }}= \left[\frac{{{\text{U}}}_{{\text{i}}}- {{\text{U}}}_{\mathrm{i }(0)}}{{\Delta {\text{U}}}_{{\text{i}}}}\right]\mathrm{ \alpha }$$
(1)

where Ui(0) is the value of Ui at the center of the study domain, ΔUi is the variation step and α is the maximum coded value of Xi: X1 = 1; X2 = 0.866; X3 = 0.816.

$${\text{U}}_{{{\text{i }}\left( 0 \right)}} = \frac{{{\text{upper limit of U}}_{{\text{i}}} + {\text{lower limit of U}}_{{\text{i}}} }}{2}$$
(2)
$$\Delta {\text{U}}_{{\text{i}}} = \frac{{{\text{upper limit of U}}_{{\text{i}}} - {\text{lower limit of U}}_{{\text{i}}} }}{2}$$
(3)

For the design of the Doehlert experimental model, the considered domain for each variable (3,4 < U1 (mM) < 33.6; 5 < U2 (min) < 35; 200 < U3 (mA) < 700) was determined following preliminary trials (data not shown).

The experimental response related to the Doehlert matrix is depicted as a quadratic polynomial model:

$${\text{Y }} = {\text{ b}}_{0} + {\text{ b}}_{{1}} {\text{X}}_{{1}} + {\text{ b}}_{{2}} {\text{X}}_{{2}} + {\text{ b}}_{{3}} {\text{X}}_{{3}} + {\text{ b}}_{{{11}}} {\text{X}}_{{1}}^{{2}} + {\text{ b}}_{{{22}}} {\text{X}}_{{2}}^{{2}} + {\text{ b}}_{{{33}}} {\text{X}}_{{3}}^{{2}} + {\text{ b}}_{{{12}}} {\text{X}}_{{1}} {\text{X}}_{{2}} + {\text{ b}}_{{{13}}} {\text{X}}_{{1}} {\text{X}}_{{3}} + {\text{ b}}_{{{23}}} {\text{X}}_{{2}} {\text{X}}_{{3}}$$
(4)

where Y is the experimental response, b0 is a constant of the model, bi is the estimation of the main effects of the factor i, bii is the estimation of the second-order effects and bij is the estimation of the interactions between factor i and factor j.

The coefficients were calculated with the least squares method by means of

$${\text{B }} = \, \left( {{\text{X}}^{{\text{T}}} {\text{X}}} \right)^{{ - {1}}} {\text{X}}^{{\text{T}}} {\text{Y}}$$
(5)

where B is the vector of estimates of the coefficients, X is the model matrix, XT is the transposed model matrix and Y is the vector of measured response.

The statistical significance of the model was verified through the variance analysis (ANOVA). The relationship of response to experimental variables was represented graphically by drawing the three-dimensional response surface and the two-dimensional iso-response curves. NEMRODW Software (Mathieu et al. 2000) was used to calculate and process data.

Results and discussion

Effect of operating parameters on the Congo red degradation

Various experiments were carried out to study the influence of the operating parameters, including pH, Fe2+ concentration, current intensity and electrolyte support concentration, on the treatment of Congo red dye by the electro-Fenton process.

Effect of pH

The effect of the initial pH (2–10) on CR degradation was investigated by the electro-Fenton process and the obtained results are shown in Fig. 1. These experiments were performed using initial CR concentration of 0.1 mM, Fe2+ concentration of 3.4 mM and current intensity of 300 mA.

Fig. 1
figure 1

Effect of the initial pH on the Congo red removal by the electro-Fenton process. Experimental conditions: [CR]0 = 0.1 mM, [Fe2+] = 3.4 mM, [Na2SO4] = 50 mM, I = 300 mA, V = 0.3 L, t = 30 min

Full size image

The result indicates that the degradation effectiveness of CR was influenced by the pH variation, the maximum CR degradation was obtained at pH 3. Moreover, it can be observed that increasing the pH from 3 to 10 diminished the CR degradation and this result is in accordance with previous studies (Wang et al. 2015). This behavior is owing to the decrease in oxidation potential of ·OH due to pH increase. Indeed, at pH higher than 6, hydroxyl radical is transformed into its conjugate base •O− (Babuponnusami and Muthukumar 2012). It should also be noted that at high pH, the production of ·OH was reduced due to the presence of insoluble ferric hydroxo complexes generated during the treatment (Babuponnusami and Muthukumar 2012). On the other hand, at pH less than 3, the reaction was slow due to the generation of complex species [Fe(H2O)6]2+, which reacts more slowly with peroxide compared to that of [Fe(OH)(H2O)5]2+ (Babuponnusami and Muthukumar 2012).

Effect of the initial Fe2+ concentration

The influence of the initial Fe2+ concentration on the CR degradation was investigated using the electro-Fenton process. Several electrolyses were carried out for 0.1 mM CR at pH 3 and current intensity 300 mA. The Fe2+ concentration was varied from 1.3 to 33.6 mM.

The obtained results (Fig. 2) indicate that the removal of CR depended on the initial Fe2+concentration. Indeed, the increase of Fe2+ concentration from 1.3 to 20.1 mM rose the degradation rate from 83.4 to 98.1% after 30 min of electrolyze. This behavior is ascribed to the high concentration of hydroxyl radicals produced with more Fe2+ (Mansour et al. 2012).

Fig. 2
figure 2

Effect of the initial Fe2+ concentration on the Congo red removal by the electro-Fenton process. Experimental conditions: [CR]0 = 0.1 mM, [Na2SO4] = 50 mM, pH = 3, I = 300 mA, V = 0.3 L, t = 30 min

Full size image

However, it can be noted that the degradation rate of CR diminished with the increase of the Fe2+ concentration from 20.1 to 33.6 mM. This behavior can be attributed to the consumption of the hydroxyl radicals by the excessive amount of ferrous ions added to the reaction medium Eq. (6) (Mansour et al. 2012).

$${\text{Fe}}^{{{\text{2}} + }} + ^{ \cdot } {\text{OH }} \to {\text{ Fe}}^{{{\text{3}} + }} + {\text{ OH}}^{ - }$$
(6)

Effect of the applied current

The effect of the current intensity on the efficiency of the electro-Fenton method was investigated by many researchers (Doumbi et al. 2022; Mansour et al. 2014, 2012, 2015a, b; Hoang et al. 2021). In order to examine the influence of this variable on the degradation of CR, the current intensity was raised from 50 to 700 mA. The CR degradation has been monitored and the results are shown in Fig. 3.

Fig. 3
figure 3

Effect of the applied current on the Congo red removal by the electro-Fenton process. Experimental conditions: [CR]0 = 0.1 mM, [Fe2+] = 3.4 mM, [Na2SO4] = 50 mM, pH = 3, V = 0.3 L, t = 30 min

Full size image

In light of the results obtained, increasing of the current intensity from 0.05 to 0.4A upgrades the CR degradation rate from 66.9 to 95.6% within 30 min of electrolyze, proving the rise of the decomposition capacity.

This improvement in the CR removal rate comes from the excess production of hydrogen peroxide and the high regeneration of Fe2+ at the cathode Eq. (7). This behavior promotes hydroxyl radical production Eq. (8), and hence enhances the treatment effectiveness (Mansour et al. 2015a).

$${\text{Fe}}^{{{3} + }} + {\text{ e}}^{ - } \to {\text{ Fe}}^{{{2} + }}$$
(7)
$${\text{Fe}}^{{{\text{2}} + }} + {\text{ H}}_{{\text{2}}} {\text{O}}_{{\text{2}}} \to {\text{ Fe}}^{{{\text{3}} + }} + {\text{ OH}}^{ - } + ^{ \cdot } {\text{OH}}~~~~~~~~~~~~\left( {{\text{Fenton's reaction}}} \right)$$
(8)

On the other hand, when the current intensity was higher than 0.4 A, the CR removal decreased due to the competitive reactions. Indeed, the oxidation of H2O to oxygen gas at the anode and the production of hydrogen gas via proton reduction at the cathode become more marked (Masomboon et al. 2010).

Effect of the initial electrolyte support concentration

The electrolyte support would be useful in an electrochemical reaction because of enhancing the conductivity of the solution and accelerating electron transfer. Therefore, it is necessary, especially in solution with insufficient conductivity.

In order to study the influence of electrolyte support concentration, the initial Na2SO4 concentration was varied from 25 to 200 mM. The obtained results (Fig. 4) reveal that the increasing of the Na2SO4 from 25 to 50 mM, raised the degradation rate of CR from 76.8 to 96.3%. Indeed, when referring to Faraday’s First Law of electrolysis, it can be noted that when the electrolyte concentration increases, the current density also increases as there are more charged ions present in the solution. This fact promotes a faster production of hydrogen peroxide which improves the electro-Fenton efficiency (Zhou et al. 2007).

Fig. 4
figure 4

Effect of the initial electrolyte support concentration on the Congo red removal by the electro-Fenton process. Experimental conditions: [CR]0 = 0.1 mM, [Fe2+] = 3.4 mM, pH = 3, I = 300 mA, V = 0.3 L, t = 30 min

Full size image

Nevertheless, the increase of Na2SO4 concentration from 50 to 200 mM reduced the treatment efficiency. This behavior is ascribed to the consuming of hydroxyl radicals by SO42− Eq. (9) (Zhou et al. 2007).

$${\text{HO}}^{ \cdot } + {\text{ SO}}_{{4}}^{{{2} - }} \to {\text{ HO}}^{ - } + {\text{ SO}}_{{4}}^{ \cdot - }$$
(9)

Determination of the optimal conditions for the removal of Congo red

The effectiveness of the electro-Fenton method is related to several parameters, such as current intensity, electrolysis time and initial Fe2+ concentration (Mansour et al. 2012). Doehlert matrix was used in order to determine the operating condition leading to the highest degradation rate. The experimental design is reported in Table 1.

Table 1 Doehlert matrix experiments and experimental results
Full size table

The polynomial model coefficients were computed using the experimental results of CR degradation (CR removal (%)) and the following model equation was proposed (Eq. (10)).

$${\text{Y}} = { 96}.{1}{-}{1}.{\text{9 X}}_{{1}} + { 5}.{\text{5 X}}_{{2}} {-}{1}0.0{\text{ X}}_{{3}} {-}{4}.{\text{5 X}}_{{1}}^{{2}} {-}{5}.{\text{1 X}}_{{2}}^{{2}} {-}{16}.{\text{8 X}}_{{3}}^{{2}} {-}0.{\text{8 X}}_{{1}} {\text{X}}_{{2}} {-} \, 0.{\text{7X}}_{{1}} {\text{X}}_{{3}} {-}{ 1}.{\text{5X}}_{{2}} {\text{X}}_{{3}}$$
(10)

The analysis of the variance for the adjusted model found the model to be statistically significant (P-value < 0.01) (Table 2). Furthermore, the correlation coefficient (R2 = 0.95) was high, indicating that in the studied domain, 95% of the response variability was described by the second-order polynomial predicted equation Eq. (10). Therefore, it can be concluded that the Y-response is appropriately described by the polynomial model, and thus the obtained equation can be applied for the prediction of the Y-values in the studied domain.

Table 2 ANOVA result for CR removal (%) by electro-Fenton treatment
Full size table

The iso-response curves of CR degradation and the corresponding three-dimensional representations are presented in Fig. 5. The interpretation of these graphs indicated that increasing applied current intensity improved the degradation rate of CR. In fact, the greater removal rate of CR was attained when the current intensity was varied from 230 to 470 mA (Fig. 5a, b). This behavior may be related to the increase in Fe2+ regeneration and hydrogen peroxide production which would increase the formation of hydroxyl radical (Atmaca 2009). On the other hand, when the current intensity was greater than 470 mA, the degradation rate of CR diminished. This fact may explain by the 4e− reduction of O2 conducting to the production of H2O (Eq. (11)), which hinders the H2O2 generation (Eq. (12)) (Özcan et al. 2008). Moreover, the produced H2O2 competes with the hydrogen gas generated at the cathode Eq. (13) (Masomboon et al. 2010), reducing thereby the formation of hydroxyl radicals (Masomboon et al. 2010).

$${\text{O}}_{{2}} + {\text{ 4e}}^{ - } + {\text{ 4H}}^{ + } \to {\text{ 2H}}_{{2}} {\text{O}}$$
(11)
$${\text{O}}_{{2}} + {\text{ 2e}}^{ - } + {\text{ 2H}}^{ + } \to {\text{ H}}_{{2}} {\text{O}}_{{2}}$$
(12)
$${\text{2H}}_{{2}} {\text{O }} + {\text{ 2e}}^{ - } \to {\text{ H}}_{{2}} + {\text{ 2OH}}^{ - }$$
(13)
Fig. 5
figure 5

a Contour plots of CR removal versus the current intensity (mA) and the electrolysis time (min); b corresponding 3D surface plot; c contour plots of CR removal versus the electrolysis time (min) and the initial Fe2+ concentration (mM); d corresponding 3D surface plot; e contour plots of CR removal versus the initial Fe2+ concentration (mM) and the current intensity (mA); f corresponding 3D surface plot. Results obtained from the Doehlert matrix (Table 2). Experimental conditions: [CR]0 = 0.1 mM, [Na2SO4] = 50 mM, pH = 3, V = 0.3 L

Full size image

In addition, it can be seen that the CR removal was enhanced by the electrolysis time. Indeed, the removal rate augmented from 87 to 96% as the reaction time increased from 6 to 22 min, respectively. This result may be explained by the continuous formation of hydroxyl radicals during treatment. Consequently, the highest removal rate of CR would be achieved for an electrolysis time ranging from 21 to 37 min (Fig. 5c and d).

On the other hand, it can be observed that an increase of the initial Fe2+ concentration would increase the removal efficiency; the maximum CR removal rate was obtained when the Fe2+ concentration was ranging between 11.5 and 26 mM (Fig. 5e and f). This trend may be explained by the larger generation of hydroxyl radicals in the existence of more Fe2+ ions in the reaction medium (Panizza and Cerisola 2009). Nevertheless, adding a high concentration of ferrous ions ([Fe2+]0 > 26 mM) reduced the degradation rate, because of the consuming of ·OH by the surplus ferrous ions Eq. (6), reducing the amount of this radical and therefore hindering the degradation reaction (Panizza and Cerisola 2009; Brillas et al. 2009).

Electro-Fenton mineralization of Congo red

The degradation of CR was carried out in the optimal operating conditions deduced from the Doehlert matrix, namely I = 360 mA, t = 30 min and [Fe2+]0 = 19 mM, conducting to a total CR degradation. Contrarily, mineralization yield remained low, 47% for 60 min electrolysis times from an initial quantity of 38.4 mg L−1 O2 (Fig. 6). This finding may be interpreted by the formation of organic intermediate products. Indeed, the degradation of CR was followed by the appearance of diverse intermediates. This attitude is consistent with the rapid destruction of CR and TOC reduction, and may be associated to the degradation of intermediates by hydroxyl radicals (Hammami et al. 2008). Hence, 81.1% TOC removal was observed after 300 min of reaction time and demonstrated that the rate of mineralization raised with the reaction time.

Fig. 6
figure 6

Time evolution of TOC removal. Experimental conditions: [CR]0 = 0.1 mM, [Fe2+] = 19 mM, [Na2SO4] = 50 mM, pH = 3, I = 360 mA, t = 300 min, V = 0.3 L

Full size image

Identification of intermediates and pathway of Congo red degradation

The proposed degradation pathway for the electro-Fenton oxidation of CR is shown in Fig. 7. As can be seen, the cleavage of C–N bonds of the chromophore group of CR at the debut of reaction, was escorted by the production of sodium 4-amino-3-diazenylnaphthalene-1-sulfonate (C1) and biphenyl-4,4′-diol (C2), previously reported in photocatalysis of CR (Yashni et al. 2021). The compound C1 was converted to 3,4-diaminonaphthalene-1-sulfonate (C3) via hydroxylation reaction. The intermediate C3 was transformed into 4-amino-3-hydroxynaphthalene-1-sulfonate (C4) which was oxidized by hydroxyl radicals to produce 4-aminonaphthalene-1-sulfonate (C5). Furthermore, the hydroxylation of the compound C5 yielded the 4-aminonaphthalen-1-ol (C6) which was transformed to naphthalene-1,4-diol (C7), 2,3-dihydronaphthalene-1,4-dione (C8), then benzene-1,2-dicarboxylic acid (C9) during the ·OH oxidation. Moreover, the compound C2 was transformed to benzene-1,4-diol and phenol via hydroxylation reaction. These last intermediates have been reported by previous studies (Wang et al. 2021; Yashni et al. 2021).

Fig. 7
figure 7

Pathway proposed for the degradation of CR by the electro-Fenton process

Full size image

On the other hand, 3,4-diaminonaphthalene-1-sulfonate (C3) and biphenyl-4,4′-diamine (C10) were formed during the cleavage of N = N double bonds of CR at the beginning of degradation by the reaction of ·OH. The intermediate C10 may also be oxidized to biphenyl-4,4′-diol (C2). Lastly, all aromatic intermediates would be oxidized by hydroxyl radicals via ring cleavage reactions to form short-chain aliphatic carboxylic acids, such as 2-hydroxybutanedioic acid, propanedioic acid, acetic acid and oxaloacetic acid.

Conclusion

The degradation of Congo red dye by electrochemical advanced oxidation process has been investigated under various operating conditions: pH, initial Fe2+ concentration, current intensity, electrolysis time and initial electrolyte support concentration. Doehlert experimental design was applied for three factors namely current intensity, initial Fe2+ concentration and electrolysis time in order to establish the optimum experimental conditions. The results analysis indicates a total Congo red degradation and a high mineralization rate, 100 and 81.1% after 30- and 300-min reaction times, respectively, under 360 mA and 19 mM Fe2+. The removal of Congo red was escorted by the production of aromatic intermediates and short-chain carboxylic acids and therefore a degradation pathway was suggested. Moreover, the obtained quadratic polynomial model was considered suitable to be applied as prediction equation in the studied domain.