Introduction

Slope instability is one of the most common types of the geological hazards and has the potential to affect human lives and cause significant economic losses [1, 2]. South Gippsland, located in the Victoria state in south-east Australia, is a mountainous terrain with relatively high risk of slope instability [3]. To mitigate potential negative impacts and to reduce the ongoing costs due to slope failures, the local authority utilises a distinctive slope-stabilisation method in which an additional pile-retaining wall is placed at toe of the roadside slopes stabilised by the geogrid-reinforced retaining walls (GR-RW) with gabion basket wall facing [4]. In particular, due to technical and economic advantages, the GR-RW has widely been used since their first introduction in 1970s [5, 6]. With the growing demands in the construction of the GR-RW in recent years, it is necessary to understand the performance of the GR-RW related to the critical design parameters, such as the facing batter angle, the geogrid embedded length, and the vertical spacing between geogrid layers. For the facing batter angle of GR-RW, Viswanadham and Mahajan [7] conducted a series of parametric studies by centrifuge modelling to study effects of reinforcement type, vertical spacing, and the slope inclination on the behaviour of the geotextile-reinforced slopes. They found that with the increase in the facing inclination from \(2\mathrm{V}:1\mathrm{H}\) to \(5\mathrm{V}:1\mathrm{H}\), the magnitude of the maximum peak strain increases, and its location also moves downward from the mid-height of the slope. In addition, the failure surface was also observed to gradually shift away from the wall facing with the increase in the slope inclination. Hu et al. [8] also conducted centrifuge tests on the geotextile-reinforced slopes with various slope inclinations, reinforcement length, and the vertical spacing to study the effect of reinforcement on failure mechanism. They concluded that the slope inclination has a significant influence on the reinforcement length and, to achieve the same reinforcement effect, the steeper slopes may need a longer reinforcement length than the gentler slope. Song et al. [9] performed the centrifuge model tests on the geocell-reinforced retaining walls to study the effect of the dimensional variables on the deformation characteristics of the structure. Different reinforcement lengths and slope inclinations were selected and the corresponding failure mechanism of the slopes were also observed. They found that the slope inclination has significant influences on the slope failure surface, but critical failure surface would not be influenced further when the slope inclination is less than a threshold value. In the studies mentioned above the centrifuge tests were employed, which can address complex geotechnical problems and provide physical data for the understanding of the mechanisms of the displacement as well as the failure [10]. Although the centrifuge model test is a straightforward method for investigating the effect of the dimension variables on the performance of the GR-RW, it is costly and time-consuming compared with the numerical modelling method.

In the current study, the numerical method is utilised as it can provide more comprehensive results based on a wider range of parameter values, and it has also been widely used by many researchers to study the behaviour of GR-RW [11,12,13,14,15,16]. For other dimensional variables investigated in this study, the reinforcement length and the vertical spacing between geogrid layers, extensive numerical studies have been conducted. Liu [17] employed a two-dimensional finite element procedure to study the end of construction and long-term deformations of GR-RW under working stress state. In the numerical model, only granular filling was considered, and no surcharge load was applied on the backfill surface. The numerical results showed that the deformation of the reinforced soil zone was mainly governed by the vertical spacing and the stiffness of the reinforcement rather than the reinforcement length. In contrast, the reinforcement length to a large extent influenced the lateral displacement at the back of the reinforced soil zone. Similar to Liu [17], Kibria et al. [18] used the finite element method (FEM) for predicting the wall-facing movement of the mechanically stabilised earth (MSE) wall. The parametric studies about the reinforcement stiffness and the reinforcement length have been conducted. They found that the inadequate reinforcement length was one of the contributing factors that caused the excessive movement of the MSE wall. A substantial decrease in the horizontal displacement was also observed when the ratio of the reinforcement length to the wall height increased from \(0.5\) to \(0.7\). Regarding the effect of the vertical spacing between geogrid layers on the behaviour of the GR-RW, several numerical studies have been conducted. Liu et al. [19] used a calibrated finite element procedure to study the long-term response of a \(8\)-metre-high GR-RW with marginal backfill soils. A parametric study focussing on the effect of the reinforcement spacing on the behaviour of the GR-RW has been conducted. The numerical results showed that the vertical spacing was critical not only to the wall-facing displacement and the geogrid tensile forces, but to their development in a long-term period. Suksiripattanapong et al. [20] also conducted numerical analysis of the reinforced earth wall by changing the wall properties (wall height, reinforcement length, reinforcement spacing, and reinforcement axial stiffness) with the assistance of the FEM. The wall was modelled assuming plane strain conditions and the perfectly elastoplastic model with Mohr–Coulomb failure criterion was adopted to represent backfills. They found that the maximum lateral movement of the wall facing increases with the increase in the reinforcement spacing, and the location of the maximum displacement of the wall facing also moves towards to the top of the wall from the mid-height.

Except for the effect of the geometric variables on the behaviour of the GR-RW, the mechanical response of reinforced soil walls subjected to various loading conditions is also critical for the development of a more advanced design methodology [12]. Yoo and Kim [21] conducted a full-scale load test and finite element analysis on a GR-RW. First, the complete monitoring data of the GR-RW under a surcharge load at the working level was used for the calibration of the finite element model. Then, the numerical analysis was performed to investigate the wall response to the surcharge load well beyond the working level. The results showed that the test GR-RW has an excellent load carrying capacity and this capacity was largely governed by the bearing capacity failure of the backfill rather than the rapture of the reinforcements. Ambauen et al. [22] developed an accurate numerical model of a reinforced soil wall using finite element analysis to study the service-state behaviour of the wall supporting spread footings. The model was compared to a full-scale laboratory testing to validate its ability in predicting the wall behaviour under surcharge loading. After a series of parametric studies, the effect of each wall property on the behaviour of the reinforced soil wall subjected to spread footing was evaluated.

As the slope instability has become a major issue for the local government authority of South Gippsland, a distinctive slope-stabilisation system comprising the embedded piles at toe of gabion-faced geogrid-reinforced retaining walls (GF-GR-RW) has been widely adopted to reinforce the slope and the road embankment. While the effect of the geometric variables of the GR-RW and the effect of the surcharge loading on the behaviour of the GR-RW has been investigated in detail, no studies have been performed to investigate the response of the integrated method subjected to the same conditions. As one integrated system, the variation of wall and reinforcement properties not only affect the behaviour of the GF-GR-RW, but the response of the embedded pile, and the pile-retaining structure also influences the behaviour of the GF-GR-RW. This coupled effect within the integrated system has not been studied. In addition, when the integrated method reinforced slope subjected to the surcharge loading condition, the behaviour of each reinforcement and the slope may be changed significantly compared with the GF-GR-RW stabilised slope.

In this study, the effectiveness of the embedded pile in improving the stability of the slope reinforced by GF-GR-RW is firstly demonstrated through comparison of Factor of Safety (FoS), wall-facing horizontal displacement and the crest settlement, and the potential failure plane under various uniform surcharge loading conditions. A series of parametric studies related to the dimension variables of GF-GR-RW, including facing inclinations, the ratio of embedded length of geogrid to slope height, and vertical spacings between geogrid layers are then conducted to investigate their influences on the stability and behaviours of the integrated method stabilised slope and the behaviours of embedded piles. The numerical results indicate that embedded piles can improve the stability of the slope and restrict the wall-facing deflections effectively. In addition, the results from the parametric study indicate that each dimension variable affects the behaviour of the slope and the pile to different extents, therefore, the significance of the effect of each dimension variable has been evaluated, and the tendency of each effect has also been described. Moreover, after a comparison of the behaviour of two integrated method stabilised slopes using the maximum and minimum geogrid amount, the effect of the geogrid amount used on the behaviour of the slope and the pile is revealed.

Study Area

Background

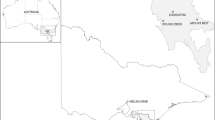
The phenomenon of the slope instability in South Gippsland area has existed for a long period (Fig. 1a). The woodland once covered \(90\%\) of the Gippsland area, but much of this has been cleared for the agriculture purpose [23]. In addition, the Gippsland area also has an undulating landscape, which makes the slope instability issue relatively worse. According to the review of the slope stability condition in the north of the South Gippsland region conducted by [24], the rainfall and the development of the weathering soil also impose negative impacts. To mitigate the negative influences of the slope instability, the gabion basket retaining wall and the GF-GR-RW will be used for the slope with relatively small scale and gentle gradient (Fig. 1b, c). Moreover, for the treatment of slope failures and the stabilisation of the roadside embankment, a distinctive integrated slope-stabilisation method that combines the embedded pile and the GF-GR-RW will be used (Fig. 1d). It is notable that a continuous wall is embedded in the concrete pile pressing against the bottom row of gabion wall facing to provide lateral support to the GF-GR-RW.

Fig. 1
figure 1

Study area details: (a) Location of South Gippsland, Victoria, Australia (Wang et al. [31]); (b) Gabion basket retaining wall; (c) GF-GR-RW; (d) Integrated method configuration

Full size image

Construction Process

Regarding the construction process of this integrated method, the installation of the embedded pile is prior to reinforced retaining walls (Fig. 2a). Each borehole is drilled by the tractor-mounted auger, the steel I-beam posts are then placed into each drilled borehole and temporarily supported when boreholes are backfilled by concrete. The length of steel I-beam posts is \(1\) metre longer than the concrete pile, and this additional length keeps protruding above the top of piles. This protruded steel I-beam post is then welded to a horizontal steel rail to form a bracing structure to the GF-GR-RW.

Fig. 2
figure 2

General construction process: (a) Pile installation is prior to the GF-GR-RW; (b) Compaction process to form the geogrid-reinforced soil zone

Full size image

Then, the GF-GR-RW is constructed adjacent to continuous steel rail wall that is embedded in the concrete piles. Each gabion basket, with a volume of \(1\) m3 is filled by rock, connected horizontally by the double-twisted wire mesh to form layers of the wall facing. The wall facing is composed of gabion basket layers that are stacked with a stepped form with the gradient within the range of inclination of typical reinforced soil walls. Moreover, each layer of the middle layer of gabion basket is wrapped by geogrid during the stacking process. The geogrid is also extended into soils, which is replaced and compacted during the stacking process to form the reinforced soil zone (Fig. 2b).

Slope Configurations and Parametric Study Design

To illustrate the effectiveness of the integrated method in increasing the slope stability, two slope configurations representing the site conditions are adopted. The first configuration is the GF-GR-RW stabilised slope (Fig. 3a). According to Fig. 3a, the foundation soil composed of the weathered bedrock is \(16\) m deep and \(60\) m wide. To minimise the boundary effect, the width of the foundation soil in front of the gabion basket wall facing is extended to \(27.8\) m and the width of the road embankment is also extended to \(30\) m. The road embankment height is \(13\) m, corresponding to \(13\) layers of the gabion basket. The geogrid is distributed horizontally as the reinforcement layers to form the reinforced soil zone.

Fig. 3
figure 3

The slope configurations analysed: (a) GF-GR-RW stabilised slope; (b) Integrated method stabilised slope (dimension in metres)

Full size image

For the second slope configuration, additional support from embedded piles has been provided to the first slope configuration (Fig. 3b). The length of concrete piles is \(12\) m and the embedded length in the weathered bedrock layer is \(6\) m. The ratio of the spacing (\(S\)) to the pile diameter (\(D\)) is \(3.5\) for the site condition (\(S=1.4\) m, \(D=0.4\) m). Then, a series of parametric studies are conducted on second slope configuration to study the effects of dimensional variables of the GF–GR–RW on the behaviour of the slope and the embedded pile. The major dimensional variables of the GF-GR-RW are slope inclination from the horizon (\(\alpha \)), the ratio of reinforcement length (\(L\)) to wall height (\(H\)), and vertical spacing (\({S}_{v}\)) between geogrid layers. A baseline case with the determined value of the dimensional variables has been selected based on the site condition, and one parameter will be deviated from the baseline case to investigate the influence of this specific factor.

The details of the investigated parameters are summarised in Table 1. It is worth noting that the uniform surcharge loading ranges from \(0 \mathrm{kPa}\) to \(80 \mathrm{kPa}\) in \(10 \mathrm{kPa}\) increments, which are applied to the backfill surface of each case so that the combined effect of the dimensional variables and the uniform surcharge loading can be investigated.

Table 1 Dimensional variables adopted in the parametric study
Full size table

Numerical Modelling

Strength Reduction Finite Element Method (SR-FEM)

The slope stability can be indicated by the value of the FoS obtained through FEM associated with strength reduction method. In SR-FEM analysis, the original effective friction angle (\({\varphi }^{{\prime}}\)) and the effective cohesion (\({c}^{{\prime}}\)) of the soil based on the Mohr–Coulomb failure criterion will be reduced progressively with the increase in the strength reduction factor (SRF) until the occurrence of the slope failure [25]. Then, SRF is the strength based FoS and can be given by:

$$FoS=\frac{{c}^{{\prime}}}{{c}_{red}}=\frac{\mathrm{tan}{\varphi }^{{\prime}}}{{\left(\mathrm{tan}{\varphi }^{{\prime}}\right)}_{red}}$$
(1)

where \({c}_{red}\) and \({\left(tan{\varphi }^{{\prime}}\right)}_{red}\) are the reduced soil shear strength.

Constitutive Models and Properties

The numerical models adopted in this chapter are developed and analysed by a geotechnical analysis software, OptumG2, which employs the Adaptive Finite Element Method (AFEM) [26]. The beam elements ‘Plate’ with the definition of strength and stiffness properties, which are used to model walls and various other thin elements, are adopted to simulate the behaviour of the continuous steel rail wall. The material type of the plate is elastoplastic with the plane strain assumption. For the embedded pile, the standard beam element (Pile Rows feature) is selected, and the parameter of \(S\) and \(D\) of the pile group can also be considered. The truss elements ‘Geogrids’ with stiffness and strength properties, which can be used to represent geogrids and other similar reinforcement types, are adopted to simulate the behaviour of the geogrid. These truss elements can yield under tensile forces with a rapture limit but cannot sustain the uniaxial compression non resist the bending. The gabion basket wall facing and the soil are presented by perfectly elastoplastic model with Mohr–Coulomb failure criterion. Under two-dimensional condition, the basic Mohr–Coulomb yield function can be expressed as:

$$F=\left|{\sigma }_{1}-{\sigma }_{3}\right|+\left({\sigma }_{1}+{\sigma }_{3}\right)\mathrm{sin}{\varphi }^{{\prime}}-2{c}{^{\prime}}\mathrm{cos}{\varphi }^{{\prime}}$$
(2)

where \({\sigma }_{1}\) and \({\sigma }_{3}\) are the major and minor principal stresses [26].

Based on main characteristics of the material and typical local area conditions described in the literature, Table 2 lists the strength properties of the solid material. The strength parameters of polyester (PET) geogrid (GGW) used in the study area are also summarised in Table 3. Based on the direct shear test and the compression test conducted by [27] on the block of the gabion basket, the effective friction angle and the effective cohesion of gabion baskets adopted in this study are \(45^\circ \) and \(560 kPa\), respectively.

Table 2 Properties of the solid materials adopted
Full size table
Table 3 Parameters of geogrid in the numerical modelling
Full size table

Boundary Conditions and Interaction Properties

In numerical models, the fixed boundary condition is applied to the bottom plane to restrain the displacements in all directions. The horizontal displacements of the left and right boundaries are also restrained by the vertical rollers.

The interaction properties can be categorised into three types: (a) the geogrid-soil interaction, (b) the geogrid-gabion basket interaction, and (c) the gabion basket-soil interaction. These interactions are modelled using the perfectly elastoplastic model with the Mohr–Coulomb failure criterion. With the increase in the relative displacement at the interface, the shear stress increases linearly at first and starts to yield at the maximum shear stress. The shear stress at the interface can be given by

$${\tau }_{max}={c}_{int}^{{\prime}}+{\sigma }_{n}^{{\prime}}\mathrm{tan}{\varphi }_{int}^{{\prime}}$$
(3)

where \({c}_{int}^{{\prime}}\) is the cohesion at the interface, \({\sigma }_{n}^{{\prime}}\) denotes the effective normal stress, \({\varphi }_{int}^{{\prime}}={\mathrm{tan}}^{-1}({c}_{rf} \mathrm{tan}{\varphi }^{{\prime}})\) represents the friction angle at the interface, and \({c}_{rf}\) is the reduction factor for the friction angle at the interface.

Table 4 lists three interaction properties adopted in this study. For the geogrid-related interfaces, the value of \(0.84\) for \({c}_{rf}\) has been adopted to calculate the friction angle at the interface [16]. The value of \({c}_{int}^{{\prime}}\) of geogrid-related interaction properties is assumed to be \(4 kPa\). For the interaction between the gabion basket and the soil, the friction angle at the interface, \({\varphi }_{int}^{{\prime}}\), is calculated based on the following equation [28]:

$${\varphi }_{int}^{{\prime}}={\mathrm{tan}}^{-1}(0.8\mathrm{tan}({\varphi }_{min}^{{\prime}}))$$
(4)

where \({\varphi }_{min}^{{\prime}}\) is the minimum friction angle of neighbouring materials. The value of \({c}_{int}^{{\prime}}\) for the interaction properties between the gabion basket and the soil is assumed to be \(4 kPa\).

Table 4 Interaction properties
Full size table

Model Validation

To ensure the validity of the numerical simulation conducted by AFEM, reinforced wall (Wall 1) studied by [12, 29, 30] has been selected. Huang et al. [13] conducted further numerical studies on this reinforced wall using three constitutive models including the Mohr–Coulomb model. The results reproduced from the current method will be compared with the tested and simulated results to guarantee the validity of the current method. The geometry of wall 1 has been shown in Fig. 4a. The wall was \(3.6\) m high and \(6\) m long, and the facing inclination was \(8^\circ \) from the vertical. The wall facing was built using concrete blocks with a height of \(150\) mm, a width of \(300\) mm, and a length of \(200\) mm. Wall 1 was reinforced with \(6\) layers of the polypropylene (PP) geogrid, with a length of \(2.22\) m and vertical spacing of \(0.6\) m. The facing block and foundation soil were simulated as elastic material, while the backfill was modelled as the elastic-perfectly plastic material with Mohr–Coulomb failure criterion. Table 5 summarises the properties of facing block, rigid foundation, and the backfill soil of Wall 1. The PP reinforcement was modelled using two-noded elastic–plastic cable elements without the consideration of the stress-rupture cutoff. The properties of the PP geogrid have been summarised in Table 6. For the interface between dissimilar materials, the linear spring-slider system with the shear strength defined by the Mohr–Coulomb yield criterion has been used, and the interface properties has been summarised in Table 7. The bottom-up process in the construction was considered in the simulation by adding the \(150\)-mm-layer sequentially. The dynamic compaction in the construction was also modelled by applying the transient uniform pressure which is \(8 \mathrm{kPa}\) to each soil lift. The typical instrumentation plan of Wall 1 has been illustrated in Fig. 4b. Approximately 300 instruments were deployed in the test wall including the strain gauges used for the geogrid, wire-line extensometers used for the measurements of reinforcement displacements, and the load rings which were used for the measurement of the connection loads. The automated data acquisition system was adopted to record the data from all instruments. A comparison of facing displacements of Wall 1 at the end of construction has then been conducted (Fig. 5a). According to Fig. 5a, the results from the current method are in good consistency with the measurements and predicted results from [13]. Another comparison of the postconstruction facing displacements under the uniform surcharge loading between the present method and the other numerical study has also been conducted (Fig. 5b). The deviation in the facing displacement is relatively small, demonstrating satisfactory agreement. Therefore, the validity of the numerical model in evaluating the stability of the slope under various loading conditions can be ensured.

Fig. 4
figure 4

The details of Wall 1 built at RMC: (a) The geometry (Hatami and Bathurst [29]); (b) Typical instrumentation plan (Bathurst et al. [30])

Full size image
Table 5 Materials properties (Data from Huang et al. [13])
Full size table
Table 6 Reinforcement properties
Full size table
Table 7 Interface properties (Data from Hatami and Bathurst [12])
Full size table
Fig. 5
figure 5

Comparison of facing displacements located at the reinforcement elevations: (a) At the end of construction; (b) Under various values of the uniform surcharge load

Full size image

Analysis of Results

Effect of Embedded Pile

To demonstrate the effect of the integrated method, the FoS of two slope configurations has been obtained by the SR-FEM, and horizontal displacements as well as the vertical crest settlement of wall facing under various values of the uniform surcharge load have been obtained through elastoplastic analysis. For clarity, the baseline case has been adopted in this section without the consideration of the effect of dimension variables.

(1) Slope stability. The FoS of two slope configurations under uniform surcharge loads are compared and depicted in Fig. 6. According to Fig. 6, when the slope is only subjected to the gravity, the FoS of the GF-GR-RW and the integrated stabilised slope are \(1.33\) and \(1.90\), respectively. The contribution from embedded piles to the stability of the slope is estimated at \(42.9\%\). As the uniform surcharge load on the backfill surface increases to \(80 \mathrm{kPa}\), the FoS of the GF-GR-RW and the integrated stabilised slope gradually decreases to \(1.11\) and \(1.51\), respectively. Under the maximum uniform surcharge load adopted in this study, the embedded pile can still improve the slope stability about \(36\%\), demonstrating the effectiveness of the integrated method.

Fig. 6
figure 6

Comparison of the Factor of Safety (FoS) between two slope configurations under uniform surcharge load

Full size image

(2) Wall-facing Deflection. Figure 7a shows the profile of horizontal displacements along the wall elevation of two slope configurations under uniform surcharge loads. The horizontal displacement of two slopes increases with the increase in the uniform surcharge load. The horizontal displacement also increases along the wall elevation and reaches the maximum at approximately the top of fourth gabion basket layer. The horizontal displacement then gradually decreases towards to the top. Comparing the horizontal displacements of two slope configurations under the same uniform surcharge load shows that the effect of the embedded pile on restricting the horizontal displacement is significant and becomes even more obvious with the increase in the uniform surcharge load. When the surcharge load reaches \(80 \mathrm{kPa}\), the reduction in the maximum horizontal displacement achieved by the embedded pile can reach \(39.7\%\).

Fig. 7
figure 7

Comparison of wall-facing deflection between two slope configurations: (a) Horizontal wall-facing displacement; (b) Vertical crest settlement

Full size image

The comparison of the vertical crest settlement between two slope configurations under different uniform surcharge loads is presented in Fig. 7b. According to Fig. 7b, the vertical settlement of two slope configurations increases with the increase in the surcharge load. For the GF-GR-RW stabilised slope, the vertical settlement increases from \(1.4\) mm to \(46.5\) mm with the increase in the surcharge load. The vertical settlement of the integrated stabilised slope increases from \(0.2\) to \(35.9\) mm. With the increase in the uniform surcharge load, the effect of the pile in reducing the vertical settlement also becomes more obvious. When the uniform surcharge load increases \(80 \mathrm{kPa}\), the reduction in the vertical settlement achieved by the embedded pile approximately reaches \(22.8\%\).

(3) Critical slip surface: The critical slip surface of the GF-GR-RW stabilised slope is basically the same under various uniform surcharge loading conditions, therefore, the critical slip surface under the highest uniform surcharge load (\(80 \mathrm{kPa}\)) is selected and depicted in Fig. 8a. According to Fig. 8a, the critical slip surface goes through the left end of the bottom geogrid layer and is out of the geogrid-reinforced soil zone, which indicates the failure mechanism of this slope configuration is an external failure mode. The critical slip plane only exists in the soil layer and not contact the lower rock layer. For the integrated stabilised slope, the potential failure plane under the \(80\mathrm{ kPa}\) uniform surcharge load is selected and shown in Fig. 8b as the value of the uniform surcharge load imposes minor impact on the critical slip surface of this slope configuration. It is notable that the pattern of the failure mechanisms is kept the same but the width and the depth of the shear band within the soil layer increases significantly. In addition, the strength of the soil around the pile has also been mobilised effectively. In general, the laterally loaded piles that placed at the toe of the road embankment can provide the lateral resisting force to the structure as well as mobilise more soil shear strength to contributes to the slope stability.

Fig. 8
figure 8

Critical slip surface of the baseline slope configurations: (a) GF-GR-RW stabilised slope; (b) Integrated method stabilised slope

Full size image

Effect of Wall-facing Inclination

In this section the effect of wall-facing inclinations on the behaviour of the slope and the pile under different uniform surcharge loads is investigated. Four facing inclinations (α) are considered, including vertical (\(90^\circ \)), \(1H:10V\)* (\(84.3^\circ \)), \(1H:5V\) (\(78.7^\circ \)), \(2H:5V\) (\(68.2^\circ \)). The baseline case has an α of \(1H:10V\)* (\(84.3^\circ \)). To study the effect of the facing inclination, other dimensional variables are kept the same with the baseline case.

(1) Slope stability. The FoS of the integrated method stabilised slope with four facing inclinations under different uniform surcharge loads is shown in Fig. 9. The FoS of four cases are approximately \(1.90\) when subjected to the gravity only. With the increase in the surcharge load to \(80 \mathrm{kPa}\), the FoS of four slopes decreases to \(\sim 1.50\), following a similar trend. The decrease in the FoS is around \(20\%\) for four cases. It is notable that with the decrease in the facing inclination (from vertical to \(2H:5V\)), the FoS of the slope increases. The slope with \(2H:5V\) facing inclination yields the highest FoS under each uniform surcharge load. Moreover, the increase in the FoS when facing inclination decreases from vertical to \(1H:10V\) is more obvious than the further increase in the FoS induced by continuous decrease in the facing inclination. This result indicates that the decrease in the facing inclination can improve the slope stability to a certain extent, but this effect decreases with further decreases in the facing inclination.

Fig. 9
figure 9

Comparison of Factor of Safety (FoS) of integrated method stabilised slope with different facing inclinations under uniform surcharge load

Full size image

(2) Wall-facing deflection. The horizontal wall-facing displacement of the integrated stabilised slope with different facing inclinations, under \(40 \mathrm{kPa}\) and \(80 \mathrm{kPa}\) uniform surcharge loads, is illustrated in Fig. 10a. The maximum horizontal displacement still yields at the top of the fourth gabion basket layer. Under \(40 \mathrm{kPa}\) surcharge load, it is notable that the decrease in the inclination induces the decrease in the horizontal displacement. The horizontal displacement under \(80 \mathrm{kPa}\) surcharge load also shows a similar tendency with the decrease in the inclination. In addition, under both \(40\mathrm{ kPa}\) and \(80 \mathrm{kPa}\) uniform surcharge loads, the reduction in the horizontal displacement induced by the decrease in the inclination also decreases. This phenomenon indicates that the effect of facing inclination decrease on the reduction in the horizontal displacement also decreases, the comparison of the FoS of the slope with various facing inclination also shows a similar trend. The reduction in maximum horizontal displacement when facing inclination decreases from vertical to \(2H:5V\) reaches \(19.5\%\) and \(26.9\%\) under \(40 \mathrm{kPa}\) and \(80 \mathrm{kPa}\) surcharge load, respectively.

Fig. 10
figure 10

Comparison of facing deflections of integrated method stabilised slope with different facing inclinations: (a) Horizontal wall-facing displacements; (b) Vertical crest settlement

Full size image

The vertical crest settlement of the reinforced slope with different facing inclinations under the uniform surcharge load is shown in Fig. 10b. The vertical settlements of four cases show an increasing trend with the increase in the uniform surcharge load. Similarly, with the distribution of the horizontal displacement, the vertical settlement decreases with the decrease in the facing inclination, and the slope with the lowest inclination (\(2H:5V\)) yields the lowest settlement under each load. As indicated in the horizontal displacement, the impact from the decrease in the inclination on the reduction of crest settlement becomes less significant. Quantitatively, when the inclination sequentially decreases from vertical to \(2H:5V\) under \(80 \mathrm{kPa}\) surcharge load, the reduction in the vertical settlement is \(8.6\) mm, \(3.7\) mm, and \(0.7\) mm, respectively. The overall reduction in the vertical settlement achieved by the decrease in the inclination is \(29.2\%\).

(3) Pile behaviour. As an integrated method, the impact of wall-facing inclinations on the pile bending moment is analysed in Fig. 11. Under \(40 \mathrm{kPa}\) uniform surcharge load, the pile shows different behaviours subjected to various facing inclinations, as demonstrated in Fig. 11.a. With the decrease in the inclination, the bending moment of the embedded part of the pile increases, while the upper half of the pile shows a reverse trend. When the inclination decreases from vertical to \(1H:10V\), the increase in the bending moment of the embedded pile part is \(204.2 \mathrm{kNm}\), while the decrease in the bending moment of the upper half pile is \(384.2 \mathrm{kNm}\). When the inclination decreases to \(2H:5V\), the changes in the bending moment of the lower half pile and the upper half pile is relatively small, which are \(46.5 \mathrm{kNm}\) and \(99.3\mathrm{ kNm}\), respectively.

Fig. 11
figure 11

Comparison of pile bending moment of integrated method stabilised slope with various facing inclinations: (a) Under \(40\mathrm{ kPa}\) surcharge load; (b) Under \(80 \mathrm{kPa}\) surcharge load

Full size image

The pile bending moment subjected to different slope gradients under \(80 kPa\) surcharge load shows a similar distribution (Fig. 11b). The changes in the bending moment induced by the decrease in the gradient from vertical to \(1H:10V\) is still more obvious than further decreases in the slope gradient. In addition, the pile bending moment for other three slope inclinations are basically the same with minor changes in the upper half pile. The effect of reducing the slope inclination on increasing the stability of the slope can be illustrated from the pile behaviour as more bearing capacity of the embedded part of piles will be mobilised. In addition, similar with the trend of FoS and wall-facing deflections, the decreasing trend in the effect of decreasing facing inclination can also be demonstrated from the changes in the bending moment of the pile which placed in the slope with different facing inclinations.

Effect of \(\mathrm{L}/\mathrm{H}\) Ratio

Four \(L/H\) ratios of GF-GR-RW, including \(0.8\), \(0.9\), \(1.0\), and \(1.1\), are adopted here to investigate the impact of the embedded geogrid length on the behaviour of slopes and piles. In the baseline model, the \(L/H\) ratio adopted is \(0.9\). The other dimension variables are kept the same with the baseline case for comparison purposes.

(1) Slope stability. The FoS of slopes with four \(L/H\) ratios under uniform surcharge loads are compared with each other, as shown in Fig. 12. When the slope is subjected to the gravity only, the FoS increases from \(1.86\) to \(2.0\) with the increase in the \(L/H\) ratio from \(0.8\) to \(1.1\). With the increase in the surcharge load, the FoS of four cases show a decreasing trend with a similar extent. Under \(80 \mathrm{kPa}\) surcharge load, the FoS of the slope ranges from \(1.48\) to \(1.58\) corresponding to the \(L/H\) ratio range. It is notable that the increase in the embedded geogrid length improves the slope stability. For GF-GR-RW reinforced slopes, there is a threshold embedded length of geogrid beyond which the slope stability will not be improved further. For the integrated method, the continuous increase in the embedded geogrid length can still serve its full function.

Fig. 12
figure 12

Comparison of Factor of Safety (FoS) of integrated method stabilised slope with various \(L/H\) ratios under uniform surcharge load

Full size image

(2) Wall-facing deflection. The horizontal wall-facing displacements of slopes with four \(L/H\) ratios are shown in Fig. 13a. Under \(40 \mathrm{kPa}\) uniform surcharge load, the maximum horizontal displacement reduces from \(12.5\) to \(7.0\) mm with the increase in the embedded geogrid length from \(0.8\) to \(1.1\) times the slope height. The reduction in the maximum horizontal displacement reaches \(44\%\). The maximum horizontal displacement decreases from \(34.4\) to \(20.9\) mm with the increase in the \(L/H\) ratio under \(80\mathrm{ kPa}\) uniform surcharge load. This reduction is about \(39.2\%\). It is notable that the effect of increasing the embedded length of geogrid on reducing horizontal displacements is significant. Similar to the distribution of the horizontal displacement with different facing inclinations, the effect of increasing the \(L/H\) ratio on restricting horizontal displacements becomes less when the embedded length of geogrid is relatively large. This distribution is different from the distribution of the FoS under the same condition.

Fig. 13
figure 13

Comparison of facing deflections of integrated method stabilised slope with various \(L/H\) ratios: (a) Horizontal wall-facing displacements; (b) Vertical crest settlement

Full size image

The vertical crest settlement of slopes with various embedded geogrid length are depicted in Fig. 13b. When the slope is only subjected to the gravity, the vertical settlement of four \(L/H\) ratios are approximately \(0.2\) mm. With the increase in the uniform surcharge load, the difference in the effect of the length of geogrid on restricting the vertical settlement appears. Under \(80 \mathrm{kPa}\) uniform surcharge load, the vertical settlement decreases from \(39.7\) to \(33\) mm with the increase in the \(L/H\) ratio from \(0.8\) to \(1.1\). The reduction in the vertical settlement reaches \(16.9\%\). The effect of the embedded length of geogrid on reducing vertical settlements also show a decreasing trend with the increase in the \(L/H\) ratio, which is similar to the distribution of horizontal displacements.

(3) Pile behaviour. The variation in the \(L/H\) ratio also imposes impacts on the pile bending moment (Fig. 14). Under \(40 \mathrm{kPa}\) uniform surcharge load as shown in Fig. 14a, the bending moment of the embedded part of the pile decreases with the increase in the embedded length of geogrid, and the bending moment of the upper half of the pile is basically the same. The value of the maximum bending moment of the lower half pile decreases from \(410.4\) to \(130.0 \mathrm{kNm}\) with the increase in the \(L/H\) ratio.

Fig. 14
figure 14

Comparison of pile bending moment of integrated method stabilised slope with different \(L/H\) ratios: (a) Under \(40 kPa\) surcharge load; (b) Under \(80 \mathrm{kPa}\) surcharge load

Full size image

Under \(80 \mathrm{kPa}\) uniform surcharge load, the distribution of the pile bending moment is similar to the \(40 \mathrm{kPa}\) uniform surcharge load (Fig. 14b). With the increase in the \(L/H\) ratio from \(0.8\) to \(1.1\), the maximum bending moment of the lower half pile decreases from \(704.4\) to \(271.5\mathrm{ kNm}\). The phenomenon that the maximum bending moment of the embedded part of the pile decreases with the increase in the embedded length of geogrid indicates that additional geogrid length can reduce the soil sliding force imposes on the pile, and the slope stability can be improved. Moreover, the changes in the pile bending moment decreases with the increase in the \(L/H\) ratio, this phenomenon is similar to the distribution of wall-facing deflections.

Effect of Spacing of Geogrid Layers

In this section, the effect of the vertical spacing between geogrid layers on the behaviour of the slope and the pile has been evaluated under the uniform surcharge load condition. Two values of \({S}_{v}\), \(1\) m and \(2\) m, have been adopted. The \({S}_{v}\) adopted in the baseline case is \(1\) m. The other dimension variables are kept the same in the analysis for comparison purposes.

(1) Slope stability. The FoS of slopes with two values of \({S}_{v}\) under uniform surcharge loads have been compared (Fig. 15). For the slope with the \({S}_{v}\) of \(1\) m, the FoS of the slope decreases from \(1.90\) to \(1.51\) with the increase in uniform surcharge load from \(0\) to \(80\mathrm{ kPa}\). The decrease in the FoS is around \(20.5\%\). When the \({S}_{v}\) of geogrid layers increases to \(2\) m, the FoS slightly decreases under each uniform surcharge load. The decrease in the FoS of the slope caused by the increase in the \({S}_{v}\) from \(1\) m to \(2\) m is around \(0.02\) for all loading conditions. This phenomenon indicates that the effect of spacing on the slope stability is less than embedded geogrid length.

Fig. 15
figure 15

Comparison of Factor of Safety (FoS) of integrated method stabilised slope with various spacings of geogrid layers under uniform surcharge load

Full size image

(2) Wall-facing deflection. For the horizontal displacement of the slope with two values of \({S}_{v}\), the distribution shows different tendencies under \(40 kPa\) and \(80 kPa\) uniform surcharge loads (Fig. 16a). Under \(40 kPa\) uniform surcharge load, the maximum horizontal displacement decreases from \(11.2\) to \(10.1\) mm when \({S}_{v}\) changes from \(2\) to \(1\) m. The reduction is around \(9.8\%\). The maximum horizontal displacement decreases from \(37\) to \(28.7\) mm with the change of \({S}_{v}\) from \(2\) to \(1\) m under \(80\mathrm{ kPa}\) uniform surcharge load. The decrease in the horizontal displacement reaches \(22.4\%\). It is notable that the effect of decreasing \({S}_{v}\) from \(2\) to \(1\) m on restricting horizontal displacements is more significant under a large uniform surcharge load (\(80\mathrm{ kPa}\)) than the small uniform surcharge load (\(40\mathrm{ kPa}\)). Although the value of \({S}_{v}\) of \(2\) m can yield reasonable FoS of the slope under each load, the smaller \({S}_{v}\) may be more appropriate for the project that has a strict requirement on horizontal displacements.

Fig. 16
figure 16

Comparison of facing deflections of integrated method stabilised slope with different spacings of geogrid layers: (a) Horizontal wall-facing displacements; (b) Vertical crest settlement

Full size image

The distribution of the vertical crest settlement shows a similar pattern to the horizontal displacement (Fig. 16b). The vertical settlement of two values of \({S}_{v}\) is basically the same, i.e., ~\(0.4\) mm when the slope is only under the gravity. With the increase in the uniform surcharge load, the effect of adopting a smaller \({S}_{v}\) on restricting the vertical settlement increases. The vertical crest settlement decreases from \(40.9\) to \(35.9\) mm with the decrease in the value of \({S}_{v}\) from \(2\) to \(1\) m under \(80 \mathrm{kPa}\) uniform surcharge load. This reduction in the vertical settlement is estimated at \(12.2\%\). The effect of the small \({S}_{v}\) value on restricting the vertical settlement increases with the increase in the uniform surcharge load, which is similar to the effect on the horizontal displacement.

(3) Pile behaviour. Figure 17 shows the pile bending moment of two \({S}_{v}\) values under \(40\mathrm{ kPa}\) and \(80 \mathrm{kPa}\) uniform surcharge loads. Under \(40\mathrm{ kPa}\) surcharge load, the pile bending moment is basically the same for two \({S}_{v}\) values (Fig. 17a). It is notable that the value of the maximum bending moment of the lower half pile decreases slightly from \(306\mathrm{ kNm}\) to \(270.6\mathrm{ kNm}\) when \({S}_{v}\) switches from \(2\) to \(1\) m, and the bending moment of the upper half pile shows a similar distribution.

Fig. 17
figure 17

Comparison of pile bending moment of integrated method stabilised slope with various spacings of geogrid layers: (a) Under \(40 \mathrm{kPa}\) surcharge load; (b) Under \(80 \mathrm{kPa}\) surcharge load

Full size image

With the increase in the uniform surcharge load to \(80\mathrm{ kPa}\), the difference in the pile bending moment induced by two \({S}_{v}\) values is insignificant (Fig. 17b). For the lower half pile, the value of the maximum bending moment decreases from \(543.2\) to \(502.5 \mathrm{kNm}\) with the decrease in \({S}_{v}\). The maximum bending moment of the upper half pile increases from \(164.5 \)to \(189.7 \mathrm{kNm}\) with the decrease of \({S}_{v}\) from \(2\) to \(1\) m. It is worth noting that the bearing capacity of the pile is mobilised to a similar extent for two values of \({S}_{v}\) under different loading conditions, therefore, the effect of the geogrid layer spacing on the pile behaviour is insignificant.

Discussion

The effectiveness of the integrated slope-stabilisation method on improving the stability of the slope and restricting wall-facing deflections has been demonstrated through the additional contribution from embedded piles. The effect of dimension variables of GF-GR-RW, including facing inclinations, the \(L/H\) ratio of geogrid layers, and the \({S}_{v}\) between geogrid layers, on the behaviour of the slope and the pile has been illustrated through a series of parametric studies. In this section, the comparison of slope and pile behaviour between the integrated method reinforced slopes that utilised the maximum (\(1H: 10V; L/H=1.1; {S}_{v}=1\) m) and minimum (\(1H: 10V; L/H=0.8; {S}_{v}=2\) m) amount of geogrid adopted in this study will be conducted.

The comparison of the FoS of the slope between the maximum and the minimum condition of the geogrid amount has been conducted (Fig. 18). According to Fig. 18, the FoS of slope with the maximum geogrid amount used is higher than the minimum condition. With the increase in the surcharge load from \(0\) to \(80 \mathrm{kPa}\), the FoS of the slope configuration that utilises the maximum geogrid amount decreases from \(2.0\) to \(1.58\), and the FoS of the slope with minimum geogrid amount decreases from \(1.84\) to \(1.46\). The difference in the FoS between two slope configurations under each load is approximately the same, i.e., ~ \(0.14\). When the geogrid amount used changes from maximum to minimum condition, the reduction in the geogrid amount is \(63.6\%\). Compared with the reduction in the geogrid, the decrease in the FoS is acceptable.

Fig. 18
figure 18

Comparison of FoS of two slope configurations used maximum and minimum geogrid amount

Full size image

The geogrid amount used influences wall-facing deflections to a larger extent, as depicted in Fig. 19. Regarding horizontal displacements, when the geogrid amount used changes from the maximum to minimum condition, the maximum horizontal displacement increases from \(7\) to \(14.5\) mm under \(40 \mathrm{kPa}\) uniform surcharge load. With the increase of the surcharge load to \(80 \mathrm{kPa}\), the maximum horizontal displacement increases from \(20.9\) to \(46.7\) mm (Fig. 19a). The vertical crest settlement increases from \(31.4\) to \(46\) mm when the geogrid amount used changes from maximum to minimum condition under \(80\mathrm{ kPa}\) uniform surcharge load (Fig. 19b). The maximum horizontal displacement is doubled for two loading conditions when the geogrid amount used decreases from the maximum to the minimum condition, and the vertical settlement also increases more than half under \(80 \mathrm{kPa}\) uniform surcharge load. This result indicates that the reduction in the amount of geogrid used imposes more significant impact on wall-facing deflections than slope stability.

Fig. 19
figure 19

Comparison of wall-facing deflections of two slope configurations used maximum and minimum geogrid amount: (a) Horizontal wall-facing displacements; (b) Vertical crest settlement

Full size image

For pile bending moment, the influence of the reduction in the geogrid amount used is also significant (Fig. 20). Under \(40 \mathrm{kPa}\) surcharge load, the maximum bending moment of the upper half pile is basically the same for two conditions, whereas the value of the maximum bending moment of the lower half pile increases significantly from \(130\) to \(430.1 \mathrm{kNm}\) with the decrease in the geogrid amount (Fig. 20a). Under \(80 \mathrm{kPa}\) surcharge load, the pile bending moment of two geogrid usage conditions show a similar distribution to \(40 \mathrm{kPa}\) loading condition (Fig. 20b). The maximum bending moment of the lower half pile also increases rapidly from \(271.5\) to \(758.5 \mathrm{kNm}\). It is notable that with the decrease in the geogrid amount used, the maximum bending moment of the lower half pile increases approximately three times for two loading conditions.

Fig. 20
figure 20

Comparison of pile bending moment of two slope configurations used maximum and minimum geogrid amount: (a) Under \(40 \mathrm{kPa}\) surcharge load; (b) Under \(80\mathrm{ kPa}\) surcharge load

Full size image

In general, the reduction in the geogrid amount imposes minor negative impacts on the stability of the slope; however, for the wall-facing deflections and the pile bending moment, the decrease in the geogrid usage would impose significant influences.

Conclusions

To treat existing slope failures and prevent further landslides, an integrated slope-stabilisation method has been widely used by the local government authority of South Gippsland in Victoria state located in south-east Australia. This integrated method combines two well-developed slope-stabilisation methods, the gabion-faced geogrid-reinforced retaining wall and the pile-retaining structure, respectively. In this study, the effectiveness of the integrated method on improving the slope stability and restricting wall-facing deflections has been demonstrated. The effect of dimension variables of the gabion-faced geogrid-reinforced retaining wall on the behaviour of the slope and the pile has been studied. The following conclusions are deduced from the analysis of the results:

  1. 1.

    The embedded piles can improve the stability of the gabion-faced geogrid-reinforced retaining wall reinforced slope around \(42.9\%\) under the gravity effect. With the increase in the uniform surcharge load to \(80 kPa\), the additional contribution from embedded pile can still improve the slope stability around \(36\%\). The effect of the embedded pile on restricting wall-facing deflections is incremental with the increase in the surcharge load. The reduction in the horizontal displacement and the vertical settlement induced by the embedded pile can reach \(39.7\%\) and \(22.8\%\) under \(80 \mathrm{kPa}\) surcharge load, respectively.

  2. 2.

    The wall-facing inclinations also influence the behaviour of the slope and the pile to a certain extent. The effect of decreasing the facing inclination on the improvement of slope stability is decremental. Compared with the effect on the slope stability, this effect influences horizontal displacements and the vertical settlement more significantly. Under \(80 \mathrm{kPa}\) surcharge load, the reduction in horizontal displacements and the vertical settlement induced by the decrease in the inclination from vertical to \(2H:5V\) can reach \(26.9\%\) and \(29.2\%\). The effect of facing inclinations on pile bending moment is also decremental, and the major changes in the pile bending moment is induced by the decrease in the facing inclination from vertical to \(1H:10V\).

  3. 3.

    With the increase of \(L/H\) ratio from \(0.8\) to \(1.1\), the FoS of the slope increase from \(1.86\) to \(2.0\) under the gravity, from \(1.48\) to \(1.58\) under \(80 \mathrm{kPa}\) uniform surcharge load. Under \(80 \mathrm{kPa}\) uniform surcharge load, the reduction in horizontal displacements and the vertical settlement achieved by the increase in \(L/H\) ratio is around \(39.2\%\) and \(16.9\%\), respectively. The maximum bending moment of the lower half pile also decreases with the increase in \(L/H\) ratio, which indicates that the increase in the embedded geogrid length can relief the sliding forces impose on the pile-retaining wall.

4. The increase in \({S}_{v}\) imposes minor negative impact on the slope stability. With the change of \({S}_{v}\) from \(2\) to m, the decrease in horizontal displacements and the vertical settlement is estimated at \(22.4\%\) and \(12.2\%\), respectively. The integrated stabilised slope with large value of \({S}_{v}\) still shows reasonable performance based on the numerical results.

As the parametric studies of the major design factors are based on a specific slope configuration from one slope site in the study area, the analysis of the results can be used as the design reference when other slope sites stabilised by the same integrated method. Decreasing the slope inclination can improve the slope stability but this effect decreases with further decreases in the inclination, however, the increase in the embedded geogrid length can improve the slope stability and decrease the maximum bending moment of pile continuously. Compared with the effect of embedded geogrid length, increasing the spacing of the geogrid within the integrated method imposes relatively less impacts on the slope stability but the horizontal wall-facing displacements increases relatively large. Therefore, when the integrated method is applied to different slope sites, the numerical results of this study can provide a rapid and simple estimation of aforementioned factors for engineers to be considered for a safe and economic design. In addition, an initial trial for the major design parameters can also be obtained for engineers to conduct further analyses.