Introduction

The mechanically stabilized earth wall is one of the major developments in retaining structures. Application of geosynthetic reinforced soil retaining walls in major public infrastructure works are increasing tremendously due to rapid urbanization and demand for effective land utilization. The reinforced soil retaining structures have three components: backfill, reinforcement and facing system. Reinforcing materials may be of relatively inextensible metal strips or extensible polymer products like geotextiles and geogrids. Wall facing may include: wrap facing, full rigid facing, segmental block facing and modular block facing [1]. The effective performance of reinforced soil retaining walls over the conventional retaining walls during recent earthquakes are reported by many researchers [2–4]. But some researchers [5–7] are also reported failures of reinforced soil structures. The dynamic studies of reinforced soil walls can be classified into three categories: analytical studies, experimental studies and numerical studies. The analytical studies were conducted by different researchers [8–14] to know about the behavior of the reinforced soil retaining walls and to establish some design curves. The dynamic behavior of reinforced soil retaining walls and slopes was studied by various physical models tests [15–23]. The numerical simulations are useful techniques to study the behavior of reinforced retaining wall structures. A properly calibrated numerical model helps to provide insight into the problem. The seismic response of reinforced soil walls in terms of wall deformation, reinforcement load, acceleration amplification were studied by many researchers [24–32]. The response of wall subjected to earthquake after 10 years and influence of creep rate of soil and reinforcements were also studied [33, 34]. Bhattacharjee and Krishna [35, 36] studied the strain behavior of backfill soil and its influence on formation of deformation zones of wrap faced reinforced soil walls. Most of the model studies are focused on analyzing the response in terms of wall displacements, lateral pressure, acceleration amplification and reinforcement load/strain against variations in different reinforcement parameters like stiffness, spacing, length etc. and seismic excitation parameters. Very few studies are available on the strain behavior of the backfill soil and corresponding reinforcement strains and deformation zones formed at backfill of reinforced soil wall.

In the present study, a full height concrete faced reinforced soil retaining wall which is termed as rigid faced reinforced soil retaining wall is considered. A numerical model of full height rigid faced reinforced soil retaining wall is developed using three dimensional explicit finite difference program FLAC3D and validated with laboratory test results available in literature. The behavior of wall in terms of octahedral shear strain in soil, horizontal displacements and vertical settlements of calibrated models are discussed. The behavior of full scale reinforced soil wall with reference to the zone of maximum octahedral shear strain is observed. The influence of zone of maximum octahedral shear strain on length of reinforcement, number of layer of reinforcement, reinforcement stiffness, backfill friction angle and facing stiffness are being studied.

Development of Numerical Model

Target Physical Model

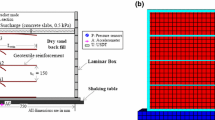
Laboratory scale shaking table tests on full height rigid faced reinforced soil retaining walls described by Krishna and Latha [21] were considered as reference case for model generation. The shaking table tests were conducted on rigid faced reinforced wall model size of 700 mm × 500 mm in plan area and 600 mm deep, constructed in a flexible laminar container. The facing was built from 12 hollow rectangular steel box sections and were bolted together with a vertical steel rod, which was fixed with the bottom plywood to represent the 600 mm high rigid wall with a fixed bottom condition. The backfill soil was filled in equal lifts of sand filling by pluviation method and with a layer of reinforcing material laid after each lift. The reinforcement materials were run through the bolts of the facing system to obtain a rigid connection between the wall and reinforcement. The four layers of geotextile reinforcement of length (L rein ) 420 mm (i.e., 0.7 times the height) were used in the model. The backfill material used in the model tests was poorly graded sand having dry unit weight of 16.2 kN/m3 corresponding to about 65 % relative density. The specific gravity of sand was 2.65 and friction angle of 43°. Four different reinforcement materials were used by Krishna and Latha [21]. The low strength geotextile was considered for the present study which is having ultimate tensile strength of 0.104 kN/m and secant modulus of 5.2 kN/m at 2 % strain. The mass per unit area of the reinforcement material was reported as 110 g/m2. A nominal surcharge of 0.5 kPa was applied after completion of all lifts. After removing the temporary supports, model wall was subjected to 20 cycles of sinusoidal motion at different frequencies. The results obtained through various instrumentations were discussed in terms of facing horizontal deformations, acceleration amplification values. The details of the test configuration and location of various instrumentations are shown in Fig. 1. An unreinforced wall was also considered to compare the results with that of reinforced wall. The unreinforced wall configuration is similar to that of rigid-faced wall but without reinforcement.

Fig. 1
figure 1

Physical model configuration of rigid faced reinforced soil retaining wall [21]

Full size image

Numerical Model

The finite difference program FLAC3D is used for development of numerical model. FLAC3D is an explicit finite difference program for engineering mechanics problems [37]. Built in constitutive models are available in FLAC3D which can be modified by using FISH programming language. The structural elements are available in FLAC3D to simulate the reinforcement used in physical models. Physical model construction and testing sequence, implemented in experimental procedure, are followed in development of numerical model. The shaking table is first generated as rigid foundation. The rigid wall is simulated and fixed at the bottom against lateral sliding. The backfill soil is built up in layers of equal thickness in the same sequence as physical model and reinforcements are placed on each layer. Various interfaces are also considered for proper interaction between dissimilar elements.

Material Properties

The model material properties used in the simulation are briefly discussed in the following.

Wall

The rigid wall facing is modeled as elastic material. The properties required for the elastic material model are mass density, shear modulus and bulk modulus.

Backfill Material

The backfill soil is modeled as elasto-plastic Mohr–Coulomb material coded with hyperbolic soil modulus proposed by Duncan et al. [38]. As the backfill is constructed in layer by layer, the confining pressure on each zone changes with change in height of fill, thereby the moduli. Hence, soil modulus is updated during construction by modified hyperbolic soil modulus model [38]. The stress dependent deformation modulus (E t ) expressed by the hyperbolic equation as [38]:

$$ E_{t} = \left[ {1 - \frac{{R_{f} (1 - \sin \phi )\,(\sigma_{1} - \sigma_{3} )}}{{2\left( {c \times \cos \phi \, + \,\sigma_{3} \sin \phi \,} \right)}}} \right]^{2} \,K_{n} \times P_{a} \,\left( {\frac{{\sigma_{3} }}{{P_{a} }}} \right)^{n} $$
(1)

where K n is the modulus number; n is the modulus exponent; c is the cohesion; σ 1 and σ 3 are the major and minor effective confining stress respectively; ϕ is the angle of internal friction; R f is the failure ratio; p a is atmospheric pressure. A small cohesion of 0.1 kPa is adopted to prevent premature yielding. Similar small value of apparent cohesion was also adopted by Hatami and Bathurst [39] for numerical simulation of reinforced soil walls. The hyperbolic model is incorporated by FISH subroutines [37] that update the soil modulus according to their stress condition. The shear behavior of granular soils under cyclic loading is modeled using non-linear and hysteretic constitutive relation that follows Massing rule [40] during loading and unloading cycles. In this model, the shear modulus is determined on the basis of stress and strain states that may vary considerably during simulation runs. The tangent shear modulus during the first cycle is expressed as

$$ G_{t} = \frac{{G_{\hbox{max} } }}{{\left[ {1 + \left( {{{G_{\hbox{max} } } \mathord{\left/ {\vphantom {{G_{\hbox{max} } } {\tau_{{\max_{oct} }} }}} \right. \kern-0pt} {\tau_{{\max_{oct} }} }}} \right)\left| {\gamma_{ \varepsilon_{oct}} } \right|} \right]^{2} }} $$
(2)

where \( G_{\hbox{max} } \) is the initial shear modulus, \( \tau_{{\max_{oct} }} \) is the maximum octahedral shear stress in 3D states which is related to shear parameters of soil through cohesion c and internal angle of friction ϕ, and \( \tau_{{\max_{oct} }} \) is the octahedral shear strain. The tangent modulus during unloading/reloading cycle is

$$ G_{t} = \frac{{G_{\hbox{max} } }}{{\left[ {1 + \left( {{{G_{\hbox{max} } } \mathord{\left/ {\vphantom {{G_{\hbox{max} } } {2\tau_{{\max_{oct} }} }}} \right. \kern-0pt} {2\tau_{\max_{oct}} }}} \right)\left| {\Delta \gamma_{oct} } \right|} \right]^{2} }} $$
(3)

where \( \Delta \gamma_{oct} \) represents the difference in octahedral shear strain during unloading/reloading cycle. In unloading case as it equals to \( \gamma_{\varepsilon_{oct}} - \gamma_{u_{oct}} \) and in reloading case it is \( \gamma_{\varepsilon_{oct}} - \gamma_{r_{oct}} \). \( \gamma_{\varepsilon_{oct}} \) is the octahedral shear strain at present state and \( \gamma_{u_{oct }} \) and \( \gamma_{r_{oct}} \) are octahedral shear strains at starting points of unloading and reloading, respectively, for that cycle. The tangent bulk modulus B t is expressed in the following form:

$$ B_{t} = K_{b} \times p_{a} \times \left( {\frac{{\sigma_{m} }}{{p_{a} }}} \right)^{n} $$
(4)

in which K b is the bulk modulus constant and n is the bulk modulus exponent.

Damping in the form of local damping ratio of 5 % is adopted for soil elements during dynamic analysis to simulate the damping of soil at low strain levels. Liu et al. [34] also considered similar non-linear cyclic hysteretic behavior of soil along with damping value for the analysis of seismic behavior of geosynthetic reinforced soil walls.

Reinforcement Material (Geotextile)

The geotextile reinforcement is modeled using the geogrid structural element available in FLAC3D. The geogrid elements are three nodded shell elements used to model flexible membrane that resist as membrane but do not resist bending loading. The geogrid element behaves as isotropic linear elastic material with no failure limit. The studies of failure of reinforced soil walls [5–7] revealed that the failure of reinforced soil wall is due to subsidence of facing system and backfill soil. The reinforcement failures rarely observed. So geogrid element without any failure limit can be used in numerical simulations. The required input parameters for geogrid element in FLAC3D are: mass, stiffness, and thickness of geogrid which are adopted as 0.11 kg/m3, 5.2 kN/m, and 0.001 m, respectively. Hysteretic behavior of geosynthetics material is not considered for simulation because the hysteretic behavior of soil is predominant one. This approach is also adopted by several researchers [24, 26, 27, 30, 32, 35].

Interface Properties

Two different interfaces are considered in the present model: interface between backfill soil and wall and interface between soil and reinforcement.

The interface between backfill soil and rigid wall controls the relative movement between them. The relative interface movement is controlled by interface normal stiffness (k n ) and shear stiffness (k s ). A recommended thumb rule is that k s and k n be set to ten times the equivalent stiffness of the stiffest neighboring zone. Thus, the maximum stiffness value is determined as [37]:

$$ k_{n} = k_{s} = 10 \times \hbox{max} \left[ {\frac{{K + \frac{4}{3}G}}{{\left( {\Delta z} \right)_{\hbox{min} } }}} \right] $$
(5)

where the parameters (∆z)min, K and G are the smallest dimensions in normal direction, bulk modulus and shear modulus of continuum zone adjacent to the interface, respectively. This approach gives the preliminary values of the interface stiffness components, and these can be adjusted to avoid intrusion to adjacent zone and to prevent excessive computation time.

The interface behavior of geogrid is represented numerically at each geogrid node by a rigid attachment in normal direction and spring-slider in the tangent plane to the geogrid surface. The orientation of the spring-slider changes in response to the shear displacement between geogrid and neighboring soil elements. The shear behavior of the geogrid–soil interface is cohesive and frictional in nature and is controlled by coupling spring properties: (1) stiffness per unit area k; (2) cohesive strength c; (3) friction angle ϕ and by effective confining stress σ m . The effective confining stress σ m acts perpendicular to the geogrid surface and computed at each geogrid node [37]. The shear strength of the interfaces between the soils and geosynthetics are determined based on interface friction angle, \( \delta = \tan^{ - 1} \left( {\frac{2}{3}\tan \phi } \right) \), [41]. The various material properties used in simulation of the validation model are listed in Table 1.

Table 1 Material properties used in numerical simulation
Full size table

Development of Numerical Model

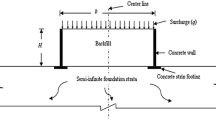
A rigid zone of size 800 mm long and 50 mm thick is considered at the base of wall to represent the shaking table. Model grid of 25 mm wide and 600 mm high is considered as the rigid wall. The lateral dimension of 100 mm is considered to observe the model response. The dimension of the physical model is 500 mm, but the 100 mm lateral dimension is considered for the ease of solving. A grid of 600 mm high and 750 mm long is generated to represent the backfill of rigid faced retaining wall. The whole grid is divided in number of zones of size 25 mm each. Four layers of geotextile reinforcement of length (L rein ) 420 mm are used in the model. Figure 2 shows the numerical grid considered to simulate the rigid faced retaining wall.

Fig. 2
figure 2

Grid adopted for numerical simulation

Full size image

Construction sequence with layers of equal thickness is followed in the numerical model generation, similar to that of physical model. The foundation zone is brought to static equilibrium before placing the rigid wall and backfill. The wall is then placed over the foundation zone and brought to static equilibrium. The horizontal movement of wall is restricted to represent temporary supports during the construction. The backfill model is generated in equal lifts. The reinforcement is placed after placing each lift. The reinforcements are extended to the wall and attached with the wall to represent rigid connection between wall and reinforcement. The structural elements in FLAC3D interacts with main grid at structural element nodes. But at the interface between wall and soil, the geogrid nodes may arbitrarily select nodes either from wall or from soil. So, finer grid is considered for wall portion so that more structural nodes interact with wall nodes. The model is brought to static equilibrium after each lift. A surcharge of 0.5 kPa is applied at top after all lifts up to full height of wall (H) and model is brought to static equilibrium. The supports of the wall are removed after the end of construction.

Boundary Conditions

The boundary conditions applied to the numerical model, in such a way that they represent the actual boundary of the physical model tests [21]. The bottom boundaries are completely fixed in vertical direction to represent the rigid boundary between the model wall and shaking table. The far end boundary elements are fixed in the x direction to represent the fixed container during construction. During construction, the model wall is fixed in horizontal direction to represent temporary facing supports. The lateral boundaries are fixed in the y direction to represent the lateral boundaries at the side of the physical model. After all layers construction is completed and the model has been brought to equilibrium, the facing supports are removed stage by stage. After the support removal in each stage, the model is brought to equilibrium. The boundary conditions of the model are shown in Fig. 3. During dynamic run free field boundary is applied to far end to represent the laminar boxes. The dynamic excitation is applied at the stiff bottom in the form of wave velocity in horizontal direction (uni-axial shaking).

Fig. 3
figure 3

Boundary conditions of the model in X–Y plane and Z–X plane

Full size image

Typical Results and Validation

Unreinforced and reinforced retaining wall models were tested for validation with sinusoidal dynamic excitation of 0.2 g base acceleration (a) at 3 Hz frequency for 20 cycles. The frequencies 2–3 Hz are represent predominant frequency of medium to high frequency earthquakes [26, 42] and also within earthquake parameters for seismic design [43]. Results are analyzed in terms of displacement, accelerations and pressures. Typical variations of displacements and accelerations with number of dynamic loading cycles at different elevations within the backfill soil of reinforced soil wall are shown in Figs. 4 and 5, respectively. The horizontal displacements increase nonlinearly with increase in number of cycles. The horizontal displacement of wall is greater at higher elevations of wall. The accelerations are amplified at higher elevations of wall.

Fig. 4
figure 4

Typical displacement histories at different elevation for a = 0.2 g and f = 3 Hz

Full size image
Fig. 5
figure 5

Typical acceleration histories obtained in numerical simulation

Full size image

The acceleration amplifications at different elevation of wall are quantified as root mean square acceleration (RMSA) amplification factor. RMSA amplification factor is the ratio of RMS acceleration values at different elevation to that of base RMS acceleration value. The RMS acceleration value are calculated according to Eq. 6 [44].

$$ {\text{RMS}} = \left[ {\frac{1}{{t_{d} }}\int\limits_{0}^{{t_{d} }} {a\left( t \right)^{2} dt} } \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} $$
(6)

where a(t) is acceleration at time t, t d is the duration of the acceleration record and dt is time interval of the acceleration record.

Figure 6 compares the variation of horizontal displacements, RMSA amplification factors and horizontal pressure increments at different elevations obtained from physical and numerical models of reinforced and unreinforced walls. The incremental pressure is the measured increase in lateral pressure during dynamic excitation on the back of the facing. The maximum horizontal displacement of unreinforced wall at an elevation of 500 mm is 12.8 mm for numerical model and that of physical model is 11.0 mm. The maximum horizontal displacement for reinforced wall at an elevation of 500 mm is 4.3 mm for numerical model and that of physical model is 4.0 mm. The acceleration amplification of unreinforced wall at an elevation of 600 mm is 1.25 for numerical model and that of physical model is 1.21. The corresponding values for reinforced wall are 1.09 for numerical model and 1.14 for physical model. The incremental pressure for unreinforced wall at an elevation of 100 mm is 0.19 kPa for numerical model and 0.06 kPa for physical model. While incremental pressure for reinforced wall is 0.33 kPa for numerical model and 0.23 kPa for physical model. Krishna and Latha [21] reported that the incremental pressure measurements were inconsistent owing to the issues related to pressure sensor sensing range (0–100 kPa) in relation to the range pressures encountered during testing (<3 kPa). So discrepancies in the incremental pressures are observed between the experimental and simulated results. The results obtained show the ability of the numerical model to capture the behavior of the physical model and confirms the validation of the model developed.

Fig. 6
figure 6

Comparison of results from numerical and physical model tests on unreinforced and reinforced (a = 0.2 g, f = 3 Hz and N L  = 4): a displacement profiles; b acceleration amplification and c incremental pressure

Full size image

Variations of octahedral shear stains, horizontal and vertical displacements along the length of backfill are analyzed for unreinforced and reinforced (N L  = 4) wall models, subjected to dynamic excitation (a = 0.2 g; f = 3 Hz), are being observed. The octahedral strain states are calculated from six strains acting on each element. The octahedral strain invariants are strain parameters independent of the choice of reference axis [45] and are expressed as

$$ \gamma_{oct} = \frac{2}{3}\left[ {\left( {\varepsilon_{xx} - \varepsilon_{yy} } \right)^{2} \,+\, \left( {\varepsilon_{yy} - \varepsilon_{zz} } \right)^{2} \,+\, \left( {\varepsilon_{zz} - \varepsilon_{xx} } \right)^{2} \,+\, 6\left( {\varepsilon_{xy}^{2} + \varepsilon_{yz}^{2} \,+\, \varepsilon_{zx}^{2} } \right)} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} $$
(7)

where ε xx , ε yy , ε zz , ε xy , ε yz and ε zx are strain parameters acting on each element in three dimensional state.

Figure 7 shows the shear strain, and displacements variations for unreinforced soil wall. In general, the maximum values of horizontal displacement (u) and vertical displacements (v) and incremental octahedral shear strain (∆γ oct ) are observed near the wall facing and they decrease gradually along the length of the backfill. Maximum horizontal displacements are 11.0, 9.0, 4.1 and 0.6 mm, at 525, 375, 225 and 75 mm elevations, respectively. The corresponding maximum vertical displacements (v) are in the range of 5.52–0.5 mm. The ∆γ oct are 10.8 % near the wall facing at 525 mm elevation and in the order of 4 % at other elevations. Figure 8 shows the similar results for a reinforced soil wall with four layers of reinforcement. The maximum u at 525 mm elevation is 4.0 mm near the wall face and it remains same up to the end of reinforcement (up to 420 mm length). From this point onwards a slight decrease in the u, up to the end of wall, is observed. Almost similar behavior has been observed at the other elevations also. The vertical displacements (v) are very low and almost uniform except, near the end of reinforcement, along the length of backfill at different elevations. The ∆γ oct are less than 0.75 % within reinforced zone but increase to 1.0 % at the end of reinforcement. Comparisons of unreinforced and reinforced wall responses show significant reductions in ∆γ oct , u, and v values. Backfill soil, near the facing is subjected to more strains in unreinforced wall and decreases gradually, while the maximum strains are near the end of reinforcement for reinforced retaining wall. These observations indicate that, the whole reinforced zone acts together as rigid body in case of reinforced retaining wall. The horizontal displacements are not reduced to minimum value near the far end boundary of wall. The model response is affected by far end boundary for both unreinforced and reinforced retaining wall and also reported in literature [21].

Fig. 7
figure 7

∆γ oct , u and v along length of backfill after dynamic excitation (a = 0.2 g and f = 3 Hz) for unreinforced wall

Full size image
Fig. 8
figure 8

∆γ oct , u and v along length of backfill of dynamic excitation for reinforced wall (a = 0.2 g and f = 3 Hz, L rein /H = 0.7 and N L  = 4)

Full size image

Response of Full Scale Reinforced Soil Retaining Wall under Seismic Excitation

Seismic behavior of a full scale rigid-faced model of 6 m high (H), 18 m long and 1 m wide with four reinforcement layers is studied, using the validated numerical model. The model parameters are kept same as that of laboratory model, except the reinforcement parameters. A 1 mm thick geotextile having mass per unit area of 230 g/m2 with, about 152 kN/m stiffness is adopted. The length of geotextile reinforcement (L rein ) is 4.2 m as per FHWA [46]. The base of wall is fixed against rotation and sliding. A surcharge of 5 kPa, resembling 20 cm thick cement concrete slab, is applied at the top of backfill. The foundation of wall is considered to be rigid hence, vertical displacements are restricted. Stability analysis has been carried out for full scale rigid-faced wall according to FHWA [46]. The factors of safety obtained for static and dynamic stability analyses are tabulated in Table 2. The safety factors shown in Table 2 indicate that the wall considered is safe against external and internal stability.

Table 2 Static and dynamic factors of safety for full scale rigid-faced model
Full size table

The full scale rigid-faced wall model is subjected to 20 cycles of sinusoidal dynamic excitation of 0.2 g acceleration (a) at 5 Hz frequency (f). The fundamental frequency of the rigid wall system is calculated based on model proposed by Wu [47] and found to be 7.07 Hz. Though 5 Hz frequency is higher than frequency range of medium to high frequency earthquake but nearer to the fundamental frequency of the rigid face wall model considered. The response of model, after dynamic excitation, is shown in Fig. 9 in the form of horizontal displacements (u), vertical displacements (v), RMSA amplification factors and horizontal pressures, near the facing and at the end of reinforcement. The maximum u are 30.1 and 12.6 mm near the facing and at the end of reinforcement; and corresponding v are 16.2 and 0.97 mm, respectively. The RMSA amplification factors are 3.36 and 2.85 at wall facing and at the end of reinforcement respectively. The horizontal pressure variation near end of reinforcement follows typical earth pressure distribution.

Fig. 9
figure 9

Horizontal, vertical displacements, RMSA amplification factor and horizontal pressure at different elevations after dynamic excitation (a = 0.2 g, f = 5 Hz L rein /H = 0.7, N L  = 4)

Full size image

The incremental octahedral shear strains (∆γ oct ), u and v displacements along the length of backfill between two reinforcement layers are presented in Fig. 10. The ∆γ oct are 1.76 and 1.14 % near the wall facing (confined to zone up to 0.4 m from facing) at elevation of 5.25 and 3.75 m respectively. The ∆γ oct at other part of backfill gradually goes down to 0.3 % at a distance of 5.3 and 2.7 m at elevation of 5.25 and 3.75 m, respectively. The u near the facing are 29.5 and 19.45 mm at elevations of 5.25 and 3.75 m, respectively. The u decrease gradually and become less than 10 mm, after the end of reinforcements. The v near the facing are 11.2 and 4.90 mm at an elevation of 5.25 and 3.75 m respectively. The v also decreases gradually and less than 1 mm within the reinforced zone. By observing the variations of ∆γ oct , u and v, two deformation zones are identified. The first zone (solid line in Fig. 10) exists totally in reinforced zone and very close to the facing which can be considered as high strain zone and shows relative settlement of reinforced zone near wall facing. The second zone (dashed line in Fig. 10) is the constant strain zone which is extending beyond reinforced zone, formed due to shear deformation within reinforced zone at higher elevation. This type of deformation zones are also observed by El-Emam and Bathurst [15] and Ling et al. [42] as surface deformations near the wall facing and some tension cracks in backfill.

Fig. 10
figure 10

∆γ oct , u and v along the length of backfill after 20 cycles of dynamic excitation (a = 0.2 g, f = 5 Hz, L rein /H = 0.7, N L  = 4)

Full size image

Effect of Backfill Friction Angle

The rigid-faced wall models with three different backfill friction angles of 30°, 38° and 43° are considered. The comparative results after seismic excitation (a = 0.2 g, f = 5 Hz) are shown in Fig. 11a. The maximum horizontal and vertical displacements of 38.44 and 18.59 mm observed near facing at elevation 5.5 m for wall with backfill friction angle 30°. About 27 and 45 % reduction in horizontal and vertical displacements near the facing are observed for change in backfill friction angle to 43°. The RMSA amplification factors at top are 3.36 and 3.38 for wall with backfill friction angle 38° and 43°. The horizontal pressures do not have any appreciable variation for wall with different backfill friction angles. Comparison of incremental octahedral shear strain (∆γ oct ) developed within soil elements after dynamic excitation for wall with different backfill friction angles is shown in Fig. 11b. The ∆γ oct near the wall facing at elevation 5.25 m are 2.4, 1.76 and 1.14 % for wall with backfill friction angles of 30°, 38° and 43°, respectively. The ∆γ oct are within the range of 0.7–0.3 % in reinforced zone and decreases to negligible value at 8 m from facing. The increase in vertical settlements (v) near the wall facing causes higher strain near facing for three different backfill soils.

Fig. 11
figure 11

a Response of model walls with backfill friction angles 30°, 38° and 43° subjected to dynamic excitation (a = 0.2 g, f = 5 Hz and L rein /H = 0.7, N L  = 4). b Comparison of ∆γ oct at backfill for wall with backfill friction angle 30°, 38° and 43° after dynamic excitation (a = 0.2 g, f = 5 Hz and L rein /H = 0.7, N L  = 4)

Full size image

Effect of Reinforcement Stiffness

Comparison of ∆γ oct in backfill soil for wall with different reinforcement stiffness of 5.2, 100 and 152 kN/m is shown in Fig. 12. The ∆γ oct near the wall facing at elevation 5.25 m are 2.7, 1.76 and 1.7 % for wall with reinforcement stiffness 5.2, 100 and 152 kN/m, respectively. At other elevations, almost same strain increments near the wall facing are observed for model walls with different reinforcement stiffness. The ∆γ oct values did not affected much with reinforcement stiffness. A high strained zone showing relative settlement is formed near the facing for three model walls.

Fig. 12
figure 12

Comparison of ∆γ oct at backfill for wall with reinforcement stiffness 5.2, 100 and 152 kN/m after dynamic excitation (a = 0.2 g, f = 5 Hz and L rein /H = 0.7, N L  = 4)

Full size image

Effect of Length of Reinforcing Layers

Three different reinforcement lengths (L rein ) 0.7H, 1.0H and 1.2H (H is the height of wall) are considered. Comparison of ∆γ oct in backfill soil for three different reinforcement lengths (L rein  = 0.7H, 1.0H and 1.2H) is shown in Fig. 13. The ∆γ oct near the facing is 1.76 and 1.14 % for reinforcement length of 0.7H and 1.0H respectively. The strain variation in soil for wall with reinforcement length 1.0H and 1.2H are almost same. Comparisons of strain in soil depict more vertical settlement near the facing for wall with reinforcement length 0.7H.

Fig. 13
figure 13

Comparison of ∆γ oct at backfill for wall with L rein / H = 0.7, 1.0 and 1.2 after dynamic excitation (a = 0.2 g, f = 5 Hz and N L = 4)

Full size image

Effect of Number of Reinforcing Layers

The rigid-faced wall with four, six and eight numbers of reinforcing layers subjected to 20 cycles of dynamic excitation of 0.2 g and frequency 5 Hz are considered. The ∆γ oct in backfill soil are compared for walls with four, six and eight layers of reinforcement in Fig. 14. Common elevations, which are not at reinforcement levels, are considered for determination of ∆γ oct . The maximum ∆γ oct is near the wall and is almost remain constant after 0.4 m from facing within reinforced zone, then decrease to negligible value at a distance of 8 m from facing at higher elevation for wall with four, six and eight layers of reinforcement. The maximum incremental shear strain at elevations 5.7 m is 2.52 % for wall with four layers of reinforcement and 2.15 % and 2.08 % for wall with six and eight layers of reinforcement. The variation of octahedral shear strain along backfill shows a zone of relative settlement near the facing and shear deformation within reinforced zone for wall with four, six and eight layers of reinforcement.

Fig. 14
figure 14

Comparison of ∆γ oct at backfill for wall with four, six and eight layers of reinforcement after dynamic excitation (a = 0.2 g, f = 5 Hz and L rein /H = 0.7)

Full size image

Effect of Facing Stiffness

Rigid-faced wall with different facing modulus of 27.4 and 15.2 GPa, resembling M30 and M10 grade concrete, are considered for analysis. Figure 15 shows comparison of ∆γ oct between two reinforcement layers after dynamic excitation. The variation of octahedral shear strain along backfill shows a zone of relative settlement near the facing and shear deformation within reinforced zone for wall with facing modulus 15.2 and 27.4 GPa. The variation of octahedral shear strain along backfill shows more relative settlement near the facing for wall with lesser facing stiffness. So the facing stiffness also one parameters to be considered for design of reinforced soil walls.

Fig. 15
figure 15

Comparison of ∆γ oct at backfill for wall with facing stiffness 27.4 GPa and 15.2 GPa after dynamic excitation (a = 0.2 g, f = 5 Hz and L rein /H = 0.7)

Full size image

Conclusions

The numerical model developed for laboratory scale rigid-faced walls is reasonably good in simulating dynamic responses and sensitive to the different material properties. In laboratory scale models, maximum shear strain developed was about 12 % near the facing for unreinforced wall, while it is about 1 %, near the end of reinforcement for reinforced wall. Displacements were significantly reduced by about 50–75 % by reinforcing layers.

Studies on full scale rigid-faced reinforced wall models showed two types of strained zones: high strain zone near the wall facing; and low strained zone extending into the retained backfill. Larger localised vertical and horizontal displacements near the wall facing indicate high strain zone (about 1–2 %); Low strain zone was marked by the extent of the retained backfill experiencing elastic strain level (around 0.3 %). The variation of length and stiffness of reinforcement, number of reinforcement layers; and backfill soil could marginally effect the strained zones, other than small changes near the wall facing at acceleration of 0.2 g.

The facing stiffness affects the response of the rigid-faced wall. The horizontal displacement of wall and vertical displacement of the backfill increases with decrease in wall stiffness. The strain increments in soil are higher for model with lesser wall stiffness.