Abstract
We give a complete classification of the torus-equivariant birational equivalence classes of smooth proper toric Deligne–Mumford stacks with trivial generic stabilizer in terms of their associated stacky fans.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
An algebraic orbifold is a smooth separated irreducible Deligne–Mumford stack of finite type over a field k (assumed to be algebraically closed of characteristic zero) with trivial generic stabilizer. Following [8, 9] we say that such orbifolds \(\mathscr {X}, \mathscr {X}'\) are birationally equivalent if there is a third algebraic orbifold \(\widehat{\mathcal {X}}\) admitting proper, birational and representable morphisms
In our paper, we consider the torus-equivariant birational classification problem for smooth proper toric Deligne–Mumford (DM) stacks with generically trivial stabilizer (see below for the precise definition). This problem was previously studied by Levchenko in [10], who considered the case of dimension 2 and obtained some birational invariants. In our paper, we give a full classification in arbitrary dimension.
2 Main result
To describe our results, we briefly recall the definition and basic properties of smooth toric DM-stacks. These were introduced in [1] and generalize the canonical cover of simplicial toric varieties (cf. [5, Theorem 4.11]). Similarly to the case of normal toric varieties, a smooth toric DM-stack is given by essentially convex-geometric data:
-
a finitely generated abelian group N of rank d; we denote the image of the natural map \(N \rightarrow N_{\mathbb {Q}}= N \hspace{0.55542pt}{\otimes }_{{\mathbb {Z}}}\hspace{1.111pt}{\mathbb {Q}}\) by \({{\overline{N}}}\),
-
a simplicial rational polyhedral fan \(\Sigma \) in \(N_{\mathbb {R}}= N \hspace{0.55542pt}{\otimes }_{{\mathbb {Z}}}\hspace{1.111pt}{\mathbb {R}}\),
-
for each ray \(\tau \in \Sigma (1)\) a vector \(\rho _\tau \in {{\overline{N}}}\) which generates \(\tau \).
Given such a tuple \(\varvec{\Sigma }= (N, \Sigma , (\rho _\tau )_{\tau \in \Sigma (1)})\), called a stacky fan, one constructs a smooth Deligne–Mumford stack \({\mathcal {X}}_{\varvec{\Sigma }}\) (see [1]). The coarse moduli space of \({\mathcal {X}}_{\varvec{\Sigma }}\) is the toric variety associated to the fan \(\Sigma \). We have that \(N = {\overline{N}}\) is torsion-free if and only if \({\mathcal {X}}_{\varvec{\Sigma }}\) is an orbifold, i.e. has generically trivial stabilizer (see [5, Lemma 7.15]). Under this assumption, for \(\sigma \in \Sigma \) we denote by \(N_\sigma \subseteq N\) the sub-lattice spanned by the \(\rho _\tau \) for \(\tau \in \sigma (1)\). The index of \(N_\sigma \) in \(N \cap \textrm{Span}_{\mathbb {Q}}\hspace{1.111pt}\sigma \) is the order of the generic stabilizer group on the torus-invariant stratum of \({\mathcal {X}}_{\varvec{\Sigma }}\) associated to \(\sigma \). We remark for later use that for a face \(\pi \subseteq \sigma \) we have \(N_\pi = N_\sigma \cap \textrm{Span}_{\mathbb {Q}}\hspace{1.111pt}\pi \).
From now on, we only work with toric orbifolds \({\mathcal {X}}_{\varvec{\Sigma }}\), i.e. smooth toric DM-stacks with generically trivial stabilizer. As for toric varieties, they contain the algebraic torus \(T = T_{{\mathcal {X}}_{\varvec{\Sigma }}} = \textrm{Spec}\hspace{0.55542pt}(k[N^\vee ])\) as an open dense substack. Following [10], we say that two such orbifolds \({\mathcal {X}}, {\mathcal {X}}'\) are T-equivariantly birationally equivalent if there exists a diagram (1) such that \(\widehat{\mathcal {X}}\) is an orbifold with an action of T and a dense equivariant embedding of T such that the maps f, g are T-equivariant.Footnote 1 It follows from [5, Theorem 7.17] that such an orbifold \(\widehat{\mathcal {X}}\) is a toric orbifold in the sense described above, i.e. given by \(\widehat{\mathcal {X}} = {\mathcal {X}}_{\hat{\varvec{\Sigma }}}\) for a stacky fan \(\hat{\varvec{\Sigma }} = (N, {\widehat{\Sigma }}, ({\widehat{\rho }}_\tau )_{\tau \in {\widehat{\Sigma }}(1)})\).
Given two toric DM-stacks \({\mathcal {X}}_{\varvec{\Sigma }'}, {\mathcal {X}}_{\varvec{\Sigma }}\) containing the same torus T, the identity on T induces a T-equivariant birational map \({\mathcal {X}}_{\varvec{\Sigma }'} \dashrightarrow {\mathcal {X}}_{\varvec{\Sigma }}\). The following proposition gives a criterion when this map is a morphism, respectively a representable morphism, in terms of the stacky fans \(\varvec{\Sigma }, \varvec{\Sigma }'\).
Proposition 2.1
Let \(\varvec{\Sigma } = (N, \Sigma , (\rho _\tau )_{\tau \in \Sigma (1)})\) and  be two stacky fans with the same underlying group N such that \(\Sigma , \Sigma '\) are full-dimensionalFootnote 2 with the same support \(|\Sigma | = |\Sigma '|\). Then the birational map \({\mathcal {X}}_{\varvec{\Sigma }'} \dashrightarrow {\mathcal {X}}_{\varvec{\Sigma }}\) extending the identity of the torus \(T = \textrm{Spec}\hspace{0.55542pt}(k[N^\vee ])\) is
be two stacky fans with the same underlying group N such that \(\Sigma , \Sigma '\) are full-dimensionalFootnote 2 with the same support \(|\Sigma | = |\Sigma '|\). Then the birational map \({\mathcal {X}}_{\varvec{\Sigma }'} \dashrightarrow {\mathcal {X}}_{\varvec{\Sigma }}\) extending the identity of the torus \(T = \textrm{Spec}\hspace{0.55542pt}(k[N^\vee ])\) is
- (a):
-
a morphism if and only if the identity on \(N_{\mathbb {R}}\) induces a map of fans
 such that for each
such that for each  and any cone \(\sigma \in \Sigma \) containing \(\tau '\), the element \(\rho '_{\tau '}\) is an integral linear combination of the \(\rho _\tau \) for \(\tau \in \sigma (1)\),
and any cone \(\sigma \in \Sigma \) containing \(\tau '\), the element \(\rho '_{\tau '}\) is an integral linear combination of the \(\rho _\tau \) for \(\tau \in \sigma (1)\), - (b):
-
a representable morphism if and only if the identity on \(N_{\mathbb {R}}\) induces a map of fans
 and for any full-dimensional cones \(\sigma \in \Sigma (d)\),
and for any full-dimensional cones \(\sigma \in \Sigma (d)\),  with
with 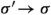 , we have an equality of sublattices \(N_\sigma = N_{\sigma '}\).
, we have an equality of sublattices \(N_\sigma = N_{\sigma '}\).
Proof
The fact that the fan-theoretic condition in (a) is sufficient is [1, Remark 4.5], and the converse implication follows from [6, Theorem 3.4]. For part (b) we note that for any cone \(\sigma \in \Sigma \), the generic stabilizer group of the associated torus-invariant subset of \({\mathcal {X}}_{\varvec{\Sigma }}\) is given by \(N \cap \textrm{Span}_{\mathbb {Q}}\hspace{1.111pt}\sigma / N_\sigma \) (as follows from [1, Proposition 4.3]). By part (a), we obtain a morphism if and only if  , and the injectivity of stabilizer groups for the representability of this morphism is then equivalent to the other inclusion
, and the injectivity of stabilizer groups for the representability of this morphism is then equivalent to the other inclusion  . We use here that it is sufficient to check the condition at the maximal cones since for a face \(\pi \subseteq \sigma \) we have \(N_\pi = N_\sigma \cap \textrm{Span}_{\mathbb {Q}}\hspace{1.111pt}\pi \).\(\square \)
. We use here that it is sufficient to check the condition at the maximal cones since for a face \(\pi \subseteq \sigma \) we have \(N_\pi = N_\sigma \cap \textrm{Span}_{\mathbb {Q}}\hspace{1.111pt}\pi \).\(\square \)
Using this proposition, we see that fixing \(\varvec{\Sigma }\), the torus-equivariant morphisms  are precisely induced by the choices of a simplicial subdivision
are precisely induced by the choices of a simplicial subdivision  and ray generators \((\rho '_{\tau '})_{\tau ' \in \Sigma '(1)}\) such that condition (a) is satisfied. Similarly, the representable morphisms correspond to subdivisions such that (b) is satisfied (in this case the ray generators are uniquely determined by condition (b)).
and ray generators \((\rho '_{\tau '})_{\tau ' \in \Sigma '(1)}\) such that condition (a) is satisfied. Similarly, the representable morphisms correspond to subdivisions such that (b) is satisfied (in this case the ray generators are uniquely determined by condition (b)).
Theorem 2.2
Let \({\mathcal {X}}_{\varvec{\Sigma }}\) and \({\mathcal {X}}_{\varvec{\Sigma }'}\) be two proper d-dimensional toric orbifolds together with an identification \(T = T_{{\mathcal {X}}_{\varvec{\Sigma }}} = T_{{\mathcal {X}}_{\varvec{\Sigma }'}}\) of their tori. Then \({\mathcal {X}}_{\varvec{\Sigma }}\) and \({\mathcal {X}}_{\varvec{\Sigma }'}\) are T-equivariantly birationally equivalent if and only if for any \(\sigma \in \Sigma (d)\) and  such that the interiors of \(\sigma \) and \(\sigma '\) intersect, we have \(N_\sigma = N_\sigma '\).
such that the interiors of \(\sigma \) and \(\sigma '\) intersect, we have \(N_\sigma = N_\sigma '\).
Proof
By definition, we have that \({\mathcal {X}}_{\varvec{\Sigma }}\) and \({\mathcal {X}}_{\varvec{\Sigma }'}\) are T-equivariantly birationally equivalent if and only if we can find a toric orbifold \(\widehat{\mathcal {X}}\) (with torus T), together with representable, proper T-equivariant birational morphisms

such that f, g restrict to the identity on T. As mentioned before, it follows from [5, Theorem 7.17] that the orbifold \(\widehat{\mathcal {X}}\) is given by \(\widehat{\mathcal {X}} = {\mathcal {X}}_{\hat{\varvec{\Sigma }}}\) for a stacky fan \(\widehat{\varvec{\Sigma }} = (N, {\hat{\Sigma }}, ({\widehat{\rho }}_\tau )_{\tau \in {\widehat{\Sigma }}(1)})\).
All toric orbifolds in diagram (2) are proper, so their fans are full-dimensional with support \(N_{\mathbb {R}}\). By Proposition 2.1, the fan \({\widehat{\Sigma }}\) is a refinement of \(\Sigma , \Sigma '\). For \(\sigma \in \Sigma (d)\) and  with overlapping interior, choose a cone \({\widehat{\sigma }} \in {\widehat{\Sigma }}(d)\) whose interior maps to \(\textrm{int}\hspace{0.55542pt}(\sigma ) \cap \textrm{int}\hspace{0.55542pt}(\sigma ')\). Then the fact that f, g are representable implies \(N_\sigma = N_{{\hat{\sigma }}} = N_{\sigma '}\) by Proposition 2.1 (b).
with overlapping interior, choose a cone \({\widehat{\sigma }} \in {\widehat{\Sigma }}(d)\) whose interior maps to \(\textrm{int}\hspace{0.55542pt}(\sigma ) \cap \textrm{int}\hspace{0.55542pt}(\sigma ')\). Then the fact that f, g are representable implies \(N_\sigma = N_{{\hat{\sigma }}} = N_{\sigma '}\) by Proposition 2.1 (b).
Conversely, assume \(N_\sigma = N_\sigma '\) for any \(\sigma \in \Sigma (d)\) and  such that the interiors of \(\sigma \) and \(\sigma '\) intersect. Then we claim that there exists an iterated stacky star subdivisionFootnote 3\({\hat{\varvec{\Sigma }}}\) of \({\varvec{\Sigma }}\) such that \({\hat{\Sigma }}\) is a refinement of \(\Sigma '\). The analogous statement for non-stacky fans is proven in [3] (see Lemmas in Sections 2.2 and 2.3 and Theorem in Section 2.4 of [3]). The proof is effective, describing a procedure for choosing the sequence of cones to subdivide. Following the same algorithm line-by-line and replacing the primitive generators of rays with the chosen generators \(\rho _\tau \) gives the desired result for stacky fans. We claim that taking \(\widehat{\mathcal {X}} = {\mathcal {X}}_{{\hat{\varvec{\Sigma }}}}\), we obtain a diagram (2) of proper representable morphisms as desired. Indeed, for the conditions of Proposition 2.1 (b), we already checked that that the underlying fan \({\widehat{\Sigma }}\) of \({\widehat{\varvec{\Sigma }}}\) refines \(\Sigma , \Sigma '\). On the other hand, the map f induced by iterated stacky star subdivision is representable, so for a cone \({\widehat{\sigma }} \in {\widehat{\Sigma }}(d)\) mapping to \(\sigma \in \Sigma (d)\) and
such that the interiors of \(\sigma \) and \(\sigma '\) intersect. Then we claim that there exists an iterated stacky star subdivisionFootnote 3\({\hat{\varvec{\Sigma }}}\) of \({\varvec{\Sigma }}\) such that \({\hat{\Sigma }}\) is a refinement of \(\Sigma '\). The analogous statement for non-stacky fans is proven in [3] (see Lemmas in Sections 2.2 and 2.3 and Theorem in Section 2.4 of [3]). The proof is effective, describing a procedure for choosing the sequence of cones to subdivide. Following the same algorithm line-by-line and replacing the primitive generators of rays with the chosen generators \(\rho _\tau \) gives the desired result for stacky fans. We claim that taking \(\widehat{\mathcal {X}} = {\mathcal {X}}_{{\hat{\varvec{\Sigma }}}}\), we obtain a diagram (2) of proper representable morphisms as desired. Indeed, for the conditions of Proposition 2.1 (b), we already checked that that the underlying fan \({\widehat{\Sigma }}\) of \({\widehat{\varvec{\Sigma }}}\) refines \(\Sigma , \Sigma '\). On the other hand, the map f induced by iterated stacky star subdivision is representable, so for a cone \({\widehat{\sigma }} \in {\widehat{\Sigma }}(d)\) mapping to \(\sigma \in \Sigma (d)\) and  , we have \(N_{{\hat{\sigma }}} = N_\sigma \). But then \(\textrm{int}\hspace{0.55542pt}(\sigma ) \cap \textrm{int}\hspace{0.55542pt}(\sigma ') \supseteq \textrm{int}\hspace{0.55542pt}({\widehat{\sigma }}) \ne \varnothing \), so by assumption
, we have \(N_{{\hat{\sigma }}} = N_\sigma \). But then \(\textrm{int}\hspace{0.55542pt}(\sigma ) \cap \textrm{int}\hspace{0.55542pt}(\sigma ') \supseteq \textrm{int}\hspace{0.55542pt}({\widehat{\sigma }}) \ne \varnothing \), so by assumption  as desired.\(\square \)
as desired.\(\square \)
As a consequence of the above result, we can give a complete classification of the birational equivalence classes of proper toric orbifolds. To state it, we introduce the following notion (which we did not find in this precise shape in the literature).
Definition 2.3
A conical polyhedral partition of \(N_{\mathbb {R}}\) is a finite collection \((C_i)_{i \in I}\) of non-empty subsets \(\varnothing \ne C_i \subseteq N_{\mathbb {R}}\) such that
-
each \(C_i\) is a finite union of full-dimensional rational polyhedral cones,
-
the union of the \(C_i\) is all of \(N_{\mathbb {R}}\),
-
the interiors of the \(C_i\) are pairwise disjoint.
We claim that for such a conical polyhedral partition, one can in fact find a fan \(\Sigma _0\) with support \(N_{\mathbb {R}}\) such that each of the \(C_i\) is a union of cones in \(\Sigma _0(d)\). Indeed, one way to obtain \(\Sigma _0\) is to subdivide \(N_{\mathbb {R}}\) at each defining hyperplane of each of the full-dimensional rational polyhedral cones used to cover the sets \(C_i\). Conversely, given a complete fan \(\Sigma _0\) and a partition I of \(\Sigma (d)\) into non-empty subsets, the sets \(C_i = \bigcup _{\sigma \in I} \sigma \) form a conical polyhedral partition.
Definition 2.4
A sublattice coloring of N is a conical polyhedral partition  indexed by a finite set
indexed by a finite set  of finite-index sublattices
of finite-index sublattices  such that for any
such that for any  , we have
, we have  .
.
Given a stacky fan \(\varvec{\Sigma }\) with an underlying fan \(\Sigma \) which is complete, we define
as the set of lattices associated to maximal cones of \(\Sigma \), and given such an  we denote by
we denote by

the associated union of maximal cones \(\sigma \) with lattice \(N_\sigma = N'\). We claim that  is a sublattice coloring of N. Indeed, by the remark below Definition 2.3 we see that \((C_{N'})_{N'}\) is a conical polyhedral partition of \(N_{\mathbb {R}}\). Thus the only non-trivial property to check is
is a sublattice coloring of N. Indeed, by the remark below Definition 2.3 we see that \((C_{N'})_{N'}\) is a conical polyhedral partition of \(N_{\mathbb {R}}\). Thus the only non-trivial property to check is  . It follows from the fact that
. It follows from the fact that  is a union of cones \(\pi \in \Sigma \) combined with the previous observation that for \(\pi \) a face of \(\sigma \in \Sigma \) we have \(N_\pi = N_\sigma \cap \textrm{Span}_{\mathbb {Q}}\hspace{1.111pt}\pi \).
is a union of cones \(\pi \in \Sigma \) combined with the previous observation that for \(\pi \) a face of \(\sigma \in \Sigma \) we have \(N_\pi = N_\sigma \cap \textrm{Span}_{\mathbb {Q}}\hspace{1.111pt}\pi \).
Corollary 2.5
The T-equivariant birational equivalence classes of proper toric orbifolds \({\mathcal {X}}_{\varvec{\Sigma }}\) with torus \(T = \textrm{Spec}\hspace{0.55542pt}(k[N^\vee ])\) are in bijection to sublattice colorings of N by sending the class \([{\mathcal {X}}_{\varvec{\Sigma }}]\) to the sublattice coloring  above.
above.
Proof
Theorem 2.2 implies that two proper toric orbifolds are birationally equivalent if and only if they have the same associated sublattice coloring. This shows that their birational equivalence classes inject into the set of sublattice colorings.
Conversely, given such a sublattice coloring  choose a fan \(\Sigma _0\) such that each \(C_{N'}\) is a union of maximal cones of \(\Sigma _0\). By performing a barycentric subdivision, we can assume without loss of generality that \(\Sigma _0\) is simplicial. For each cone \(\sigma \in \Sigma _0\) choose
choose a fan \(\Sigma _0\) such that each \(C_{N'}\) is a union of maximal cones of \(\Sigma _0\). By performing a barycentric subdivision, we can assume without loss of generality that \(\Sigma _0\) is simplicial. For each cone \(\sigma \in \Sigma _0\) choose  such that \(\sigma \subseteq C_{N'}\) and define \(N_\sigma = \textrm{Span}\hspace{0.55542pt}(\sigma ) \cap {N'}\). By the definition of sublattice coloring, this sublattice \(N_\sigma \subseteq N\) is independent of the choice of the set \(C_{N'}\) containing \(\sigma \). We would like to construct a stacky fan \(\varvec{\Sigma }_0'\) whose underlying fan \(\Sigma _0'\) refines \(\Sigma _0\) and such that the lattices on the cones of \(\Sigma _0'\) are the restrictions of the lattices \(N_\sigma \).
such that \(\sigma \subseteq C_{N'}\) and define \(N_\sigma = \textrm{Span}\hspace{0.55542pt}(\sigma ) \cap {N'}\). By the definition of sublattice coloring, this sublattice \(N_\sigma \subseteq N\) is independent of the choice of the set \(C_{N'}\) containing \(\sigma \). We would like to construct a stacky fan \(\varvec{\Sigma }_0'\) whose underlying fan \(\Sigma _0'\) refines \(\Sigma _0\) and such that the lattices on the cones of \(\Sigma _0'\) are the restrictions of the lattices \(N_\sigma \).
To obtain \(\varvec{\Sigma }_0'\), observe that associated to each cone \(\sigma \) of \(\Sigma _0\) we have two lattices: the lattice \(N_\sigma \) above, and its sublattice \(N_\sigma '\) spanned by the primitive generators \(\rho _\tau \in \tau \cap N_\tau \cong {\mathbb {N}}\) of the rays \(\tau \in \sigma (1)\). We define the multiplicity \(\textrm{mult}\hspace{0.55542pt}(\sigma )\) as the index of \(N_\sigma '\) in \(N_\sigma \). If some of the multiplicities are strictly greater than 1, we can perform iterated star subdivision on \(\Sigma _0\) to reduce their multiplicities, as explained in [2, Section 8.2] (adapting the procedure explained there to use the lattices \(N_\sigma \) for operations on the cone \(\sigma \)). After finitely many steps we arrive at a simplicial refinement \(\Sigma _0'\) of \(\Sigma _0\) with multiplicity 1 on each of the cones, giving the desired stacky fan \(\varvec{\Sigma }_0' = (N, \Sigma _0', (\rho _{\tau '})_{\tau ' \in \Sigma _0'(1)})\).\(\square \)
In particular, the above result easily shows that fixing the torus T there are infinitely many T-equivariant birational equivalence classes of proper toric orbifolds \({\mathcal {X}}\) with torus T, even when fixing a bound \(b \geqslant 2\) on the size of the stabilizer groups of points in \({\mathcal {X}}\). This is in stark contrast to the classical case of toric varieties, which are all birationally equivalent.Footnote 4
Remark 2.6
The proofs of Theorem 2.2 and Corollary 2.5 featured many combinatorial and convex geometric operations (like the multiplicity reduction above). A more conceptual and geometric approach is possible via the theory of possibly singular toric DM-stacks and their associated KM fans in the sense of [7]. Here a (lattice) KM fan is a triple \(F=(N, \Sigma , (N_\sigma )_{\sigma \in \Sigma })\) of a rational polyhedral fan \(\Sigma \) in the lattice N together with choices of sublattices \(N_\sigma \subseteq N\) associated to its cones which are finite index in \(\textrm{Span}\hspace{0.55542pt}(\sigma ) \cap N\) and compatible under face inclusions. Associated to F, the paper [7] defines a toric, but possibly singular DM-stack \({\mathcal {X}}(F)\). Any stacky fan \(\varvec{\Sigma }\) defines a KM fan F by taking \(N_\sigma \) to be the lattice spanned by the chosen ray generators \(\rho _\tau \) of \(\sigma \) as before. The constructed toric DM-stacks \({\mathcal {X}}(\varvec{\Sigma })\) and \({\mathcal {X}}(F)\) agree and for a KM fan F, we have that \({\mathcal {X}}(F)\) is smooth if and only if F comes from a stacky fan.
With this formalism in mind, we can sketch a geometric interpretation of the proofs presented above. Indeed, given complete stacky fans \(\varvec{\Sigma }, \varvec{\Sigma }'\) with compatible lattices on their maximal cones as in Theorem 2.2, choose any common refinement \(\Sigma ''\) of their underlying fans. Then the cones \(\sigma ''\) of \(\Sigma ''\) carry natural sublattices \(N_{\sigma ''}\) of \(N \cap \textrm{Span}\hspace{0.55542pt}(\sigma )\) induced from the associated lattices of their coarsenings in \(\Sigma , \Sigma '\) (which are compatible by assumption). Denote by  the associated KM fan. By functoriality, the associated toric DM-stack \({\mathcal {X}}(F'')\) admits toric maps to \({\mathcal {X}}_{\varvec{\Sigma }}, {\mathcal {X}}_{\varvec{\Sigma }'}\) which are representable by [7, Theorem 3.11.2]. Composing these with a toric resolution of singularities \(\widehat{\mathcal {X}} \rightarrow {\mathcal {X}}(F'')\) gives the diagram (2) showing that \({\mathcal {X}}_{\varvec{\Sigma }}, {\mathcal {X}}_{\varvec{\Sigma }'}\) are T-equivariantly birationally equivalent.
the associated KM fan. By functoriality, the associated toric DM-stack \({\mathcal {X}}(F'')\) admits toric maps to \({\mathcal {X}}_{\varvec{\Sigma }}, {\mathcal {X}}_{\varvec{\Sigma }'}\) which are representable by [7, Theorem 3.11.2]. Composing these with a toric resolution of singularities \(\widehat{\mathcal {X}} \rightarrow {\mathcal {X}}(F'')\) gives the diagram (2) showing that \({\mathcal {X}}_{\varvec{\Sigma }}, {\mathcal {X}}_{\varvec{\Sigma }'}\) are T-equivariantly birationally equivalent.
Similarly, in Corollary 2.5 given a sublattice coloring \((C_{N'})_{N'}\) choose a fan \(\Sigma _0\) such that each \(C_{N'}\) is a union of maximal cones of \(\Sigma _0\). Given a cone \(\sigma \in \Sigma _0\) contained in some \(C_{N'}\), we obtain the lattice  (which is independent of the choice of \(C_{N'}\) containing \(\sigma \) by the definition of sublattice colorings). Again we obtain a KM fan \(F=(N, \Sigma _0, (N_\sigma )_\sigma )\), and we can choose any toric resolution \(\widehat{\mathcal {X}}\) of \({\mathcal {X}}(F)\), whose birational equivalence class then induces the given sublattice coloring \((C_{N'})_{N'}\).
(which is independent of the choice of \(C_{N'}\) containing \(\sigma \) by the definition of sublattice colorings). Again we obtain a KM fan \(F=(N, \Sigma _0, (N_\sigma )_\sigma )\), and we can choose any toric resolution \(\widehat{\mathcal {X}}\) of \({\mathcal {X}}(F)\), whose birational equivalence class then induces the given sublattice coloring \((C_{N'})_{N'}\).
Notes
By composing f, g with the action of suitable points in T(k) on \({\mathcal {X}}, {\mathcal {X}}'\) we can assume without loss of generality these maps restrict to the identity on T.
Here we say that a rational polyhedral fan in \(N_{\mathbb {R}}\cong {\mathbb {R}}^d\) is full-dimensional if each cone of the fan is a face of a d-dimensional cone inside the fan. This condition is automatic for complete fans.
This is a variant of the usual star subdivision of a fan along a cone which takes into account the chosen ray generators \(\rho _\tau \), see [4] for the definition.
We thank the referee for pointing out this observation.
References
Borisov, L.A., Chen, L., Smith, G.G.: The orbifold Chow ring of toric Deligne-Mumford stacks. J. Amer. Math. Soc. 18(1), 193–215 (2005)
Danilov, V.I.: The geometry of toric varieties. Uspekhi Mat. Nauk 33(2), 85–134 (1978) (in Russian)
De Concini, C., Procesi, C.: Complete symmetric varieties. II. Intersection theory. In: Hotta, R. (ed.) Algebraic Groups and Related Topics. Advanced Studies in Pure Mathematics, vol. 6, pp. 481–513. North-Holland, Amsterdam (1985)
Edidin, D., More, Y.: Partial desingularizations of good moduli spaces of Artin toric stacks. Michigan Math. J. 61(3), 451–474 (2012)
Fantechi, B., Mann, E., Nironi, F.: Smooth toric Deligne–Mumford stacks. J. Reine Angew. Math. 648, 201–244 (2010)
Geraschenko, A., Satriano, M.: Toric stacks I: the theory of stacky fans. Trans. Amer. Math. Soc. 367(2), 1033–1071 (2015)
Gillam, W.D., Molcho, S.: A Theory of Stacky Fans (2015). arXiv:1512.07586
Kresch, A., Tschinkel, Yu.: Birational types of algebraic orbifolds. Sb. Math. 212(3), 319–331 (2021)
Kresch, A., Tschinkel, Yu.: Birational geometry of Deligne–Mumford stacks (2023). arXiv:2312.14061
Levchenko, D.: Birational invariants of toric orbifold surfaces. Ann. Univ. Ferrara Sez. VII Sci. Mat. 69(2), 463–471 (2023)
Acknowledgements
Our deep gratitude goes to Andrew Kresch, for his guidance to the literature on toric orbifolds, numerous pieces of advice on technical challenges related to stacky fans and detailed feedback on a preliminary version of the present article, improving exposition and clarity of our arguments. We also thank Sam Molcho for pointing out the theory of KM fans and helpful suggestions concerning toric resolution of singularities. We are also grateful to the referee for pointing out many interesting questions and observations, some of which we comment on above.
Funding
Open access funding provided by Swiss Federal Institute of Technology Zurich.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schmitt, J. Birational classification of toric orbifolds. European Journal of Mathematics 10, 13 (2024). https://doi.org/10.1007/s40879-023-00724-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40879-023-00724-y



 such that for each
such that for each  and any cone
and any cone  and for any full-dimensional cones
and for any full-dimensional cones  with
with 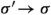 , we have an equality of sublattices
, we have an equality of sublattices