Abstract
We consider infinite-dimensional properties in coarse geometry for hyperspaces consisting of finite subsets of metric spaces with the Hausdorff metric. We see that several infinite-dimensional properties are preserved by taking the hyperspace of subsets with at most n points. On the other hand, we prove that, if a metric space contains a sequence of long intervals coarsely, then its hyperspace of finite subsets is not coarsely embeddable into any uniformly convex Banach space. As a corollary, the hyperspace of finite subsets of the real line is not coarsely embeddable into any uniformly convex Banach space. It is also shown that every (not necessarily bounded geometry) metric space with straight finite decomposition complexity has metric sparsification property.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Asymptotic dimension introduced by Gromov [17] and coarse embeddability into a Hilbert space (abbr. CE) are fundamental in coarse geometry. In fact, it was proved by Yu [33, 34] that every proper metric space with finite asymptotic dimension (abbr. FAD) and every bounded geometry metric space with CE satisfy the coarse Baum–Connes conjecture. Every metric space with FAD satisfies CE, and the following notions between FAD and CE are well-known: asymptotic property C (abbr. APC) [12]; finite decomposition complexity (abbr. FDC) [18, 19]; weak finite decomposition complexity (abbr. wFDC) [19]; APC-decomposition complexity (abbr. APCDC) [4]; straight finite decomposition complexity (abbr. sFDC) [13]; property A [34]; metric sparsification property (abbr. MSP) [8]. The definitions of these notions can be found in Definition 2.3. Among these properties, the following implications hold for metric spaces. Here we consider the Higson–Roe condition for property A (abbr. A(HR)) which is equivalent to the original definition of property A for metric spaces of bounded geometry [20, Lemma 3.5].

Implications 1, 6, 7 and 10 were proved in [19, Theorem 4.1], [4, Appendix A], [14, Theorem 4.2] and [9, Proposition 2.10], respectively. Equivalence 9 is obtained by theorems in [7] and [30, Theorem 4.1] for metric spaces of bounded geometry. Implication 11 was proved in [7, Corollary 3.5 and Theorem 3.8] for locally finite metric spaces. Implications 2, 3, 4 and 5 are immediate from their definitions. In Appendix, we show that implication 8 holds for every metric space. To the best of authors’ knowledge, it is unknown whether there is a relationship between APC and (w)FDC and whether arrows 3, 4, 5, 6, 7 and 8 can be reversed or not (see [27, Open Questions 2.7.8 and 2.7.9] and [26, Question in 9.4]).
Let (X, d) be a metric space and n a positive integer. In this paper we consider the above properties of the hyperspace \([X]^{<\omega }\) consisting of all non-empty finite subsets of X with the Hausdorff metric (see Sect. 2 for the definition) and its metric subspace \([X]^{\leqslant n}\) consisting of all non-empty subsets of X with at most n points.
Radul and Shukel’ [28] proved the inequality \(\mathrm{asdim}\,[X]^{\leqslant n}\!\leqslant n\, \mathrm{asdim}\,X\) holds whenever X has FAD (see also [21, Theorem 4.6] and [2, Theorem 24.2 and Example 24.15]). In particular, if X has FAD, then \([X]^{\leqslant n}\) has FAD. On the other hand, Dranishnikov and Zarichnyi [14, Proposition 3.6] proved that if X satisfies sFDC, then so does \([X]^{\leqslant n}\) by means of coarsely m-to-1 maps (for the definition, see Sect. 2). Actually, they proved that there exists a coarsely \(n^n\)-to-1 surjective map from the n-th product \(X^n\) of a metric space X to \([X]^{\leqslant n}\) (see Theorem 4.1) and apply the following two theorems.
-
(1)
sFDC is preserved under taking finite products (which follows from [5, Theorem 5.2]).
-
(2)
sFDC is preserved through coarsely m-to-1 maps [16, Theorems 8.4 and 8.7].
In Sect. 3, we show that wFDC and APCDC are preserved under taking finite products by applying theorems in [4], and that they are also preserved through coarsely m-to-1 maps. Applying these results and theorems in [5, 10, 14, 16], we obtain that APC, MSP, wFDC and APCDC are closed under taking hyperspaces of subsets with at most n points in Sect. 4.
Concerning the hyperspace \([X]^{<\omega }\), it was proved in [11, Proposition 2.3] that if X is a metric space of asymptotic dimension zero, then so is \([X]^{<\omega }\). The situation is completely different if a metric space X has positive dimension. In that case, \(\mathrm{asdim}\,X^n\!\geqslant n\) as Banakh proved in [1], and thus \(\mathrm{asdim}\,[X]^{<\omega }\!=\infty \) using the above-mentioned coarsely \(n^n\)-to-1 surjective map from \(X^n\) to \([X]^{\leqslant n}\). Moreover, in Sect. 5, we prove that if a metric space X contains a sequence of long intervals coarsely, then \([X]^{<\omega }\) is not coarsely embeddable into any uniformly convex Banach space, and hence \([X]^{<\omega }\) does not satisfy CE (Corollary 5.4). For example, every unbounded geodesic space contains a sequence of long intervals coarsely.
Note that every metric space containing a sequence of long intervals coarsely has positive asymptotic dimension. In Sect. 6, we show that the converse does not hold in general by giving an example of a locally finite metric space of positive asymptotic dimension which does not contain a sequence of long intervals coarsely.
2 Preliminaries
For a set A and \(n\in {\mathbb {N}}\), let |A|, \([A]^{<\omega }\) and \([A]^{\leqslant n}\) denote the cardinal number of a set A, the set of all non-empty finite subsets of A, and the set \(\{ F\in [A]^{<\omega }\,{:}\, |F|\leqslant n\}\), respectively. By \({\mathbb {R}}\) we denote the real line with the usual metric. Let \({\mathbb {R}}_{\geqslant 0}\) (resp. \({\mathbb {Z}}\), \({\mathbb {N}}\)) be the set of all non-negative real numbers (resp. integers, positive integers), respectively. Throughout this paper, every subset of a metric space is assumed to be its metric subspace.
Let X be a metric space. For the sake of simplicity, the metric on X will be denoted by \(d_X\) if it is not specified. Let B(x, R) denote the open ball centred at \(x\in X\) with radius \(R\geqslant 0\). For every pair of subsets \(Y,Z\subseteq X\) and every \(R\geqslant 0\), denote
For \(R\geqslant 0\), a family  of subsets of X is said to be R-disjoint if \(\mathrm{dist}\,(U,V) \geqslant R\) for every
of subsets of X is said to be R-disjoint if \(\mathrm{dist}\,(U,V) \geqslant R\) for every  with \(U \ne V\). The metric space X
with \(U \ne V\). The metric space X
-
is locally finite if \(|B(x,R)|\) is finite for every \(x\in X\) and \(R\in {\mathbb {R}}_{\geqslant 0}\);
-
has bounded geometry if there exist \(R\in {\mathbb {R}}_{\geqslant 0}\) and \(\delta :{\mathbb {R}}_{\geqslant 0}\rightarrow {\mathbb {N}}\) such that, for every \(x\in X\) and \(S\in {\mathbb {R}}_{\geqslant 0}\), the ball B(x, S) can be covered by at most \(\delta (S)\) balls of radius R.
We assume that the set \([X]^{<\omega }\) is equipped with the Hausdorff metric \(d^{\mathrm{H}}:[X]^{<\omega }{\times }\, [X]^{<\omega }\rightarrow {\mathbb {R}}_{\geqslant 0}\) defined as follows: for every \(Y,Z\in [X]^{<\omega }\),
Note that the inclusion \(i:X\rightarrow [X]^{<\omega }\), defined by letting \(i(x)=\{x\}\), for every \(x\in X\), is an isometric embedding. For \(n \in {\mathbb {N}}\) we assume that \([X]^{\leqslant n}\) is the metric subspace of \([X]^{<\omega }\). Because of the previous observation, for every \(n\in {\mathbb {N}}\), \([X]^{\leqslant n}\) contains a copy of X.
For metric spaces \(X_1, \dots , X_n\), the product set \(\prod _{\,i=1}^{\,n} X_i\) is assumed to have the maximum metric d defined by
for \(x=(x_i), y=(y_i)\in \prod _{\,i=1}^{\,n} X_i\).
A family of metric spaces is called a metric family. For a metric family  , let
, let

Then  is uniformly bounded if
is uniformly bounded if  .
.
By a map  between metric families
between metric families  and
and  , we mean a set of maps \(f:X_f \rightarrow Y_f\) such that
, we mean a set of maps \(f:X_f \rightarrow Y_f\) such that  and
and  . A restriction
. A restriction  of a map
of a map  between metric families is itself a map between metric families such that, for every \(g\in G\), there exists \(f\in F\) satisfying \(X^\prime _g\subseteq X_f\), \(Y_g^\prime \subseteq Y_f\), and \(g=f{{\,\mathrm{\!\upharpoonright }\,}}_{X_g^\prime }\). A map \(F:{\mathscr {X}} \rightarrow {\mathscr {Y}}\) is said to be
between metric families is itself a map between metric families such that, for every \(g\in G\), there exists \(f\in F\) satisfying \(X^\prime _g\subseteq X_f\), \(Y_g^\prime \subseteq Y_f\), and \(g=f{{\,\mathrm{\!\upharpoonright }\,}}_{X_g^\prime }\). A map \(F:{\mathscr {X}} \rightarrow {\mathscr {Y}}\) is said to be
-
bornologous if there exists a non-decreasing function \(\rho _+ :{\mathbb {R}}_{\geqslant 0}\rightarrow {\mathbb {R}}_{\geqslant 0}\) such that for every \(f \in F\) and for every \(x,x' \!\in X_f\), we have
$$\begin{aligned} d_{Y_f} (f(x),f(x')) \leqslant \rho _+ (d_{X_f}(x,x')), \end{aligned}$$ -
a coarse embedding if it is bornologous and there exists a non-decreasing function \(\rho _- :{\mathbb {R}}_{\geqslant 0}\rightarrow {\mathbb {R}}_{\geqslant 0}\) such that \(\lim _{t \rightarrow \infty } \rho _-(t)=\infty \) and for every \(f \in F\) and for every \(x,x'\! \in X_f\), we have \( \rho _- (d_{X_f}(x,x'))\leqslant d_{Y_f} (f(x),f(x'))\),
-
coarsely surjective if there exists \(S >0\) such that for every
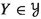 there exists \(f \in F\) satisfying \(Y=Y_f =N(f(X_f),S)\),
there exists \(f \in F\) satisfying \(Y=Y_f =N(f(X_f),S)\), -
a coarse equivalence if it is a coarsely surjective coarse embedding, and
-
coarsely n-to-1 if it is bornologous and there exists a non-decreasing function \(c :{\mathbb {R}}_{\geqslant 0}\rightarrow {\mathbb {R}}_{\geqslant 0}\) such that for every \(f \in F\), for every \(y \in Y_f\) and for every \(R>0\), there exist n points \(x_1,\dots ,x_n \in X_f\) such that \(f^{-1} (B(y,R)) \subseteq \bigcup _{i=1}^n B(x_i,c(R))\).
The functions \(\rho _+\), \(\rho _-\) and c above are called control functions. For metric spaces X and Y, a map \(f :X\rightarrow Y\) is said to be bornologous (resp., a coarse embedding, coarsely surjective, a coarse equivalence, coarsely n-to-1) if so is the map \(\{f\}:\{X\}\rightarrow \{Y\}\).
A metric family  (resp., a metric space X) is said be coarsely embeddable into a metric family
(resp., a metric space X) is said be coarsely embeddable into a metric family  (resp., a metric space Y) if there exists a coarse embedding
(resp., a metric space Y) if there exists a coarse embedding  (resp., \(f :X \rightarrow Y\)). A metric family
(resp., \(f :X \rightarrow Y\)). A metric family  is said to refine a metric family
is said to refine a metric family  (or \({\mathscr {X}}\prec {\mathscr {Y}}\)) if for every
(or \({\mathscr {X}}\prec {\mathscr {Y}}\)) if for every  there exists
there exists  such that \(X \subseteq Y\). For a map
such that \(X \subseteq Y\). For a map  and
and  let
let  .
.
Proposition 2.1
For metric spaces X and Y and a map \(f :X \rightarrow Y\), define \({\overline{f}} :[X]^{<\omega } \rightarrow [Y]^{<\omega }\) by letting \({{\overline{f}}}(A)=\{f(a)\,{:}\, a\in A\}\) for \(A \in [X]^{<\omega }\). Then the following hold:
-
(1)
f is bornologous if and only if \({{\overline{f}}}\) is;
-
(2)
f is a coarse embedding if and only if \({{\overline{f}}}\) is;
-
(3)
f is coarsely surjective if and only if \({{\overline{f}}}\) is;
-
(4)
f is a coarse equivalence if and only if \({{\overline{f}}}\) is.
Proof
(1) To show the “only if” part, assume that f is bornologous and let \(\rho _+\) be the control function. Define \(\rho _+':{\mathbb {R}}_{\geqslant 0}\rightarrow {\mathbb {R}}_{\geqslant 0}\) by \(\rho _+'(t) = \inf \, \{\rho _+ (s) \,{:}\, t< s \}\) for \(t \in {\mathbb {R}}_{\geqslant 0}\). Then we have \(d_Y^\mathrm{H}({\overline{f}}(A),{\overline{f}}(B)) \leqslant \rho _+'(d_X^{\mathrm{H}}(A, B))\) for any \(A, B \in [X]^{<\omega }\). The “if” part is obvious. Item (2) can be proved similarly. Item (3) is straightforward. Item (4) follows from (2) and (3).\(\square \)
Example 2.2
For any \(k \in {\mathbb {N}}\), \([{\mathbb {R}}^k]^{<\omega }\) is coarsely equivalent to \([{\mathbb {Z}}^k]^{<\omega }\), and \([{\mathbb {R}}_{\geqslant 0}]^{<\omega }\) is coarsely equivalent to \([{\mathbb {N}}]^{<\omega }\). Moreover, for every \(k,n\in {\mathbb {N}}\), \([{\mathbb {R}}^k]^{\leqslant n}\) is coarsely equivalent to \([{\mathbb {Z}}^k]^{\leqslant n}\), and \([{\mathbb {R}}_{\geqslant 0}]^{\leqslant n}\) is coarsely equivalent to \([{\mathbb {N}}]^{\leqslant n}\).
Let us recall the definitions of properties cited in the introduction. For \(n\in {\mathbb {N}}\), a metric space X is said to have asymptotic dimension at most n (\(\mathrm{asdim}\,X\leqslant n\)) if, for every \(R\geqslant 0\), there exist \(n+1\) uniformly bounded families  of subsets of X such that
of subsets of X such that  covers X and
covers X and  is R-disjoint for every \(i\in \{0,\dots ,n\}\). For \(k \in {\mathbb {N}}\) and \(R>0\), a metric family
is R-disjoint for every \(i\in \{0,\dots ,n\}\). For \(k \in {\mathbb {N}}\) and \(R>0\), a metric family  is said to be (k, R)-decomposable over a metric family
is said to be (k, R)-decomposable over a metric family  [19], denoted by
[19], denoted by  , if for every
, if for every  there exist \(k+1\) subfamilies
there exist \(k+1\) subfamilies  such that
such that  covers X and
covers X and  is R-disjoint for every \(i\in \{0,\dots ,k\}\). Note that, for \(n \in {\mathbb {N}}\), a metric space X satisfies \(\mathrm{asdim}\,X\leqslant n\) if and only if, for every \(R\in {\mathbb {R}}_{\geqslant 0}\), there exists a uniformly bounded family
is R-disjoint for every \(i\in \{0,\dots ,k\}\). Note that, for \(n \in {\mathbb {N}}\), a metric space X satisfies \(\mathrm{asdim}\,X\leqslant n\) if and only if, for every \(R\in {\mathbb {R}}_{\geqslant 0}\), there exists a uniformly bounded family  of subsets of X such that \(\{X\}\xrightarrow {(n,R)}{\mathscr {Y}}\). For \((R_i) \in {\mathbb {R}}_{\geqslant 0}^{\mathbb {N}}\), a metric family
of subsets of X such that \(\{X\}\xrightarrow {(n,R)}{\mathscr {Y}}\). For \((R_i) \in {\mathbb {R}}_{\geqslant 0}^{\mathbb {N}}\), a metric family  is said to be uniformly \((R_i)\)-decomposable over a metric family
is said to be uniformly \((R_i)\)-decomposable over a metric family  [4], denoted by
[4], denoted by  , if there exists \(k\in {\mathbb {N}}\) such that for every
, if there exists \(k\in {\mathbb {N}}\) such that for every  there exist subfamilies
there exist subfamilies  such that
such that  covers X and
covers X and  is \(R_i\)-disjoint for every \(i\in \{0,\dots ,k\}\). Let \({\mathfrak {B}}\) be the class of uniformly bounded metric families and set \({\mathfrak {D}}_0 ={\mathrm{w}}{\mathfrak {D}}_0={\mathfrak {C}}_0={\mathfrak {B}}\). For an ordinal \(\alpha >0\), define classes \({\mathfrak {D}}_\alpha \), \({\mathrm{w}}{\mathfrak {D}}_\alpha \) and \({\mathfrak {C}}_\alpha \) of metric families recursively by letting
is \(R_i\)-disjoint for every \(i\in \{0,\dots ,k\}\). Let \({\mathfrak {B}}\) be the class of uniformly bounded metric families and set \({\mathfrak {D}}_0 ={\mathrm{w}}{\mathfrak {D}}_0={\mathfrak {C}}_0={\mathfrak {B}}\). For an ordinal \(\alpha >0\), define classes \({\mathfrak {D}}_\alpha \), \({\mathrm{w}}{\mathfrak {D}}_\alpha \) and \({\mathfrak {C}}_\alpha \) of metric families recursively by letting

For a set X, let \(\ell _1(X)\) denote the Banach space of all functions \(f :X \rightarrow {\mathbb {R}}\) such that the \(\ell _1\)-norm \(\Vert f\Vert \) defined by \(\sum _{x \in X} |f(x)|\) is finite. For \(f \in \ell _1(X)\), the set \({{\,\mathrm{supp}\,}}f \) is defined as \(\{x \in X \,{:}\, f(x)>0\}\). Let \(\ell _1 (X)_{1,+}\) denote the set of all functions \(f \in \ell _1(X)\) such that \(\Vert f\Vert =1\) and \(f(x)\geqslant 0\) for any \(x \in X\). Every \(\mu \in \ell _1 (X)_{1,+}\) is identified with a probability measure on X by letting \(\mu (A) = \sum _{x \in A} \mu (x)\) for \(A \subset X\). If X is countable, then \(\ell _1 (X)_{1,+}\) is the set of all Borel probability measures on X with the discrete topology.
Definition 2.3
A metric space X is said to have
-
(1)
finite asymptotic dimension (or FAD) if \(\mathrm{asdim}\,X\leqslant m\) for some \(m\in {\mathbb {N}}\),
-
(2)
asymptotic property C (or APC) if \(\{X\} \in {\mathfrak {C}}_1\), that is, for any \((R_i) \in {\mathbb {R}}_{\geqslant 0}^{\mathbb {N}}\) there exist \(k \in {\mathbb {N}}\) and uniformly bounded families
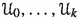 of X such that
of X such that 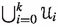 covers X and
covers X and 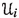 is \(R_i\)-disjoint for every \(i\in \{0,\dots ,k\}\),
is \(R_i\)-disjoint for every \(i\in \{0,\dots ,k\}\), -
(3)
finite decomposition complexity (or FDC) if \(\{X\} \in {\mathfrak {D}}_\alpha \) for some ordinal \(\alpha \),
-
(4)
weak finite decomposition complexity (or wFDC) if \(\{X\} \in {\mathrm{w}}{\mathfrak {D}}_\alpha \) for some ordinal \(\alpha \),
-
(5)
APC-decomposition complexity (or APCDC) if \(\{X\} \in {\mathfrak {C}}_\alpha \) for some ordinal \(\alpha \),
-
(6)
straight finite decomposition complexity (or sFDC) if for any \((R_i) \in {\mathbb {R}}_{\geqslant 0}^{\mathbb {N}}\) there exist \(k \in {\mathbb {N}}\) and families
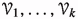 of subsets of X such that
of subsets of X such that  and
and  is uniformly bounded,
is uniformly bounded, -
(7)
metric sparsification property (or MSP) if there exist \(c>0\) and a function \(s:{\mathbb {R}}_{\geqslant 0}\rightarrow {\mathbb {R}}_{\geqslant 0}\) such that for every \(R\geqslant 0\) and for every \(\mu \in \ell _1(X)_{1,+}\) there exists an R-disjoint family
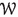 of subsets of X such that
of subsets of X such that 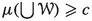 and
and 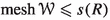 ,
, -
(8)
the Higson–Roe condition for property A (or A(HR)) if, for every \(\varepsilon >0\) and for every \(R>0\), there exist \(S>0\) and a map \(\xi :X\rightarrow \ell _1(X)\) such that \(\Vert \xi (x)\Vert =1\) and \({{\,\mathrm{supp}\,}}\xi (x) \subseteq B(x, S)\) for every \(x \in X\), and that \(\Vert \xi (x)-\xi (y)\Vert \leqslant \varepsilon \) for every \(x , y \in X\) with \(d_X(x,y)\leqslant R\).
Remark 2.4
A(HR) and MSP are equivalent to the original definition of property A of Yu [34] for metric spaces of bounded geometry according to [20, Lemma 3.5] (see also [32, Proposition 3.2], [27, Theorem 4.2.1]), [7] and [30, Theorem 4.1].
Remark 2.5
Dydak and Virk in [16, Theorem 8.4] proved that a metric space X has sFDC if and only if it is of countable asymptotic dimension [15, Definition 7.1], that is, there exists \((n_i) \in {\mathbb {N}}^{{\mathbb {N}}}\) such that for any \((R_i) \in {\mathbb {R}}_{\geqslant 0}^{\mathbb {N}}\) there exist \(k \in {\mathbb {N}}\) and families \({\mathscr {V}}_1,\dots ,{\mathscr {V}}_k\) of subsets of X satisfying  where
where  is uniformly bounded.
is uniformly bounded.
3 Preservation under products and coarsely n-to-1 maps
In this section, we show facts on preservation of some coarse infinite-dimensional properties (especially, wFDC and APCDC) under products and coarsely n-to-1 maps, which will be applied in Sect. 4.
Bell, Głodkowski and Nagórko in [4] proved the following.
Theorem 3.1
Let \(\alpha \) be an ordinal.
-
(1)
([4, Theorem 3.1]) If
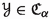 and a metric family
and a metric family 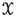 is coarsely embeddable into
is coarsely embeddable into 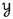 , then
, then 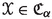 . In particular, if
. In particular, if 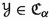 and
and 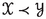 , then
, then 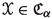 .
. -
(2)
([4, Fibering Permanence]) If
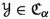 and a metric family
and a metric family 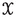 admits a bornologous map
admits a bornologous map 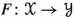 and an ordinal \(\gamma \) such that
and an ordinal \(\gamma \) such that 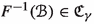 for every uniformly bounded
for every uniformly bounded 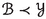 , then
, then 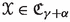 .
.
By a similar argument as in Theorem 3.1, we also have the following.
Lemma 3.2
Let \(\alpha \) be an ordinal.
-
(1)
If
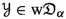 and a metric family
and a metric family 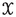 is coarsely embeddable into
is coarsely embeddable into  , then
, then 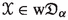 . In particular, if
. In particular, if 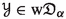 and
and 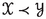 , then
, then 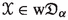 .
. -
(2)
If
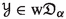 and a metric family
and a metric family 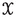 admits a bornologous map
admits a bornologous map 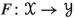 and an ordinal \(\gamma \) such that
and an ordinal \(\gamma \) such that 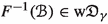 for every uniformly bounded
for every uniformly bounded 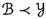 , then
, then 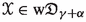 .
.
The following lemma follows from [25, Lemma 3.6] and [16, Lemma 2.7].
Lemma 3.3
Let X and Y be metric spaces, \(f :X \rightarrow Y\) a coarsely n-to-1 map with a control function \(c:{\mathbb {R}}_{\geqslant 0}\rightarrow {\mathbb {R}}_{\geqslant 0}\), and \(R>0\). Let  be a \(2c(2nR+1)\)-disjoint family of subsets of X. Then there exist n families
be a \(2c(2nR+1)\)-disjoint family of subsets of X. Then there exist n families  of subsets of Y such that each
of subsets of Y such that each  is R-disjoint,
is R-disjoint,  and
and  .
.
Proof
For the sake of convenience, we give a direct proof based on [25, Lemma 3.6] (see also [6, Lemma 3]) and [16, Lemma 2.7]. For  , define \(g_U :Y \rightarrow {\mathbb {R}}\) by letting \(g_U(y) =\mathrm{dist}\,(\{y\} , Y \, {\setminus }\, N(f(U),2nR))\), \(y \in Y\). For
, define \(g_U :Y \rightarrow {\mathbb {R}}\) by letting \(g_U(y) =\mathrm{dist}\,(\{y\} , Y \, {\setminus }\, N(f(U),2nR))\), \(y \in Y\). For  , let
, let

For \(i \in \{ 1,2,\dots , n\}\), set  . We show that
. We show that  , \(i\in \{1,2,\dots ,n\}\) are the required families.
, \(i\in \{1,2,\dots ,n\}\) are the required families.
To show that each  is R-disjoint, it suffices to show that the family
is R-disjoint, it suffices to show that the family  consists of pairwise disjoint subsets. Let
consists of pairwise disjoint subsets. Let  with
with  and
and  . Then we can take
. Then we can take  and
and  . If
. If  , then we have \(g_A(y)> g_{A'}(y)\), which implies
, then we have \(g_A(y)> g_{A'}(y)\), which implies  . Hence
. Hence  .
.
To show that  , let
, let  . Choose
. Choose  satisfying \(y \in f(U_y)\). Then \(g_{U_y}(y)\geqslant 2nR\). Let
satisfying \(y \in f(U_y)\). Then \(g_{U_y}(y)\geqslant 2nR\). Let  . Since \(f :X \rightarrow Y\) is a coarsely n-to-1 map with the control function \(c:{\mathbb {R}}_{\geqslant 0}\rightarrow {\mathbb {R}}_{\geqslant 0}\), there exist n points \(x_1,\dots ,x_n \in X\) satisfying \(f^{-1} (B(y,2nR+1)) \subseteq \bigcup _{i=1}^n B(x_i,c(2nR+1))\). For every
. Since \(f :X \rightarrow Y\) is a coarsely n-to-1 map with the control function \(c:{\mathbb {R}}_{\geqslant 0}\rightarrow {\mathbb {R}}_{\geqslant 0}\), there exist n points \(x_1,\dots ,x_n \in X\) satisfying \(f^{-1} (B(y,2nR+1)) \subseteq \bigcup _{i=1}^n B(x_i,c(2nR+1))\). For every  , we have \(g_A(y) >0\), which implies \(y \in N(f(A), 2nR)\), and hence \( f(A) \cap B(y,2nR+1)\ne \varnothing \). Thus
, we have \(g_A(y) >0\), which implies \(y \in N(f(A), 2nR)\), and hence \( f(A) \cap B(y,2nR+1)\ne \varnothing \). Thus

where the last inequality follows from the fact that  is \(2c(2nR+1)\)-disjoint. Since \(g_{U_y} (y) \geqslant 2nR\) and there are at most n elements of
is \(2c(2nR+1)\)-disjoint. Since \(g_{U_y} (y) \geqslant 2nR\) and there are at most n elements of  between 0 and \(g_{U_y} (y) \) in \({\mathbb {R}}\), there exists
between 0 and \(g_{U_y} (y) \) in \({\mathbb {R}}\), there exists  such that
such that

Then we have  , and hence
, and hence  . This and
. This and  imply that
imply that  , and hence
, and hence  .
.
Finally, we show that  . Let
. Let  . Then
. Then  for some
for some  . Fix
. Fix  . Then
. Then  , and for every
, and for every  , we have \(g_A(y) >0\), and hence \(y \in N(f(A),2nR)\). Thus
, we have \(g_A(y) >0\), and hence \(y \in N(f(A),2nR)\). Thus  . Therefore
. Therefore  .\(\square \)
.\(\square \)
Theorem 3.4
Let \(n \in {\mathbb {N}}\) and let \(\alpha \) be an ordinal.
-
(1)
If
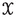 and
and 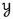 are metric families with a coarsely n-to-1 coarsely surjective map
are metric families with a coarsely n-to-1 coarsely surjective map 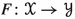 such that
such that 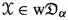 , then
, then 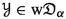 .
. -
(2)
If
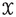 and
and 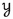 are metric families with a coarsely n-to-1 coarsely surjective map
are metric families with a coarsely n-to-1 coarsely surjective map 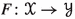 such that
such that 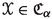 , then
, then 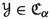 .
.
Proof
(1) We prove it by transfinite induction on \(\alpha \). The conclusion for \(\alpha =0\) holds since, if  is uniformly bounded and
is uniformly bounded and  is bornologous and coarsely surjective,
is bornologous and coarsely surjective,  is uniformly bounded.
is uniformly bounded.
Suppose that \(\alpha >0\) and (1) holds for every \(\beta < \alpha \). Let  and
and  be metric families with a coarsely n-to-1 coarsely surjective map
be metric families with a coarsely n-to-1 coarsely surjective map  such that
such that  . Let \(\rho _+\) and c be two control functions of F being bornologous and coarsely n-to-1, respectively. Since F is coarsely surjective,
. Let \(\rho _+\) and c be two control functions of F being bornologous and coarsely n-to-1, respectively. Since F is coarsely surjective,  is coarsely embeddable into the family
is coarsely embeddable into the family  . Indeed, take \(S>0\) so that, for every
. Indeed, take \(S>0\) so that, for every  , there exists \(f_Y \in F\) satisfying \(Y=N_Y(f_Y(X_{f_Y}), S)\). Then, for every
, there exists \(f_Y \in F\) satisfying \(Y=N_Y(f_Y(X_{f_Y}), S)\). Then, for every  , we can choose a function \(g_Y:Y \rightarrow f_Y(X_{f_Y})\) such that \(d(g_Y(y) , y) \leqslant S\) for any \(y \in Y\). Then
, we can choose a function \(g_Y:Y \rightarrow f_Y(X_{f_Y})\) such that \(d(g_Y(y) , y) \leqslant S\) for any \(y \in Y\). Then  is a coarse embedding from
is a coarse embedding from  into
into  . Thus, by (1) of Lemma 3.2, it suffices to show that
. Thus, by (1) of Lemma 3.2, it suffices to show that  .
.
Since  , there exists \(k \in {\mathbb {N}}\) satisfying
, there exists \(k \in {\mathbb {N}}\) satisfying

Let \(R>0\). We want to find \(\beta <\alpha \) and  satisfying
satisfying  . In order to do that, take \(\beta <\alpha \) and
. In order to do that, take \(\beta <\alpha \) and  with
with  .
.
Let \(f \in F\). Since  , there are
, there are  such that
such that  and each
and each  is c(2nR)-disjoint. Applying Lemma 3.3, for each \(i \in \{0,\dots , k\}\), choose families
is c(2nR)-disjoint. Applying Lemma 3.3, for each \(i \in \{0,\dots , k\}\), choose families  of subsets of \(Y_f\) satisfying
of subsets of \(Y_f\) satisfying  , each
, each  is R-disjoint and
is R-disjoint and  . For each
. For each  , let \(f_U\) be the restriction map \(f{{\,\mathrm{\!\upharpoonright }\,}}_{U}:U \rightarrow N_{Y_f}(f(U),2nR)\).
, let \(f_U\) be the restriction map \(f{{\,\mathrm{\!\upharpoonright }\,}}_{U}:U \rightarrow N_{Y_f}(f(U),2nR)\).
Set

Then  . Since
. Since  , we have
, we have  by (1) of Lemma 3.2. It is easy to see that
by (1) of Lemma 3.2. It is easy to see that  is coarsely n-to-1 with the control functions \(\rho _+\) and c and coarsely surjective with respect to the constant 2nR. Thus, by the induction hypothesis, we have
is coarsely n-to-1 with the control functions \(\rho _+\) and c and coarsely surjective with respect to the constant 2nR. Thus, by the induction hypothesis, we have  . This and
. This and  imply
imply  .
.
To show  , let \(f \in F\). Then the families
, let \(f \in F\). Then the families  , \(i\in \{0,\dots , k\}\) and \(j\in \{1,\dots , n\}\), are all R-disjoint and
, \(i\in \{0,\dots , k\}\) and \(j\in \{1,\dots , n\}\), are all R-disjoint and

Therefore  , and we have
, and we have  .
.
We can also prove (2) by a similar argument.\(\square \)
As an immediate consequence of Theorem 3.4, the following result descends.
Corollary 3.5
Let \(n\in {\mathbb {N}}\), and \(f:X\rightarrow Y\) be a coarsely n-to-1 coarsely surjective map between metric spaces. Then
-
(1)
Y has wFDC whenever X has wFDC;
-
(2)
Y has APCDC whenever X has APCDC.
Using Lemma 3.2 we can also prove the following result concerning finite products.
Proposition 3.6
Let \(n \in {\mathbb {N}}\).
-
(1)
If a metric space X has wFDC, then so does \(X^n\).
-
(2)
If a metric space X has APCDC, then so does \(X^n\).
Proof
(1) Assume that X has wFDC. We prove that \(X^n\) has wFDC by induction on n. The case \(n=1\) is trivial. Assume that \(n>1\) and \(X^{n-1}\) has wFDC. Then there exist ordinals \(\alpha \) and \(\beta \) such that \(\{X^{n-1}\} \in {\mathrm{w}}{\mathfrak {D}}_\alpha \) and \(\{X\} \in {\mathrm{w}}{\mathfrak {D}}_\beta \). Let \(p:X^n \rightarrow X\) be the n-th projection. To apply (2) of Lemma 3.2, let \(F=\{p\} :\{X^n\} \rightarrow \{X\}\) and let  be a uniformly bounded metric family with
be a uniformly bounded metric family with  . Then
. Then  . For each
. For each  , let \(g_B :X^{n-1} \, {\times }\, B \rightarrow X^{n-1}\) be the projection and let
, let \(g_B :X^{n-1} \, {\times }\, B \rightarrow X^{n-1}\) be the projection and let  . Then
. Then  is a coarse embedding with the control function \(\rho _-, \rho _+ :{\mathbb {R}}_{\geqslant 0}\rightarrow {\mathbb {R}}_{\geqslant 0}\) defined by
is a coarse embedding with the control function \(\rho _-, \rho _+ :{\mathbb {R}}_{\geqslant 0}\rightarrow {\mathbb {R}}_{\geqslant 0}\) defined by  and \(\rho _+(t)=t\), for every \(t\in {\mathbb {R}}_{\geqslant 0}\). Thus, by (1) of Lemma 3.2 and the fact that \(\{X^{n-1}\} \in {\mathrm{w}}{\mathfrak {D}}_\alpha \), we have
and \(\rho _+(t)=t\), for every \(t\in {\mathbb {R}}_{\geqslant 0}\). Thus, by (1) of Lemma 3.2 and the fact that \(\{X^{n-1}\} \in {\mathrm{w}}{\mathfrak {D}}_\alpha \), we have  . Therefore, by (2) of Lemma 3.2, we have \(\{X^n\} \in {\mathrm{w}}{\mathfrak {D}}_{\alpha +\beta }\), and hence \(X^n\) has wFDC.
. Therefore, by (2) of Lemma 3.2, we have \(\{X^n\} \in {\mathrm{w}}{\mathfrak {D}}_{\alpha +\beta }\), and hence \(X^n\) has wFDC.
We can also prove (2) by the same argument as above applying Theorem 3.1.\(\square \)
Concerning MSP, we have the following lemma on finite products which follows from [16, Theorem 7.9].
Lemma 3.7
Let \(n \in {\mathbb {N}}\). If a metric space X has MSP, then so does \(X^n\).
Proof
We give a direct proof for the sake of convenience. Assume that X has MSP. Let c and \(s:{\mathbb {R}}_{\geqslant 0}\rightarrow {\mathbb {R}}_{\geqslant 0}\) be a positive constant and a function for X being MSP, respectively. We claim that \(c^n\) and s are as required for \(X^n\) being MSP by induction on n. The case \(n=1\) is obvious. Suppose that the claim holds for \(n-1\). To show that \(c^n\) and s are as required for \(X^n\), let \(R\geqslant 0\) and \(\mu \in \ell _1(X^n)_{1,+}\). Define \(\mu _1 \in \ell _1(X^{n-1})_{1,+}\) by letting \(\mu _1 (x) = \mu (\{x\} \, {\times }\, X)\) for each \(x \in X^{n-1}\). Then, by induction hypothesis, there exists an R-disjoint family  of \(X^{n-1}\) such that
of \(X^{n-1}\) such that  and
and  . Define \(\mu _2 \in \ell _1(X)_{1,+}\) by letting
. Define \(\mu _2 \in \ell _1(X)_{1,+}\) by letting  for each \(x\in X\). Since X has MSP, there exists an R-disjoint family
for each \(x\in X\). Since X has MSP, there exists an R-disjoint family  of X such that
of X such that  and
and  . Let
. Let  . Then
. Then  is an R-disjoint family of \(X^n\) such that
is an R-disjoint family of \(X^n\) such that  and
and  . \(\square \)
. \(\square \)
4 Infinite-dimensionality of hyperspaces of subsets with at most n points
Let \(n\in {\mathbb {N}}\). In the introduction we have already recalled that, if a metric space X satisfies FAD, then \([X]^{\leqslant n}\) satisfies FAD [28] and, if X satisfies sFDC, then so does \([X]^{\leqslant n}\) [14]. In particular, in the proof of the last result Dranishnikov and Zarichnyi proved the following.
Theorem 4.1
(see [14, Proposition 3.6]) Let \(f:X^n \rightarrow [X]^{\leqslant n}\) be the map defined by \(f(x_1,x_2,\dots ,x_n) = \{ x_1, x_2, \dots , x_n \}\) for \((x_1, x_2, \dots , x_n) \in X^n\). Then f is coarsely \(n^n\)-to-1 and surjective.
By the same argument as in the proof of [14, Proposition 3.6], we also have the following corollary as a consequence of theorems in [5, 10, 16], Theorem 4.1, and results proved in Sect. 3.
Corollary 4.2
Let \(n\in {\mathbb {N}}\).
-
(1)
If a metric space X satisfies APC, then so does \([X]^{\leqslant n}\).
-
(2)
If a metric space X satisfies MSP, then so does \([X]^{\leqslant n}\).
-
(3)
If a metric space X satisfies wFDC, then so does \([X]^{\leqslant n}\).
-
(4)
If a metric space X satisfies APCDC, then so does \([X]^{\leqslant n}\).
-
(5)
If a metric space X with bounded geometry satisfies property A, then so does \([X]^{\leqslant n}\).
Proof
(1) Assume that a metric space X has APC. Then, by [5, Theorem 3.1] or [10, Theorem 3.1], so is \(X^n\). This, [16, Theorem 6.2] and Theorem 4.1 imply that \([X]^{\leqslant n}\) has APC.
Item (2) follows from Lemma 3.7, Theorem 4.1 and [16, Theorem 7.9].
Items (3) and (4) can be shown, similarly to the previous items, applying Proposition 3.6 and Corollary 3.5.
Item (5) follows from (2) and the equivalence 9 in (\(\dagger \)) in the introduction (see Remark 2.4) since, if X has bounded geometry, then so does \([X]^{\leqslant n}\).\(\square \)
Question 4.3
Let \(n \in {\mathbb {N}}\) and let X be a (not necessarily bounded geometry) metric space with A(HR). Does \([X]^{\leqslant n}\) have A(HR)?
Question 4.4
Let \(n \in {\mathbb {N}}\) and let X be a metric space with FDC. Does \([X]^{\leqslant n}\) have FDC?
Question 4.5
Let \(n \in {\mathbb {N}}\) and let X be a metric space being CE. Is \([X]^{\leqslant n}\) CE?
5 Infinite-dimensionality of hyperspaces of finite subsets
As already mentioned in the introduction, the following dichotomy descends from Theorem 4.1.
Corollary 5.1
Let X be a metric space. Then:
-
(1)
\(\mathrm{asdim}\,X=0\) if and only if \(\mathrm{asdim}\,[X]^{<\omega }=0\);
-
(2)
\(\mathrm{asdim}\,X>0\) if and only if \(\mathrm{asdim}\,[X]^{<\omega }=\infty \).
Proof
Item (1) is proved in [11, Proposition 2.3] and also implies the “if” implication in (2). Suppose now that \(\mathrm{asdim}\,X>0\). According to [1, Theorem 1], \(\mathrm{asdim}\,X^n\geqslant n\). Let now \(f:X^n\rightarrow [X]^{\leqslant n}\) be the coarsely \(n^n\)-to-1 surjective map defined in Theorem 4.1. Since f is also bornologous, [16, Theorem 6.1] implies that \(n\leqslant \mathrm{asdim}\,X^n\leqslant \mathrm{asdim}\,[X]^{\leqslant n}\). Thus \(\mathrm{asdim}\,[X]^{<\omega }=\infty \) as, for every \(n\in {\mathbb {N}}\), \([X]^{\leqslant n}\) is a subspace of \([X]^{<\omega }\).\(\square \)
For a sequence \(\{X_k\}_{k\in {\mathbb {N}}}\) of metric spaces, a metric space X is said to contain \(\{X_k\}_{k\in {\mathbb {N}}}\) coarsely if the family \(\{X_k \,{:}\, k \in {\mathbb {N}} \}\) is coarsely embeddable into \(\{X\}\). Moreover, the space X is said to contain a coarse disjoint union of \(\{X_k\}_{k\in {\mathbb {N}}}\) if there exists a coarse embedding \(\{i_k:X_k\rightarrow X\,{:}\,k\in {\mathbb {N}}\}\) such that \(\mathrm{dist}\,(i_m(X_m),i_k(X_k))\rightarrow \infty \) as \(m,k\rightarrow \infty \). A sequence \(\{I_k\}_{k\in {\mathbb {N}}}\) is called a sequence of long intervals if each \(I_k\) is a closed interval in \({\mathbb {R}}\) and \(\mathrm{diam}\,I_k \rightarrow \infty \). In this section, we shall prove the following.
Theorem 5.2
If a metric space X contains a sequence of long intervals coarsely, then \([X]^{<\omega }\) contains a coarse disjoint union of any sequence of finite metric spaces.
Example 5.3
A metric space X is said to be geodesic if for every \(x, y\in X\) there exists a isometric embedding \(\gamma :[0,d_X(x,y)] \rightarrow X\) such that \(\gamma (0) =x\) and \(\gamma (d_X(x,y))=y\). It is easy to see that every unbounded geodesic metric space contains a sequence of long intervals coarsely. Thus, if an unbounded geodesic metric space can be coarsely embedded into a metric space X, then X contains a sequence of long intervals coarsely. Every box space of a finitely generated residually finite infinite group (see [29, Definition 11.24] for definition) also contains a sequence of long intervals coarsely.
Recall that a Banach space \((X,\Vert \cdot \Vert )\) is uniformly convex if, for every \(0<\varepsilon \leqslant 2\) there exists \(\delta >0\) so that for any two vectors with \(\Vert x\Vert =\Vert y\Vert =1\), the condition \(\Vert x-y\Vert \geqslant \varepsilon \) implies that \(\Vert (x+y)/2\Vert \leqslant 1-\delta \). Lafforgue [23] constructed a sequence \(\{X_k\}_{k\in {\mathbb {N}}}\) of expander graphs such that no uniformly convex Banach space contains \(\{X_k\}_{k\in {\mathbb {N}}}\) coarsely. Since every Hilbert space is a uniformly convex Banach space, this and Theorem 5.2 yield the following.
Corollary 5.4
Let X be a metric space containing a sequence of long intervals coarsely. Then \([X]^{<\omega }\) is not coarsely embeddable into any uniformly convex Banach space. In particular, \([X]^{<\omega }\) is not CE.
To prove Theorem 5.2, we will apply the following lemmas:
Lemma 5.5
Let X be a metric space containing a sequence \(\{I_k\}_{k\in {\mathbb {N}}}\) of long intervals coarsely. Then X contains a coarse disjoint union of a sequence of long intervals.
Proof
Let us fix a coarse embedding \(\{i_k:I_k\rightarrow X:k\in \mathbb N\}\). Let \(\rho _- :{\mathbb {R}}_{\geqslant 0}\rightarrow {\mathbb {R}}_{\geqslant 0}\) be a non-decreasing function such that \(\lim _{t \rightarrow \infty } \rho _-(t)=\infty \) and for every \(k \in {\mathbb {N}}\) and for every \(x,x' \!\in I_k\), we have \( \rho _- (d_{I_k}(x,x'))\leqslant d_{X} (i_k(x),i_k(x'))\).
By induction on n, we find \(k_n \in {\mathbb {N}}\) and a subinterval \(J_n\subseteq I_{k_n}\) satisfying \(\mathrm{diam}\,J_n=n\) and, for every \(m < n\), we have \(k_m<k_n\) and \(\mathrm{dist}\,(i_{k_m} (J_m), i_{k_n} (J_n)) \geqslant n\). Indeed, let \(k_1=1\) and \(J_1=I_1\), and assume that \(J_m\subseteq I_{k_m}\) has been defined for \(m<n\). Since \(\lim _{t \rightarrow \infty } \rho _-(t)=\infty \), there is \(t_n \in {\mathbb {R}}_{\geqslant 0}\) satisfying \(\mathrm{diam}\,N(\bigcup _{m<n}i_{k_m}(J_m), n) < \rho _-(t_n)\). Since \(\mathrm{diam}\,I_k \rightarrow \infty \), we can take \(k_n \in {\mathbb {N}}\) satisfying \(\mathrm{diam}\,I_{k_n} > 3\max \{ n,t_n \}\). Then we have \(\mathrm{diam}\,i_{k_n}^{-1} ( N(\bigcup _{m<n}i_{k_m}(J_m), n) )\leqslant t_n\). Thus there is a closed subinterval \(J_n \subseteq I_{k_n}\) of diameter n such that \(J_n \cap i_{k_n}^{-1}(N(\bigcup _{m<n}i_{k_m}(J_m), n) )= \varnothing \), and hence \(i_{k_n}(J_n) \cap N(\bigcup _{m<n}i_{k_m}(J_m), n) = \varnothing \).
Then the sequence \(\{J_n\}_{n\in {\mathbb {N}}}\) and the coarse embedding \(\{i_{k_n}{{\,\mathrm{\!\upharpoonright }\,}}_{J_n}:J_n\rightarrow X: n\in {\mathbb {N}}\}\) are as required.\(\square \)
Lemma 5.6
For every \(r>0\) and \(m\in {\mathbb {N}}\) there exists \(M>0\) such that the product space \([-r,r]^m\) with the maximum metric can be isometrically embedded into \([[0,M]]^{<\omega }\).
Proof
For every \(r>0\) and \(m\in {\mathbb {N}}\), let \(M=4mr+m+r\) and define \(\phi :[-r,r]^m \rightarrow [[0,M]]^{<\omega }\) by
For \(x=(x_1,x_2,\dots , x_m), y=(y_1,y_2,\dots , y_m) \in [-r,r]^m \) and \(i,j \in \{1,2,\dots ,m\}\), we have \(|x_i -y_i|\leqslant 2r\) and \(|i(4r+1) +x_i -(j(4r+1 ) +y_j)| \geqslant 4r+1 -|x_i-y_j|\geqslant 2r+1 \) whenever \(i\ne j\). Thus \(d^{\mathrm{H}}( \phi (x), \phi (y)) = \max \, \{ |x_j-y_j| \,{:}\, j \in \{ 1,2,\dots , m\}\}\), which shows that \(\phi \) is isometric. \(\square \)
Lemma 5.7
Every finite metric space X can be isometrically embedded into \([-\mathrm{diam}\,X ,\mathrm{diam}\,X]^X\) with the maximum metric.
Proof
Fix \(x_0 \in X\). Then the Kuratowski embedding [22] \(\psi :X \rightarrow [-\mathrm{diam}\,X ,\mathrm{diam}\,X]^X\) defined by \(\psi (x) =(d_X(x,z) -d_X(x_0,z ))_{z \in X}\), \(x \in X\), shows the lemma. \(\square \)
By Lemmas 5.6 and 5.7, we have the following.
Corollary 5.8
For every finite metric space X, there exists \(M>0\) such that X can be isometrically embedded into \([[0,M]]^{<\omega }\).
Proof of Theorem 5.2
Let X be a metric space containing a sequence of long intervals coarsely and \(\{X_k\}_{k\in {\mathbb {N}}}\) a sequence of finite metric spaces. By Lemma 5.5, X contains a coarse disjoint union of a sequence \(\{I_n\}_{n\in {\mathbb {N}}}\) of long intervals coarsely. Take a coarse embedding \(\{i_n:I_n\rightarrow X:n\in {\mathbb {N}}\}\) such that \(\mathrm{dist}\,(i_m(I_m),i_n(I_n))\rightarrow \infty \) as \(m,n\rightarrow \infty \). For each \(n \in {\mathbb {N}}\), let \({\overline{i}}_n :[I_n]^{<\omega }\! \rightarrow [X]^{<\omega }\) be the map defined by \({\overline{i}}_n (A) ={i_n} (A)\) for \(A \in [I_n]^{<\omega }\). By the same reason as in Proposition 2.1, we have that \(\{{{\overline{i}}}_n:[I_n]^{<\omega }\!\rightarrow [X]^{<\omega }:n\in {\mathbb {N}}\}\) is a coarse embedding. By Corollary 5.8 and the fact that \(\mathrm{diam}\,I_n \rightarrow \infty \), we can take a strictly increasing sequence \(\{n_k\}_{k\in {\mathbb {N}}}\) in \({\mathbb {N}}\) and isometric embeddings \(\phi _k :X_k \rightarrow [I_{n_k}]^{<\omega }\), \(k \in {\mathbb {N}}\). Since
for \(k,m \in {\mathbb {N}}\), the coarse embedding \(\{\overline{i}_{n_k}\,{\circ }\, \phi _k:X_k\rightarrow [X]^{<\omega }:k\in {\mathbb {N}}\}\) is as required. \(\square \)
Note that, if a metric space X contains a sequence of long intervals coarsely, then \(\mathrm{asdim}\,X >0\). In the next section, we show that the converse does not hold in general.
6 A metric space of positive asymptotic dimension which does not contain a sequence of long intervals coarsely
Let X be a metric space and \(R\in {\mathbb {R}}_{\geqslant 0}\). A finite sequence \(\{x_i\}_{i=0}^m\) of points in X is called an R-path of length m connecting \(x_0\) and \(x_m\) if \(d(x_{i-1},x_i)\leqslant R\) for every \(i \in \{1,\dots ,m\}\). The space X is called R-connected if, for every \(x,y \in X\), there exists an R-path of finite length connecting x and y. Note that, for a metric space X, \(\mathrm{asdim}\,X>0\) if and only if there exists \(R\in {\mathbb {R}}_{\geqslant 0}\) such that, for every \(S\in {\mathbb {R}}_{\geqslant 0}\), there exists an R-connected subset A of X satisfying \(\mathrm{diam}\,A \geqslant S\).
In this section, we give an example of an unbounded 1-connected locally finite metric space which does not contain a sequence of long intervals coarsely. Before providing the example, let us recall a standard construction. A weighted non-directed graph is a triple \(\Gamma _w=(V,E,w)\) where (V, E) is a non-directed graph and w is a weight function, i.e., a map \(w:E\rightarrow {\mathbb {R}}_{\geqslant 0}\). For the sake of simplicity, we write w(x, y) instead of \(w(\{x,y\})\), for every \(\{x,y\}\in E\). If \(\Gamma _w=(V,E,w)\) is a weighted graph and (V, E) is connected (i.e., for every pair of points there exists a path connecting them), we can define the weighted path metric on V as follows: for every \(x,y\in V\),
In the sequel, we identify the graph \(\Gamma _w\) with its vertex set V.
Example 6.1
We construct an unbounded 1-connected locally finite metric space \(\Gamma \) which does not contain a sequence of long intervals coarsely.
In order to define \(\Gamma \), we first need to define some special subspaces \(\Gamma ^{(m)}\), where \(m\in \mathbb N\, {\setminus }\, \{1\}\). Fix then \(m\in \mathbb N\, {\setminus }\, \{1\}\). For every \(i \in \{0,\dots , m-1\}\) and \({{\overline{k}}}\in \{0,\dots ,m-1\}^{i}\), let \(\Gamma _{{{\overline{k}}}}^{m,i}=\{x_{\overline{k},0}^{m,i},\dots ,x_{{{\overline{k}}},m}^{m,i}\}\) be the weighted complete graph of \(m+1\) vertices with the weight function \(w^{m,i}_{\overline{k}}\) defined as follows: for every \(0\leqslant j_1<j_2\leqslant m\),
where we let \(\{0,\dots , m-1\}^0 = \{\varepsilon \}\) with the empty word \(\varepsilon \). Moreover, let
with respect to the equivalence relation \(\approx \) defined as follows: for every \(i \in \{0,\dots , m-2 \}\) and \((k_0,\dots ,k_i)\in \{0,\dots ,m-1\}^{i+1}\),
Note that the equivalence \(\approx \) agrees with the weights of the edges since \(m\geqslant 2\). Finally, define the non-directed graph \(\Gamma =\bigl (\bigsqcup _{\,m\in {\mathbb {N}}\, {\setminus }\, \{1\}}\Gamma ^{(m)}\bigr )/_{\cong }\), where \(\cong \) is the equivalence relation defined as follows: for every \(m\in {\mathbb {N}}\, {\setminus }\, \{1\}\), \(x_m^{m,0}\cong x_0^{m+1,0}\). By gluing together the weight functions of the single pieces, also the edges of the non-directed connected graph \(\Gamma \) can be endowed with a weight function, and so we can equip \(\Gamma \) with its weighted path metric. With that choice, \(\Gamma \) is a locally finite, unbounded metric space. Moreover, one can easily check that it is 1-connected; as an illustrative example, consider the following chain of elements connecting \(x_0^{3,0}\) and \(x_1^{3,0}\)
where \(\rightarrow \) indicates a jump of length 1. For the sake of simplicity, in the sequel we identify all \(\Gamma ^{(m)}\), \(\Gamma ^{m,i}_{{{\overline{k}}}}\) and \(x^{m,i}_{{\overline{k}},j}\) with their images in \(\Gamma \), respectively.
For \(m\in {\mathbb {N}}\, {\setminus }\, \{1\}\), \(i \in \{0,\dots , m-1\}\) and \({\overline{k}} \in \{0,\dots ,m-1 \}^{i}\), set
where \({\overline{k}} \in \{0,\dots ,m-1 \}^{i}\) is also considered as the map \({\overline{k}} :\{0,1,\dots ,i-1\} \rightarrow \{0,\dots ,m-1 \}\). Then \(U_{{\overline{k}}}^{m,i}\) coincides with the set
in \(\Gamma \), and
We also observe that, if \({\overline{k}} ,\overline{k'}\! \in \{0,\dots ,m-1 \}^{i}\) and \(U_{{\overline{k}}}^{m,i} \!\cap U_{\overline{k'}}^{m,i}= \varnothing \), then \(\mathrm{dist}\,\bigl (U_{{\overline{k}}}^{m,i} , U_{\overline{k'}}^{m,i} \bigr )\geqslant m+1-i\). Note that \(U_{\varepsilon }^{m,0}\) coincides with \(\Gamma ^{(m)}\) and \(U_{{\overline{k}}}^{m,i-1} = \bigcup _{j=1}^{m-1} U_{{\overline{k}},j} ^{m,i}\) for every \(i\in \{1,\dots ,m-1\}\) and \({\overline{k}} \in \{ 0,\dots , m-1\}^{i-1}\).
We want to prove that \(\mathrm{asdim}\,\Gamma =1\). Since \(\Gamma \) is 1-connected and unbounded, \(\mathrm{asdim}\,\Gamma >0\). In order to show that \(\mathrm{asdim}\,\Gamma \leqslant 1\), fix an arbitrary \(R\in {\mathbb {N}}\). We are using a different but equivalent definition of asymptotic dimension, namely, we want to construct a uniformly bounded cover  of \(\Gamma \) such that, for every \(x \in \Gamma \),
of \(\Gamma \) such that, for every \(x \in \Gamma \),  (see, for example, [3, Theorem 2.1.2]). Let \(U_0 = \bigcup _{i=2}^{2R} \Gamma ^{(i)}\). Then the cover
(see, for example, [3, Theorem 2.1.2]). Let \(U_0 = \bigcup _{i=2}^{2R} \Gamma ^{(i)}\). Then the cover

satisfies the desired properties. In fact, \(|\{U\in {\mathscr {U}}: B(x,R)\cap U\ne \varnothing \}|\leqslant 2\) for every \(x \in \Gamma \), and, by (6.1),  is uniformly bounded.
is uniformly bounded.
Finally, we want to show that \(\Gamma \) does not contain a sequence \(\{I_m\}_{m\in {\mathbb {N}}}\) of long intervals coarsely. Suppose, by contradiction, that there exists a coarse embedding \(\{f_m:I_m\rightarrow \Gamma :m\in {\mathbb {N}}\}\) with control functions \(\rho _-\) and \(\rho _+\). Since \(\Gamma \) is unbounded and \(\lim _{t \rightarrow \infty }\rho _-(t) =\infty \), there exists \(R\in {\mathbb {N}}\) such that \(S=\lfloor \rho _+(R)\rfloor \geqslant 1\), and \(k\in {\mathbb {N}}\) such that \(k> S\) and \(\rho _-(kR)\ge 4(S+2)^2\). Since \(\mathrm{diam}\,I_m \rightarrow \infty \) and \(\lim _{t \rightarrow \infty }\rho _-(t) =\infty \), there is \(l \in {\mathbb {N}}\) satisfying \(\mathrm{diam}\,\bigl (\bigcup _{j=2}^{k+2}\Gamma ^{(j)}\bigr ) + S+ \rho _+(kR) < \rho _-(\mathrm{diam}\,I_l)\leqslant \mathrm{diam}\,(f_l(I_l))\). Then we can take \(x,y \in I_l\) satisfying \(\rho _+(kR)< d_{\Gamma }(f_l(x), f_l(y))\) and \(f_l([x,y]) \cap \bigcup _{j=2}^{k+2}\Gamma ^{(j)}=\varnothing \). Note that \(|x-y|>kR\) since \(\rho _+(kR)<d_{\Gamma }(f_l(x), f_l(y))\leqslant \rho _+(|x-y| )\). Thus \(f_l(\{x, x+R, \dots , x+kR \}) \subset \Gamma \, {\setminus }\, \bigcup _{j=2}^{k+2}\Gamma ^{(j)}\subset \bigcup _{m>k+2}\Gamma ^{(m)} = \bigcup _{m>k+2}\bigcup _{{\overline{k}}\in \{0,\dots ,m-1 \}^{m-S}} U^{m,m-S}_{{\overline{k}}} \). Since \(\{f_l(x+jR)\}_{j=0}^k\) is an S-path connecting \(f_l(x)\) and \(f_l(x+kR)\) in \( \Gamma {\setminus } \bigcup _{j=2}^{k+2}\Gamma ^{(j)}\) and \(d_\Gamma (f(x), f(x+kR)) \geqslant \rho _-(kR)>4(S+2)^2 >4 \,\mathrm{diam}\,U^{m,m-S}_{{\overline{k}}}\) for every \(m>k+2\) and \({\overline{k}} \in \{0,\dots , m-1 \}^{m-S}\), there exist \(n>k+2\), \({\overline{l}} \in \{0,\dots , m-1 \}^{n-S-1}\) and \(j\in \{1,\dots ,m-2\}\) such that
Thus, in particular, \(f_l(\{x,\dots ,x+kR\})\) entirely crosses \(U^{n,n-S}_{{\overline{k}},j}\), and an S-path doing that needs at least \(n+1-2=n-1\) points; more precisely, \(|f_l(\{x,\dots ,x+kR\})\cap U^{n,n-S}_{{\overline{k}},j}|\geqslant n-1\). However, this leads to a contradiction since \(|f_l(\{x,\dots ,x+kR\})|\leqslant k+1<n-1\).
Concerning Theorem 5.2, we may ask the following question.
Question 6.2
Is it true that, if a metric space X satisfies \(\mathrm{asdim}\,X>0\), then the space \([X]^{<\omega }\) contains a coarse disjoint union of any sequence of finite metric space coarsely?
In particular, we do not know whether the following specialisation of Question 6.2 holds.
Question 6.3
For the metric space \(\Gamma \) in Example 6.1, does \([\Gamma ]^{<\omega }\) contain a coarse disjoint union of any sequence of finite metric space coarsely?
Question 6.4
Let X be a metric space with bounded geometry satisfying \(\mathrm{asdim}\,X>0\). Does X contain a sequence of long intervals coarsely?
Data Availibility
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Banakh, I., Banakh, T.: On the asymptotic dimension of products of coarse spaces (2020). arXiv:2001.04300 (to appear in Topology Appl.)
Banakh, T., Brydun, V., Karchevska, L., Zarichnyi, M.: The \(\ell _p\)-metrization of functors with finite supports (2020). arXiv:2004.02017
Bell, G., Dranishnikov, A.: Asymptotic dimension in Bȩdlewo. Topology Proc. 38, 209–236 (2011)
Bell, G., Głodkowski, D., Nagórko, A.: Decomposition theorems for asymptotic property C and property A. Topol. Appl. 256, 248–261 (2019)
Bell, G.C., Moran, D.S.: On constructions preserving the asymptotic topology of metric spaces. North Carolina J. Math. Stat. 1, 46–57 (2015)
Brodskiy, N., Dydak, J.: Coarse dimensions and partitions of unity. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 102(1), 1–19 (2008)
Brodzki, J., Niblo, G.A., Špakula, J., Willett, R., Wright, N.: Uniform local amenability. J. Noncommut. Geom. 7(2), 583–603 (2013)
Chen, X., Tessera, R., Wang, X., Yu, G.: Metric sparsification and operator norm localization. Adv. Math. 218(5), 1496–1511 (2008)
Dadarlat, M., Guentner, E.: Uniform embeddability of relatively hyperbolic groups. J. Reine Angew. Math. 612, 1–15 (2007)
Davila, T.: On asymptotic property C (2016). arXiv:1611.05988v1
Dikranjan, D., Protasov, I., Zava, N.: Hyperballeans of groups. Topol. Appl. 263, 172–198 (2019)
Dranishnikov, A.N.: Asymptotic topology. Russian Math. Surveys 55(6), 1085–1129 (2000)
Dranishnikov, A., Zarichnyi, M.: Asymptotic dimension, decomposition complexity, and Haver’s property C. Topol. Appl. 169, 99–107 (2014)
Dranishnikov, A., Zarichnyi, M.: Remarks on straight finite decomposition complexity. Topol. Appl. 227, 102–110 (2017)
Dydak, J.: Coarse amenability and discreteness. J. Aust. Math. Soc. 100(1), 65–77 (2016)
Dydak, J., Virk, Ž: Preserving coarse properties. Rev. Mat. Complut. 29(1), 191–206 (2016)
Gromov, M.: Asymptotic invariants of infinite groups. In: Niblo, G.A., Roller, M.A. (eds.) Geometric Group Theory, Vol. 2 (Sussex, 1991). London Mathematical Society Lecture Note Series, vol. 182, pp. 1–295. Cambridge University Press, Cambridge (1993)
Guentner, E., Tessera, R., Yu, G.: A notion of geometric complexity and its application to topological rigidity. Invent. Math. 189(2), 315–357 (2012)
Guentner, E., Tessera, R., Yu, G.: Discrete groups with finite decomposition complexity. Groups Geom. Dyn. 7(2), 377–402 (2013)
Higson, N., Roe, J.: Amenable group actions and the Novikov conjecture. J. Reine Angew. Math. 519, 143–153 (2000)
Kucab, J., Zarichnyi, M.: On asymptotic power dimension. Topol. Appl. 201, 124–130 (2016)
Kuratowski, C.: Quelques problèmes concernant les espaces métriques non-séparables. Fund. Math. 25, 534–545 (1935)
Lafforgue, V.: Un renforcement de la propriété (T). Duke Math. J. 143(3), 559–602 (2008)
Mendel, M., Naor, A.: Nonlinear spectral calculus and super-expanders. Publ. Math. Inst. Hautes Études Sci. 119, 1–95 (2014)
Miyata, T., Virk, Ž: Dimension-raising maps in a large scale. Fund. Math. 223(1), 83–97 (2013)
Nicas, A., Rosenthal, D., et al.: Hyperbolic dimension and decomposition complexity. In: Broaddus, N. (ed.) Topological Methods in Group Theory. London Mathematical Society Lecture Note Series, vol. 451, pp. 146–167. Cambridge University Press, Cambridge (2018)
Nowak, P.W., Yu, G.: Large Scale Geometry. EMS Textbooks in Mathematics. European Mathematical Society, Zürich (2012)
Radul, T.M., Shukel’, O.: Functors of finite degree and asymptotic dimension. Mat. Stud. 31(2), 204–206 (2009)
Roe, J.: Lectures on Coarse Geometry. University Lecture Series, vol. 31. American Mathematical Society, Providence (2003)
Sako, H.: Property A and the operator norm localization property for discrete metric spaces. J. Reine Angew. Math. 690, 207–216 (2014)
Shukel’, O.: Functors of finite degree and asymptotic dimension zero. Mat. Stud. 29(1), 101–107 (2008)
Tu, J.-L.: Remarks on Yu’s “property A’’ for discrete metric spaces and groups. Bull. Soc. Math. France. 129(1), 115–139 (2001)
Yu, G.: The Novikov Conjecture for groups with finite asymptotic dimension. Ann. Math. 147(2), 325–355 (1998)
Yu, G.: The coarse Baum-Connes conjecture for spaces which admit a uniform embedding into Hilbert space. Invent. Math. 139(1), 201–240 (2000)
Acknowledgements
We would like to thank the referees for their careful reading and the comments that improved our work. The third named author would like to thank the Division of Mathematics, Physics and Earth Sciences of the Graduate School of Science and Engineering of Ehime University and the second named author for hosting his visit in June 2018.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funding
Open access funding provided by Institute of Science and Technology (IST Austria).
Author information
Authors and Affiliations
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The first named author was supported by the NSF through grant OIA-1937095. The second named author was supported by JSPS KAKENHI grant No. 19K03467.
Appendix: Straight finite decomposition complexity implies metric sparsification property
Appendix: Straight finite decomposition complexity implies metric sparsification property
According to [14] and [7], every bounded geometry metric space with sFDC satisfies MSP. In this appendix, we show that the assumption of bounded geometry can be dropped in this fact.
Theorem 6.5
Let X be a metric space with sFDC. Then X satisfies MSP.
Proof
Let \(R>0\). Since X has sFDC, there exist families  of subsets of X such that
of subsets of X such that

and  is uniformly bounded. Let
is uniformly bounded. Let

and fix an arbitrary \(\mu \in \ell _1(X)_{1,+}\). Set \(X_0^0=X\), \(A_0=\{0\}\) and  . Obviously,
. Obviously,  is R-disjoint.
is R-disjoint.
Claim 1
For every \(i \in \{1,\dots ,n\}\), there exist  and \(\pi _i:A_i \rightarrow A_{i-1}\) such that for every \(\alpha \in A_{i-1}\),
and \(\pi _i:A_i \rightarrow A_{i-1}\) such that for every \(\alpha \in A_{i-1}\),
-
(1)
\(X _\alpha ^0= \bigcup _{\beta \in \pi _i^{-1}(\alpha )} X_\beta ^0\), and
-
(2)
there are \(B_\alpha ^0 , B_\alpha ^1 \subseteq A_i\) such that \(\pi _i^{-1}(\alpha )= B_\alpha ^0 \cup B_\alpha ^1\), \(B_\alpha ^0 \cap B_\alpha ^1 = \varnothing \) and \(\{ X_\beta ^0 \,{:}\, \beta \in B_\alpha ^l \}\) is \(2^{i+3}R\)-disjoint for each \(l \in \{0,1\}\).
Proof of Claim 1
We construct  and \(\pi _i\) by induction on i. Assume that
and \(\pi _i\) by induction on i. Assume that  has been obtained. Let \(\alpha \in A_{i-1}\). Since
has been obtained. Let \(\alpha \in A_{i-1}\). Since  , there exist
, there exist  such that
such that  and
and  is \(2^{i+3}R\)-disjoint for each \(l \in \{0,1\}\). We may assume
is \(2^{i+3}R\)-disjoint for each \(l \in \{0,1\}\). We may assume  by replacing
by replacing  with
with  .
.
Let  and define \(\pi _i :A_i \rightarrow A_{i-1}\) by letting \(\pi _i ((\alpha ,X')) = \alpha \) for \((\alpha ,X') \in A_i\). Set \(X^0_\beta =X'\) for each \(\beta =(\alpha ,X') \in A_i\),
and define \(\pi _i :A_i \rightarrow A_{i-1}\) by letting \(\pi _i ((\alpha ,X')) = \alpha \) for \((\alpha ,X') \in A_i\). Set \(X^0_\beta =X'\) for each \(\beta =(\alpha ,X') \in A_i\),  and
and  for each \(\alpha \in A_{i-1}\) and \(l \in \{0,1\}\). Then
for each \(\alpha \in A_{i-1}\) and \(l \in \{0,1\}\). Then  and \(\pi _i \) satisfy (1) and (2).\(\square \)
and \(\pi _i \) satisfy (1) and (2).\(\square \)
For each \(i,j \in \{ 0,1,\dots , n\}\) with \(i<j\), let
and let \(\pi _i^i:A_i \rightarrow A_i\) be the identity map.
Claim 2
For every \(k \in \{1,\dots ,n\}\) and \(i\in \{k,k+1, \dots , n \}\), there exist a family  of subsets and a subset \(Z_k\) in X such that
of subsets and a subset \(Z_k\) in X such that
-
(1)
\(X^k_\alpha =\bigcup _{\beta \in \pi _i^{-1}(\alpha )} X_\beta ^k\) for every \(\alpha \in A_{i-1}\) if \(i>k\),
-
(2)
\(\bigl \{X^k_\beta \,{:}\, \beta \in B_\alpha ^l\bigr \}\) is \(\bigl (2^{i+3}-\sum _{j=1}^{k}2^{j+2}\bigr )R\)-disjoint for every \(\alpha \in A_{i-1}\) and \(l \in \{0,1\}\),
-
(3)
 ,
, -
(4)
 is R-disjoint,
is R-disjoint, -
(5)
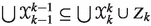 , and
, and -
(6)
\(\mu (Z_k) \leqslant 2^{-k-1}\).
Proof of Claim 2
We construct  by induction on k. The families
by induction on k. The families  taken above satisfy (1)–(4). Assume that families
taken above satisfy (1)–(4). Assume that families  satisfying (1)–(4) have been defined. For \(j \in \{ 1,2,3,\dots , 2^{k+1}\}\), let
satisfying (1)–(4) have been defined. For \(j \in \{ 1,2,3,\dots , 2^{k+1}\}\), let
Note that the family \(\{W^j_\lambda \,{ :}\, \lambda \in A_{k-1} \}\) is R-disjoint since so is  , and the family \(\{W_j \,{:}\, j \in \{1,2,3,\dots , 2^{k+1} \}\}\) is a family of pairwise disjoint subsets of X. Since \(\sum _{j=1}^{2^{k+1}} \mu (W_j) = \mu \bigl (\bigcup _{j=1}^{2^{k+1}}W_j\bigr ) \leqslant \mu (X) =1\), there exists \(j_k \in \{1,2,3,\dots ,2^{k+1}\}\) such that \(\mu (W_{j_k}) \leqslant 2^{-k-1}\). For \( i\in \{k,k+1, \dots , n\}\) and \(\beta \in A_i\), let \(\lambda = \pi _{k-1}^i (\beta )\) and
, and the family \(\{W_j \,{:}\, j \in \{1,2,3,\dots , 2^{k+1} \}\}\) is a family of pairwise disjoint subsets of X. Since \(\sum _{j=1}^{2^{k+1}} \mu (W_j) = \mu \bigl (\bigcup _{j=1}^{2^{k+1}}W_j\bigr ) \leqslant \mu (X) =1\), there exists \(j_k \in \{1,2,3,\dots ,2^{k+1}\}\) such that \(\mu (W_{j_k}) \leqslant 2^{-k-1}\). For \( i\in \{k,k+1, \dots , n\}\) and \(\beta \in A_i\), let \(\lambda = \pi _{k-1}^i (\beta )\) and
Note that

Set  for \( i\in \{k,k+1, \dots , n\}\) and \(Z_k =W_{j_k}\). Then \(Z_k\) satisfies (6).
for \( i\in \{k,k+1, \dots , n\}\) and \(Z_k =W_{j_k}\). Then \(Z_k\) satisfies (6).
To show (1), suppose that \(i>k\) and \(\alpha \in A_{i-1}\). Let \(\lambda = \pi _{k-1}^{i-1} (\alpha )\). Since \(\pi ^{i-1}_{k} (\alpha ) \in \pi _k^{-1}(\lambda ) =B_\lambda ^0\cup B_\lambda ^1\), either \(\pi ^{i-1}_{k} (\alpha ) \in B_\lambda ^0\) or \(\pi ^{i-1}_{k} (\alpha ) \in B_\lambda ^1\). If \(\pi ^{i-1}_{k} (\alpha ) \in B_\lambda ^0\), then
If \(\pi ^{i-1}_{k} (\alpha ) \in B_\lambda ^1\), then
For \(\alpha \in A_{i-1}\), \(l \in \{0,1\}\) and \(\beta , \beta ' \in B_\alpha ^l\) with \(\beta \ne \beta '\), because of (**), we have
which shows (2). For \(\alpha \in A_n\), we have

which implies (3).
To show (4), let \(\beta , \beta ' \!\in A_k\) with \(\beta \ne \beta '\). If \(\pi _k(\beta ) \ne \pi _k(\beta ')\), then
If \(\pi _k(\beta ) = \pi _k(\beta ')\), \(\beta \in B_\alpha ^0\) and \(\beta ' \!\in B_\alpha ^1\) for \(\alpha = \pi _k(\beta )\), then \(\mathrm{dist}\,(X^k_\beta , X^k_{\beta '}) \geqslant R\) since \(X^k_\beta \subseteq N(X^{k-1}_\beta \!,(j_k-1)R)\) and \(X^k_{\beta '} \cap N\bigl (\bigcup _{\gamma \in B_{\alpha }^0}X^{k-1}_\gamma \!, j_k R\bigr ) =\varnothing \). If \(\pi _k(\beta ) = \pi _k(\beta ')\) and \(\beta , \beta ' \!\in B_\alpha ^l\) for \(\alpha = \pi _k(\beta )\) and \(l \in \{0,1\}\), then \(\mathrm{dist}\,(X^k_\beta , X^k_{\beta '}) \geqslant R\) since \(\{X^k_\gamma \,{:}\, \gamma \in B_\alpha ^l\}\) is \((2^{k+3}-\sum _{j=1}^{k}2^{i+2})R\)-disjoint by (2) and \((2^{k+3}-\sum _{j=1}^{k}2^{i+2})R=2^3R>R\).
To show (5), let  and assume \(x\notin Z_k\). Since
and assume \(x\notin Z_k\). Since  , there is \(\lambda \in A_{k-1}\) such that \(x \in X^{k-1}_\lambda = \bigcup _{\beta \in \pi ^{-1}_k(\lambda )} X_\beta ^{k-1}\). Choose \(\beta \in \pi _k^{-1}(\lambda )\) satisfying \(x \in X^{k-1}_\beta \). Since \(x \notin Z_k\), we have \(x \notin W^{j_k}_\lambda \). This and \(x \in X^{k-1}_\lambda \) imply either \(x \notin N\bigl (\bigcup _{\gamma \in B_\lambda ^0}X^{k-1}_\gamma \!, j_kR\bigr )\) or \(x \in N\bigl (\bigcup _{\gamma \in B_\lambda ^0}X^{k-1}_\gamma \!, (j_k-1)R\bigr )\). If \(x \notin N\bigl (\bigcup _{\gamma \in B_\lambda ^0}X^{k-1}_\gamma \!, j_kR\bigr )\), then \(\beta \in B_\lambda ^1\) and
, there is \(\lambda \in A_{k-1}\) such that \(x \in X^{k-1}_\lambda = \bigcup _{\beta \in \pi ^{-1}_k(\lambda )} X_\beta ^{k-1}\). Choose \(\beta \in \pi _k^{-1}(\lambda )\) satisfying \(x \in X^{k-1}_\beta \). Since \(x \notin Z_k\), we have \(x \notin W^{j_k}_\lambda \). This and \(x \in X^{k-1}_\lambda \) imply either \(x \notin N\bigl (\bigcup _{\gamma \in B_\lambda ^0}X^{k-1}_\gamma \!, j_kR\bigr )\) or \(x \in N\bigl (\bigcup _{\gamma \in B_\lambda ^0}X^{k-1}_\gamma \!, (j_k-1)R\bigr )\). If \(x \notin N\bigl (\bigcup _{\gamma \in B_\lambda ^0}X^{k-1}_\gamma \!, j_kR\bigr )\), then \(\beta \in B_\lambda ^1\) and  . Suppose \(x \in N\bigl (\bigcup _{\gamma \in B_\lambda ^0}X^{k-1}_\gamma \!, (j_k-1)R\bigr )\). Then there exists \(\gamma \in B_\lambda ^0\) such that \(x \in N\bigl (X^{k-1}_\gamma , (j_k-1)R\bigr )\). This and \(x \in X^{k-1}_\lambda \) imply
. Suppose \(x \in N\bigl (\bigcup _{\gamma \in B_\lambda ^0}X^{k-1}_\gamma \!, (j_k-1)R\bigr )\). Then there exists \(\gamma \in B_\lambda ^0\) such that \(x \in N\bigl (X^{k-1}_\gamma , (j_k-1)R\bigr )\). This and \(x \in X^{k-1}_\lambda \) imply  .
.
Thus the families  satisfy (1)–(6).\(\square \)
satisfy (1)–(6).\(\square \)
Since  satisfies (3) and (4) in Claim 2,
satisfies (3) and (4) in Claim 2,  (see (*) for the definition of S), and the family
(see (*) for the definition of S), and the family  is R-disjoint. By (5), we have
is R-disjoint. By (5), we have  . This and (6) imply
. This and (6) imply  , and hence
, and hence  . Therefore X satisfies MSP.\(\square \)
. Therefore X satisfies MSP.\(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Weighill, T., Yamauchi, T. & Zava, N. Coarse infinite-dimensionality of hyperspaces of finite subsets. European Journal of Mathematics 8, 335–355 (2022). https://doi.org/10.1007/s40879-021-00515-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-021-00515-3




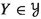 there exists
there exists 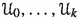 of X such that
of X such that 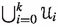 covers X and
covers X and 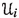 is
is 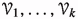 of subsets of X such that
of subsets of X such that 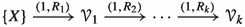 and
and 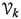 is uniformly bounded,
is uniformly bounded,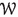 of subsets of X such that
of subsets of X such that 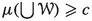 and
and 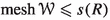 ,
,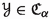 and a metric family
and a metric family 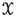 is coarsely embeddable into
is coarsely embeddable into 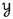 , then
, then 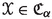 . In particular, if
. In particular, if 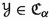 and
and 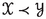 , then
, then 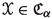 .
.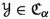 and a metric family
and a metric family 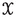 admits a bornologous map
admits a bornologous map 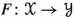 and an ordinal
and an ordinal 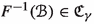 for every uniformly bounded
for every uniformly bounded 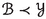 , then
, then 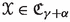 .
.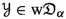 and a metric family
and a metric family 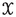 is coarsely embeddable into
is coarsely embeddable into  , then
, then 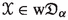 . In particular, if
. In particular, if 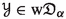 and
and 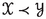 , then
, then 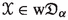 .
.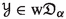 and a metric family
and a metric family 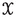 admits a bornologous map
admits a bornologous map 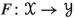 and an ordinal
and an ordinal 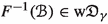 for every uniformly bounded
for every uniformly bounded 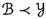 , then
, then 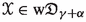 .
.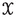 and
and 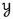 are metric families with a coarsely n-to-1 coarsely surjective map
are metric families with a coarsely n-to-1 coarsely surjective map 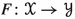 such that
such that 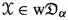 , then
, then 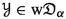 .
.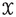 and
and 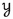 are metric families with a coarsely n-to-1 coarsely surjective map
are metric families with a coarsely n-to-1 coarsely surjective map 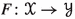 such that
such that 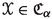 , then
, then 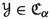 .
. ,
, is R-disjoint,
is R-disjoint,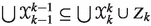 , and
, and