Abstract
Given a continuous function \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\), we denote the so-called “big Lip” and “little lip” functions by  and
and  respectively. We are interested in the following question. Given a set \(E \subset {\mathbb {R}}\), is it possible to find a continuous function f such that
respectively. We are interested in the following question. Given a set \(E \subset {\mathbb {R}}\), is it possible to find a continuous function f such that  or
or  ? For monotone continuous functions we provide a rather straightforward answer. For arbitrary continuous functions the answer is much more difficult to find. We introduce the concept of uniform density type (UDT) and show that if E is \(G_\delta \) and UDT then there exists a continuous function f satisfying
? For monotone continuous functions we provide a rather straightforward answer. For arbitrary continuous functions the answer is much more difficult to find. We introduce the concept of uniform density type (UDT) and show that if E is \(G_\delta \) and UDT then there exists a continuous function f satisfying  , that is, E is a
, that is, E is a  set. In the other direction we show that every
set. In the other direction we show that every  set is \(G_\delta \) and weakly dense. We also show that the converse of this statement is not true, namely that there exist weakly dense \(G_{{\delta }}\) sets which are not
set is \(G_\delta \) and weakly dense. We also show that the converse of this statement is not true, namely that there exist weakly dense \(G_{{\delta }}\) sets which are not  . We say that a set \(E\subset \mathbb {R}\) is
. We say that a set \(E\subset \mathbb {R}\) is  if there is a continuous function f such that
if there is a continuous function f such that  . We introduce the concept of strongly one-sided density and show that every
. We introduce the concept of strongly one-sided density and show that every  set is a strongly one-sided dense \(F_\sigma \) set.
set is a strongly one-sided dense \(F_\sigma \) set.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Throughout this note we assume that \(f:{\mathbb {R}} \rightarrow {\mathbb {R}}\) is continuous. Then the so-called “big Lip” and “little lip” functions are defined as follows:

where

As far as we know the definition of  first appeared in [9] and later reappeared in [12].
first appeared in [9] and later reappeared in [12].
In order to connect these functions to more customary ones, after denoting the Dini derivatives by \(D^{+}f(x), D^{-}f(x), D_{+}f(x), D_{-}f(x)\) (for the definitions see for example [3, p. 317]), one can easily check that

Note also that if f is differentiable at x, then  . Moreover,
. Moreover,  if and only if \(f'(x)=0\). The connection of
if and only if \(f'(x)=0\). The connection of  to the Dini derivatives is quite weak as the following example shows. Suppose that \(g({-1}/{2^{n^2}})=g(1/2^{n^2})=(-1)^{n}/2^{n^2}\), \(n=1,2,\dots \), and \(g(x)=0\) otherwise. The function g is not continuous, but one can easily see that by a slight modification of g one can obtain a continuous function f for which \(D^{+}f(0)=D^{-}f(0)=1\), \(D_{+}f(0)=D_{-}f(0)=-1\) while
to the Dini derivatives is quite weak as the following example shows. Suppose that \(g({-1}/{2^{n^2}})=g(1/2^{n^2})=(-1)^{n}/2^{n^2}\), \(n=1,2,\dots \), and \(g(x)=0\) otherwise. The function g is not continuous, but one can easily see that by a slight modification of g one can obtain a continuous function f for which \(D^{+}f(0)=D^{-}f(0)=1\), \(D_{+}f(0)=D_{-}f(0)=-1\) while  .
.
We also define

The behaviour of the two functions,  and
and  , is intimately related to the differentiability of f. For example, the Rademacher–Stepanov Theorem [14] tells us that if \( {\mathbb {R}}\backslash L_f\) has measure zero, then f is differentiable almost everywhere on \( {\mathbb {R}}\). On the other hand, in ([1], 2006) Balogh and Csörnyei construct a continuous function \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) such that
, is intimately related to the differentiability of f. For example, the Rademacher–Stepanov Theorem [14] tells us that if \( {\mathbb {R}}\backslash L_f\) has measure zero, then f is differentiable almost everywhere on \( {\mathbb {R}}\). On the other hand, in ([1], 2006) Balogh and Csörnyei construct a continuous function \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) such that  almost everywhere, but f is nowhere differentiable. However, in the same paper, they also show that if \( {\mathbb {R}}\backslash l_f\) is countable and
almost everywhere, but f is nowhere differentiable. However, in the same paper, they also show that if \( {\mathbb {R}}\backslash l_f\) is countable and  is locally integrable, then f is again differentiable almost everywhere on \( {\mathbb {R}}\).
is locally integrable, then f is again differentiable almost everywhere on \( {\mathbb {R}}\).
More recently, progress has been made on characterizing the sets \(L_f\) and \(l_f\) for continuous functions ([8], 2018) and characterizing the sets of non-differentiability for continuous functions with either  or
or  ([11], 2016). There are still a number of open problems concerning the relationship between \(L_f\) (\(l_f\)) and the differentiability properties of f.
([11], 2016). There are still a number of open problems concerning the relationship between \(L_f\) (\(l_f\)) and the differentiability properties of f.
We also mention the very recent result ([15], 2019) about little Lipschitz maps of analytic metric spaces with sufficiently high packing dimension onto cubes in \( {\mathbb {R}}^n\).
It is an interesting problem to characterize the functions  and
and  for continuous functions f. This is in the spirit of the well-known problem of characterizing the functions f which are derivatives. (See [4, 16, 19, 20].) In this note, we take a first step in this direction by investigating when it is possible for
for continuous functions f. This is in the spirit of the well-known problem of characterizing the functions f which are derivatives. (See [4, 16, 19, 20].) In this note, we take a first step in this direction by investigating when it is possible for  (or
(or  ) to be a characteristic function. Given a set \(E \subset {\mathbb {R}}\), we say that E is
) to be a characteristic function. Given a set \(E \subset {\mathbb {R}}\), we say that E is  (
( ) if there is a continuous function f defined on \( {\mathbb {R}}\) such that
) if there is a continuous function f defined on \( {\mathbb {R}}\) such that  (
( ). So we are interested in determining which sets E are
). So we are interested in determining which sets E are  or
or  . (See [13] for a related problem.)
. (See [13] for a related problem.)
It turns out that it is straightforward to decide this in the special case where f is monotone. We say that E is monotone  (
( ) if there is a continuous, monotone function f such that
) if there is a continuous, monotone function f such that  (
( ). In Theorems 3.1 and 3.4 we show that monotone
). In Theorems 3.1 and 3.4 we show that monotone  and
and  sets can be characterized using simple density conditions. The details for this are laid out in Sect. 3.
sets can be characterized using simple density conditions. The details for this are laid out in Sect. 3.
In Sect. 4 we see that  sets are weakly dense \(G_{{\delta }}\) sets (Definition 2.1, Theorem 4.1) and
sets are weakly dense \(G_{{\delta }}\) sets (Definition 2.1, Theorem 4.1) and  sets are strongly one-sided dense \(F_{\sigma }\) sets (Definition 3.2, Theorem 4.6). In Theorem 4.3 we show that a set E is
sets are strongly one-sided dense \(F_{\sigma }\) sets (Definition 3.2, Theorem 4.6). In Theorem 4.3 we show that a set E is  if and only if \(\mathbb {R}\) can be divided into three sets such that they give a ternary decomposition with respect to E in the sense of Definition 4.2. In Theorem 4.7 it is proved that countable disjoint unions of closed and strongly one-sided dense sets are
if and only if \(\mathbb {R}\) can be divided into three sets such that they give a ternary decomposition with respect to E in the sense of Definition 4.2. In Theorem 4.7 it is proved that countable disjoint unions of closed and strongly one-sided dense sets are  .
.
In Sect. 5 we consider a more difficult problem of characterizing general  sets. Given a measurable set, we introduce a two-parameter family of sets describing its levels of density and use this to define uniform density type (UDT) sets.
sets. Given a measurable set, we introduce a two-parameter family of sets describing its levels of density and use this to define uniform density type (UDT) sets.
Definition 1.1
Suppose that \(E\subseteq \mathbb {R}\) is measurable and \(\gamma ,\delta >0\). Let

where |E| denotes the Lebesgue measure of the set E.
We say that E has uniform density type (UDT) if there exist sequences \(\gamma _n\nearrow 1\) and \(\delta _n\searrow 0\) such that \(E\subseteq \bigcap _{k=1}^{\infty } \bigcup _{n=k}^{\infty }E^{\gamma _n,\delta _n}\).
Our main result from Sect. 5, Theorem 5.6, states that \(G_\delta \) sets which are UDT are  . As we show in [5], the converse of this statement does not hold. There exist
. As we show in [5], the converse of this statement does not hold. There exist  sets which are not UDT.
sets which are not UDT.
Finally, in Sect. 6 we show that the UDT condition in Theorem 5.6 cannot be replaced with one of the weaker density conditions from Sect. 3.
Summarizing the main results of this paper, we show that

and that the second implication cannot be reversed.
2 Preliminary definitions and results
The union of disjoint sets A and B is denoted by \(A\sqcup B\). For any \(S,T\subset {\mathbb {R}}\) and \(x \in {\mathbb {R}}\) we define d(S, T) to be the lower distance from S to T, that is  . Let \(d(x,S)=d(\{x\},S)\). (We recall that we defined |S| to be the Lebesgue measure of S.)
. Let \(d(x,S)=d(\{x\},S)\). (We recall that we defined |S| to be the Lebesgue measure of S.)
In the space of continuous functions defined on an interval I we use the supremum norm  and the metric topology generated by this norm.
and the metric topology generated by this norm.
Definition 2.1
Given a sequence of non-degenerate closed intervals \(\{I_n\}\), we write \(I_n\rightarrow x\) if \(x \in I_n\) for all \(n \in \mathbb {N}\) and \(|I_n|\rightarrow 0\). The measurable set E is weakly dense at x if there exists \(I_n \rightarrow x\) such that \({|E \cap I_n|}/{|I_n|}\rightarrow 1\). The set E is weakly dense if E is weakly dense at x for each \(x \in E\). The set E is strongly dense at x if for every sequence \(\{I_n\}\) such that \(I_n \rightarrow x \) we have \( {|E \cap I_n|}/{|I_n|}\rightarrow 1\). We say that E is strongly dense if E is strongly dense at x for each \(x \in E\).
Note: E being strongly dense at x, just means that x is a point of density of E. (See Remark 3.3.)
In this paper a.e. always means almost everywhere with respect to the Lebesgue measure.
Lemma 2.2
If \(E\subset {\mathbb {R}}\) and \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) such that  then \(|f(a)-f(b)|\leqslant |[a,b]\cap E|\) for every \(a,b\in {\mathbb {R}}\) (where \(a<b\)) so f is Lipschitz and hence absolutely continuous.
then \(|f(a)-f(b)|\leqslant |[a,b]\cap E|\) for every \(a,b\in {\mathbb {R}}\) (where \(a<b\)) so f is Lipschitz and hence absolutely continuous.
Proof
Let \( {\varepsilon }>0\). For every \(x\in {\mathbb {R}}\) we fix \(r_x\in (0, {\varepsilon })\) such that \(M_f(x,r_x)<1+ {\varepsilon }\). We select a finite set \(H\subset {\mathbb {R}}\) for which  is a minimal cover of [a, b]. Then every \(y\in {\mathbb {R}}\) is contained by at most two of these open intervals. If \(x\in {\mathbb {R}}\), \(r>0\) and \(y\in (x-r,x+r)\), we have \(|f(x)-f(y)|\leqslant rM_f(x,r)\). Thus
is a minimal cover of [a, b]. Then every \(y\in {\mathbb {R}}\) is contained by at most two of these open intervals. If \(x\in {\mathbb {R}}\), \(r>0\) and \(y\in (x-r,x+r)\), we have \(|f(x)-f(y)|\leqslant rM_f(x,r)\). Thus
Hence f is Lipschitz as a, b and \( {\varepsilon }\) were chosen arbitrarily.
Since f is Lipschitz, it is absolutely continuous. Therefore \(f'\) exists almost everywhere and  . Since \(|f'| \leqslant \mathbf {1}_E \) a.e., we obtain that
. Since \(|f'| \leqslant \mathbf {1}_E \) a.e., we obtain that  . \(\square \)
. \(\square \)
3 Necessary and/or sufficient conditions for monotone  and
and  sets
sets
For monotone  and
and  sets it is rather easy to obtain necessary and sufficient conditions.
sets it is rather easy to obtain necessary and sufficient conditions.
Theorem 3.1
The set E is monotone  if and only if E is weakly dense and \(E^\mathrm{c}\) is strongly dense.
if and only if E is weakly dense and \(E^\mathrm{c}\) is strongly dense.
Proof
Assume that E is monotone  . Then we can choose a continuous, monotone increasing function f such that
. Then we can choose a continuous, monotone increasing function f such that  . By Lemma 2.2, f is Lipschitz and therefore differentiable a.e. Since
. By Lemma 2.2, f is Lipschitz and therefore differentiable a.e. Since  and f is increasing, we conclude that \(f'(x)= \mathbf {1}_E (x)\) a.e. and we have
and f is increasing, we conclude that \(f'(x)= \mathbf {1}_E (x)\) a.e. and we have

From (1) and the definition of  it is straightforward to show that E is weakly dense and \(E^\mathrm{c}\) is strongly dense.
it is straightforward to show that E is weakly dense and \(E^\mathrm{c}\) is strongly dense.
Now assume that E is weakly dense and \(E^\mathrm{c}\) is strongly dense. Then let  by selecting an arbitrary \(x_{0}\). It is straightforward to show that
by selecting an arbitrary \(x_{0}\). It is straightforward to show that  and therefore E is monotone
and therefore E is monotone  . \(\square \)
. \(\square \)
For the characterization of monotone  sets we need a few new definitions.
sets we need a few new definitions.
Definition 3.2
Suppose that \(I_n \rightarrow x\). If each \(I_n\) is centered at x we say that \(\{I_n\}\) center converges to x and we write \(I_n {\mathop {\rightarrow }\limits ^\mathrm{c}} x\).
The set E is weakly center dense at x if there exists a sequence \(\{I_n\}\) such that \(I_n {\mathop {\rightarrow }\limits ^\mathrm{c}} x,\) and \({|E \cap I_n|}/{|I_n|}\rightarrow 1\). The set E is weakly center dense if E is weakly center dense at every point \(x \in E\).
The set E is strongly one-sided dense at x if for any sequence \(\{I_n\}=\{[x-r_n,x+r_n]\}\) such that \(r_n \searrow 0\) we have  . The set E is strongly one-sided dense if E is strongly one-sided dense at every point \(x \in E\).
. The set E is strongly one-sided dense if E is strongly one-sided dense at every point \(x \in E\).
Remark 3.3
It is easy to see that if E is right- or left-dense in the ordinary Lebesgue density sense then it is strongly one-sided dense. The reverse implication is not true. Indeed, it is not difficult to see that the set

is strongly one-sided dense at 0 according to our notation but it is not right- or left-dense in the ordinary Lebesgue density sense.
The observant reader will note that we have not defined strongly center dense or weakly one-sided dense. The reason for this is that defining these terms in the obvious way would be redundant since strongly center dense sets would be equivalent to strongly dense sets and weakly one-sided dense sets would be equivalent to weakly dense sets. We also observe that the following implications hold:
Note that neither of the above implications is reversible: a closed interval is strongly one-sided dense and weakly dense, but not strongly dense or weakly center dense.
Theorem 3.4
The set E is monotone  if and only if E is strongly one-sided dense and \(E^\mathrm{c}\) is weakly center dense.
if and only if E is strongly one-sided dense and \(E^\mathrm{c}\) is weakly center dense.
Proof
The proof of Theorem 3.4 is straightforward and similar to the proof of Theorem 3.1. We leave it up to the reader.\(\square \)
4 Necessary and/or sufficient conditions for general  and
and 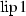 sets
sets
In Theorem 4.1 we give a necessary condition for a set to be  . We will see in Sect. 6 (Theorem 6.3) that this condition is not sufficient.
. We will see in Sect. 6 (Theorem 6.3) that this condition is not sufficient.
Theorem 4.1
If \(E\subset {\mathbb {R}}\) is  then E is a weakly dense \(G_\delta \) set.
then E is a weakly dense \(G_\delta \) set.
Proof
Suppose that E is  . Lemma 2.2 implies that E is weakly dense. Let \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) be such that
. Lemma 2.2 implies that E is weakly dense. Let \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) be such that  . Since
. Since

and the sets on the right are open, we obtain that E is \(G_\delta \).\(\square \)
The next definition will be used to obtain a necessary and sufficient condition for  sets in Theorem 4.3.
sets in Theorem 4.3.
Definition 4.2
Let E be a measurable subset of \( \mathbb {R} \) and suppose that \(E_1,E_0,E_{-1}\) are pairwise disjoint measurable sets whose union is \( \mathbb {R} \). Then we say that \(E_1,E_0,E_{-1}\) is a ternary decomposition of \(\, \mathbb {R} \) with respect to E if the following conditions hold:
-
for all \(x \in E \;\text {either}\; E_1 \;\text {or}\;E_{-1} \;\text {is weakly dense at}\;x\),
-
for all \(x \notin E \;\text {and}\; \forall I_n \rightarrow x \;\text {we have}\;\frac{||E_1 \cap I_n| - |E_{-1}\cap I_n||}{|I_n|} \rightarrow 0\).
If \(E_1,E_0,E_{-1}\) is a ternary decomposition of \( \mathbb {R} \) with respect to E we write \(E \sim (E_1,E_0,E_{-1})\).
Theorem 4.3
A set E is  if and only if there is a ternary decomposition of \(\, \mathbb {R} \) with respect to E.
if and only if there is a ternary decomposition of \(\, \mathbb {R} \) with respect to E.
Proof
Suppose that \(E \sim (E_1,E_0,E_{-1})\). Define

Then straightforward calculations show that  .
.
Working in the opposite direction, now assume that  . Then by Lemma 2.2, f is Lipschitz and hence f is differentiable almost everywhere and wherever \(f'(x)\) is defined \(f'(x)\) is equal to either 1, 0 or \(-1\). For \(i=1,-1\) define \(E_i=\{x\,{ :}\, f'(x)=i\}\) and let \(E_0=\mathbb {R} \backslash (E_1 \,{\cup }\, E_{-1})\). By absolute continuity of f we have that
. Then by Lemma 2.2, f is Lipschitz and hence f is differentiable almost everywhere and wherever \(f'(x)\) is defined \(f'(x)\) is equal to either 1, 0 or \(-1\). For \(i=1,-1\) define \(E_i=\{x\,{ :}\, f'(x)=i\}\) and let \(E_0=\mathbb {R} \backslash (E_1 \,{\cup }\, E_{-1})\). By absolute continuity of f we have that

and it is straightforward to show that \(E\sim (E_1,E_0,E_{-1})\).\(\square \)
Remark 4.4
Suppose that \(E \sim (E_1,E_0,E_{-1})\). Then we can find \(F_1,F_0,F_{-1}\) such that \(E \sim (F_1,F_0,F_{-1})\) and \(E = F_1 \cup F_{-1}\).
To verify that Remark 4.4 is true assume that \(E \sim (E_1,E_0,E_{-1})\). By the Lebesgue density theorem, almost every element in a set is a density point of the set and hence it follows from the definition of a ternary decomposition that \(|E_i \backslash E|=0\) for \(i =1,-1\) and \(|E_0 \cap E|=0\). Thus, if we define \(F_1=E\backslash E_{-1}\), \(F_{-1}=E_{-1} \cap E\), and  , then we have \(E \sim (F_1,F_0,F_{-1})\) and \(E = F_1 \cup F_{-1}\).
, then we have \(E \sim (F_1,F_0,F_{-1})\) and \(E = F_1 \cup F_{-1}\).
Remark 4.5
Although Theorem 4.3 gives a characterization of  sets, it is not always easy to verify whether or not a given set E has a ternary decomposition. One simple example is \(E=(0,\infty )\). In this case, one can verify that \(E_0=(-\infty ,0]\), \(E_{-1}=\bigcup _{n=1}^\infty (1/({2n+1}), 1/{2n}]\), \(E_1=\bigl (\bigcup _{n=1}^\infty (1/{2n},1/({2n-1})]\bigr )\cup (1,\infty )\) gives a ternary decomposition of \( {\mathbb {R}}\) with respect to E and therefore E is
sets, it is not always easy to verify whether or not a given set E has a ternary decomposition. One simple example is \(E=(0,\infty )\). In this case, one can verify that \(E_0=(-\infty ,0]\), \(E_{-1}=\bigcup _{n=1}^\infty (1/({2n+1}), 1/{2n}]\), \(E_1=\bigl (\bigcup _{n=1}^\infty (1/{2n},1/({2n-1})]\bigr )\cup (1,\infty )\) gives a ternary decomposition of \( {\mathbb {R}}\) with respect to E and therefore E is  .
.
Next we want to find some necessary and some sufficient conditions for  sets. For this purpose we will need to use Lemma 2.2.
sets. For this purpose we will need to use Lemma 2.2.
Theorem 4.6
If \(E\subset {\mathbb {R}}\) is  then E is a strongly one-sided dense \(F_\sigma \) set.
then E is a strongly one-sided dense \(F_\sigma \) set.
Proof
Suppose that E is  . Lemma 2.2 implies that E is strongly one-sided dense. Let \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) such that
. Lemma 2.2 implies that E is strongly one-sided dense. Let \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) such that  . As
. As

and the sets on the right are open, the set \(E^\mathrm{c}\) is \(G_\delta \) hence E is \(F_\sigma \).\(\square \)
Theorem 4.6 provides a necessary condition for a function to be  . The following result provides a sufficient condition.
. The following result provides a sufficient condition.
Theorem 4.7
Suppose that \(E=\bigsqcup _{n=1}^\infty E_n\) where for each \(n \in \mathbb {N} \), \(E_n\) is closed and strongly one-sided dense. Then E is  .
.
We should note that simple examples show that the converse of Theorem 4.7 does not hold. For example, non-empty, open sets are  , but no non-empty, open set can be expressed as a disjoint, countable union of closed sets.
, but no non-empty, open set can be expressed as a disjoint, countable union of closed sets.
We note that apart from unions of non-degenerate closed intervals, it is not completely trivial to construct closed and strongly one-sided dense sets. However, in [5, Theorem 3.1] we construct a nowhere dense closed set which has SUDT and hence is strongly one-sided dense.
Remark 4.8
A result analogous to Theorem 4.7 for  sets is not true. If E is dense in \( \mathbb {R} \) and each \(E_n\) is nowhere dense, then E is not
sets is not true. If E is dense in \( \mathbb {R} \) and each \(E_n\) is nowhere dense, then E is not  . Indeed, according to Theorem 4.1, if E were
. Indeed, according to Theorem 4.1, if E were  , it would be \(G_{\delta }\) as well. However, a dense \(G_{\delta }\) set cannot be written as a countable union of nowhere dense sets according to Baire’s category theorem.
, it would be \(G_{\delta }\) as well. However, a dense \(G_{\delta }\) set cannot be written as a countable union of nowhere dense sets according to Baire’s category theorem.
The proof of Theorem 4.7 depends on the following:
Lemma 4.9
Suppose that E is closed and strongly one-sided dense. Let \(\varepsilon >0\). Then there exists a continuous function f such that
-
(i)
 ,
, -
(ii)
\(0 \leqslant f(x) \leqslant \varepsilon \) for all \(x \in \mathbb {R}\).
Proof
For every \(i\in {\mathbb {Z}}\) define  and choose \(x_i\in E_i\) such that \(|E\cap [a_{i-1},x_i]|=|E\cap [x_i,a_i]|\). For each \(i\in \mathbb {Z}\) define \(E^+_i=E\cap [a_{i-1},x_i]\) and \(E^-_i=E\cap [x_i,a_i]\) and let
and choose \(x_i\in E_i\) such that \(|E\cap [a_{i-1},x_i]|=|E\cap [x_i,a_i]|\). For each \(i\in \mathbb {Z}\) define \(E^+_i=E\cap [a_{i-1},x_i]\) and \(E^-_i=E\cap [x_i,a_i]\) and let  and
and  . Define
. Define  . It is easy to verify that (i) and (ii) hold.\(\square \)
. It is easy to verify that (i) and (ii) hold.\(\square \)
Proof of Theorem 4.7
Assume that \(E=\bigsqcup _{n=1}^\infty E_n\), where each \(E_n\) is closed and strongly one-sided dense. Redefining \(E_1,E_2,\ldots \) we can suppose that if \(n\geqslant 2\) then \(E_n\) is bounded.
Using Lemma 4.9 we choose \(f_1\) such that (i) and (ii) of Lemma 4.9 hold with f replaced by \(f_1\), E replaced by \(E_1\) and \(\varepsilon =1\). Using Lemma 4.9 for each \(n \in \mathbb {N}\cap [2,\infty )\) we recursively choose \(f_n\geqslant 0\) such that (i) holds with f replaced by \(f_n\) and E replaced with \(E_n\) such that

(we note that the right-hand side is positive, as \(E_n\) is compact and \(\bigcup _{k=1}^{n-1} E_k\) is closed). Obviously, for every \(n\in {\mathbb {N}}\),
Let \(f(x)=\sum _{n=1}^\infty f_n\). Suppose that \(x\in E_{n_0}\) for some \(n_0\in {\mathbb {N}}\), and \( {\varepsilon } >0\). Using
we infer

Let

For every \(y\in [x-r,x+r]\) we have

Thus  .
.
Now let \(x\notin E\) and \(\varepsilon >0\) be arbitrary. If x is not an accumulation point of E then obviously  . Otherwise, set
. Otherwise, set  and
and  . For every \(y\in [x-r,x+r]\),
. For every \(y\in [x-r,x+r]\),

Since \(r\rightarrow 0\) as \(n_1\rightarrow \infty \) (and \(n_1\rightarrow \infty \) as \( {\varepsilon }\rightarrow 0\)), we obtain  . \(\square \)
. \(\square \)
The refereeing procedure for this paper took a while and during this time in [6] we managed to obtain a characterization of  sets as countable unions of closed sets which are strongly one-sided dense. The above special case in Theorem 4.7 has a simpler proof than the main result of [6].
sets as countable unions of closed sets which are strongly one-sided dense. The above special case in Theorem 4.7 has a simpler proof than the main result of [6].
5
\(G_{{\delta }}\) uniform density type sets are 
In this section we prove our main result: Theorem 5.6, which asserts that \(G_\delta \) sets which are also UDT are  . Recall that the sets \(E^{\gamma ,\delta }\) were defined in Definition 1.1.
. Recall that the sets \(E^{\gamma ,\delta }\) were defined in Definition 1.1.
Lemma 5.1
For any \(\gamma ,\delta >0\) the set \(E^{\gamma ,\delta }\) is closed.
Proof
For \(r>0\) we introduce the notation

Then we obviously have

Note that the functions \(x \mapsto \frac{|(x-r,x)\cap E|}{r}\) and \(x \mapsto \frac{|(x,x+r)\cap E|}{r}\) are obviously continuous for any r and hence

is also continuous, which immediately yields that each upper level set \(E_r^{\gamma }\) is closed. Consequently, their intersection \(E^{\gamma ,\delta }\) is also closed. \(\square \)
Proposition 5.2
UDT sets are strongly one-sided dense.
Remark 5.3
There are strongly one-sided dense sets which are not UDT, however the construction of such sets is not that easy. We wrote a short note, [7] on this topic.
Proof
Suppose E is UDT. Then there exist sequences \(\gamma _n\nearrow 1\) and \(\delta _n\searrow 0\) such that \(E\subseteq \bigcap _{k=1}^{\infty } \bigcup _{n=k}^{\infty }E^{\gamma _n,\delta _n}\). Let \(x\in E\) and \(\gamma <1\). Choose k such that \(\gamma _{n}>\gamma \) when \(n\geqslant k\). Then there exists \(n(\gamma , x)\geqslant k\) such that \(x\in E^{\gamma _{n(\gamma , x)},\delta _{n(\gamma , x)}}\), that is

Since this is true for any \(0<\gamma <1\), we see that E is strongly one-sided dense at x. \(\square \)
The following notion is closely related to UDT.
Definition 5.4
We say that E has strong uniform density type (SUDT) if there exist sequences \(\gamma _n\nearrow 1\) and \(\delta _n\searrow 0\) such that \(E\subseteq \bigcup _{k=1}^{\infty } \bigcap _{n=k}^{\infty }E^{\gamma _n,\delta _n}\).
For the following proposition assume that all sets which occur in its statement are measurable subsets of \(\mathbb {R}\).
Proposition 5.5
-
(i)
If a set E has SUDT then it also has UDT.
-
(ii)
Any interval has SUDT (and hence UDT).
-
(iii)
If \(E_1, E_2, \dots \) have UDT (resp. SUDT) then \(E= \bigcup _{m=1}^{\infty }E_m\) also has UDT (resp. SUDT).
-
(iv)
There exists E which has SUDT but its closure \(\overline{E}\) is not strongly one-sided dense and hence does not have UDT.
Proof
Statements (i) and (ii) are obvious.
In (iii) we will examine the UDT case, the proof of the SUDT case is basically the same. For each set \(E_m\) choose a pair of sequences \((\gamma _{m,n})_{n=1}^\infty , (\delta _{m,n})_{n=1}^\infty \) such that \(\gamma _{m,n}\nearrow 1\) and \(\delta _{m,n}\searrow 0\) such that \(E_m\subseteq \bigcap _{k=1}^{\infty } \bigcup _{n=k}^{\infty }E^{\gamma _{m,n},\delta _{m,n}}\). Then a straightforward diagonalization argument shows that we can choose sequences \((\gamma _n)_{n=1}^\infty \) and \((\delta _n)_{n=1}^\infty \) such that \(\gamma _n\nearrow 1\) and \(\delta _n\searrow 0\) and for every \(m\in {\mathbb {N}}\) there is an \(n_m\in {\mathbb {N}}\) for which
Thus for every \(m\in {\mathbb {N}}\) and \(n>n_m\) we have that  , hence
, hence

This implies
that is E has UDT.
Finally, for (iv) consider

By (iii), E has SUDT as it is a countable union of intervals. Note that its closure is \(\overline{E}=E\cup \{0\}\). But in intervals of the form \((0,2^n-2^{n-2})\), \(n\in {\mathbb {Z}}\), the set \(\overline{E}\) has density

and for any interval of the form \((-r,0)\) for \(r>0\) the set \(\overline{E}\) has density 0. Consequently, E is not strongly-one sided dense at 0 and therefore not UDT. \(\square \)
The following theorem is the main result of this paper.
Theorem 5.6
Assume that E is \(G_\delta \) and E has UDT. Then there exists a continuous function f satisfying  , that is, the set E is
, that is, the set E is  .
.
In order to prove the theorem we will need a pair of definitions and a couple of technical lemmas.
Definition 5.7
By a vicinity U of a function \(f:\mathbb {R}\rightarrow \mathbb {R}\) we mean the set of functions of the following form:

where r(x) is a fixed, continuous, non-negative function, called the radius of U.
Definition 5.8
Suppose that f is continuous on the interval [a, b] and \(f_l,f_u\) are continuous on [a, b] with \(f_l< f < f_u\) on (a, b) and \(f_l(a)=f_u(a)=f(a)\) and \(f_l(b)=f_u(b)=f(b)\). Then we say that \((f_l,f_u)\) is an envelope for f on [a, b] and we write \(f \in (f_l,f_u)\) on [a, b].
For each of the following lemmas we assume that E is as in the statement of Theorem 5.6 and that  . Observe that \(\phi (y)-\phi (x) = |[x,y]\cap E|\) for \(x\leqslant y\).
. Observe that \(\phi (y)-\phi (x) = |[x,y]\cap E|\) for \(x\leqslant y\).
Lemma 5.9
Assume that f is continuous and monotone on [a, b] and \(f\in (f_l,f_u)\) on [a, b]. Furthermore, let \(0< \delta < \epsilon \leqslant 1\) and assume that
Then, there exists a continuous function g on [a, b] such that
-
\(g \in (f_l,f_u)\) on [a, b],
-
g is locally piecewise monotone on (a, b), that is any compact subinterval of (a, b) can be divided into finitely many subintervals on each of which g is monotone,
-
on any interval of monotonicity of g there exists a constant K depending only on the interval such that
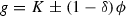 .
.
Proof
We first note the following useful fact, which follows from the inequalities \(0<\delta < \epsilon \) and inequality (7):
Given any interval \([r,s] \subset (a,b)\), we can choose \(t\in (r,s)\) such that

Next, we note that in order to prove the lemma it suffices to prove that for any subinterval \([c,d]\subset (a,b)\) we can construct a continuous function g on [c, d] such that
-
(i)
\(f_l(x)< g(x) < f_u(x)\) on [c, d],
-
(ii)
\(g(c)=f(c)\) and \(g(d)=f(d)\),
-
(iii)
g is piecewise monotone on [c, d],
-
(iv)
 on each interval of monotonicity of g, recall that we use constants K which depend on the interval considered.
on each interval of monotonicity of g, recall that we use constants K which depend on the interval considered.
Assume that \([c,d] \subset (a,b)\). Let

Using the uniform continuity of \(f_{u}\) and \(f_{l}\) on [c, d] choose a positive integer n such that

For \(i=0,1,2,\ldots , n\) let \(c_{2i}=c+i({d-c})/n\) so we have \(c=c_0<c_2<c_4<\cdots <c_{2n}=d\). Using (8) for each \(i=1,2,\ldots , n\) we choose \(c_{2i-1} \in (c_{2i-2},c_{2i})\) such that
Next, for each \(j=0,1,2,\ldots ,2n-1\) we define g in  by
by

We see that for \(j=0,1,2,\ldots , n-1\) we have g is monotone increasing on \([c_{2j},c_{2j+1}]\) and monotone decreasing on \([c_{2j+1},c_{2j+2}]\). Furthermore,  on each interval \([c_i,c_{i+1}]\) for \(i=0,1,2,\ldots , 2n-1\) with suitable constants \(K_{i}\). We also see that (ii) holds and (i) follows from inequality (9). \(\square \)
on each interval \([c_i,c_{i+1}]\) for \(i=0,1,2,\ldots , 2n-1\) with suitable constants \(K_{i}\). We also see that (ii) holds and (i) follows from inequality (9). \(\square \)
Lemma 5.10
Suppose that f is continuous on [a, b], \(f\in (f_l,f_u)\) on [a, b], and H is a closed set such that \(H \subset (a,b)\backslash E\). Furthermore, assume that \(0< \delta < \epsilon \leqslant 1\) and (7) holds. Then there exists a function g continuous on [a, b] with
-
(i)
\(g\in (f_l,f_u)\) on [a, b],
-
(ii)
\(g(a)=f(a)\), \(g(b)=f(b)\),
-
(iii)
\(g'=0\) on H,
-
(iv)
\(|g(x)-g(y)|\leqslant (1-\delta )|\phi (x)-\phi (y)|\,\) for all \(x,y \in [a,b]\).
Proof
Write (a, b) as a countable union of non-overlapping closed intervals [c, d] which satisfy

Assume that [c, d] is a closed subinterval of (a, b) satisfying (10). It suffices to show that we can define g on [c, d] such that
and
We treat the case where \(c,d \in H\). If either c or d is not in H, one can proceed similarly: this argument is left to the reader. We note that if \(|E \,{\cap }\, (c,d)| = 0\), then it follows from inequality (7) that f is constant on [c, d] and we simply define \(g=f\) on [c, d]. Thus we may as well assume that \(|E \,{\cap }\, (c,d)|>0\). We also assume without loss of generality that \(f(d)\geqslant f(c)\). Next we choose finitely many intervals \(I_i=(c_{2i-1},c_{2i})\), \(i=1,2,\ldots ,n\), which are contiguous to \(H\cap [c,d]\) and such that \(c\leqslant c_1< c_2 \leqslant c_3< c_4 \leqslant \cdots \leqslant c_{2n-1}<c_{2n}\leqslant d\) and

Furthermore, we choose \(\gamma \) so that

and note that \(\gamma < 1-\delta \). Using this fact, on each interval \([c_{2i-1},c_{2i}]\) one can define a monotone function \(g_i\) so that
and
We also extend \(g_i\) to the entire interval [c, d] by defining \(g_i=0\) on \([c,c_{2i-1}]\) and \(g_i=g_i(c_{2i})\) on \([c_{2i},d]\). Finally, we define \(g=f(c)+\sum _{i=1}^n g_i\) on [c, d]. Then using (10) it is straightforward to verify that (11)–(14) hold and we are done with the proof.\(\square \)
Proof of Theorem 5.6
Throughout this proof the value of the constant K will depend on the interval with which it is associated. Fix sequences \(\gamma _n\) and \(\delta _n\) witnessing the UDT property of E. Let \(E= \bigcap _{n=1}^{\infty }G_n\), where each set \(G_n\) is open and \(G_{n+1}\subset G_n\) for all \(n \in {\mathbb {N}}\). We also assume, as we may, that each component of \(G_n\) intersects E. We also denote the complement of \(G_n\) by \(F_n\). Thus \((F_n)_{n=1}^{\infty }\) is an increasing sequence of closed sets. Let  be the integral function of the characteristic function of E. We will construct a sequence of functions \((f_n)_{n=1}^{\infty }\) together with a sequence of vicinities \((U_n)_{n=1}^\infty \) with the following properties (recall that the vicinity was defined in Definition 5.7):
be the integral function of the characteristic function of E. We will construct a sequence of functions \((f_n)_{n=1}^{\infty }\) together with a sequence of vicinities \((U_n)_{n=1}^\infty \) with the following properties (recall that the vicinity was defined in Definition 5.7):
-
(i)
\(f_n\) is differentiable on \(F_n\) and its derivative vanishes there.
-
(ii)
For any \(m\geqslant {n}\) we have \(f_m{\restriction } _{F_n} = f_n{\restriction } _{F_n}\).
-
(iii)
For any \(x,y\in \mathbb {R}\) we have \(|f_n(x)-f_n(y)|\leqslant (1-2^{-3n})|\phi (x)-\phi (y)|\).
-
(iv)
If (a, b) is an interval contiguous to \(F_n\), then for any
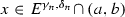 there exists \(y_n(x)\in (a,b)\) such that \(|x-y_n(x)|\leqslant \delta _n\) and
there exists \(y_n(x)\in (a,b)\) such that \(|x-y_n(x)|\leqslant \delta _n\) and  . Moreover, \(y_n(x)\) may be chosen so that \(|y_n(x)-x|\) is bounded away from 0 on each compact subset of (a, b). Additionally, \(f_n\) is locally monotone on (a, b) and on each interval of monotonicity we have
. Moreover, \(y_n(x)\) may be chosen so that \(|y_n(x)-x|\) is bounded away from 0 on each compact subset of (a, b). Additionally, \(f_n\) is locally monotone on (a, b) and on each interval of monotonicity we have  .
. -
(v)
Each \(U_n\) has a continuous radius \(r_n\) satisfying
 for all \(x \in {\mathbb {R}}\) and \(r_n(x)>0\) for all \(x \in G_n\) and \(r_n(x), r_n(y_n(x)) < 2^{-2n}\gamma _n|x-y_n(x)|\) for all \(x \in E^{\gamma _n,\delta _n}\). Moreover, \(f_m \in U_n\) for all \(m \geqslant n\) and \(U_{n+1}\subset U_n\) for all \(n \in {\mathbb {N}}\).
for all \(x \in {\mathbb {R}}\) and \(r_n(x)>0\) for all \(x \in G_n\) and \(r_n(x), r_n(y_n(x)) < 2^{-2n}\gamma _n|x-y_n(x)|\) for all \(x \in E^{\gamma _n,\delta _n}\). Moreover, \(f_m \in U_n\) for all \(m \geqslant n\) and \(U_{n+1}\subset U_n\) for all \(n \in {\mathbb {N}}\). -
(vi)
For any \(m\geqslant {n}\) and \(x \in G_n \cap E^{\gamma _n,\delta _n}\) we have

-
(vii)
For any \(g \in U_n\) we have \(g'=0\) on \(F_n\).
Assume for the moment that we have established (i)–(vii). From (v) it follows that the \(f_n\)s converge uniformly to some function f. Then, \(f \in U_n\) for all \(n \in {\mathbb {N}}\) so by (vii) we may conclude that  on \(\bigcup _{n=1}^\infty F_n= {\mathbb {R}}\backslash E\) and therefore
on \(\bigcup _{n=1}^\infty F_n= {\mathbb {R}}\backslash E\) and therefore  on \( {\mathbb {R}} \backslash E\). On the other hand, if \(x\in E\), we have \(x\in E^{\gamma _n,\delta _n}\) for infinitely many choices of n as E has UDT. Hence by (iv) and (vi) there exists \(y_n(x)\) satisfying \(|x-y_n(x)|<\delta _n\) and
on \( {\mathbb {R}} \backslash E\). On the other hand, if \(x\in E\), we have \(x\in E^{\gamma _n,\delta _n}\) for infinitely many choices of n as E has UDT. Hence by (iv) and (vi) there exists \(y_n(x)\) satisfying \(|x-y_n(x)|<\delta _n\) and  for all \(m \geqslant n\), which yields
for all \(m \geqslant n\), which yields  . As we have
. As we have  , we deduce that
, we deduce that  . On the other hand, by (iii),
. On the other hand, by (iii),  everywhere and we have
everywhere and we have  for \(x\in E\) which concludes the proof.
for \(x\in E\) which concludes the proof.
In the following we construct the \(f_n\)s and \(U_n\)s and verify that (i)–(vii) are valid. We begin by constructing \(f_1\) and then define the other functions recursively.
To begin we set \(f_0=f_0^*\equiv 0\) and we also define \(f_1=0\) on \(F_1\). Set
Now, consider an interval (a, b) contiguous to \(F_1\) see Fig. 1. We need to ensure that \(f_1\) has derivative 0 at a and b. Note that \(f_0\in (\mathscr {E}_1,\mathscr {E}^1)\) on [a, b]. Now applying Lemma 5.9 with \(f=f_0\), \(\delta =2^{-3}\), \( \epsilon =1\) and \((f_l,f_u)=(\mathscr {E}_1,\mathscr {E}^1)\) we can define \(f_1\) on [a, b] so that
and on any interval of monotonicity [c, d] of \(f_1\) we have

Note that by defining \(f_1\) in this fashion on each contiguous interval of \(F_1\) we ensure that \(f_1\) is differentiable on \(F_1\) with \(f_1'=0\) on \(F_1\). It follows that (i) is satisfied for \(n=1\) and it is easy to see that (iii) holds as well. (Regarding these properties, in the upcoming steps of the construction we will require that \(f_n\in (\mathscr {E}_1,\mathscr {E}^1)\) on [a, b] as well. This will make sure that the limit function f is differentiable on \(F_1\) and its derivative vanishes there as desired.)
We next demonstrate that (iv) holds. We assume without loss of generality that \(\gamma _1 \geqslant 1/2\) and let  . Choose a maximal interval of monotonicity
. Choose a maximal interval of monotonicity  of \(f_1\) containing x. We can assume without loss of generality that x is in the left half of
of \(f_1\) containing x. We can assume without loss of generality that x is in the left half of  so that
so that  . Since \(x\in (a,b)\), it is impossible that \(x=a\). In case of \(c'\not =a\) we set \(c=c'\). If
. Since \(x\in (a,b)\), it is impossible that \(x=a\). In case of \(c'\not =a\) we set \(c=c'\). If  then we set \(c=c'+({x-c'})/{2}= a+({x-a})/{2}\). In both cases \( x \in [c,({c+d})/2]\). Using (15) set
then we set \(c=c'+({x-c'})/{2}= a+({x-a})/{2}\). In both cases \( x \in [c,({c+d})/2]\). Using (15) set

Choose

Suppose first that \(x \in [c+\delta ,({c+d})/2]\). In this case \(f_1\) is monotone on \([x-\delta ,x+\delta ]\) and using the definition of \(f_1\), the fact that \(x \in E^{\gamma _1,\delta _1}\) and the fact that \(\delta \leqslant \delta _1\), we see that  must hold for either \(y=x-\delta \) or \(y=x+\delta \).
must hold for either \(y=x-\delta \) or \(y=x+\delta \).
Now suppose that \(x \in [c,c+\delta ]\). Since \(x \in E^{\gamma _1,\delta _1}\) and \(100\delta \leqslant \delta _1\) we have that  . Suppose first that \(|E\cap [x,x\,{+}\,100\delta ]|\geqslant 100\gamma _1\delta \) and let \(y=x+100\delta \). In this case, since \([x,y]\subset [c,d]\), by the definition of \(f_1\), we obtain
. Suppose first that \(|E\cap [x,x\,{+}\,100\delta ]|\geqslant 100\gamma _1\delta \) and let \(y=x+100\delta \). In this case, since \([x,y]\subset [c,d]\), by the definition of \(f_1\), we obtain  . Now suppose that \(|E\,{\cap }\, [x\,{-}\,100\delta ,x]|\geqslant 100\gamma _1\delta \). Note that \([x-100\delta ,c]\subset [e,c]\). Setting \(y=x-100\delta \),
. Now suppose that \(|E\,{\cap }\, [x\,{-}\,100\delta ,x]|\geqslant 100\gamma _1\delta \). Note that \([x-100\delta ,c]\subset [e,c]\). Setting \(y=x-100\delta \),  and
and  , we get \(|f_1(x)-f_1(y)|\geqslant S_1-S_2\). On the other hand, we know that
, we get \(|f_1(x)-f_1(y)|\geqslant S_1-S_2\). On the other hand, we know that  and
and  . Using the fact that \(\gamma _1\geqslant 1/2\), we see that
. Using the fact that \(\gamma _1\geqslant 1/2\), we see that

Summing up, we see that in each of the two cases considered: \(x \in [c,c+\delta ]\) or \( x \in [c+\delta ,({c+d})/2]\), we can choose \(y=y_1(x)\) such that \(\delta \leqslant |x-y| \leqslant \delta _1\) and  . Note that the definition of \(\delta \) in (16) ensures that \(|x-y_1(x)|\) is bounded away from 0 on each compact subset of (a, b). This establishes (iv).
. Note that the definition of \(\delta \) in (16) ensures that \(|x-y_1(x)|\) is bounded away from 0 on each compact subset of (a, b). This establishes (iv).
Using the fact that \(|x-y_1(x)|\) is bounded away from 0 on each compact subset of (a, b), we see that we can define a continuous, non-negative function \(r_1\leqslant \mathscr {E}^1\) so that \(r_1=0\) on \(F_1\), \(r_1>0\) on \(G_1\) and \(r_1(x) ,r_1(y_1(x)) < 2^{-2} |x-y_1(x)|\) for all  and \(\Vert r_1\Vert _\infty \leqslant 1/2\). Letting \(U_1\) be the vicinity of \(f_1\) with radius \(r_1\) we see that for any \(g \in U_1\) we have \(g \in (-\mathscr {E}_{1},\mathscr {E}_{1})\) on any interval [a, b] contiguous to \(F_1\). It follows that (v)–(vii) have been established provided that we assume that at later steps \(f_{m}\in U_{m} \subset U_{1}\) for \(m>1\).
and \(\Vert r_1\Vert _\infty \leqslant 1/2\). Letting \(U_1\) be the vicinity of \(f_1\) with radius \(r_1\) we see that for any \(g \in U_1\) we have \(g \in (-\mathscr {E}_{1},\mathscr {E}_{1})\) on any interval [a, b] contiguous to \(F_1\). It follows that (v)–(vii) have been established provided that we assume that at later steps \(f_{m}\in U_{m} \subset U_{1}\) for \(m>1\).
Now assume that we have already defined the functions \(f_1,f_2,\dots ,f_{n-1}\) and the decreasing sequence of vicinities \(U_1,U_2,\dots ,U_{n-1}\) with radii \(r_1,r_2,\ldots , r_{n-1}\) for some \(n\geqslant {2}\) so that they have the prescribed properties. Since \(r_{n-1}\) is continuous and positive on \(G_{n-1}\), it follows that \(r_{n-1}\) is bounded away from 0 on all compact subsets of \(G_{n-1}\). Now we would like to define \(f_n\) and \(U_n\). First we define an auxiliary function \(f_n^*\). Roughly \(f_n^*\) will be defined so that it has the same increment as \(f_{n-1}\) in any interval of monotonicity of \(f_{n-1}\), but has vanishing derivative on \(F_{n}\).
To this end consider an interval (a, b) contiguous to \(F_{n-1}\). See Fig. 2. On this figure the function \(f_{n-1}\) is drawn with a continuous line, the boundaries of the vicinity \(U_{n-1}\) are marked with dotted lines, the envelope boundaries \(\mathscr {E}_{n-1}\) and \(\mathscr {E}^{n-1}\) used in step \(n-1\) are marked with dashed lines, finally the auxiliary function \(f_{n-1}^{*}\) used at the previous step is marked with a dash-dot line.
By assumption we have

and clearly \(f_{n-1}\in (f_{n-1}-{r_{n-1}}/3,f_{n-1}+{r_{n-1}}/3)\) on [a, b]. Let \( {\delta }'\) satisfy \(2^{-3n}< {\delta }' < 2^{-3(n-1)}\). Then by Lemma 5.10 used with \( {\varepsilon }=2^{-3(n-1)}\) and \( {\delta }= {\delta }'\) we can define \(f_n^*\) on [a, b] so that

Now define  and let \(\mathscr {E}_n=f_n^*- \epsilon _n\) and \(\mathscr {E}^n=f_n^*+ \epsilon _n\). Let
and let \(\mathscr {E}_n=f_n^*- \epsilon _n\) and \(\mathscr {E}^n=f_n^*+ \epsilon _n\). Let  be contiguous to \(F_n\) in (a, b) so we have \(f_n^* \in (\mathscr {E}_n,\mathscr {E}^n)\) on
be contiguous to \(F_n\) in (a, b) so we have \(f_n^* \in (\mathscr {E}_n,\mathscr {E}^n)\) on  . See Fig. 3. Noting that (17) holds, we can apply Lemma 5.9 with \( {\varepsilon }= {\delta }'\) and \( {\delta }=2^{-3n}\) to define a function \(f_n\) such that on each
. See Fig. 3. Noting that (17) holds, we can apply Lemma 5.9 with \( {\varepsilon }= {\delta }'\) and \( {\delta }=2^{-3n}\) to define a function \(f_n\) such that on each  we have that \(f_n \in (\mathscr {E}_n,\mathscr {E}^n)\), that \(f_n\) is locally monotone and that on each interval of monotonicity we have
we have that \(f_n \in (\mathscr {E}_n,\mathscr {E}^n)\), that \(f_n\) is locally monotone and that on each interval of monotonicity we have  .
.
From our construction we see that (i)–(iii) hold. On the other hand, (iv) is verified in a similar way as in the case \(n=1\). Finally, we consider (v)–(vii). We can define \(r_n \in C[a,b]\) such that  and \(r_n >0\) on each interval
and \(r_n >0\) on each interval  contiguous to \(F_{n}\). Moreover, as \(|x-y_n(x)|\) is bounded away from 0 on each compact subset of each such contiguous interval
contiguous to \(F_{n}\). Moreover, as \(|x-y_n(x)|\) is bounded away from 0 on each compact subset of each such contiguous interval  , we can choose \(r_n\) such that if the vicinity \(U_n\) has radius \(r_n\) we have for any function \(g\in U_n\) that
, we can choose \(r_n\) such that if the vicinity \(U_n\) has radius \(r_n\) we have for any function \(g\in U_n\) that  . Note that \(r_n \leqslant \epsilon _n\) guarantees \(U_n\subseteq U_{n-1}\). Thus, for a sufficiently small \(r_n\) the condition \( r_n(x),r_n(y(x)) < 2^{-2n}\gamma _n |x-y_n(x)|\) is satisfied for all \(x\in E^{\gamma _{n},\delta _{n}}\)and therefore (v) is verified. Moreover (vi) and (vii) follow easily as well.
. Note that \(r_n \leqslant \epsilon _n\) guarantees \(U_n\subseteq U_{n-1}\). Thus, for a sufficiently small \(r_n\) the condition \( r_n(x),r_n(y(x)) < 2^{-2n}\gamma _n |x-y_n(x)|\) is satisfied for all \(x\in E^{\gamma _{n},\delta _{n}}\)and therefore (v) is verified. Moreover (vi) and (vii) follow easily as well.
By our earlier observations this concludes the proof: (v) guarantees that the sequence \((f_n)\) has a uniform limit function f, for which  in E by (iv) and (v). On the other hand,
in E by (iv) and (v). On the other hand,  in the complement of E by (ii) and (v), as f has a vanishing derivative there by the choice of the vicinities.\(\square \)
in the complement of E by (ii) and (v), as f has a vanishing derivative there by the choice of the vicinities.\(\square \)
Note that sets of full measure are trivially UDT sets so an interesting consequence of Theorem 5.6 is that \(G_\delta \) sets of full measure are  , yielding the following surprising corollary.
, yielding the following surprising corollary.
Corollary 5.11
The set of irrational numbers is  . That is, in terms of Dini derivatives, there exists a continuous function f with
. That is, in terms of Dini derivatives, there exists a continuous function f with

6 A weakly dense \(G_\delta \) set which is not  1
1
Recall that in Sect. 4 we proved that  sets are weakly dense, \(G_\delta \) sets (Theorem 4.1). In this section (Theorem 6.3) we show that weakly dense, \(G_\delta \) sets need not be
sets are weakly dense, \(G_\delta \) sets (Theorem 4.1). In this section (Theorem 6.3) we show that weakly dense, \(G_\delta \) sets need not be  . For the proof of the theorem we will need the following:
. For the proof of the theorem we will need the following:
Lemma 6.1
Suppose that \(E\subset {\mathbb {R}}\), \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) and  . Then for every \(x\in E\) and \( {\varepsilon }>0\) there is a \(y\in E\cap (x- {\varepsilon },x+ {\varepsilon })\) for which \(|f(x)-f(y)|>(1- {\varepsilon })|x-y|\).
. Then for every \(x\in E\) and \( {\varepsilon }>0\) there is a \(y\in E\cap (x- {\varepsilon },x+ {\varepsilon })\) for which \(|f(x)-f(y)|>(1- {\varepsilon })|x-y|\).
Proof
Take  such that \(|f(x)-f(y')|>(1-{{\varepsilon }}/{2})|x-y'|\) and \(|x-y'|< {\varepsilon }\). We can assume that \( {\varepsilon }<1\) and
such that \(|f(x)-f(y')|>(1-{{\varepsilon }}/{2})|x-y'|\) and \(|x-y'|< {\varepsilon }\). We can assume that \( {\varepsilon }<1\) and  . There is a
. There is a  for which
for which  and Lemma 2.2 implies that
and Lemma 2.2 implies that
\(\square \)
Remark 6.2
Recall Definition 2.1. It is easy to see that the following two statements are equivalent:
-
E is weakly dense at x,
-
for every \( {\varepsilon }>0\) there is an \(r\in (0, {\varepsilon })\) such that

Theorem 6.3
There exists a weakly dense, \(G_\delta \) set \(E\subset {\mathbb {R}}\) which is not  .
.
Proof
We use recursion to define E. Set  . Suppose that n is a non-negative integer and for some
. Suppose that n is a non-negative integer and for some  we have already defined a non-degenerate closed interval \(F_{i_0,\ldots ,i_n}\) (see Fig. 4). Let \(U_{i_0,\ldots ,i_n}\) be the left half of \(F_{i_0,\ldots ,i_n},\) that is
we have already defined a non-degenerate closed interval \(F_{i_0,\ldots ,i_n}\) (see Fig. 4). Let \(U_{i_0,\ldots ,i_n}\) be the left half of \(F_{i_0,\ldots ,i_n},\) that is

For every \(i_{n+1}\in \{1,\ldots ,4^{n+1}\}\) let

We define \(U_{i_0,\dots ,i_n}\) and \(F_{i_0,\ldots ,i_n}\) recursively in this way for every \(n\in {\mathbb {N}}\) and  . We are now ready to define E. First define
. We are now ready to define E. First define

and let \(\mathscr {I}_1=\{(i_n)\in \mathscr {I} \,{:}\, i_n=1 \text{ for } \text{ infinitely } \text{ many } n \in \mathbb {N}\}\). Set

and

The set F is a Cantor set minus countably many Cantor sets, hence it is \(G_\delta \). For every \(n\in {\mathbb {N}}\) and  there is an open set \(U'_{i_0,\ldots ,i_n}\) such that
there is an open set \(U'_{i_0,\ldots ,i_n}\) such that  . Thus U is also \(G_\delta \). This implies that
. Thus U is also \(G_\delta \). This implies that

is also \(G_\delta \).
If \(x\in U\) then E is clearly weakly dense at x. If \(x\in F\) and \( {\varepsilon }>0\) then using (18) take \(n\in {\mathbb {N}}\) and  such that \(x\in F_{i_0,\ldots ,i_n,1}\) and
such that \(x\in F_{i_0,\ldots ,i_n,1}\) and  . By the definition of \(F_{i_0,\ldots ,i_n,1}\) we have \( 4 \cdot 4^{n+1} |F_{i_0,\ldots ,i_n,1}| =|F_{i_0,\ldots ,i_n}| \), hence
. By the definition of \(F_{i_0,\ldots ,i_n,1}\) we have \( 4 \cdot 4^{n+1} |F_{i_0,\ldots ,i_n,1}| =|F_{i_0,\ldots ,i_n}| \), hence
By \((\min F_{i_0,\ldots ,i_n}, x) \subset (x- {\varepsilon },x)\) and (19) we obtain that E is weakly dense at x.
We use proof by contradiction to show that E is not  . Assume the existence of a function \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) such that
. Assume the existence of a function \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) such that  . We will show that there is a point \(x^*\in {\mathbb {R}}\) for which
. We will show that there is a point \(x^*\in {\mathbb {R}}\) for which  . We will define \((i_0,i_1,\ldots )\in {\mathscr {I}}\) recursively so that \(\{x^*\}=\bigcap _{n=0}^\infty F_{i_0,\ldots ,i_n}\). Set
. We will define \((i_0,i_1,\ldots )\in {\mathscr {I}}\) recursively so that \(\{x^*\}=\bigcap _{n=0}^\infty F_{i_0,\ldots ,i_n}\). Set  and
and  . Suppose that \(n\in {\mathbb {N}}\) and we have already defined a non-negative integer \(a_{n-1}\) and \(i_m\in \{1,\ldots ,4^m\}\) for every \(m\in \{0,\ldots ,a_{n-1}\}\). Let
. Suppose that \(n\in {\mathbb {N}}\) and we have already defined a non-negative integer \(a_{n-1}\) and \(i_m\in \{1,\ldots ,4^m\}\) for every \(m\in \{0,\ldots ,a_{n-1}\}\). Let  . Observe that \(\{y_{n}\}=\bigcap _{l=1}^{{\infty }}F_{i_{0},\ldots ,i_{a_{n-1}},1^{l}}\), where
. Observe that \(\{y_{n}\}=\bigcap _{l=1}^{{\infty }}F_{i_{0},\ldots ,i_{a_{n-1}},1^{l}}\), where  . By Lemma 6.1 used with \(x=y_{n}\) and
. By Lemma 6.1 used with \(x=y_{n}\) and  we can find an \(x_n\in E\) satisfying \(|y_{n}-x_{n}|< {\varepsilon }\) and
we can find an \(x_n\in E\) satisfying \(|y_{n}-x_{n}|< {\varepsilon }\) and

This implies that \(x_{n}\in F_{i_0,\ldots , i_{a_{n-1}}}.\) Since \(x_{n}\not =y_{n}\) there exists \(a_{n}>a_{n-1}\) such that  while \(y_{n}\in F_{i_0,\ldots , i_{a_{n}-1},1}.\) The property \(x_{n}\in F_{i_0,\ldots , i_{a_{n}-1}}\) defines \(i_{m}\) for \(m\in \{a_{n-1}+1,\dots ,a_{n}-1\}.\) We might be able to find many \(x_{n}\)s satisfying the above property but we select an \(x_{n}\) for which \(a_{n}\) is minimal among the possible choices. Then \(i_{m}=1\) for every \(m\in \{a_{n-1}+1,\dots ,a_{n}-1\}.\)
while \(y_{n}\in F_{i_0,\ldots , i_{a_{n}-1},1}.\) The property \(x_{n}\in F_{i_0,\ldots , i_{a_{n}-1}}\) defines \(i_{m}\) for \(m\in \{a_{n-1}+1,\dots ,a_{n}-1\}.\) We might be able to find many \(x_{n}\)s satisfying the above property but we select an \(x_{n}\) for which \(a_{n}\) is minimal among the possible choices. Then \(i_{m}=1\) for every \(m\in \{a_{n-1}+1,\dots ,a_{n}-1\}.\)
If \(k\in {\mathbb {N}}\),  , \(j_{k+1},j'_{k+1}\in \{1,\ldots ,4^{k+1}\}\), \(j_{k+1} < j'_{k+1}\), \(z\in F_{j_0,\ldots ,j_k,j_{k+1}}\) and
, \(j_{k+1},j'_{k+1}\in \{1,\ldots ,4^{k+1}\}\), \(j_{k+1} < j'_{k+1}\), \(z\in F_{j_0,\ldots ,j_k,j_{k+1}}\) and  , then by Lemma 2.2 and the elementary fact
, then by Lemma 2.2 and the elementary fact
we obtain

This applied with \(z=y_{n}\),  and \(k=a_{n}-1\) would imply that for \(x_{n}\not \in U_{i_0,\ldots ,i_{a_n-1}}\) we would have \(|f(x_{n})-f(y_{n})|\leqslant \frac{2}{3}|x_{n}-y_{n}|\), contradicting (20). Hence \(x_n\in U_{i_0,\ldots ,i_{a_n-1}}\).
and \(k=a_{n}-1\) would imply that for \(x_{n}\not \in U_{i_0,\ldots ,i_{a_n-1}}\) we would have \(|f(x_{n})-f(y_{n})|\leqslant \frac{2}{3}|x_{n}-y_{n}|\), contradicting (20). Hence \(x_n\in U_{i_0,\ldots ,i_{a_n-1}}\).
For every \(x\in U_{i_0,\ldots ,i_{a_n-1}}\) and \(y\in F_{i_0,\ldots ,i_{a_n-1},4^{a_n}}\) again Lemma 2.2 and (21) imply that

Next we define \(i_{a_{n}}\). We select an integer \(i_{a_n}\in \{1,\ldots ,4^{a_n}\}\) (let it be the least one) such that for every \(\widetilde{x}\in U_{i_0,\ldots ,i_{a_n-1}}\) and \(\widetilde{y}\in F_{i_0,\ldots ,i_{a_n}}\) we have
Since \(x_n\in U_{i_0,\ldots ,i_{a_n-1}}\) and \(y_{n}\in E\cap F_{i_0,\ldots ,i_{a_n-1},1}\) by (20) we have that \(i_{a_n}\) is larger than one.
As there are \(w\in F_{i_0,\ldots ,i_{a_n-1},i_{a_n}-1}\) and \(v\in U_{i_0,\ldots ,i_{a_n-1}}\) for which

(see Fig. 5 below) for every \(\widetilde{y}\in F_{i_0,\ldots ,i_{a_n}}\) we obtain

We define \(a_n\) and \(i_0,\ldots ,i_{a_n}\) recursively for every \(n\in {\mathbb {N}}\).
Set  . From (25) we have
. From (25) we have  . We claim that
. We claim that
for every  . Suppose that an \(\widehat{x}\) does not satisfy (26). Since f is continuous and it is constant on every complementary interval of the closure of E, we can assume that \(\widehat{x}\in E\). By (22) there is a \(k\in {\mathbb {N}}\) such that \(\widehat{x}\in U_{i_0,\ldots ,i_{k-1}}\) and \(x^*\in F_{i_0,\ldots ,i_{k-1},i_k}\). Since \(i_{a_n} > 1\) for every \(n\in {\mathbb {N}}\) we have
. Suppose that an \(\widehat{x}\) does not satisfy (26). Since f is continuous and it is constant on every complementary interval of the closure of E, we can assume that \(\widehat{x}\in E\). By (22) there is a \(k\in {\mathbb {N}}\) such that \(\widehat{x}\in U_{i_0,\ldots ,i_{k-1}}\) and \(x^*\in F_{i_0,\ldots ,i_{k-1},i_k}\). Since \(i_{a_n} > 1\) for every \(n\in {\mathbb {N}}\) we have  . This implies
. This implies

Since (23) shows that \(k\ne a_n\) for any \(n\in {\mathbb {N}}\), from the definition of \((a_n)_{n=0}^\infty \) we obtain

Moreover (22) implies that

Hence by (27), (28) and (29) we have
which is impossible.
Thus  , which is a contradiction.\(\square \)
, which is a contradiction.\(\square \)
7 Open problems
As mentioned in the introduction, there are a number of problems in this area which are still open. We list some of these below.
-
Characterize
 sets. This paper and [5] provide progress in this direction, but there is still more work to be done.
sets. This paper and [5] provide progress in this direction, but there is still more work to be done. -
Characterize the sets \(E \subset \mathbb {R}\) for which there is a continuous function f such that
 . See [8] for a partial result on this problem. The corresponding problem with
. See [8] for a partial result on this problem. The corresponding problem with  in place of
in place of  turns out to be quite straightforward.
turns out to be quite straightforward. -
Characterize the sets E which are sets of non-differentiability for continuous functions \(f:\mathbb {R}\rightarrow \mathbb {R}\) such that
 everywhere. See [11] for partial results in this direction.
everywhere. See [11] for partial results in this direction.
References
Balogh, Z.M., Csörnyei, M.: Scaled-oscillation and regularity. Proc. Amer. Math. Soc. 134(9), 2667–2675 (2006)
Banach, S.: Über die Baire’sche Kategorie gewisser Funktionenmengen. Stud. Math. 3, 174–179 (1931)
Bruckner, A.M., Bruckner, J.B., Thomson, B.S.: Elementary Real Analysis. 2nd edn. ClassicalRealAnalysis.com (2008)
Bruckner, A.M., Leonard, J.L.: Derivatives. Amer. Math. Monthly 73(4) Part II, 24–56 (1966)
Buczolich, Z., Hanson, B., Maga, B., Vértesy, G.: Lipschitz one sets modulo sets of measure zero. Math. Slovaca 70(3), 567–584 (2020)
Buczolich, Z., Hanson, B., Maga, B., Vértesy, G.: Characterization of lip sets. J. Math. Anal. Appl. 489(2), # 124175 (2020)
Buczolich, Z., Hanson, B., Maga, B., Vértesy, G.: Strong one-sided density without uniform density (2021). arXiv:2101.09471
Buczolich, Z., Hanson, B., Rmoutil, M., Zürcher, T.: On sets where \(\text{ lip }\, f\) is finite. Studia Math. 249(1), 33–58 (2019)
Cheeger, J.: Differentiability of Lipschitz functions on metric measure spaces. Geom. Funct. Anal. 9(3), 428–517 (1999)
Hanson, B.: Linear dilatation and differentiability of homeomorphisms of \(\mathbb{R}^n\). Proc. Amer. Math. Soc. 140(10), 3541–3547 (2012)
Hanson, B.H.: Sets of non-differentiability for functions with finite lower scaled oscillation. Real Anal. Exchange 41(1), 87–99 (2016)
Keith, S.: A differentiable structure for metric measure spaces. Adv. Math. 183(2), 271–315 (2004)
Maliszewski, A.: Characteristic functions and products of bounded derivatives. Proc. Amer. Math. Soc. 123(7), 2203–2211 (1995)
Malý, J., Zajíçek, L.: On Stepanov type differentiability theorems. Acta Math. Hungar. 145(1), 174–190 (2015)
Malý, J., Zindulka, O.: Mapping analytic sets onto cubes by little Lipschitz functions. Eur. J. Math. 5(1), 91–105 (2019)
Preiss, D., Tartaglia, M.: On characterizing derivatives. Proc. Amer. Math. Soc. 123(8), 2417–2420 (1995)
Saks, S.: Theory of the Integral, 2nd edn. Dover, New York (1964)
Stepanoff, W.: Über totale Differenzierbarkeit. Math. Ann. 90(3–4), 318–320 (1923)
Weil, C.E.: On properties of derivatives. Trans. Amer. Math. Soc. 114(2), 363–376 (1965)
Zahorski, Z.: Sur la première dérivée. Trans. Amer. Math. Soc. 69(1), 1–54 (1950)
Acknowledgements
We are thankful for the referees’ comments, which improved the presentation and readability of this paper.
Funding
Open access funding provided by Eötvös Loránd University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Zoltán Buczolich was supported by the Hungarian National Research, Development and Innovation Office–NKFIH, Grant 124003. Balázs Maga was supported by the ÚNKP-18-2 New National Excellence of the Hungarian Ministry of Human Capacities, and by the Hungarian National Research, Development and Innovation OfficeNKFIH, Grant 124749. Gáspár Vértesy was supported by the ÚNKP-18-3 New National Excellence Program of the Ministry of Human Capacities, and by the Hungarian National Research, Development and Innovation OfficeNKFIH, Grant 124749.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Buczolich, Z., Hanson, B., Maga, B. et al. Big and little Lipschitz one sets. European Journal of Mathematics 7, 464–488 (2021). https://doi.org/10.1007/s40879-021-00458-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-021-00458-9
Keywords
- Lipschitz functions
- Big and little lip functions
- Uniform density properties
- One-sided density
- Weak density
- Strong uniform density



 and
and  sets
sets and
and 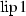 sets
sets ,
,
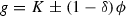 .
. on each interval of monotonicity of g, recall that we use constants K which depend on the interval considered.
on each interval of monotonicity of g, recall that we use constants K which depend on the interval considered.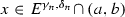 there exists
there exists  . Moreover,
. Moreover,  .
. for all
for all 



 1
1


 sets. This paper and [
sets. This paper and [ . See [
. See [ in place of
in place of  turns out to be quite straightforward.
turns out to be quite straightforward. everywhere. See [
everywhere. See [