Abstract
We study the surface of Gauss double points associated to a very general quartic surface and the natural morphisms associated to it.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 The result
We work over \({\mathbb {C}}\), the complex number field. In this paper \(X\subset {\mathbb {P}}^3\) is a very general quartic surface. In particular there are no lines inside it. We explicitly describe a singular surface \(\Sigma _{\mathrm{dou}}\) naturally associated to X. This surface is classically known as the “developable touching the surface along UK”, see [4, Chapter XVII, 607, 608]. For a general surface of degree d inside \({\mathbb {P}}^3\) the corresponding developable surface is studied in [2], where the reader can also find a modern study of Salmon’s treatise. In this paper the point of view is different, because we want to relate the geometry of \(\Sigma _{\mathrm{dou}}\) to the geometry of the surface of bitangent lines to X and for this we need a careful study of \(\Sigma _{\mathrm{dou}}\).
In order to introduce and to study \(\Sigma _{\mathrm{dou}}\) we revise some aspects of the geometry of quartic surfaces. We ground our exposition on [7]. The book [7] contains both a well written modern account about the projective Gauss map and a very nice description of the geometry of a general quartic surface.
Given the surface X, it is well known that its bitangents describe a smooth algebraic surface S inside the Gassmannian \(\mathbb {G}(2,4)\) of lines of \({\mathbb {P}}^3\). If \({\mathscr {Q}}_{S}\) is the restriction to S of the universal bundle \({\mathscr {Q}}\) over \(\mathbb {G}(2,4)\), it is also well known that inside its Grothendieck’s projectivisation \({\mathbb {P}}({\mathscr {Q}}_{S})\) we can define the surface \(Y\subset {\mathbb {P}}({\mathscr {Q}})\) of contact points associated to S. Namely, a point \(y\in Y\) is a couple  where l is a bitangent line of X and \(p\in l\cap X\). The geometry of Y is quite well known, see Proposition 4.4 and [1, 7]. Together with S and Y there is a third surface which naturally comes with the geometry of X. To describe it, we consider a point \(p\in X\) and denote by \(T_pX\) the projective tangent space of X at p. It is known that the closure of the loci of the points \(p\in X\) for which the hyperplane section \(X_p:=T_pX\cap X\) has geometrical genus strictly less than 2 is a 1-dimensional subscheme \(C_{{\mathrm{dou}}}\) inside X, see Theorem 3.13. Cayley called \(C_{{\mathrm{dou}}}\) the node-couple curve, see [4, Chapter XVII, 607], where it is denoted by UK.
where l is a bitangent line of X and \(p\in l\cap X\). The geometry of Y is quite well known, see Proposition 4.4 and [1, 7]. Together with S and Y there is a third surface which naturally comes with the geometry of X. To describe it, we consider a point \(p\in X\) and denote by \(T_pX\) the projective tangent space of X at p. It is known that the closure of the loci of the points \(p\in X\) for which the hyperplane section \(X_p:=T_pX\cap X\) has geometrical genus strictly less than 2 is a 1-dimensional subscheme \(C_{{\mathrm{dou}}}\) inside X, see Theorem 3.13. Cayley called \(C_{{\mathrm{dou}}}\) the node-couple curve, see [4, Chapter XVII, 607], where it is denoted by UK.
We will see that for a general point \(p\in C_{\mathrm{dou}}\) there exists another unique singular point  such that \(T_pX=T_{p'}X\). Clearly, both
such that \(T_pX=T_{p'}X\). Clearly, both  and since \(p\ne p'\) there exists a unique line
and since \(p\ne p'\) there exists a unique line  passing through \(p,p'\). Clearly,
passing through \(p,p'\). Clearly,  . The new singular surface we mentioned above is the locus
. The new singular surface we mentioned above is the locus  obtained by the closure of the surface swept by the lines \(l_{p,p'}\) where \(p\in C_{\mathrm{dou}}\) is a general point. We give a description of the geometry of \(\Sigma _{\mathrm{dou}}\). In the case of a quartic surface, we think right to call \(\Sigma _{\mathrm{dou}}\) the almost ruled surface of Gauss double points because it matches perfectly with the modern classification of points on a general quartic surface that we adopted, see Proposition 3.3.
obtained by the closure of the surface swept by the lines \(l_{p,p'}\) where \(p\in C_{\mathrm{dou}}\) is a general point. We give a description of the geometry of \(\Sigma _{\mathrm{dou}}\). In the case of a quartic surface, we think right to call \(\Sigma _{\mathrm{dou}}\) the almost ruled surface of Gauss double points because it matches perfectly with the modern classification of points on a general quartic surface that we adopted, see Proposition 3.3.
The projective bundle \({\mathbb {P}}({\mathscr {Q}}_S)\) is easily seen to coincide with the following incidence variety:  . One of the most basic morphisms associated to the geometry of X is the forgetful one:
. One of the most basic morphisms associated to the geometry of X is the forgetful one:

Nevertheless it has not been deeply studied yet. We denote by \(B(f)\hookrightarrow {\mathbb {P}}^3\) its branch locus and by \(R(f)\hookrightarrow {\mathbb {P}}({\mathscr {Q}}_S)\) its ramification one. We prove that there exists a curve \(C\subset S\) which parameterises the bitangent lines associated to the couples  where \(T_pX=T_{p'}X\). Geometrically \(C\subset S\) is birational to the quotient of
where \(T_pX=T_{p'}X\). Geometrically \(C\subset S\) is birational to the quotient of  by the natural involution \(p\mapsto p'\) where
by the natural involution \(p\mapsto p'\) where  .
.
In particular, we can construct the ruled surface \(\pi _C:\Sigma \rightarrow C\) obtained by the pull-back of the natural morphism \(\pi _S:{\mathbb {P}}({\mathscr {Q}}_S)\rightarrow S\) via the natural inclusion \(C\hookrightarrow S\).
Main Theorem
If X is a very general quartic surface then S and Y are smooth surfaces and \(C_{\mathrm{dou}},C^{\vee }_{\mathrm{dou}}\) are singular curves whose singularities are fully classified. The morphism \(f:{\mathbb {P}}({\mathscr {Q}}_S)\rightarrow {\mathbb {P}}^3\) is finite of degree 12. The almost ruled surface of Gauss double points \(\Sigma _{\mathrm{dou} }\) has degree 160 and osculates the quartic X along \(C_{\mathrm{dou}}\). It holds:
- (i):
-
\(B(f)=X\cup \Sigma _{\mathrm{dou} }\),
- (ii):
-
\(R(f)=Y\cup \Sigma \).
Moreover, the natural morphism \(f:{\mathbb {P}}({\mathscr {Q}}_S)\rightarrow {\mathbb {P}}^3\) induces by restriction two morphisms \(\rho :Y\rightarrow X\) and \(\rho _{\mathrm{dou}}:\Sigma \rightarrow \Sigma _{\mathrm{dou} }\) of degree respectively 6 and 1.
For the proof of Main Theorem, see Sect. 4.6. Actually we need a detailed description of the geometry associated to the curves \(C_{\mathrm{dou}},C^{\vee }_{\mathrm{dou}}\). This geometry is described in Proposition 2.5. The proof of Proposition 2.5 is postponed to Sect. 4.5.
Finally we would like to mention that this work was originally motivated by Diophantine problems: smooth quartic surfaces are particularly interesting in Diophantine geometry, since they lie at the frontier between rational surfaces, for which the distribution of rational points is well understood, and surfaces of general type, for which it is conjectured that their rational points are never Zariski-dense. For quartic surfaces defined over a number field, it is widely believed that their rational points become Zariski-dense after a suitable finite extension of their field of definition, but this is proved only in very particular cases, and no example with Picard number 1 is known where this density can be proved.
Quartic surfaces are limiting cases also for the problem of integral points on open subsets of \({\mathbb {P}}^3\): the complement of a surface of degree \(\leqslant 3\) in \({\mathbb {P}}^3\) is known to have potential density of integral points; for complements of smooth surfaces of degree 5 or more, Vojta’s conjecture predicts degeneracy (but no case is known for the complement of a smooth surface). The complement of quartic surface should have a potentially dense set of integral points, but again this is still a widely open problem. Again by Vojta’s conjecture, we expect that removing the union of a quartic surface and any other surface from \({\mathbb {P}}^3\) produces an affine variety with degenerate sets of integral points. As a by product of this work and our previous work [1], we could, for instance, deduce the finiteness of the set of integral points, over every ring of S-integers, on the complement of the union of a quartic surface X and its associated surface \(\Sigma _{\mathrm {dou}}\) to be described in the present work. We intend to devote a future paper to the arithmetic applications of these geometrical investigations.
2 The morphism of bitangents
We agree that a general point on a variety M satisfies a property \({\mathscr {P}}\) if there exists an open dense subset of M satisfying the property \({\mathscr {P}}\), and that a very general point on M satisfies a property \({\mathscr {P}}\) if there exists a countable union \(\mathscr {Z}\) of closed proper subsets of X such that all the points outside \(\mathscr {Z}\) satisfy the property \({\mathscr {P}}\).
In this section we introduce some of the geometrical objects which appear in the statement of Main Theorem. Let V be a complex vector space of dimension 4 and let \(V^{\vee }\) its \(\mathbb {C}\)-dual. We set \({\mathbb {P}}^3:={\mathbb {P}}(V^{\vee })\). Let \(F\in {\mathrm{Sym}}^{4}\, V\) and let \(X:=(F\,{=}\,0)\subset {\mathbb {P}}^3\) be the associated quartic surface. In this paper, unless otherwise stated, we assume that X is a very general quartic. We shall use the Yau–Zaslow formula, see [3, Formula 13.4.2]. The surface X comes naturally with three other surfaces that we are going to describe.
2.1 The surface of bitangents
Let \(\mathbb {G}:=\mathbb {G}(2, V^{\vee })\) be the Grassmann variety which parameterises the lines of \({\mathbb {P}}^3\).
Definition 2.1
A line \(l\subset {\mathbb {P}}^3\) is a bitangent line to X if the subscheme  is non-reduced over each supporting point.
is non-reduced over each supporting point.
Definition 2.2
We call  the variety of bitangents to X.
the variety of bitangents to X.
2.2 The surface of contact points
We have the standard exact sequence of vector bundles on \(\mathbb {G}\):

A point \(\alpha \in {\mathscr {Q}}^{\vee }\) is a couple  where
where  ,
,  . We denote by \({\mathbb {P}}({\mathscr {Q}})\) the variety
. We denote by \({\mathbb {P}}({\mathscr {Q}})\) the variety  . By definition \({\mathbb {P}}({\mathscr {Q}})\) coincides with the universal family of lines over \(\mathbb {G}\):
. By definition \({\mathbb {P}}({\mathscr {Q}})\) coincides with the universal family of lines over \(\mathbb {G}\):

We denote by \(\pi _{\mathbb {G}}:{\mathbb {P}}({\mathscr {Q}})\rightarrow \mathbb {G}\) the natural projection and following the mainstream we call the sequence

the universal exact sequence. By the inclusion \(j_{S}:S\hookrightarrow \mathbb {G}\) we can define \({\mathscr {Q}}_{S}:=j_{S}^{\star }{\mathscr {Q}}\). It remains to define the variety of contact points.
Definition 2.3
We call  the variety of contact points.
the variety of contact points.
Obviously, there is an embedding \(j_Y:Y\hookrightarrow {\mathbb {P}}({\mathscr {Q}}_{S})\) and the natural morphism \(\pi _{S}:{\mathbb {P}}({\mathscr {Q}}_{S}) \rightarrow S\) restricts to a morphism \(\pi :Y\rightarrow S\) which we call the forgetful morphism.
2.3 The double cover subscheme
We need to introduce the subscheme of X given by the points p for which the restriction of X to the tangent plane of X at p is a curve \(X_p\) of geometrical genus less than 2. It is a 1-dimensional subscheme \(C_{{\mathrm{dou}}}\) inside X. Following the literature:
Definition 2.4
We call  the double cover subscheme of X.
the double cover subscheme of X.
We will see in Propositions 3.12 and 3.14 that if X is general then \(C_{{\mathrm{dou}}}\) is an irreducible singular curve.
2.3.1 The double cover subscheme and Gauss map
On X it is defined the Gauss map \(\varphi _{{\mathrm{Gauss}}}:X\rightarrow ({\mathbb {P}}^3)^{\vee }\) which is a morphism. We set
Let \(\nu _{{\mathrm{dou}}} :{\widetilde{ C_{{\mathrm{dou}}}}}\rightarrow C_{{\mathrm{dou}}}\) and \(\nu _{{\mathrm{dou}}}^{\vee }:{\widetilde{ C^{\vee }_{{\mathrm{dou}}}} }\rightarrow C_{{\mathrm{dou}}}^{\vee }\) be the normalisation morphisms. The following proposition is of interest in itself, for the proof see Sect. 4.5.
Proposition 2.5
There exist embeddings
such that the following diagram is commutative:

where \(\pi _{{\mathrm{dou}}}:{\widetilde{ C_{{\mathrm{dou}}}}}\rightarrow {\widetilde{ C^{\vee }_{{\mathrm{dou}}}}}\) is a 2-to-1 branched covering induced by the restriction of \(\pi :Y\rightarrow S\) to \( {\widetilde{ C_{{\mathrm{dou}}}}}\).
2.4 The almost ruled surface of Gauss double points
We will need to consider also a third surface naturally associated to X. We found no reference on it. We will see that for a general point \(p\in C_{\mathrm{dou}}\) there exists another unique singular point  such that \(T_pX=T_{p'}X\). Clearly, both
such that \(T_pX=T_{p'}X\). Clearly, both  and since \(p\ne p'\) there exists a unique line
and since \(p\ne p'\) there exists a unique line  passing through \(p,p'\). We will show that
passing through \(p,p'\). We will show that  . On the other hand, the natural morphism \(\rho _{{\mathbb {P}}^3}:{\mathbb {P}}({\mathscr {Q}})\rightarrow {\mathbb {P}}^3\) restricted to \({\mathbb {P}}({\mathscr {Q}}_{S})\) gives a morphism \(f:{\mathbb {P}}({\mathscr {Q}}_{S})\rightarrow {\mathbb {P}}^3\). We will show that the image \(\Sigma _{\mathrm{dou} }:=f(\pi _S^{-1}( {j^{\vee }_{ \mathrm{dou}}}{\widetilde{ C^{\vee }_{{\mathrm{dou}}}} } ))\) is a surface inside \({\mathbb {P}}^3\) which is the closure of the surface swept by the lines \(l_{p,p'}\) as \(p\in C_{\mathrm{dou}}\) is a general point.
. On the other hand, the natural morphism \(\rho _{{\mathbb {P}}^3}:{\mathbb {P}}({\mathscr {Q}})\rightarrow {\mathbb {P}}^3\) restricted to \({\mathbb {P}}({\mathscr {Q}}_{S})\) gives a morphism \(f:{\mathbb {P}}({\mathscr {Q}}_{S})\rightarrow {\mathbb {P}}^3\). We will show that the image \(\Sigma _{\mathrm{dou} }:=f(\pi _S^{-1}( {j^{\vee }_{ \mathrm{dou}}}{\widetilde{ C^{\vee }_{{\mathrm{dou}}}} } ))\) is a surface inside \({\mathbb {P}}^3\) which is the closure of the surface swept by the lines \(l_{p,p'}\) as \(p\in C_{\mathrm{dou}}\) is a general point.
Definition 2.6
We call the subscheme \(\Sigma _{\mathrm{dou} }\hookrightarrow {\mathbb {P}}^3\) given by the closure of the surface swept by the lines \(l_{p,p'}\) where \(p\in C_{\mathrm{dou}}\) is a general point the almost ruled surface of Gauss double points.
2.5 The basic morphism
Note that geometrically \({\mathbb {P}}({\mathscr {Q}}_{S})\) is easily seen as

We introduced above a basic object of this geometry: the morphism \(f:{\mathbb {P}}({\mathscr {Q}}_{S})\rightarrow {\mathbb {P}}^3\). It is obtained by projecting to the second factor and is called the morphism of bitangents. We want to understand its branch locus subscheme \(B(f)\hookrightarrow {\mathbb {P}}^3\) and its ramification one \(R(f)\hookrightarrow {\mathbb {P}}({\mathscr {Q}}_S)\).
3 Special curves on a quartic surface
3.1 Singularities of a plane quartic
We recall a basic fact on irreducible plane quartics. Its proof is easy.
Lemma 3.1
Let \(C\subset {\mathbb {P}}^2\) be an irreducible plane quartic. Then C has at most three singularities. If \(g(C)=1\) then the following cases occur:
- (i):
-
a point of multiplicity 3, or
- (ii):
-
a tacnode, or
- (iii):
-
two nodes, or
- (iv):
-
a node and a cusp, or
- (v):
-
two cusps.
If \(g(C)=2\) then C has exactly one node or one cusp.
3.2 Classification of points of a general quartic surface
Let  be as above a general homogeneous polynomial of degree 4 and let \(X:=V(F)\subset {\mathbb {P}}^3\) be the corresponding quartic surface. Since X is smooth, we can define the Gauss map which maps a point \(X\ni p\) to its tangent space seen as a point of the dual projective space
be as above a general homogeneous polynomial of degree 4 and let \(X:=V(F)\subset {\mathbb {P}}^3\) be the corresponding quartic surface. Since X is smooth, we can define the Gauss map which maps a point \(X\ni p\) to its tangent space seen as a point of the dual projective space

Clearly, \(\varphi _{{\mathrm{Gauss}}}:X\rightarrow ({\mathbb {P}}^3)^{\vee }\) is a morphism since X is smooth. In the rest of this section we strongly rely on [7]. Actually, by the stability property of the Gauss map, cf. [7, Section 2.1], we know the analytic behaviour of the Gauss map in an analytic neighborhood of any point \(p\in X\). It follows that for any point \(p\in X\) it holds that \(d\varphi _{ {\mathrm{Gauss}}, p}\ne 0\), see [7, Proposition 2.15].
Proposition 3.2
Let X be a general quartic surface. Then:
- (i):
-
All tangent curves are irreducible.
- (ii):
-
Tangent curves have only singularities of multiplicity 2 (and the second fundamental form is non-zero for any \(p\in X\)).
- (iii):
-
All rational tangent curves are nodal.
- (iv):
-
There are no elliptic cuspidal tangent curves on X.
Proof
(i) follows since  . For (ii), see [7, Lemma 2.1.4]. For (iii), see [7, Fact 1.4.8, p. 21]. For (iv), see [7, Lemma 2.1.6]. \(\square \)
. For (ii), see [7, Lemma 2.1.4]. For (iii), see [7, Fact 1.4.8, p. 21]. For (iv), see [7, Lemma 2.1.6]. \(\square \)
It is interesting to stress here that Proposition 3.2 (iv) means that if X is a general quartic then there are no elliptic hyperplane sections with two cusps. This should be read together with Lemma 3.1 (v). This leads to a full classification of the possible hyperplane sections
Proposition 3.3
([7, Proposition 2.1.7]) Let X be a very general quartic \(X\subset {\mathbb {P}}^3\). Let \(p\in X\) and \(X_p=T_pX\cap X\). The couple \((X_p,p)\) is one of the following types:
- (a):
-
General case: \(g(X_p)=2\) and \(X_p\) has only one node.

- (b):
-
Simple parabolic point: \(g(X_p)=2\) and \(X_p\) has only one cusp.

- (c):
-
Simple Gauss double point: \(g(X_p)=1\) and \(X_p\) has only two nodes.

- (d):
-
Parabolic Gauss double point: \(g(X_p)=1\) and \(X_p\) has a cusp on p and a node on another point \(p'\ne p\).

- (e):
-
Dual to parabolic Gauss double point: \(g(X_p)=1\) and \(X_p\) has a cusp on \(p'\ne p\) and a node on p.

- (f):
-
Gauss swallowtail: \(g(X_p)=1\) and \(X_p\) has one tacnode.

- (g):
-
Gauss triple point: \(g(X_p)=0\) and \(X_p\) has three distinct nodes.

By Proposition 3.3 and by calculation of the Milnor numbers of nodes, cusps, and tacnodes we get the full classification of the singular points of the image  .
.
Proposition 3.4
([7, Proposition 2.19]) Let  . Then
. Then  if p is a simple parabolic point or a simple Gauss double point and
if p is a simple parabolic point or a simple Gauss double point and  if p is a parabolic Gauss double point, dual to parabolic Gauss double point, a Gauss swallowtail, or a Gauss triple point.
if p is a parabolic Gauss double point, dual to parabolic Gauss double point, a Gauss swallowtail, or a Gauss triple point.
3.3 The parabolic curve of a general quartic surface
There are three curves on X which contain important information on X. The first one is the following.
Definition 3.5
We define the parabolic curve \(C_{{\mathrm{par}}}\subset X\) to be the ramification locus of the Gauss map \(\varphi :X\rightarrow X^*\). A point \(p\in X\) is called parabolic if \(p\in C_{{\mathrm{par}}}\).
3.3.1 The asymptotic directions
We recall that locally we can consider a neighbourhood of the point \(p=(0,0,0)\) with coordinates \((x,y,z)\in \mathbb {C}^3\) such that locally \(T_pS\) is given by \((z=0)\). Hence the germ of S at p is given by  . In particular, the local analytic expression of the Hessian of F is
. In particular, the local analytic expression of the Hessian of F is
Then each principal direction, that is those giving the tangents to the branches of \(X_p\) at p, is obtainable by the vector \(v\in T_pS\) such that for the induced quadratic form it holds \({\mathrm{Hess}}_{(S,p)}(v,v)=0\). Following a notation coming from differential geometry these two directions are called asymptotic directions at p. In particular, if \(X_p\) has a cusp on p then there exists a unique direction v such that \({\mathrm{Hess}}_{(S,p)}(v,\dots )\equiv 0\) and the line \(\langle v\rangle \subset T_pS\) is the direction of ramification of \(\varphi _{\mathrm{Gauss}}\) that is  .
.
3.3.2 Classification of the parabolic points
By a local analysis it follows that
Proposition 3.6
Let X be a general quartic. A point \(p\in X\) is parabolic iff p is a cusp or a tacnode of \(X_p\). The parabolic curve \(C_{{\mathrm{par}}}\) is the zero locus of the determinant of the Hessian of X. Moreover, \(C_{{\mathrm{par}}}\) is a smooth element of the linear system |8h|. In particular, \(C_{{\mathrm{par}}}\) has genus 129.
Proof
We noted above that \(C_{\mathrm{par}}\) is the locus where the Gauss morphism is not a smooth one. Hence by the local analytic description of the Gauss map the claim follows. See [7, Proposition 2.2.4]. \(\square \)
3.4 The flecnodal curve
The second curve inside X which is useful for understanding the geometry of X is the one containing all the hyperflexes.
Definition 3.7
A line \(l\subset {\mathbb {P}}^3\) is called a hyperflex line if the subscheme \(X_{|l}\hookrightarrow l\) is supported over a unique point \(p\in X\cap l\). In this case the line l is called a hyperflex line of X at p.
Definition 3.8
A point \(p\in X\) is called a hyperflex if there exists a hyperflex line through it. We define the hyperflex curve  to be the reduced scheme of hyperflexes.
to be the reduced scheme of hyperflexes.
We sum up the results on \(C_{{\mathrm{hf}}}\) we need.
Proposition 3.9
([7, Subsection 2.3.3 and Corollary 2.4.6]) Let X be a general quartic. Then:
- (i):
-
\(C_{{\mathrm{hf}}}\) is irreducible.
- (ii):
-
If \(p \in C_{{\mathrm{hf}}}\) is a general point then X has exactly one hyperflex in p.
- (iii):
-
\(C_{{\mathrm{hf}}}\) has geometric genus 201.
- (iv):
-
If \(p\in C_{{\mathrm{hf}}}\) has two distinct hyperflexes then p is a singular point of \(C_{{\mathrm{hf}}}\).
- (v):
-
\(C_{{\mathrm{hf}}}\in |20h|\).
3.4.1 Swallowtail points, parabolic curve and the flecnodal curve
On the parabolic curve \(C_{{\mathrm{par}}}\) there is unicity of asymptotic directions. This enables us to construct the subbundle \({\mathscr {L}}\subset TX_{|C_{{\mathrm{par}}}}\) of asymptotic directions. By Proposition 3.6 we can build the standard tangent sequence

It is well known that the scheme where \(\nu _{C_{{\mathrm{par}}}|{\mathscr {L}}}\) vanishes is the one given by Gauss swallowtails, see [7, Remark 2.2.7].
Proposition 3.10
([7, Section 2.4, p. 39]) Every swallowtail is a simple zero of \(\nu _{C_{{\mathrm{par}}}|{\mathscr {L}}}\). A point \(p\in C_{{\mathrm{par}}}\) is a Gauss swallowtail iff \(p\in C_{{\mathrm{hf}}}\), that is set theoretically

Moreover, every \(p\in C_{{\mathrm{par}}}\cap C_{{\mathrm{hf}}}\) is a smooth point both of \(C_{{\mathrm{hf}}}\) and \(C_{\mathrm{par}}\) and
Corollary 3.11
([7, Proposition 2.4.5]) There are 320 Gauss swallowtails.
3.5 The double cover curve
By the classification of points of a general quartic surface it is natural to consider the closure of the locus of simple Gauss double points. This gives the third curve on X whose importance in understanding the geometry of X has been recognised by many authors, see [7] and the bibliography of [7]. We introduced in Definition 2.4 the double cover curve  as the subset of points \(x\in X\) such that \(g(X_p)\leqslant 1\). By Theorem 3.3, as a set \(C_{\mathrm{dou}}\) consists exactly of simple Gauss points, parabolic Gauss double points, dual to parabolic Gauss double points, Gauss swallowtails, and Gauss triple points.
as the subset of points \(x\in X\) such that \(g(X_p)\leqslant 1\). By Theorem 3.3, as a set \(C_{\mathrm{dou}}\) consists exactly of simple Gauss points, parabolic Gauss double points, dual to parabolic Gauss double points, Gauss swallowtails, and Gauss triple points.
Proposition 3.12
([7, Proposition 2.5.6]) The subset  is a closed irreducible subscheme of pure dimension 1.
is a closed irreducible subscheme of pure dimension 1.
Note that there exists a rational involution
which sends the node \(p\in X_p\cap C_{\mathrm{dou}}\) to the other node  if p is a general point of \(C_{\mathrm{dou}}\). The computation of the degree of \(C_{\mathrm{dou}}\) requires a certain amount of work on its image \(C_{\mathrm{dou}}^{\vee }\) through the Gauss morphism. Using the apolarity theory we can easily see that letting \({\mathrm{Pol}}_p(X)\) stand for the polar cubic surface to X with respect to the point p, we can define the curve
if p is a general point of \(C_{\mathrm{dou}}\). The computation of the degree of \(C_{\mathrm{dou}}\) requires a certain amount of work on its image \(C_{\mathrm{dou}}^{\vee }\) through the Gauss morphism. Using the apolarity theory we can easily see that letting \({\mathrm{Pol}}_p(X)\) stand for the polar cubic surface to X with respect to the point p, we can define the curve

By construction \(D_p=\varphi _{\mathrm{Gauss}}^{-1}(p^{\perp }\,{\cap }\, X^{\vee })\). In other words we can interpret geometrically the Gauss morphism as induced by the morphism  given by the sublinear system of the polar cubics. This gives
given by the sublinear system of the polar cubics. This gives
Theorem 3.13
([7, Proposition 2.5.20, Corollary 2.5.21]) The curve \(C_{\mathrm{dou}}\) belongs to |80h| while \(C_{\mathrm{dou}}^{\vee }\) has degree 480.
The curve \(C_{\mathrm{dou}}\) is singular. We sketch the local analysis necessary to understand the local geometry of \(C_{\mathrm{dou}}\), but we stress that it requires the deep Yau–Zaslow formula which says that there are exactly 3200 nodal rational curves inside the linear system \(|{\mathscr {O}}_X(1)|\) if X is general. By Proposition 3.3 (vii) we know that each one of these rational nodal curves is a tangent section with three nodes. Each node determines the tangent section and since there are only nodes, there are exactly three nodes. By our previous notation this means that these 3200 nodal rational curves are exactly the hyperplane sections with Gauss triple points. This implies that there are exactly 9600 Gauss triple points. By the local analysis which uses the local stability of the Gauss morphism we have that \(C_{\mathrm{dou}}\) and \(C_{\mathrm{par}}\) intersect only at the 320 Gauss swallowtails, see Corollary 3.11, with multiplicity two and with multiplicity one at the parabolic Gauss double point, see [7, Proposition 2.5.15]. Hence we obtain that there are 1920 parabolic Gauss double points and so there are also 1920 dual to a parabolic Gauss double point. The above analysis leads to the following
Proposition 3.14
The double cover curve  is irreducible and it has only ordinary singularities. More precisely,
is irreducible and it has only ordinary singularities. More precisely,
- (i):
-
\(C_{\mathrm{dou}}\) has a node at each point of any Gauss triple.
- (ii):
-
\(C_{\mathrm{dou}}\) has a cusp at each dual to a parabolic Gauss double point.
- (iii):
-
Gauss swallowtails are smooth points of
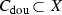 .
. - (iv):
-
\(C_{\mathrm{dou}}\) is smooth at any parabolic Gauss double point.
Finally there are precisely 9600 Gauss triple points and 1920 parabolic Gauss double points. In particular, the genus of \(C_{\mathrm{dou}}\) is 1281.
Proof
It follows by the detailed analysis on the geometry of \(C_{\mathrm{dou}}\) done in [7, Section 2.5]. \(\square \)
Proposition 3.15
([7, Section 2.7]) The dual curve \(C^{\vee }_{\mathrm{dou}}\) has a three-branched node in correspondence to the triplet of Gauss triple points and a cusp at each one of the points corresponding to parabolic Gauss double points. Hence it has genus 561.
4 The almost ruled surface
4.1 Numerical invariants associated to the surfaces of bitangents
We need to recall briefly some results mainly taken from [6, 7]. We stress that we set  and that
and that  is a very general quartic surface. In particular, there are no lines contained inside X. The next proposition is well known, possibly since very long time ago, but we include a proof of it because in the sequel we need analogue techniques and notation to write the ramification divisor R(f).
is a very general quartic surface. In particular, there are no lines contained inside X. The next proposition is well known, possibly since very long time ago, but we include a proof of it because in the sequel we need analogue techniques and notation to write the ramification divisor R(f).
Proposition 4.1
The scheme \(S\subset \mathbb {G}\) which parameterises bitangents to a smooth quartic surface \(X\subset {\mathbb {P}}^3\) with no lines is a smooth surface.
Proof
We fix a line \(l\subset {\mathbb {P}}^3\) which is bitangent to X. W.l.o.g. we can assume that \(l:=(x_2\,{=}\,x_3\,{=}\,0)\) and that the two points in \(X\cap l\) are \(P=(1\,{:}\,0\,{:}\,0\,{:}\,0)\), \(P_{\lambda }=(1\,{:}\,\lambda \,{:}\,0\,{:}\,0)\) where we do not assume \(\lambda \ne 0\). Then
where  are homogeneous forms of degree 3. We recall that by generality \(l\not \subset X\).
are homogeneous forms of degree 3. We recall that by generality \(l\not \subset X\).
We consider an open neighbourhood  of
of  and let \((u_0,u_1,u_2,u_3)\) be a regular parameterisation of \(U'\) of
and let \((u_0,u_1,u_2,u_3)\) be a regular parameterisation of \(U'\) of  inside \(\mathbb {G}\); this means that for points
inside \(\mathbb {G}\); this means that for points  close to
close to  inside \(U'\) we can write
inside \(U'\) we can write

We look for conditions on the tangent vector  to be inside the Zariski tangent space
to be inside the Zariski tangent space  of S at
of S at  . This means that if in
. This means that if in  , where
, where  , we write
, we write
then there exists a polynomial  of degree at most 2 in the variables \(x_0, x_1\) with \(f=q^2\). Since
of degree at most 2 in the variables \(x_0, x_1\) with \(f=q^2\). Since  , where \(g(x_0\,{:}\,x_1):=G(x_0\,{:}\,x_1\,{:}\,0\,{:}\,0)\) and \(h(x_0\,{:}\,x_1):=H(x_0\,{:}\,x_1\,{:}\,0\,{:}\,0)\), this is possible iff \(x_{1} (x_{1}-\lambda x_{0})\) is a factor of
, where \(g(x_0\,{:}\,x_1):=G(x_0\,{:}\,x_1\,{:}\,0\,{:}\,0)\) and \(h(x_0\,{:}\,x_1):=H(x_0\,{:}\,x_1\,{:}\,0\,{:}\,0)\), this is possible iff \(x_{1} (x_{1}-\lambda x_{0})\) is a factor of  . We distinguish now two cases: \(\lambda =0\) or \(\lambda \ne 0\). If \(\lambda \ne 0\) then we obtain that
. We distinguish now two cases: \(\lambda =0\) or \(\lambda \ne 0\). If \(\lambda \ne 0\) then we obtain that  iff
iff

The above linear system has rank \(\leqslant 1\) iff P or \(P_{\lambda }\) is a singular point of X. If \(\lambda =0\) the condition is equivalent to

and again the rank is less or equal to 1 iff P is a singular point. \(\square \)
4.1.1 Basic diagrams
We need a description of \(S\subset \mathbb {G}\) and of its invariants. Denote by \(H_{\mathbb {G}}\) the hyperplane section of the Plücker embedding \(\mathbb {G}\hookrightarrow {\mathbb {P}}(\bigwedge ^{2} V^{\vee })\). We have the universal exact sequence, its restriction over S and we stress that \({\mathscr {O}}_\mathbb {G}(H_{\mathbb {G}})={\mathrm{det}}\,{\mathscr {Q}}={\mathrm{det}}\,{\mathscr {S}}\).
Now we consider the standard conormal sequence of X inside \({\mathbb {P}}^3\):
We partially maintain the notation of [6] to help the reader to check some of our assertions. Following [6] we can build the following diagram:

where the inclusion \(J_X:{\mathbb {P}}(\Omega ^1_X(1))\rightarrow {\mathbb {P}}(\Omega ^1_{{\mathbb {P}}^3|X}(1))\) is given by sequence (4.1) and the morphism \({\mathbb {P}}({\mathscr {Q}}_S)\rightarrow {\mathbb {P}}(\Omega ^1_{{\mathbb {P}}^3|X}(1))\) is the restriction over S of the standard diagram

and \(\rho ':{\mathbb {P}}(\Omega ^1_{{\mathbb {P}}^3|X}(1))\rightarrow {\mathbb {P}}(V^\vee )\) is the obvious restriction.
4.1.2 Geometrical interpretation
By construction the \({\mathbb {P}}^1\)-bundle \(\pi _{\mathbb {G}}:{\mathbb {P}}({\mathscr {Q}})\rightarrow \mathbb {G}\) is the universal family of \(\mathbb {G}\), and the \({\mathbb {P}}^2\)-bundle \(\rho :{\mathbb {P}}(\Omega ^1_{{\mathbb {P}}^3}(1))\rightarrow {\mathbb {P}}^3\) is the projective bundle of the tangent directions on \({\mathbb {P}}^3\); that is  where
where  is the vector space given by the tangent space to \({\mathbb {P}}^3\) at the point p. The isomorphism \({\mathbb {P}}(\Omega ^1_{{\mathbb {P}}^3}(1))\cong {\mathbb {P}}({\mathscr {Q}})\) is well known.
is the vector space given by the tangent space to \({\mathbb {P}}^3\) at the point p. The isomorphism \({\mathbb {P}}(\Omega ^1_{{\mathbb {P}}^3}(1))\cong {\mathbb {P}}({\mathscr {Q}})\) is well known.
We denote by N the divisor on \({\mathbb {P}}(\Omega ^1_{{\mathbb {P}}^3}(1))\) and by R the divisor on \(\mathbb {P}({\mathscr {Q}})\) such that
Since no confusion can arise we denote by R also the restriction to \({\mathbb {P}}({\mathscr {Q}}_S)\) of R, hence \(\pi _{S\star }{\mathscr {O}}_{{\mathbb {P}}({\mathscr {Q}}_S)}(R)={\mathscr {Q}}_S\). We also denote by T the divisor on \({\mathbb {P}}(\Omega ^1_X(1))={\mathbb {P}}(\Omega ^1_X)\) such that
Lemma 4.2
For the 3-fold \({\mathbb {P}}(\Omega ^1_X(1))\) it holds

Proof
Trivial since X is smooth. \(\square \)
4.1.3 Useful divisor classes
We can relate classes which are easily seen by the geometry of \(\rho _X:{\mathbb {P}}(\Omega ^1_X(1))\rightarrow X\) to ones which can be better seen via the morphism  . We think it does not create any confusion to write R for the class
. We think it does not create any confusion to write R for the class  which comes from the divisor R on \({\mathbb {P}}({\mathscr {Q}}_S)\) via the inclusion \({\mathbb {P}}({\mathscr {Q}}_S)\hookrightarrow {\mathbb {P}}(\Omega ^1_{{\mathbb {P}}^3|X}(1))\). Finally we set
which comes from the divisor R on \({\mathbb {P}}({\mathscr {Q}}_S)\) via the inclusion \({\mathbb {P}}({\mathscr {Q}}_S)\hookrightarrow {\mathbb {P}}(\Omega ^1_{{\mathbb {P}}^3|X}(1))\). Finally we set  and
and  . One can easily check:
. One can easily check:
Lemma 4.3
It holds on  :
:
- (i):
-
\(R\sim \rho _{X}^{\star }h\).
- (ii):
-
\(N_{|{\mathbb {P}}(\Omega ^1_X(1))}\sim T +\rho _{X}^{\star }h\).
- (iii):
-
\(H_X\sim T+2\rho _{X}^{\star }h\).
4.1.4 The surface of contact points as a double cover
Inside S there is the subscheme \(B_{\mathrm{hf}}\hookrightarrow S\) which parameterises the hyperflex lines. In Proposition 3.9 we recalled a description of the corresponding curve \(C_{\mathrm{hf}}\subset X\). Using the surface of contact points Y, see Definition 2.3, and \(B_{\mathrm{hf}}\) we have an important information on S.
Proposition 4.4
([7, Proposition 3.11], see also [1]) There exists a non-trivial 2-torsion element  such that the surface of contact points Y can be realised as a subscheme of
such that the surface of contact points Y can be realised as a subscheme of  . The restriction of the natural projection
. The restriction of the natural projection  induces a 2-to-1 cover \(\pi :Y\rightarrow S\) branched over \(B_{\mathrm{hf}}\in |2H_{\mathbb {G}|S}|\). In particular Y is a smooth surface. Moreover, as a class inside \({\mathbb {P}}({\mathscr {Q}}_S)\) we have that \(Y\in |2R+\pi _S^{\star }(\sigma )|\).
induces a 2-to-1 cover \(\pi :Y\rightarrow S\) branched over \(B_{\mathrm{hf}}\in |2H_{\mathbb {G}|S}|\). In particular Y is a smooth surface. Moreover, as a class inside \({\mathbb {P}}({\mathscr {Q}}_S)\) we have that \(Y\in |2R+\pi _S^{\star }(\sigma )|\).
By diagram (4.2) and by a slight abuse of notation we obtain the following basic diagram:

The fact that Y is a divisor both in \({\mathbb {P}}(\Omega ^1_X(1))\) and in \({\mathbb {P}}({\mathscr {Q}}_S)\) makes possible to link the geometry of X to the geometry of S via the one of Y. In particular, it is noteworthy that we can try to obtain special curves on S via special curves on X and viceversa. First we recall that since X is general  , where we recall that \(h:=H_{{\mathbb {P}}^3_{|X}}\). Hence
, where we recall that \(h:=H_{{\mathbb {P}}^3_{|X}}\). Hence

Proposition 4.5
([6, Proposition 2.3]) As a class inside  it holds that
it holds that
4.1.5 The class of S in the Chow ring of \(\mathbb {G}\)
It is quite natural to introduce the following classes inside the Chow ring \(\bigoplus _{i=1}^{4}{\mathrm{CH}}^{i}(\mathbb {G})\) associated to the fundamental ladder, point, line, plane, \(p\in l\subset h\subset {\mathbb {P}}^3\):  ,
,  ,
,  . It is well known that
. It is well known that
and that the divisorial class of \(\sigma _l\) is the class \(H_{\mathbb {G}}\).
Lemma 4.6
([7, Lemma 3.30]) The following identity holds in the Chow ring of \(\mathbb {G}\):

In particular  .
.
4.1.6 Numerical invariants
Theorem 4.7
([7, Cohomological study, pp. 41–45]) For the surfaces S, Y we have the following formulae:
- (i):
-
\(K_{S}=3H_{\mathbb {G}|S}+\sigma \), \(q(S)=0\), \(p_g(S)=45\), \(h^1(S_X,\Omega ^1_{S}) =100\), \(c_2(S)=192\),
- (ii):
-
\(K_Y=\pi ^{\star }(4H_{\mathbb {G}|S})\), \(q(Y)=0\), \(p_g(Y)=171\).
4.2 The dual geometry
We consider the following open set of \(C_{\mathrm{dou}}\):

We set \((C_{\mathrm{dou}}^{0})^{\vee } :=\varphi _{\mathrm{Gauss}}(C_{\mathrm{dou}}^{0})\).
Lemma 4.8
The restriction of the Gauss morphism to \(C_{\mathrm{dou}}^{0}\) induces a 2-degree étale covering \(\tau :C_{\mathrm{dou}}^{0}\rightarrow (C_{\mathrm{dou}}^{0})^{\vee }\).
Proof
If p is a simple Gauss double point, it comes together with a unique other point \({\hat{p}} \in T_pX\) where \(X_p\) has the other node exactly on \(\hat{p}\) and \(T_{\hat{p}}X=T_pX\); that is \(\varphi _{\mathrm{Gauss}}(p)=\varphi _{\mathrm{Gauss}}({\hat{p}})\). By definition of the double cover curve there are no other points of \(C_{\mathrm{dou}}^{0}\) over \(\varphi _{\mathrm{Gauss}}(p)\). \(\square \)
We define \(\Sigma _{\mathrm{dou}}^{0}\subset {\mathbb {P}}^3\) the open surface swept by the lines \(l_{p,\hat{p}}:=\langle p,\hat{p} \rangle \subset {\mathbb {P}}^3\) where \(p\in C_{\mathrm{dou}}^{0}\). We notice that: 1)  and 2) if \(p_1\ne p\) then
and 2) if \(p_1\ne p\) then  . This implies that we can define an injective morphism
. This implies that we can define an injective morphism  defined by
defined by  . By the normalisation morphism \(\nu _{{\mathrm{dou}}}^{\vee }:{\widetilde{ C^{\vee }_{{\mathrm{dou}}}} }\rightarrow C_{{\mathrm{dou}}}^{\vee }\) we obtain a global morphism generically of degree 1:
. By the normalisation morphism \(\nu _{{\mathrm{dou}}}^{\vee }:{\widetilde{ C^{\vee }_{{\mathrm{dou}}}} }\rightarrow C_{{\mathrm{dou}}}^{\vee }\) we obtain a global morphism generically of degree 1:
We set
In Definition 2.6 we called \(\Sigma _{\mathrm{dou} }\hookrightarrow {\mathbb {P}}^3\) the almost ruled surface of Gauss double points.
Lemma 4.9
If  is the projective closure of \(\Sigma _{\mathrm{dou}}^{0}\) then it holds that
is the projective closure of \(\Sigma _{\mathrm{dou}}^{0}\) then it holds that  . Moreover, \(C_{\mathrm{dou}}\hookrightarrow \Sigma _{\mathrm{dou}}\).
. Moreover, \(C_{\mathrm{dou}}\hookrightarrow \Sigma _{\mathrm{dou}}\).
Proof
By Proposition 3.14, \(C_{\mathrm{dou}}\) is irreducible, then the first claim follows by the universal property of \(\mathbb {G}\). By construction it holds that \(C_{\mathrm{dou}}^{0}\hookrightarrow \Sigma _{\mathrm{dou}}\) then \(C_{\mathrm{dou}}\hookrightarrow \Sigma _{\mathrm{dou}}\) since \(C_{\mathrm{dou}}\) is the closure inside \({\mathbb {P}}^3\) of \(C_{\mathrm{dou}}^{0}\). \(\square \)
Let \(\pi _C:\Sigma \rightarrow C\) be the ruled surface obtained by the pull-back of \(\pi _S:{\mathbb {P}}({\mathscr {Q}}_S)\rightarrow S\) via the natural inclusion \(C\hookrightarrow S\).
Lemma 4.10
The curve C is irreducible and the surface \(\Sigma \) is irreducible.
Proof
By Proposition 3.14 and by its construction the curve C is irreducible. Since \(\pi _S:{\mathbb {P}}({\mathscr {Q}}_S)\rightarrow S\) is a fiber bundle, the claim follows. \(\square \)
Consider again the surface  of Gauss double points. Note that the pull-back \(\Sigma ^{0}\rightarrow (C_{\mathrm{dou}}^{0})^{\vee }\) of \(\pi _C:\Sigma \rightarrow C\) via the inclusion
of Gauss double points. Note that the pull-back \(\Sigma ^{0}\rightarrow (C_{\mathrm{dou}}^{0})^{\vee }\) of \(\pi _C:\Sigma \rightarrow C\) via the inclusion  is a smooth open ruled surface. Now we obviously have
is a smooth open ruled surface. Now we obviously have
Corollary 4.11
There exists a rational map \(\mu :\Sigma _{\mathrm{dou} }\dashrightarrow {\widetilde{ C^{\vee }_{{\mathrm{dou}}}} }\) which induces the natural structure of smooth ruled surface on \(\Sigma ^{0}\rightarrow ( C_{\mathrm{dou}}^{0}) ^{\vee }\).
Proof
The pull-back \(\pi ':{\widetilde{\Sigma }} \rightarrow {\widetilde{ C^{\vee }_{{\mathrm{dou}}}} }\) of \(\pi _S:{\mathbb {P}}({\mathscr {Q}}_S)\rightarrow S\) via the morphism \(j^{\vee }_{{\mathrm{dou}}}:{\widetilde{ C^{\vee }_{{\mathrm{dou}}}} }\rightarrow S\) is a smooth surface which is mapped birationally onto \(\Sigma _{\mathrm{dou}}\) in a way compatible with the morphism \(\varphi _{\mathrm{Gauss}|C_{\mathrm{dou}}}:C_{\mathrm{dou}}\rightarrow C^{\vee }_{\mathrm{dou}}\). \(\square \)
Lemma 4.12
The almost ruled surface of Gauss double points is irreducible and it osculates X along \(C_{\mathrm{dou}}\); that is the restriction \(\Sigma _{{\mathrm{dou}}|X}\) is a subscheme of X which contains \(2C_{\mathrm{dou}}\).
Proof
By construction we saw that \(\Sigma _{\mathrm{dou}}= f(\Sigma )\). Then the first claim follows by Lemma 4.10. We show that the open ruled surface \(\Sigma ^{0}\) osculates X along \(C_{\mathrm{dou}}^{0}\). This follows by definition since any fiber l of \(\Sigma ^{0}\rightarrow (C_{\mathrm{dou}}^{0} )^{\vee }\) osculates X along the corresponding two simple Gauss points \(p,\hat{p}\) such that  .
.
\(\square \)
4.3 The geometry of the morphism of bitangents
Now we start the study of the morphism \(f:{\mathbb {P}}({\mathscr {Q}}_S)\rightarrow {\mathbb {P}}^3\).
Lemma 4.13
The morphism \(f:{\mathbb {P}}({\mathscr {Q}}_S)\rightarrow {\mathbb {P}}^3\) is finite of degree 12.
Proof
Let \(p\in {\mathbb {P}}^3\) be such that the f-fiber is of positive dimension. This means that there are infinite bitangent lines through p. Then the polar cubic \({\mathrm{Pol}}_{p}(X)\) has at least a component swept by lines through p. The restriction of \({\mathrm{Pol}}_{p}(X)\) to X is non-reduced. This implies that this restriction is a divisor of type \(2D+A\). Since we are assuming that  , X does not contain curves of degree \(\leqslant 3\). Then the only possibility is that D is a hyperplane section. This implies that S contains the rational curve which parameterises the pencil of lines contained in a plane and passing through p. This is a contradiction. Indeed there exists an unramified covering \(S_X\rightarrow S\) where \(S_X\) is an irregular surface; the details of the proof are in [6, Propositions 2.4 and 3.1]. Another self-contained proof is in [7, Lemma 1.1]. See also [1, Section 3]. Finally by [7, Corollary A.3, p. 53] it is known that the Albanese morphism
, X does not contain curves of degree \(\leqslant 3\). Then the only possibility is that D is a hyperplane section. This implies that S contains the rational curve which parameterises the pencil of lines contained in a plane and passing through p. This is a contradiction. Indeed there exists an unramified covering \(S_X\rightarrow S\) where \(S_X\) is an irregular surface; the details of the proof are in [6, Propositions 2.4 and 3.1]. Another self-contained proof is in [7, Lemma 1.1]. See also [1, Section 3]. Finally by [7, Corollary A.3, p. 53] it is known that the Albanese morphism  is a closed immersion. In particular there are no rational curves on S. \(\square \)
is a closed immersion. In particular there are no rational curves on S. \(\square \)
4.3.1 The ramification divisor
Lemma 4.14
The surface of contact points is a subdivisor of R(f) of multiplicity 1. Moreover the induced morphism \(\rho :Y\rightarrow X\) is of degree 6 and \(f^{\star }{\mathscr {O}}_{{\mathbb {P}}^3}(X)={\mathscr {O}}_{{\mathbb {P}}({\mathscr {Q}}_S)}(2Y)\).
Proof
By definition \(f^{-1}(X)= Y\). Since any bitangent line through a point \(p\in X\) is contained in \(T_pX\), any bitangent line through p gives a ramification point for the morphism \({\widetilde{X_p}}\rightarrow {\mathbb {P}}^1\) given by the pencil of lines inside \(T_pX\) with focal point p. This and Lemma 4.13 imply that the induced morphism \(\rho :Y\rightarrow X\) is finite of degree 6. Since \(f^{-1}(X)= Y\) then the Chow groups projection formula implies that \(12[X] =f_{\star }f^{\star }[X]=f_{\star }a[Y]=af_{\star }[Y]=6a[X]\). Thus \(a=2\). \(\square \)
Lemma 4.15
The surface \(\Sigma \) belongs to R(f).
Proof
This follows easily by a local count. We use notation of Proposition 4.1. We consider a line \(l\subset {\mathbb {P}}^3\) which is bitangent to X. W.l.o.g. we can assume that \(l:=(x_2\,{=}\,x_3\,{=}\,0)\) and that the two points where l is tangent to X are \(P=(1\,{:}\,0\,{:}\,0\,{:}\,0)\), \(P_{\lambda }(1\,{:}\,\lambda \,{:}\,0\,{:}\,0)\). For a while assume \(\lambda \ne 0\). The general point \(p\in l\) is then given by a parameter \(t\in \mathbb {C}\) and \(p=(1\,{:}\,t\,{:}\,0\,{:}\,0)\). We easily can write the tangent space to \({\mathbb {P}}({\mathscr {Q}}_S)\) at the point  . Indeed let \(w_1={x_1}/{x_0}-t\), \(w_2={x_2}/{x_0}\), \(w_3={x_3}/{x_0}\) be such that \((w_1,w_2,w_3)\) is a system of local coordinates around the point \(p\in {\mathbb {P}}^3\) and let \((u_0,u_1,u_2,u_3)\) be a local system of coordinates at the point
. Indeed let \(w_1={x_1}/{x_0}-t\), \(w_2={x_2}/{x_0}\), \(w_3={x_3}/{x_0}\) be such that \((w_1,w_2,w_3)\) is a system of local coordinates around the point \(p\in {\mathbb {P}}^3\) and let \((u_0,u_1,u_2,u_3)\) be a local system of coordinates at the point  , that is a line r near to l is parameterised by
, that is a line r near to l is parameterised by
Then (locally) inside  , where we take coordinates \((w_1,w_2,w_3,u_0,u_1,u_2,u_3)\), the tangent space
, where we take coordinates \((w_1,w_2,w_3,u_0,u_1,u_2,u_3)\), the tangent space  is (locally) given by
is (locally) given by

by the proof of Proposition 4.1. The morphism \(f:{\mathbb {P}}({\mathscr {Q}}_S)\rightarrow {\mathbb {P}}^3\) is given by the restriction to \({\mathbb {P}}({\mathscr {Q}}_S)\) of the natural projection \(\rho :{\mathbb {P}}({\mathscr {Q}})={\mathbb {P}}(\Omega ^1_{{\mathbb {P}}^3})\rightarrow {\mathbb {P}}^3\), which is, locally, \((w_1,w_2,w_3,u_0,u_1,u_2,u_3)\mapsto (w_1,w_2,w_3)\). Now suppose for a while we are in the general case where \(h(1\,{:}\,0)=H(1\,{:}\,0\,{:}\,0\,{:}\,0)\ne 0\) and \(h(1\,{:}\,\lambda )=H(1\,{:}\,\lambda \,{:}\,0\,{:}\,0)\ne 0\). We take \((w_1, u_0,u_1)\) as local coordinates for the threefold \({\mathbb {P}}({\mathscr {Q}}_S)\) around the point  . The matrix of the differential
. The matrix of the differential  is then given by
is then given by
Hence its determinant is zero iff  ; we immediately see that
; we immediately see that  is the local equation of \(Y\subset {\mathbb {P}}({\mathscr {Q}}_S)\). The condition
is the local equation of \(Y\subset {\mathbb {P}}({\mathscr {Q}}_S)\). The condition  is independent of t. This last condition means that when it is satisfied this occurs for all the points which belong to the bitangent line l. Finally it is a trivial verification on the equation
is independent of t. This last condition means that when it is satisfied this occurs for all the points which belong to the bitangent line l. Finally it is a trivial verification on the equation
of X to see that generically the condition \(0={\mathrm{det}} \bigl ( {\begin{matrix} g(1:0) &{} h(1:0) \\ g(1:\lambda )&{} h(1:\lambda ) \end{matrix}} \bigr )\) occurs iff \(T_PX=T_{P_{\lambda }}X\) and \(X_P=T_PX\cap X\) is a quartic with two nodes respectively on P and on \(P_{\lambda }\). Analogue computations hold if we are in more special cases where \(h(1\,{:}\,\lambda )=0\) and \(h(1\,{:}\,0)\ne 0\) or \(h(1\,{:}\,\lambda )\ne 0\) and \(h(1\,{:}\,0)= 0\) or \(g(1\,{:}\,\lambda )=0\) and \(g(1\,{:}\,0)\ne 0\) or \(g(1\,{:}\,\lambda )\ne 0\) and \(g(1\,{:}\,0)= 0\) or where \(\lambda =0\). All these verifications are analogue to the one shown above. The condition above means that the open surface \(\Sigma _0:=\pi _{S}^{-1}( (j_{\mathrm{dou}}^{0})^{\vee } ( (C_{\mathrm{dou}}^{0})^{\vee } ))\) is inside R(f). This implies the claim. \(\square \)
Lemma 4.16
The divisor R(f) is linearly equivalent to \(Y +\pi _{S}^{\star } (4H_{\mathbb {G}|S})\).
Proof
By Theorem 4.7, \(K_{S}=3H_{\mathbb {G}|S}+\sigma \). Since the first Chern class of \({\mathscr {Q}}_S\) is \(H_{\mathbb {G}|S}\), by the standard formula of the canonical class divisor we conclude that \(K_{{\mathbb {P}}({\mathscr {Q}}_S)}\sim -2R+\pi _{S}^{\star } (4H_{\mathbb {G}|S}+\sigma )\). By Proposition 4.13 we know that \(K_{{\mathbb {P}}({\mathscr {Q}}_S)} \sim f^{\star } (K_{{\mathbb {P}}^{3}}) +R(f)\sim f^{\star }(-X)+R(f)\) since \(X\in |4H_{ {\mathbb {P}}^{3} }|\). Then since \(\sigma \sim -\sigma \), it holds that
By Proposition 4.14 we know that sheaf theoretically \(f^{\star }{\mathscr {O}}_{{\mathbb {P}}^3}(X)={\mathscr {O}}_{{\mathbb {P}}({\mathscr {Q}}_S)}(2Y)\) and by Proposition 4.4 we know that \(Y\in |2R+\pi _S^{\star }(\sigma )|\). This implies that \(f^{\star }(X) -(2R+\pi _{S}^{\star } (\sigma ))\sim Y\). Hence by substitution inside equation (4.3) we have
\(\square \)
4.3.2 The branch divisor
We now study the branch divisor of \(f:{\mathbb {P}}({\mathscr {Q}}_S)\rightarrow {\mathbb {P}}^3\). The claim follows by a delicate computation on Chow groups. Since there is no possibility of misunderstanding we will indicate the Chow class [A] of the cycle A simply by A. We recall here that a line l inside \({\mathbb {P}}^3\) is given as  .
.
Proposition 4.17
\(B(f)=X+\Sigma _{\mathrm{dou}}\). In particular, for the almost ruled surface of Gauss double points has degree 160.
Proof
By projection formula

By Lemma 4.16
hence

Since \(\sigma \) is a torsion element and \(R= f^{\star }(H_{{\mathbb {P}}^3})\) it follows that

It remains to compute the natural number:  . We can find it by divisors restriction on Y. Inside
. We can find it by divisors restriction on Y. Inside  the class Y is numerically equivalent to \(2f^{\star }(H_{{\mathbb {P}}^3})\). Then in the Chow algebra of \({\mathbb {P}}({\mathscr {Q}}_S)\) it holds that
the class Y is numerically equivalent to \(2f^{\star }(H_{{\mathbb {P}}^3})\). Then in the Chow algebra of \({\mathbb {P}}({\mathscr {Q}}_S)\) it holds that

We point out that the number  coincides with the intersection number of the following two divisors on Y: \((f^{\star }(H_{{\mathbb {P}}^3}))_{| Y}\) and \((\pi _{S}^{\star } (H_{\mathbb {G}|S}))_{| Y}\). Now we carry on this computation on Y seen as a divisor inside \({\mathbb {P}}(\Omega ^1_X(1)))\), where we can use the conversion rules recalled in Lemma 4.3. By Proposition 4.5 we know that as a class inside \({\mathrm{Pic}}({\mathbb {P}}(\Omega ^1_X(1)))\), \(Y\in |6T\,{+}\,8 \rho _{X}^{\star }(h)|\). Then
coincides with the intersection number of the following two divisors on Y: \((f^{\star }(H_{{\mathbb {P}}^3}))_{| Y}\) and \((\pi _{S}^{\star } (H_{\mathbb {G}|S}))_{| Y}\). Now we carry on this computation on Y seen as a divisor inside \({\mathbb {P}}(\Omega ^1_X(1)))\), where we can use the conversion rules recalled in Lemma 4.3. By Proposition 4.5 we know that as a class inside \({\mathrm{Pic}}({\mathbb {P}}(\Omega ^1_X(1)))\), \(Y\in |6T\,{+}\,8 \rho _{X}^{\star }(h)|\). Then

and since on  it holds that
it holds that  ,
,  and
and  it follows that
it follows that

We showed that  . On the other hand by Lemma 4.15 we know that \(\Sigma _{\mathrm{dou}}\) is a subdivisor of B(f) since \(f(\Sigma )=\Sigma _{\mathrm{dou}}\). By Lemma 4.12 we know that \(\Sigma _{\mathrm{dou}}\) restricts on X at least to \(2C_{\mathrm{dou}}\). By Theorem 3.13, \(C_{\mathrm{dou}}\in |80h|\). Then \(\Sigma _{\mathrm{dou}}\in |b H_{{\mathbb {P}}^3}|\) where \(b\geqslant 160\). Moreover by Lemma 4.14 we certainly have that \(6X+\Sigma _{\mathrm{dou}}\) is at least a subdivisor of \(f_{\star } R(f)\), but
. On the other hand by Lemma 4.15 we know that \(\Sigma _{\mathrm{dou}}\) is a subdivisor of B(f) since \(f(\Sigma )=\Sigma _{\mathrm{dou}}\). By Lemma 4.12 we know that \(\Sigma _{\mathrm{dou}}\) restricts on X at least to \(2C_{\mathrm{dou}}\). By Theorem 3.13, \(C_{\mathrm{dou}}\in |80h|\). Then \(\Sigma _{\mathrm{dou}}\in |b H_{{\mathbb {P}}^3}|\) where \(b\geqslant 160\). Moreover by Lemma 4.14 we certainly have that \(6X+\Sigma _{\mathrm{dou}}\) is at least a subdivisor of \(f_{\star } R(f)\), but

This implies that \(b=160\) and that \(X+\Sigma _{\mathrm{dou}}\) is exactly the divisor B(f). \(\square \)
Remark 4.18
We stress that the degree of \(\Sigma _{\mathrm{dou}}\) is computed also in [2, (4.21), p. 24].
4.4 Geometrical consequences on the geometry of Gauss curves
By Proposition 4.17 and by its proof we can complete the geometrical picture behind Proposition 2.5.
Lemma 4.19
\(R(f)=Y+\Sigma \). In particular, \(\Sigma \in |\pi _{S}^{\star } (4H_{\mathbb {G}|S})|\).
Proof
Consider the two morphisms \(f:{\mathbb {P}}({\mathscr {Q}}_S)\rightarrow {\mathbb {P}}^3\) and \(\pi _S:{\mathbb {P}}({\mathscr {Q}}_S)\rightarrow S\). The divisor \(Y+\Sigma \) is a subdivisor of R(f) and by Lemma 4.16, \(R(f)\sim Y +\pi _{S}^{\star } (4H_{\mathbb {G}|S})\). By construction \(\Sigma \in |\pi _{S}^{\star } (C)|\). Hence C is a subdivisor of a divisor \(D\in |4H_{\mathbb {G}|S}|\) but looking to the f-direction, by the same technique used in the proof of Lemma 4.17 we have that

hence \(C\in |4H_{\mathbb {G}|S}|\), and the claim follows. \(\square \)
4.5 The proof of Proposition 2.5
By the proof of Lemma 4.19, \(C\in |4H_{\mathbb {G}|S}|\) and by Lemma 4.10, C is irreducible. Hence by Lemma 4.6 and by Theorem 4.7 (i) it holds that C is an irreducible curve of arithmetical genus \(\rho _{a}(C)=561\). By Proposition 3.15 we know that \({\widetilde{ C^{\vee }_{{\mathrm{dou}}}} }\) has genus 561. Then the morphism \(j^{\vee }_{{\mathrm{dou}}}:{\widetilde{ C^{\vee }_{{\mathrm{dou}}}} }\rightarrow C\subset S\) is an embedding.
By Proposition 4.4 we know that \(\pi :Y\rightarrow S\) is branched on the curve of hyperflexes which is in \(|2H_{\mathbb {G}|S}|\). Then an analogue argument shows that \(j_{{\mathrm{dou}}} :{\widetilde{ C_{{\mathrm{dou}}}}}\hookrightarrow Y\) too is an embedding. By construction we have that diagram (2.1) is commutative.
4.6 The proof of Main Theorem
We showed in Proposition 4.1 that S is smooth. By Proposition 4.4 we know that Y is smooth. By Proposition 3.14 we have a full classification of the singularities of the double cover curve  . By Proposition 3.15 we have a full classification of the singularities of the dual curve \(C^{\vee }_{\mathrm{dou}}\). By Lemma 4.13 the morphism \(f:{\mathbb {P}}({\mathscr {Q}}_S)\rightarrow {\mathbb {P}}^3\) is finite of degree 12. By the proof of Proposition 4.17 we know that \(\Sigma _{\mathrm{dou}}\) is a surface of degree 160. By Lemma 4.12 and by the proof of Proposition 4.17 we know that \(\Sigma _{{\mathrm{dou}}_{| X}}\) is exactly \(2C_{\mathrm{dou}}\). Finally, by Proposition 4.17, \(B(f)=X+\Sigma _{\mathrm{dou}}\), by Lemma 4.19, \(R(f)=Y+\Sigma \), by Lemma 4.14 the morphism \(f_{| Y}=\rho :Y\rightarrow X\) is of degree 6, and by the proof of Lemma 4.19 and by construction the morphism \(f_{|\Sigma }:\Sigma \rightarrow \Sigma _{\mathrm{dou}}\) is birational.
. By Proposition 3.15 we have a full classification of the singularities of the dual curve \(C^{\vee }_{\mathrm{dou}}\). By Lemma 4.13 the morphism \(f:{\mathbb {P}}({\mathscr {Q}}_S)\rightarrow {\mathbb {P}}^3\) is finite of degree 12. By the proof of Proposition 4.17 we know that \(\Sigma _{\mathrm{dou}}\) is a surface of degree 160. By Lemma 4.12 and by the proof of Proposition 4.17 we know that \(\Sigma _{{\mathrm{dou}}_{| X}}\) is exactly \(2C_{\mathrm{dou}}\). Finally, by Proposition 4.17, \(B(f)=X+\Sigma _{\mathrm{dou}}\), by Lemma 4.19, \(R(f)=Y+\Sigma \), by Lemma 4.14 the morphism \(f_{| Y}=\rho :Y\rightarrow X\) is of degree 6, and by the proof of Lemma 4.19 and by construction the morphism \(f_{|\Sigma }:\Sigma \rightarrow \Sigma _{\mathrm{dou}}\) is birational.
References
Corvaja, P., Zucconi, F.: Bitangents to the quartic surface and infinitesimal deformations (2019). arXiv:1910.01365
Dedieu, T.: Some classical formulae for curves and surfaces. In: Notes of the Seminar on Degenerations and Enumeration of Curves on Surfaces, held in Rome Tor Vergata (2015–2017). https://hal.archives-ouvertes.fr/hal-02914653/document
Huybrechts, D.: Lectures on K3 Surfaces. Cambridge Studies in Advanced Mathematics, vol. 158. Cambridge University Press, Cambridge (2016)
Salmon, G.: A Treatise on the Analytic Geometry of Three Dimensions, 4th edn. Hodges, Figgis, Dublin (1882)
Tikhomirov, A.S.: The geometry of the Fano surface of the double cover of \({\mathbb{P}}^{3}\) branched in a quartic. Math. USSR-Izv. 16(2), 373–397 (1981)
Welters, G.E.: Abel–Jacobi isogenies for certain types of Fano threefolds Mathematical Centre Tracts, vol. 141. Mathematical Centrum, Amsterdam (1981)
Witaszek, J.: The Geometry of Smooth Quartics. MSc Thesis, Bonn University Bonn (2014). http://wwwf.imperial.ac.uk/~jw2214/masterthesis.pdf
Acknowledgements
The authors thank Piercarlo Craighero for useful discussions, Jakub Witaszek for useful comments and for giving us the permission to use his pictures, and finally Thomas Dedieu who informed us that the surface of Gauss double points was classically studied, e.g. in [4].
Funding
Open access funding provided by Università degli Studi di Udine within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Corvaja, P., Zucconi, F. The surface of Gauss double points. European Journal of Mathematics 8, 871–892 (2022). https://doi.org/10.1007/s40879-021-00456-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-021-00456-x











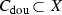 .
.