Abstract
We study the real loci of toric degenerations of complex varieties with reducible central fibre. We show that the topology of such degenerations can be explicitly described via the Kato–Nakayama space of the central fibre as a log space. We furthermore provide generalities of real structures in log geometry and their lift to Kato–Nakayama spaces. A key point of this paper is a description of the Kato–Nakayama space of a toric degeneration and its real locus, both as bundles determined by tropical data. We provide several examples including real toric degenerations of K3-surfaces and a toric degeneration of local \({\mathbb {P}}^2\).






Similar content being viewed by others
Notes
The discussion in [17] is on the complement of a part \({\widetilde{\Delta }}\subset B\) of the codimension two skeleton of the barycentric subdivision. There is a retraction of
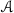 to a subset of \({\widetilde{\Delta }}\). However, the discussion on monomials works on any cell
to a subset of \({\widetilde{\Delta }}\). However, the discussion on monomials works on any cell 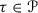 not contained in
not contained in  and with
and with 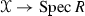 locally toroidal at some point of \(X_\tau \).
locally toroidal at some point of \(X_\tau \).This condition is non-trivial only if \(x\in \partial B\).
References
Argüz, H.: Topological torus fibrations on Calabi–Yau manifolds via Kato–Nakayama spaces (2020). arXiv:2003.11589 (to appear in the Proceedings of the 26th Gökova Geometry Topology Conference)
Argüz, H., Prince, T.: Real Lagrangians in Calabi–Yau threefolds. Proc. London Math. Soc. 121(2), 287–311 (2020)
Argüz, H., Prince, T.: On the cohomology groups of real Lagrangians in Calabi–Yau threefolds (2020). arXiv:2002.03957 (to appear in Experimental Mathematics)
Bihan, F.: Asymptotic behaviour of Betti numbers of real algebraic surfaces. Comment. Math. Helv. 78(2), 227–244 (2003)
Castaño-Bernard, R., Matessi, D.: The fixed point set of anti-symplectic involutions of Lagrangian fibrations. Rend. Semin. Mat. Univ. Politec. Torino 68(3), 235–250 (2010)
Degtyarev, A.I., Kharlamov, V.M.: Topological properties of real algebraic varieties: du côté de chez Rokhlin. Russian Math. Surveys 55(4), 735–814 (2000)
Delaunay, C.: Real structures on smooth compact toric surfaces. In: Goldman, R., Krasuaskas, R. (eds.) Topics in Algebraic Geometry and Geometric Modeling. Contemporary Mathematics, vol. 334, pp. 267–290. American Mathematical Society, Providence (2003)
Duistermaat, J.J.: On global action-angle coordinates. Comm. Pure Appl. Math. 33(6), 687–706 (1980)
Fukaya, K., Oh, Y.-G., Ohta, H., Ono, K.: Antisymplectic involution and Floer cohomology. Geom. Topol. 21(1), 1–106 (2017)
Fulton, W.: Introduction to Toric Varieties. Annals of Mathematics Studies, vol. 131. Princeton University Press, Princeton (1993)
Georgieva, P.: Open Gromov–Witten disk invariants in the presence of an anti-symplectic involution. Adv. Math. 301, 116–160 (2016)
Gillam, W.D.: Oriented real blowup (2011). http://www.math.boun.edu.tr/instructors/wdgillam/orb.pdf
Gross, M.: Topological mirror symmetry. Invent. Math. 144(1), 75–137 (2001)
Gross, M.: Special Lagrangian fibrations I: topology. In: Saito, M.-H., et al. (eds.) Integrable Systems and Algebraic Geometry, pp. 156–193. World Scientific, River Edge (1998)
Gross, M.: Special Lagrangian fibrations. II. Geometry. In: Yau, S.-T. (ed.) Surveys in Differential Geometry: Differential Geometry Inspired by String Theory. Surveys in Differential Geometry, vol. 5, pp. 341–403. International Press, Boston (1999)
Gross, M., Hacking, P., Keel, S.: Mirror symmetry for log Calabi–Yau surfaces I. Publ. Math. Inst. Hautes Études Sci. 122, 65–168 (2015)
Gross, M., Hacking, P., Siebert, B.: Theta functions on varieties with effective anti-canonical class (2016). arXiv:1601.07081v1
Gross, M., Siebert, B.: Mirror symmetry via logarithmic degeneration data I. J. Differential Geom. 72(2), 169–338 (2006)
Gross, M., Siebert, B.: Mirror symmetry via logarithmic degeneration data II. J. Algebraic Geom. 19(4), 679–780 (2010)
Gross, M., Siebert, B.: From real affine to complex geometry. Ann. Math. 174(3), 1301–1428 (2011)
Gross, M., Siebert, B.: An invitation to toric degenerations. In: Leung, N.C., Yau, S.-T. (eds.) Surveys in Differential Geometry, Vol. XVI. Geometry of Special Holonomy and Related Topics. Surveys in Differential Geometry, vol. 16, pp. 43–78. International Press, Somerville (2011)
Haase, C., Zharkov, I.: Integral affine structures on spheres: complete intersections. Int. Math. Res. Not. 2005(51), 3153–3167 (2005)
Haase, C., Zharkov, I.: Integral affine structures on spheres and torus fibrations of Calabi–Yau toric hypersurfaces I (2002). arXiv:0205321
Haase, C., Zharkov, I.: Integral affine structures on spheres and torus fibrations of Calabi–Yau toric hypersurfaces II (2003). arXiv:0301222
Hartshorne, R.: Algebraic Geometry. Graduate Texts in Mathematics, vol. 52. Springer, New York (1977)
Hatcher, A.E.: Concordance Spaces, Higher Simple-Homotopy Theory and Applications. In: Milgram, R.J. (ed.) Algebraic and Geometric Topology, Part I. Proceedings of Symposia in Pure Mathematics, vol. 32. American Mathematical Society, Providence (1978)
Huisman, J.: Real Abelian Varieties with Complex Mmultiplication. PhD thesis, Vrije Universiteit (1992)
Itenberg, I.: Topology of real algebraic \(T\)-surfaces. Rev. Mat. Univ. Complut. Madrid 10(special issue), 131–152 (1997)
Itenberg, I., Katzarkov, L., Mikhalkin, G., Zharkov, I.: Tropical homology. Math. Ann. 374(1–2), 963–1006 (2019)
Itenberg, I., Viro, O.: Asymptotically maximal real algebraic hypersurfaces of projective space. In: Proceedings of Gökova Geometry-Topology Conference, pp. 91–105. GGT, Gökova (2006)
Kato, F.: Log smooth deformation theory. Tohoku Math. J. 48(3), 317–354 (1996)
Kato, K.: Logarithmic structures of Fontaine-Illusie. In: Igusa, J.-I., et al. (eds.) Algebraic Analysis, Geometry, and Number Theory, pp. 191–224. Johns Hopkins University Press, Baltimore (1989)
Kato, K., Nakayama, C.: Log Betti cohomology, log étale cohomology, and log de Rham cohomology of log schemes over \({ C}\). Kodai Math. J. 22(2), 161–186 (1999)
Moishezon, B.: Complex Surfaces and Connected Sums of Complex Projective Planes. Lecture Notes in Mathematics, vol. 603. Springer, Berlin (1977)
Moser-Jauslin, L., Terpereau, R.: Real structures on horospherical varieties. Michigan Math. J. (2020). https://doi.org/10.1307/mmj/20195793
Nakayama, C., Ogus, A.: Relative rounding in toric and logarithmic geometry. Geom. Topol. 14(4), 2189–2241 (2010)
Nikulin, V.V.: Integral symmetric bilinear forms and some of their applications. Math. USSR-Izv. 14(1), 103–167 (1980)
Nikulin, V.V., Saito, S.: Real \(K3\) surfaces with non-symplectic involution and applications. Proc. London Math. Soc. 90(3), 591–654 (2005)
Ogus, A.: Lectures on Logarithmic Algebraic Geometry. Cambridge Studies in Advanced Mathematics, vol. 178. Cambridge University Press, Cambridge (2018)
Pandharipande, R., Solomon, J., Walcher, J.: Disk enumeration on the quintic 3-fold. J. Amer. Math. Soc. 21(4), 1169–1209 (2008)
Parker, B.: Exploded manifolds. Adv. Math. 229(6), 3256–3319 (2012)
Renaudineau, A., Shaw, K.: Bounding the Betti numbers of real hypersurfaces near the tropical limit (2018). arXiv:1805.02030
Ruan, W.-D.: Lagrangian torus fibration of quintic hypersurfaces. I. Fermat quintic case. In: Vafa, C., Yau, S.-T. (eds.) Winter School on Mirror Symmetry, Vector Bundles and Lagrangian Submanifolds. AMS/IP Studies in Advanced Mathematics, vol. 23, pp. 297–332. American Mathematical Society, Providence (2001)
Ruan, W.-D.: Lagrangian torus fibration of quintic Calabi-Yau hypersurfaces. II. Technical results on gradient flow construction. J. Symplectic Geom. 1(3), 435–521 (2002)
Ruan, W.-D.: Lagrangian torus fibration of quintic Calabi-Yau hypersurfaces. III. Symplectic topological SYZ mirror construction for general quintics. J. Differential Geom. 63(2), 171–229 (2003)
Ruddat, H., Sibilla, N., Treumann, D., Zaslow, E.: Skeleta of affine hypersurfaces. Geom. Topol. 18(3), 1343–1395 (2014)
Ruddat, H., Siebert, B.: Period integrals from wall structures via tropical cycles, canonical coordinates in mirror symmetry and analyticity of toric degenerations (2019). arXiv:1907.03794
Ruddat, H., Zharkov, I.: Compactifying torus fibrations over integral affine manifolds with singularities (2020). arXiv:2003.08521
Ruddat, H., Zharkov, I.: Tailoring a pair of pants (2020). arXiv:2001.08267
Siebenmann, L.C.: Deformation of homeomorphisms on stratified sets. I, II. Comment. Math. Helv. 47, 137–163 (1972)
Solomon, J.: Intersection Theory on the Moduli Space of Holomorphic Curves with Lagrangian Boundary Conditions. Ph.D. Thesis, Massachusetts Institute of Technology (2006). arXiv:math/0606429
Strominger, A., Yau, S.-T., Zaslow, E.: Mirror symmetry is \(T\)-duality. Nuclear Phys. B 479(1–2), 243–259 (1996)
Viro, O.: Outline of results. http://www.math.stonybrook.edu/~oleg/math/research-st.html
Acknowledgements
This work was a part of my PhD thesis, which would not be possible without the support of my adviser Bernd Siebert. I am also indebted to Mark Gross for many useful conversations; a major part of this paper was written during a visit to the University of Cambridge hosted by him. I am grateful to Tom Coates and Dimitri Zvonkine for their useful suggestions which improved the exposition of the paper. Finally, many thanks to anonymous referees for their very useful feedback and corrections.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This project has received funding from the “Research Training Group 1670 Mathematics inspired by String Theory” at Universität Hamburg funded by the Deutsche Forschungsgemeinschaft (DFG), the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No. 682603), and from Fondation Mathématiques Jacques Hadamard.
Rights and permissions
About this article
Cite this article
Argüz, H. Real loci in (log) Calabi–Yau manifolds via Kato–Nakayama spaces of toric degenerations. European Journal of Mathematics 7, 869–930 (2021). https://doi.org/10.1007/s40879-021-00454-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-021-00454-z




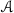 to a subset of
to a subset of 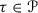 not contained in
not contained in  and with
and with 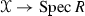 locally toroidal at some point of
locally toroidal at some point of