Abstract
We study a subset of square free positive braids and we give a few algebraic characterizations of them and one geometric characterization: the set of positive braids whose closures are unlinks. We describe canonical forms of these braids and of their conjugacy classes.
Similar content being viewed by others
References
Ali, U., Berceanu, B.: Canonical form of positive braids. J. Algebra Appl. 14(1), # 1450076 (2015)
Artin, E.: Theory of braids. Ann. Math. 48, 101–126 (1947)
Ashraf, R., Berceanu, B.: Recurrence relations for HOMFLY polynomial and rational specializations (2010). arXiv:1003.1034
Ashraf, R., Berceanu, B., Riasat, A.: Fibonacci numbers and positive braids. Ars Combin. 122, 299–306 (2015). arXiv:1005.1145
Ashraf, R., Berceanu, B., Riasat, A.: What could be a simple permutation? (2010). arXiv:1007.3869
Berceanu, B.: Artin algebras—applications in topology. PhD thesis, University of Bucharest (1995) (in Romanian)
Berceanu, B., Nizami, A.R.: Recurrence relation for Jones polynomials. J. Korean Math. Soc. 51(3), 443–462 (2014). arXiv:1002.3735
Birman, J.: Braids, Links, and Mapping Class Groups. Annals of Mathematics Studies, vol. 82. Princeton University Press, Princeton (1975)
Bokut, L.A., Fong, Y., Ke, W.-F., Shiao, L.S.: Gröbner–Shirshov bases for braid semigroup. In: Shum, K.P., et al. (eds.) Advances in Algebra, pp. 60–72. World Scientific, River Edge (2003)
El-Rifai, E.A., Morton, H.R.: Algorithms for positive braids. Q. J. Math. 45(180), 479–497 (1994)
Garside, F.A.: The braid groups and other groups. Q. J. Math. 20, 235–254 (1969)
Kassel, C., Turaev, V.: Braid Groups. Graduate Texts in Mathematics, vol. 247. Springer, New York (2008)
Lickorish, W.B.R.: An Introduction to Knot Theory. Graduate Texts in Mathematics, vol. 175. Springer, New York (1997)
Moran, S.: The Mathematical Theory of Knots and Braids. North-Holland Mathematics Studies, vol. 82. North-Holland, Amsterdam (1983)
Paris, L.: Braid groups and Artin groups. In: Papadopoulos, A. (ed.) Handbook on Teichmüller Theory, vol. II. EMS, Zürich (2008)
Author information
Authors and Affiliations
Corresponding author
Additional information
In memoriam Ştefan Papadima.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research was partially supported by Higher Education Commission of Pakistan.
Appendix
Appendix
In this section we consider only positive braids: we compute the left least common multiple \((\mathrm{lcm}_{\,\mathrm L})\) of a generator \(x_{i}\) and of the very simple braid, U(a, b) and D(c, d) respectively. The simplest case appears in Garside [11].
Lemma 7.1
(Garside) Suppose that  .
.
-
(a)
If \(|i-j|\geqslant 2\), then
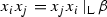 .
. -
(b)
If \(i+1=j\), then \(x_{i}x_{i+1}x_{i}=x_{i+1}x_{i}x_{i+1}\,|_{\mathrm{L}}\,\beta \).
Lemma 7.2
-
(a)
If \(x_{i}x_{i+1},x_{i+2}\in \mathrm{Div}_{\mathrm{L}}(\beta )\), then \(x_{i}x_{i+1}(x_{i+2}x_{i+1})=x_{i+2}(x_{i} x_{i+1}x_{i+2})\,|_{\mathrm{L}}\,\beta \).
-
(b)
if \(x_{i+1}x_{i+2},x_{i}\in \mathrm{Div}_{\mathrm{L}}(\beta )\), then \(x_{i}(x_{i+1} x_{i}x_{i+2}x_{i+1})=x_{i+1}x_{i+2}(x_{i}x_{i+1} x_{i+2})\,|_{\mathrm{L}}\,\beta \).
-
(c)
if \(x_{i+2}x_{i+1},x_{i}\in \mathrm{Div}_{\mathrm{L}}(\beta )\), then \(x_{i}(x_{i+2} x_{i+1}x_{i})=x_{i+2}x_{i+1}x_{i}(x_{i+1})\,|_{\mathrm{L}}\,\beta \).
-
(d)
if \(x_{i+1}x_{i},x_{i+2}\in \mathrm{Div}_{\mathrm{L}}\beta \), then \(x_{i+1}x_{i}(x_{i +2}x_{i+1}x_{i})=x_{i+2}(x_{i+1}x_{i}x_{i+2} x_{i+1})\,|_{\mathrm{L}}\,\beta \).
Proof
(a): Garside Lemma (a) implies that  , therefore \(x_{i+2}\,|_{\mathrm{L}}\,x_{i+1} \beta '\), and case (b) of Garside Lemma implies that
, therefore \(x_{i+2}\,|_{\mathrm{L}}\,x_{i+1} \beta '\), and case (b) of Garside Lemma implies that  .
.
(b): Garside Lemma (b) implies \(x_{i+1}x_{i+2}\beta ' =\beta =x_{i+1}x_{i}x_{i+1}\beta ^{'''}\), therefore \(x_{i}x_{i+1}\) and \(x_{i+2}\) are left divisors of \(x_{i+2}\beta '\); case (a) of this lemma gives the result.
(c) and (d) can be checked in a similar way. \(\square \)
Using Lemmas 7.1 and 7.2 one can start an induction to prove the next results (or one can find a proof in [1]).
Proposition 7.3
Suppose that \(x_{i},U(a,b)\in \mathrm{Div}_{\mathrm{L}}(\beta )\), \(a+1\leqslant b\). We have the following implications:
-
(a)
if \(i\notin \mathrm{e}\text {-}\mathrm{supp} U(a,b)\), then
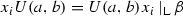 ;
; -
(b)
if \(i=a-1\), then
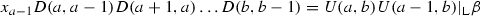 ;
; -
(c)
if \(i=a\), then \(\mathrm{lcm}_{\,\mathrm L}(x_{a},U(a,b))=U(a,b)\);
-
(d)
if \(i\in [a+1,b]\), then
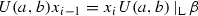 ;
; -
(e)
if \(i=b+1\), then
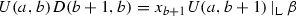 .
.
Proposition 7.4
Suppose that \(x_{i},D(c,d)\in \mathrm{Div}_{\mathrm{L}} (\beta )\ (c\geqslant d+1)\). We have the following implications:
-
(a)
if \(i\notin \mathrm{e}\text {-}\mathrm{supp}D(c,d)\) then
 ;
; -
(b)
if \(i=d-1\), then
 ;
; -
(c)
if \(i\in [d,c-1]\), then
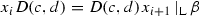 ;
; -
(d)
if \(i=c\), then \(\mathrm{lcm}_{\,\mathrm L}(x_{c},D(c,d))=D(c,d)\);
-
(e)
if \(i=c+1\), then
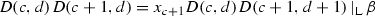 .
.
Proposition 7.5
Given  and a cycle \(\gamma \),
and a cycle \(\gamma \),  , we have the following implications:
, we have the following implications:
-
(a)
if \(x_{b-1}\,|_{\mathrm{L}}\,\gamma \beta \), then \(x_{b-1}\,|_{\mathrm{L}}\,\beta \);
-
(b)
if \(x_{e+1}\,|_{\mathrm{L}}\,\gamma \beta \), then \(x_{e+1}\,|_{\mathrm{L}}\,\beta \).
Proof
Induction on the length of \(\gamma \) and Garside Lemma 7.1 give the result. \(\square \)
Rights and permissions
About this article
Cite this article
Ashraf, R., Berceanu, B. Simple braids. European Journal of Mathematics 6, 646–660 (2020). https://doi.org/10.1007/s40879-020-00404-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-020-00404-1



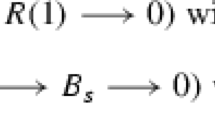
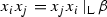 .
.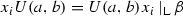 ;
;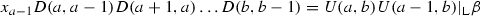 ;
;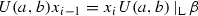 ;
;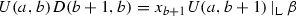 .
. ;
; ;
;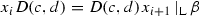 ;
;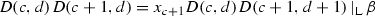 .
.