Abstract
Stanley introduced two classes of lattice polytopes associated to posets, which are called the order polytope \({{\mathscr {O}}}_P\) and the chain polytope \({{\mathscr {C}}}_P\) of a poset P. It is known that, given a poset P, the Ehrhart polynomials of \({{\mathscr {O}}}_P\) and \({{\mathscr {C}}}_P\) are equal to the order polynomial of P that counts the P-partitions. In this paper, we introduce the enriched order polytope of a poset P and show that it is a reflexive polytope whose Ehrhart polynomial is equal to that of the enriched chain polytope of P and the left enriched order polynomial of P that counts the left enriched P-partitions, by using the theory of Gröbner bases. The toric rings of enriched order polytopes are called enriched Hibi rings. It turns out that enriched Hibi rings are normal, Gorenstein, and Koszul. The above result implies the existence of a bijection between the lattice points in the dilations of  and
and  . Towards such a bijection, we give the facet representations of enriched order and chain polytopes.
. Towards such a bijection, we give the facet representations of enriched order and chain polytopes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A lattice polytope in \({\mathbb {R}}^n\) is a convex polytope all of whose vertices are in \({\mathbb {Z}}^n\). In [18], Stanley introduced a class of lattice polytopes associated to finite partially ordered sets (poset for short). Let \((P, <_P )\) be a finite poset on  . The order polytope
. The order polytope  of P is the convex polytope consisting of the set of points \((x_1,\ldots ,x_n) \in {\mathbb {R}}^n\) such that
of P is the convex polytope consisting of the set of points \((x_1,\ldots ,x_n) \in {\mathbb {R}}^n\) such that
-
\(0 \leqslant x_i \leqslant 1\) for \(1 \leqslant i \leqslant n\),
-
 if
if  .
.
Then  is a lattice polytope of dimension n. In fact, each vertex of
is a lattice polytope of dimension n. In fact, each vertex of  corresponds to a filter of P. Here, a subset F of P is called a filter of P if \(i \in F\) and \(j \in P\) together with
corresponds to a filter of P. Here, a subset F of P is called a filter of P if \(i \in F\) and \(j \in P\) together with  guarantee \(j \in F\). For a subset
guarantee \(j \in F\). For a subset  , we define the (0, 1)-vector
, we define the (0, 1)-vector  , where \({\mathbf {e}}_1,\ldots ,{\mathbf {e}}_n\) are the canonical unit coordinate vectors of \({\mathbb {R}}^n\). Then one has
, where \({\mathbf {e}}_1,\ldots ,{\mathbf {e}}_n\) are the canonical unit coordinate vectors of \({\mathbb {R}}^n\). Then one has  , where
, where  is the set of filters of P. Moreover, there is a close interplay between the combinatorial structure of P and the geometric structure of
is the set of filters of P. Moreover, there is a close interplay between the combinatorial structure of P and the geometric structure of  . Assume that P is naturally labeled, i.e., \(i < j\) if
. Assume that P is naturally labeled, i.e., \(i < j\) if  . Let \({\mathbb {Z}}_{\geqslant 0}\) be the set of nonnegative integers. A map \(f :P \rightarrow {\mathbb {Z}}_{\geqslant 0}\) is called a P-partition if for all \(x,y \in P\) with
. Let \({\mathbb {Z}}_{\geqslant 0}\) be the set of nonnegative integers. A map \(f :P \rightarrow {\mathbb {Z}}_{\geqslant 0}\) is called a P-partition if for all \(x,y \in P\) with  , f satisfies \(f(x) \leqslant f(y)\). We identify a P-partition f with a lattice point \((f(1),\ldots ,f(n)) \in {\mathbb {Z}}^n\). Since every P-partition \(f :P \rightarrow {\mathbb {Z}}_{\geqslant 0}\) with \(f(i) \leqslant 1\) is a filter of P, the set of P-partitions \(f :P \rightarrow {\mathbb {Z}}_{\geqslant 0}\) with \(f(i) \leqslant 1\) coincides with
, f satisfies \(f(x) \leqslant f(y)\). We identify a P-partition f with a lattice point \((f(1),\ldots ,f(n)) \in {\mathbb {Z}}^n\). Since every P-partition \(f :P \rightarrow {\mathbb {Z}}_{\geqslant 0}\) with \(f(i) \leqslant 1\) is a filter of P, the set of P-partitions \(f :P \rightarrow {\mathbb {Z}}_{\geqslant 0}\) with \(f(i) \leqslant 1\) coincides with  . Moreover, the set of P-partitions \(f :P \rightarrow {\mathbb {Z}}_{\geqslant 0}\) with \(f(i) \leqslant m\) coincides with
. Moreover, the set of P-partitions \(f :P \rightarrow {\mathbb {Z}}_{\geqslant 0}\) with \(f(i) \leqslant m\) coincides with  for \(0 < m \in {\mathbb {Z}}\). Here, for a convex polytope
for \(0 < m \in {\mathbb {Z}}\). Here, for a convex polytope  ,
,  is the m-th dilated polytope.
is the m-th dilated polytope.
In the present paper, we define a new class of lattice polytopes associated to finite posets from a viewpoint of the theory of enriched P-partitions. For a filter F of P, we set
 and
and
 , where
, where
 is the set of minimal elements of F. For a subset
is the set of minimal elements of F. For a subset
 and a vector
\(\varepsilon =(\varepsilon _1,\ldots ,\varepsilon _r) \in \{-1,1\}^{r}\), we define the
\((-1,0,1)\)-vector
and a vector
\(\varepsilon =(\varepsilon _1,\ldots ,\varepsilon _r) \in \{-1,1\}^{r}\), we define the
\((-1,0,1)\)-vector
 . The enriched order polytope
. The enriched order polytope
 of a finite (not necessarily naturally labeled) poset P on
of a finite (not necessarily naturally labeled) poset P on
 is the lattice polytope of dimension n which is the convex hull of
is the lattice polytope of dimension n which is the convex hull of

Then
 coincides with the set (1) above, Lemma 4.1. Now, we discuss a relation between
coincides with the set (1) above, Lemma 4.1. Now, we discuss a relation between
 and the theory of enriched P-partitions. Again, we assume that P is naturally labeled. A map
and the theory of enriched P-partitions. Again, we assume that P is naturally labeled. A map
 is called an enriched P-partition [19] if, for all
\(x, y \in P\) with
is called an enriched P-partition [19] if, for all
\(x, y \in P\) with
 , f satisfies
, f satisfies
-
\(|f(x)| \leqslant |f(y)|\);
-
\(|f(x)| = |f(y)| \, \Rightarrow f(y) > 0\).
On the other hand, Petersen [17] introduced a slightly different notion “left enriched P-partitions” as follows. A map \(f:P \rightarrow {\mathbb {Z}}\) is called a left enriched P-partition if, for all \(x, y \in P\) with  , f satisfies the following conditions:
, f satisfies the following conditions:
-
(i)
\(|f(x)| \leqslant |f(y)|\);
-
(ii)
\(|f(x)| = |f(y)| \, \Rightarrow f(y) \geqslant 0\).
Then the set of left enriched P-partitions \(f:P \rightarrow {\mathbb {Z}}\) with \(|f(i)| \leqslant 1\) coincides with  . Contrary to the case of order polytopes, the set of left enriched P-partitions \(f :P \rightarrow {\mathbb {Z}}\) with \(|f(i)| \leqslant m\) does not always coincide with the set of lattice points
. Contrary to the case of order polytopes, the set of left enriched P-partitions \(f :P \rightarrow {\mathbb {Z}}\) with \(|f(i)| \leqslant m\) does not always coincide with the set of lattice points  for \(m >1\), Example 4.2. However, we will show that the number \(\Omega _P^{(\ell )}(m)\) of left enriched P-partitions \(f:P \rightarrow {\mathbb {Z}}\) with \(|f(i)| \leqslant m\) is equal to
for \(m >1\), Example 4.2. However, we will show that the number \(\Omega _P^{(\ell )}(m)\) of left enriched P-partitions \(f:P \rightarrow {\mathbb {Z}}\) with \(|f(i)| \leqslant m\) is equal to  . Namely,
. Namely,
Theorem 1.1
For a naturally labeled finite poset P on  , let
, let

be the Ehrhart polynomial of  , and let \(\Omega _P^{(\ell )}(m)\) be the left enriched order polynomial of P. Then one has
, and let \(\Omega _P^{(\ell )}(m)\) be the left enriched order polynomial of P. Then one has

where \({\overline{P}}\) is the dual poset of P.
In this paper, in order to show Theorem 1.1, we investigate the toric ring of the enriched order polytope  . In [5], Hibi studied the toric ring of the order polytope
. In [5], Hibi studied the toric ring of the order polytope  . The toric ideal
. The toric ideal  possesses a squarefree quadratic Gröbner basis, that is a Gröbner basis consisting of binomials whose initial monomials are squarefree and of degree 2. This implies that the toric ring
possesses a squarefree quadratic Gröbner basis, that is a Gröbner basis consisting of binomials whose initial monomials are squarefree and of degree 2. This implies that the toric ring  is a normal Cohen–Macaulay domain and Koszul. In particular,
is a normal Cohen–Macaulay domain and Koszul. In particular,  possesses a flag regular unimodular triangulation. The toric ring
possesses a flag regular unimodular triangulation. The toric ring  is called the Hibi ring of P. See [4, Chapter 6]. We call the toric ring
is called the Hibi ring of P. See [4, Chapter 6]. We call the toric ring  the enriched Hibi ring of P.
the enriched Hibi ring of P.
Theorem 1.2
Let P be a finite poset on  . Then
. Then  is a reflexive polytope with a flag regular unimodular triangulation. Moreover, the toric ring
is a reflexive polytope with a flag regular unimodular triangulation. Moreover, the toric ring  is normal, Gorenstein, and Koszul.
is normal, Gorenstein, and Koszul.
First, in Sect. 2, we introduce known results on two poset polytopes introduced by Stanley [18], that is, the order polytope  and the chain polytope
and the chain polytope  of a poset P. A squarefree quadratic Gröbner basis of the toric ideal of each of
of a poset P. A squarefree quadratic Gröbner basis of the toric ideal of each of  and its applications will be extended to “enriched case” in the following sections. In Sect. 3, we study the notion of enriched chain polytopes
and its applications will be extended to “enriched case” in the following sections. In Sect. 3, we study the notion of enriched chain polytopes  [16] because we need to compare the toric ideals of enriched order polytopes and that of enriched chain polytopes in order to prove Theorem 1.1. In Sect. 4, we discuss fundamental properties of enriched order polytopes. In Sect. 5, we study the toric ideals of enriched order polytopes and their applications. By proving that the toric ideal of
[16] because we need to compare the toric ideals of enriched order polytopes and that of enriched chain polytopes in order to prove Theorem 1.1. In Sect. 4, we discuss fundamental properties of enriched order polytopes. In Sect. 5, we study the toric ideals of enriched order polytopes and their applications. By proving that the toric ideal of  possesses a squarefree quadratic Gröbner basis consisting of binomials whose initial monomials do not contain the variable corresponding to the origin, we show Theorem 1.2 (Corollary 5.3). Moreover, by comparing the initial ideals of toric ideals of two enriched poset polytopes, Theorem 5.4, we will complete the proof of Theorem 1.1. Note that Theorem 1.1 implies the existence of a bijection between
possesses a squarefree quadratic Gröbner basis consisting of binomials whose initial monomials do not contain the variable corresponding to the origin, we show Theorem 1.2 (Corollary 5.3). Moreover, by comparing the initial ideals of toric ideals of two enriched poset polytopes, Theorem 5.4, we will complete the proof of Theorem 1.1. Note that Theorem 1.1 implies the existence of a bijection between  and
and  . In Sect. 6, towards such a bijection, we consider an elementary geometric property, the facet representations of enriched order and chain polytopes, Proposition 6.1 and Theorem 6.2. The number of facets is discussed in Corollary 6.3 and Proposition 6.5. Finally, we show that
. In Sect. 6, towards such a bijection, we consider an elementary geometric property, the facet representations of enriched order and chain polytopes, Proposition 6.1 and Theorem 6.2. The number of facets is discussed in Corollary 6.3 and Proposition 6.5. Finally, we show that  is rarely unimodularly equivalent to
is rarely unimodularly equivalent to  , Proposition 6.6.
, Proposition 6.6.
2 Two poset polytopes
In this section, we review properties of order polytopes and chain polytopes. Let \({(P,<_P )}\) be a finite poset on  . Recall that the order polytope
. Recall that the order polytope  is the convex hull of
is the convex hull of

In [18], Stanley introduced another lattice polytope associated to P as well as the order polytope  . An antichain of P is a subset of P consisting of pairwise incomparable elements of P. Let
. An antichain of P is a subset of P consisting of pairwise incomparable elements of P. Let  denote the set of antichains of P. Note that the empty set \(\varnothing \) is an antichain of P. The chain polytope
denote the set of antichains of P. Note that the empty set \(\varnothing \) is an antichain of P. The chain polytope  of P is the convex hull of
of P is the convex hull of

Then  is a lattice polytope of dimension n. The order polytope
is a lattice polytope of dimension n. The order polytope  and the chain polytope
and the chain polytope  have similar properties.
have similar properties.
First, we study the Ehrhart polynomials of  and
and  . Let
. Let  be a general lattice polytope of dimension n. Given a positive integer m, we define
be a general lattice polytope of dimension n. Given a positive integer m, we define

The study on  originated in Ehrhart [3] who proved that
originated in Ehrhart [3] who proved that  is a polynomial in m of degree n with the constant term 1. Moreover, the leading coefficient of
is a polynomial in m of degree n with the constant term 1. Moreover, the leading coefficient of  coincides with the usual Euclidean volume of
coincides with the usual Euclidean volume of  . We say that
. We say that  is the Ehrhart polynomial of
is the Ehrhart polynomial of  . An Ehrhart polynomial often coincides with a counting function of a combinatorial object. A map \(f :P \rightarrow {\mathbb {Z}}_{\geqslant 0}\) is called an order preserving map if for all \(x,y \in P\) with
. An Ehrhart polynomial often coincides with a counting function of a combinatorial object. A map \(f :P \rightarrow {\mathbb {Z}}_{\geqslant 0}\) is called an order preserving map if for all \(x,y \in P\) with  , f satisfies \(f(x) \leqslant f(y)\). Let \(\Omega _P(m)\) denote the number of order preserving maps \(f :P \rightarrow {\mathbb {Z}}_{\geqslant 0}\) with \(f(i) \leqslant m\). Then \(\Omega _P(m)\) is a polynomial in m of degree n and called the order polynomial of P. Stanley showed a relation between the Ehrhart polynomials of
, f satisfies \(f(x) \leqslant f(y)\). Let \(\Omega _P(m)\) denote the number of order preserving maps \(f :P \rightarrow {\mathbb {Z}}_{\geqslant 0}\) with \(f(i) \leqslant m\). Then \(\Omega _P(m)\) is a polynomial in m of degree n and called the order polynomial of P. Stanley showed a relation between the Ehrhart polynomials of  and
and  and the order polynomial \(\Omega _P(m)\). In fact,
and the order polynomial \(\Omega _P(m)\). In fact,
Proposition 2.1
([18, Theorem 4.1]) Let P be a finite poset on  . Then one has
. Then one has

On the other hand,  and
and  are not always unimodularly equivalent. Here, two lattice polytopes
are not always unimodularly equivalent. Here, two lattice polytopes  of dimension n are unimodularly equivalent if there exist a unimodular matrix \(U \in {\mathbb {Z}}^{n \times n}\) and a lattice point \({\mathbf {w}}\in {\mathbb {Z}}^n\) such that
of dimension n are unimodularly equivalent if there exist a unimodular matrix \(U \in {\mathbb {Z}}^{n \times n}\) and a lattice point \({\mathbf {w}}\in {\mathbb {Z}}^n\) such that  , where \(f_U\) is the linear transformation in \({\mathbb {R}}^n\) defined by U, i.e., \(f_U({\mathbf {x}})={\mathbf {x}}U\) for all \({\mathbf {x}}\in {\mathbb {R}}^n\). In [7], Hibi and Li characterized when
, where \(f_U\) is the linear transformation in \({\mathbb {R}}^n\) defined by U, i.e., \(f_U({\mathbf {x}})={\mathbf {x}}U\) for all \({\mathbf {x}}\in {\mathbb {R}}^n\). In [7], Hibi and Li characterized when  and
and  are unimodularly equivalent. In fact,
are unimodularly equivalent. In fact,
Proposition 2.2
([7, Corollary 2.3]) Let P be a finite poset on  . Then the following conditions are equivalent:
. Then the following conditions are equivalent:
-
(i)
The order polytope
 and the chain polytope
and the chain polytope  are unimodularly equivalent.
are unimodularly equivalent. -
(ii)
The number of the facets of
 is equal to that of
is equal to that of  .
. -
(iii)
The following poset is not a subposet of P.
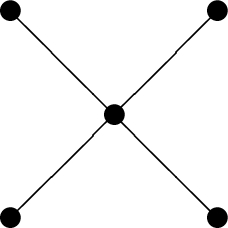
Next, we review the toric ideals of order polytopes and chain polytopes. First, we recall basic materials and notation on toric ideals. Let  be the Laurent polynomial ring in \(n+1\) variables over a field K. If \({\mathbf {a}}= (a_{1}, \ldots , a_{n}) \in {\mathbb {Z}}^{n}\), then \(\mathbf{t}^{{\mathbf {a}}}s\) is the Laurent monomial
be the Laurent polynomial ring in \(n+1\) variables over a field K. If \({\mathbf {a}}= (a_{1}, \ldots , a_{n}) \in {\mathbb {Z}}^{n}\), then \(\mathbf{t}^{{\mathbf {a}}}s\) is the Laurent monomial  . Let
. Let  be a lattice polytope and
be a lattice polytope and  . Then, the toric ring of
. Then, the toric ring of  is the subalgebra
is the subalgebra  of
of  generated by
generated by  over K. We regard
over K. We regard  as a homogeneous algebra by setting each \(\deg {\mathbf {t}}^{{\mathbf {a}}_i}s=1\). Let
as a homogeneous algebra by setting each \(\deg {\mathbf {t}}^{{\mathbf {a}}_i}s=1\). Let  denote the polynomial ring in d variables over K with each
denote the polynomial ring in d variables over K with each  . The toric ideal
. The toric ideal  of
of  is the kernel of the surjective homomorphism
is the kernel of the surjective homomorphism  defined by \(\pi (x_i)={\mathbf {t}}^{{\mathbf {a}}_i}s\) for \(1 \leqslant i \leqslant d\). It is known that
defined by \(\pi (x_i)={\mathbf {t}}^{{\mathbf {a}}_i}s\) for \(1 \leqslant i \leqslant d\). It is known that  is generated by homogeneous binomials. See, e.g., [4, 20].
is generated by homogeneous binomials. See, e.g., [4, 20].
Now, we study the toric ideals of  and
and  . Remark that
. Remark that  and
and  are unimodularly equivalent and
are unimodularly equivalent and  . A subset I of P is called a poset ideal of P if \(i \in I\) and \(j \in P\) together with
. A subset I of P is called a poset ideal of P if \(i \in I\) and \(j \in P\) together with  guarantee \(j \in I\). Let
guarantee \(j \in I\). Let  denote the set of poset ideals of P, ordered by inclusion. If
denote the set of poset ideals of P, ordered by inclusion. If  and
and  are incomparable in
are incomparable in  , then we write \(I \not \sim J\). Then the order polytope
, then we write \(I \not \sim J\). Then the order polytope  is the convex hull of
is the convex hull of

Let  denote the polynomial ring over K in variables \(x_I\), where
denote the polynomial ring over K in variables \(x_I\), where  . In particular, the origin corresponds to the variable \(x_{\varnothing }\). Then the toric ideal
. In particular, the origin corresponds to the variable \(x_{\varnothing }\). Then the toric ideal  is the kernel of the ring homomorphism
is the kernel of the ring homomorphism  defined by
defined by  . Let
. Let  be a reverse lexicographic order on
be a reverse lexicographic order on  such that \(x_I <_{P} x_J\) if \(I \subsetneq J\). In [5], Hibi essentially proved that
such that \(x_I <_{P} x_J\) if \(I \subsetneq J\). In [5], Hibi essentially proved that  possesses a squarefree quadratic Gröbner basis. In fact,
possesses a squarefree quadratic Gröbner basis. In fact,
Proposition 2.3
([5]) Work with the same notation as above. Then

is a Gröbner basis of  with respect to a reverse lexicographic order
with respect to a reverse lexicographic order  . Moreover,
. Moreover,  is a normal Cohen–Macaulay domain and Koszul.
is a normal Cohen–Macaulay domain and Koszul.
Recently, the toric ring  is called the Hibi ring of P and studied by many authors from several viewpoints. One can find some of them in [4, Note of Chapter 6].
is called the Hibi ring of P and studied by many authors from several viewpoints. One can find some of them in [4, Note of Chapter 6].
For a poset ideal I of P, we denote by  the set of maximal elements of I. Then
the set of maximal elements of I. Then  is an antichain of P and every antichain of P is the set of maximal elements of a poset ideal. On the other hand, for an antichain A of P, the poset ideal of P generated by A is the smallest poset ideal of P which contains A. Every poset ideal of P can be obtained by this way. Hence
is an antichain of P and every antichain of P is the set of maximal elements of a poset ideal. On the other hand, for an antichain A of P, the poset ideal of P generated by A is the smallest poset ideal of P which contains A. Every poset ideal of P can be obtained by this way. Hence  and
and  have a one-to-one correspondence. Let
have a one-to-one correspondence. Let  denote the polynomial ring over K in variables \(x_{\max (I)}\), where
denote the polynomial ring over K in variables \(x_{\max (I)}\), where  . Then the toric ideal
. Then the toric ideal  is the kernel of the ring homomorphism
is the kernel of the ring homomorphism  defined by \(\pi _{{\mathscr {C}}}(x_{\max (I)})=s \prod _{i \in \max (I)} t_i\). Let
defined by \(\pi _{{\mathscr {C}}}(x_{\max (I)})=s \prod _{i \in \max (I)} t_i\). Let  be a reverse lexicographic order on
be a reverse lexicographic order on  such that
such that  if \(I \subsetneq J\). Given poset ideals
if \(I \subsetneq J\). Given poset ideals  , let
, let  denote the poset ideal of P generated by
denote the poset ideal of P generated by  . Note that
. Note that  . The following lemma is fundamental and important.
. The following lemma is fundamental and important.
Lemma 2.4
Let P be a finite poset and  . For
. For  , the following conditions are equivalent:
, the following conditions are equivalent:
-
(i)
\(p \in J\);
-
(ii)
 ;
; -
(iii)
 ;
; -
(iv)
 .
.
Proof
First, (ii) \(\Rightarrow \) (i) is trivial. Suppose \(p \in J\). Since p does not belong to  , p is not a maximal element in J. Hence we have
, p is not a maximal element in J. Hence we have  . Thus (i) \(\Rightarrow \) (iv) holds. Suppose
. Thus (i) \(\Rightarrow \) (iv) holds. Suppose  . Then there exists an element \(q \in I \cup J\) such that
. Then there exists an element \(q \in I \cup J\) such that  . If q belongs to I, then \(p \notin \), a contradiction. Thus \(q \in J\), and hence \(p \in I \cap J\). If
. If q belongs to I, then \(p \notin \), a contradiction. Thus \(q \in J\), and hence \(p \in I \cap J\). If  holds, then there exists an element
holds, then there exists an element  such that
such that  . This contradicts to the hypothesis
. This contradicts to the hypothesis  . Thus (iv) \(\Rightarrow \) (ii) holds. Finally, we have (ii) \(\Leftrightarrow \) (iii) by
. Thus (iv) \(\Rightarrow \) (ii) holds. Finally, we have (ii) \(\Leftrightarrow \) (iii) by  .\(\square \)
.\(\square \)
In [6], Hibi and Li essentially proved that  possesses a squarefree quadratic Gröbner basis. In fact,
possesses a squarefree quadratic Gröbner basis. In fact,
Proposition 2.5
([6]) Work with the same notation as above. Then

is a Gröbner basis of  with respect to a reverse lexicographic order
with respect to a reverse lexicographic order  . Moreover,
. Moreover,  is a normal Cohen–Macaulay domain and Koszul.
is a normal Cohen–Macaulay domain and Koszul.
From Propositions 2.3 and 2.5 we can prove the following.
Proposition 2.6
Work with the same notation as above. Then one has

Furthermore, we obtain  .
.
Proof
From Propositions 2.3 and 2.5, we have

Hence it follows that the map \(x_{I} \mapsto x_{\max (I)}\) induces an isomorphism from  to
to  . Therefore, the first claim follows.
. Therefore, the first claim follows.
Since both  and
and  are squarefree, both
are squarefree, both  and
and  possess a unimodular triangulation, and hence the Ehrhart polynomial coincides with the Hilbert polynomial of its toric ring for each of
possess a unimodular triangulation, and hence the Ehrhart polynomial coincides with the Hilbert polynomial of its toric ring for each of  and
and  , see [4, Section 4.2] or [20, Chapters 8 and 13]. Moreover, for an ideal I of \(K[{\mathbf {x}}]\) and a monomial order < on \(K[{\mathbf {x}}]\), the Hilbert polynomial of \(K[{\mathbf {x}}]/I\) is equal to that of \(K[{\mathbf {x}}]/\mathrm{in}_{<}(I)\). Therefore, the second claim follows.\(\square \)
, see [4, Section 4.2] or [20, Chapters 8 and 13]. Moreover, for an ideal I of \(K[{\mathbf {x}}]\) and a monomial order < on \(K[{\mathbf {x}}]\), the Hilbert polynomial of \(K[{\mathbf {x}}]/I\) is equal to that of \(K[{\mathbf {x}}]/\mathrm{in}_{<}(I)\). Therefore, the second claim follows.\(\square \)
3 Enriched chain polytopes
In this section, we recall the definition and properties of enriched chain polytopes given in [16]. Let \((P, <_P )\) be a finite poset on  . The enriched chain polytope
. The enriched chain polytope  of P is the convex hull of
of P is the convex hull of

Then  is a lattice polytope of dimension n. It is easy to see that
is a lattice polytope of dimension n. It is easy to see that  is centrally symmetric (i.e., for any facet
is centrally symmetric (i.e., for any facet  of
of  ,
,  is also a facet of
is also a facet of  ), and the origin of \({\mathbb {R}}^n\) is the unique interior lattice point of
), and the origin of \({\mathbb {R}}^n\) is the unique interior lattice point of  . Remark that
. Remark that  .
.
A lattice polytope  of dimension n is called reflexive if the origin of \({\mathbb {R}}^n\) is a unique lattice point belonging to the interior of
of dimension n is called reflexive if the origin of \({\mathbb {R}}^n\) is a unique lattice point belonging to the interior of  and its dual polytope
and its dual polytope

is also a lattice polytope, where \(\langle {\mathbf {x}},{\mathbf {y}}\rangle \) is the usual inner product of \({\mathbb {R}}^n\). It is known that reflexive polytopes correspond to Gorenstein toric Fano varieties, and they are related to mirror symmetry, see, e.g., [1, 2]. In each dimension there exist only finitely many reflexive polytopes up to unimodular equivalence [13] and all of them are known up to dimension 4 [12]. Recently, several classes of reflexive polytopes were constructed by an algebraic technique on Gröbner bases, cf., [10, 11, 15]. The algebraic technique is based on the following lemma that follows from the argument in [9, Proof of Lemma 1.1].
Lemma 3.1
Let  be a lattice polytope of dimension n such that the origin of \({\mathbb {R}}^n\) is contained in its interior. Suppose that any lattice point in \({\mathbb {Z}}^n\) is a linear integer combination of the lattice points in
be a lattice polytope of dimension n such that the origin of \({\mathbb {R}}^n\) is contained in its interior. Suppose that any lattice point in \({\mathbb {Z}}^n\) is a linear integer combination of the lattice points in  . If there exists a monomial order such that the initial ideal of
. If there exists a monomial order such that the initial ideal of  is generated by squarefree monomials which do not contain the variable corresponding to the origin, then
is generated by squarefree monomials which do not contain the variable corresponding to the origin, then  is reflexive and has a regular unimodular triangulation. Moreover,
is reflexive and has a regular unimodular triangulation. Moreover,  is a normal Gorenstein domain.
is a normal Gorenstein domain.
In order to use Lemma 3.1 for enriched chain polytopes  , we study the toric ideal of
, we study the toric ideal of  . Let
. Let  denote the polynomial ring over K in variables \(x_{A}^{\varepsilon }\), where
denote the polynomial ring over K in variables \(x_{A}^{\varepsilon }\), where  and \(\varepsilon =(\varepsilon _1,\ldots ,\varepsilon _n) \in \{-1,0,1\}^{n}\) with
and \(\varepsilon =(\varepsilon _1,\ldots ,\varepsilon _n) \in \{-1,0,1\}^{n}\) with
Then the toric ideal  is the kernel of a ring homomorphism
is the kernel of a ring homomorphism  defined by
defined by  . In addition,
. In addition,

is the toric ideal  . For \(\varepsilon =(\varepsilon _1,\ldots ,\varepsilon _n) \in \{-1,0,1\}^n\), we write
. For \(\varepsilon =(\varepsilon _1,\ldots ,\varepsilon _n) \in \{-1,0,1\}^n\), we write  . We identify the variable \(x^{\varepsilon ^{+}}_A\) on
. We identify the variable \(x^{\varepsilon ^{+}}_A\) on  with the variable \(x_A\) on
with the variable \(x_A\) on  . It is known [20, Proposition 1.11] that there exists a nonnegative weight vector
. It is known [20, Proposition 1.11] that there exists a nonnegative weight vector  such that
such that  . Then we define the weight vector
. Then we define the weight vector  on
on  such that the weight of each variable \(x_A^\varepsilon \) with respect to
such that the weight of each variable \(x_A^\varepsilon \) with respect to  is the weight of the variable \(x_A^{\varepsilon ^+}\) with respect to
is the weight of the variable \(x_A^{\varepsilon ^+}\) with respect to  . In addition, let \({\mathbf {w}}_{\#}\) be the weight vector on
. In addition, let \({\mathbf {w}}_{\#}\) be the weight vector on  such that the weight of each variable \(x_A^\varepsilon \) with respect to \({\mathbf {w}}_{\#}\) is |A|. Fix any monomial order \(\prec \) on
such that the weight of each variable \(x_A^\varepsilon \) with respect to \({\mathbf {w}}_{\#}\) is |A|. Fix any monomial order \(\prec \) on  as a tie-breaker. Let
as a tie-breaker. Let  be a monomial order on
be a monomial order on  such that
such that  if and only if one of the following holds:
if and only if one of the following holds:
-
The weight of u is less than that of v with respect to \({\mathbf {w}}_\#\).
-
The weight of u is the same as that of v with respect to \({\mathbf {w}}_\#\), and the weight of u is less than that of v with respect to
 .
. -
The weight of u is the same as that of v with respect to \({\mathbf {w}}_\#\) and
 , and \(u \prec v\).
, and \(u \prec v\).
The following proposition was given in [16, Theorem 1.3]:
Proposition 3.2
([16]) Work with the same notation as above. Let  be the set of all binomials
be the set of all binomials

where  , \(\varepsilon _p\ne \mu _p\), and
, \(\varepsilon _p\ne \mu _p\), and  , together with all binomials
, together with all binomials

where  with \(I \not \sim J\), and
with \(I \not \sim J\), and
-
(a)
for any
 , we have \(\varepsilon _p =\varepsilon '_p =\mu _p=\mu '_p \);
, we have \(\varepsilon _p =\varepsilon '_p =\mu _p=\mu '_p \); -
(b)
for any
 , we have
, we have 
-
(c)
for any
 , we have
, we have 
Then  is a Gröbner basis of
is a Gröbner basis of  with respect to a monomial order
with respect to a monomial order  . The initial monomial of each binomial is the first monomial. In particular, the initial ideal is generated by squarefree quadratic monomials which do not contain the variable \(x_\varnothing ^\mathbf{0}\).
. The initial monomial of each binomial is the first monomial. In particular, the initial ideal is generated by squarefree quadratic monomials which do not contain the variable \(x_\varnothing ^\mathbf{0}\).
By Lemma 3.1 and Proposition 3.2, we have the following immediately.
Corollary 3.3
([16]) Let P be a finite poset on  . Then
. Then  is a reflexive polytope with a flag regular unimodular triangulation. Moreover,
is a reflexive polytope with a flag regular unimodular triangulation. Moreover,  is a normal Gorenstein domain and Koszul.
is a normal Gorenstein domain and Koszul.
Next, we study Ehrhart polynomials of enriched chain polytopes. Assume that P is naturally labeled. Let \(\Omega ^{(\ell )}_P(m)\) denote the number of left enriched P-partitions \(f :P \rightarrow {\mathbb {Z}}\) with \(|f(i)| \leqslant m\). Then \(\Omega ^{(\ell )}_P(m)\) is a polynomial in m of degree n and called the left enriched order polynomial of P.
Proposition 3.4
([16, Theorem 0.2]) Let P be a naturally labeled finite poset on  . Then one has
. Then one has

4 Fundamental properties of enriched order polytopes
In this section, we discuss some fundamental properties of enriched order polytopes. First, we consider the set of lattice points in enriched order polytopes.
Lemma 4.1
Let P be a finite poset on  . Then one has
. Then one has

In addition, the origin is the unique interior lattice point in  .
.
Proof
Let  . It is enough to show that
. It is enough to show that  . Let
. Let  . Since
. Since  is the convex hull of X, there exist \({\mathbf {a}}_1,\dots , {\mathbf {a}}_s \in X\) such that \({\mathbf {x}}= \sum _{i=1}^s \lambda _i {\mathbf {a}}_i \), where \(\lambda _i > 0 \), \( \sum _{i=1}^s \lambda _i =1\). Then each \({\mathbf {a}}_i\) is a \((-1,0,1)\)-vector, and hence so is \({\mathbf {x}}\). It is easy to see that \(x_k = 1\) (resp. \(x_k = - 1\)) if and only if k-th component of \({\mathbf {a}}_i\) is equal to 1 (resp. \(-1\)) for all \(i = 1,2,\ldots ,s\). Suppose that
is the convex hull of X, there exist \({\mathbf {a}}_1,\dots , {\mathbf {a}}_s \in X\) such that \({\mathbf {x}}= \sum _{i=1}^s \lambda _i {\mathbf {a}}_i \), where \(\lambda _i > 0 \), \( \sum _{i=1}^s \lambda _i =1\). Then each \({\mathbf {a}}_i\) is a \((-1,0,1)\)-vector, and hence so is \({\mathbf {x}}\). It is easy to see that \(x_k = 1\) (resp. \(x_k = - 1\)) if and only if k-th component of \({\mathbf {a}}_i\) is equal to 1 (resp. \(-1\)) for all \(i = 1,2,\ldots ,s\). Suppose that  . If \(x_k = 0\), then \(|x_k| \leqslant |x_\ell |\) and the equality holds if and only if \(x_\ell =0\). Suppose that \(|x_k| =1\). Then k-th component of \({\mathbf {a}}_i\) is equal to \(x_k \) for all \(i = 1,2,\ldots ,s\). Since each \({\mathbf {a}}_i\) is a left enriched P-partition, \(\ell \)-th component of \({\mathbf {a}}_i\) is equal to 1 for all \(i = 1,2,\ldots ,s\). Hence \(x_\ell = 1\). In particular, \(|x_k| = |x_\ell |\) and \(x_\ell \geqslant 0\). Thus \({\mathbf {x}}\) is a left enriched P-partition, that is, \({\mathbf {x}}\) belongs to X.
. If \(x_k = 0\), then \(|x_k| \leqslant |x_\ell |\) and the equality holds if and only if \(x_\ell =0\). Suppose that \(|x_k| =1\). Then k-th component of \({\mathbf {a}}_i\) is equal to \(x_k \) for all \(i = 1,2,\ldots ,s\). Since each \({\mathbf {a}}_i\) is a left enriched P-partition, \(\ell \)-th component of \({\mathbf {a}}_i\) is equal to 1 for all \(i = 1,2,\ldots ,s\). Hence \(x_\ell = 1\). In particular, \(|x_k| = |x_\ell |\) and \(x_\ell \geqslant 0\). Thus \({\mathbf {x}}\) is a left enriched P-partition, that is, \({\mathbf {x}}\) belongs to X.
Since  is an n-dimensional subpolytope of a cube \([-1,1]^n\), it follows that each nonzero vector \({\mathbf {x}}\in X\) belongs to the boundary of
is an n-dimensional subpolytope of a cube \([-1,1]^n\), it follows that each nonzero vector \({\mathbf {x}}\in X\) belongs to the boundary of  . Suppose that the origin \(\mathbf{0} \in {\mathbb {R}}^n\) belongs to the boundary of
. Suppose that the origin \(\mathbf{0} \in {\mathbb {R}}^n\) belongs to the boundary of  . Then there exists a facet
. Then there exists a facet  of
of  which contains \(\mathbf{0}\). Let
which contains \(\mathbf{0}\). Let  with \(\mathbf{0} \ne {\mathbf {a}}= (a_1,\dots , a_n) \in {\mathbb {R}}^n\) be the supporting hyperplane of
with \(\mathbf{0} \ne {\mathbf {a}}= (a_1,\dots , a_n) \in {\mathbb {R}}^n\) be the supporting hyperplane of  and let
and let  \((\ne \varnothing )\) be a subposet of P. We may assume that
\((\ne \varnothing )\) be a subposet of P. We may assume that  satisfies \(a_i >0\). Let
satisfies \(a_i >0\). Let  be a filter of P. Then
be a filter of P. Then  and hence
and hence  satisfies \( \langle {\mathbf {a}},{\mathbf {y}}\rangle = a_i > 0\) and
satisfies \( \langle {\mathbf {a}},{\mathbf {y}}\rangle = a_i > 0\) and  satisfies \( \langle {\mathbf {a}},{\mathbf {y}}' \rangle = - a_i < 0\). This contradicts that \({{\mathscr {H}}}\) is a supporting hyperplane of
satisfies \( \langle {\mathbf {a}},{\mathbf {y}}' \rangle = - a_i < 0\). This contradicts that \({{\mathscr {H}}}\) is a supporting hyperplane of  .\(\square \)
.\(\square \)
Next, we consider lattice points in the dilated polytopes of an enriched order polytope. The following example shows that, contrary to the case of order polytopes, the set of left enriched P-partitions \(f :P \rightarrow {\mathbb {Z}}\) with \(|f(i)| \leqslant m\) does not always coincide with the set of lattice points  if \(m >1\).
if \(m >1\).
Example 4.2
Let P be a poset on \(\{1,2\}\) with  . Then the set of left enriched P-partitions \(f :P \rightarrow {\mathbb {Z}}\) with \(|f(i)| \leqslant 2\) is
. Then the set of left enriched P-partitions \(f :P \rightarrow {\mathbb {Z}}\) with \(|f(i)| \leqslant 2\) is
and

Thus two sets are different. On the other hand, the cardinality of each set is the same. Moreover, it follows that  .
.
5 The toric ideals of enriched order polytopes
In this section, we discuss the toric ideals of enriched order polytopes. Let P be a finite poset on  . For a poset ideal I of P, we set
. For a poset ideal I of P, we set  and
and  . Then lattice points in
. Then lattice points in  can be written by poset ideals of P:
can be written by poset ideals of P:

Contrary to the case of order polytopes, the enriched order polytopes  and
and  are not always unimodularly equivalent.
are not always unimodularly equivalent.
Example 5.1
Let P be the following poset on \(\{1,2,3\}\):

Then  has five facets and
has five facets and  has six facets. Thus
has six facets. Thus  and
and  are not unimodularly equivalent. On the other hand, it follows that
are not unimodularly equivalent. On the other hand, it follows that

Now, we consider the toric ideals  . Let
. Let  be the polynomial ring over K in variables \(x_I^{\varepsilon }\), where
be the polynomial ring over K in variables \(x_I^{\varepsilon }\), where  and \(\varepsilon =(\varepsilon _1,\ldots ,\varepsilon _n) \in \{-1,0,1\}^{n}\) with
and \(\varepsilon =(\varepsilon _1,\ldots ,\varepsilon _n) \in \{-1,0,1\}^{n}\) with

Then the toric ideal  is the kernel of a ring homomorphism
is the kernel of a ring homomorphism  defined by
defined by  . In addition,
. In addition,

is the toric ideal  . We define a reverse lexicographic order
. We define a reverse lexicographic order  on
on  such that
such that  if \(I \subsetneq J\).
if \(I \subsetneq J\).
Theorem 5.2
Work with the same notation as above. Let  be the set of all binomials
be the set of all binomials

where  , \(\varepsilon _p \ne \mu _p\), and
, \(\varepsilon _p \ne \mu _p\), and  , together with all binomials
, together with all binomials

where  with \(I \not \sim J\), and
with \(I \not \sim J\), and
-
(a)
for any
 , we have \(\varepsilon _p =\varepsilon '_p =\mu _p=\mu '_p\);
, we have \(\varepsilon _p =\varepsilon '_p =\mu _p=\mu '_p\); -
(b)
for any
 , we have
, we have 
-
(c)
for any
 , we have
, we have 
Then  is a Gröbner basis of
is a Gröbner basis of  with respect to a monomial order
with respect to a monomial order  . The initial monomial of each binomial is the first monomial. In particular, the initial ideal is generated by squarefree quadratic monomials which do not contain the variable \(x_\varnothing ^\mathbf{0}\).
. The initial monomial of each binomial is the first monomial. In particular, the initial ideal is generated by squarefree quadratic monomials which do not contain the variable \(x_\varnothing ^\mathbf{0}\).
Proof
It is easy to see that any binomial of type (2) belongs to  . By Lemma 2.4, it follows that any binomial of type (3) belongs to
. By Lemma 2.4, it follows that any binomial of type (3) belongs to  . Hence
. Hence  is a subset of
is a subset of  . Moreover, the initial monomial of each binomial is the first monomial. Assume that
. Moreover, the initial monomial of each binomial is the first monomial. Assume that  is not a Gröbner basis of
is not a Gröbner basis of  with respect to
with respect to  . Let
. Let

By [4, Theorem 3.11], there exists a nonzero irreducible homogeneous binomial  such that neither u nor v belongs to
such that neither u nor v belongs to  . For
. For  and \(\varepsilon , \mu \in \{-1,0,1\}^n\), if
and \(\varepsilon , \mu \in \{-1,0,1\}^n\), if  satisfies \(\varepsilon _i \ne \mu _i\), then
satisfies \(\varepsilon _i \ne \mu _i\), then  . On the other hand, for
. On the other hand, for  with \(I \not \sim J\) and for \(\varepsilon , \mu \in \{-1,0,1\}^n\), if \(\varepsilon _p=\mu _p\) for any
with \(I \not \sim J\) and for \(\varepsilon , \mu \in \{-1,0,1\}^n\), if \(\varepsilon _p=\mu _p\) for any  , then
, then  . Hence u and v are of the form
. Hence u and v are of the form

where  and
and  for \(k =1,2,\dots , r\) such that
for \(k =1,2,\dots , r\) such that
-
(a)
\(I_1 \subset \dots \subset I_r\) and \(J_1 \subset \dots \subset J_r\).
-
(b)
For any p and q, and for any
 , we obtain
, we obtain  .
. -
(c)
For any p and q, and for any
 , we obtain
, we obtain 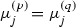 .
.
Since u and v satisfy conditions (b) and (c) and since f belongs to  , it then follows that
, it then follows that  and \(\varepsilon _r=\mu _r\). Hence one has
and \(\varepsilon _r=\mu _r\). Hence one has  . This contradicts the assumption that f is irreducible.\(\square \)
. This contradicts the assumption that f is irreducible.\(\square \)
By Lemma 3.1 and Theorem 5.2, we have the following immediately.
Corollary 5.3
Let P be a finite poset on  . Then
. Then  is a reflexive polytope with a flag regular unimodular triangulation. Moreover,
is a reflexive polytope with a flag regular unimodular triangulation. Moreover,  is a normal Gorenstein domain and Koszul.
is a normal Gorenstein domain and Koszul.
Theorem 5.4
Work with the same notation as above. Then one has

Furthermore, we obtain

Proof
From Theorem 5.2,  is generated by all monomials
is generated by all monomials

where  , \(\varepsilon _p\ne \mu _p\), and
, \(\varepsilon _p\ne \mu _p\), and  together with all monomials
together with all monomials

where  with \(I \not \sim J\) and \(\varepsilon _p =\varepsilon '_p\) for each
with \(I \not \sim J\) and \(\varepsilon _p =\varepsilon '_p\) for each  . Moreover, from Proposition 3.2,
. Moreover, from Proposition 3.2,  is generated by all monomials
is generated by all monomials

where  , \(\varepsilon _p\ne \mu _p\), and
, \(\varepsilon _p\ne \mu _p\), and  together with all monomials
together with all monomials

where  with \(I \not \sim J\) and \(\varepsilon _p =\varepsilon '_p\) for each
with \(I \not \sim J\) and \(\varepsilon _p =\varepsilon '_p\) for each  . Hence it follows that the map
. Hence it follows that the map  , where \(\varepsilon _i' = \varepsilon _i\) for
, where \(\varepsilon _i' = \varepsilon _i\) for  and \(\varepsilon _i' = 0\) for
and \(\varepsilon _i' = 0\) for  , induces an isomorphism for the first claim. By the argument in the last part of the proof of Proposition 2.6, we have
, induces an isomorphism for the first claim. By the argument in the last part of the proof of Proposition 2.6, we have  and
and  . Since
. Since  , the second claim follows.\(\square \)
, the second claim follows.\(\square \)
6 Facets of enriched order polytopes and enriched chain polytopes
Theorem 1.1 implies the existence of a bijection between  and
and  . Towards such a bijection, in this section, we consider an elementary geometric property, the facet representations of enriched order polytopes and enriched chain polytopes.
. Towards such a bijection, in this section, we consider an elementary geometric property, the facet representations of enriched order polytopes and enriched chain polytopes.
Let P be a finite poset on  . Given elements i, j of P, we say that j covers i if \(i < j\) and there exists no \(k \in P\) such that \(i< k < j\). If j covers i in P, then we write \(i \lessdot j\). A chain of P is a totally ordered subset of P. A chain of the form \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) is called a saturated chain. A saturated chain \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) is called maximal if
. Given elements i, j of P, we say that j covers i if \(i < j\) and there exists no \(k \in P\) such that \(i< k < j\). If j covers i in P, then we write \(i \lessdot j\). A chain of P is a totally ordered subset of P. A chain of the form \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) is called a saturated chain. A saturated chain \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) is called maximal if  and
and  . First, we give the facet representations of enriched chain polytopes which easily follows from [16, Lemma 1.1] and the facet representations of chain polytopes [18].
. First, we give the facet representations of enriched chain polytopes which easily follows from [16, Lemma 1.1] and the facet representations of chain polytopes [18].
Proposition 6.1
Let P be a finite poset on  . Then
. Then  is the solution set of the linear inequalities
is the solution set of the linear inequalities

where \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) is a maximal chain of P, and  . In addition, each of the above inequalities is facet defining.
. In addition, each of the above inequalities is facet defining.
On the other hand, the facet representations of enriched order polytopes are as follows.
Theorem 6.2
Let P be a finite poset on  . Then
. Then  is the solution set of the following linear inequalities:
is the solution set of the following linear inequalities:
-
(a)
 , where \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) is a saturated chain of P with
, where \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) is a saturated chain of P with  ;
; -
(b)
 , where \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) is a maximal chain of P.
, where \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) is a maximal chain of P.
In addition, each of the above inequalities is facet defining.
Proof
The proof is induction on n. If \(n=1\), then the assertion is trivial. Assume \(n \geqslant 2\).
Let \({{\mathscr {Q}}} \subset {\mathbb {R}}^n\) be the solution set of the above linear inequalities. Since \(2^{s-1} - \sum _{j=2}^{s} 2^{s-j} = 1\) holds for any positive integer s, it is easy to see that  satisfies (a) and (b) for any filter F of P, and for any \(\varepsilon \in \{-1,1\}^{|F_{\min }|}\). Since
satisfies (a) and (b) for any filter F of P, and for any \(\varepsilon \in \{-1,1\}^{|F_{\min }|}\). Since  is the convex hull of such vectors, we have
is the convex hull of such vectors, we have  . In order to prove
. In order to prove  , let \(\mathbf{x} = (x_1, \dots , x_n) \in {{\mathscr {Q}}}\). First, we will show that \(|x_i| \leqslant 1\) for each
, let \(\mathbf{x} = (x_1, \dots , x_n) \in {{\mathscr {Q}}}\). First, we will show that \(|x_i| \leqslant 1\) for each  . Let \(i= i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) be a saturated chain of P with
. Let \(i= i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) be a saturated chain of P with  . Then \(\mathbf{x}\) satisfies the following r inequalities:
. Then \(\mathbf{x}\) satisfies the following r inequalities:

If \(r=1\), then \(x_i \leqslant 1\) is trivial. Let \(r \geqslant 2\). Then the inequality given by a linear combination  of the above inequalities is \(2^{r-1} x_{i_1} \leqslant 2^{r-1}\), and hence
of the above inequalities is \(2^{r-1} x_{i_1} \leqslant 2^{r-1}\), and hence  . Suppose that i belongs to a maximal chain \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\), say, \(i = i_k\). Then \(\mathbf{x}\) satisfies
. Suppose that i belongs to a maximal chain \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\), say, \(i = i_k\). Then \(\mathbf{x}\) satisfies  above and
above and

Then the inequality given by a linear combination

of the above inequalities is  , and hence we have
, and hence we have  .
.
We now prove that \(\mathbf{x}\) belongs to  by induction on n. Suppose that \(x_i = 0\) for some
by induction on n. Suppose that \(x_i = 0\) for some  . Then \((x_1,\dots ,x_{i-1},x_{i+1},\dots ,x_n) \in {\mathbb {R}}^{n-1}\) satisfies inequalities (a) and (b) for the subposet
. Then \((x_1,\dots ,x_{i-1},x_{i+1},\dots ,x_n) \in {\mathbb {R}}^{n-1}\) satisfies inequalities (a) and (b) for the subposet  of P. By the assumption of induction, \((x_1,\dots ,x_{i-1},x_{i+1},\dots ,x_n)\) belongs to
of P. By the assumption of induction, \((x_1,\dots ,x_{i-1},x_{i+1},\dots ,x_n)\) belongs to  . It then follows that \(\mathbf{x}\) belongs to
. It then follows that \(\mathbf{x}\) belongs to  . Thus we may assume that \(x_i \ne 0\) for any
. Thus we may assume that \(x_i \ne 0\) for any  . Let
. Let  . Note that \(0 < \lambda \leqslant 1\). Let
. Note that \(0 < \lambda \leqslant 1\). Let

where  , and \(\varepsilon \in \{-1,1\}^{|F_{\min } |}\) corresponds to the sign of \(x_i\) for each
, and \(\varepsilon \in \{-1,1\}^{|F_{\min } |}\) corresponds to the sign of \(x_i\) for each  . We now show that the vector \(\mathbf{y}\) satisfies
. We now show that the vector \(\mathbf{y}\) satisfies
-
(c)
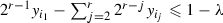 , where \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) is a saturated chain of P with
, where \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) is a saturated chain of P with  ;
; -
(d)
 , where \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) is a maximal chain of P.
, where \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) is a maximal chain of P.
Inequality (c). If either  or
or  holds, then
holds, then

If  and
and  , then
, then  and hence
and hence

Inequality (d). If  , then we have
, then we have

If  , then
, then  and hence
and hence

If \(\lambda =1\), then we have \(\mathbf{y}=\mathbf{0}\) by inequalities (c) and (d). Hence  . If \(\lambda \ne 1\), then \(\frac{1}{1-\lambda }\, \mathbf{y}\) belongs to \({{\mathscr {Q}}}\) by inequalities (c) and (d). From the definition of \(\lambda \), there exists
. If \(\lambda \ne 1\), then \(\frac{1}{1-\lambda }\, \mathbf{y}\) belongs to \({{\mathscr {Q}}}\) by inequalities (c) and (d). From the definition of \(\lambda \), there exists  such that \(y_i=0\). By the assumption of induction, \(\frac{1}{1-\lambda }\, \mathbf{y}\) belongs to
such that \(y_i=0\). By the assumption of induction, \(\frac{1}{1-\lambda }\, \mathbf{y}\) belongs to  , and hence \(\mathbf{y}\) belongs to
, and hence \(\mathbf{y}\) belongs to  . Thus
. Thus  belongs to
belongs to  .
.
Finally, we will prove that each of inequalities (a) and (b) is facet defining. Let

where \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) is a saturated chain of P with  , and let
, and let

where \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) is a maximal chain of P. It is enough to show that

Let \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) be a saturated chain of P with  . If
. If  , then let \(i = i_1\). If
, then let \(i = i_1\). If  , then let i be an arbitrary element in
, then let i be an arbitrary element in  . Note that, if
. Note that, if  , then \(i_2 \lessdot i_3 \lessdot \cdots \lessdot i_r\) is a maximal chain of
, then \(i_2 \lessdot i_3 \lessdot \cdots \lessdot i_r\) is a maximal chain of  . Let
. Let  . Then
. Then

is unimodularly equivalent to a facet of  by the assumption of induction. Hence
by the assumption of induction. Hence  . Since \((1,\dots ,1) \in {\mathbb {R}}^n\) belongs to
. Since \((1,\dots ,1) \in {\mathbb {R}}^n\) belongs to  , we have
, we have  . On the other hand, for a maximal chain \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) of P, let \(i = i_1\) if
. On the other hand, for a maximal chain \(i_1 \lessdot i_2 \lessdot \cdots \lessdot i_r\) of P, let \(i = i_1\) if  , and let i be an arbitrary element in
, and let i be an arbitrary element in  otherwise. Note that, if
otherwise. Note that, if  , then \(i_2 \lessdot i_3 \lessdot \cdots \lessdot i_r\) is a maximal chain of
, then \(i_2 \lessdot i_3 \lessdot \cdots \lessdot i_r\) is a maximal chain of  . Then
. Then

is unimodularly equivalent to a facet of  by the assumption of induction. Hence
by the assumption of induction. Hence  . Since \((1,\dots ,1) - 2 \mathbf{e}_i \in {\mathbb {R}}^n\) belongs to
. Since \((1,\dots ,1) - 2 \mathbf{e}_i \in {\mathbb {R}}^n\) belongs to  , we have
, we have  as desired.\(\square \)
as desired.\(\square \)
Given a polytope  of dimension n, let \(f_{n-1} ({\mathscr {P}})\) be the number of the facets of
of dimension n, let \(f_{n-1} ({\mathscr {P}})\) be the number of the facets of  . It is known [7, Corollary 1.2] that
. It is known [7, Corollary 1.2] that  for any poset P.
for any poset P.
Corollary 6.3
Let P be a finite poset on  . Then we have the following:
. Then we have the following:
-
(a)
Let
 (resp.
(resp.  ) be the number of saturated (resp. maximal) chains of P that contains a maximal element of P. Then
) be the number of saturated (resp. maximal) chains of P that contains a maximal element of P. Then  .
. -
(b)
Let \(\mathrm{mc}_\ell (P)\) be the number of maximal chains of P of length \(\ell \). Then
 .
.
Moreover, we have  .
.
Proof
The formulas of the number of facets follows from Proposition 6.1 and Theorem 6.2. Each maximal chain of P of length \(\ell \) contains exactly \(\ell +1\) saturated chains of P that contains a maximal element of P. Since \(\ell + 2 \leqslant 2^{\ell +1}\) for any integer \(\ell \geqslant 0\), we have  .\(\square \)
.\(\square \)
In [8, Lemma 3.8], tight upper bounds for  and
and  are given. Given an integer \(n\geqslant 2\), let
are given. Given an integer \(n\geqslant 2\), let

It is known [14, Theorem 1] that \(\mu _n\) is the maximum number of cliques possible in a graph with n vertices.
Proposition 6.4
([8, Lemma 3.8]) Let P be a finite poset on  with \(n \geqslant 5\). Then we have
with \(n \geqslant 5\). Then we have  , and
, and  In addition, both upper bounds are tight.
In addition, both upper bounds are tight.
We give tight upper bounds for the number of facets of enriched order and chain polytopes.
Proposition 6.5
Let P be a finite poset on  . Then we have
. Then we have  and
and

In addition, both upper bounds are tight.
Proof
The proof for  is induction on n. If \(n=1\), then
is induction on n. If \(n=1\), then  has two facets. Let \(n \geqslant 2\) and let M be the set of all minimal elements of P. If \(|M| = m\), then we have
has two facets. Let \(n \geqslant 2\) and let M be the set of all minimal elements of P. If \(|M| = m\), then we have

by the assumption of induction. Note that  if P is a chain.
if P is a chain.
By explicit computation, for \(n=1, 2,3,4\), the maximum value of the number of facets of  is 2, 4, 6, 10, respectively. (Note that
is 2, 4, 6, 10, respectively. (Note that  if P is an antichain.) Thus the assertion for
if P is an antichain.) Thus the assertion for  holds for \(n \leqslant 4\). Assume \(n \geqslant 5\). Let P be a poset on
holds for \(n \leqslant 4\). Assume \(n \geqslant 5\). Let P be a poset on  . Let \(P_1 = P\) and let \(M_1\) be the set of all maximal elements of \(P_1\). If \(P_1\) is not an antichain, then let
. Let \(P_1 = P\) and let \(M_1\) be the set of all maximal elements of \(P_1\). If \(P_1\) is not an antichain, then let  and let \(M_2\) be the set of all maximal elements of \(P_2\). In general, if \(P_i\) is not an antichain, then
and let \(M_2\) be the set of all maximal elements of \(P_2\). In general, if \(P_i\) is not an antichain, then  and let \(M_{i+1}\) be the set of all maximal elements of \(P_{i+1}\). By this procedure, we get a sequence of posets \(P_1, \dots , P_r\) such that \(P_r\) is an antichain. Then we have
and let \(M_{i+1}\) be the set of all maximal elements of \(P_{i+1}\). By this procedure, we get a sequence of posets \(P_1, \dots , P_r\) such that \(P_r\) is an antichain. Then we have

We show that

is equal to
for \(n \geqslant 5\). Suppose that \(m_1, \dots , m_r\), where \(1 \leqslant r \leqslant n\),  , and \(1 \leqslant m_i \in {\mathbb {Z}}\) give the maximum value of (4). If \(m_i < m_{i+1}\) for some i, then
, and \(1 \leqslant m_i \in {\mathbb {Z}}\) give the maximum value of (4). If \(m_i < m_{i+1}\) for some i, then
where \((m_i',m_{i+1}') = (m_{i+1},m_i)\) and \(m_k' = m_k\) if  . This is a contradiction. Hence we have \(m_1 \geqslant m_2 \geqslant \cdots \geqslant m_r\). If \(m_1 \geqslant 4\), then
. This is a contradiction. Hence we have \(m_1 \geqslant m_2 \geqslant \cdots \geqslant m_r\). If \(m_1 \geqslant 4\), then
Hence
where \(m_0' = \lfloor ({m_1+1})/{2} \rfloor \), \(m_1' = m_1-m_0'\) and \(m_k' = m_k\) if \(k \notin \{0, 1\}\). This is a contradiction. Thus we have \(m_1 \leqslant 3\). It is easy to see that \(m_r \ne 1\). Therefore
Since \(2 + 2 + 2 + 2 = 3 + 3 +2\) and  , there are at most three \(m_i\)’s that are equal to 2. If \(n = 3k+1\), then \(m_1 = \cdots = m_{r-2} =3\) and \(m_{r-1} = m_r=2\). If \(n = 3k+2\), then \(m_1 = \cdots = m_{r-1} =3\) and \(m_r=2\). If \(n = 3k \geqslant 6\), then there are two possibilities:
, there are at most three \(m_i\)’s that are equal to 2. If \(n = 3k+1\), then \(m_1 = \cdots = m_{r-2} =3\) and \(m_{r-1} = m_r=2\). If \(n = 3k+2\), then \(m_1 = \cdots = m_{r-1} =3\) and \(m_r=2\). If \(n = 3k \geqslant 6\), then there are two possibilities:
Since  , it follows that \(m_1,\dots ,m_r\) satisfies (5).
, it follows that \(m_1,\dots ,m_r\) satisfies (5).
Thus the maximum value is equal to

A poset that attains the maximum value is the ordinal sum  of antichains \(A_1,\dots ,A_r\) such that \(|A_i| = m_i\).\(\square \)
of antichains \(A_1,\dots ,A_r\) such that \(|A_i| = m_i\).\(\square \)
Finally, we discuss when the numbers of facets of  and
and  coincide.
coincide.
Proposition 6.6
Let P be a finite poset on  . Then the following conditions are equivalent:
. Then the following conditions are equivalent:
-
(i)
P is an antichain.
-
(ii)
 and
and  are unimodularly equivalent.
are unimodularly equivalent. -
(iii)
 is centrally symmetric.
is centrally symmetric. -
(iv)
The number of the facets of
 is equal to that of
is equal to that of  .
.
Proof
First, (ii) \(\Rightarrow \) (iv) is trivial.
(ii) \(\Rightarrow \) (iii): Note that  is always centrally symmetric, and that the origin is the unique interior lattice point in each of
is always centrally symmetric, and that the origin is the unique interior lattice point in each of  and
and  . Hence if
. Hence if  and
and  are unimodularly equivalent, then
are unimodularly equivalent, then  is also centrally symmetric.
is also centrally symmetric.
(iii) \(\Rightarrow \) (i): Assume that  is centrally symmetric. Then since
is centrally symmetric. Then since  , one has
, one has  . By the definition of
. By the definition of  , this implies that each element of P is a minimal element of P. Hence P is an antichain.
, this implies that each element of P is a minimal element of P. Hence P is an antichain.
(i) \(\Rightarrow \) (ii): If P is an antichain, then we have  .
.
(iv) \(\Rightarrow \) (i): Suppose that the number of the facets of  is equal to that of
is equal to that of  . By the argument in the proof of Corollary 6.3, each maximal chain of P of length \(\ell \) must satisfy \(\ell + 2 = 2^{\ell +1}\), and hence \(\ell = 0\). Thus P is an antichain.\(\square \)
. By the argument in the proof of Corollary 6.3, each maximal chain of P of length \(\ell \) must satisfy \(\ell + 2 = 2^{\ell +1}\), and hence \(\ell = 0\). Thus P is an antichain.\(\square \)
References
Batyrev, V.V.: Dual polyhedra and mirror symmetry for Calabi–Yau hypersurfaces in toric varieties. J. Algebraic Geom. 3(3), 493–535 (1994)
Cox, D.A., Little, J.B., Schenck, H.K.: Toric Varieties. Graduate Studies in Mathematics, vol. 124. American Mathematical Society, Providence (2011)
Ehrhart, E.: Polynomês Arithmétiques et Méthode des Polyédres en Combinatorie. International Series of Numerical Mathematics, vol. 35. Birkhäuser, Boston (1977)
Herzog, J., Hibi, T., Ohsugi, H.: Binomial Ideals. Graduate Texts in Mathematics, vol. 279. Springer, Cham (2018)
Hibi, T.: Distributive lattices, affine semigroup rings and algebras with straightening laws. In: Nagata, M., Matsumura, H. (eds.) Commutative Algebra and Combinatorics. Advanced Studies in Pure Mathematics, vol. 11, pp. 93–109. North-Holland, Amsterdam (1987)
Hibi, T., Li, N.: Chain polytopes and algebras with straightening laws. Acta Math. Vietnam. 40(3), 447–452 (2015)
Hibi, T., Li, N.: Unimodular equivalence of order and chain polytopes. Math. Scand. 118(1), 5–12 (2016)
Hibi, T., Li, N., Li, T.X., Mu, L., Tsuchiya, A.: Order-chain polytopes. Ars Math. Contemp. 16(2), 299–317 (2019)
Hibi, T., Matsuda, K., Ohsugi, H., Shibata, K.: Centrally symmetric configurations of order polytopes. J. Algebra 443, 469–478 (2015)
Hibi, T., Tsuchiya, A.: Facets and volume of Gorenstein Fano polytopes. Math. Nachr. 290(16), 2619–2628 (2017)
Hibi, T., Tsuchiya, A.: Reflexive polytopes arising from perfect graphs. J. Combin. Theory Ser. A 157, 233–246 (2018)
Kreuzer, M., Skarke, H.: Complete classification of reflexive polyhedra in four dimensions. Adv. Theor. Math. Phys. 4(6), 1209–1230 (2000)
Lagarias, J.C., Ziegler, G.M.: Bounds for lattice polytopes containing a fixed number of interior points in a sublattice. Canadian J. Math. 43(5), 1022–1035 (1991)
Moon, J.W., Moser, L.: On cliques in graphs. Israel J. Math. 3, 23–28 (1965)
Ohsugi, H., Hibi, T.: Reverse lexicographic squarefree initial ideals and Gorenstein Fano polytopes. J. Commut. Algebra 10(2), 171–186 (2018)
Ohsugi, H., Tsuchiya, A.: Enriched chain polytopes. (to appear in Israel J. Math.)
Petersen, T.K.: Enriched $P$-partitions and peak algebras. Adv. Math. 209(2), 561–610 (2007)
Stanley, R.P.: Two poset polytopes. Discrete Comput. Geom. 1(1), 9–23 (1986)
Stembridge, J.R.: Enriched $P$-partitions. Trans. Amer. Math. Soc. 349(2), 763–788 (1997)
Sturmfels, B.: Gröbner Bases and Convex Polytopes. University Lecture Series, vol. 8. American Mathematical Society, Providence (1996)
Acknowledgements
The authors are grateful to an anonymous referee for his/her useful comments. In particular, the last section was added following referee’s advice.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors were partially supported by JSPS KAKENHI 18H01134 and 16J01549.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ohsugi, H., Tsuchiya, A. Enriched order polytopes and enriched Hibi rings. European Journal of Mathematics 7, 48–68 (2021). https://doi.org/10.1007/s40879-020-00403-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-020-00403-2
Keywords
- Reflexive polytope
- Flag triangulation
- Left enriched partition
- Left enriched order polynomial
- Gröbner basis
- Toric ideal




 if
if  .
. and the chain polytope
and the chain polytope  are unimodularly equivalent.
are unimodularly equivalent. is equal to that of
is equal to that of  .
.
 ;
; ;
; .
. .
. , and
, and  , we have
, we have  , we have
, we have 
 , we have
, we have 
 , we have
, we have  , we have
, we have 
 , we have
, we have 
 , we obtain
, we obtain  .
. , we obtain
, we obtain 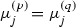 .
. , where
, where  ;
; , where
, where 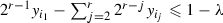 , where
, where  ;
; , where
, where  (resp.
(resp.  ) be the number of saturated (resp. maximal) chains of P that contains a maximal element of P. Then
) be the number of saturated (resp. maximal) chains of P that contains a maximal element of P. Then  .
. .
. and
and  are unimodularly equivalent.
are unimodularly equivalent. is centrally symmetric.
is centrally symmetric. is equal to that of
is equal to that of  .
.