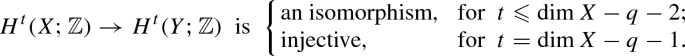Abstract
The goal of this article is to define partially ample subvarieties of projective varieties, generalizing Ottem’s work on ample subvarieties, and also to show their ubiquity. As an application, we obtain a connectedness result for pre-images of subvarieties by morphisms, reminiscent to a problem posed by Fulton–Hansen in the late 1970s. Similar criteria are not available in the literature.
References
Andreotti, A., Grauert, H.: Théorème de finitude pour la cohomologie des espaces complexes. Bull. Soc. Math. France 90, 193–259 (1962)
Arapura, D.: Partial regularity and amplitude. Amer. J. Math. 128(4), 1025–1056 (2006)
Bott, R.: On a theorem of Lefschetz. Michigan Math. J. 6, 211–216 (1959)
Białynicki-Birula, A.: Some theorems on actions of algebraic groups. Ann. Math. 98, 480–497 (1973)
Buchsbaum, D., Eisenbud, D.: Generic free resolutions and a family of generically perfect ideals. Adv. Math. 18(3), 245–301 (1975)
Debarre, O.: Théorèmes de connexité pour les produits d’espaces projectifs et les grassmanniennes. Amer. J. Math. 118(6), 1347–1367 (1996)
Faltings, G.: Formale geometrie und homogene Räume. Invent. Math. 64(1), 123–165 (1981)
Fulger, M., Lehmann, B.: Positive cones of dual cycle classes. Algebraic Geom. 4(1), 1–28 (2017)
Fulton, W., Hansen, J.: A connectedness theorem for projective varieties, with applications to intersections and singularities of mappings. Ann. Math. 110(1), 159–166 (1979)
Halic, M.: Subvarieties with partially ample normal bundle. Math. Z. https://doi.org/10.1007/s00209-018-2175-1
Halic, M., Tajarod, R.: About the cohomological dimension of certain stratified varieties. Proc. Amer. Math. Soc. 145(12), 5157–5167 (2017)
Hansen, J.: A connectedness theorem for flagmanifolds and Grassmannians. Amer. J. Math. 105(3), 633–639 (1983)
Hartshorne, R.: Cohomological dimension of algebraic varieties. Ann. Math. 88, 403–450 (1968)
Hartshorne, R.: Ample Subvarieties of Algebraic Varieties. Lecture Notes in Mathematics, vol. 156. Springer, Berlin (1970)
Hironaka, H., Matsumura, H.: Formal functions and formal embeddings. J. Math. Soc. Japan 20, 52–82 (1968)
Hyry, E., Järvilehto, T.: Coefficient ideals and the Gorenstein property of blowups. Comm. Algebra 33(12), 4617–4629 (2005)
Kawasaki, T.: On macaulayfication of Noetherian schemes. Trans. Amer. Math. Soc. 352(6), 2517–2552 (2000)
Kollár, J.: Higher direct images of dualizing sheaves. I. Ann. Math. 123(1), 11–42 (1986)
Matsumura, S.: Asymptotic cohomology vanishing and a converse to the Andreotti–Grauert theorem on surfaces. Ann. Inst. Fourier (Grenoble) 63(6), 2199–2221 (2013)
Ogus, A.: Local cohomological dimension of algebraic varieties. Ann. Math. 98, 327–365 (1973)
Ottem, J.Chr.: Ample subvarieties and \(q\)-ample divisors. Adv. Math. 229(5), 2868–2887 (2012)
Peternell, Th.: Submanifolds with ample normal bundles and a conjecture of Hartshorne. In: Bates, D.J., et al. (eds.) Interactions of Classical and Numerical Algebraic Geometry. Contemporary Mathematics, vol. 496, pp. 317–330. American Mathematical Society, Providence (2009)
Sommese, A.J.: Submanifolds of Aabelian varieties. Math. Ann. 233(3), 229–256 (1978)
Totaro, B.: Line bundles with partially vanishing cohomology. J. Eur. Math. Soc. (JEMS) 15(3), 731–754 (2013)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Background material
Appendix A: Background material
1.1 A.1 Cohomological q-ampleness
This notion was introduced by Arapura and Totaro.
Definition A.1
Let Y be a projective scheme,  an ample line bundle.
an ample line bundle.
- (i)
([24, Theorem 7.1]) An invertible sheaf \({\mathscr {L}}\) on Y is q-ample if, for any coherent sheaf \({\mathscr {G}}\) on X, holds: there exists \(\mathop {\mathrm{ct}}^{{\mathscr {G}}}\) such that for all \(a\geqslant \mathop {\mathrm{ct}}^{{\mathscr {G}}}\) and all \(t>q\),
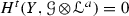 .
.It is enough to verify the property for
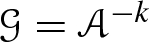
, \(k\geqslant 1\) (cf. [24, Theorem 6.3, 7.1]).
- (ii)
([2, Lemmas 2.1, 2.3]) A locally free sheaf \({\mathscr {E}}\) on Y is q-ample if \({\mathscr {O}}_{\mathbb {P}({\mathscr {E}}^\vee )}(1)\) on
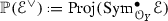 is q-ample. It is equivalent saying that, for any coherent sheaf \({\mathscr {G}}\) on Y, there is
is q-ample. It is equivalent saying that, for any coherent sheaf \({\mathscr {G}}\) on Y, there is 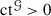 such that:
such that: 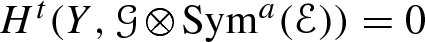
, for all \(t>q\) and all \(a\geqslant \mathop {\mathrm{ct}}^{{\mathscr {G}}}\).
The q-amplitude of\({\mathscr {E}}\), denoted by \(q^{\mathscr {E}}\), is the smallest integer q with this property. Note that \({\mathscr {E}}\) is q-ample if and only if so is \({\mathscr {E}}_{Y_{\mathrm{red}}}\) (cf. [24, Corollary 7.2]). Also, any locally free quotient \({\mathscr {F}}\) of \({\mathscr {E}}\) is still q-ample; indeed,
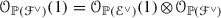 .
.
1.2 A.2 q-Positivity
Proposition A.2
([23, Proposition 1.7]) For a globally generated, locally free sheaf \({\mathscr {E}}\) on Y, the following statements are equivalent:
- (i)
\({\mathscr {E}}\) is q-ample (cf. Definition A.1);
- (ii)
The fibres of the morphism \(\mathbb {P}({\mathscr {E}}^\vee )\rightarrow |{\mathscr {O}}_{\mathbb {P}({\mathscr {E}}^\vee )}(1)|\) are at most q-dimensional.
We say that \({\mathscr {E}}\) is Sommese-q-ample if it satisfies any of these conditions.
Definition A.3
(cf. [1]) Suppose X is a smooth, complex projective variety. A line bundle \({\mathscr {L}}\) on X is q-positive, if it admits a Hermitian metric whose curvature is positive definite on a subspace of \({\mathscr {T}}_{X,x}\) of dimension at least \(\dim X-q\), for all \(x\in X\); equivalently, the curvature has at each point \(x\in X\) at most q negative or zero eigenvalues.
Theorem A.4
-
(i)
([1, Proposition 28]) q-positive line bundles are q-ample.
-
(ii)
([19, Theorem 1.4]) Assume \({\mathscr {E}}\) is globally generated. Then it holds:
$$\begin{aligned} {\mathscr {E}}\text { is Sommese-}q\text {-ample}\;\;\Longleftrightarrow \;\; {\mathscr {O}}_{\mathbb {P}({\mathscr {E}}^\vee )}(1)\text { is }q\text {-positive.} \end{aligned}$$ -
(iii)
([3, 21]) Let
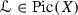 be q-positive and \(Y\in |{\mathscr {L}}|\) a smooth divisor. Then it holds:
be q-positive and \(Y\in |{\mathscr {L}}|\) a smooth divisor. Then it holds: 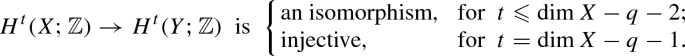
Rights and permissions
About this article
Cite this article
Halic, M. Partially ample subvarieties of projective varieties. European Journal of Mathematics 6, 400–419 (2020). https://doi.org/10.1007/s40879-019-00325-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-019-00325-8


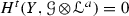 .
.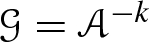
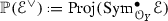 is q-ample. It is equivalent saying that, for any coherent sheaf
is q-ample. It is equivalent saying that, for any coherent sheaf 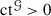 such that:
such that: 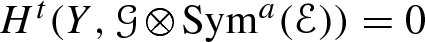
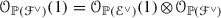 .
.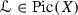 be q-positive and
be q-positive and