Abstract
We study a certain Artin–Schreier family of elliptic curves over the function field  . We prove an asymptotic estimate on the special values of their L-function in terms of the degree of their conductor; we show that the special values are, in a sense, ‘asymptotically as large as possible’. We also provide an explicit expression for their L-function. The proof of the main result uses this expression and a detailed study of the distribution of character sums related to Kloosterman sums. Via the BSD conjecture, the main result translates into an analogue of the Brauer–Siegel theorem for these elliptic curves.
. We prove an asymptotic estimate on the special values of their L-function in terms of the degree of their conductor; we show that the special values are, in a sense, ‘asymptotically as large as possible’. We also provide an explicit expression for their L-function. The proof of the main result uses this expression and a detailed study of the distribution of character sums related to Kloosterman sums. Via the BSD conjecture, the main result translates into an analogue of the Brauer–Siegel theorem for these elliptic curves.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \({\mathbb {F}}_q\) be a finite field of odd characteristic p and  . Consider a nonisotrivial elliptic curve E defined over K, and its associated L-functionFootnote 1L(E, T). Via a cohomological interpretation, Grothendieck has proven that, even though L(E, T) is a priori defined as a formal power series in T, it is actually a polynomial with integral coefficients, whose degree we denote by b(E). Moreover, L(E, T) satisfies the expected functional equation relating L(E, T) to \(L(E, 1/q^2T)\).
. Consider a nonisotrivial elliptic curve E defined over K, and its associated L-functionFootnote 1L(E, T). Via a cohomological interpretation, Grothendieck has proven that, even though L(E, T) is a priori defined as a formal power series in T, it is actually a polynomial with integral coefficients, whose degree we denote by b(E). Moreover, L(E, T) satisfies the expected functional equation relating L(E, T) to \(L(E, 1/q^2T)\).
Define \(\rho (E)\) to be the order of vanishing of L(E, T) at the central point \(T=q^{-1}\) and the special value of L(E, T) by  . These invariants both appear in the conjecture of Birch and Swinnerton-DyerFootnote 2 through which they are related to ‘arithmetic’ invariants of E.
. These invariants both appear in the conjecture of Birch and Swinnerton-DyerFootnote 2 through which they are related to ‘arithmetic’ invariants of E.
We will be interested in comparing the size of the special value \(L^*(E, 1)\) to the degree b(E) of the L-function. It is relatively straightforward to prove that

and it seems natural to ask about the optimality of such bounds. In other words, given a family  of nonisotrivial elliptic curves E over K with \(b(E)\rightarrow \infty \), we investigate the asymptotic behaviour of the ratio
of nonisotrivial elliptic curves E over K with \(b(E)\rightarrow \infty \), we investigate the asymptotic behaviour of the ratio  as E runs through
as E runs through  . Does this ratio have a limit? If so, what is this limit?
. Does this ratio have a limit? If so, what is this limit?
These questions are still wide open and, as far as the author knows, they have only been settled for a very limited number of special families  (see [10, Theorem 7.12], [7, Corollary 5.1], [8, Theorem 4.2] and [6, Theorem 9]). These examples are known as ‘Kummer families’ of elliptic curves: one obtains them by pulling-back an elliptic curve \(E_1/K\) by the map \(t\mapsto t^d\) for larger and larger integers d which are coprime to q. In those cases, the ratio in (1) does have a limit, and this limit is 0.
(see [10, Theorem 7.12], [7, Corollary 5.1], [8, Theorem 4.2] and [6, Theorem 9]). These examples are known as ‘Kummer families’ of elliptic curves: one obtains them by pulling-back an elliptic curve \(E_1/K\) by the map \(t\mapsto t^d\) for larger and larger integers d which are coprime to q. In those cases, the ratio in (1) does have a limit, and this limit is 0.
In this article, we answer the two questions above for an ‘Artin–Schreier family’ of elliptic curves over K. More precisely, we prove
Theorem A
Let \({\mathbb {F}}_q\) be a finite field of odd characteristic p and  . Fix \(\gamma \in {\mathbb {F}}_q^\times \) and, for all integers \(a\geqslant 1\), let \(E_{a,\gamma }\) be the elliptic curve over K given by the affine Weierstrass model
. Fix \(\gamma \in {\mathbb {F}}_q^\times \) and, for all integers \(a\geqslant 1\), let \(E_{a,\gamma }\) be the elliptic curve over K given by the affine Weierstrass model

Then, as \(a\rightarrow \infty \), the limit below exists and is 0:

The name of ‘Artin–Schreier family’ stems from its construction: starting with the elliptic curve \(E_{\gamma }/K\) given by  , one obtains \(E_{a, \gamma }\) by pulling back \(E_{\gamma }\) by the Artin–Schreier map
, one obtains \(E_{a, \gamma }\) by pulling back \(E_{\gamma }\) by the Artin–Schreier map  for any \(a\geqslant 1\). This family of elliptic curves \(\{E_{a, \gamma }\}_{a\geqslant 1}\) was previously studied in [18] where, among other things, the authors prove that \(E_{a, \gamma }\) satisfies the BSD conjecture. Following [18, Section 7.3], we note the ressemblance between \(E_{a, \gamma }\) and a Legendre elliptic curve. We refer to Theorem 7.1 for a more quantitative version of (2).
for any \(a\geqslant 1\). This family of elliptic curves \(\{E_{a, \gamma }\}_{a\geqslant 1}\) was previously studied in [18] where, among other things, the authors prove that \(E_{a, \gamma }\) satisfies the BSD conjecture. Following [18, Section 7.3], we note the ressemblance between \(E_{a, \gamma }\) and a Legendre elliptic curve. We refer to Theorem 7.1 for a more quantitative version of (2).
Once again, prior to Theorem A, the only known examples of families of elliptic curves exhibiting a behaviour such as (2) were Kummer families. We also remark that the strategy of proof of (2) significantly differs from the one used in our previous works [6,7,8]; we comment further on this difference and on the reason for adopting a new approach in Remark 7.2.
From Theorem A and from the BSD conjecture, we will deduce (see Theorem 8.1):
Theorem B
Let \({\mathbb {F}}_q\) be a finite field of odd characteristic and  . For any \(\gamma \in {\mathbb {F}}_q^\times \) and any integer \(a\geqslant 1\), the Tate–Shafarevich group
. For any \(\gamma \in {\mathbb {F}}_q^\times \) and any integer \(a\geqslant 1\), the Tate–Shafarevich group  is finite. Furthermore, one has
is finite. Furthermore, one has

where \(\mathrm{Reg}(E_{a, \gamma })\) denotes the Néron–Tate regulator of \(E_{a, \gamma }\), and \(H(E_{a, \gamma })\) its exponential differential height (see Sects. 2.1–2.3 for definitions).
Following [10], we view this result as an analogue of the Brauer–Siegel theorem for the sequence of elliptic curves \(\{E_{a, \gamma }\}_{a\geqslant 1}\). We further comment on this result in Sect. 8.
Let us give an outline of the proof of Theorem A as we describe the structure of the paper and state the other results contained in it. In Sect. 2, we start by reviewing the construction of the elliptic curves \(E_{a, \gamma }\) and by computing some of their invariants. We also recall the definition of their L-function and state the BSD conjecture (proven by Pries and Ulmer for \(E_{a, \gamma }\), cf. [18]).
In the following two sections, we compute the L-function of \(E_{a, \gamma }\); the relevant objects are introduced in Sect. 3. In particular, a central role is played by angles of some Kloosterman sums. For the purpose of this introduction let us only say that, to any place \(v\ne 0, \infty \) of K, we will attach a character sum  . The sum
. The sum  is a real number satisfying
is a real number satisfying  where \(d_v\) is the degree of v. Hence there exists an angle
where \(d_v\) is the degree of v. Hence there exists an angle  such that
such that  . The reader is referred to Sects. 3.2 and 4.4 for precise definitions. Section 4 is devoted to the calculation of the L-function itself, which results in the following expression:
. The reader is referred to Sects. 3.2 and 4.4 for precise definitions. Section 4 is devoted to the calculation of the L-function itself, which results in the following expression:
Theorem C
For all integers \(a\geqslant 1\), we denote by  the set of places \(v\ne 0, \infty \) of K whose degree \(d_v\) divides a. Then, for all \(\gamma \in {\mathbb {F}}_q^\times \), the L-function of \(E_{a, \gamma }\) is given by
the set of places \(v\ne 0, \infty \) of K whose degree \(d_v\) divides a. Then, for all \(\gamma \in {\mathbb {F}}_q^\times \), the L-function of \(E_{a, \gamma }\) is given by

where, for all  , \(\theta _v\in (0,\pi )\) is as above (see Sects. 3.2 and 4.4 for a precise definition).
, \(\theta _v\in (0,\pi )\) is as above (see Sects. 3.2 and 4.4 for a precise definition).
This result is proven by a ‘point-counting’ argument, directly from the definition of \(L(E_{a, \gamma }, T)\), through manipulations of character sums over finite fields. Given the paucity of tables of L-functions of elliptic curves over K of large conductor, such an explicit expression of \(L(E_{a, \gamma }, T)\) may be of independent interest.
As a by-product, Theorem C yields a closed formula for the analytic rank  . Using that the BSD conjecture is proven for \(E_{a, \gamma }\), we recover a result of [18] stating that the ranks of \(E_{a, \gamma }(K)\) are unbounded as \(a\rightarrow \infty \); more precisely, we show in Corollary 4.8 that
. Using that the BSD conjecture is proven for \(E_{a, \gamma }\), we recover a result of [18] stating that the ranks of \(E_{a, \gamma }(K)\) are unbounded as \(a\rightarrow \infty \); more precisely, we show in Corollary 4.8 that  .
.
From Theorem C, we also derive (Proposition 4.7 and (27)) an explicit expression for the special value \(L^*(E_{a, \gamma }, 1)\). In the notations of (3), we obtain an expression of the shape

where, \(b(E_{a, \gamma })\gg q^a\), as will be shown in Sect. 2.2. Estimating the first term is straightforward: it is  as \(a\rightarrow \infty \) and thus does not play any role in the asymptotics. In order to prove the limit in Theorem A, we have to investigate the behaviour of the second term: specifically, we need to show that it is
as \(a\rightarrow \infty \) and thus does not play any role in the asymptotics. In order to prove the limit in Theorem A, we have to investigate the behaviour of the second term: specifically, we need to show that it is  too. The size of this term visibly depends on how the angles
too. The size of this term visibly depends on how the angles  distribute in the interval
distribute in the interval  . Since \(t\mapsto \log \sin ^2 t\) tends to \(-\infty \) at 0 and \(\pi \), this size also depends on how close the angles \(\theta _v\) can be to the endpoints of \((0,\pi )\). Therefore we devote Sects. 5 and 6 to studying the distribution of the angles
. Since \(t\mapsto \log \sin ^2 t\) tends to \(-\infty \) at 0 and \(\pi \), this size also depends on how close the angles \(\theta _v\) can be to the endpoints of \((0,\pi )\). Therefore we devote Sects. 5 and 6 to studying the distribution of the angles  in more detail. The two main results in these sections can be stated as follows:
in more detail. The two main results in these sections can be stated as follows:
Theorem D
Notations being as above:
-
(i
– Theorem 6.6) For all continuously differentiable functions
 ,
, 
-
(ii
– Corollary 5.5) There is a constant \(c>0\) such that
 for all
for all  .
.
By the work of Katz, it is known that the angles of Kloosterman sums become equidistributed in  with respect to the Sato–Tate measure (see [11]). It turns out that the same statement holds for the angles
with respect to the Sato–Tate measure (see [11]). It turns out that the same statement holds for the angles  (see Theorem 6.5). The proof relies on an adaptation of Katz’s method in [11, Chapter 3] and results of Fu and Liu in [5]. This equidistribution result, however, is not sufficient for our purpose: we need a more effective version such as Theorem D (i). The effective version (Theorem 6.6) follows from Theorem 6.5 after a more detailed analysis using tools from equidistribution theory (see [17]).
(see Theorem 6.5). The proof relies on an adaptation of Katz’s method in [11, Chapter 3] and results of Fu and Liu in [5]. This equidistribution result, however, is not sufficient for our purpose: we need a more effective version such as Theorem D (i). The effective version (Theorem 6.6) follows from Theorem 6.5 after a more detailed analysis using tools from equidistribution theory (see [17]).
The main goal of Sect. 5 is to prove Theorem D (ii); we actually prove a more general result there (see Theorem 5.1). The proof has a Diophantine approximation flavour and the main tool is a version of Liouville’s inequality, as found in [16].
Combining the two results in Theorem D and approximating \(t\mapsto \log \sin ^2 t\) by sufficiently regular functions, we prove (Theorem 7.3) that

Theorem A then follows rather easily (see Theorem 7.1), since (5) implies that the second term in (4) is indeed  as \(a\rightarrow \infty \). Finally, Sect. 8 is devoted to the proof of Theorem B (see Theorem 8.1).
as \(a\rightarrow \infty \). Finally, Sect. 8 is devoted to the proof of Theorem B (see Theorem 8.1).
Throughout this article, we fix a finite field\({\mathbb {F}}_q\)of characteristic\(p\geqslant 3\), and we denote by the function field of the projective line\({\mathbb {P}}^1_{/{\mathbb {F}}_q}\).
the function field of the projective line\({\mathbb {P}}^1_{/{\mathbb {F}}_q}\).
2 The Artin–Schreier family of elliptic curves \(E_{a, \gamma }\)
In this section, we explain in some detail how the curves \(E_{a, \gamma }\) are constructed and we collect elementary facts about them. We also setup some notations and conventions that will be in force for the rest of the paper. For a nice account of the theory of elliptic curves over K, the reader may consult [21].
For all integers \(a\geqslant 1\), we let  . For any \(\gamma \in {\mathbb {F}}_q^\times \) and any \(a\geqslant 1\), we consider the elliptic curve \(E_{a, \gamma }\) defined over K by the affine Weierstrass model:
. For any \(\gamma \in {\mathbb {F}}_q^\times \) and any \(a\geqslant 1\), we consider the elliptic curve \(E_{a, \gamma }\) defined over K by the affine Weierstrass model:

The sequence \(\{E_{a, \gamma }\}_{a\geqslant 1}\) is called an Artin–Schreier family of elliptic curves over K. This terminology comes from the following observations. Let \(E_\gamma /K\) be the elliptic curve given by  . Then, for all \(a\geqslant 1\), the curve \(E_{a, \gamma }\) is the pullback of \(E_\gamma \) under the Artin–Schreier map \({\mathbb {P}}^1_{/{\mathbb {F}}_q} \!\rightarrow {\mathbb {P}}^1_{/{\mathbb {F}}_q}\) given by
. Then, for all \(a\geqslant 1\), the curve \(E_{a, \gamma }\) is the pullback of \(E_\gamma \) under the Artin–Schreier map \({\mathbb {P}}^1_{/{\mathbb {F}}_q} \!\rightarrow {\mathbb {P}}^1_{/{\mathbb {F}}_q}\) given by  . Hence, studying \(E_{a, \gamma }\) over
. Hence, studying \(E_{a, \gamma }\) over  is equivalent to studying \(E_\gamma \) over the Artin–Schreier extension
is equivalent to studying \(E_\gamma \) over the Artin–Schreier extension  of
of  , where
, where  .
.
These elliptic curves \(E_{a, \gamma }\) were studied in [18, Sections 6.4, 7.3] where, among other things, it was shown that they satisfy the BSD conjecture (see Sect. 2.3). In their paper, Pries and Ulmer construct the curves \(E_{a, \gamma }\) as follows. For any \(\gamma \in {\mathbb {F}}_q^\times \), we let \(f_\gamma :{\mathbb {P}}^1_{/K}\!\rightarrow {\mathbb {P}}^1_{/K}\) be the map  . Consider the curve
. Consider the curve  defined over K by
defined over K by

in the  -coordinates on
-coordinates on  . This curve is smooth of genus 1 and admits one K-rational point
. This curve is smooth of genus 1 and admits one K-rational point  . The curve \(Z_{a, \gamma }\) is given in the affine (x, y)-coordinates on \(\mathbb {A}^2_{/K}\) by
. The curve \(Z_{a, \gamma }\) is given in the affine (x, y)-coordinates on \(\mathbb {A}^2_{/K}\) by

The change of coordinates

then brings \(Z_{a, \gamma }\) into the affine Weierstrass form

One finally passes from \(E^\circ _{a, \gamma }\) to \(E_{a, \gamma }\) by means of the 2-isogeny \(\phi :E^\circ _{a, \gamma }\!\rightarrow E_{a, \gamma }\) given by

From the model (6), it is straightforward to compute the j-invariant \(j(E_{a, \gamma })\) of \(E_{a, \gamma }\) and obtain that

As a rational function of t, the j-invariant \(j(E_{a, \gamma })\) is visibly nonconstant and separable. In particular, the curve \(E_{a, \gamma }\) is not isotrivial.
We also would like to point out that \(E_{a, \gamma }\) is ‘almost’ a Legendre curve. More precisely, in the setting of [1], the curve \(E_{a, \gamma }\) can be obtained as follows. Starting from the Legendre elliptic curve \(E_{0, \gamma }/K\) given by

one takes a quadratic twist by  , obtaining \(E'_{0, \gamma }\) defined by
, obtaining \(E'_{0, \gamma }\) defined by

Pulling back \(E'_{0, \gamma } \) along  , one recovers the curve \(E_{a, \gamma }\) defined by (6).
, one recovers the curve \(E_{a, \gamma }\) defined by (6).
2.1 Bad reduction and invariants
For any place v of K, we denote by \(d_v\) or \(\deg v\) the degree of v and by \({\mathbb {F}}_{v}\) the residue field at v. We identify finite places of K with monic irreducible polynomials in  ; we also identify the residue field at \(v\ne \infty \) with
; we also identify the residue field at \(v\ne \infty \) with  if
if  is the monic irreducible polynomial corresponding to v.
is the monic irreducible polynomial corresponding to v.
Let us describe the reductions of \(E_{a, \gamma }\) at places of K and compute its relevant invariants. A straightforward computation of the discriminant of the model (6) of \(E_{a, \gamma }\) gives that

The finite places of bad reduction of \(E_{a, \gamma }\) are then the monic irreducible divisors of \(\Delta \) in  . By a routine application of Tate’s algorithm (see [19, Chapter IV, Section 9] for instance), one can give a more precise description:
. By a routine application of Tate’s algorithm (see [19, Chapter IV, Section 9] for instance), one can give a more precise description:
Proposition 2.1
Let \(Z_{a, \gamma }\) be the set of places of K that divide  . Then \(E_{a, \gamma }\) has good reduction outside \(S= Z_{a, \gamma }\cup \{\infty \}\). The reduction of \(E_{a, \gamma }\) at places \(v\in S\) is as follows:
. Then \(E_{a, \gamma }\) has good reduction outside \(S= Z_{a, \gamma }\cup \{\infty \}\). The reduction of \(E_{a, \gamma }\) at places \(v\in S\) is as follows:
Place v of K | Reduction type of \(E_{a, \gamma }\) at v | \(\mathrm{ord}_{v}\Delta _{\min }(E_{a, \gamma })\) |
|
|---|---|---|---|
| Multiplicative (of type \(\mathbf I _{4}\)) | 4 | 1 |
| Multiplicative (of type \(\mathbf I _2\)) | 2 | 1 |
\(\infty \) | Split multiplicative (of type \(\mathbf I _{4q^a}\)) | \(4q^a\) | 1 |
In this table, for all places v of bad reduction for \(E_{a, \gamma }\), we have denoted by \(\mathrm{ord}_{v}\Delta _{\min }(E_{a, \gamma })\) (resp.  ) the valuation at v of the minimal discriminant of \(E_{a, \gamma }\) (resp. of the conductor of \(E_{a, \gamma }\)). See [19, Chapter IV, Section 9], [21, Lecture 1, Section 8] for the definitions of these local invariants.
) the valuation at v of the minimal discriminant of \(E_{a, \gamma }\) (resp. of the conductor of \(E_{a, \gamma }\)). See [19, Chapter IV, Section 9], [21, Lecture 1, Section 8] for the definitions of these local invariants.
From this local information, one deduces the values of the following global invariants (we refer to [21, Lecture 1] for their definition). The minimal discriminant divisor \(\Delta _{\min }(E_{a, \gamma })\) has degree \({\deg \Delta _{\min }(E_{a, \gamma }) = 12 q^{a}}\), and the conductor  has degree
has degree  . Indeed, since both
. Indeed, since both  and
and  are squarefree in
are squarefree in  , one has
, one has

Hence the exponential differential height \(H(E_{a, \gamma })\) is \(q^{q^a}\) since, by definition (see [21, Lecture 3, Section 2]), it is given by  . Summarising these calculations, we have
. Summarising these calculations, we have

Remark 2.2
As is clear from comparing (8) and the third column of the table in Proposition 2.1, the discriminant \(\Delta \) of the Weierstrass model (6) has the same valuation as \({\Delta _{\min }(E_{a, \gamma })}\) at all finite places of K. Therefore, the model (6) is a minimal integral model of \(E_{a, \gamma }\) at all places \(v\ne \infty \) of K.
2.2 Definitions of L-function, analytic rank and special value
For any place v of K, with degree \(d_v\) and residue field \({\mathbb {F}}_v\), we denote by \((\widetilde{E_{a, \gamma }})_v\) the reduction modulo v of a minimal integral model of \(E_{a, \gamma }\) at v: \((\widetilde{E_{a, \gamma }})_v\) is thus a plane cubic curve over \({\mathbb {F}}_{v}\). By definition, the L-function of \(E_{a, \gamma }\) is the power series in T given by

where the products are over places of K where \(E_{a, \gamma }\) has good (resp. bad) reduction, and whereFootnote 3

We refer to [1, Section 2.2] and [21, Lecture 1, Section 9, Lecture 3, Section 6] for more details.
Since \(E_{a, \gamma }\) is not isotrivial, a theorem of Grothendieck shows that \(L(E_{a, \gamma }, T)\) is actually a polynomial in T with integral coefficients whose degree is denoted by \(b(E_{a, \gamma })\). Further, by the Grothendieck–Ogg–Shafarevich formula and our computation in (9) of the degree of  , we know that
, we know that

In Sect. 4, we will compute the polynomial \(L(E_{a, \gamma }, T)\) explicitly. For now, we only note that it makes sense to define the following two quantities:
Definition 2.3
Let \(\rho (E_{a, \gamma })\) be the analytic rank of\(E_{a, \gamma }\), i.e., \(\rho (E_{a, \gamma })\) is the multiplicity of \(T=q^{-1}\) as a root of \(L(E_{a, \gamma }, T)\). Further, define the special value of\(L(E_{a, \gamma }, T)\)at\(T=q^{-1}\) to be

Remark 2.4
The special value \(L^*(E_{a, \gamma }, 1)\) is ‘usually’ defined as the first nonzero coefficient in the Taylor expansion around \(s=1\) of the function \(s\mapsto L(E_{a, \gamma }, q^{-s})\). Our definition (12) differs from that more ‘usual’ one by a factor \((\log q)^\rho \). We prefer to use the normalisation (12) because it ensures that \(L^*(E_{a,\gamma }, 1)\in {\mathbb {Q}}^*\). This choice is consistent with our normalisation of \(\mathrm{Reg}(E_{a, \gamma })\), see Sect. 2.3.
2.3 The BSD conjecture
The Mordell–Weil theorem implies that \(E_{a, \gamma }(K)\) is a finitely generated abelian group (cf. [21, Lecture 1, Theorem 5.1]). Since the canonical Néron–Tate height is quadratic on \(E_{a, \gamma }(K)\), it induces a \({\mathbb {Z}}\)-bilinear pairing 
 , which is nondegenerate modulo \(E_{a, \gamma }(K)_{{\text {tors}}}\) (cf. [19, Chapter III, Theorem 4.3]). We can then define the Néron–Tate regulator of \(E_{a, \gamma }\) by
, which is nondegenerate modulo \(E_{a, \gamma }(K)_{{\text {tors}}}\) (cf. [19, Chapter III, Theorem 4.3]). We can then define the Néron–Tate regulator of \(E_{a, \gamma }\) by

for any choice of a \({\mathbb {Z}}\)-basis \(P_1, \ldots , P_r \in E_{a, \gamma }(K)\) of \(E_{a, \gamma }(K)/E_{a, \gamma }(K)_{{\text {tors}}}\). Note that we normalise  to have values in \({\mathbb {Q}}\): we may do so since, in our context, this height pairing has an interpretation as an intersection pairing on the minimal regular model of \(E_{a, \gamma }\) (see [19, Chapter III, Section 9]).
to have values in \({\mathbb {Q}}\): we may do so since, in our context, this height pairing has an interpretation as an intersection pairing on the minimal regular model of \(E_{a, \gamma }\) (see [19, Chapter III, Section 9]).
Let us also recall that the Tate–Shafarevich group of \(E_{a, \gamma }\) is defined by

see [21, Lecture 1, Section 11] for more details. In Theorem 2.5, we will see that  is finite.
is finite.
It has been conjectured by Birch, Swinnerton-Dyer and Tate that the ‘analytically defined’ quantities \(\rho (E_{a, \gamma })\) and \(L^*(E_{a, \gamma }, 1)\) have an arithmetic interpretation (see [20, Conjecture B]). Even though this conjecture is still open in general, it has been proven by Pries and Ulmer for \(E_{a, \gamma }\) in [18]. Let us state their result as follows:
Theorem 2.5
(Pries–Ulmer) For all \(\gamma \in {\mathbb {F}}_q^\times \) and all integers \(a\geqslant 1\), the elliptic curve \(E_{a, \gamma }/K\) satisfies the full Birch and Swinnerton-Dyer conjecture. That is to say,
-
The Tate–Shafarevich group
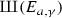 is finite.
is finite. -
The rank of \(E_{a, \gamma }(K)\) is equal to \(\rho (E_{a, \gamma })=\mathrm{ord}_{T=q^{-1}}L(E_{a, \gamma }, T)\).
-
Moreover, one has
 (13)
(13)where \(\tau (E_{a, \gamma })\) denotes the Tamagawa number of \(E_{a, \gamma }\).
Proof
We only sketch a proof and refer the interested reader to [18, Section 3] for more details. As we have seen at the beginning of this section, \(E_{a, \gamma }\) is 2-isogenous to \(E^\circ _{a, \gamma }\). Since \(E_{a, \gamma }\) and \(E^\circ _{a, \gamma }\) are linked by an isogeny of degree prime to the characteristic of K, [15, Chapter I, Theorem 7.3] implies that the BSD conjecture holds for \(E_{a, \gamma }\) if and only if it does for \(E^\circ _{a, \gamma }\). Hence Theorem 2.5 will follow if we prove that \(E^\circ _{a, \gamma }\) satisfies the BSD conjecture.
We have also shown that \(E^\circ _{a, \gamma }\) is birational to the curve  which, by construction, is given in affine coordinates by an equation of the form
which, by construction, is given in affine coordinates by an equation of the form  where \(f_\gamma \) is a certain rational function on \(\mathbb {P}^1_{/K}\) and
where \(f_\gamma \) is a certain rational function on \(\mathbb {P}^1_{/K}\) and  is a separable additive polynomial. Under these conditions, [18, Corollary 3.1.4] proves that \(E^\circ _{a, \gamma }\) satisfies the BSD conjecture.
is a separable additive polynomial. Under these conditions, [18, Corollary 3.1.4] proves that \(E^\circ _{a, \gamma }\) satisfies the BSD conjecture.
The crucial point of their proof is the following: given the specific shape of the equation of \(Z_{a, \gamma }\) to which \(E^\circ _{a, \gamma }\) is birational, the minimal regular model  over \({\mathbb {F}}_q\) of the curve \(E^\circ _{a, \gamma }/K\) is dominated by a product of curves
over \({\mathbb {F}}_q\) of the curve \(E^\circ _{a, \gamma }/K\) is dominated by a product of curves  over \({\mathbb {F}}_q\) (where
over \({\mathbb {F}}_q\) (where  is actually the curve defined in Remark 3.3). The Tate conjecture (T) asserts that the order of the pole of the zeta function of a surface \(S/{\mathbb {F}}_q\) equals the rank of the Néron–Severi group of S (see [20, Conjecture C], or [21, Lecture 2, Sections 10–13]). Conjecture (T) is proven for surfaces that are dominated by products of curves. In particular, (T) holds for the surface
is actually the curve defined in Remark 3.3). The Tate conjecture (T) asserts that the order of the pole of the zeta function of a surface \(S/{\mathbb {F}}_q\) equals the rank of the Néron–Severi group of S (see [20, Conjecture C], or [21, Lecture 2, Sections 10–13]). Conjecture (T) is proven for surfaces that are dominated by products of curves. In particular, (T) holds for the surface  . On the other hand, it is known that conjecture (T) for
. On the other hand, it is known that conjecture (T) for  is equivalent to the BSD conjecture for the generic fiber of
is equivalent to the BSD conjecture for the generic fiber of  , i.e., for the elliptic curve \(E^\circ _{a, \gamma }/K\) ([21, Lecture 2, Theorem 8.1]). Hence the result. \(\square \)
, i.e., for the elliptic curve \(E^\circ _{a, \gamma }/K\) ([21, Lecture 2, Theorem 8.1]). Hence the result. \(\square \)
In Sect. 7 we give bounds on the special value \(L^*(E_{a, \gamma }, 1)\) on the left-hand side of (13) and, in Sect. 8, we deduce from these an estimate on the asymptotically significant quantities on the right-hand side of (13). For completeness, let us recall here the following bounds (which we will need to prove Theorem 8.1).
Proposition 2.6
Let E be a nonisotrivial elliptic curve over K. Then
-
(i)
\(|E(K)_{{\mathrm{tors}}}| \ll _q 1\),
-
(ii)
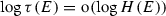 as \(H(E)\rightarrow \infty \).
as \(H(E)\rightarrow \infty \).
Proof
The first bound is an analogue for elliptic curves over  of Merel’s uniform bound on torsion for elliptic curves over \({\mathbb {Q}}\). There are several proofs of (i) and we refer the reader to [21, Lecture 1, Section 7] for a survey and a sketch of proof (by a modular method). The bound (ii) on the Tamagawa number is a consequence of [10, Theorem 1.22] in the case when E is semistable or \(p>3\). A self-contained (and elementary) proof for all elliptic curves over K can also be found in[6, Théorème 1.5.4]. \(\square \)
of Merel’s uniform bound on torsion for elliptic curves over \({\mathbb {Q}}\). There are several proofs of (i) and we refer the reader to [21, Lecture 1, Section 7] for a survey and a sketch of proof (by a modular method). The bound (ii) on the Tamagawa number is a consequence of [10, Theorem 1.22] in the case when E is semistable or \(p>3\). A self-contained (and elementary) proof for all elliptic curves over K can also be found in[6, Théorème 1.5.4]. \(\square \)
3 The sums  and the sets
and the sets 
The goal of this section is to introduce the objects which appear in the L-function of \(E_{a, \gamma }\). We fix a finite field \({\mathbb {F}}_q\) of odd characteristic and a nontrivial additive character \(\psi _q\) on \({\mathbb {F}}_q\), which we assume to take values in the cyclotomic field \({\mathbb {Q}}(\zeta _p)\). For instance, a standard choice of \(\psi _q\) is the map  where \(\zeta _p\) is a primitive \(p\hbox {th}\) root of unity and
where \(\zeta _p\) is a primitive \(p\hbox {th}\) root of unity and  is the trace map.
is the trace map.
For any finite extension \({\mathbb {F}}\) of \({\mathbb {F}}_q\), we denote by  the relative trace and we ‘lift’ \(\psi _q\) to a nontrivial additive character
the relative trace and we ‘lift’ \(\psi _q\) to a nontrivial additive character  on \({\mathbb {F}}\) by putting
on \({\mathbb {F}}\) by putting  .
.
3.1 Kloosterman sums
For a finite field \({\mathbb {F}}\) of odd characteristic p, a nontrivial additive character \(\psi \) on \({\mathbb {F}}\) with values in the cyclotomic field \({\mathbb {Q}}(\zeta _p)\), and a parameter \(\alpha \in {\mathbb {F}}^\times \), we define the Kloosterman sum by
by

As a sum of \(p\hbox {th}\) roots of unity,  is an algebraic integer in \({\mathbb {Q}}(\zeta _p)\). For our purpose, it is convenient to normalise the sum by a \(-1\) sign. Let us gather in one proposition several classical facts about the Kloosterman sums that will be useful in this article.
is an algebraic integer in \({\mathbb {Q}}(\zeta _p)\). For our purpose, it is convenient to normalise the sum by a \(-1\) sign. Let us gather in one proposition several classical facts about the Kloosterman sums that will be useful in this article.
Proposition 3.1
Let \({\mathbb {F}}, \psi \) and \(\alpha \) be as above. Then:
-
(i)
 is a totally real algebraic integer in \({\mathbb {Q}}(\zeta _p)\), i.e.,
is a totally real algebraic integer in \({\mathbb {Q}}(\zeta _p)\), i.e., 
-
(ii)
 satisfies ‘Salié’s formula’:
satisfies ‘Salié’s formula’:  (14)
(14)where \(\lambda :{\mathbb {F}}^\times \!\rightarrow \{\pm 1\}\) is the unique multiplicative character on \({\mathbb {F}}^\times \) of exact order 2 (extended by
 to the whole of \({\mathbb {F}}\)).
to the whole of \({\mathbb {F}}\)). -
(iii)
If \({\mathbb {F}}\) contains \({\mathbb {F}}_q\), one has
 .
. -
(iv)
There exist two algebraic integers
 and
and  such that
such that  and, for any finite extension
and, for any finite extension  ,
, 
The pair
 is uniquely determined by \({\mathbb {F}}, \psi , \alpha \).
is uniquely determined by \({\mathbb {F}}, \psi , \alpha \). -
(v)
 and
and  have magnitude \(|{\mathbb {F}}|^{1/2}\) in any complex embedding. In particular, in any complex embedding of \({\mathbb {Q}}(\zeta _p)\), the sum
have magnitude \(|{\mathbb {F}}|^{1/2}\) in any complex embedding. In particular, in any complex embedding of \({\mathbb {Q}}(\zeta _p)\), the sum  satisfies
satisfies  (‘Weil bound’).
(‘Weil bound’). -
(vi)
In any complex embedding of \({\mathbb {Q}}(\zeta _p)\), one has

Proof
The reader can confer [14, Chapter 5, Section 5] and [22, Section 3] for proofs of these classical results about Kloosterman sums: (i) and (iii) are easily checked; items (ii), (iv) and (v) are [14, Theorems 5.47, 5.43 and 5.44], respectively; (vi) is proven in [22, Corollary 3.2]. \(\square \)
3.2 The sums 
Assume a parameter \(\gamma \in {\mathbb {F}}_q^\times \) is given. A place \(v\ne 0, \infty \) of K with degree \(d_v\) corresponds to a monic irreducible polynomial  of degree \(d_v\), with \(B_v\ne t\). Choose a root \(\beta _v\in \overline{{\mathbb {F}}_q}{}^{\,\times }\) of \(B_v\): we claim that the value of the Kloosterman sum
of degree \(d_v\), with \(B_v\ne t\). Choose a root \(\beta _v\in \overline{{\mathbb {F}}_q}{}^{\,\times }\) of \(B_v\): we claim that the value of the Kloosterman sum  does not depend on the choice of \(\beta _v\). Indeed, given one such \(\beta _v\) the \(d_v-1\) other choices are of the form \({\beta _v}^{q^{j}}\) (with
does not depend on the choice of \(\beta _v\). Indeed, given one such \(\beta _v\) the \(d_v-1\) other choices are of the form \({\beta _v}^{q^{j}}\) (with  ) because the \(d_v\) different roots of \(B_v\) in \(\overline{{\mathbb {F}}_q}\) are all conjugate under the action of the Galois group \(\mathrm{Gal}({\mathbb {F}}_v/{\mathbb {F}}_q)\). A repeated application of Proposition 3.1 (iii) then proves the claim. Therefore the following definition makes sense:
) because the \(d_v\) different roots of \(B_v\) in \(\overline{{\mathbb {F}}_q}\) are all conjugate under the action of the Galois group \(\mathrm{Gal}({\mathbb {F}}_v/{\mathbb {F}}_q)\). A repeated application of Proposition 3.1 (iii) then proves the claim. Therefore the following definition makes sense:
Definition 3.2
Let \({\mathbb {F}}_q\) be a finite field of characteristic p, \(\psi _q\) be a nontrivial additive character on \({\mathbb {F}}_q\) and \(\gamma \in {\mathbb {F}}_q^\times \). For any place \(v\ne 0, \infty \) of  corresponding to a monic irreducible
corresponding to a monic irreducible  , we let
, we let

for any choice of \(\beta _v\in \overline{{\mathbb {F}}_q}{}^{\,\times }\) such that \(B_v(\beta _v)=0\).
Note that  depends on \({\mathbb {F}}_q\) and \(\psi _q\), but we chose not to include these in the notation for brevity.
depends on \({\mathbb {F}}_q\) and \(\psi _q\), but we chose not to include these in the notation for brevity.
For any place \(v\ne 0, \infty \), Proposition 3.1 (iv)–(v) shows that there exists a unique pair  of conjugate algebraic integers, which have magnitude \(|{\mathbb {F}}_v|^{1/2} = q^{d_v/2}\) in any complex embedding and such that
of conjugate algebraic integers, which have magnitude \(|{\mathbb {F}}_v|^{1/2} = q^{d_v/2}\) in any complex embedding and such that

In other words, we denote by  the pair of algebraic integers
the pair of algebraic integers  .
.
Remark 3.3
These sums  appear in the zeta function of a curve over \({\mathbb {F}}_q\). Namely, consider the hyperelliptic curve
appear in the zeta function of a curve over \({\mathbb {F}}_q\). Namely, consider the hyperelliptic curve  over \({\mathbb {F}}_q\) defined as a smooth projective model of the affine curve \(\wp _a(y)= x+\gamma /x\). A computation, which probably goes back to Weil, shows that the zeta function of
over \({\mathbb {F}}_q\) defined as a smooth projective model of the affine curve \(\wp _a(y)= x+\gamma /x\). A computation, which probably goes back to Weil, shows that the zeta function of  is given by
is given by

where the product is over all places \(v\ne 0, \infty \) of K whose degrees divide a (see [22]).
3.3 The sets 
Definition 3.4
For any integer \(a\geqslant 1\), we denote by  the set of places v of K, with
the set of places v of K, with  , whose degree \(d_v\) divides a. In the identification between finite places of K and monic irreducible polynomials,
, whose degree \(d_v\) divides a. In the identification between finite places of K and monic irreducible polynomials,  corresponds to the set
corresponds to the set  . Equivalently,
. Equivalently,  is the set of closed points on the multiplicative group \({\mathbb {G}}_m={\mathbb {P}}^1\smallsetminus \{0, \infty \}\) over \({\mathbb {F}}_q\) whose degree divides a.
is the set of closed points on the multiplicative group \({\mathbb {G}}_m={\mathbb {P}}^1\smallsetminus \{0, \infty \}\) over \({\mathbb {F}}_q\) whose degree divides a.
In what follows, we will frequently need the following estimates, which we record here for convenience.
Lemma 3.5
Given a finite field \({\mathbb {F}}_q\), one has
-
(i)
 for all \(a\geqslant 1\).
for all \(a\geqslant 1\). -
(ii)
 for all \(a\geqslant 1\).
for all \(a\geqslant 1\).
The involved constants are effective and depend at most on q.
Proof
For all \(n\geqslant 1\), we denote by \(\pi _q(n)\) the number of places \(v\ne 0, \infty \) of K of degree \(d_v=n\). In other words, \(\pi _q(n)\) is the number of closed points of degree n of \({\mathbb {G}}_m\) over \({\mathbb {F}}_q\).
The ‘Prime Number Theorem’ for  states that
states that  for all \(n\geqslant 1\) where the hidden constant can be given explicitly (see [2, Proposition 6.3] for example). On the other hand, it is clear from the definition that
for all \(n\geqslant 1\) where the hidden constant can be given explicitly (see [2, Proposition 6.3] for example). On the other hand, it is clear from the definition that  . The estimate of \(\pi _q(n)\) and this relation directly imply (i). From this, one easily deduces (ii). \(\square \)
. The estimate of \(\pi _q(n)\) and this relation directly imply (i). From this, one easily deduces (ii). \(\square \)
4 The L-function
With the notations introduced in the previous section, we can now state our first main result:
Theorem 4.1
Let \({\mathbb {F}}_q\) be a finite field of odd characteristic p and  . For any \(\gamma \in {\mathbb {F}}_q^\times \) and any integer \(a\geqslant 1\), consider the elliptic curve \(E_{a, \gamma }/K\) given by (6). The L-function of \(E_{a, \gamma }\) is given by
. For any \(\gamma \in {\mathbb {F}}_q^\times \) and any integer \(a\geqslant 1\), consider the elliptic curve \(E_{a, \gamma }/K\) given by (6). The L-function of \(E_{a, \gamma }\) is given by

where  are the algebraic integers associated to
are the algebraic integers associated to  (see (15) and (16)).
(see (15) and (16)).
The proof of this theorem occupies the rest of the present section. Our strategy is loosely based on the computation in [3, Section 3.2]: to give an expression of \(L(E_{a, \gamma }, T)\), we rely on an explicit ‘point-counting’ argument with character sums. This requires showing an identity for counting solutions to ‘Artin–Schreier equations’ in terms of character sums, as well as a relation between the character sums that appear in the argument and the sums  introduced above. We first give in the next subsection a proof of these two facts, and then prove Theorem 4.1 in Sect. 4.2.
introduced above. We first give in the next subsection a proof of these two facts, and then prove Theorem 4.1 in Sect. 4.2.
Remark 4.2
Before moving on to the proof of this theorem, we note the following:
1. Even though the sums  for
for  individually depend on the choice of a nontrivial additive character \(\psi _q\) on \({\mathbb {F}}_q\), the L-function
individually depend on the choice of a nontrivial additive character \(\psi _q\) on \({\mathbb {F}}_q\), the L-function  does not. Indeed, changing the choice of \(\psi _q\) amounts to permuting the factors in (17).
does not. Indeed, changing the choice of \(\psi _q\) amounts to permuting the factors in (17).
2. Note that  . Thus, as a polynomial in T, the L-function \(L(E_{a, \gamma }, T)\) has degree
. Thus, as a polynomial in T, the L-function \(L(E_{a, \gamma }, T)\) has degree  . This is consistent with the expected degree, see (11).
. This is consistent with the expected degree, see (11).
3. For any integer \(a\geqslant 1\), the L-function of the base change of \(E_{a, \gamma }\) to  admits a somewhat simpler expression. Indeed, for all \(\gamma \in {\mathbb {F}}_q^\times \) and \(a\geqslant 1\), the L-function of
admits a somewhat simpler expression. Indeed, for all \(\gamma \in {\mathbb {F}}_q^\times \) and \(a\geqslant 1\), the L-function of  is given by
is given by

where, for all \(\beta \in {\mathbb {F}}_{q^a}^\times \), \({{\textsf {kl}}}_{\beta }\) and \({{\textsf {kl}}}'_{\beta }\) are the two algebraic integers associated to the Kloosterman sum  . This follows directly from (17).
. This follows directly from (17).
4. Recall the elliptic curves \(E^\circ _{a, \gamma }\) introduced at the beginning of Sect. 2 and given by (7). Since isogenous elliptic curves share the same L-function (by [15, Chapter I, Lemma 7.1]), Theorem 4.1 also shows that the L-function of \(E^\circ _{a, \gamma }\) is given by (17).
5. It is perhaps illuminating to comment on the appearance of Kloosterman sums in \(L(E_{a, \gamma }, T)\). Choosing a prime \(\ell \ne p\), we denote by  the ith \(\ell \)-adic étale cohomology group of a smooth projective variety \(X/{\mathbb {F}}_q\). Let
the ith \(\ell \)-adic étale cohomology group of a smooth projective variety \(X/{\mathbb {F}}_q\). Let  denote the minimal regular model of \(E^\circ _{a, \gamma }\). The cohomological interpretation of L-functions of Grothendieck implies that \(L(E^\circ _{a, \gamma }, T)\) is essentially the ‘interesting part’ of the zeta function of the surface
denote the minimal regular model of \(E^\circ _{a, \gamma }\). The cohomological interpretation of L-functions of Grothendieck implies that \(L(E^\circ _{a, \gamma }, T)\) is essentially the ‘interesting part’ of the zeta function of the surface  , i.e., \(L(E^\circ _{a, \gamma }, T)\) is a factor of the characteristic polynomial of the Frobenius \({\text {Frob}}_q\) acting on
, i.e., \(L(E^\circ _{a, \gamma }, T)\) is a factor of the characteristic polynomial of the Frobenius \({\text {Frob}}_q\) acting on  .
.
By the construction of \(E^\circ _{a, \gamma }\) in Sect. 2,  is a smooth model of a quotient of
is a smooth model of a quotient of  by the action of a certain finite group \(G_a\), where
by the action of a certain finite group \(G_a\), where  is the curve introduced in Remark 3.3 (see [18, Section 7.3] for a more detailed presentation). In particular,
is the curve introduced in Remark 3.3 (see [18, Section 7.3] for a more detailed presentation). In particular,  can be seen as a subspace of
can be seen as a subspace of  , itself a subspace of
, itself a subspace of  . Hence, by Künneth’s formula, \(L(E^\circ _{a, \gamma }, T)\) divides the characteristic polynomial of \({\text {Frob}}_q\) acting on
. Hence, by Künneth’s formula, \(L(E^\circ _{a, \gamma }, T)\) divides the characteristic polynomial of \({\text {Frob}}_q\) acting on  .
.
As was noted in Remark 3.3, the numerator of the zeta function of  , i.e., the characteristic polynomial of \({\text {Frob}}_q\) acting on
, i.e., the characteristic polynomial of \({\text {Frob}}_q\) acting on  , involves Kloosterman sums
, involves Kloosterman sums  . Hence, the eigenvalues of \({\text {Frob}}_q\) acting on
. Hence, the eigenvalues of \({\text {Frob}}_q\) acting on  are products of the form
are products of the form  . Being a factor of the characteristic polynomial of \({\text {Frob}}_q\) acting on
. Being a factor of the characteristic polynomial of \({\text {Frob}}_q\) acting on  , the L-function \(L(E^\circ _{a, \gamma }, T)\) has to involve some of the products
, the L-function \(L(E^\circ _{a, \gamma }, T)\) has to involve some of the products  .
.
Working out the details of this sketchy computation could lead to a different proof of Theorem 4.1.
4.1 Point-counting and character sums
For any finite finite field \({\mathbb {F}}\) of odd characteristic, we fix a nontrivial additive character \(\psi \) on \({\mathbb {F}}\), and we denote by \(\lambda :{\mathbb {F}}^\times \rightarrow \{\pm 1\}\) the unique quadratic character on \({\mathbb {F}}^\times \), extended to the whole of \({\mathbb {F}}\) by  .
.
For any \(\gamma \in {\mathbb {F}}^\times \) and \(\beta \in {\mathbb {F}}\), we consider the following double character sum:

Up to a trivial term, we identify the character sum  as the square of a Kloosterman sum:
as the square of a Kloosterman sum:
Proposition 4.3
Notations being as above, we have

In order to prove this identity, we begin by recording the following ‘point-counting’ lemma:
Lemma 4.4
For any \(z\in {\mathbb {F}}\) and \(\gamma \in {\mathbb {F}}^\times \), consider

We have

where \(\delta _{z,0}=1\) if \(z=0\) and \(\delta _{z,0}=0\) otherwise.
Proof
Let us start by splitting the set  into the two disjoint subsets
into the two disjoint subsets  and
and  . Computing \(|X_0|\) is straightforward: if \(z=0\), any pair (u, 0) with \(u\in {\mathbb {F}}\) belongs to \(X_0\) and, if \(z\ne 0 \), no such pair belongs to
. Computing \(|X_0|\) is straightforward: if \(z=0\), any pair (u, 0) with \(u\in {\mathbb {F}}\) belongs to \(X_0\) and, if \(z\ne 0 \), no such pair belongs to  . Therefore, we have
. Therefore, we have  .
.
To count the number of elements in \(X_1\), let us introduce an auxiliary set

which we also split into two parts:  and
and  . The two maps
. The two maps
are easily checked to be well-defined and inverse to each other. Thus, we have \(|X_1|=|Y_1|\) and the lemma will be proven once we have related \(|Y_1|\) to the character sum in (18). Grouping points \((x,y)\in Y_1\) according to their x-coordinates, we obtain that:

Since  and \(|X_1|=|Y_1|\), we conclude that (18) holds. \(\square \)
and \(|X_1|=|Y_1|\), we conclude that (18) holds. \(\square \)
Proof of Proposition 4.3
We treat the case where \(\beta =0\) first: we have to prove that

This identity follows easily upon using the following equality (see [14, Theorem 5.48]):

It remains to prove the proposition in the case where \(\beta \ne 0\). If \(\beta \ne 0\), the character \(x\mapsto \psi (\beta x)\) is nontrivial, and we can expand  as a double character sum using Salié’s formula (14): we obtain that
as a double character sum using Salié’s formula (14): we obtain that

The last line follows from the first by letting  . For a given \(z\in {\mathbb {F}}\), notice that
. For a given \(z\in {\mathbb {F}}\), notice that
which is the discriminant of the quadratic equation  with unknown V. Hence, the number of solutions \(v\in {\mathbb {F}}\) to this equation is given by
with unknown V. Hence, the number of solutions \(v\in {\mathbb {F}}\) to this equation is given by

Therefore we can rewrite the inner sum (over \(u\in {\mathbb {F}}\)) in (19) as

where  is the set introduced in Lemma 4.4. In that same Lemma 4.4, we have proven that
is the set introduced in Lemma 4.4. In that same Lemma 4.4, we have proven that

On multiplying this identity by \(\psi (\beta z)\) and summing over all \(z\in {\mathbb {F}}\), we deduce from (19) that

Indeed, the sum  vanishes because \(x\mapsto \psi (\beta x)\) is nontrivial. This concludes the proof. \(\square \)
vanishes because \(x\mapsto \psi (\beta x)\) is nontrivial. This concludes the proof. \(\square \)
In the proof of Theorem 4.1, we will also need the following ‘counting lemma’:
Lemma 4.5
Let \({\mathbb {F}}_q\) be a finite field and \(\psi _q\) be a nontrivial additive character on \({\mathbb {F}}_q\). For any finite extension \({\mathbb {F}}\) of \({\mathbb {F}}_q\) and any \(z\in {\mathbb {F}}\), one has

Proof
For the duration of the proof, we write \({\mathbb {F}}={\mathbb {F}}_{q^n}\) and we let  ; note that
; note that  . The map \(\wp _a:{\mathbb {F}}_{q^n}\rightarrow {\mathbb {F}}_{q^n}\) is an \({\mathbb {F}}_{q^b}\)-linear endomorphism of \({\mathbb {F}}_{q^n}\) whose kernel is \({\mathbb {F}}_{q^b}\). In particular, the image of \(\wp _a\) must have dimension
. The map \(\wp _a:{\mathbb {F}}_{q^n}\rightarrow {\mathbb {F}}_{q^n}\) is an \({\mathbb {F}}_{q^b}\)-linear endomorphism of \({\mathbb {F}}_{q^n}\) whose kernel is \({\mathbb {F}}_{q^b}\). In particular, the image of \(\wp _a\) must have dimension  . The trace
. The trace  is a surjective \({\mathbb {F}}_{q^b}\)-linear map, so that its kernel H is a sub-\({\mathbb {F}}_{q^b}\)-vector space of \({\mathbb {F}}_{q^n}\) of dimension \(n/b -1\). Recall that
is a surjective \({\mathbb {F}}_{q^b}\)-linear map, so that its kernel H is a sub-\({\mathbb {F}}_{q^b}\)-vector space of \({\mathbb {F}}_{q^n}\) of dimension \(n/b -1\). Recall that  on \({\mathbb {F}}_{q^n}\), thus we have \({{\text {Im}}}\,\wp _a\subset H\). Since these two subspaces have the same dimension, they coincide. This shows that, for \(z\in {\mathbb {F}}_{q^n}\),
on \({\mathbb {F}}_{q^n}\), thus we have \({{\text {Im}}}\,\wp _a\subset H\). Since these two subspaces have the same dimension, they coincide. This shows that, for \(z\in {\mathbb {F}}_{q^n}\),

On the other hand, for a given \(z\in {\mathbb {F}}_{q^n}\), we notice that

because \(t={{\mathrm{tr}}}_{q^n/q^b}\) is \({\mathbb {F}}_{q^b}\)-linear. Combining the two displayed equalities, we obtain the result. \(\square \)
4.2 Proof of Theorem 4.1
We start by giving a ‘concrete’ expression for \(L(E_{a, \gamma }, T)\) in terms of the number of rational points on the reductions of \(E_{a, \gamma }\) at places of K. To that end, we introduce the following notations: for any \(n\geqslant 1\) and any \(\tau \in {\mathbb {P}}^1({\mathbb {F}}_{q^n})\), denote by \(v_\tau \) the place of K corresponding to \(\tau \) and by \((\widetilde{E_{a, \gamma }})_\tau \) the reduction of a integral minimal model of \(E_{a, \gamma }\) at \(v_\tau \) (a cubic plane curve over \({\mathbb {F}}_{{v_\tau }}\), not necessarily smooth). We then let

With these notations, we have:
Lemma 4.6
The L-function of \(E_{a, \gamma }\) is given by

Proof
Starting from definition (10) of the L-function of \(E_{a, \gamma }\), expanding the logarithm of \(L(E_{a, \gamma }, T)\) as a power series in T and rearranging terms yields the desired expression for \(L(E_{a, \gamma }, T)\). See [1, Section 2.2] or [3, Section 3.2] for more details. \(\square \)
The next step is to find a more tractable expression of the inner sums in (20). For any finite extension \({\mathbb {F}}_{q^n}\) of \({\mathbb {F}}_q\), we again let \(\lambda :{\mathbb {F}}_{q^n}^\times \rightarrow \{\pm 1\}\) be the unique nontrivial character of \({\mathbb {F}}_{q^n}^\times \) of order 2. For any \(\tau \in {\mathbb {P}}^1({\mathbb {F}}_{q^n})\), we choose an affine Weierstrass model \(y^2=f_\tau (x)\) of \((\widetilde{E_{a, \gamma }})_\tau \) (with  monic of degree 3): a standard computation then yields that
monic of degree 3): a standard computation then yields that

Since \(E_{a, \gamma }\) has split multiplicative reduction at \(\infty \) (see Proposition 2.1), we have \(A_{a, \gamma }(\infty , q^n) = 1\). Moreover, by Remark 2.2, we may choose

for any \(\tau \in {\mathbb {F}}_{q^n}\). Summing identity (21) over all \(\tau \in {\mathbb {F}}_{q^n}\) for this choice of \(f_\tau (x)\), we obtain that

We know from Lemma 4.5 that, for any \(z\in {\mathbb {F}}_{q^n}\),

Therefore, we deduce that

where \(M_{q^n}(\beta , \gamma )\) is the double character sum that we studied in Sect. 4.1 (with \({\mathbb {F}}={\mathbb {F}}_{q^n}\)). Proposition 4.3, together with our computation of \(A_{a, \gamma }(\infty , q^n)\), then leads to

For each \(\beta \in {\mathbb {F}}_{q^n}^\times \), Proposition 3.1 (iv) proves the existence of two algebraic integers  and
and  whose product is \(|{\mathbb {F}}_{q^n}|=q^n\) and whose sum is \({\text {Kl}}_{q^n}(\psi _{q^n}; \gamma \beta ^2)\). We thus have
whose product is \(|{\mathbb {F}}_{q^n}|=q^n\) and whose sum is \({\text {Kl}}_{q^n}(\psi _{q^n}; \gamma \beta ^2)\). We thus have

Hence, for all \(n\geqslant 1\), (22) can be rewritten as

For any \(\beta \in {\mathbb {F}}_{q^a}^\times \), we let  be the degree of \(\beta \) over \({\mathbb {F}}_q\). Such a \(\beta \) also belongs to \({\mathbb {F}}_{q^n}\) if and only if \(d_\beta \) divides n, i.e., if and only if \({\mathbb {F}}_{q^n}\) is an extension of \({\mathbb {F}}_{q^{d_\beta }}\). Therefore, by Proposition 3.1 (iv) one has
be the degree of \(\beta \) over \({\mathbb {F}}_q\). Such a \(\beta \) also belongs to \({\mathbb {F}}_{q^n}\) if and only if \(d_\beta \) divides n, i.e., if and only if \({\mathbb {F}}_{q^n}\) is an extension of \({\mathbb {F}}_{q^{d_\beta }}\). Therefore, by Proposition 3.1 (iv) one has

For brevity, we temporarily write

and  . We deduce from (23) that
. We deduce from (23) that

Upon multiplying both sides of this identity by  and summing over all \(n\geqslant 1 \), we arrive at
and summing over all \(n\geqslant 1 \), we arrive at

and exchanging the order of summation (setting \(m=n/d_\beta \)) leads to

Moreover, as we have explained in Sect. 3.2, for each \(\beta \in {\mathbb {F}}_{q^a}^\times \) with degree \(d_\beta \), the triple  is constant along the Galois orbit
is constant along the Galois orbit  , i.e., the closed point of \({\mathbb {G}}_m\) corresponding to \(\beta \). Consequently, for a closed point v of \({\mathbb {G}}_m\) whose degree divides a, we may define
, i.e., the closed point of \({\mathbb {G}}_m\) corresponding to \(\beta \). Consequently, for a closed point v of \({\mathbb {G}}_m\) whose degree divides a, we may define  to be
to be  for any choice of \(\beta \in v\). Each term
for any choice of \(\beta \in v\). Each term  (for \(i=1, 2, 3\)) appears \(d_v=d_\beta \) times in (24) and we may thus rewrite the sum over \(\beta \in {\mathbb {F}}_{q^a}^\times \) there as a sum over closed points of \({\mathbb {G}}_m\) whose degrees divide a:
(for \(i=1, 2, 3\)) appears \(d_v=d_\beta \) times in (24) and we may thus rewrite the sum over \(\beta \in {\mathbb {F}}_{q^a}^\times \) there as a sum over closed points of \({\mathbb {G}}_m\) whose degrees divide a:

Exponentiating this identity and replacing the  ’s by their value (see Sect. 3.2) concludes the calculation of the L-function of \(E_{a, \gamma }\) over K. \(\square \)
’s by their value (see Sect. 3.2) concludes the calculation of the L-function of \(E_{a, \gamma }\) over K. \(\square \)
4.3 Rank and special value
From the factored expression of \(L(E_{a, \gamma }, T)\) obtained in Theorem 4.1, one can deduce explicit expressions of the analytic rank \(\rho (E_{a, \gamma })\) and of the special value \(L^*(E_{a, \gamma }, 1)\) (as defined in Sect. 2.2).
Proposition 4.7
For any \(\gamma \in {\mathbb {F}}_q^\times \) and any integer \(a\geqslant 1\), we have


Proof
For each  , let
, let

be the corresponding factor of \(L(E_{a, \gamma }, T)\) (as in Theorem 4.1). The factor  has a simple zero at \(T=q^{-1}\) and neither of the other two factors of \(g_v(T)\) vanishes at \(T=q^{-1}\). Indeed, neither of
has a simple zero at \(T=q^{-1}\) and neither of the other two factors of \(g_v(T)\) vanishes at \(T=q^{-1}\). Indeed, neither of  and
and  can equal \(q^{d_v}\) since
can equal \(q^{d_v}\) since  is strictly smaller than \(2q^{d_v/2}\) by Proposition 3.1 (vi). Hence, \(g_v(T)\) has a simple zero at \(T=q^{-1}\) and we have
is strictly smaller than \(2q^{d_v/2}\) by Proposition 3.1 (vi). Hence, \(g_v(T)\) has a simple zero at \(T=q^{-1}\) and we have

which proves (24). Next, by definition (cf. (12)) of the special value \(L^*(E_{a, \gamma }, 1)\), we have

Besides, a straightforward computation yields

Combining the last two displayed identities directly leads to the desired expression for \(L^*(E_{a, \gamma }, 1)\). \(\square \)
Since the curve \(E_{a, \gamma }\) satisfies the BSD conjecture (see Theorem 2.5), Proposition 4.7 implies that  . It is worthwhile to note that the Mordell–Weil rank of \(E_{a, \gamma }(K)\) is actually independent of \(\gamma \in {\mathbb {F}}_q^\times \) [this is evident from (24)]. By Lemma 3.5 (i), we therefore have
. It is worthwhile to note that the Mordell–Weil rank of \(E_{a, \gamma }(K)\) is actually independent of \(\gamma \in {\mathbb {F}}_q^\times \) [this is evident from (24)]. By Lemma 3.5 (i), we therefore have

In particular, this yields that \(\mathrm{rank}\,E_{a, \gamma }(K)\gg _q q^a/a\), and we retrieve the following result of ‘unbounded rank’ (see [18, Corollary 2.7.3]).
Corollary 4.8
(Pries–Ulmer) Let \({\mathbb {F}}_q\) be a finite field of odd characteristic and  . For all \({\gamma \in {\mathbb {F}}_q^\times }\), the rank of \(E_{a, \gamma }(K)\) is unbounded as \(a\geqslant 1\) tends to infinity.
. For all \({\gamma \in {\mathbb {F}}_q^\times }\), the rank of \(E_{a, \gamma }(K)\) is unbounded as \(a\geqslant 1\) tends to infinity.
Let us also compare (26) to the upper bound of [2, Proposition 6.9], which states that

From Sect. 2.1, we know that  ; hence (26) shows that \(\mathrm{rank}\,E_{a, \gamma }(K)\) attains Brumer’s upper bound (up to constants depending on q).
; hence (26) shows that \(\mathrm{rank}\,E_{a, \gamma }(K)\) attains Brumer’s upper bound (up to constants depending on q).
4.4 Angles of the sums 
For any place  , we know that
, we know that  is a totally real algebraic integer with
is a totally real algebraic integer with  in any complex embedding (see items (i), (iv), (v) in Proposition 3.1). Thus, there exists a unique angle
in any complex embedding (see items (i), (iv), (v) in Proposition 3.1). Thus, there exists a unique angle  such that
such that

Note that the individual angles \(\varvec{\theta }_\gamma (v)\) depend on a choice of complex embedding \({\mathbb {Q}}(\zeta _p)\hookrightarrow {\mathbb {C}}\), but that the set  does not.
does not.
We can then rewrite the expression of \(L^*(E_{a, \gamma }, 1)\) obtained in Proposition 4.7 in terms of these angles:

In Sect. 7, we will prove upper and lower bounds on the size of \(L^*(E_{a, \gamma }, 1)\) in terms of the degree \(b(E_{a, \gamma })\) of the L-function. From the above expression, it is obvious that this size crucially depends on how the angles  are distributed in
are distributed in  when \(a\rightarrow \infty \). Therefore, we spend the next two sections describing this distribution in some detail.
when \(a\rightarrow \infty \). Therefore, we spend the next two sections describing this distribution in some detail.
5 Small angles of Kloosterman sums
In this section, we work in the following setting. Let \({\mathbb {F}}\) be a finite field of odd characteristic p, and \(\psi \) be a nontrivial additive character on \({\mathbb {F}}\). We assume that \(\psi \) takes values in \({\mathbb {Q}}(\zeta _p)\) and we pick a complex embedding \({\mathbb {Q}}(\zeta _p)\hookrightarrow {\mathbb {C}}\).
For any \(\alpha \in {\mathbb {F}}^\times \) the Kloosterman sum  is a totally real algebraic integer with
is a totally real algebraic integer with  [see Proposition 3.1 (i), (iv) and (v)]. Thus there is a well-defined angle
[see Proposition 3.1 (i), (iv) and (v)]. Thus there is a well-defined angle  associated to the Kloosterman sum by
associated to the Kloosterman sum by

Further, as was noted in Proposition 3.1 (vi), the angle  cannot equal 0 or \(\pi \) since
cannot equal 0 or \(\pi \) since  ‘never attains the Weil bound’. In this section, we investigate how close
‘never attains the Weil bound’. In this section, we investigate how close  can be to 0 and \(\pi \); we prove the following result, which may be of independent interest.
can be to 0 and \(\pi \); we prove the following result, which may be of independent interest.
Theorem 5.1
There exists an effectively computable constant  (depending at most on p) such that the following holds: for any finite field \({\mathbb {F}}\) of characteristic p, any nontrivial additive character \(\psi \) on \({\mathbb {F}}\) and any \(\alpha \in {\mathbb {F}}^\times \), one has
(depending at most on p) such that the following holds: for any finite field \({\mathbb {F}}\) of characteristic p, any nontrivial additive character \(\psi \) on \({\mathbb {F}}\) and any \(\alpha \in {\mathbb {F}}^\times \), one has

Moreover  is a suitable value of the constant.
is a suitable value of the constant.
Before we start the proof, we recall for convenience the following version of Liouville’s inequality:
Theorem 5.2
(Liouville’s inequality) Let  be a polynomial of degree N. For any algebraic number \(z\in {\overline{\mathbb {Q}}}\), let \(D_z\) be its degree over \({\mathbb {Q}}\) and h(z) denote its logarithmic absolute Weil height.
be a polynomial of degree N. For any algebraic number \(z\in {\overline{\mathbb {Q}}}\), let \(D_z\) be its degree over \({\mathbb {Q}}\) and h(z) denote its logarithmic absolute Weil height.
Either \(P(z)= 0\) or

in any complex embedding of \({\mathbb {Q}}(z)\), where \(\Vert P\Vert _1\) is the sum of the absolute values of the coefficients of P.
See the introduction of [16] and the proof of Lemma 5 in loc.cit. for this version and its proof.
Proof of Theorem 5.1
We let \({\mathbb {F}}, \psi \) and \(\alpha \) be as in the statement of Theorem 5.1; we choose an embedding \({\overline{\mathbb {Q}}}\hookrightarrow {\mathbb {C}}\) which is compatible with our choice of \({\mathbb {Q}}(\zeta _p)\hookrightarrow {\mathbb {C}}\). By Proposition 3.1 (iv), we can write

for two algebraic integers  of magnitude \(|{\mathbb {F}}|^{1/2}\) whose product is \(|{\mathbb {F}}|\). In the given complex embedding,
of magnitude \(|{\mathbb {F}}|^{1/2}\) whose product is \(|{\mathbb {F}}|\). In the given complex embedding,  and
and  are complex conjugates: one of them thus has nonnegative imaginary part, i.e., equals
are complex conjugates: one of them thus has nonnegative imaginary part, i.e., equals  by Proposition 3.1 (v). Without loss of generality, we may and do assume that it is
by Proposition 3.1 (v). Without loss of generality, we may and do assume that it is  . Consider the algebraic number
. Consider the algebraic number  and write
and write  . We have
. We have
Lemma 5.3
The ratio z has degree \(D_z\leqslant 2(p-1)\) and height \(h(z)\leqslant \log \sqrt{|{\mathbb {F}}|}\). Moreover, \(z\ne \pm 1\).
Proof
By Proposition 3.1 (i) and (iv), we know that  , and, further, that
, and, further, that  and
and  are the two roots of
are the two roots of  ; it is then clear that the degree of
; it is then clear that the degree of  over \({\mathbb {Q}}\) is
over \({\mathbb {Q}}\) is  . We thus have
. We thus have

as was to be shown. Since  , we infer that \(|z|=1\) in any complex embedding of L, therefore the archimedean places of L do not contribute to h(z). We deduce further that z is a unit at all finite places of L which are not above p; hence these places do not contribute to h(z) either. It remains to consider finite places \({\mathfrak {P}}\) of L lying above p: since both
, we infer that \(|z|=1\) in any complex embedding of L, therefore the archimedean places of L do not contribute to h(z). We deduce further that z is a unit at all finite places of L which are not above p; hence these places do not contribute to h(z) either. It remains to consider finite places \({\mathfrak {P}}\) of L lying above p: since both  and
and  are algebraic integers, the contribution of \(\mathfrak {P}\) to h(z) is
are algebraic integers, the contribution of \(\mathfrak {P}\) to h(z) is  . By summing these, we conclude that \(h(z)\leqslant \frac{1}{2}\log |{\mathbb {F}}|\).
. By summing these, we conclude that \(h(z)\leqslant \frac{1}{2}\log |{\mathbb {F}}|\).
Finally, Proposition 3.1 (vi) shows that  , and the last assertion easily follows. \(\square \)
, and the last assertion easily follows. \(\square \)
Upon applying Liouville’s inequality (28) to z with \(P=X\pm 1\) and using Lemma 5.3, we obtain that

Noting that the the graph of \(t\mapsto |{\sin t}|\) lies below its tangents at \(t=\pi /2\), one sees that  for all
for all  . From this inequality and the lower bound (29) on \(|z-1|\), we deduce that
. From this inequality and the lower bound (29) on \(|z-1|\), we deduce that

where  . To get the lower bound on
. To get the lower bound on  , we use the lower bound on \(|z+1|\) in (29) and the inequality stating that
, we use the lower bound on \(|z+1|\) in (29) and the inequality stating that  for all
for all  . This concludes the proof of Theorem 5.1. \(\square \)
. This concludes the proof of Theorem 5.1. \(\square \)
Let us deduce two corollaries from Theorem 5.1. The first one can be viewed as a slight improvement on the Weil bound on Kloosterman sums (i.e., an effective version of Proposition 3.1 (vi)):
Corollary 5.4
For any finite field \({\mathbb {F}}\) of characteristic \(p\geqslant 3\), any nontrivial additive character \(\psi \) on \({\mathbb {F}}\) and any \(\alpha \in {\mathbb {F}}^\times \), we have

where  is the constant in Theorem 5.1.
is the constant in Theorem 5.1.
Proof
By construction, we have  . Theorem 5.1 implies that
. Theorem 5.1 implies that  lies in \([Q, \pi -Q]\) with
lies in \([Q, \pi -Q]\) with  . The corollary follows from the elementary observation that
. The corollary follows from the elementary observation that

\(\square \)
The second corollary is more central to our study of the size of \(L^*(E_{a, \gamma }, 1)\), cf. Sect. 7.1.
Corollary 5.5
Let \({\mathbb {F}}_q\) be a finite field of characteristic \(p\geqslant 3\) equipped with a nontrivial additive character \(\psi _q\). For any \(\gamma \in {\mathbb {F}}_q^\times \) and any integer \(a\geqslant 1\), the angles \(\varvec{\theta }_{\gamma }(v)\) for \(v\in P_{q}(a)\) defined in Sect. 4.4 satisfy

where  is the constant in Theorem 5.1.
is the constant in Theorem 5.1.
Proof
For all  , the residue field \({\mathbb {F}}_v\) is a subfield of \({\mathbb {F}}_{q^a}\) and we may choose \(\beta _v\) as in Sect. 3.2. Upon noting that \(|{\mathbb {F}}_v|\leqslant q^a\), the corollary immediately follows from Theorem 5.1 applied to \({\mathbb {F}}={\mathbb {F}}_{v}\),
, the residue field \({\mathbb {F}}_v\) is a subfield of \({\mathbb {F}}_{q^a}\) and we may choose \(\beta _v\) as in Sect. 3.2. Upon noting that \(|{\mathbb {F}}_v|\leqslant q^a\), the corollary immediately follows from Theorem 5.1 applied to \({\mathbb {F}}={\mathbb {F}}_{v}\),  and \(\alpha =\gamma \beta _v^2\). \(\square \)
and \(\alpha =\gamma \beta _v^2\). \(\square \)
6 Distribution of the sums 
In this section, we fix again a finite field \({\mathbb {F}}_q\) of odd characteristic p, an element \(\gamma \in {\mathbb {F}}_q^\times \) and a nontrivial additive character \(\psi _q\) on \({\mathbb {F}}_q\) with values in \({\mathbb {Q}}(\zeta _p)\). For any finite extension \({\mathbb {F}}/{\mathbb {F}}_q\), we continue denoting by  the composition
the composition  of \(\psi _q\) with the trace
of \(\psi _q\) with the trace  .
.
Loosely speaking, we show that, as \(a\rightarrow \infty \), the numbers  with \(v\in P_q(a)\) (see Sect. 3.2) are asymptotically distributed in \([-2, 2]\) as ‘the traces of random matrices in \({\text {SU}}(2, {\mathbb {C}})\)’. In order to make this statement more precise and to prove it, we begin by introducing the necessary notations and notions.
with \(v\in P_q(a)\) (see Sect. 3.2) are asymptotically distributed in \([-2, 2]\) as ‘the traces of random matrices in \({\text {SU}}(2, {\mathbb {C}})\)’. In order to make this statement more precise and to prove it, we begin by introducing the necessary notations and notions.
Choose a prime number \(\ell \ne p\), an algebraic closure \(\overline{{\mathbb {Q}}_\ell }\) of \({\mathbb {Q}}_\ell \), an embedding \({\overline{\mathbb {Q}}}\hookrightarrow \overline{{\mathbb {Q}}_\ell }\), and a field isomorphism \(\overline{{\mathbb {Q}}_\ell }\simeq {\mathbb {C}}\). Through this isomorphism, we view \(\psi _q\) as a \(\overline{{\mathbb {Q}}_\ell }\)-valued additive character on \({\mathbb {F}}_q\).
We fix a separable closure \(K^{{\text {sep}}}\) of K. The set of places \(v\ne 0, \infty \) of K can be identified with the set of closed points of the multiplicative group  over \({\mathbb {F}}_q\). For a finite extension \({\mathbb {F}}/{\mathbb {F}}_q\) and a point \(\alpha \in {\mathbb {G}}_m({\mathbb {F}})\), we denote by
over \({\mathbb {F}}_q\). For a finite extension \({\mathbb {F}}/{\mathbb {F}}_q\) and a point \(\alpha \in {\mathbb {G}}_m({\mathbb {F}})\), we denote by  the geometric Frobenius of \({\mathbb {G}}_m\) at \(\alpha \), which we view as a conjugacy class in the profinite group \(\mathrm{Gal}(K^{{\text {sep}}}/K)\). For any closed point v of \({\mathbb {G}}_m\), we choose \(\beta _v\in v\) and we let
the geometric Frobenius of \({\mathbb {G}}_m\) at \(\alpha \), which we view as a conjugacy class in the profinite group \(\mathrm{Gal}(K^{{\text {sep}}}/K)\). For any closed point v of \({\mathbb {G}}_m\), we choose \(\beta _v\in v\) and we let  .
.
6.1 Angles of Kloosterman sums
Let us start by redefining the angles  from a representation-theoretic point of view. The reader is referred to [11, Chapter 3] or [4] for more detailed presentations.
from a representation-theoretic point of view. The reader is referred to [11, Chapter 3] or [4] for more detailed presentations.
In [11, Chapter 4], Katz has constructed a lisse \(\overline{{\mathbb {Q}}_\ell }\)-sheaf  on \({\mathbb {G}}_m\) whose Frobenius traces are Kloosterman sums (
on \({\mathbb {G}}_m\) whose Frobenius traces are Kloosterman sums ( is the so-called Kloosterman sheaf). Taking a suitable Tate twist, one obtains a lisse \(\overline{{\mathbb {Q}}_\ell }\)-sheaf
is the so-called Kloosterman sheaf). Taking a suitable Tate twist, one obtains a lisse \(\overline{{\mathbb {Q}}_\ell }\)-sheaf  of rank 2 on \({\mathbb {G}}_m\) which is pure of weight 0.
of rank 2 on \({\mathbb {G}}_m\) which is pure of weight 0.
By definition,  ‘is’ a continuous 2-dimensional \(\overline{{\mathbb {Q}}_\ell }\)-representation
‘is’ a continuous 2-dimensional \(\overline{{\mathbb {Q}}_\ell }\)-representation
which is unramified outside \(\{0, \infty \}\) and which satisfies the following. For all places \(v\ne 0, \infty \) of K, the eigenvalues of \(\kappa ({\text {Fr}}_v)\) have magnitudeFootnote 4 1 (‘pure of weight 0’) and the trace of \(\kappa ({\text {Fr}}_v)\) is

where \(\beta _v\in {\mathbb {G}}_m(\overline{{\mathbb {F}}_q})\) is a choice of element in the closed point of \({\mathbb {G}}_m\) corresponding to v, as in Sect. 3.2. Note that, even though \({\text {Fr}}_v\) is only defined up to conjugation in \(\mathrm{Gal}(K^{{\text {sep}}}/K)\), the trace \(\text {Trace}(\kappa (\text {Fr}_v))\) is well-defined.
Katz has shown that the image of \(\mathrm{Gal}(K^{{\text {sep}}}/K)\) under \(\kappa \) is contained in \({\text {SL}}(2, \overline{{\mathbb {Q}}_\ell })\) (in other words, the representation \(\kappa \) has trivial determinant, see [11, Chapter 11]). Via the chosen isomorphism \(\overline{{\mathbb {Q}}_\ell }\simeq {\mathbb {C}}\), we may view \(\kappa (\mathrm{Gal}(K^{{\text {sep}}}/K))\) as a subgroup of \({\text {SL}}(2, {\mathbb {C}})\). The special unitary group  is a maximal compact subgroup of \({\text {SL}}(2, {\mathbb {C}})\) and, since \({\text {SL}}(2, {\mathbb {C}})\) is semisimple, such an H is uniquely determined up to conjugation. For any place \(v\ne 0, \infty \), let \(\kappa ({\text {Fr}}_v)^{\text {s.s.}}\) be the semisimplification of \(\kappa ({\text {Fr}}_v)\): the closure of the subgroup of \({\text {SL}}(2, {\mathbb {C}})\) generated by all the \(\kappa ({\text {Fr}}_v)^{\text {s.s.}}\) is compact and thus, up to conjugation in \({\text {SL}}(2, {\mathbb {C}})\), lies in H.
is a maximal compact subgroup of \({\text {SL}}(2, {\mathbb {C}})\) and, since \({\text {SL}}(2, {\mathbb {C}})\) is semisimple, such an H is uniquely determined up to conjugation. For any place \(v\ne 0, \infty \), let \(\kappa ({\text {Fr}}_v)^{\text {s.s.}}\) be the semisimplification of \(\kappa ({\text {Fr}}_v)\): the closure of the subgroup of \({\text {SL}}(2, {\mathbb {C}})\) generated by all the \(\kappa ({\text {Fr}}_v)^{\text {s.s.}}\) is compact and thus, up to conjugation in \({\text {SL}}(2, {\mathbb {C}})\), lies in H.
We denote by \(H^\natural \) the set of conjugacy classes of H and we equip \(H^\natural \) with the measure \(\mu ^\natural \) obtained as the direct image of the Haar measure on H normalised to have total mass 1. The trace of \(M\in H\) (or of any element in its conjugacy class) is the sum of two conjugate complex number of magnitude 1, so it is a real number in \([-2,2]\). More precisely, a matrix \(M\in H\) is conjugate (in H) to a diagonal matrix  for some unique
for some unique  and \({{\mathrm{Trace}}}\, M = 2\cos \theta _M\). Hence, the set \(H^\natural \) endowed with \(\mu ^\natural \) can be identified with the interval
and \({{\mathrm{Trace}}}\, M = 2\cos \theta _M\). Hence, the set \(H^\natural \) endowed with \(\mu ^\natural \) can be identified with the interval  endowed with the Sato–Tate measure
endowed with the Sato–Tate measure  (see [11, Chapter 13]). We identify any angle \(\theta \in [0, \pi ]\) with the conjugacy class of
(see [11, Chapter 13]). We identify any angle \(\theta \in [0, \pi ]\) with the conjugacy class of  , which we also denote by the same symbol \(\theta \).
, which we also denote by the same symbol \(\theta \).
We are now ready to (re)define angles of Kloosterman sums. For any finite extension \({\mathbb {F}}/{\mathbb {F}}_q\) and any \(\alpha \in {\mathbb {G}}_m({\mathbb {F}})\), the semisimplification of  is \({\text {SL}}(2,{\mathbb {C}})\)-conjugate to an element of H, and we can define
is \({\text {SL}}(2,{\mathbb {C}})\)-conjugate to an element of H, and we can define  to be the conjugacy class in H of this element. In the identification between \(H^\natural \) and
to be the conjugacy class in H of this element. In the identification between \(H^\natural \) and  , this gives us a well-defined angle
, this gives us a well-defined angle  , see [11, Section 3.3].
, see [11, Section 3.3].
For any finite extension \({\mathbb {F}}/{\mathbb {F}}_q\) and any \(\alpha \in {\mathbb {G}}_m({\mathbb {F}})\), we thus have

so that the new definition of  coincides with the one given at the beginning of Sect. 5.
coincides with the one given at the beginning of Sect. 5.
Definition 6.1
Fix a finite field \({\mathbb {F}}_q\) equipped with a nontrivial additive character \(\psi _q\) and \(\gamma \in {\mathbb {F}}_q^\times \). For any place \(v\ne 0, \infty \) of K, let \(\varvec{\theta }_\gamma (v)\) be the angle associated to the Kloosterman sum  by the construction above. In other words, we put
by the construction above. In other words, we put  .
.
Remark 6.2
Let \({\mathbb {F}}\) be the finite extension of \({\mathbb {F}}_q\) with  . For any \(\alpha \in {\mathbb {G}}_m({\mathbb {F}})\), let w be the closed point of \({\mathbb {G}}_m\) corresponding to \(\alpha \) (that is to say, w is the \(\mathrm{Gal}(\overline{{\mathbb {F}}_q}/{\mathbb {F}}_q)\)-orbit of \(\alpha \)). The residue field \({\mathbb {F}}_w\) is then a subfield of \({\mathbb {F}}\) and
. For any \(\alpha \in {\mathbb {G}}_m({\mathbb {F}})\), let w be the closed point of \({\mathbb {G}}_m\) corresponding to \(\alpha \) (that is to say, w is the \(\mathrm{Gal}(\overline{{\mathbb {F}}_q}/{\mathbb {F}}_q)\)-orbit of \(\alpha \)). The residue field \({\mathbb {F}}_w\) is then a subfield of \({\mathbb {F}}\) and  as conjugacy classes in \(\mathrm{Gal}(K^{{\text {sep}}}/K)\). Therefore
as conjugacy classes in \(\mathrm{Gal}(K^{{\text {sep}}}/K)\). Therefore  and
and

In particular, when v is a closed point of \({\mathbb {G}}_m\) whose degree divides a and when \(\beta _v\in v\), by our definition  , the above relation reads
, the above relation reads

6.2 Statement of results
Denote by \(\mu _{\mathrm{ST}}\) the Sato–Tate measure \(\frac{2}{\pi }\sin ^2\theta {\,\text {d}}\theta \) on  . A sequence of Borel measures
. A sequence of Borel measures  on
on  is said to converge weak-\(*\)to\(\mu _{\mathrm{ST}}\) if, for every continuous \({\mathbb {C}}\)-valued function f on
is said to converge weak-\(*\)to\(\mu _{\mathrm{ST}}\) if, for every continuous \({\mathbb {C}}\)-valued function f on  , the sequence of integrals \(\int _{[0, \pi ]} f{\,\text {d}}\mu _i\) converges to \(\int _{[0,\pi ]}f{\,\text {d}}\mu _{\mathrm{ST}}\) as \(i\rightarrow \infty \).
, the sequence of integrals \(\int _{[0, \pi ]} f{\,\text {d}}\mu _i\) converges to \(\int _{[0,\pi ]}f{\,\text {d}}\mu _{\mathrm{ST}}\) as \(i\rightarrow \infty \).
Our results concern two sequences of probability measures that we now introduce.
Definition 6.3
We fix a finite field \({\mathbb {F}}_q\) of characteristic \(p\geqslant 3\), a nontrivial additive character \(\psi _q\) on \({\mathbb {F}}_q\) and \(\gamma \in {\mathbb {F}}_q^\times \). For an integer \(a\geqslant 1\), we again denote by  the set of closed points of \({\mathbb {G}}_m\) whose degrees divide a. For all integers \(a\geqslant 1\), we define
the set of closed points of \({\mathbb {G}}_m\) whose degrees divide a. For all integers \(a\geqslant 1\), we define

where  denotes the Dirac delta measure at
denotes the Dirac delta measure at  . For all finite extensions \({\mathbb {F}}/{\mathbb {F}}_q\), we also define
. For all finite extensions \({\mathbb {F}}/{\mathbb {F}}_q\), we also define

In what follows, we abbreviate \(\nu {({\mathbb {F}}_q, \psi _q, \gamma ; a)}\) by \(\nu _a\) and \(\xi {({\mathbb {F}}_q, \psi _q, \gamma ; {\mathbb {F}}_{q^a})}\) by \(\xi _a\).
Clearly, both \(\nu _a\) and \(\xi _a\) are Borel measures on  with total mass 1. It follows from the discussion in Sect. 6.1 that we may view \(\nu _a\) and \(\xi _a\) as measures on \(H^\natural \); we use both points of view interchangeably. Moreover, we note that \(\xi _a\) is also given byFootnote 5
with total mass 1. It follows from the discussion in Sect. 6.1 that we may view \(\nu _a\) and \(\xi _a\) as measures on \(H^\natural \); we use both points of view interchangeably. Moreover, we note that \(\xi _a\) is also given byFootnote 5

where \(\tfrac{a}{\deg v}\cdot \varvec{\theta }_{\gamma }(v)\) is to be understood modulo \(\pi \) (see Remark 6.2).
Remark 6.4
In terms of the measure \(\nu _a\), Corollary 5.5 can be reinterpreted as follows: given \({\mathbb {F}}_q, \psi _q\) and \(\gamma \) as above, for any \(a\geqslant 1\) the support of the probability measure \(\nu _a\) on  is contained in
is contained in  .
.
We can now state the two main results of this section. First we show that the angles  are asymptotically equidistributed with respect to the Sato–Tate measure as \(a\rightarrow \infty \). Namely,
are asymptotically equidistributed with respect to the Sato–Tate measure as \(a\rightarrow \infty \). Namely,
Theorem 6.5
Assume we are given a datum \({\mathbb {F}}_q, \psi _q, \gamma \) as above. Then the sequences  and
and  of Borel probability measures both converge weak-\(*\) to the Sato–Tate measure \(\mu _{\mathrm{ST}}\) when \(a\rightarrow \infty \).
of Borel probability measures both converge weak-\(*\) to the Sato–Tate measure \(\mu _{\mathrm{ST}}\) when \(a\rightarrow \infty \).
This statement concretely means that, for all continuous functions f on  , we have
, we have

It will be proven in Propositions 6.7 and 6.9 by a suitable adaptation of the arguments in [11, Chapter 3] and [5, Section 2].
In the course of proving Theorem 7.3, we will need a more effective version of (31): indeed, we require an estimate of the rate at which \(\int _{[0,\pi ]} f {\,\text {d}}\nu _a\) converges to \(\int _{[0, \pi ]} f{\,\text {d}}\mu _{\mathrm{ST}}\), at least for a smaller class of functions f. This is the object of the second result in this section:
Theorem 6.6
Assume we are given a datum \({\mathbb {F}}_q, \psi _q, \gamma \) as above. For any continuously differentiable function g on \([0,\pi ]\), we have

This will follow from the proof of Theorem 6.5 coupled with tools from distribution theory (see [17]).
The proofs will also show that the constants in Theorems 6.5 and 6.6 are effective and depend at most on q (and neither on the choice of \(\psi _q\) nor on the value of \(\gamma \in {\mathbb {F}}_q^\times \)).
6.3 Equidistribution of \(\varvec{\theta }_\gamma (v)\)’s
In this subsection, we prove Theorem 6.5 in two steps (Propositions 6.7 and 6.9). Let us first make a reduction (see [11, Sections 3.4, 3.5] for more details). We need to show that, for all complex-valued continuous functions f on  , we have
, we have
Since \(H={\text {SU}}(2, {\mathbb {C}})\) is compact and since  can be identified with \(H^\natural \), there is a natural correspondence between the space of continuous functions on
can be identified with \(H^\natural \), there is a natural correspondence between the space of continuous functions on  and the space
and the space  of continuous central functions on H. When
of continuous central functions on H. When  is endowed with the topology of the supremum norm, the Peter–Weyl theorem asserts that the vector subspace generated by characters of irreducible finite-dimensional representations of H is dense in
is endowed with the topology of the supremum norm, the Peter–Weyl theorem asserts that the vector subspace generated by characters of irreducible finite-dimensional representations of H is dense in  . By density, Theorem 6.5 will follow if we can show that, for all irreducible finite-dimensional representations \(\Lambda \) of H,
. By density, Theorem 6.5 will follow if we can show that, for all irreducible finite-dimensional representations \(\Lambda \) of H,
If \(\Lambda _0\) is trivial, \({\mathrm{Trace}}\Lambda _0\) is the trivial character \(\varvec{1}\) on H and the above limits clearly hold because the measures \(\nu _a\), \(\xi _a\) and \(\mu ^\natural \) on \(H^\natural \) all have total mass 1. Now, when \(\Lambda \) is a nontrivial irreducible finite-dimensional representation of H, \(\int _{H^\natural }{{\mathrm{Trace}}}\,\Lambda {\,\text {d}}\mu ^\natural \) on the right-hand side vanishes by orthogonality of characters. Hence, the proof of Theorem 6.5 reduces to that of the following statementFootnote 6: for any nontrivial irreducible finite-dimensional representation\(\Lambda \)of\(H={\text {SU}}(2, {\mathbb {C}})\), one has
We actually prove slightly more precise estimates.
Proposition 6.7
Fix \({\mathbb {F}}_q, \psi _q\) and \(\gamma \in {\mathbb {F}}_q^\times \) as in Sect. 6.2. Let \(\Lambda \) be a nontrivial irreducible representation of \(H=\mathrm{SU}(2, {\mathbb {C}})\). For all \(a\geqslant 1\), one has
Proof
For any finite extension \({\mathbb {F}}/{\mathbb {F}}_q\), notice that

where  denotes the unique nontrivial character of order 2 on \({\mathbb {F}}^\times \). Therefore, one has
denotes the unique nontrivial character of order 2 on \({\mathbb {F}}^\times \). Therefore, one has

For any multiplicative character \(\chi \) on \({\mathbb {F}}_q^\times \) and any finite extension \({\mathbb {F}}/{\mathbb {F}}_q\), we denote by  the character on \({\mathbb {F}}^\times \) ‘lifted’ by the norm
the character on \({\mathbb {F}}^\times \) ‘lifted’ by the norm  . The crucial input is a result of Fu and Liu (see [5, Lemma 4]) who have proven that, for every multiplicative character \(\chi \) on \({\mathbb {F}}_q\), one has
. The crucial input is a result of Fu and Liu (see [5, Lemma 4]) who have proven that, for every multiplicative character \(\chi \) on \({\mathbb {F}}_q\), one has
Applying this inequality successively to both multiplicative characters on \({\mathbb {F}}_q\) whose order divides 2, we deduce from (33) that

Therefore, for any finite extension \({\mathbb {F}}/{\mathbb {F}}_q\), we have proven that

Specialising to \({\mathbb {F}}={\mathbb {F}}_{q^a}\) yields the desired estimate since \(\xi _a=\xi {({\mathbb {F}}_q, \psi _q, \gamma ; {\mathbb {F}}_{q^a})}\). \(\square \)
Remark 6.8
Let us suggest an alternative way of proving Proposition 6.7. Denote again by  the Kloosterman sheaf (suitably twisted to be pure of weight 0) whose existence was proven by Katz. For a given \(\gamma \in {\mathbb {F}}_q^\times \), consider the morphism \(f:{\mathbb {G}}_m\rightarrow {\mathbb {G}}_m\) given by \(\beta \mapsto \gamma \beta ^2\), and put
the Kloosterman sheaf (suitably twisted to be pure of weight 0) whose existence was proven by Katz. For a given \(\gamma \in {\mathbb {F}}_q^\times \), consider the morphism \(f:{\mathbb {G}}_m\rightarrow {\mathbb {G}}_m\) given by \(\beta \mapsto \gamma \beta ^2\), and put  . Then
. Then  is again a lisse \(\overline{{\mathbb {Q}}_\ell }\)-sheaf of rank 2 on \({\mathbb {G}}_m\) which is pure of weight 0. Moreover, for all places \(v\ne 0, \infty \) of K, one has
is again a lisse \(\overline{{\mathbb {Q}}_\ell }\)-sheaf of rank 2 on \({\mathbb {G}}_m\) which is pure of weight 0. Moreover, for all places \(v\ne 0, \infty \) of K, one has

In the case where \(\gamma =1\), [5, Remark 1] sketches a proof that  satisfies the assumptions of [11, Sections 3.1–3.3]. One could therefore prove Proposition 6.7 by making use of [11, Section 3.6]. This argument should carry over, mutatis mutandis, to the case of an arbitrary \(\gamma \ne 0\).
satisfies the assumptions of [11, Sections 3.1–3.3]. One could therefore prove Proposition 6.7 by making use of [11, Section 3.6]. This argument should carry over, mutatis mutandis, to the case of an arbitrary \(\gamma \ne 0\).
To complete the proof of Theorem 6.5, it remains to show that  also converges (weak-\(*\)) to \(\mu _{\mathrm{ST}}\).
also converges (weak-\(*\)) to \(\mu _{\mathrm{ST}}\).
Proposition 6.9
Fix a datum \({\mathbb {F}}_q, \psi _q\) and \(\gamma \in {\mathbb {F}}_q^\times \) as in Sect. 6.2. Let \(\Lambda \) be a nontrivial irreducible representation of \(H=\mathrm{SU}(2, {\mathbb {C}})\). For all \(a\geqslant 1\), one has

Proof
Consider the measure  on \(H^\natural \) (or
on \(H^\natural \) (or  ). By (30), we have
). By (30), we have

Let  , where \(\pi _q(b)\) denotes the number of places \(v\ne 0, \infty \) of K with \(\deg v= b\). As is clear from the right-most expression above, \(\omega _a\) is a sum of \(N_a\) Dirac delta measures supported at points of \(H^\natural \). By straightforward estimates using the ‘Prime Number Theorem’ for \({\mathbb {F}}_q[t]\) (see Lemma 3.5), one can show that
, where \(\pi _q(b)\) denotes the number of places \(v\ne 0, \infty \) of K with \(\deg v= b\). As is clear from the right-most expression above, \(\omega _a\) is a sum of \(N_a\) Dirac delta measures supported at points of \(H^\natural \). By straightforward estimates using the ‘Prime Number Theorem’ for \({\mathbb {F}}_q[t]\) (see Lemma 3.5), one can show that

Since, for any \(z\in K\), the eigenvalues of \(\Lambda (z)\) all have magnitude 1, we have \({|{{\mathrm{Trace}}}\,\Lambda (z)|\leqslant \dim \Lambda }\). Hence we find that

Now we notice that

where  and
and  , again by Lemma 3.5. Therefore, combining (32) in the previous proposition and inequality (34), we deduce that
, again by Lemma 3.5. Therefore, combining (32) in the previous proposition and inequality (34), we deduce that

This concludes the proof of the proposition and, by the discussion at the beginning of this subsection, that of Theorem 6.5. \(\square \)
6.4 Effectivity of the equidistribution
The nontrivial irreducible representations of \(H={\text {SU}}(2, {\mathbb {C}})\) are exactly the symmetric powers \({\text {Symm}}^n({{\text {std}}})\) of the standard representation \({{\text {std}}}:H\hookrightarrow {\text {GL}}(2, {\mathbb {C}})\). Moreover, if \(\Lambda _n = {\text {Symm}}^n({{\text {std}}})\) for some \({n\geqslant 1}\), then \(\Lambda _n\) has dimension \(n+1\) and the trace function \({\mathrm{Trace}}\,\Lambda _n:H^\natural \rightarrow {\mathbb {R}}\) corresponds to the mapFootnote 7 in the identification of \(H^\natural \) with
in the identification of \(H^\natural \) with  .
.
It is convenient to denote by  , the ‘\(n\hbox {th}\) moment’ of
, the ‘\(n\hbox {th}\) moment’ of  , i.e.,
, i.e.,

With this notation, the result of Proposition 6.9 can be rewritten as follows. Given a datum \({\mathbb {F}}_q, \psi _q,\gamma \in {\mathbb {F}}_q^\times \) as in Sect. 6.2 and an integer \(n\geqslant 1\), one has

To measure ‘how far’ from being perfectly equidistributed with respect to the Sato–Tate distribution the angles \(\varvec{\theta }_{\gamma }(v)\) are, it is customary to introduce the stardiscrepancy :
:

where the supremums are taken over  . This definition is the direct analogue of the star discrepancy for the uniform measure (see [12, Chapter 2, Section 1]) in the context of \(\mu _{\mathrm{ST}}\). The interest of finding good upper bounds on
. This definition is the direct analogue of the star discrepancy for the uniform measure (see [12, Chapter 2, Section 1]) in the context of \(\mu _{\mathrm{ST}}\). The interest of finding good upper bounds on  is exemplified by the following result, which is similar to Koksma’s inequality (see [12, Chapter 2, Theorem 5.1]).
is exemplified by the following result, which is similar to Koksma’s inequality (see [12, Chapter 2, Theorem 5.1]).
Theorem 6.10
(Niederreiter) For any function  of total bounded variation
of total bounded variation  , one has
, one has

This statement is essentiallyFootnote 8 in [17, Corollary 2], the proof of which is based on an adaptation to the Sato–Tate context of the proof of Koksma’s inequality for the uniform measure (see [12, p. 143]).
Note that, for a continuously differentiable function g,  . Therefore, Theorem 6.6 follows directly from Theorem 6.10 and the following:
. Therefore, Theorem 6.6 follows directly from Theorem 6.10 and the following:
Proposition 6.11
The star discrepancy of  is bounded by
is bounded by

Proof
Niederreiter has proven in [17] a variant of the ‘Erdős–Turán inequality’ in the Sato–Tate context. Just as the Erdős–Turán theorem (see [12, Chapter 2, Theorem 2.5]), his result gives an upper bound on  in terms of ‘exponential sums’, here the moments
in terms of ‘exponential sums’, here the moments  defined in (35). Let us state [17, Lemma 3] as followsFootnote 9: for any odd positive integer N, we have
defined in (35). Let us state [17, Lemma 3] as followsFootnote 9: for any odd positive integer N, we have

As was noted in (36), Proposition 6.9 reads:  . Also remark that
. Also remark that

Hence, for all odd \(N\geqslant 1\), (37) leads to  . Choosing N to be the largest odd integer smaller than \((a^{-1}q^{a/2})^{1/2}\), we have \(N^{-1}\ll a^{1/2}q^{-a/4}\) and we obtain the desired bound. \(\square \)
. Choosing N to be the largest odd integer smaller than \((a^{-1}q^{a/2})^{1/2}\), we have \(N^{-1}\ll a^{1/2}q^{-a/4}\) and we obtain the desired bound. \(\square \)
7 Bounds on the special value
By Definition 2.3, the special value \(L^*(E_{a, \gamma }, 1)\) is the value at \(T=q^{-1}\) of a polynomial with integral coefficients of degree \(\leqslant b(E_{a, \gamma })\). Therefore, \(L^*(E_{a, \gamma }, 1)\) is of the form \(n/q^{b(E_{a, \gamma })}\) for some integer \(n\geqslant 1\), and we deduce the following ‘trivial’ lower bound on \(L^*(E_{a, \gamma }, 1)\):

On the other hand, using techniques from classical complex analysis, Hindry and Pacheco show the following upper bound on \(L^*(E_{a, \gamma }, 1)\) (see [10, Theorem 7.5]):

In this section, we prove the main theorem of this article (Theorem A in the introduction), which provides a significant improvement on (38):
Theorem 7.1
Let \({\mathbb {F}}_q\) be a finite field of odd characteristic p and  . There exist positive constants \(C_1, C_2\) (depending at most on q and p) such that the following holds. For all \(\gamma \in {\mathbb {F}}_q^\times \) and all integers \(a\geqslant 1\), the special value \(L^*(E_{a, \gamma }, 1)\) satisfies
. There exist positive constants \(C_1, C_2\) (depending at most on q and p) such that the following holds. For all \(\gamma \in {\mathbb {F}}_q^\times \) and all integers \(a\geqslant 1\), the special value \(L^*(E_{a, \gamma }, 1)\) satisfies

We will prove this Theorem in Sect. 7.2. The upper bound in (39) does not radically improve on the upper bound of Hindry and Pacheco (loc. cit.) but, since our proof is rather short, we decided to include it here for completeness. Our proof of the lower bound in (39), on the other hand, is much more involved: the crucial step is the computation of a ‘Sato–Tate limit’, using the results of Sects. 5 and 6 (see the next subsection). For later use (in Sect. 8), we note that Theorem 7.1 implies that

Remark 7.2
In [6,7,8], the author has also proven, for other families of elliptic curves, lower bounds on special values of L-functions which are similar to (39). However, the approach used in those papers for proving such bounds significantly differs from the strategy of proof of Theorem 7.1: let us investigate what comes out of our previous method for the sequence \(\{E_{a, \gamma }\}_{a\geqslant 1}\) at hand.
The proof of Proposition 4.7 implies that

The product \(\Pi _1\) is an integer and can be shown to satisfy  as \(a\rightarrow \infty \) [see (41) and its proof], hence it is negligible for our purpose. As for the second term \(\Pi _2\), by construction of the special value, it is of the form
as \(a\rightarrow \infty \) [see (41) and its proof], hence it is negligible for our purpose. As for the second term \(\Pi _2\), by construction of the special value, it is of the form

The proofs of [7, Theorem 4.1] and [8, Theorem 4.2] are essentially based on the observation that to prove the desired lower bound on\(\log L^*(E_{a, \gamma }, 1)\), it issufficientto show that the exponent\(e_{a, \gamma }\)is as\(a\rightarrow \infty \). Let us show that this asymptotic relation does not hold here.
as\(a\rightarrow \infty \). Let us show that this asymptotic relation does not hold here.
To do so, we keep track of the contribution to the exponent \(e_{a, \gamma }\) of each factor in the product \(\Pi _2\). Fix a prime ideal \({\mathfrak {P}}\) of \({\overline{\mathbb {Q}}}\) above p and denote by \(\mathrm{ord}_{\mathfrak {P}}\) the \(\mathfrak {P}\)-adic valuation on \({\overline{\mathbb {Q}}}\) so normalised that \(\mathrm{ord}_{\mathfrak {P}}(q)=1\). For any  , one has \(\mathrm{ord}_{\mathfrak {P}}(q^{d_v})=d_v\) and it can be shown that
, one has \(\mathrm{ord}_{\mathfrak {P}}(q^{d_v})=d_v\) and it can be shown that  . Indeed, we know from Proposition 3.1 that
. Indeed, we know from Proposition 3.1 that  and
and  are algebraic integers whose product is \(|{\mathbb {F}}_v|=q^{d_v}\) and whose sum is
are algebraic integers whose product is \(|{\mathbb {F}}_v|=q^{d_v}\) and whose sum is  . Besides it is known that
. Besides it is known that  (see [22, Proposition 3.1 (v)] for instance). Hence one of
(see [22, Proposition 3.1 (v)] for instance). Hence one of  or
or  is a \(\mathfrak {P}\)-adic unit, so that the other has \(\mathfrak {P}\)-adic valuation \(d_v\).
is a \(\mathfrak {P}\)-adic unit, so that the other has \(\mathfrak {P}\)-adic valuation \(d_v\).
A quick computation then shows that the \(v\hbox {th}\) factor of \(\Pi _2\) has \(\mathfrak {P}\)-adic valuation  , i.e., is of the form
, i.e., is of the form

Taking the product of these factors over  , we deduce that (cf. (11)):
, we deduce that (cf. (11)):

Since \(e_{a, \gamma }\) is not  here, this ‘p-adic valuation’ method only yields a much weaker lower bound on the special value \(L^*(E_{a, \gamma }, 1)\) than the one in (39), namely,
here, this ‘p-adic valuation’ method only yields a much weaker lower bound on the special value \(L^*(E_{a, \gamma }, 1)\) than the one in (39), namely,

This is why we rely instead on studying the distribution of the angles  in
in  .
.
7.1 Evaluation of a Sato–Tate limit
In this subsection, we show the following result, which is the crucial input in our proof of the lower bound in Theorem 7.1. For any integer \(a\geqslant 1\), we again denote by \(\nu _a=\nu ({\mathbb {F}}_q, \psi _q, \gamma ;a)\) the probability measure on  introduced in Sect. 6.2.
introduced in Sect. 6.2.
Theorem 7.3
Let \({\mathbb {F}}_q\) be a finite field equipped with a nontrivial additive character \(\psi _q\), and \(\gamma \in {\mathbb {F}}_q^\times \). Then
More concretely, this statement means that

the evaluation of the integral on the right-hand side being a routine exercise in calculus.
Proof
For conciseness, we denote by  the function given by
the function given by  if \(t\ne 0, \pi \) and
if \(t\ne 0, \pi \) and  . Once and for all, pick a nondecreasing continuously differentiable function
. Once and for all, pick a nondecreasing continuously differentiable function  such that \(\phi _0 \equiv 0\) on
such that \(\phi _0 \equiv 0\) on  and \(\phi _0\equiv 1\) on
and \(\phi _0\equiv 1\) on  . For all \(\epsilon \in (0, 1)\), we define a function
. For all \(\epsilon \in (0, 1)\), we define a function  by
by

and we let  . By construction, \(w_\epsilon \) is a continuously differentiable function on
. By construction, \(w_\epsilon \) is a continuously differentiable function on  such that \(w_\epsilon \leqslant w\) on
such that \(w_\epsilon \leqslant w\) on  , \(w\equiv w_\epsilon \) on
, \(w\equiv w_\epsilon \) on  , and \(w_\epsilon \equiv 0\) on
, and \(w_\epsilon \equiv 0\) on  . Furthermore, we have the following analytic estimates:
. Furthermore, we have the following analytic estimates:
Lemma 7.4
Notations being as above, for all \(\epsilon \in (0, 1)\), we have
-
(i)
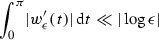 ,
, -
(ii)
 .
.
The constants depend only on the choice of \(\phi _0\).
We postpone the proof of this lemma until the end of the subsection, and we now prove that \(\int _{[0, \pi ]} w {\,\text {d}}\nu _a\) converges to \(\int _{[0, \pi ]} w{\,\text {d}}\mu _{\mathrm{ST}}\) when \(a\rightarrow \infty \). For any \(\epsilon \in (0,1)\), note that

Let us bound each of these three terms using the results in Sects. 5 and 6.
For \(\epsilon >0\) sufficiently small, we claim that the first term \(T_1\) vanishes. Indeed, \(w\equiv w_\epsilon \) on  and, as we pointed out in Remark 6.4, Corollary 5.5 shows that the support of \(\nu _a\) is contained in
and, as we pointed out in Remark 6.4, Corollary 5.5 shows that the support of \(\nu _a\) is contained in  . Therefore, for any
. Therefore, for any  , w and \(w_\epsilon \) coincide (at least) on the support of \(\nu _a\), so that we have \(T_1=0\). Next, the function \(w_\epsilon \) being continuously differentiable on
, w and \(w_\epsilon \) coincide (at least) on the support of \(\nu _a\), so that we have \(T_1=0\). Next, the function \(w_\epsilon \) being continuously differentiable on  , we can use our effective equidistribution result (Theorem 6.6) to control the second term \(T_2\). Precisely, Theorem 6.6 yields
, we can use our effective equidistribution result (Theorem 6.6) to control the second term \(T_2\). Precisely, Theorem 6.6 yields

where the rightmost upper bound is Lemma 7.4 (i). Finally, Lemma 7.4 (ii) proves the estimate  .
.
In summary, for all \(\epsilon >0\) such that  , we have
, we have

Upon choosing \(\epsilon = (q^{a})^{ -\gamma }\) where  , we conclude that
, we conclude that

which proves Theorem 7.3. We even obtain a more quantitative version of (40):

where the implicit constant depends at most on q and p (and the choice of the auxiliary function \(\phi _0\)). \(\square \)
Proof of Lemma 7.4
Since both w and \(w_\epsilon \) are symmetric around \(\pi /2\), it is sufficient to prove (i) and (ii) where the integrals are replaced by integrals over  . We also note that, for all \(t\in (0, \pi /2]\), one has
. We also note that, for all \(t\in (0, \pi /2]\), one has  . This follows from the classical estimate: \(\sin t\geqslant \frac{2t}{\pi }\) for
. This follows from the classical estimate: \(\sin t\geqslant \frac{2t}{\pi }\) for  .
.
To prove (i), we study separately the integrals over \((0,\epsilon )\) and over  . Since w and \(w_\epsilon \) coincide on
. Since w and \(w_\epsilon \) coincide on  , we have
, we have

by the classical estimate mentioned above. Hence we have

On the interval \((0,\epsilon )\), we use the fact that \(w_\epsilon = w\phi _\epsilon \) to deduce that

where \(\Vert \phi _0'\Vert _\infty \) denotes the supnorm of \(\phi '_0\) on  . By the upper bound on
. By the upper bound on  at the beginning of the proof and the fact that \(\phi _\epsilon \equiv 0\) on
at the beginning of the proof and the fact that \(\phi _\epsilon \equiv 0\) on  , we obtain that
, we obtain that

and from there, that

Summing the contributions of \(\int _0^\epsilon \) and \(\int _\epsilon ^{\pi /2}\), we conclude that (i) holds, with a constant depending only on \(\phi _0\). We now show that (ii) holds: by the symmetry of \(w-w_\epsilon \) and since \(w\equiv w_\epsilon \) on  , it suffices to prove that
, it suffices to prove that

By construction of \(\phi _\epsilon \), we notice that

where inequality \((*)\) follows from the upper bound on  given at the beginning of the proof. \(\square \)
given at the beginning of the proof. \(\square \)
7.2 Proof of Theorem 7.1
In (25) and (27), we have proven that

Therefore, we have

and we estimate the terms \(A_1\) and \(A_2\) separately. First of all, we deduce from Lemma 3.5 (ii) that

And, since we know by (11) that \({q^a\ll b(E_{a, \gamma }) \ll q^a}\), this yields
Let us now bound \(A_2\). Recall from Sect. 7.1 that  denotes the function
denotes the function  . It is clear that \(A_2\) is nonnegative, and that one can write
. It is clear that \(A_2\) is nonnegative, and that one can write

By (11) again, we have \(b(E_{a, \gamma })\gg q^a\) and, since Lemma 3.5 (ii) yields that  , we see that
, we see that  . Moreover, by Theorem 7.3, we have
. Moreover, by Theorem 7.3, we have
Putting these estimates together, we infer that
Summing the inequalities (41) and (42), we finally obtain that

This concludes the proof of Theorem 7.1. \(\square \)
8 Application to an analogue of the Brauer–Siegel theorem
In this section, we deduce from Theorem 7.1 and from the BSD conjecture that the following theorem holds (stated as Theorem B in the introduction).
Theorem 8.1
Let \({\mathbb {F}}_q\) be a finite field of odd characteristic and  . For all \(\gamma \in {\mathbb {F}}_q^\times \) and all integers \(a\geqslant 1\), consider the elliptic curve \(E_{a, \gamma }/K\) as above. Then the Tate–Shafarevich group
. For all \(\gamma \in {\mathbb {F}}_q^\times \) and all integers \(a\geqslant 1\), consider the elliptic curve \(E_{a, \gamma }/K\) as above. Then the Tate–Shafarevich group  is finite and, as \(a\rightarrow \infty \),
is finite and, as \(a\rightarrow \infty \),

Alternatively, (43) can be rewritten under the form: for all \(\epsilon >0\),

The upper bound in (44) was essentially conjectured by Lang for elliptic curves over \({\mathbb {Q}}\) with finite Tate–Shafarevich groupsFootnote 10 (see [13, Conjecture 1]). Theorem 8.1 thus provides an unconditional example where this conjecture holds for elliptic curves over  . The lower bound in (44) further proves that the exponent 1 of the height is optimal, in the sense that 1 cannot be replaced by any smaller number.
. The lower bound in (44) further proves that the exponent 1 of the height is optimal, in the sense that 1 cannot be replaced by any smaller number.
One may also view Theorem 8.1 as an analogue of the Brauer–Siegel theorem for the elliptic curves \(E_{a, \gamma }\). The Brauer–Siegel theorem states that, as F runs through a sequence of number fields of given degree n over \({\mathbb {Q}}\) and whose discriminants \(\Delta _F\) tend, in absolute value, to \(+\infty \), one has

where  denotes the class group of F and R(F) its regulator of units. At least formally, (44) is very similar to (45). A more detailed analogy is explained in [9] and [10].
denotes the class group of F and R(F) its regulator of units. At least formally, (44) is very similar to (45). A more detailed analogy is explained in [9] and [10].
Proof
We know from Theorem 2.5 that the BSD conjecture holds for \(E_{a, \gamma }\). In particular, the Tate–Shafarevich group  is indeed finite and the special value \(L^*(E_{a, \gamma }, 1)\) satisfies (13). The BSD formula (13) and Proposition 2.6 then imply the estimate:
is indeed finite and the special value \(L^*(E_{a, \gamma }, 1)\) satisfies (13). The BSD formula (13) and Proposition 2.6 then imply the estimate:

Therefore, to conclude the proof of Theorem 8.1, it remains to show that

or, alternatively, that

because, by (9), \(\log H(E_{a, \gamma })\) and \(b(E_{a, \gamma })\) have the same order of magnitude asymptotically as \(a\rightarrow \infty \). But we have already proven in Theorem 7.1 that this asymptotic estimate holds. \(\square \)
Note added in proof
Ulmer recently uploaded a preprint [23] in which he develops an algebraic approach to proving an analogue of the Brauer-Siegel theorem for some elliptic curves over K (see Sect. 8). His strategy to do so is based on finding lower bounds on an invariant he introduces: the ‘dimension of  ’.
’.
We would like to point out that the sequence \(\{E_{a, \gamma }\}_{a\geqslant 1}\) provides an example where the approach of [23] fails to be conclusive. Indeed, Theorem 8.1 shows that the Brauer-Siegel ratio of \(E_{a, \gamma }\) is large; even though Proposition 4.2 in [23] and our Remark 7.2 imply that  .
.
Notes
Since the base field K is fixed and all the invariants of E we consider are relative to K, we drop the dependency on K from the notations.
Hereafter abbreviated as BSD.
When \(E_{a, \gamma }\) has bad reduction at v, note that \(a_v\) equals 0 (resp. \(+1\), \(-1\)) if \(E_{a, \gamma }\) has additive (resp. split multiplicative, nonsplit multiplicative) reduction at v.
Here we view \(\kappa ({\text {Fr}}_v)\in \overline{{\mathbb {Q}}_\ell }\) as an element of \({\mathbb {C}}\) by means of the chosen isomorphism \(\overline{{\mathbb {Q}}_\ell }\simeq {\mathbb {C}}\).
The measure \(\xi _a\) is the measure denoted by \(X_a\) in [11, Section 3.5] applied to our situation.
This is an analogue in the Sato–Tate context of Weyl’s criterion for uniform distribution (see [12, Chapter 4, Section 1]).
so that \({{\mathrm{Trace}}}\,\Lambda _n(\theta )=U_n(\cos \theta )\), where \(U_n\) is the \(n\hbox {th}\) Chebyshev polynomial of the second kind.
Instead of considering the measure \(\mu _{\mathrm{ST}}\) on
 , Niederreiter works on the interval \([-1, 1]\) endowed with the direct image of \(\mu _{\mathrm{ST}}\) under \(t\mapsto \cos t\) (the ‘semi-circle measure’); the translation to our setting is straightforward.
, Niederreiter works on the interval \([-1, 1]\) endowed with the direct image of \(\mu _{\mathrm{ST}}\) under \(t\mapsto \cos t\) (the ‘semi-circle measure’); the translation to our setting is straightforward.Note though that Lang uses a different normalisation of the height: his (naive) height has an exponent 1 / 12 instead of our exponent 1.
References
Baig, S.: Hall, Chr.: Experimental data for Goldfeld’s conjecture over function fields. Exp. Math. 21(4), 362–374 (2012)
Brumer, A.: The average rank of elliptic curves I. Invent. Math. 109(3), 445–472 (1992)
Conceição, R.P., Hall, Chr., Ulmer, D.: Explicit points on the Legendre curve II. Math. Res. Lett. 21(2), 261–280 (2014)
Fisher, B.: Equidistribution theorems. In: Columbia University Number Theory Seminar (New York, 1992). Astérisque, vol. 228(3), pp. 69–79. Société Mathématique de France, Paris (1995)
Fu, L., Liu, C.: Equidistribution of Gauss sums and Kloosterman sums. Math. Z. 249(2), 269–281 (2005)
Griffon, R.: Analogues du Théorème de Brauer–Siegel pour Quelques Familles de Courbes Elliptiques. PhD thesis, Université Paris Diderot (2016). http://math.leidenuniv.nl/~griffonrmm/thesis/Griffon_thesis.pdf
Griffon, R.: Analogue of the Brauer–Siegel theorem for Legendre elliptic curves. J. Number Theory 193, 189–212 (2018)
Griffon, R.: Explicit \(L\)-functions and a Brauer–Siegel theorem for Hessian elliptic curves. J. Théor. Nombres Bordeaux. arXiv:1709.02761 (to appear)
Hindry, M.: Why is it difficult to compute the Mordell–Weil group? In: Zannier, U. (ed.) Diophantine Geometry. Centro di Ricerca Matematica Ennio De Giorgi Series, vol. 4, pp. 197–219. Edizioni della Normale, Pisa (2007)
Hindry, M., Pacheco, A.: An analogue of the Brauer–Siegel theorem for abelian varieties in positive characteristic. Moscow Math. J. 16(1), 45–93 (2016)
Katz, N.M.: Gauss Sums, Kloosterman Sums, and Monodromy Groups. Annals of Mathematics Studies, vol. 116. Princeton University Press, Princeton (1988)
Kuipers, L., Niederreiter, H.: Uniform Distribution of Sequences. Dover, New York (2006)
Lang, S.: Conjectured Diophantine estimates on elliptic curves. In: Artin, M., Tate, J. (eds.) Arithmetic and Geometry, Vol. I. Progress in Mathematics, vol. 35, pp. 155–171. Birkhäuser, Boston (1983)
Lidl, R., Niederreiter, H.: Finite fields, 2nd edn. In: Encyclopedia of Mathematics and Its Applications, vol. 20. With a foreword by P.M. Cohn. Cambridge University Press (1997)
Milne, J.S.: Arithmetic Duality Theorems. Perspectives in Mathematics, vol. 1. Academic Press, Boston (1986)
Mignotte, M., Waldschmidt, M.: On algebraic numbers of small height: linear forms in one logarithm. J. Number Theory 47(1), 43–62 (1994)
Niederreiter, H.: The distribution of values of Kloosterman sums. Arch. Math. (Basel) 56(3), 270–277 (1991)
Pries, R., Ulmer, D.: Arithmetic of abelian varieties in Artin–Schreier extensions. Trans. Amer. Math. Soc. 368(12), 8553–8595 (2016)
Silverman, J.H.: Advanced Topics in the Arithmetic of Elliptic Curves. Graduate Texts in Mathematics, vol. 151. Springer, New York (1994)
Tate, J.T.: On the conjectures of Birch and Swinnerton-Dyer and a geometric analog. In: Séminaire Bourbaki, vol. 9, Exp. No. 306, pp. 415–440. Société Mathématique de France, Paris (1965/1966)
Ulmer, D.: Elliptic curves over function fields. In: Popescu, C. et al. (eds.) Arithmetic of \(L\)-Functions. IAS/Park City Math. Series, vol. 18, pp. 211–280. American Mathematical Society, Providence (2011)
van der Geer, G., van der Vlugt, M.: Kloosterman sums and the \(p\)-torsion of certain Jacobians. Math. Ann. (Basel) 290(3), 549–563 (1991)
Ulmer, D.: On the Brauer-Siegel ratio for abelian varieties over function fields. arXiv:1806.01961 (preprint)
Acknowledgements
It is a pleasure to thank Marc Hindry and Douglas Ulmer for their encouragements and for some useful comments on earlier versions of this work. The author would also like to thank Bruno Anglès, Peter Bruin and Peter Koymans for fruitful discussions about various parts of the paper. Thanks are also due to the referee for their careful reading and valuable suggestions to improve the exposition.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work has been carried out at Universiteit Leiden, whose financial support and perfect working conditions are gratefully acknowledged. The author is also partially supported by the ANR project ‘FLAIR’ (Grant ANR-17-CE40-0012).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Griffon, R. Bounds on special values of L-functions of elliptic curves in an Artin–Schreier family. European Journal of Mathematics 5, 476–517 (2019). https://doi.org/10.1007/s40879-018-0284-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-018-0284-3
Keywords
- Elliptic curves over function fields in characteristic p
- Explicit computation of L-functions
- Special values of L-functions
- BSD conjecture
- Kloosterman sums
- Sato–Tate distribution




 ,
, 
 for all
for all  .
.


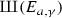 is finite.
is finite.
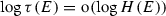 as
as  and the sets
and the sets 
 is a totally real algebraic integer in
is a totally real algebraic integer in 
 satisfies ‘Salié’s formula’:
satisfies ‘Salié’s formula’: 
 to the whole of
to the whole of  .
. and
and  such that
such that  and, for any finite extension
and, for any finite extension  ,
, 
 is uniquely determined by
is uniquely determined by  and
and  have magnitude
have magnitude  satisfies
satisfies  (‘Weil bound’).
(‘Weil bound’).


 for all
for all  for all
for all 

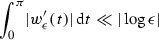 ,
, .
. , Niederreiter works on the interval
, Niederreiter works on the interval