Besov spaces generated by the Neumann Laplacian

Abstract

We give a definition of Besov spaces generated by the Neumann Laplacian and study their fundamental properties. As a by-product of these results, the fractional Leibniz rule in these Besov spaces is obtained.

Appendices

Appendix

Proposition A.1

Let . Then the following assertions are equivalent:

• (i) 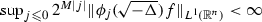for any $M \in {\mathbb {N}}$;

• (ii) .

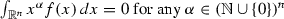When $\mathrm{\Omega }={\mathbb {R}}^n$, Proposition A.1 implies that letting , we have

$$\begin{aligned} f \in {\mathscr {Z}}({\mathbb {R}}^n)\; \text {if and only if }\;f \in {\mathscr {S}}_0({\mathbb {R}}^n). \end{aligned}$$

This means that when $\mathrm{\Omega }={\mathbb {R}}^n$, ${\mathscr {Z}}({\mathbb {R}}^n)$ corresponds to ${\mathscr {S}}_0({\mathbb {R}}^n)$.

Proof

Let $f \in {\mathscr {S}}({\mathbb {R}}^n)$. We divide the proof into two steps.

First step. We prove that assertion (ii) is equivalent to the following:

(64)

Indeed, assertion (ii) implies that

Hence it follows that

(65)

for any $M\in {\mathbb {N}}$. Here, since

it follows that

for any $j \leqslant 0$ and $M\in {\mathbb {N}}$. Therefore we deduce from (65) that

for any $j \leqslant 0$ and $M\in {\mathbb {N}}$, which implies (64). Conversely, suppose (64). Then

for any $j \leqslant 0$ and $M\in {\mathbb {N}}$, which implies that

(66)

for any $M\in {\mathbb {N}}$. Since is $C^\infty$ on ${\mathbb {R}}^n$, we conclude from (66) that

which implies assertion (ii). Thus the equivalence between (ii) and (64) is proved.

Second step. It is sufficient to show that assertion (i) is equivalent to (64) by the first step. Suppose (i). Then, by $L^1$–$L^\infty$-boundedness of the Fourier transform ${\mathscr {F}}$, we find that

for any $j \leqslant 0$. Hence, multiplying both sides by $2^{M|j|}$ and taking the supremum with respect to $j\leqslant 0$, we get (64). Conversely, suppose that (64) holds. We estimate

As for $j\leqslant 0$, we deduce from $L^1$–$L^\infty$-boundedness of that there exists a constant $C>0$ such that

for any $j \leqslant 0$. As for the second factor, applying [18, Section 1.5.2, Theorem] to it, we find that there exists a constant such that

for any $j \leqslant 0$, where C is independent of j. Hence, combining the last three inequalities, we infer assertion (i). $\square$

Appendix

Lemma B.1

Assume that $\mathrm{\Omega }$ is a Lipschitz domain in ${\mathbb {R}}^n$. Let $\phi \in {\mathscr {S}}({\mathbb {R}})$. Then the operators and belong to for any $\alpha ,\theta >0$. Furthermore, there exists a constant $C>0$ such that

(67)

(68)

for any $\theta >0$.

The proof of Lemma B.1 is similar to that of [12, Lemmas 6.3 and 7.1]. Here, we use the fact that $C^\infty _0({\mathbb {R}}^n)|_{\mathrm{\Omega }}$ is dense in $H^1(\mathrm{\Omega })$, which is the main difference from the previous paper [12]. Indeed, instead of this fact, in the Dirichlet Laplacian case we used the density of $C^\infty _0(\mathrm{\Omega })$ in $H^1_0(\mathrm{\Omega })$.

Lemma B.2

([12, Lemma 6.2]) Let $\mathrm{\Omega }$ be an open set in ${\mathbb {R}}^n$. Assume that $\alpha >n/2$ and $\theta >0$. If $A\in {\mathscr {A}}_{\alpha ,\theta }$, then there exists a constant $C>0$, depending only on n and $\alpha$, such that

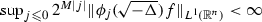for any .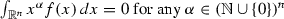