Abstract
In Hirschfeld (J Austral Math Soc 4(1):83–89, 1964), the existence of the cubic surface which arises from a double-six over the finite field of order four was considered. In Hirschfeld (Rend Mat Appl 26:115–152, 1967), the existence and the properties of the cubic surfaces over the finite fields of odd and even order was discussed and classified over the fields of order seven, eight, nine. In this paper, cubic surfaces with twenty-seven lines over the finite field of thirteen elements are classified.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and preliminaries
Let  be the n-dimensional projective space over a field K. When \(K= \mathbf {F}_{q}\), it is denoted by
be the n-dimensional projective space over a field K. When \(K= \mathbf {F}_{q}\), it is denoted by  . The projective general linear group
. The projective general linear group  is the group of projectivities of
is the group of projectivities of  .
.
The projective plane  over \(\mathbf {F}_q\) contains
over \(\mathbf {F}_q\) contains  points and
points and  lines, [10]. There are \(q+1\) points on a line and \(q+1\) lines through a point. A point
lines, [10]. There are \(q+1\) points on a line and \(q+1\) lines through a point. A point  is in
is in  where
where  and not all zero. In
and not all zero. In  , there are 183 points and 183 lines; there are 14 points on every line and 14 lines passing through every point.
, there are 183 points and 183 lines; there are 14 points on every line and 14 lines passing through every point.
The space  contains
contains  points and planes, as well as
points and planes, as well as  lines. There are
lines. There are  lines through every point and \(q+1\) planes through a line. In
lines through every point and \(q+1\) planes through a line. In  , planes and lines are characterised as follows: a subset \(\mathrm{\Pi }_2\) is a plane if and only if it has
, planes and lines are characterised as follows: a subset \(\mathrm{\Pi }_2\) is a plane if and only if it has  points and meets every line; a subset \(\mathrm{\Pi }_1\) is a line if and only if it has \(q+1\) points and meets every plane. A point
points and meets every line; a subset \(\mathrm{\Pi }_1\) is a line if and only if it has \(q+1\) points and meets every plane. A point  is in
is in  where
where  and not all zero. In
and not all zero. In  , there are 2380 points and planes, and 31110 lines. Also, there are 183 lines passing through a point and 14 planes through a line.
, there are 2380 points and planes, and 31110 lines. Also, there are 183 lines passing through a point and 14 planes through a line.
A k-arc in  is a set of k points no three of which are collinear. When k achieves its maximum value, a k-arc is an oval. For q odd, an oval is a
is a set of k points no three of which are collinear. When k achieves its maximum value, a k-arc is an oval. For q odd, an oval is a  -arc, and this is the set of rational points of a conic. For q even, an oval is a
-arc, and this is the set of rational points of a conic. For q even, an oval is a  -arc; here, an oval may be constructed as a conic plus its nucleus, which is the intersection of all its tangent lines. For \(q=2^h\) with \(h\geqslant 4\), there exist other types of ovals.
-arc; here, an oval may be constructed as a conic plus its nucleus, which is the intersection of all its tangent lines. For \(q=2^h\) with \(h\geqslant 4\), there exist other types of ovals.
In  , the variety V(F) is the set of points \((x_0, x_1,\ldots ,x_n)\) such that
, the variety V(F) is the set of points \((x_0, x_1,\ldots ,x_n)\) such that

for the homogeneous polynomial F. In particular, a cubic surface \(\mathscr {F}\) in  is the zero set of a homogeneous cubic equation in four variables over K:
is the zero set of a homogeneous cubic equation in four variables over K:

where  , \(i+j+k+l=3\), and
, \(i+j+k+l=3\), and  . Therefore, to determine a cubic surface, 19 conditions are required since there are 20 monomials of degree 3 in four variables.
. Therefore, to determine a cubic surface, 19 conditions are required since there are 20 monomials of degree 3 in four variables.
Theorem 1.1
(Cayley and Salmon [4]) A non-singular cubic surface over the complex field contains exactly twenty-seven lines.
Cayley stated that there is great difficulty in conceiving the complete figure formed by the twenty-seven lines, indeed this can hardly be accomplished till a more perfect notation is discovered”.
A long first list of enumerative properties of 27 lines, most of which are implicit in Cayley’s paper, was systematically expounded by Steiner [13] in 1857.
In 1858, Schläfli found the required notation for the complete figure formed by these 27 lines. The formulation for a double-six in Schläfli’s theorem is as follows.
Theorem 1.2
(Schläfli [12]) Given five skew lines \(a_1, a_2, a_3 , a_4, a_5\) with a single transversal \(b_6\) such that each set of four \(a_i\) omitting  has a unique further transversal
has a unique further transversal  , then the five lines \(b_1, b_2, b_3, b_4, b_5\) also have a transversal \(a_6\). These twelve lines form a double-six; that is, a double-six in
, then the five lines \(b_1, b_2, b_3, b_4, b_5\) also have a transversal \(a_6\). These twelve lines form a double-six; that is, a double-six in  is the set of 12 lines
is the set of 12 lines
such that each line only meets the five lines which are not in the same row or column.
Theorem 1.3
([9]) A double-six lies on a unique cubic surface \(\mathscr {F}\) with 15 further lines \(c_{ij}\) given by the intersection of  and
and  where
where  is the plane containing \(a_i\) and
is the plane containing \(a_i\) and  .
.
The main related problems are stated in [9].
-
(i)
When does a double-six exist over \(\mathbf {F}_{q}\)?
-
(ii)
What are the particular properties of cubic surfaces over \(\mathbf {F}_{q}\)?
-
(iii)
Classify the cubic surfaces with twenty-seven lines over \(\mathbf {F}_{q}\).
The first two problems are answered in [9].
Theorem 1.4
([8]) A necessary and sufficient condition for the existence of a double-six, and so of a cubic surface with 27 lines, is the existence in a plane over the same field of a plane 6-arc not on a conic. This occurs when \(q \ne 2,3,5\).
In [7] and [8], the smallest cases, namely, \(\mathbf {F}_4, \mathbf {F}_7, \mathbf {F}_8,\mathbf {F}_9\), are resolved. Sadeh [11] constructed the cubic surfaces in  and gave their groups of projectivities.
and gave their groups of projectivities.
A point is an Eckardt point if it lies on exactly three lines of the cubic surface \(\mathscr {F}\).
Let \(G(\mathscr {F})\) be the group of projectivities which fixes the cubic surface \(\mathscr {F}\) [6], and let \(e_3\) be the total number of Eckardt points of \(\mathscr {F}\). In Table 1, a summary for \(4\leqslant q \leqslant 11\) is given.
A surface which is projectively equivalent to one with equation
is an equianharmonic surface, and denoted by \(\mathscr {E}\).
A surface which is projectively equivalent to one with equation

is a diagonal surface, and denoted by \(\mathscr {D}\).
In this paper, the projective classification of cubic surfaces \(\mathscr {F}\) with 27 lines in  is done by classifying the 6-arcs not lying on a conic in the plane; projectively distinct arcs do not necessarily represent projectively distinct surfaces. Complete arcs in
is done by classifying the 6-arcs not lying on a conic in the plane; projectively distinct arcs do not necessarily represent projectively distinct surfaces. Complete arcs in  were classified by Ali [1].
were classified by Ali [1].
2 Structure of the cubic surface
Here, \(\mathscr {F}\) denotes a non-singular cubic surface with twenty-seven lines, [2]. Consider \(\mathscr {F}\) with 27 lines of the form \(a_i, b_i, c_{ij}\), where  , with the 12 lines \(a_i, b_i\) in the form of a double-six (1), and
, with the 12 lines \(a_i, b_i\) in the form of a double-six (1), and  . Let
. Let  . Each line of \(\mathscr {F}\) meets 10 others; that is,
. Each line of \(\mathscr {F}\) meets 10 others; that is,

The 27 lines form 36 double-sixes: \(D,\ 15\; D_{ij},\ 20\; D_{ijk}\). Here,
Lemma 2.1
([9]) Let \(\mathscr {F}\) be a non-singular cubic surface, let P be a point of the surface and let  denote the tangent plane at P.
denote the tangent plane at P.
-
(i)
If P is on no line of \(\mathscr {F}\), then
 meets \(\mathscr {F}\) in an irreducible cubic with a double point at P.
meets \(\mathscr {F}\) in an irreducible cubic with a double point at P. -
(ii)
If P is on exactly one line of \(\mathscr {F}\), then
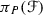 meets \(\mathscr {F}\) in the line plus a conic through P.
meets \(\mathscr {F}\) in the line plus a conic through P. -
(iii)
If P is on exactly two lines of \(\mathscr {F}\), then
 meets \(\mathscr {F}\) these two lines plus another line forming a triangle.
meets \(\mathscr {F}\) these two lines plus another line forming a triangle. -
(iv)
If P is on exactly three lines of \(\mathscr {F}\), then
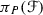 meets \(\mathscr {F}\) in these three concurrent lines.
meets \(\mathscr {F}\) in these three concurrent lines.
In cases (iii) and (iv) of Lemma 2.1,  is a tritangent plane since, in (iii), it is the tangent plane at each vertex of the triangle and, in case (iv), it is the tangent plane at the coincident points.
is a tritangent plane since, in (iii), it is the tangent plane at each vertex of the triangle and, in case (iv), it is the tangent plane at the coincident points.
Through each line there are five tritangent planes; therefore, there are  tritangent planes altogether, namely,
tritangent planes altogether, namely,

In case (iv) of Lemma 2.1, P is an Eckardt point. The number of Eckardt points is an isomorphism invariant of cubic surfaces. In some cases, cubic surfaces are characterised by their number of Eckardt points. For example, a cubic surface with 10 Eckardt points is a diagonal surface and a cubic surface with 18 Eckardt points is an equianharmonic surface. An Eckardt point may be of two types:

There are at most 30 of the first type and 15 of the second type.
Any two tritangent planes having no line of a cubic surface \(\mathscr {F}\) in common are uniquely associated with a third in such a way that the nine lines of \(\mathscr {F}\) in these three planes form another set of three similarly associated planes: the two trihedra form a trihedral pair. For example, let two tritangent planes \(V(F_1)\) and \(V(F_2)\) be made up of \(a_1, b_2, c_{12}\) and \(a_3, b_4, c_{34}\) with no common line. They are uniquely associated with a third tritangent plane \(V(F_3)\) containing \(c_{14}, c_{23}, c_{56}\). These nine lines of the cubic surface give two trihedra. The first trihedron consist of three planes given by  and second by
and second by  . Such a pair of trihedra is called a Steiner trihedral pair. It is customary to arrange the nine lines of intersection of the planes in a trihedral pair in the form of an array, such as this one:
. Such a pair of trihedra is called a Steiner trihedral pair. It is customary to arrange the nine lines of intersection of the planes in a trihedral pair in the form of an array, such as this one:
Here, the rows represent for the planes of type \(F_i\) and the columns represent the planes of type \(G_i\). This particular trihedral pair is denoted \(T_{12,34}\).
The 45 tritangent planes form  trihedral pairs which come in three types:
trihedral pairs which come in three types:

Theorem 2.2
([9]) Let the planes of a trihedral pair belonging to cubic surface \(\mathscr {F}\) be given by \(V(F_1), V(F_2), V(F_3)\) and \(V(G_1), V(G_2), V(G_3)\). Then the cubic surface can be written as
for some \(\lambda \) in \(\mathbf {F}_{q}\backslash \{0\}\).
The cubic surface can be created by any of the 120 trihedral pairs. In this paper, trihedral pairs are used to classify the cubic surfaces over a particular finite field. A trihedral pair is special if the three planes of one trihedron meet in a line, which is the line on which the three Eckardt points from the other trihedron are collinear. The existence of Eckardt points and their collinearities gives the set of special trihedral pairs.
Lemma 2.3
([9]) Any two Eckardt points not on the same line of \(\mathscr {F}\) are collinear with a third Eckardt point.
The possible collinearities are as follows:
3 Techniques
Cubic surfaces in three-dimensional projective space are the blow-up of six points in the plane. To see this, the Clebsch map from the cubic surface onto a plane is considered.
Theorem 3.1
(Clebsch [5]) A general cubic surface is the image of a birational map from a projective plane given by the linear system of cubics through six points.
Let \(\mathscr {F}\) be a cubic surface given by  , for some linear forms
, for some linear forms  . A point
. A point  is on \(\mathscr {F}\) if and only if
is on \(\mathscr {F}\) if and only if
that is, there exists  such that the following system has a non-trivial unique solution:
such that the following system has a non-trivial unique solution:
Since \(F_i\) and \(G_i\) are linear forms in the four variables \(x_0, x_1, x_2, x_3\), solving the system for the \(x_i\) gives

where each  determines a cubic curve in the plane. Therefore, there is a mapping \(\mathrm{\Phi }\) from the surface onto the plane that maps plane sections of \(\mathscr {F}\) to cubic curves through the set \(\mathscr {S}\) of six points, where
determines a cubic curve in the plane. Therefore, there is a mapping \(\mathrm{\Phi }\) from the surface onto the plane that maps plane sections of \(\mathscr {F}\) to cubic curves through the set \(\mathscr {S}\) of six points, where  , [9, Section 20.4].
, [9, Section 20.4].
Let \(S=\{P_1, P_2, P_3, P_4, P_5, P_6\}\) be a 6-arc not on a conic in  , let
, let  be the line through \(P_i\) and
be the line through \(P_i\) and  , and let
, and let  be the conic through the five points of
be the conic through the five points of  . Let \(\mathscr {F}\) be the corresponding cubic surface with twenty-seven lines in
. Let \(\mathscr {F}\) be the corresponding cubic surface with twenty-seven lines in  . Consider Clebsch’s mapping \(\mathrm{\Phi }\) of \(\mathscr {F}\) to the plane:
. Consider Clebsch’s mapping \(\mathrm{\Phi }\) of \(\mathscr {F}\) to the plane:

It takes the \(q+1\) points of the line \(a_i\) of \(\mathscr {F}\) in  to
to  . So there is a set of six points forming a 6-arc not on a conic under \(\mathrm{\Phi }\). Each of the remaining points of \(\mathscr {F}\) is mapped to a separate point of the plane. The points of the line \(b_i\) map to the points of the conic \(C_i\), and the points of the line \(c_{ij}\) map to the points of the line
. So there is a set of six points forming a 6-arc not on a conic under \(\mathrm{\Phi }\). Each of the remaining points of \(\mathscr {F}\) is mapped to a separate point of the plane. The points of the line \(b_i\) map to the points of the conic \(C_i\), and the points of the line \(c_{ij}\) map to the points of the line  :
:

Corollary 3.2
In \(,\) a cubic surface with 27 lines has  points.
points.
Proof
From above, there are  points on \(\mathscr {F}\). \(\square \)
points on \(\mathscr {F}\). \(\square \)
Note 3.3
In  , the number of points on the 27 lines of a cubic surface is
, the number of points on the 27 lines of a cubic surface is  .
.
Let \(V(F_1)\) be the plane section of the corresponding cubic surface \(\mathscr {F}\) consisting of \(c_{ij}, c_{kl}, c_{mn}\) and \(V(f_1)\) be the cubic curve in  which is made up of three lines namely
which is made up of three lines namely  . Then
. Then

Also, the image of the B-point  , the intersection of three bisecants of S, is the Eckardt point of the form \(E_{ij,kl,mn}\), since it is the intersection of \(c_{ij}, c_{kl} , c_{mn}\).
, the intersection of three bisecants of S, is the Eckardt point of the form \(E_{ij,kl,mn}\), since it is the intersection of \(c_{ij}, c_{kl} , c_{mn}\).
Let \(V(F_2)\) be the plane section of the corresponding cubic surface \(\mathscr {F}\) consisting of \(a_{i}, b_{j} , c_{ij}\), let \(V(f_2)\) be the cubic curve in  which is made up of a conic
which is made up of a conic  and a tangent line
and a tangent line  . Then
. Then

Also, if there exists a tangent line  touching
touching  at \(P_i\), Eckardt points of the form \(E_{ij}\) exist since it is the intersection of the \(a_{i}, b_{j} , c_{ij}\).
at \(P_i\), Eckardt points of the form \(E_{ij}\) exist since it is the intersection of the \(a_{i}, b_{j} , c_{ij}\).
In this paper, the method explained in [3] has been used to classify the sets of six points in  , no three collinear, not all on a conic. Some notation needs to be introduced.
, no three collinear, not all on a conic. Some notation needs to be introduced.
Let \(\mathscr {Y}\) denote the object to be classified, let \(\mathscr {X}\) be the class of sub-objects, and let G be the group which acts on the finite sets \(\mathscr {X}\) and \(\mathscr {Y}\). Let \(\mathscr {R}\) be a relation between \(\mathscr {X}\) and \(\mathscr {Y}\); also, G acts on \(\mathscr {R}\). The orbits of G on \(\mathscr {Y}\) are isomorphism classes of \(\mathscr {Y}\). Assume that the orbits of G on \(\mathscr {X}\) are classified and the relation \(\mathscr {R}\) is a G-invariant. With this method, the objects \(\mathscr {Y}\) can be classified by the classification of the sub-objects \(\mathscr {X}\).
Let \(P_1, \ldots ,P_m\) be the representatives for the orbits of G on \(\mathscr {X}\); so

Let \(Q_1, \ldots , Q_n\) be the representatives for orbits of G on \(\mathscr {Y}\); so

For  , let the up-set of \(P_i\) be
, let the up-set of \(P_i\) be

For  , let the down-set of
, let the down-set of  be
be

Let \(T_{i,k}\) be representatives of the orbits of  ; so
; so

where \(k=1, \ldots , k_i\) and \(\mathscr {T}_{i,k}= {\mathrm {Orb}}_{{\mathrm {Stab}}_G(P_i)}(T_{i,k})\). Let \(S_{j,l}\) be representatives of the orbits of  on
on  ; so
; so

where  and
and  .
.
Lemma 3.4
([3]) There is a bijection between the set of orbits  and the set of orbits
and the set of orbits  .
.
4 Algorithms
Two algorithms are now described: the arc-lifting algorithm and the classification algorithm.
4.1 Arc-lifting algorithm
This algorithm is used for the construction of the cubic surface with twenty-seven lines in  arising from a 6-arc not on a conic in
arising from a 6-arc not on a conic in  .
.
The algorithm’s input is

and the algorithm’s output is

The algorithm proceeds in four stages.
At the first stage, for a given 6-arc S not on a conic, the plane cubic curves through S are found. At the second stage, the Clebsch map is used to obtain the equations of the tritangent planes corresponding to the cubic surface \(\mathscr {F}\).
At the third stage, the possible arrangements of 120 trihedral pairs are found which yield eighteen conditions to determine the cubic surface. At the last stage, the nineteenth condition gives the parameter \(\lambda \) that determines the equation of the corresponding non-singular cubic surface.
Stage 1: Find the cubic curves through
 in
in

-
1.
Calculate six different conics
 through
through 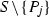 , where \(j=1,\ldots , 6\).
, where \(j=1,\ldots , 6\). -
2.
Calculate 15 different bisecants
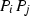 on the plane through each pair, where \(i,j=1, \ldots , 6\).
on the plane through each pair, where \(i,j=1, \ldots , 6\). -
3.
Calculate 30 different cubic curves through S of the form
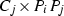 .
. -
4.
Calculate 15 different cubic curves through S of the form
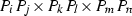 .
. -
5.
Fix four linearly independent cubic curves as base curves, say
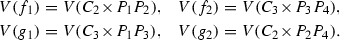
Stage 2: Find the tritangent planes of
\(\mathscr {F}\)
in

The tritangent plane  is the image of the cubic curve
is the image of the cubic curve  and the tritangent plane \(c_{ij}c_{kl}c_{mn}\) is the image of the cubic curve
and the tritangent plane \(c_{ij}c_{kl}c_{mn}\) is the image of the cubic curve  .
.
Considering four base cubic plane curves, the four associated base tritangent planes can be written as follows:

Calculate the remaining 41 tritangent planes as linear combinations of \(x_0, x_1, x_2, x_3\).
Stage 3: Find the trihedral pairs of
\(\mathscr {F}\)
in

Pick a trihedral pair related to four base tritangent planes \(V(F_1), V(F_2), V(G_1), V(G_2)\) and four base cubic curves \(V(f_1), V(f_2), V(g_1), V(g_2)\), say \(T_{14,23}\):
In stage two, 45 tritangent planes are already calculated as the linear combination of \(x_0, x_1, x_2, x_3\). Therefore, \(F_i\) and \(G_i\) are linear forms in the four coordinates. From Theorem 2.2, it is known that every cubic surface can be written in 120 ways in the form

Stage 4: Find the equation of the cubic surface \(\mathscr {F}\) in  with 27 lines
with 27 lines
The parameter \(\lambda \) can be found as the following way. The Clebsch map is surjective; that is, every point in  is an image of a point (or points) on the cubic surface \(\mathscr {F}\) as follows:
is an image of a point (or points) on the cubic surface \(\mathscr {F}\) as follows:

where \(V(f_1), V(f_2), V(g_1), V(g_2)\) are base cubic curves in the plane. Taking a point  not on the base cubic curves in
not on the base cubic curves in  , the point
, the point  is found on \(\mathscr {F}\). The parameter \(\lambda \) is found by evaluating
is found on \(\mathscr {F}\). The parameter \(\lambda \) is found by evaluating  in (2).
in (2).
4.2 The classification algorithm
This algorithm is used for the classification of cubic surfaces with twenty-seven lines in  . The algorithm’s input is
. The algorithm’s input is

and the algorithm’s output is

The algorithm proceeds in five stages.
In the first stage, for each 6-arc the arc-lifting algorithm is used. In the second stage, for each 6-arc we find the set of special trihedral pairs, say \(\mathbf {T}\). In the third stage, we classify the set of six points in  . In the fourth stage, for each 6-arc we find the automorphism group of the cubic surface \(\mathscr {F}\) which acts on the set of special trihedral pairs, \(\mathbf {T}\). In the last stage, we check the projectivity between cubic surfaces with the same number of Eckardt points and the isomorphic group of projectivities if there exists one.
. In the fourth stage, for each 6-arc we find the automorphism group of the cubic surface \(\mathscr {F}\) which acts on the set of special trihedral pairs, \(\mathbf {T}\). In the last stage, we check the projectivity between cubic surfaces with the same number of Eckardt points and the isomorphic group of projectivities if there exists one.
Stage 1: For each 6-arc, process the arc-lifting program
For each 6-arc, the corresponding cubic surface is constructed with its 27 lines, 45 tritangent planes and 120 trihedral pairs, giving a particular set \(\mathbf {T}\) of trihedral pairs.
Stage 2: For each corresponding cubic surface, find the set of special trihedral pairs
In this stage, there are three steps as follows.
-
1.
Find all possible Eckardt points. Here,
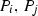 are the points from the related 6-arc not on a conic and
are the points from the related 6-arc not on a conic and 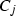 is a conic through
is a conic through 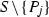 where \(j=1, \ldots , 6\) and
where \(j=1, \ldots , 6\) and 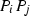 ’s are bisecants through 6-arc; If
’s are bisecants through 6-arc; If 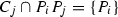 then print “\(E_{ij}\) is an Eckardt point”; if else
then print “\(E_{ij}\) is an Eckardt point”; if else 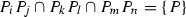 where
where 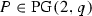 then print “\(E_{ij,kl,mn}\) is an Eckardt point”; else print failed; end
then print “\(E_{ij,kl,mn}\) is an Eckardt point”; else print failed; end
-
2.
Find all possible sets of three collinear Eckardt points. The coordinates of an Eckardt point are obtained by intersecting the required three lines. Then, for each triple of Eckardt points, it is determined whether or not they are collinear. Alternatively, Lemma 2.3 can be used to see the possible collinearities.
-
3.
Find the special trihedral pairs. Every trihedral pair gives two possible collinear triples of Eckardt points. For every collinear triple of Eckardt points, there is only one associated trihedral pair, which is called special.
Stage 3: The classification of the sets of six points in 
In this stage, all projective transformations between six points in  are obtained. The process in Lemma 3.4 is repeated five times to classify the sets of six points of
are obtained. The process in Lemma 3.4 is repeated five times to classify the sets of six points of  . Let \(\mathscr {X}_i\) be the set of i-subsets of
. Let \(\mathscr {X}_i\) be the set of i-subsets of  and let \(\mathscr {Y}_i\) be the set of
and let \(\mathscr {Y}_i\) be the set of  -subsets of
-subsets of  , with \(\mathscr {R}\) the inclusion relation.
, with \(\mathscr {R}\) the inclusion relation.
Consider the action of the group  on
on  and hence on trihedral pairs and cubic surfaces. Let
and hence on trihedral pairs and cubic surfaces. Let  be a set of special trihedral pairs and \(G(\mathscr {F})\) the group of projectivities of \(\mathscr {F}\) which fixes \(\mathscr {F}\).
be a set of special trihedral pairs and \(G(\mathscr {F})\) the group of projectivities of \(\mathscr {F}\) which fixes \(\mathscr {F}\).
Stage 4: For each corresponding cubic surface, find its automorphism group
In this stage, the orbit-stabiliser theorem and Lemma 3.4 are used. There are three steps.
-
1.
Pick a trihedral pair from the set of special trihedral pairs, say \(T_1\). Find the stabiliser of \(T_1\):
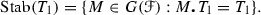
The elements M are obtained from the previous stage. Two more tests are applied to show that M fixes the cubic surface \(\mathscr {F}\). One is “does it preserve the
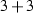 partition of trihedral pair \(T_1\)” and another one is “does it preserve the equation of the cubic surface
partition of trihedral pair \(T_1\)” and another one is “does it preserve the equation of the cubic surface 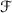 ”.
”. -
2.
Consider the set of special trihedral pairs
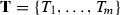 ; each has six planes. Find the orbit of \(T_1\):
; each has six planes. Find the orbit of \(T_1\): 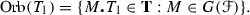
-
3.
Use the orbit-stabiliser theorem to find the automorphism group of \(\mathscr {F}\):
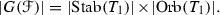
Stage 5: Find the projectively equivalent and distinct cubic surfaces in 
Two cubic surfaces \( \mathscr {F}\) and  with the same number of Eckardt points and isomorphic group of projectivities are projectively equivalent if and only if there exists a projectivity between them. Let T be a trihedral pair of \(\mathscr {F}\) and \(T'\) be a trihedral pair of
with the same number of Eckardt points and isomorphic group of projectivities are projectively equivalent if and only if there exists a projectivity between them. Let T be a trihedral pair of \(\mathscr {F}\) and \(T'\) be a trihedral pair of  . If the projectivity S in
. If the projectivity S in  is such that
is such that  also transforms \(\mathscr {F}\) to
also transforms \(\mathscr {F}\) to  , then \( \mathscr {F}\) and
, then \( \mathscr {F}\) and  are projectively equivalent; otherwise, \( \mathscr {F}\) and
are projectively equivalent; otherwise, \( \mathscr {F}\) and  are projectively distinct (Table 2).
are projectively distinct (Table 2).
5 Cubic surfaces with 27 lines over \(\mathbf {F}_{13}\)
From Theorem 1.4, such a surface \(\mathscr {F}\) in  exists and has 261 points.
exists and has 261 points.
Theorem 5.1
There are four projectively distinct cubic surfaces with 27 lines in  , namely,
, namely,  .
.


Proof
Two algorithms from the previous section have been used to prove the theorem. The projectively distinct 6-arcs not on a conic in  are shown in Table 3. In Table 4, the projectively distinct non-singular cubic surfaces
are shown in Table 3. In Table 4, the projectively distinct non-singular cubic surfaces  can be seen with their related plane 6-arcs, automorphism groups, and equations. \(\square \)
can be seen with their related plane 6-arcs, automorphism groups, and equations. \(\square \)
In Table 4, the order of the coefficients is the natural one as follows:

Let \(\mathbf {C}_n,\mathbf {S}_n\) and \(\mathbf {D}_n\) be the cyclic group of order n, the symmetric group of degree n and the dihedral group of order 2n. In Table 4,

where  is the Heisenberg group extended by a group of order 4.
is the Heisenberg group extended by a group of order 4.
References
Ali, A.H.: The Classification of Arcs in Galois Plane of Order Thirteen. Ph.D. Thesis. University of Sussex (1993)
Baker, H.F.: Principles of Geometry, III. Cambridge University Press, Cambridge (1921–1933) (Ungar, 1960–1968)
Betten, A.: The packings of PG(3,3). Des. Codes Cryptogr. 79(3), 583–595 (2016)
Cayley, A.: On the triple tangent planes of surfaces of the third order. Cambridge Dublin Math. J. 4, 252–260 (1849)
Clebsch, A.: Die Geometrie auf den Flächen dritter Ordnung. J. Reine Angew. Math. 65, 359–380 (1866)
Edge, W.L.: Quadrics over GF(2) and their relevance for the cubic surface group. Canad. J. Math. 11, 625–645 (1959)
Hirschfeld, J.W.P.: The double-six of lines over PG(3,4). J. Austral. Math. Soc. 4(1), 83–89 (1964)
Hirschfeld, J.W.P.: Classical configurations over finite fields: I. The double-six and the cubic surface with 27 lines. Rend. Mat. Appl. 26, 115–152 (1967)
Hirschfeld, J.W.P.: Finite Projective Spaces of Three Dimensions. Oxford Mathematical Monographs. Oxford University Press, New York (1985)
Hirschfeld, J.W.P.: Projective Geometries over Finite Fields. Oxford Mathematical Monographs, 2nd edn. Oxford University Press, New York (1998)
Sadeh, A.R.: The Classification of \(k\)-arcs and Cubic Surfaces with Twenty-Seven Lines over the Field of Eleven Elements. Ph.D. Thesis. University of Sussex (1984)
Schläfli, L.: An attempt to determine the twenty-seven lines upon a surface of the third order, and to divide such surfaces into species in reference to the reality of the lines upon the surface. Quart. J. Pure and Appl. Math. 2(55–65), 110–120 (1858)
Steiner, J.: Über die Flächen dritten grades. J. Reine Angew. Math. 53, 133–141 (1857)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Betten, A., Hirschfeld, J.W.P. & Karaoglu, F. Classification of cubic surfaces with twenty-seven lines over the finite field of order thirteen. European Journal of Mathematics 4, 37–50 (2018). https://doi.org/10.1007/s40879-017-0182-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-017-0182-0





 meets
meets  meets
meets  meets
meets  meets
meets  through
through 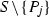 , where
, where 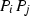 on the plane through each pair, where
on the plane through each pair, where 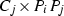 .
.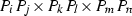 .
.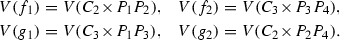
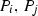 are the points from the related 6-arc not on a conic and
are the points from the related 6-arc not on a conic and 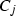 is a conic through
is a conic through 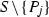 where
where 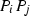 ’s are bisecants through 6-arc; If
’s are bisecants through 6-arc; If 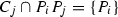 then print “
then print “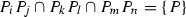 where
where 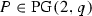 then print “
then print “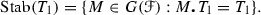
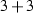 partition of trihedral pair
partition of trihedral pair 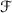 ”.
”.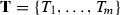 ; each has six planes. Find the orbit of
; each has six planes. Find the orbit of