Abstract
We construct a functor \(T\) from the category of endomorphisms of vector spaces to the category of Com-PreLie algebras. For any endomorphism \(f\) of a vector space \(V\), we describe the enveloping algebra of the pre-Lie algebra \(T(V,f)\), the dual Hopf algebra and the associated group of characters. For \(f=\mathrm{Id}_V\), we find the algebra of formal diffeomorphisms, seen as a subalgebra of the Connes–Kreimer Hopf algebra of rooted trees in the context of QFT; for other well-chosen nilpotent \(f\), we obtain the groups of Fliess operators in Control Theory. An algebraic study of these Com-PreLie Hopf algebras is carried out: gradations, generation, subobject generated by \(V\), etc.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Hopf algebra \(H\) of coordinates of the group of Fliess operators \(G\), used to study the feedback in Control Theory, is described in [11]. This Hopf algebra is studied in the one-dimensional case in [10], and it is shown it is a right-sided Hopf algebra in the sense of [15]. Consequently, its dual Lie algebra \({\mathfrak {g}}\), which is the Lie algebra of \(G\), inherits a right pre-Lie algebra structure. It is proved that \({\mathfrak {g}}\) is in fact a Hopf Com-PreLie algebra, that is to say:
-
1.
\({\mathfrak {g}}\) has a commutative product
 and a coproduct \(\Delta \), making it a commutative Hopf algebra.
and a coproduct \(\Delta \), making it a commutative Hopf algebra. -
2.
\({\mathfrak {g}}\) has a nonassociative product \({\bullet }\) satisfying the (right) pre-Lie axiom: for all \(a,b,c\in {\mathfrak {g}}\), \(a{\bullet } (b{\bullet }c)- (a{\bullet }b){\bullet }c =a{\bullet } (c{\bullet }b)-(a{\bullet } c){\bullet }b\). The Lie bracket of \({\mathfrak {g}}\) is the antisymmetrization of \({\bullet }\).
-
3.
For all \(a,b,c \in {\mathfrak {g}}\), \((a{\bullet }b) {\bullet }c-a{\bullet } (b{\bullet }c)=(a{\bullet } c){\bullet }b-a {\bullet }(c{\bullet }b)\).
-
4.
For all
 , with Sweedler’s notations.
, with Sweedler’s notations.
Our aim in this text is to give a generalization of the construction of \({\mathfrak {g}}\) and its relative \(H\) and \(G\), and to study some general properties of this construction. Let us take any linear endomorphism \(f\) of a vector space \(V\). We inductively define a pre-Lie product \({\bullet }\) on the shuffle Hopf algebra  , making it a Com-PreLie Hopf algebra denoted by \(T(V,f)\) (Definition 2.1 and Theorem 2.2). For example, if \(x_1,x_2,x_3 \in V\) and \(w \in T(V)\), then
, making it a Com-PreLie Hopf algebra denoted by \(T(V,f)\) (Definition 2.1 and Theorem 2.2). For example, if \(x_1,x_2,x_3 \in V\) and \(w \in T(V)\), then

Here are some examples:
-
1.
Take \(V\) be one-dimensional and \(f=\mathrm{Id}\). Taking a basis \((x)\) of \(V\), we obtain a pre-Lie product on \({\mathbb {K}}[x]\) given by
$$\begin{aligned} x^i{\bullet }x^j=\left( {\begin{array}{c}i+j\\ i-1\end{array}}\right) x^{i+j}. \end{aligned}$$We shall prove that \({\mathbb {K}}[x]\) admits a basis \((y_n)_{n\ge 1}\) such that for all \(i,j \ge 0\),
$$\begin{aligned}{}[y_i,y_j]=(i-j)y_{i+j}. \end{aligned}$$Hence, \({\mathbb {K}}[x]_+=\mathrm{Vect}(y_i: i\ge 1)\) is isomorphic, as a Lie algebra, to the Faà di Bruno Lie algebra [7–9]. This case is studied in Sect. 4.1.
-
2.
Take \(V=\mathrm{Vect}(x_0,x_1)\) and \(f:V \rightarrow V\), with matrix in the basis \((x_0,x_1)\) given by
$$\begin{aligned} \left( \begin{matrix} 0&{}1\\ 0&{}0 \end{matrix}\right) . \end{aligned}$$The Com-PreLie Hopf algebra \(T(V,f)\) is precisely the one obtained from the group of Fliess operators in dimension \(1\). In dimension \(n \ge 2\), the group of Fliess operators admits a decomposition into a direct product of \(n\) subgroups \(G_1,\ldots ,G_n\). The group \(G_i\) is obtained from the Com-PreLie Hopf algebra \(T(V_i,f_i)\), where \(V_i=\mathrm{Vect}(x_0,\ldots ,x_n)\), and \(f_i\) is defined by \(f_i(v_j)=\delta _{ij}v_0\). These cases are studied in Sect. 4.2.
For any linear endomorphism \(f\), the Com-PreLie Hopf algebra \(T(V,f)\) is graded by the length of words. We study the existence of other gradations of \(T(V)\) as a pre-Lie algebra in Proposition 2.11. This holds for the pre-Lie algebra of Fliess operators. In this case, the dimension of the homogeneous parts of the gradation are given by the Fibonacci polynomials, Theorem 4.8, and consequently \(K\langle x_1,\ldots ,x_n\rangle \) is a minimal space of generators of \(T(V_i,f_i)\). In the one-dimensional case, we get in this way a result which was already proved in [10], where a presentation of the pre-Lie algebra of Fliess operators in dimension one is described.
According to [18, 19], we can give a description of the enveloping algebra \(\fancyscript{U}(T(V,f))\) in Theorems 2.13 and 2.14. We describe the dual Hopf algebra in Theorem 2.16 and its group of characters in Theorem 2.17; this group is in a certain sense the exponentiation of the lie algebra \(T(V,f)\). Because of the usual problems of duality of a infinite-dimensional Hopf algebra, we have to restrict here to the case where \(f\) is locally nilpotent. This holds in the Fliess operators case, and we indeed recover the group of Fliess operators in this way.
Using a generic case, we give systems of generators of \(T(V,f)\) as a pre-Lie algebra and as a Com-PreLie algebra. We also study the pre-Lie and Com-PreLie subalgebra of \(T(V,f)\) generated by a subspace \(W\) in the next section. We use for this a description of free Com-PreLie algebras in terms of partitioned trees [10]. First, the generic case proves that the pre-Lie subalgebra generated by \(V\) can be free, Theorem 3.18 and its Corollary 3.20; we give in Theorem 3.21 and Corollary 3.22 equivalent conditions for \(T_+(V,f)\) to be generated as a pre-Lie or as a Com-PreLie algebra by a subspace of \(V\) in terms of the codimension of \(\hbox {Im}\,f\). Applied to the Faà di Bruno case, this gives by duality an injection of the Faà di Bruno Hopf algebra into the Connes–Kreimer Hopf algebra of rooted trees, and we get in this way the subalgebra of formal diffeomorphisms defined in [3, 4].
This paper is organized in the following way. The first section groups all the algebraic structures associated to the linear endomorphism \(V\): the Com-PreLie algebra \(T(V,f)\), its enveloping algebra, the dual Hopf algebra and the associated group of characters. We also study the gradations of \(T(V,f)\) here. Generation by \(V\) and morphisms from free Com-PreLie algebras to \(T(V,f)\) are studied in the second section; it uses the notion of admissible words, whose study is reported to the appendix. The last section deals with the two main examples, the diagonalizable case, which leads to the Faà di Bruno Lie algebra, and the Fliess operators cases.
Notation
We denote by \({\mathbb {K}}\) a commutative field of characteristic zero. All the objects (algebra, coalgebras, pre-Lie algebras, etc.) in this text will be taken over \({\mathbb {K}}\).
2 Algebraic structures associated to a linear endomorphism
Notation
1. Let \(V\) be a \({\mathbb {K}}\)-vector field. We denote by \(T(V)\) the free associative, unitary algebra generated over \({\mathbb {K}}\) by \(V\):
As a vector space, it is generated by the set of words with letters in \(V\); the unit is the empty word \(\emptyset \) and the product is the concatenation of words. The augmentation ideal of \(T(V)\) is
2. We denote by \(\mathrm{Sh}(k,l)\) the set of \((k,l)\)-shuffles, that is to say permutations \(\sigma \in \mathfrak {S}_{k+l}\) such that \(\sigma (1)<\cdots <\sigma (k)\) and \(\sigma (k+1)<\cdots <\sigma (k+l)\).
3. \(T(V)\) is a commutative dendriform algebra (or Zinbiel algebra [5, 6, 13, 14, 16]), with the half-shuffle product \(\prec \): if \(k,l\ge 1\) and \(x_1,\ldots ,x_k,y_1,\ldots ,y_l \in V\), then
the \(n\)-th symmetric group acts on words of length \(n\) is by permutation of the letters. By convention, if \(w\) is a nonempty word, \(\emptyset {\prec } w=0\) and \(w {\prec } \emptyset =w\); note that \(\emptyset {\prec } \emptyset \) is not defined.
4. The induced commutative, associative product is the usual shuffle product  [21]:
[21]:

For all \(x,y \in V\) and \(u,v \in T(V)\),

Examples
If \(a,b,c,d\in V\), then

2.1 Construction of \(T(V,f)\)
We now fix a vector space \(V\) and a linear endomorphism \(f:V\rightarrow V\).
Definition 2.1
We define a bilinear product \({\bullet }\) on \(T(V)\) by induction on the length of words in the following way: for all \(x \in V\) and \(w,w'\in T(V)\), put

Examples
If \(x_1,x_2,x_3\in V\) and \(w\in T(V)\), then

Theorem 2.2
-
1.
For all \(a,b,c \in T(V)\),
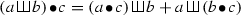 .
. -
2.
For all words \(a,b,c \in A\) with \((a,b) \ne (\emptyset ,\emptyset )\), \((a{\prec } b) {\bullet }c=(a{\bullet } c){\prec } b+a{\prec } (b{\bullet }c)\).
-
3.
For all \(a,b,c \in T(V)\), \((a{\bullet } b){\bullet }c -a{\bullet }(b{\bullet } c)=(a{\bullet }c) {\bullet }b-a{\bullet } (c{\bullet }b)\).
-
4.
For all
 .
.
By points 1 and 3,  is a Com-PreLie algebra [17]. This structure is denoted by \(T(V,f)\).
is a Com-PreLie algebra [17]. This structure is denoted by \(T(V,f)\).
Proof
1. We assume that \(a,b,c\) are words. If \(a=\emptyset \), then

If \(b=\emptyset \), then  . We now assume that \(a\ne \emptyset \) and \(b \ne \emptyset \). We prove the result by induction on \(n=\mathrm{lg}(a)+\mathrm{lg}(b)\). This is obvious if \(n\le 1\). Let us assume the result at rank \(n-1\). We put \(a=xu\) and \(b=yv\). Then
. We now assume that \(a\ne \emptyset \) and \(b \ne \emptyset \). We prove the result by induction on \(n=\mathrm{lg}(a)+\mathrm{lg}(b)\). This is obvious if \(n\le 1\). Let us assume the result at rank \(n-1\). We put \(a=xu\) and \(b=yv\). Then

2. If \(a=\emptyset \), \((\emptyset {\prec } b) {\bullet } c=0=(\emptyset { \bullet } b){\prec } c+\emptyset {\prec } (b {\bullet }c)\). If \(a=xu\), then

3. We assume that \(a,b,c\) are words and we proceed by induction on \(\mathrm{lg}(a)\). If \(a=\emptyset \), then
If \(a=xu\), then

The second and third terms are obviously symmetric in \(b\) and \(c\). By the induction hypothesis applied to \(u\), the first term is also symmetric in \(b\) and \(c\), so the pre-Lie relation is satisfied for \(a,b,c\).
4. Let us assume that \(a\) and \(b\) are words. We proceed by induction on the length of \(a\). If \(a=\emptyset \), then

If the length of \(a\) is \(\ge 1\), we put \(a=xu\). Applying the induction hypothesis to \(u\), we have


Hence, the result holds for all words \(a\) and \(b\). \(\square \)
Let us now give a closed formula for the pre-Lie product of two words.
Definition 2.3
Let \(k,l \in \mathbb {N}\). For all \(\sigma \in {\mathfrak {S}}_{k+l}\), we put
with the convention \(m_k(\sigma )=0\) if there is no \(i \in \{1,\ldots ,k\}\) such that \(\sigma (i)=i\).
Proposition 2.4
Let \(k,l \in \mathbb {N}\) and let \(x_1,\ldots ,x_{k+l} \in V\). Then

Proof
By induction on \(k\). If \(k=0\), then \(x_1\ldots x_k=\emptyset \). For all \(\sigma \in \mathrm{Sh}(0,l)\), \(m_0(\sigma )=0\) by convention, so
Let us assume the result at rank \(k-1\).

so the result holds for all \(k\). \(\square \)
Remark 2.5
In particular, if \(x_1,\ldots ,x_k \in V\), then
The pre-Lie product \({\bullet }\) is generally nonassociative, as proved in the following proposition.
Proposition 2.6
The following conditions are equivalent:
-
1.
\(\bullet \) is trivial.
-
2.
\(\bullet \) is associative.
-
3.
\(f=0\).
Proof
1 \(\Rightarrow \) 2. Obvious.
2 \(\Rightarrow \) 3. Let \(x\in V\). Then
so \(f^2=0\). Moreover,

Let us assume that \(f(x) \ne 0\). There exists \(g \in V^*\) such that \(g(f(x))=1\).
so there exists \(\lambda \in {\mathbb {K}}\) such that \(x=\lambda f(x)\). Then \(f(x)=\lambda f^2(x)=0\): this is a contradiction. Finally, \(f(x)=0\).
3 \(\Rightarrow \) 1. This is a direct consequence of Proposition 2.4. \(\square \)
Corollary 2.7
We have
Consequently, \(T(V,f){\bullet } T(V,f)\subseteq T_+(V,f)\).
Proof
We put
Proposition 2.4 directly implies that \(T(V,f){\bullet } T(V,f)\subseteq W\). Let
for \(1\le i \le n\). Let us prove that \(w \in T(V,f) {\bullet }T(V,f)\) by induction on \(i\). If \(i=1\), then
Let us assume the result at all ranks \(j<i\). So

If \(\sigma \in \mathrm{Sh}(i,n-i)\) is different from the identity of \({\mathfrak {S}}_n\), then \(m_i(\sigma )<i\). By the induction hypothesis, \(x_1\ldots x_i{\bullet }x_{i+1}\ldots x_n-x_1\ldots x_{i-1}f(x_i)x_{i+1}\ldots x_n \in T(V,f){ \bullet } T(V,f)\), so \(x_1\ldots x_{i-1}f(x_i)x_{i+1}\ldots x_n \in T(V,f) {\bullet }T(V,f)\). Finally, \(W=T(V,f){\bullet }T(V,f)\). \(\square \)
Notice that \({\mathbb {K}}\emptyset \) is a trivial pre-Lie subalgebra of \(T(V,f)\), and \(T_+(V,f)\) is a pre-Lie ideal of \(T(V,f)\). Hence
Proposition 2.8
As a Lie algebra, \(T(V,f)= T_+(V,f){\rtimes } {\mathbb {K}}\emptyset \). The right action of \(\emptyset \) on \(T(V,f)\) is given by
Proof
It remains to compute the bracket \([x_1\ldots x_k,\emptyset ]\). First
The result comes then from Proposition 2.4. \(\square \)
2.2 Functoriality
Lemma 2.9
Let \(W\) be a subspace of \(V\). We put
Then \(I\) is a Com-PreLie ideal of \(T(V,f)\) if and only if \(f(W)\subseteq W\). Moreover, if it is the case and if \(f\) is surjective, then \(I\) is generated by \(W\) as a Com-PreLie ideal.
Proof
\(I\) is clearly an ideal for the shuffle product. Let us assume that it is an ideal for \({\bullet }\) For all \(w\in W\), \(w \in I\), so \(w{\bullet }\emptyset =f(w) \in I\cap V=W\): \(W\) is stable under \(f\). Conversely, if \(f(W)\subseteq W\), by Proposition 2.4, \(I\) is an ideal for \({\bullet }\).
Let us assume that \(f\) is surjective. We denote by \(J\) the Com-PreLie ideal of \(T(V,f)\) generated by \(W\). As \(I\) is a Com-PreLie ideal of \(T(V,f)\) which contains \(W\), \(J \subseteq I\). Let \(w=x_1\ldots x_n \in V^{\otimes (i-1)}{\otimes } W{\otimes } V^{\otimes (n-i)}\), and let us prove that \(w \in J\) by induction on \(n\). If \(n=1\), then \(w\in W \subseteq J\). Let us assume the result at rank \(n-1\). If \(i\ge 2\), then \(x_2\ldots x_n \in J\). As \(f\) is surjective, there exists \(y_1 \in V\) such that \(f_1(y_1)=x_1\). Then
If \(i=1\), then \(x_1\in J\) and

We already proved that \(x_2 \ldots x_i x_1 x_{i+1}\ldots x_n\in J\) for all \(2\le i \le n\), so \(w \in J\). As a conclusion, \(I\subseteq J\). \(\square \)
Proposition 2.10
Let \(V_1,V_2\) be two vector spaces and \(f_1:V_1\rightarrow V_1\), \(f_2:V_2\rightarrow V_2\) be two endomorphisms. If \(f:V_1\rightarrow V_2\) satisfies \(f {\circ }f_1=f_2 {\circ }f\), then the following map is a morphism of Com-PreLie algebras:
Moreover, the image of this morphism is \(T(\mathrm{Im}\,f,(f_2)_{| \mathrm{Im}\,f})\) and its kernel is
If \(f_1\) its surjective, \(\mathrm{Ker}\,F\) is generated, as a Com-PreLie ideal, by \(\mathrm{Ker}\,f\).
Proof
The map \(F\) is clearly an algebra morphism from  to
to  . Let \(x_1,\ldots ,x_{k+l} \in V_1\). By Proposition 2.4,
. Let \(x_1,\ldots ,x_{k+l} \in V_1\). By Proposition 2.4,

So \(F\) is a pre-Lie algebra morphism. By Lemma 2.9, if \(f_1\) is surjective, then \(\mathrm{Ker}\,F\) is generated by \(\mathrm{Ker}\,f\). \(\square \)
2.3 Gradations of \(T(V,f)\)
By Proposition 2.4, the Com-PreLie algebra \(T(V,f)\) is graded by the the length of words. This is not a connected gradation of the pre-Lie algebra \(T(V,f)\), as \(\emptyset \) is homogeneous of degree \(0\). Let us now define other gradations, when \(V\) itself is graded.
Proposition 2.11
Let us assume that \(V\) admits a gradation \((V_n)_{n\ge 0}\) such that \(f\) is homogeneous of degree \(N \in {\mathbb {N}}\). For all \(n \ge 0\), we put
Then \((T(V,f)_n)_{n\ge 0}\) is a gradation of the pre-Lie algebra \(T(V,f)\).
Proof
Let \(u=x_1\ldots x_k\) and \(v=y_1\ldots y_l\) be two words of \(T(V,f)\) with homogeneous letters. Then \(u\) is homogeneous of degree \(\mathrm{deg}\,u=\mathrm{deg}\,x_1+\cdots +\mathrm{deg}\,x_k+N\) and \(v\) is homogeneous of degree \(\mathrm{deg}\,v=\mathrm{deg}\,y_1+\cdots +\mathrm{deg}\,y_l+N\). Let us prove that \(u{\bullet }v\) is homogeneous of degree \(\mathrm{deg}\,u+\mathrm{deg}\,v\). We proceed by induction on \(k\). If \(k=0\), then \(u=\emptyset \), \(u{\bullet }v=0\) and the result is obvious. If \(k\ge 1\), then

By the induction hypothesis, \(x_1\ldots x_k {\bullet } y\) is homogeneous of degree \(\mathrm{deg}\,x_2+\cdots +\mathrm{deg}\,x_k+N+\mathrm{deg}\,v\), so \(x_1 (x_2\ldots x_k {\bullet }y)\) is homogeneous of degree \(\mathrm{deg}\,x_1+\cdots +\mathrm{deg}\,x_k+N+\mathrm{deg}\,v=\mathrm{deg}\,u+\mathrm{deg}\,v\). Moreover, \(f(x_1)\) is homogeneous of degree \(\mathrm{deg}\,x_1+N\) and  is homogeneous of degree \(\mathrm{deg}\,x_2+\cdots +\mathrm{deg}\,x_k+\mathrm{deg}\,y_1+\cdots +\mathrm{deg}\,y_l+N\), so
is homogeneous of degree \(\mathrm{deg}\,x_2+\cdots +\mathrm{deg}\,x_k+\mathrm{deg}\,y_1+\cdots +\mathrm{deg}\,y_l+N\), so  is homogeneous of degree \(\mathrm{deg}\,x_1+N+\mathrm{deg}\,x_2+\cdots +\mathrm{deg}\,x_k+\mathrm{deg}\,y_1+\cdots +\mathrm{deg}\,y_l+N=\mathrm{deg}\,u+\mathrm{deg}\,v\). Finally, \(u{\bullet }v\) is homogeneous of degree \(\mathrm{deg}\,u+\mathrm{deg}\,v\). \(\square \)
is homogeneous of degree \(\mathrm{deg}\,x_1+N+\mathrm{deg}\,x_2+\cdots +\mathrm{deg}\,x_k+\mathrm{deg}\,y_1+\cdots +\mathrm{deg}\,y_l+N=\mathrm{deg}\,u+\mathrm{deg}\,v\). Finally, \(u{\bullet }v\) is homogeneous of degree \(\mathrm{deg}\,u+\mathrm{deg}\,v\). \(\square \)
Under the hypothesis of Proposition 2.11, \(T(V,f)\) is a bigraded pre-Lie algebra, with
If the gradation of \(V\) is finite-dimensional, then the bigradation of \(T(V,f)\) is finite-dimensional. We put
We obtain
Corollary 2.12
-
1.
Under the hypothesis of Proposition 2.11,
$$\begin{aligned} F_{T(V,f)}(X,Y)=\frac{X^N}{1-F_V(X)Y}. \end{aligned}$$ -
2.
Under the hypothesis of Proposition 2.11, if for all \(i\ge 0\), \(V_i\) is finite-dimensional and \(V_0=(0)\), then for all \(n \ge 0\), \(T(V,f)_n\) is finite-dimensional and
$$\begin{aligned} \sum _{n \ge 0} \mathrm{dim}\,T(V,f)_n\,X^n=\frac{X^N}{1-F_V(X)}. \end{aligned}$$Moreover, if \(N \ge 1\), then \(T(V,f)_0=(0)\).
Proof
1. Indeed, putting \(p_i=\mathrm{dim}\,V_i\) for all \(i\), we have
2. Take \(Y=1\) in the first point. \(\square \)
2.4 Enveloping algebra of \(T(V,f)\)
We use here the Oudom–Guin construction of the enveloping algebra on \(S(T(V,f))\) [18, 19]. In order to avoid confusions between the product of \(S(V)\) and the concatenation of words, we shall denote by \(\times \) the product of \(S(T(V,f))\) and by \(1\) its unit. We extend the pre-Lie product into a product from \(S(T(V,f)) {\otimes } S(T(V,f))\) into \(S(T(V,f))\) in the following way:
-
1.
If \(u_1,\ldots ,u_k \in T(V,f)\), \((u_1 {\times } \cdots {\times } u_k){\bullet }1=u_1 {\times }\cdots {\times } u_k\).
-
2.
If \(u,u_1,\ldots ,u_k \in T(V,f)\),
$$\begin{aligned} u{\bullet }(u_1{\times } \cdots {\times } u_k)=(u{\bullet }(u_1{\times } \cdots {\times } u_{k-1})){\bullet }u_k-u {\bullet }((u_1{\times } \cdots {\times }u_{k-1}) {\bullet }u_k). \end{aligned}$$ -
3.
If \(x,y,z\in S(T(V,f))\), \((x{\times } y) {\bullet }z=(x {\bullet }z^{(1)}) {\times }(y{\bullet } z^{(2)})\), where \(\Delta (z)=z^{(1)}{\otimes } z^{(2)}\) is the usual coproduct of \(S(T(V,f))\), defined by
$$\begin{aligned} \Delta (u_1{\times } \cdots {\times } u_k)= (u_1{\otimes } 1+1{\otimes } u_1){\times } \cdots {\times } (u_k {\otimes } 1+1{\otimes } u_k), \end{aligned}$$for all \(u_1,\ldots , u_k \in T(V,f)\).
In particular, if \(u_1,\ldots ,u_k,u\in T(V,f)\), then
Denoting by \(\star \) the associative product induced on \(S(T(V,f))\) by \(\bullet \), for all \(x,y\in S(T(V,f))\), we have
Notation
Let \(w_1,\ldots ,w_k \in T(V,f)\). For all \(I=\{i_1,\ldots ,i_p\}\subseteq \{1,\ldots ,k\}\), we put

With these notations, the coproduct of \(S(T(V,f))\) is given by
Theorem 2.13
Let \(w_1,\ldots ,w_k \in T(V,f)\), \(k\ge 0\), \(x\in V\), and \(w\in T(V,f)\). Then
-
1.
If \(k\ge 1\), \(\emptyset {\bullet } (w_1{\times } \cdots {\times } w_k)=0\).
-
2.
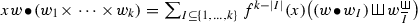 .
. -
3.
\(\emptyset {\star } (w_1{\times } \cdots {\times } w_k)=\emptyset {\times } w_1{\times } \cdots {\times } w_k\).
-
4.
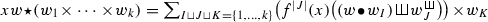 .
.
Proof
1. We proceed by induction on \(k\). If \(k=1\), \(\emptyset {\bullet }w_1=0\). Let us assume the result at rank \(k_1\). Then
By the induction hypothesis, both terms of this sum are equal to zero.
2. If \(k=0\), then

If \(k=1\), then

Let us assume the result at rank \(k-1\). For all \(I\subseteq \{1,\ldots ,k-1\}\), we denote by \(\widetilde{I}\) its complement in \(\{1,\ldots ,k-1\}\) and by \(\overline{I}=\widetilde{I}\cup \{k\}\) its complement in \(\{1,\ldots ,k\}\). Then

where \(w'_j=w_j\) if \(j\ne i\) and \(w'_i=w_i {\bullet }w_k\).
3 and 4. For all \(u\in T(V,f)\),
The results come then directly from points 1 and 2.\(\square \)
Theorem 2.14
Let \(x_1,\ldots ,x_i \in V\), \(w_1,\ldots ,w_k \in T(V,f)\), \(i\ge 1\), and \(k\ge 0\). If \(w=x_1\ldots x_i\), then

Proof
By induction on \(i\). If \(i=1\), then

so the result holds if \(k=1\). Let us assume the result at rank \(i-1\). Then

The induction hypothesis applied to \(x_2\ldots x_i{\bullet }w_J\) gives the result.\(\square \)
Remark 2.15
In particular,  .
.
2.5 Dual Hopf algebra
By duality, if \(f\) is locally nilpotent, the symmetric algebra \(S(T(V,f))\), with its usual product \(\times \), inherits a Hopf algebra structure. Let us describe its coproduct \(\mathrm \Delta \), dual to the product \(\star \) on \(S(T(V^*,f^*))\).
Theorem 2.16
Let us assume that \(f\) is locally nilpotent. We define a coproduct \(\widetilde{\Delta }\) on \(S(T(V,f))\) in the following way:
-
1.
\(\widetilde{\Delta }(\emptyset )=\emptyset {\otimes } 1\).
-
2.
If \(x \in V\) and \(u\in T(V,f)\), put
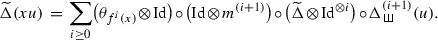
We used the iterated products \(m^{(j)}:S(T(V,f))^{\otimes j}\rightarrow S(T(V,f))\) and the iterated coproducts
 .
.
For all \(w\in T(V,f)\), we put \(\Delta (w)=\widetilde{\Delta }(w)+1 {\otimes } w\). With this coproduct, \(S(T(V,f))\) is a Hopf algebra.
Proof
We denote by \(g\) the transpose of \(f\). As \(S(T(V,f))\) is the dual of the enveloping algebra of a right pre-Lie algebra, for all \(w\in T(V,f)\),
We let \(\widetilde{\Delta }(w)=\Delta (w)-1{\otimes } w\) for all \(w\in T(V,f)\). Let \(v,v_1,\ldots ,v_k\) be words in \(T(V^*,f^*)\). If \(v\ne \emptyset \), then \(v{\bullet }v_1{\times } \cdots {\times } v_k \in T_+(V^*,f^*)\), so
If \(v=\emptyset \), then
So \(\widetilde{\Delta }(\emptyset )=\emptyset {\otimes } 1\). Let \(v_1,\ldots ,v_k \in T(V^*,f^*)\). Then

Let \(y\in V^*\) and \(v,v_1,\ldots ,v_k \in T(V^*,f^*)\). Then

This implies the announced result. \(\square \)
Examples
Let \(x_1,x_2 \in V\).
In particular, the second line shows that the condition of local nilpotence of \(f\) is necessary in order to obtain a coproduct with values in \(S(T(V,f)){\otimes } S(T(V,f))\).
2.6 Group of characters
Let us now describe the character group \(G\) associated to \(f\). Any character of \(S(T(V^*,f^*))\) is the extension of a linear map from \(T(V^*,f^*)\) to \({\mathbb {K}}\), so, as a set, we identify \(G\) and \( \prod _{n=0}^\infty (V^{**})^{\otimes n}\). The composition of \(G\) is denoted by \(\diamond \). We shall consider the following subset of \(G'\):
We give \(G'\) and \(\overline{T}(V)\) their usual ultrametric topology.
We shall prove that this is a subgroup of \(G\). Note that \(G=\overline{T}(V)\) if and only if \(V\) is finite-dimensional.
Theorem 2.17
We inductively define a continuous composition \(\widetilde{\diamond }\) on \(\overline{T}(V)\): for all \(v \in \overline{T}(V)\),
-
1.
\(\emptyset \widetilde{\diamond }v=\emptyset \).
-
2.
if \(x\in V\) and \(u \in G\),
 .
.
Then for all \(u,v \in G\), \(u{\diamond } v=u\widetilde{\diamond }v+v\).
Proof
We define a composition \(\widetilde{\triangleleft }\) on \(\overline{T}(V)\) by \(u\widetilde{\triangleleft }v(w)=(u{\otimes } v){\circ }\widetilde{\Delta }(w)\) for all \(w \in T(V,f)\). Then, for all \(w \in T(V,f)\),
So \(u{\diamond } v=u\widetilde{\triangleleft }v+v\).
Let \(w \in T(V,f)\). Then \((\emptyset \widetilde{\triangleleft }v)(w)=(\emptyset {\otimes } v){\circ }\widetilde{\Delta }(w)\). If \(w \ne \emptyset \), we observed that \(\widetilde{\Delta }(w)\in T_+(V,f) {\otimes } T(V,f)\), so \((\emptyset {\otimes } v){\circ }\widetilde{\Delta }(w)=0\). Hence, \(\emptyset \widetilde{\triangleleft }v=\lambda \emptyset \) for a particular \(\lambda \). If \(w=\emptyset \), we obtain \((\emptyset \widetilde{\triangleleft }v)(w)=\emptyset (\emptyset )v(1)=1\), so \(\lambda =1\).
Let us compute \(xu\widetilde{\triangleleft }v\). First, \(xu\widetilde{\triangleleft }v(\emptyset )=(xu {\otimes } v)(\emptyset {\otimes } 1)=0\). Let us take \(y\in V^*\) and \(w \in T(V^*,f^*)\). Then

So the composition \(\widetilde{\triangleleft }\) defined in this proof is the composition \(\widetilde{\diamond }\) defined in Theorem 2.17. Moreover, an easy induction on the length proves that for all words \(u\) and all \(w \in \overline{T}(V)\), \(u\widetilde{\diamond }w \in \overline{T}(V)\). By linearity and continuity, \(\overline{T}(V)\widetilde{\diamond } \overline{T}(V) \subseteq \overline{T}(V)\). \(\square \)
Now, by induction on \(k\) we get
Corollary 2.18
For all \(x_1,\ldots ,x_k \in V\) and \(v\in G\), we have

3 From free Com-PreLie algebras to \(T(V,f)\)
3.1 Free Com-PreLie algebras
Let us recall the construction of free Com-Prelie algebras [10].
Definition 3.1
-
1.
A partitioned forest is a pair \((F,I)\) such that:
-
\(F\) is a rooted forest (the edges of \(F\) being oriented from the roots to the leaves).
-
\(I\) is a partition of the vertices of \(F\) with the following condition: if \(x,y\) are two vertices of \(F\) which are in the same part of \(I\), then either they are both roots, or they have the same direct ascendant.
The parts of the partition are called blocks.
-
-
2.
We shall say that a partitioned forest is a partitioned tree if all the roots are in the same block.
-
3.
Let \({\fancyscript{D}}\) be a set. A partitioned tree decorated by \({\fancyscript{D}}\) is a pair \((t,d)\), where \(t\) is a partitioned tree and \(d\) is a map from the set of vertices of \(t\) into \({\fancyscript{D}}\). For any vertex \(x\) of \(t\), \(d(x)\) is called the decoration of \(x\).
-
4.
The set of isoclasses of partitioned trees will be denoted by \({\fancyscript{PT}}\). For any set \({\fancyscript{D}}\), the set of isoclasses of partitioned trees decorated by \({\fancyscript{D}}\) will be denoted by \({\fancyscript{PT}}({\fancyscript{D}})\).
Examples
We represent partitioned trees by the Hasse graph of the underlying rooted forest, the blocks of cardinality \(\ge 2\) being represented by horizontal edges of different colors. Here are the partitioned trees with \(\le 4\) vertices:

Definition 3.2
Let \(t=(t,I)\) and \(t'=(t',J) \in {\fancyscript{PT}}\).
-
1.
Let \(s\) be a vertex of \(t'\). The partitioned tree \(t{\bullet }_s t'\) is defined as follows:
-
As a rooted forest, \(t {\bullet }_s t'\) is obtained by grafting all the roots of \(t'\) on the vertex \(s\) of \(t\).
-
We put \(I=\{I_1,\ldots ,I_k\}\) and \(J=\{J_1,\ldots ,J_l\}\). The partition of the vertices of this rooted forest is \(I\sqcup J=\{I_1,\ldots ,I_k,J_1,\ldots ,J_l\}\).
-
-
2.
The partitioned tree
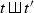 is defined as follows:
is defined as follows:-
As a rooted forest,
 is \(tt'\).
is \(tt'\). -
We put \(I=\{I_1,\ldots ,I_k\}\) and \(J=\{J_1,\ldots ,J_l\}\) and we assume that the set of roots of \(t\) is \(I_1\) and the set of roots of \(t'\) is \(J_1\). The partition of the vertices of
 is \(\{I_1\sqcup J_1,I_2,\ldots ,I_k,J_1,\ldots ,J_l\}\).
is \(\{I_1\sqcup J_1,I_2,\ldots ,I_k,J_1,\ldots ,J_l\}\).
-
Examples
-
1.
Here are the three possible graftings
 and
and  .
. -
2.
Here are the two possible graftings
 and
and  .
. -
3.
 .
.
These operations are similarly defined for decorated partitioned trees.
The free nonunitary Com-PreLie algebra is described in [10].
Proposition 3.3
Let \({\fancyscript{D}}\) be a set. The free nonunitary Com-PreLie algebra \(\mathrm{ComPrelie}({\fancyscript{D}})\) generated by \({\fancyscript{D}}\) is the vector space generated by \({\fancyscript{PT}}({\fancyscript{D}})\). We extend  by bilinearity and the pre-Lie product \(\bullet \) is defined on in the following way: if \(t,t'\in {\fancyscript{PT}}({\fancyscript{D}})\), put
by bilinearity and the pre-Lie product \(\bullet \) is defined on in the following way: if \(t,t'\in {\fancyscript{PT}}({\fancyscript{D}})\), put
It satisfies the following universal property: if \(A\) is a Com-PreLie algebra and \(a_d \in {\fancyscript{D}}\) for all \(d \in {\fancyscript{D}}\), there exists a unique Com-PreLie algebra morphism \(\phi :\mathrm{ComPrelie}({\fancyscript{D}})\rightarrow A\) such that  for all \(d \in {\fancyscript{D}}\).
for all \(d \in {\fancyscript{D}}\).
Rooted trees are identified with partitioned rooted trees such that any block has cardinality one. The free pre-Lie algebra \(\mathrm{Prelie}({\fancyscript{D}})\), which is based on decorated rooted trees [2], is seen as a pre-Lie subalgebra of \(\mathrm{ComPrelie}({\fancyscript{D}})\).
3.2 A generic case
Definition 3.4
-
1.
Let \({\fancyscript{D}}\) be a set. The set of biletters in \({\fancyscript{D}}\) is \(\mathbb {N}{\times } {\fancyscript{D}}\). A biletter will be denoted by \(\left( {\begin{array}{c}k\\ d\end{array}}\right) \), with \(k\in \mathbb {N}\) and \(d\in {\fancyscript{D}}\). A biword in \({\fancyscript{D}}\) is a word in biletters in \({\fancyscript{D}}\).
-
2.
Let \(V_{\fancyscript{D}}\) be the space generated by the biletters in \({\fancyscript{D}}\). We define a map \(f_{\fancyscript{D}}:V_{\fancyscript{D}}\rightarrow V_{\fancyscript{D}}\) by \(f_{\fancyscript{D}}\bigl (\left( {\begin{array}{c}k\\ i\end{array}}\right) \bigr ) =\left( {\begin{array}{c}k+1\\ i\end{array}}\right) \) for all \(k\ge 0\) and \(d\in {\fancyscript{D}}\).
-
3.
The pre-Lie subalgebra \(T(V_{\fancyscript{D}},f_{\fancyscript{D}})\) generated by the billeters \(\left( {\begin{array}{c}0\\ d\end{array}}\right) \), \(d \in {\fancyscript{D}}\), is denoted by \({\mathfrak {g}}_{\fancyscript{D}}\).
The pair \((V_{\fancyscript{D}},f_{\fancyscript{D}})\) satisfies a universal property
Proposition 3.5
Let \(V\) be a vector space, \(g:V\rightarrow V\) a linear map, and for all \(d\in {\fancyscript{D}}\), \(x_d \in V\). There exists a unique linear map \(F:V_{\fancyscript{D}}\rightarrow V\) such that \(F{\circ } f_{\fancyscript{D}}=g{\circ }F\) and \(F\left( {\begin{array}{c}0\\ d\end{array}}\right) =x_d\) for all \(d\in {\fancyscript{D}}\).
This map is \(F\left( {\begin{array}{c}k\\ d\end{array}}\right) =g^k(x_d)\).
3.3 Generation of \(T(V_{\fancyscript{D}},f_{\fancyscript{D}})\)
We now assume that \({\fancyscript{D}}\) is a totally ordered set. Consequently, the set of biletters \(\left( {\begin{array}{c}0\\ d\end{array}}\right) \), \(d\in {\fancyscript{D}}\), is also totally ordered.
Proposition 3.6
-
1.
The pre-Lie algebra \(T(V_{\fancyscript{D}},f_{\fancyscript{D}})\) is generated by the set of words in biletters \(\left( {\begin{array}{c}0\\ d\end{array}}\right) \), \(d\in {\fancyscript{D}}\). Moreover, this set is a minimal set of generators.
-
2.
The Com-PreLie algebra \(T(V_{\fancyscript{D}},f_{\fancyscript{D}})\) is generated by \(\emptyset \) and the set of Lyndon words in biletters \(\left( {\begin{array}{c}0\\ d\end{array}}\right) \), \(d\in {\fancyscript{D}}\). Moreover, this set is a minimal set of generators.
Proof
1. We denote by \(W\) the subspace of \(V_{\fancyscript{D}}\) generated by the biletters \(\left( {\begin{array}{c}0\\ d\end{array}}\right) \), \(d\in {\fancyscript{D}}\). Let \(A\) be the pre-Lie subalgebra of \(T(V_{\fancyscript{D}},f_{\fancyscript{D}})\) generated by \(T(W)\). Let \(w=x_1\ldots x_n\) be a word in biletters \(\left( {\begin{array}{c}i\\ d\end{array}}\right) \), \(i\ge 0\), \(d\in {\fancyscript{D}}\). If all its biletters are of the form \(\left( {\begin{array}{c}0\\ d\end{array}}\right) \), then it belongs to \(T(W) \subseteq A\). Let us now assume that it contains at least one biletter \(\left( {\begin{array}{c}i\\ d\end{array}}\right) \), with \(i\ge 1\). We prove that \(w\in A\) by induction on \(n\). If \(n=1\), we put \(x_1=\left( {\begin{array}{c}i\\ d\end{array}}\right) \), and
So the result is true at rank \(1\). Let us assume it at all ranks \(<n\), \(n \ge 2\). Let \(k\) be the smallest integer such that \(x_k=\left( {\begin{array}{c}i\\ d\end{array}}\right) \), with \(i\ge 1\). We proceed by induction on \(k\). If \(k=1\), then by the induction hypothesis on \(n\), \(x_2,\ldots , x_n \in A\), and by Theorem 2.14,
Let us assume the result at all ranks \(<k\), \(k\ge 2\). We already know that \(x_1\ldots x_{k-1}\left( {\begin{array}{c}0\\ d\end{array}}\right) \), and \( x_{k+1}\ldots x_n \in A\). By Theorem 2.14,
So \(x_1\ldots x_n \in A\). Finally, \(T(V_{\fancyscript{D}},f_{\fancyscript{D}})\) is generated by \(T(W)\) as a pre-Lie algebra.
As \(\mathrm{Im}\,f_{\fancyscript{D}}\cap W=(0)\), by Corollary 2.7,
So \(T(W)\) is a minimal subspace of generators of \(T(V_{\fancyscript{D}},f_{\fancyscript{D}})\).
2. Let \(W'\) be the subspace of \(T(V_{\fancyscript{D}},f_{\fancyscript{D}})\) generated by \(\emptyset \) and the Lyndon words in biletters \(\left( {\begin{array}{c}0\\ d\end{array}}\right) \). We denote by \(B\) the Com-PreLie subalgebra of \(T(V_{\fancyscript{D}},f_{\fancyscript{D}})\) generated by \(W\). Then \(B\) contains the subalgebra generated by \(W'\) (for the product  ), that is to say the shuffle algebra \(T(W)\). By the first point, \(B=T(V_{\fancyscript{D}},f_{\fancyscript{D}})\).
), that is to say the shuffle algebra \(T(W)\). By the first point, \(B=T(V_{\fancyscript{D}},f_{\fancyscript{D}})\).
Let us prove now the minimality of \(W'\). First, Lyndon words are a minimal system of generators of the shuffle algebra \(T(W)\). Moreover, \(T(V_{\fancyscript{D}},f_{\fancyscript{D}}) {\bullet } T(V_{\fancyscript{D}},f_{\fancyscript{D}})\) is contained in the set of words in biletters \(\left( {\begin{array}{c}i\\ d\end{array}}\right) \), so

Consequently, \(W'\) is a minimal subspace of generators of  . \(\square \)
. \(\square \)
Corollary 3.7
Let \(V\) be a vector space and let \(g:V\rightarrow V\). Let \(W\) be a subspace of \(V\) such that
Then \(T(V,g)\) is generated, as a pre-Lie algebra, by \(T(W)\). We give \(W\) a totally ordered basis \((w_d)_{d\in D}\). Then \(T(V,g)\) is generated, as a Com-PreLie algebra, by \(\emptyset \) and the set of Lyndon words in letters \(w_d\), \(d\in {\fancyscript{D}}\).
Proof
Let \(f:V_{\fancyscript{D}}\rightarrow V\) be the unique map such that \(f{\circ }f_{\fancyscript{D}}=g {\circ }f\), and let \(F:T(V_{\fancyscript{D}},f_{\fancyscript{D}}) \rightarrow T(V,g)\) be obtained by functoriality. We obtain
so \(\mathrm{Im}\,F=T(\mathrm{Im}\,f)=T(V,g)\). As \(T(V_{\fancyscript{D}},f_{\fancyscript{D}})\) is generated, as a pre-Lie algebra, by the words in biletters \(\left( {\begin{array}{c}0\\ d\end{array}}\right) \), \(T(V,g)\) is generated by their images, that is to say words in \(W\).
As \(T(V_{\fancyscript{D}},f_{\fancyscript{D}})\) is generated, as a Com-PreLie algebra, by \(\emptyset \) and the Lyndon words in biletters \(\left( {\begin{array}{c}0\\ d\end{array}}\right) \), \(d\in {\fancyscript{D}}\), \(T(V,g)\) is generated by their images, that is to say \(\emptyset \) and the Lyndon words in letters \(w_d\), \(d\in {\fancyscript{D}}\). \(\square \)
Remark 3.8
-
1.
If \(W\) is \(1\)-dimensional, that is to say if \((V,g)\) is cyclic, then \(T(V,g)\) is generated, as a Com-PreLie algebra, by \(\emptyset \) and any nonzero element of \(W\).
-
2.
These sets of generators are not necessarily minimal. For example, if \(g\) is surjective, we shall prove in Lemma 4.6 that \(\emptyset \) and \(W\) generate \(T(V,g)\), even if \(V\) is not one-dimensional.
3.4 A morphism from partitioned trees to words in biletters
Our aim is now to prove that \({\mathfrak {g}}_{\fancyscript{D}}\), the pre-Lie subalgebra of \(T(V_{\fancyscript{D}},f_{\fancyscript{D}})\) generated by the biletters \(\left( {\begin{array}{c}0\\ d\end{array}}\right) \), \(d\in {\fancyscript{D}}\), is free. We shall use the following morphism.
Definition 3.9
We denote by \({\Phi }_{\mathrm{CPL}}\) the Com-PreLie algebra morphism defined by

Its restriction to \(\mathrm{Prelie}({\fancyscript{D}})\) is denoted by \({\Phi }_\mathrm{PL}\). Note that \({\mathfrak {g}}_{\fancyscript{D}}={\Phi }_\mathrm{PL}(\mathrm{ComPrelie}({\fancyscript{D}}))\).
Examples
Let \(a,b,c,d \in {\fancyscript{D}}\).

Remark 3.10
\({\Phi }_{\mathrm{CPL}}\) is not injective: for any \(d \in {\fancyscript{D}}\),  . However, we will prove that the restriction \({\Phi }_\mathrm{PL}\) is injective, Theorem 3.18.
. However, we will prove that the restriction \({\Phi }_\mathrm{PL}\) is injective, Theorem 3.18.
By the universal property of \(V_{\fancyscript{D}}\) and the factoriality of the construction of \(T(V,f)\) we have
Theorem 3.11
Let \(V\) be a vector space, \(f:V\rightarrow V\) a linear map and \(x_d \in V\) for all \(d\in {\fancyscript{D}}\). The following map is a Com-PreLie algebra morphism:
Moreover, denoting by \(W\) the smallest subspace of \(V\) stable under \(f\) and containing all \(x_d\), the image of \(\varphi _{(V,f)}\) is \(T(W)\).
Definition 3.12
Let \(t\) be a partitioned tree decorated by \({\fancyscript{D}}\).
-
1.
The number of vertices of \(t\) is denoted by \(|t|\).
-
2.
Let \(s\) be a vertex of \(t\).
-
The fertility of \(s\) is the number of blocks \(B\) such that there is an edge from \(s\) to any vertex of \(B\). It is denoted by \(\mathrm{fert}(t)\).
-
The decoration of \(s\) is denoted by \(d(s)\).
-
-
3.
A linear extension of \(t\) is a bijection \(\sigma :\{1,\ldots ,|t|\}\rightarrow \mathrm{Vert}(t)\) such that if \(x\) is a child of \(y\), then \(\sigma ^{-1}(x)>\sigma ^{-1}(y)\) (the edges of \(t\) being oriented from the roots to the leaves). The set of linear extensions of \(t\) is denoted by \(L(t)\).
Let us now give a direct description of \({\Phi }_{\mathrm{CPL}}\).
Proposition 3.13
For all partitioned tree decorated by \({\fancyscript{D}}\),
Proof
By induction on \(n=|t|\). It is obvious if \(n=0\) or \(n=1\). Let us assume the result at all ranks \(<n\). Two cases can occur.
First case. Let us assume that \(t\) has several roots. We can write  , with \(t_1,t_2\) two partitioned trees with \(<n\) vertices. Let us denote by \(k\) and \(l\) the number of vertices of \(t_1\) and \(t_2\). Then
, with \(t_1,t_2\) two partitioned trees with \(<n\) vertices. Let us denote by \(k\) and \(l\) the number of vertices of \(t_1\) and \(t_2\). Then
Hence, by the induction hypothesis applied to \(t_1\) and \(t_2\),

Second case. Let us assume that \(t\) has a single root. Let  be the partitioned tree obtained by deleting the root of \(t\), where \(t_1,\ldots ,t_k\) are partitioned trees with a single root. If \(d\) is the decoration of the root of \(t\), then
be the partitioned tree obtained by deleting the root of \(t\), where \(t_1,\ldots ,t_k\) are partitioned trees with a single root. If \(d\) is the decoration of the root of \(t\), then  . We put \(w_i={\Phi }_{\mathrm{CPL}}(t_i)\) for all \(i\). Then, by Theorem 2.13,
. We put \(w_i={\Phi }_{\mathrm{CPL}}(t_i)\) for all \(i\). Then, by Theorem 2.13,

Moreover, for all \(\sigma \in L(t)\), \(\sigma (1)\) is the root of \(t\). Hence
Finally,
So the result holds for all partitioned trees \(t\). \(\square \)
Remark 3.14
If \(t\) is a partitioned tree with \(k\) blocks, then
Moreover, this is an equality if and only if \(t\) is a rooted tree. Hence, for all partitioned trees of degree \(n\), \({\Phi }_{\mathrm{CPL}}(t)\) is a sum of biwords of length \(n\), such that the sum of its upper letters is \(\le n-1\). Consequently, \({\Phi }_{\mathrm{CPL}}\) is not surjective.
3.5 Freeness of \({\mathfrak {g}}_{\fancyscript{D}}\)
We now prove that the restriction of \({\Phi }_\mathrm{CPL}\) to the the free pre-Lie algebra \(\mathrm{Prelie}({\fancyscript{D}})\) is injective. We shall use certain families of biwords.
Definition 3.15
Let \(w=\left( {\begin{array}{c}a_1\ldots a_n\\ d_1\ldots d_n\end{array}}\right) \) be a biword.
-
1.
We shall say that \(w\) is admissible if:
-
For all \(1\le i \le n\), \(a_i+\cdots +a_n\le n-i\).
-
\(a_1+\cdots +a_n=n-1\).
-
-
2.
We shall say that \(w\) is \(\sigma \)-admissible if it can be written as \(w=w_1\ldots w_k\), with \(w_1,\ldots ,w_k\) admissible.
Examples
-
1.
Here are the possible upper words for admissible words of length \(\le 4\):
$$\begin{aligned} 0;\quad 10;\quad 200,\;110;\quad 3000,\;2100,\;1200,\;2010,\;1110. \end{aligned}$$ -
2.
Here are the possible upper words for \(\sigma \)-admissible words of length \(\le 4\):
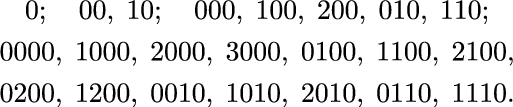
Remark 3.16
If \(w=\left( {\begin{array}{c}a_1\ldots a_n\\ d_1\ldots d_n\end{array}}\right) \) is admissible and \(n\ge 1\), then \(a_n\le n-n=0\), so \(a_n=0\).
Lemma 3.17
-
1.
Let \(w=\left( {\begin{array}{c}a_1\ldots a_n\\ d_1\ldots d_n\end{array}}\right) \) be a \(\sigma \)-admissible biword. Then it can be uniquely written as \(w=w_1\ldots w_k\), with \(w_1,\ldots ,w_k\) admissible. Moreover, \(a_1+\cdots +a_n=n-k\).
-
2.
Let \(w=\left( {\begin{array}{c}a_1\ldots a_n\\ d_1\ldots d_n\end{array}}\right) \) be a \(\sigma \)-admissible word. Then for all \(1\le i\le n\), \(a_i+\cdots +a_n\le n-i\).
-
3.
Let \(w=\left( {\begin{array}{c}a_1\ldots a_n\\ d_1\ldots d_n\end{array}}\right) \) be a word such that for all \(1\le i\le n\), \(a_i+\cdots +a_n \le n-i\). We put \(k=n-(a_1+\cdots +a_n)\). Then \(k\ge 1\) and for \(d\in {\fancyscript{D}}\), \(\left( {\begin{array}{c}ka_1\ldots a_n\\ dd_1\ldots d_n\end{array}}\right) \) is admissible.
Proof
1. Let \(w=w_1\ldots w_k=w'_1\ldots w'_l\) be two decompositions of \(w\) in admissible words. Then
Similarly, \(a_1+\cdots +a_n=n-l\), so \(k=l\). Let us assume that \(w_1\) is formed by the first \(i\) biletters of \(w\), \(w'_1\) is formed by the first \(j\) biletters of \(w\), with \(i<j\). As \(w_1\) and \(w'_1\) are admissible, \(a_1+\cdots +a_j=j-1\) and \(a_1+\cdots +a_i=i-1\), so \(a_{i+1}+\cdots +a_j=(j-1)-(i-1)=j-i\). As \(w'_1\) is admissible, \(a_{i+1}+\cdots +a_j \le j-i-1\): this is a contradiction. So \(i=j\), and \(w_1=w'_1\); hence, \(w_2\ldots w_k=w'_2\ldots w'_k\). Iterating the process, \(w_2=w'_2,\ldots , w_k=w'_k\).
2. We put \(w=w_1\ldots w_k\), where \(w_1,\ldots ,w_k\) are admissible. We put, for all \(i\), \(w_i=\left( {\begin{array}{c}a_{i1}\ldots a_{il_i}\\ d_{i1}\ldots d_{il_i}\end{array}}\right) \). For all \(i,j\), we have
Hence, if \(w=\left( {\begin{array}{c}a_1\ldots a_n\\ d_1\ldots d_n\end{array}}\right) \), for all \(1\le i\le n\), \(a_i+\cdots +a_n\le n-i\).
3. We put \(b_1\ldots b_{n+1}=ka_1\ldots a_n\). If \(2\le i\le n+1\), then
Moreover, \(b_1+\cdots +b_{n+1}=k+a_1+\cdots +a_n=n=(n+1)-1\). So \(\left( {\begin{array}{c}b_1\ldots b_{n+1}\\ d_1\ldots d_{n+1}\end{array}}\right) \) is admissible. \(\square \)
Theorem 3.18
The map \({\Phi }_\mathrm{PL}:\mathrm{Prelie} ({\fancyscript{D}})\rightarrow T(V_{\fancyscript{D}},f_{\fancyscript{D}})\) is injective.
Proof
We shall consider the subalgebra (for the product  ) generated by \(\mathrm{Prelie}({\fancyscript{D}})\) in \(\mathrm{ComPrelie}({\fancyscript{D}})\). We denote it by \({\fancyscript{H}}_{\fancyscript{D}}\). A basis of \({\fancyscript{H}}_{\fancyscript{D}}\) is given by the set of partitioned trees decorated by \({\fancyscript{D}}\) such that any block has cardinality \(1\), except the block containing the roots. Forgetting the blocks, these special partitioned trees are identified with rooted forests. Here are for example rooted forests with \(\le 4\) vertices:
) generated by \(\mathrm{Prelie}({\fancyscript{D}})\) in \(\mathrm{ComPrelie}({\fancyscript{D}})\). We denote it by \({\fancyscript{H}}_{\fancyscript{D}}\). A basis of \({\fancyscript{H}}_{\fancyscript{D}}\) is given by the set of partitioned trees decorated by \({\fancyscript{D}}\) such that any block has cardinality \(1\), except the block containing the roots. Forgetting the blocks, these special partitioned trees are identified with rooted forests. Here are for example rooted forests with \(\le 4\) vertices:

Let \({\fancyscript{W}}_n\) be the set of \(\sigma \)-admissible words of length \(n\) and let \({\fancyscript{W}}\) be the union of \({\fancyscript{W}}_n\). We choose a total order on \({\fancyscript{W}}\) such that:
-
1.
If \(u\in {\fancyscript{W}}_m\) and \(v\in {\fancyscript{W}}_n\) with \(m>n\), then \(u>v\).
-
2.
For all \(n\ge 0\) and all \(d\in {\fancyscript{D}}\) the following map is increasing:
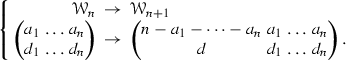
Note that this map takes its values in the set of admissible words, by Lemma 3.17.
-
3.
If \(u=u_1\ldots u_k\) and \(v=v_1\ldots v_l\) are two elements of \({\fancyscript{W}}_n\) decomposed into admissible words, and if for a particular index \(i\), \(u_k=v_l\), \(u_{k-1}=v_{l-1}\), \(\ldots \), \(u_{k-i+1}=v_{k-i+1}\) and \(u_{k-i}>v_{l-i}\), then \(u>v\).
For any decorated rooted forest \(F\) (still identified with a partitioned tree by putting all the roots in the same block), we inductively define a biword \(w_F\) in the following way:
-
\(w_1=\emptyset \).
-
If \(F\) is not a tree, we put \(F=t_1\ldots t_k\), indexed so that \(w_{t_1}\le \cdots \le w_{t_k}\). Then \(w_F=w_{t_1}\ldots w_{t_k}\).
-
If \(F\) is a tree, let \(d\) be the decoration of its root and let \(t_1\ldots t_k\) be the forest obtained by deleting the root of \(F\), its trees being indexed so that \(w_{t_1}\le \cdots \le w_{t_k}\). Then \(w_F=\left( {\begin{array}{c}k\\ d\end{array}}\right) w_{t_1}\ldots w_{t_k}\).
First step. Let us prove that for all rooted forest \(F\):
-
1.
The coefficient of \(w_F\) in \({\Phi }_{\mathrm{CPL}}(F)\) is not zero.
-
2.
\(w_F\) is \(\sigma \)-admissible. Moreover, if \(F\) is a tree, \(w_F\) is admissible.
We proceed by induction on the number \(n\) of vertices of \(F\). If \(n=0\), this is obvious. Let us assume the result at all ranks \(<k\). If \(F\) is not a tree, we put \(F=t_1\ldots t_k\). By the induction hypothesis, \(w_{t_1},\ldots , w_{t_k}\) are admissible, so \(w_{t_1}\ldots w_{t_k}\) is \(\sigma \)-admissible. For all \(1\le i \le k\), there exists a linear extension \(\sigma _i\) of \(t_i\) such that
Then \(\sigma =\sigma _1{\otimes } \cdots {\otimes }\sigma _k\) is a linear extension of \(F\) and
so this biword appears in \({\Phi }_{\mathrm{CPL}}(F)\). If \(F\) is a tree, keeping the notations of the the definition of \(w_F\), by the induction hypothesis, \(w_{t_1},\ldots ,w_{t_k}\) are admissible. By Lemma 3.17, \(\left( {\begin{array}{c}k\\ d\end{array}}\right) w_{t_1}\ldots w_{t_k}\) is admissible. For all \(1\le i \le k\), there exists a linear extension \(\sigma _i\) of \(t_i\) such that
Then \(\sigma =(1){\otimes } \sigma _1{\otimes } \cdots {\otimes }\sigma _k\) is a linear extension of \(F\) and
so this biword appears in \({\Phi }_{\mathrm{CPL}}(F)\).
Second step. Let \(F,G\) be two forests such that \(w_F=w_G\). As \(w=w_F=w_G\) appears in \({\Phi }_{\mathrm{CPL}}(F)\) and \({\Phi }_{\mathrm{CPL}}(G)\), then the number of vertices of \(F\) and \(G\) is the length \(n\) of \(w\). Let us prove that \(F=G\) by induction on \(n\). It is obvious if \(n=1\). Let us assume the result at all ranks \(<n\). Let us put \(F=t_1\ldots t_k\), and \(G=t'_1\ldots t'_l\). As the biwords \(w_{t_i}\) are admissible, by Lemma 3.17, the sum of letters of \(w\) is \(n-k\); similarly, this sum is \(n-l\), so \(k=l\). If \(k\ge 2\), by the unicity of the decomposition of \(w\) into admissible biwords, \(w_{t_i}=w_{t'_i}\) for all \(i\). By the induction hypothesis, \(t_i=t'_i\) for all \(i\), so \(F=G\). If \(k=1\), considering the first biletter of \(w\), the roots of \(F\) and \(G\) have the same decoration and the same fertility. Considering the biword obtained by deleting the first biletter of \(w\), if \(F'\) and \(G'\) are the forests obtained by deleting the roots of \(F\) and \(G\), the induction hypothesis implies that \(F'=G'\); hence, \(F=G\).
Third step. For all forests \(F\), we put
By the preceding observations, \(w'_F\) exists and \(w'_F \ge w_F\). Let us prove that \(w'_F=w_F\) for any forest \(F\). We proceed by induction on the number \(n\) of vertices of \(F\). It is obvious if \(F=1\). Let us assume the result at all ranks \(<n\).
We put \(w'_F=w_1 \ldots w_k\), with \(w_1\ldots w_k\) admissible, and \(f\) the linear extension of \(F\) corresponding to \(w'_F\). For all \(1\le i \le k\), let \(X_i\) be the subset of the vertices of \(F\) corresponding to the biletters of \(w_i\). If \(x \in X_i\) and \(y\in X_j\) is a child of \(x\) in \(F\), then as \(f\) is a linear extension of \(F\), \(j \ge i\). So for all \(1\le i\le k\), \(F_i=X_i\sqcup \cdots \sqcup X_k\) is an ideal of \(F\), and \(w_i\ldots w_k\) appears in \({\Phi }_{\mathrm{CPL}}(F_i)\). By Lemma 3.17, the sum of the first letters of \(w_i\ldots w_k\) is \(|F_i|-(k-i+1)=|F_i|-\mathrm{lg}(F_i)\), so \(F_i\) is a forest of \(k-i+1\) trees.
Let us assume there exists an index \(i\) such that \(F_i\) is not the disjoint union of a tree formed by the vertices in \(X_i\) and \(F_{i+1}\). We choose \(i\) maximal; for all \(j>i\), let \(t_j\) be the tree formed by the vertices of \(X_j\) such that \(F_{i+1}=t_{i+1}\ldots t_k\). As \(F_i\) is a forest of length \(k-i+1\), and \(X_i\) does not form a subtree of \(F_i\), \(X_i\) forms a forest \(s_1\ldots s_l\) with \(l>1\), and at least one of \(s_p\), say \(s_l\) for example, has for a child a root of one of \(t_j\). Let \(t\) be the subtree of \(F\) containing \(s_l\) and \(t_j\). Then a word of the form \(\ldots w_t w_{t_{j+1}}\ldots w_{t_k}\) appears in \({\Phi }_{\mathrm{CPL}}(F)\). As \(|t|>|t_j|\), by the first condition on the order on admissible words, \(w_{t_{j+1}}>w_{t_j}\). By the third condition on the order, \(\ldots w_t w_{t_{j+1}}\ldots w_{t_k}>w_{t_1}\ldots w_{t_k}=w'_F\): this contradicts the maximality of \(w'_F\). We obtain that \(F=t_1\ldots t_k\), the vertices of \(t_i\) corresponding via \(f\) to the billetters of \(w_i\) for all \(i\). Consequently, \(w_i\le w'_{t_i}=w_{t_i}\) for all \(i\).
Let us assume that \(i<j\) and \(w_i>w_j\). Shuffling the biletters corresponding to the vertices of \(t_i\) and \(t_j\), \(w_1\ldots w_j \ldots w_i \ldots w_k\) also appears in \({\Phi }_{\mathrm{CPL}}(F)\) and is strictly greater than \(w'_F\), by the third condition on the order: a contradiction. So \(w_1\le \cdots \le w_k\).
Let us assume that \(k\ge 2\). We put \(F=t'_1\ldots t'_k\), with \(w_{t'_1}\le \cdots \le w_{t'_k}\), such that \(w_F=w_{t'_1}\ldots w_{t'_k}\). By the induction hypothesis, for all \(i\), \(w_{t'_i}=w'_{t'_i}\). In particular, \(w_k\le w'_{t_k}\le w_{t'_k}\), as \(t_k\) is one of \(t'_j\). If \(w_k<w_{t'_k}\), then \(w_1\ldots w_k<w_F\) by the third condition of the total order, and this contradicts the maximality of \(w'_F\). So \(w_k=w'_{t'_k}\). Moreover, \(w_1\ldots w'_{t_k}\) also appears in \({\Phi }_{\mathrm{CPL}}(F)\); by maximality of \(w'_F\), necessarily \(w'_{t_k}\le w_k\), so \(w'_{t_k}=w_k\). By the second step, \(t_k=t'_k\). We then obtain that \(t_1\ldots t_{k-1}=t'_1\ldots t'_{k-1}\) and that \(w'_{t_1\ldots t_{k-1}}=w_1\ldots w_{k-1}\). By the induction hypothesis, \(w_1\ldots w_{k-1}=w_{t'_1}\ldots w_{t'_{k-1}}\), so \(w'_F=w_F\).
Let us assume that \(k=1\). Let \(d\) the decoration of the root of \(F\), \(l\) its fertility and \(G\) be the forest obtained by deleting the root of \(F\). Then \({\Phi }_{\mathrm{CPL}}(F)=\left( {\begin{array}{c}l\\ d\end{array}}\right) {\Phi }_{\mathrm{CPL}}(G)\). By the second condition on the total order on \(\sigma \)-admissible biwords, \(w'_F=\left( {\begin{array}{c}l\\ d\end{array}}\right) w'_G\). By the induction hypothesis, \(w'_G=w_G\), so \(w'_F=w_F\).
Last step. Let \(x=\sum a_F F\) be a nonzero element of \({\fancyscript{H}}_{\fancyscript{D}}\). As \(F\rightarrow w_F\) is injective by the second step, let us totally order the set of decorated rooted forests such that \(F<G\) if and only if \(w_F<w_G\). Let \(F_0\) be the maximal forest such that \(a_F\ne 0\). If \(F<F_0\), then \(w_F<w_{F_0}\); as \(w_F=w'_F\), \(w_{F_0}\) does not appear in \({\Phi }_{\mathrm{CPL}}(F)\). If \(F>F_0\), \(a_F=0\). So the coefficient of \(w_F\) in \({\Phi }_{\mathrm{CPL}}(F)\) is \(a_{F_0}\) times the coefficient of \(w_{F_0}\) in \({\Phi }_{\mathrm{CPL}}(F_0)\), which is not zero. So \({\Phi }_{\mathrm{CPL}}(x)\ne 0\): \({\Phi }_{\mathrm{CPL}}\) is injective.
Remark 3.19
-
1.
We even prove that the restriction of \({\Phi }_{\mathrm{CPL}}\) to \({\fancyscript{H}}_{\fancyscript{D}}\) is injective.
-
2.
Although it contains a free pre-Lie subalgebra, \(T_+(V_{\fancyscript{D}},f_{\fancyscript{D}})\) is not free. Let us assume it is free. As the length of words gives a connected gradation of \(T_+(V_{\fancyscript{D}},f_{\fancyscript{D}})\), it is freely generated by any graded complement of \(T_+(V_{\fancyscript{D}},f_{\fancyscript{D}}){\bullet }T_+(V_{\fancyscript{D}},f_{\fancyscript{D}})\). Let us choose \(d\in {\fancyscript{D}}\). Then it is not difficult to prove that we can choose a complement of \(T_+(V_{\fancyscript{D}},f_{\fancyscript{D}}){\bullet }T_+(V_{\fancyscript{D}},f_{\fancyscript{D}})\) which contains \(\left( {\begin{array}{c}0\\ d\end{array}}\right) , \left( {\begin{array}{c}1\\ d\end{array}}\right) \) and \(\left( {\begin{array}{c}00\\ dd\end{array}}\right) \), which implies that the pre-Lie subalgebra generated by these three elements is free. Hence, the following pre-Lie morphism is injective:

But
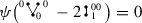 : this is a contradiction. So \(T_+(V_{\fancyscript{D}},f_{\fancyscript{D}})\) is not free.
: this is a contradiction. So \(T_+(V_{\fancyscript{D}},f_{\fancyscript{D}})\) is not free.
Corollary 3.20
The pre-Lie subalgebra \({\mathfrak {g}}_{\fancyscript{D}}\) of \(T(V_{\fancyscript{D}},f_{\fancyscript{D}})\) is freely generated by the biletters \(\left( {\begin{array}{c}0\\ d\end{array}}\right) \), \(d\in {\fancyscript{D}}\).
We shall give more results on the morphism \({\Phi }_{\mathrm{CPL}}\) and the admissible words in the appendix.
3.6 Prelie subalgebra generated by \(V\)
We here consider the pre-Lie subalgebra of \(V\) generated by \(V\). We denote by \(\mathrm{Prelie}(V)\) the free pre-Lie algebra generated by \(V\). This is the space of rooted trees decorated by \(V\), each vertex being linear in its decoration. The pre-Lie product is also given by grafting. We shall also consider the free Com-PreLie algebra generated by \(V\). This is the space of partitioned trees decorated by \(V\), each vertex being linear in its decoration. We consider the two morphisms

Note that \(\phi _\mathrm{PL}\) is the restriction of \(\phi _{\mathrm{CPL}}\) on \(\mathrm{Prelie}(V)\subseteq \mathrm{ComPrelie}(V)\).
Combining Theorem 3.11 and Proposition 3.13, \(\phi _{\mathrm{CPL}}=\varphi _{(V,f)}{\circ }{\Phi }_{\mathrm{CPL}}\). Hence, for all partitioned tree \(t\) decorated by \(V\), we have
Theorem 3.21
-
1.
\(\phi _\mathrm{PL}\) is surjective if and only if \(f(V)=V\).
-
2.
\(\phi _{\mathrm{CPL}}\) is surjective if and only if the codimension of \(f(V)\) in \(V\) is \(\le 1\).
Proof
1. \(\Rightarrow \). The length of words is a gradation of \(T(V,f)\); moreover, \(\phi _{\mathrm{CPL}}\) is homogeneous for this gradation. Hence

If \(\phi _\mathrm{PL}\) is surjective, then \(f(V){\otimes } V =V{\otimes } V\), so \(f(V)=V\).
1. \(\Leftarrow \). Let \(v_1\ldots v_n \in V^{\otimes n}\). As \(f(V)=V\), for all \(1\le i \le n-1\), there exists \(w_i \in V\) such that \(f(w_i)=v_i\). Let \(t\) be the ladder with \(n\) vertices, decorated from the root to the leaf by \(w_1,\ldots ,w_{n-1},v_n\). Then \(L(t)\) is reduced to a single element, and \(\phi _\mathrm{PL}(t)=f(w_1)\ldots f(w_{n-1})v_n=v_1\ldots v_n\). So \(\phi _\mathrm{PL}\) is surjective.
2. \(\Rightarrow \). By homogeneity of \(\phi _{\mathrm{CPL}}\),

Let us assume that the codimension of \(f(V)\) in \(V\) is \(\ge 2\). Let \(x,y \in V\), linearly independent, such that \(f(V)\cap \mathrm{Vect}(x,y)=(0)\). There exists a linear map \(g:V\rightarrow V\) such that \(g(f(V))=(0)\) and \(g(x)=x\), \(g(y)=y\). As \(\phi _{\mathrm{CPL}}\) is surjective, we can write
Hence
So \(xy=yx\), and consequently \(x\) and \(y\) are linearly independent: this is a contradiction. So the codimension of \(f(V)\) in \(V\) is \(\le 1\).
2. \(\Leftarrow \). If \(f(V)=V\), then by the first point, \(\phi _\mathrm{PL}\), and consequently \(\phi _{\mathrm{CPL}}\), is surjective. Let us assume that the codimension of \(f(V)\) in \(V\) is \(1\). Let us choose \(x \in V\) such that \(V=f(V){\oplus }\mathrm{Vect}(x)\). In order to prove that \(\phi _{\mathrm{CPL}}\) is surjective, it is enough to prove that \(v_1\ldots v_n \in \mathrm{Im}\,\phi _{\mathrm{CPL}}\) for all \(n\ge 1\) and \(v_1,\ldots ,v_n \in \{x\} \cup f(V)\). We proceed by induction on \(n\). If \(n=1\), then  . Let us assume the result at rank \(n-1\). Let \(k\) be the greatest integer such that \(v_1=\cdots =v_k=x\), with the convention that \(k=0\) if \(v_1\ne x\). We proceed by induction on \(k\). If \(k=0\), let us put \(v_1=f(w_1)\). By the induction on \(n\), there exists \(P \in \mathrm{ComPrelie}(V)\) such that \(\phi _{\mathrm{CPL}}(P)=v_2\ldots v_n\). Then
. Let us assume the result at rank \(n-1\). Let \(k\) be the greatest integer such that \(v_1=\cdots =v_k=x\), with the convention that \(k=0\) if \(v_1\ne x\). We proceed by induction on \(k\). If \(k=0\), let us put \(v_1=f(w_1)\). By the induction on \(n\), there exists \(P \in \mathrm{ComPrelie}(V)\) such that \(\phi _{\mathrm{CPL}}(P)=v_2\ldots v_n\). Then

Let us assume the result at rank \(k-1\), with \(k\ge 1\). By the induction hypothesis on \(n\), there exists \(X \in \mathrm{ComPrelie}(V)\) such that \(\phi _{\mathrm{CPL}}(X)=x^{k-1}v_{k+1}\ldots v_n\). Then

By the induction hypothesis on \(k\), for all \(k+1\le i \le n\), \(x^{k-1}v_{k+1}\ldots v_i x v_{i+1}\ldots v_n \in \mathrm{Im}\,\phi _{\mathrm{CPL}}\). So \(k x^k kv_{k+1}\ldots v_n \in \mathrm{Im}\,\phi _{\mathrm{CPL}}\). As the characteristic of the base field is zero, \(v_1\ldots v_n =x^k kv_{k+1}\ldots v_n \in \mathrm{Im}\,\phi _{\mathrm{CPL}}\). So \(\phi _{\mathrm{CPL}}\) is surjective.
Corollary 3.22
-
1.
The subspace \(V\) generates the pre-Lie algebra \(T_+(V)\) if and only if \(f(V)=V\). The subspace \(V\) generates the Com-PreLie algebra \(T_+(V)\) if and only if the codimension of \(f(V)\) in \(V\) is \(\le 1\).
-
2.
Let \(W\) be a subspace of \(V\). We put
$$\begin{aligned} \overline{W}=\sum _{k=0}^\infty f^k(W), \end{aligned}$$that is to say the smallest subspace of \(V\) stable by \(f\) which contains \(W\).
-
2a.
\(K\emptyset { \oplus } W\) generates the pre-Lie algebra \(T(V,f)\) if and only if \(\overline{W}=V\) and \(f(V)=V\).
-
2b.
\(K\emptyset {\oplus } W\) generates the Com-PreLie algebra \(T(V,f)\) if and only if \(\overline{W}=V\) and the codimension of \(f(V)\) in \(V\) is \(\le 1\).
-
2a.
Proof
1. It is a direct consequence of Theorem 3.21.
2a. We denote by \(A\) the pre-Lie subalgebra of \(T(V,f)\) generated by \(K\emptyset {\oplus } W\) and by \(A'\) the pre-Lie subalgebra of \(T(V,f)\) generated by \(\overline{W}\). Let us prove that \(A=K\emptyset {\oplus } A'\). First, for all \(w_1,\ldots , w_k \in \overline{W}\),
as \(\overline{W}\) is stable under \(f\). As \(\emptyset {\circ }w=0\) for any \(w \in A'\), \(K\emptyset {\oplus } A'\) is a pre-Lie subalgebra which contains \(W\), so it contains \(A\). For any \(x \in W\) and any \(k\ge 0\), we have
so \(\overline{W} \subseteq A\), which implies \(A'\subseteq A\) and \(K\emptyset {\oplus } A'\subseteq A\).
\(\Rightarrow \). If \(A=T(V,f)\), then \(A'=T(V,f)\). Comparing the homogeneous component of degree \(1\), \(\overline{W}=V\). By the first point, \(f(V)=V\).
\(\Leftarrow \). In this case, \(A'=T_+(V)\), so \(A=K\emptyset {\oplus } T_+(V)=T(V)\).
Point 2b is proved similarly.\(\square \)
4 Examples
4.1 The diagonalizable case
We here assume that the endomorphism \(f\) is diagonalizable. Let \((x_d)_{d\in {\fancyscript{D}}}\) be a basis of \(V\) such that \(f(x_d)=\lambda _d x_d\) for all \(d\in {\fancyscript{D}}\). We now construct the pre-Lie algebra \(T_+(V,f)\) as the dual of a Hopf subalgebra of the Connes–Kreimer Hopf algebra \({\fancyscript{H}}_\mathrm{CK}^{\fancyscript{D}}\) of rooted trees decorated by \({\fancyscript{D}}\) [1, 3]. As an algebra, it is the free commutative, associative algebra generated by the set of rooted trees decorated by \({\fancyscript{D}}\). Its coproduct is given by admissible cuts: for any tree \(t\),
For example,

The enveloping algebra of \(\mathrm{Prelie}({\fancyscript{D}})\) and \({\fancyscript{H}}_\mathrm{CK}^{\fancyscript{D}}\) are in duality by the pairing [12, 20]
where \(s_F\) is the number of symmetries of the forest \(F\). As the characteristic of \({\mathbb {K}}\) is zero, this pairing is nondegenerate. Consequently, the subspace of \({\fancyscript{H}}_\mathrm{CK}^{\fancyscript{D}}\) generated by the set of rooted trees inherits a pre-Lie cobracket defined by \(\delta =(\pi {\otimes } \pi ){\circ }{\Delta }\), where \(\pi \) is defined by
Following [3, 4], for all \(d \in {\fancyscript{D}}\), we define a linear map \(N_d:{\fancyscript{H}}_\mathrm{CK}^{\fancyscript{D}}\rightarrow {\fancyscript{H}}_\mathrm{CK}^{\fancyscript{D}}\) by

for any forest \(F\). We shall also need the following map:
Proposition 4.1
For all \(d\in {\fancyscript{D}}\),
-
1.
For all \(x,y\in {\fancyscript{H}}_\mathrm{CK}^{\fancyscript{D}}\), \(N_d(xy)=N_d(x)y+xN_d(y)\).
-
2.
\(N_d {\circ }\pi = \pi {\circ }N_d\).
-
3.
For all \(x\in {\fancyscript{H}}_\mathrm{CK}^{\fancyscript{D}}\),
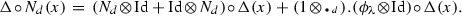
-
3.
If \(x\) is a linear span of trees,
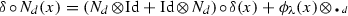 .
.
Proof
1. This is obvious if \(x\) and \(y\) are forests, as \(V(xy)=V(x)\sqcup V(y)\).
2. If \(F\) is a tree, then \(N_d(F)\) is a linear span of trees, so \(N_d {\circ }\pi (F)=N_d(F)=\pi {\circ } N_d(F)\). If \(F\) is a forest which is not a tree, then \(N_d(F)\) is a linear span of forests which are not trees, so \(N_d {\circ }\pi (F)=0=\pi {\circ }N_d(F)\).
3. Let \(F\) be a forest, and \(s\in V(F)\). We denote by \(l\) the leaf decorated by \(d\) grafted onto \(F\) to obtain  . There are the following three types of admissible cuts of \(G\):
. There are the following three types of admissible cuts of \(G\):
-
Admissible cuts \(c\) such that \(s \in V(P^c(G))\). Then \(R^c(G)=R^{c_{| F}}(F)\) and
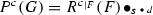 .
. -
Admissible cuts \(c\) such that \(s,\ell \in V(R^c(G))\). Then
 and \(P^c(G)=R^{c_{|F}}(F)\).
and \(P^c(G)=R^{c_{|F}}(F)\). -
Admissible cuts \(c\) such that \(s \in V(R^c(G))\) and \(\ell \in V(P^c(G))\). Then \(R^c(G)=R^{c_{| F}}(F)\) and
 .
.
Summing all these possibilities, we obtain

4. Let \(t\) be a tree. We put \({\Delta }(t)=t{\otimes } 1+\sum t'{\otimes } t''\), where \(\sum t'{\otimes } t''\) is a sum of tensors such that the left part is a forest and the right part is a tree. Then

Hence

which proves the last point. \(\square \)
Definition 4.2
Let \(d_1,\ldots ,d_n \in {\fancyscript{D}}\), \(n \ge 1\). We inductively defined \(t_{d_1\ldots d_n}\) in the following way:
-
1.
If \(n=1\),
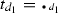 .
. -
2.
If \(n \ge 2\), \(t_{d_1\ldots d_n}=N_{d_n}(t_{d_1\ldots d_{n-1}})\).
We denote by \({\fancyscript{H}}_\lambda \) the subalgebra of \({\fancyscript{H}}_\mathrm{CK}^{\fancyscript{D}}\) generated by the elements \(t_{d_1\ldots d_n}\).
Examples
If \(a,b,c,d \in {\fancyscript{D}}\), then

Proposition 4.3
\({\fancyscript{H}}_\lambda \) is stable under \(N_d\) for all \(d \in {\fancyscript{D}}\) and under \(\phi _\lambda \), and is a Hopf subalgebra of \({\fancyscript{H}}_\mathrm{CK}^{\fancyscript{D}}\).
Proof
We consider
As \(N_d\) and \(\phi _\lambda \) are derivations, this is a subalgebra of \({\fancyscript{H}}_\lambda \). For all nonempty words \(w=d_1\ldots d_n\), \(N_d(t_w)=t_{wd}\) and \(\phi _\lambda (t_w)=(\lambda _{d_1}+\cdots +\lambda _{d_n})t_w\), so \(A\) contains the generators of \({\fancyscript{H}}_\lambda \): \(A={\fancyscript{H}}_\lambda \), which proves the first point. Let us prove that \({\Delta }(t_w) \in {\fancyscript{H}}_\lambda {\otimes } {\fancyscript{H}}_\lambda \) for all nonempty words \(w\) by induction on the length \(n\). If \(n=1\), then  for a particular \(d\), so \({\Delta }(t_w)=t_w{\otimes } 1+1{\otimes } t_w \in {\fancyscript{H}}_\lambda {\otimes } {\fancyscript{H}}_\lambda \). Let us assume the result at rank \(n-1\). We put \(w=w'd\), with \(d \in {\fancyscript{D}}\). By the induction hypothesis, \({\Delta }(t_w') \in {\fancyscript{H}}_\lambda {\otimes } {\fancyscript{H}}_\lambda \). Then
for a particular \(d\), so \({\Delta }(t_w)=t_w{\otimes } 1+1{\otimes } t_w \in {\fancyscript{H}}_\lambda {\otimes } {\fancyscript{H}}_\lambda \). Let us assume the result at rank \(n-1\). We put \(w=w'd\), with \(d \in {\fancyscript{D}}\). By the induction hypothesis, \({\Delta }(t_w') \in {\fancyscript{H}}_\lambda {\otimes } {\fancyscript{H}}_\lambda \). Then

As \({\fancyscript{H}}_\lambda \) is stable under \(N_d\) and \(\phi _\lambda \) and contains  , this belongs to \({\fancyscript{H}}_\lambda {\otimes } {\fancyscript{H}}_\lambda \). So \({\fancyscript{H}}_\lambda \) is a Hopf subalgebra of \({\fancyscript{H}}_\mathrm{CK}^{\fancyscript{D}}\).\(\square \)
, this belongs to \({\fancyscript{H}}_\lambda {\otimes } {\fancyscript{H}}_\lambda \). So \({\fancyscript{H}}_\lambda \) is a Hopf subalgebra of \({\fancyscript{H}}_\mathrm{CK}^{\fancyscript{D}}\).\(\square \)
As its generators are linear spans of trees, \({\fancyscript{H}}_\lambda \) is stable under \(\pi \). As it is also stable under \({\Delta }\), the vector space generated by the elements \(t_w\) is stable under \(\delta \), so is a pre-Lie coalgebra. Let us give a formula for this pre-Lie cobracket.
Proposition 4.4
Let \(d_1,\ldots ,d_n \in {\fancyscript{D}}\). For all \(J=\{i_1,\ldots ,i_k\}\subseteq \{1,\ldots ,n\}\), with \(i_1<\cdots <i_k\), we put
-
\(w_J=d_{i_1}\ldots d_{i_k}\).
-
\(m(J)=\max \{i: \{1,\ldots ,i\} \subseteq J\}\), with the convention \(m(J)=0\) if \(1 \notin J\).
Then
Proof
By induction on \(n\). It is obvious if \(n=1\), as \(\delta (t_{d_1})=0\). Let us assume the result at rank \(n-1\).

So the result holds for all \(n\).\(\square \)
Let us assume that all \(\lambda _d\) are nonzero. For all words \(w=d_1\ldots d_n\), in \(t_w\) appears only one ladder, that is to say a tree with no ramification: its vertices, from the root to the unique leaf, are decorated by \(d_1,\ldots ,d_n\), and its coefficient is \(\lambda _{d_1} \ldots \lambda _{d_{n-1}}\). So the elements \(t_w\) are linearly independent. Dually, identifying the dual basis \((t^*_{d_1\ldots d_n})_{d_1,\ldots ,d_n\in {\fancyscript{D}}}\) of the graded dual of the pre-Lie coalgebra of the generators of \({\fancyscript{H}}_\lambda \) and the basis \((x_{d_1}\ldots x_{d_n})_{d_1,\ldots ,d_n \in {\fancyscript{D}}}\), we obtain a pre-Lie algebra structure on the space \(T(V)\). If \(d_1,\ldots ,d_{k+l} \in {\fancyscript{D}}\), then
as if \(i\le m_k(\sigma )\), \(\sigma ^{-1}(i)=i\) and \(f\bigl (x_{d_{\sigma ^{-1}(i)}}\bigr )=\lambda _{d_i} x_{d_i}\). Hence, we obtain the pre-Lie algebra \((T(V,f),\circ )\).
If \(x\) is an eigenvector of \(f\) with eigenvalue \(\lambda \), the preceding formula gives
Let us assume that \(\lambda \ne 0\). For all \(k\ge 0\), we put \(y_k=(k+1)!x^k/\lambda \). As the characteristic of \({\mathbb {K}}\) is zero, \((y_k)_{k\ge 0}\) is a basis of \({\mathbb {K}}[x]\). We obtain
so \([y_k,y_l]=(k-l)y_{k+l}\). Hence, if \(\lambda \ne 0\), \({\mathbb {K}}[x]_+\subseteq T(V,f)\) is isomorphic, as a Lie algebra, to the Faà di Bruno Lie algebra [7–9].
Remark 4.5
In particular, if \(V\) is one-dimensional and \(f=\mathrm{Id}_V\), we can work with a single decoration and delete it everywhere. The dual of the enveloping algebra of \(T(V,f)\) is the subalgebra of \({\fancyscript{H}}_\mathrm{CK}\) generated by the elements \(t_n\) inductively defined by  and \(t_{n+1}=N(t_n)\),
and \(t_{n+1}=N(t_n)\),

This is the Connes–Moscovici subalgebra of \({\fancyscript{H}}_\mathrm{CK}\) [3, 4].
4.2 Examples from Control Theory
We now consider the group of Fliess operators [11]. We fix an integer \(n\ge 1\). We denote by \(X^*\) the set of words in letters \(x_0,\ldots ,x_n\). As a set, the group of Fliess operators is isomorphic to \(G_\mathrm{Fliess}={\mathbb {K}}\langle \langle x_0,\ldots ,x_n\rangle \rangle ^n \approx {\mathbb {K}}^n\langle \langle x_0,\ldots ,x_n\rangle \rangle \). Let us now describe the composition. Let \(c,d=(d_1,\ldots ,d_n) \in G_\mathrm{Fliess}\). We put
with \(c_w \in {\mathbb {K}}^n\) for all \(w \in X^*\).
-
For all \(0\le i\le n\), we consider

with \(d_0=0\). If \(w=x_{i_1}\ldots x_{i_k} \in X^*\), we put \(\widetilde{D}_w=\widetilde{D}_{x_{i_1}}\!{\circ }\cdots {\circ }\widetilde{D}_{x_{i_k}}\). By convention, \(\widetilde{D}_\emptyset =\mathrm{Id}_{G_\mathrm{Fliess}}\).
-
The composition \(c \widetilde{\diamond }d\) is defined by
$$\begin{aligned} c \widetilde{\diamond }d=\!\sum _{w\in X^*}\!\! c_w \widetilde{D}_w(\emptyset ). \end{aligned}$$In particular, \(\emptyset \widetilde{\diamond }d=\widetilde{D}_\emptyset (\emptyset )=\emptyset \).
-
The product of \(G_\mathrm{Fliess}\) is then given by \(c {\diamond } d=c\widetilde{\diamond }d+d\).
Let \(0\le i\le n\), \(c,d \in G_\mathrm{Fliess}\). We keep the same notation as before.

In other words,
-
\(\widetilde{\diamond }\) is \({\mathbb {K}}^n\)-linear on the left.
-
For all \(d \in {\mathbb {K}}\langle \langle x_0,\ldots ,x_n\rangle \rangle ^n\), \(\emptyset \widetilde{\diamond }d=\emptyset \).
-
For all \(c,d \in {\mathbb {K}}\langle \langle x_0,\ldots ,x_n\rangle \rangle ^n\),
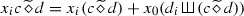 , with the convention \(d_0=0\).
, with the convention \(d_0=0\).
Notation
Let \(\epsilon _i\) be the \(i\)-th element of the canonical basis. We put \(G_i=\epsilon _i {\mathbb {K}}\langle \langle x_0,\ldots , x_n\rangle \rangle ^n\).
From the left \({\mathbb {K}}^n\)-linearity and \(\epsilon _i\epsilon _j= \delta _{ij}\epsilon _i\) we easily get
Lemma 4.6
If \(c,d \in {\mathbb {K}}\langle \langle x_0,\ldots ,x_n\rangle \rangle \), then

Theorem 4.7
-
1.
For all \(1\le i \le n\), \(G_i\) is a subgroup of \(G\). Moreover, it is isomorphic to the group of characters associated to \((V,f_i)\), with \(V=\mathrm{Vect} (x_0,\ldots ,x_n)\) and
$$\begin{aligned} f_i:\left\{ \begin{array}{rcl} V&{}\,\rightarrow &{}\,V\\ x_j&{}\,\rightarrow &{}\,\delta _{ij}x_0. \end{array}\right. \end{aligned}$$ -
2.
The group \(G\) is the direct product of the subgroups \(G_i\), \(1\le i \le n\).
Proof
1. As a set, we identify \(G_i\) with \({\mathbb {K}}\langle \langle x_0,\ldots ,x_n\rangle \rangle \), via the multiplication by \(\epsilon _i\). In this group, if \(u,v \in {\mathbb {K}}\langle \langle x_0,\ldots ,x_n\rangle \rangle \), by Lemma 4.6,

We consider the character group associated to \(f_i\). As \(f_i^2=0\), the second statement of Theorem 2.17 becomes

So \(G_i\) is isomorphic to this group of characters, via the multiplication by \(\epsilon _i\).
2. Let \(1\le i,j \le n\), with \(i\ne j\). Then, by Lemma 4.6, if \(u,v \in {\mathbb {K}}\langle \langle x_0,\ldots ,x_n\rangle \rangle \), then

An easy induction on the length then proves that for all words \(u\) and all \(v\in {\mathbb {K}}\langle \langle x_0,\ldots ,x_n\rangle \rangle \), \((\epsilon _iu)\widetilde{\diamond }(\epsilon _jv)=\epsilon _i u\). By continuity of \(\widetilde{\diamond }\), for all \(u,v \in {\mathbb {K}}\langle \langle x_0,\ldots , x_n\rangle \rangle \), \((\epsilon _iu)\widetilde{\diamond }(\epsilon _jv)=\epsilon _i u\). Hence, for all \(u,v \in {\mathbb {K}}\langle \langle x_0,\ldots ,x_n\rangle \rangle \),
As a conclusion, \(G\) is the direct sum of the subgroups \(G_i\).
The Lie algebra of \(G_i\) is the pre-Lie algebra \(T(V,f_i)={\mathbb {K}}\langle x_0,\ldots ,x_n\rangle \) with the composition associated to \(f_i\). Let us give a few results on this pre-Lie algebra.
Theorem 4.8
\(T(V,f_i)\) inherits a gradation such that \(x_i\) is homogeneous of degree \(1\) for all \(1\le i \le n\) and \(x_0\) is homogeneous of degree \(0\). The formal series of this gradation is
Proof
We put \(V_1=\mathrm{Vect}(x_1,\ldots ,x_n)\) and \(V_2=\mathrm{Vect}(x_0)\). It defines a gradation of \(V\) such that \(f_i\) is homogeneous of degree \(1\). We apply Corollary 2.12.\(\square \)
Examples
These are the Fibonacci polynomials, see sequence A011973 in [22]. Here are several specializations of these sequences, which can be found in [22]:
These sequences are generically called generalized Fibonacci sequences. If \(n=1\), this is the Fibonacci sequence; if \(n=2\), this is the Pell sequence.
Remark 4.9
By Corollary 3.7, \(T(V,f_i)\) is generated, as a pre-Lie algebra, by \({\mathbb {K}}\langle x_1,\ldots ,x_n\rangle \). Moreover, by Corollary 3.22, \(T_+(V,f_i)\) is generated, as a Com-Prelie algebra, by \(\mathrm{Vect}(x_0,\ldots ,x_n)\) if and only if \(n=1\). We recover in this way a result of [10].
References
Broadhurst, D.J., Kreimer, D.: Towards cohomology of renormalization: bigrading the combinatorial Hopf algebra of rooted trees. Comm. Math. Phys. 215(1), 217–236 (2000)
Chapoton, F., Livernet, M.: Pre-Lie algebras and the rooted trees operad. Int. Math. Res. Notices 2001(8), 395–408 (2001)
Connes, A., Kreimer, D.: Hopf algebras, renormalization and noncommutative geometry. Comm. Math. Phys. 199(1), 203–242 (1998)
Connes, A., Moscovici, H.: Hopf algebras, cyclic cohomology and the transverse index theorem. Comm. Math. Phys. 198(1), 199–246 (1998)
Dokas, I.: Zinbiel algebras and commutative algebras with divided powers. Glasg. Math. J. 52(2), 303–313 (2010)
Eilenberg, S., Mac Lane, S.: On the groups of \(H(\Pi, n)\). I. Ann. Math. 58(1), 55–106 (1953)
Figueroa, H., Gracia-Bondía, J.M.: On the antipode of Kreimer’s Hopf algebra. Modern Phys. Lett. A 16(22), 1427–1434 (2001)
Foissy, L.: Faà di Bruno subalgebras of the Hopf algebra of planar trees from combinatorial Dyson–Schwinger equations. Adv. Math. 218(1), 136–162 (2008)
Foissy, L.: Hopf subalgebras of rooted trees from Dyson–Schwinger equations. In: Motives, Quantum Field Theory, and Pseudodifferential Operators. Clay Mathematics Proceedings, vol. 12, pp. 189–210. American Mathematical Society, Providence (2010)
Foissy, L.: The Hopf algebra of Fliess operators and its dual pre-Lie algebra (2014). arXiv:1304.1726
Gray, W.S., Duffaut, E., Luis, A.: A Faà di Bruno Hopf algebra for a group of Fliess operators with applications to feedback. Syst. Control Lett. 60(7), 441–449 (2011)
Hoffman, M.E.: Combinatorics of rooted trees and Hopf algebras. Trans. Am. Math. Soc. 355(9), 3795–3811 (2003)
Loday, J.-L.: Cup-product for Leibniz cohomology and dual Leibniz algebras. Math. Scand. 77(2), 189–196 (1995)
Loday, J.-L.: Scindement d’associativité et algèbres de Hopf. In: Actes des Journées Mathématiques à la Mémoire de Jean Leray. Séminaires et Congrès, vol. 9, pp. 155–172. Société Mathématique de France, Paris (2004)
Loday, J.-L., Ronco, M.: Combinatorial Hopf algebras. In: Quanta of Maths, Clay Mathematics Proceedings, vol. 11, pp. 347–383. American Mathematical Society, Providence (2010)
MacLane, S.: The homology products in \(K(\Pi, n)\). Proc. Am. Math. Soc. 5(4), 642–651 (1954)
Mansuy, A.: Preordered forests, packed words and contraction algebras (2013). arXiv:1305.0343
Oudom, J.-M., Guin, D.: Sur l’algèbre enveloppante d’une algèbre pré-Lie. C. R. Math. Acad. Sci. Paris 340(5), 331–336 (2005)
Oudom, J.-M., Guin, D.: On the Lie enveloping algebra of a pre-Lie algebra. J. K-Theory 2(1), 147–167 (2008)
Panaite, F.: Relating the Connes–Kreimer and Grossman–Larson Hopf algebras built on rooted trees. Lett. Math. Phys. 51(3), 211–219 (2000)
Reutenauer, C.: Free Lie Algebras. London Mathematical Society Monographs. Oxford Science Publications. The Clarendon Press/Oxford University Press, New York (1993)
Sloane, N.J.A.: The On-Line Encyclopedia of Integer Sequences. Springer, Berlin (2000). http://oeis.org/
Author information
Authors and Affiliations
Corresponding author
Additional information
The research leading these results was partially supported by the French National Research Agency under the reference ANR-12-BS01-0017.
Originally submitted to the Central European Journal of Mathematics in February 2014, but withdrawn due to imposition of publishing fees and resubmitted in May 2014 to the European Journal of Mathematics.
Appendix
Appendix
1.1 Admissible words and Dyck paths
Recall that a Dyck path of length \(2n\) is a path from \((0,0)\) to \((n,n)\), made of steps \(\rightarrow \) and \(\uparrow \), always staying under the diagonal, but possibly touching it in other points that \((0,0)\) and \((n,n)\). The set of Dyck paths of length \(2n\) is denoted by \(D(n)\).
Examples
Note that a nonempty Dyck path always starts by \(\rightarrow \) and ends by \(\uparrow \).
Lemma 4.10
Let \(\rightarrow \,\uparrow ^{a_1}\rightarrow \, \uparrow ^{a_2} \rightarrow \cdots \rightarrow \, \uparrow ^{a_n}\) be a path starting from \((0,0)\), with \(a_1,\ldots ,a_n \ge 0\).
-
It is a path from \((0,0)\) to \((n,n)\) if and only if \(a_1+\cdots +a_n=n\).
-
This path is under the diagonal if and only if for all \(1\le i\le n\), \(a_1+\cdots +a_i\le i\).
Proof
The path contains \(n\rightarrow \) and \(a_1+\cdots +a_n {\uparrow }\), so is a path from \((0,0)\) to \((n,a_1+\cdots +a_n)\). The second property is immediate. \(\square \)
Notation
For all \(n\ge 1\), we denote by \({\fancyscript{W}}(n)\) the set of first lines of admissible biwords of length \(n\), that is to say words \(a_1\ldots a_n\) with letters in \(\mathbb {N}\), such that:
-
For all \(1\le i\le n\), \(a_i+\cdots +a_n\le n-i\).
-
\(a_1+\cdots +a_n=n-1\).
We denote by \({\fancyscript{W}}_\sigma (n)\) the set of first lines of \(\sigma \)-admissible biwords of length \(n\), that is to say words \(w_1\ldots w_k\) of length \(k\) such that \(w_1,\ldots , w_k\) are admissible words.
Proposition 4.11
For all \(n \ge 0\), the following map is a bijection:
Proof
First, \(\theta _n\) is well defined: if \(a_1\ldots a_{n+1} \in {\fancyscript{W}}(n+1)\), by definition \(a_{n+1}=0\). Moreover, \(a_1+\cdots +a_n=a_1+\cdots +a_{n+1}=n+1-1=n\). By Lemma 4.10, it is a path from \((0,0)\) to \((n,n)\). For all \(1\le i \le n\), \(a_i+\cdots +a_n=a_i+\cdots +a_{n+1}\le n+1-i\). By Lemma 4.10, it is under the diagonal, so it is indeed in \(D(n)\).
\(\theta _n\) is injective: if \(\theta _n(a_1 \ldots a_{n+1}) =\theta _n(b_1\ldots b_{n+1})\), then immediately \(a_1=b_1,\ldots ,a_n=b_n\); moreover, \(a_{n+1}=b_{n+1}=0\).
\(\theta _n\) is surjective: if \(P\) is a Dyck path of length \(n\), as it starts by \(\rightarrow \) and contains exactly \(n\) \(\rightarrow \) and \(\uparrow \), it can be written under the form \(\rightarrow \,\uparrow ^{a_n}\cdots \rightarrow \,\uparrow ^{a_1}\), with \(a_1+\cdots +a_n=n\). As it is under the diagonal, by Lemma 4.10, for all \(1\le i \le n\), \(a_i+\cdots +a_n\le n+1-i\). So \(a_1\ldots a_n0 \in {\fancyscript{W}}(n+1)\) and \(\theta (a_1\ldots a_n0)=P\). \(\square \)
Corollary 4.12
For all \(n \ge 1\), \(|{\fancyscript{W}}(n)|\) is the \((n-1)\)-th Catalan number \(\frac{1}{n}\left( {\begin{array}{c}2n-2\\ n-1\end{array}}\right) \).
Corollary 4.13
-
1.
For all \(n\ge 0\), \(|{\fancyscript{W}}_\sigma (n)|\) is the \(n\)-th Catalan number \(\frac{1}{n+1}\left( {\begin{array}{c}2n\\ n\end{array}}\right) \).
-
2.
Let \(a_1,\ldots , a_n\) be a word with letters in \(\mathbb {N}\). It is \(\sigma \)-admissible if and only if for all \(1\le i \le n\), \(a_i+\cdots +a_n\le n-i\).
Proof
1. Let \(C(X)\) be the formal series of Catalan numbers, then
Then the formal series of admissible words is
so \(f^2(X)-f(X)+X=0\) or, equivalently,
By the unicity of decomposition of \(\sigma \)-admissible words in Lemma 3.17, the formal series of \(\sigma \)-admissible words is
so \(|{\fancyscript{W}}_\sigma (n)|\) is the \(n\)-th Catalan number.
2. We denote by \({\fancyscript{W}}'_\sigma (n)\) the set of words \(a_1\ldots a_n\) such that for all \(i\), \(a_i+\cdots +a_n \le n-i\). By Lemma 3.17, \({\fancyscript{W}}_\sigma (n)\subseteq {\fancyscript{W}}'_\sigma (n)\). By Lemma 3.17, the following map is well defined:
It is clearly injective, so \(|{\fancyscript{W}}'_\sigma (n)|\le |{\fancyscript{W}}(n+1)|=|{\fancyscript{W}}_\sigma (n)|\). So \({\fancyscript{W}}_\sigma ( n)={\fancyscript{W}}_\sigma '(n)\).\(\square \)
1.2 Image of the morphism \({\Phi }_\mathrm{CPL}\)
Proposition 4.14
\({\mathfrak {g}}_{\fancyscript{D}}={\Phi }_\mathrm{PL}(\mathrm{Prelie}({\fancyscript{D}}))\) is included in the space generated by admissible words and \({\Phi }_\mathrm{CPL}(\mathrm{ComPrelie}({\fancyscript{D}}))\) is included in the space generated by \(\sigma \)-admissible words.
Proof
Let \(t\) be a partitioned tree with \(n\) vertices and \(k\) blocks, and let \(f\) be a linear extension of \(t\). We put \(\mathrm{fert}(f(i))=a_i\) for all \(i\). It is not difficult to prove that \(a_1+\cdots +a_n=k-1\). As \(k\le n\), \(a_1+\cdots +a_n\le n-1\); if \(t\) is a rooted tree, \(k=n\) and \(a_1+\cdots +a_n=n-1\). Let us prove that \(a_i+\cdots +a_n\le n-i\) for all \(1\le i\le n\) by induction on \(n\). It is obvious if \(n=0\). If \(n\ge 1\), we already proved the result if \(i=1\). Let us assume that \(i\ge 2\). We put \(t'=f^{-1}(\{2,\ldots ,n\})\). As \(f\) is a linear extension of \(t\), \(t'\) is an ideal of \(t\), and \(b_1\ldots b_{n-1}=a_2\ldots a_n\) appears in \({\Phi }_\mathrm{CPL}(t')\). By the induction hypothesis,
Finally, if \(t\) is a partitioned tree, any biword appearing in \({\Phi }_\mathrm{CPL}(t)\) is \(\sigma \)-admissible; if \(t\) is a rooted tree, any biword appearing in \({\Phi }_\mathrm{CPL}(t)\) is admissible. \(\square \)
Remark 4.15
It is not difficult to see that \({\mathfrak {g}}_{\fancyscript{D}}\) is strictly included in the space of admissible words and that \({\Phi }_\mathrm{CPL}(\mathrm{ComPrelie}({\fancyscript{D}}))\) is strictly included in the space of \(\sigma \)-admissible words.
Corollary 4.16
The space of \(\sigma \)-admissible words, with the shuffle product  and the pre-Lie product \(\bullet \) of \(T(V_{\fancyscript{D}},f_{\fancyscript{D}})\), is a Com-Prelie algebra.
and the pre-Lie product \(\bullet \) of \(T(V_{\fancyscript{D}},f_{\fancyscript{D}})\), is a Com-Prelie algebra.
Proof
Let \(w\) be a \(\sigma \)-admissible biwords. Let us first prove that there exists a partitioned tree \(t\) such that \(w\) appears in \({\Phi }_\mathrm{CPL}(t)\). We proceed by induction on the length \(n\) of \(w\). If \(n=0\), then we take \(t=1\). Let us assume the result at all ranks \(<n\). If \(w=a_1\ldots a_n\) is admissible, then the second point implies that \(a_2\ldots a_n\) is \(\sigma \)-admissible, and \(a=1\left( {\begin{array}{c}n-a_1-\cdots -a_n\\ d\end{array}}\right) \) for a certain \(d\in {\fancyscript{D}}\). By the induction hypothesis, there exists a forest \(t'\) such that \(a_2\ldots a_n\) appears in \({\Phi }_\mathrm{CPL}(t')\). Then \(a_1\ldots a_n\) appears in  . If \(w=w_1\ldots w_k\), with \(w_1,\ldots , w_k\) admissible and \(k\ge 2\), then for all \(i\) there exists \(t_i\) such that \(w_i\) appears in \({\Phi }_\mathrm{CPL}(t_i)\). Hence, \(w_1\ldots w_k\), being a particular shuffling of \(w_1,\ldots ,w_k\), appears in
. If \(w=w_1\ldots w_k\), with \(w_1,\ldots , w_k\) admissible and \(k\ge 2\), then for all \(i\) there exists \(t_i\) such that \(w_i\) appears in \({\Phi }_\mathrm{CPL}(t_i)\). Hence, \(w_1\ldots w_k\), being a particular shuffling of \(w_1,\ldots ,w_k\), appears in  .
.
Let us consider now two \(\sigma \)-admissible biwords \(u\) and \(u'\). There exists admissible forests \(t\) and \(t'\) such that \(u\) appears in \({\Phi }_\mathrm{CPL}(t)\) and \(u'\) appears in \({\Phi }_\mathrm{CPL}(t')\). Then any word appearing in  or in \(u{\bullet }u'\) appears in
or in \(u{\bullet }u'\) appears in  or in \({\Phi }_\mathrm{CPL}(t){\bullet }{\Phi }_\mathrm{CPL}(t')={\Phi }_\mathrm{CPL}(t{\bullet } t')\), so is \(\sigma \)-admissible by Proposition 4.14. \(\square \)
or in \({\Phi }_\mathrm{CPL}(t){\bullet }{\Phi }_\mathrm{CPL}(t')={\Phi }_\mathrm{CPL}(t{\bullet } t')\), so is \(\sigma \)-admissible by Proposition 4.14. \(\square \)
Rights and permissions
About this article
Cite this article
Foissy, L. A pre-Lie algebra associated to a linear endomorphism and related algebraic structures. European Journal of Mathematics 1, 78–121 (2015). https://doi.org/10.1007/s40879-014-0032-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-014-0032-2





 and a coproduct
and a coproduct  , with Sweedler’s notations.
, with Sweedler’s notations.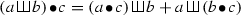 .
. .
.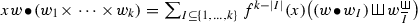 .
.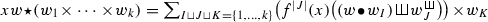 .
.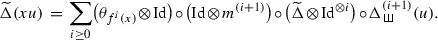
 .
. .
. is defined as follows:
is defined as follows: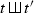 is
is  is
is  and
and  .
. and
and  .
. .
.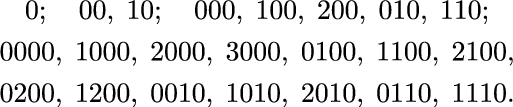
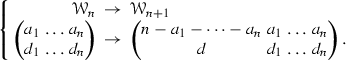

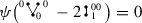 : this is a contradiction. So
: this is a contradiction. So 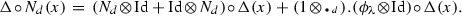
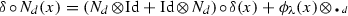 .
.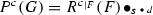 .
. and
and  .
.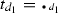 .
.
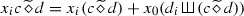 , with the convention
, with the convention