New Insights into the Failure Front Phenomenon and the Equation of State of Soda-Lime Glass Under Planar Plate Impact

Abstract

A systematic study has been performed to gather more detailed experimental information on the equation of state and the Hugoniot elastic limit (HEL) of soda-lime glass as well as the failure front phenomenon. The key innovations of this study comprise experimental as well as analytical aspects. On the one hand, an extensive planar plate impact (PPI) test series has been carried out over a wide range of shock loading stress levels instrumented with two high-speed cameras and laser interferometers (PDV and VISAR). On the other hand, a systematic analysis concept has been developed and evaluated, including a combination of Lagrange diagrams with velocity profile data and a derivation of the equation of state together with an error estimation. Impact velocities ranged from 500 to 3000 m/s resulting in loadings of the soda-lime glass targets between 3.5 and 20.8 GPa. For stress levels between 3.5 and 6.7 GPa two high-speed cameras with 5 Mfps, positioned at the side and rear of the specimens, enabled the observation of shock waves and two different kinds of failure fronts. Therefore, visual information could be gathered not only in the purely elastic regime, but also in the transition region above 4 GPa and at stress levels beyond the HEL. The HEL of the soda-lime glass is determined to $\left(5.0 \pm 0.2\right) \mathrm{GPa}$. For the onset of an internal failure front a minimum longitudinal stress between 3.8 and 3.9 GPa is identified. The evaluated failure front velocities range from 800 to 2100 m/s. From the observed release response a minimum spall strength of 6.7 GPa and release wave velocities between 5740 and 9500 m/s are deduced.

Introduction

The continuous enhancement of ballistic threats poses permanently increasing requirements for the protective capabilities of armor systems. For military vehicles, for example the transparent parts of the armor should not present a weak point. In order to further improve transparent armor and support the development of new designs, it is essential to understand the response to shock loading. This can be achieved efficiently by combining ballistic tests with numerical simulations. Hereby, basic research experiments are used as input to establish the constitutive material models.

The focus of this work is to gain new insights on the critical properties of soda-lime glass (SLG) during shock loading. SLG is a well-established material for the use in transparent armor systems and has therefore been the subject of intensive research since decades.

A crucial material property and focus of many studies is the so-called Hugoniot Elastic Limit (HEL), which is the principal compressive stress at the limit of the elastic response under one-dimensional strain conditions. Unfortunately, there is much ambiguity in the determined values of the HEL (Table 1). This is because SLG exhibits no clear two-wave structure in its shock wave profiles, which makes the common analysis methods of ductile materials barely applicable. For example, Grady et al. [1] stated that some measured values were uncertain since a clear-cut method for the evaluation of stress levels is missing: “Maximum compressive stresses achieved in tests AT-2 and AT-8 were about 6–7 GPa although values are uncertain because of the lack of a clear-cut method of evaluation stress levels from these particular wave profiles” [1] (p. 9). “The peak compression states of stress, strain and particle velocity (Hugoniot states) were extracted from the wave profile data by approximating the measured wave profiles by two shocks; an elastic shock with a velocity of 5.83 km/s and amplitude selected at 0.4 km/s and a deformational shock wave of velocity determined by the arrival of the wave midpoint” [1] (p. 5).

Table 1 Selection of HEL values for soda-lime glass from other authors

This method is referred to as “selective analysis” in the following. As SLG exhibits a convex shaped Hugoniot, a different concept, the so-called “incremental analysis” is used within the scope of the present work, which is an incremental analysis of the differential form of the Rankine-Hugoniot. A detailed description of both methods is outlined in the Appendix (Section “Details of the “Incremental Analysis” Applied for the Evaluation of Surface Velocity Measurements”).

Besides the HEL, much research effort has been dedicated to the determination of the material strength of SLG under shock loading. Table 2 provides a selection of tensile spall strength and compressive shear strength data evaluated by other authors. These values differ widely, also depending on the state of the glass (intact or failed) at the point of measurement.

Table 2 Selection of strength values for soda-lime glass from other authors

For brittle materials, the transition from the intact to the failed state can be accompanied by a phenomenon, which is often referred to as failure wave or failure front. The assumption of its existence rationalized some of the conflicting results of previous studies. However, the nature of this phenomenon has not yet been conclusively understood.

First systematic investigations of the failure wave were conducted by Rasorenov, Kanel, et al. [2, 3]. They used explosive charges and planar plate impact (PPI) tests to induce a plane shock wave in optical K19 glass (similar to SLG). At loads up to 4.2 GPa, they observed a “failure wave” which initially moved at 1500 m/s and was slowed down to less than 1000 m/s after travelling a distance of 3 mm. They further noticed that at high pressures no failure wave arose which was attributed to plastic deformation preventing brittle fracture.

In contradiction, Brar et al. [4, 5] observed a failure wave at loadings above the HEL, moving with a velocity of 2200 m/s. A further discrepancy to Rasorenov et al. was that Raiser et al. [6] could not observe a reflection of the shock waves at the failure front.

Orphal et al. [7] later introduced the term failure front. They observed the phenomenon during the impact of multiple co-axial spaced gold rods into borosilicate glass. Their conclusion was that the failure front stops shortly after the driving stress ceases, but is reinitiated by the impact of the next rod. They therefore assumed that the failure front cannot be a diffusion-like phenomenon but is rather a result of nucleation and growth of cracks and densification.

Table 3 summarizes the failure front velocities for reported peak loads in SLG determined in previous studies from other authors.

Table 3 Summary of failure front velocities in soda-lime glass from other authors

Simha and Gupta [8] found that the discrepancies of the determined failure front velocities are due to the fact that longitudinal and lateral gauge data indicate different features. They observed a strongly time-dependent material response and concluded that the lateral stress measurements of previous studies cannot be interpreted in terms of a moving wave or front. They also pointed out that deriving a wave velocity even from longitudinal gauge data is difficult.

Apart from the experiments using stress gauges, several studies have focused on visualizing the onset and propagation of the damage in transparent materials. Senf et al. [9, 10] developed edge-on-impact experiments, which enabled the observation of crack nucleation and propagation in single glass plates. This procedure has later been continued and improved by Strassburger et al. [11,12,13,14,15]. The more complex morphology of damage in multi-layer glass laminates was studied by Bless et al. [16] for high velocity impact (1118 m/s).

Strassburger et al. also developed an experimental technique, which facilitated the visualization of damage propagation in a complex laminate target during projectile penetration [17]. A combination of high-speed imaging, photonic Doppler velocimetry and numerical simulations revealed a clear correlation between damage propagation, glass layer deformation and projectile position.

Various studies have also focused on the visualization of fracture propagation along glass bars (e.g. [18,19,20].). However, Walley concludes in a review paper [21] that even though some differences between the behavior of soda-lime and borosilicate glass during symmetric rod impact have been reported, the origin of these differences is still not understood and has not been conclusively demonstrated. Gorfain et al. [22] used reported experimental characterization data of SLG to develop a complete set of parameters for the latest computational constitutive model of Holmquist and Johnson [23]. They were able to simulate the development of failure fronts during Taylor rod impact with reasonable propagation velocities. However, clear difficulties reproducing the experimental observed radial expansion and discrete jet phenomena were still apparent.

Some studies have also investigated the existence of failure fronts in other brittle materials, although it is still controversial if they exist in materials apart from silica glasses, as reported by Walley [21]. For example, Zubkov et al. [24] observed a failure front in polymethylmethacrylate (PMMA) by means of synchrotron radiation.

Bourne et al. [25] were the first to use high-speed photography for the visualization of the failure front propagation in SLG during PPI at loadings up to the HEL. They observed a ramping behavior of SLG through the whole elastic range which, to their knowledge, had been overlooked before. Grady et al. [1] later specified that the ramping is caused by dispersing precursor waves, which can be caused either by exceeding the HEL or by elastic softening under compression.

Bourne et al. [25] were also able to visualize an uneven failure front at an impact load of 2.5 GPa. The front was moving at 2000 m/s and was initialized by the release wave from the back of the projectile. At a higher impact load of almost 5 GPa, they observed a different behavior. In this case, the failure front was moving closely behind the shock front at 5500 m/s. This high velocity was in certain contradiction with earlier findings and the discrepancy could not be explained.

In additional test series [26, 27], they estimated a threshold stress of 4 GPa for the onset of a failure front, which lies below the value of the HEL. Furthermore, they examined the influence of an internal interface layer with polished or pre-damaged surfaces. By means of lateral strain gauges and high-speed imaging with 5 Mfps, they revealed that the polished interface resulted in a delay of the failure propagation and a change in the failure front velocity.

As far as the authors know, the only other effort to visualize the compressive failure front in PPI tests aside from Bourne et al. [25, 28, 29], was undertaken by Chocron et al. [30]. They conducted PPI tests with borosilicate glass in the elastic range at stress levels between 0.7 GPa and 2.0 GPa. While they could clearly observe a failure front at stress levels of 0.8 GPa, the simultaneously recorded velocity profiles did not show the expected recompression signal. They assumed that the recompression wave resulting from the reflection at the failure front was too small to be distinguished from the signal noise. From this, they wrapped up that previous studies could maybe mistakenly have concluded the non-existence of the failure front at low velocities. They also observed failure nucleation sites trailing the shock wave, which were getting closer to the shock front at higher impact velocities.

In summary, in the reviewed literature, a number of questions remain open. In particular, these are the conflicting values for the reported HEL, the required stress levels for the initiation of a failure front and the failure front velocities. Therefore, we performed a systematic study to gather more detailed experimental information on the equation of state and the HEL of soda-lime glass. Furthermore, new insights into the failure front phenomena could be gained by means of additional high-speed video observation.

The key innovations of this study comprise experimental as well as analytical aspects. On the one hand, an extensive PPI test series has been carried out over a wide range of shock loading stress levels instrumented by two high-speed cameras and laser interferometers (PDV and VISAR). On the other hand, a systematic analysis concept has been developed and evaluated, including a combination of Lagrange diagrams with velocity profile data and a derivation of the equation of state (EOS) together with an error estimation.

Impact velocities ranged from 500 to 3000 m/s giving a load of the SLG targets between 3.5 and 20.8 GPa. For stress levels between 3.5 and 6.7 GPa two high-speed cameras with 5 Mfps enabled the observation of shock waves and failure fronts in side and rear views of the specimen. Therefore, visual information could be gathered not only in the purely elastic regime, but also in the transition region above 4 GPa and at stress levels beyond the HEL.

Experimental Details

Test Material

Specimen were manufactured from commercial grade SLG sheets of three different thicknesses: $\left(2.86\pm 0.05\right) \mathrm{mm}$, $\left(4.85\pm 0.05\right) \mathrm{mm}$ and $\left(7.85\pm 0.05\right) \mathrm{mm}$.

For the tests with high-speed video observation 50 mm × 50 mm square shaped specimens with polished side faces were cut. For all other tests, round discs with a diameter of 33 mm or 40 mm were prepared by means of water jet cutting.

Table 4 provides a summary of the typical material parameters. Values were taken from literature data or calculated by means of the conversion formulae of the elastic properties.

Table 4 Literature data for soda-lime glass

Planar Plate Impact Tests

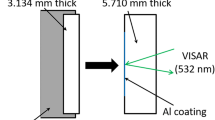
PPI experiments [31] were conducted with three different acceleration facilities with diverse gun barrel diameters at Fraunhofer EMI (two single-stage facilities located in Freiburg and a two-stage facility at the EMI location in Kandern). The general setup of the impact experiments is depicted in Fig. 1.

Fig. 1

Scheme of experimental setup for a direct planar plate impact test. Not to scale; the detailed arrangement depends on the specific facility used for the tests

The specimen geometry is flat such that a uniaxial state of strain is obtained in the specimen during the time period of interest. In all tests, a massive polycarbonate (PC) sabot was used to accelerate the impactor plate in a gun barrel. The sabots were produced to fit smoothly in the specific gun barrels. Impactor plates were made from commercial C45 steel or aluminum 6061 T6511 (denoted as Al in the following). All tests were conducted as direct impacts, in which the specimen plate is observed directly by the laser interferometer (no window applied). In order to establish a reflection of the laser light only from the surface of the specimen, a thin layer of gold was vapor-deposited on each specimen.

Table 5 provides a summary of all analyzed PPI tests conducted at the two-stage light gas gun. For tests with numbers 0112, 0113 and 0114 a shortened sabot was used (70 mm length instead of 150 mm), which reduced the total weight of the projectile-sabot-combination by more than 50%.

Table 5 Summary of all analyzed PPI tests conducted at the two-stage light gas gun (v_P = impact velocity)

The bore diameter of the second acceleration stage was 45 mm; the sabots had lengths of 150 mm and 70 mm with masses of 270 g and 122 g respectively.

In addition, a summary of all evaluated PPI tests conducted at the single-stage guns (powder or gas) is shown in Table 6. For most of these tests, a 70 mm gun barrel was used and the sabots had a total length of 50 mm and a mass without impactor plate of about 190 g. The impact velocity v_P was determined by a shortcut trigger arrangement of three pins in the muzzle region of the gun with a typical accuracy of ± 3%. For three tests (0855, 0856 and 0857), another single-stage accelerator operated with propellant was used. In those tests, a gun barrel with an 18.35 mm bore was utilized. The total length of the sabots was 32 mm, the mass of the sabots themselves was 8.7 g and impact velocities were calculated using a well-known impact velocity-amount of propellant-relationship (accuracy better than ± 2%). The chambers of the single-stage facilities were evacuated to the level of typically 2 mbar or below.

Table 6 Summary of all evaluated PPI tests conducted at single-stage guns (v_P = impact velocity)

In case of the single-stage accelerators, a VISAR [32,33,34] interferometric system was utilized for measuring the free surface velocity in the center of the rear face of the specimen. The focus point of the VISAR had a diameter of approximately 0.5 mm. The accuracy of the velocity measurement with the VISAR was ± 2% since typically 1.0 to 1.5 fringes were captured [35] during the experiments. The time resolution of the system is better than 2 ns.

In combination with the two-stage accelerator a two-beam PDV [36,37,38] was used. With one (collimated) beam the complete acceleration path of the sabot was measured, giving the impact velocity with an accuracy of at least ± 1%. This beam was positioned slightly above the SLG target measuring the projectile velocity either directly at the front face of the projectile plate (if the projectile diameter was larger than the target) or at the front face of the sabot. The other beam was used, as in case of the VISAR measurements mentioned above, to determine the free surface velocity of the specimens in their rear face center region. This beam of the PDV was focused and had a diameter of approximately 1 mm. In case of the PDV, the time resolution ${\sigma }_{t}$ and the accuracy of the velocity measurement ${\sigma }_{v}$ are connected to the wavelength ${\lambda }_{0}$ of the laser by the relation $2{\sigma }_{v}\cdot 2{\sigma }_{t}=\frac{{\lambda }_{0}}{2\pi }$ and depend strongly on the parameters of the applied short-time Fourier transform analysis [39]. For the measured loading curves, minimal time resolutions between 3 to 8 ns could be achieved. The chamber of the two-stage facility was evacuated to the level of typically 7 mbar or below.

In all tests the specimens fragmented completely to fine dust, so that no fragments could be recovered.

Setup for High Speed Videos

Some measurements conducted with the 70 mm single stage facility were accompanied by high-speed video camera observation (tests 4042 and 4143 to 4146, see Table 6). In order to give the camera a free view onto the specimen the specimen holder system indicated in Fig. 1 was replaced by a simplified specimen holder technique. The specimen were glued with a two-component epoxy onto a glass bar. The glass bar was fixed in a two angle-y-alignment unit so that the specimen could be oriented perpendicularly to the shot axis as in all other experiments.

High-speed videos were recorded with two sub-microsecond cameras. One camera observed the specimen directly from the side (side view, in order to make wave propagation processes visible and determine wave propagation speeds). A second camera observed the rear side of the specimen by the help of a mirror. As the cameras were exactly synchronized, it was possible to clearly distinguish waves at the specimen lateral surface (edge) from waves in the specimen center by comparing pictures from the different views at certain times. This rear side perspective is also used for receiving a qualitative impression of the effects of the waves and the resulting damage in the glass. The angle of observation as well as the portion of the specimen visible in the rear side view videos differ slightly from experiment to experiment, since the mirror is individually positioned in each experiment and destroyed in the test.

The time step between adjacent video images was set to 0.2 µs. A maximum of 128 images (400 × 250 pixels) could be recorded in each test by each camera. Results of the high speed videos are discussed in “New Insights Into the Failure Front Phenomenon” section.

Experimental Results

The measured free surface velocity v_fs as a function of time is presented in Fig. 2 for all tests with an aluminum projectile and in Fig. 3 for the configurations with the steel projectiles. All velocity curves were shifted in such a way that they reach a value of v_fs = 300 m/s at t₀. This point of time is set to be the arrival time of the elastic wave. The 300 m/s are selected in order to ensure that the amplitude of the air shock lies below this value while the rise of the velocity signal is still steep (approximately the midpoint of the elastic precursor). This is quite similar to Grady’s method of selecting an amplitude of 400 m/s [1].

Fig. 2

Velocity profiles of tests with an aluminum (Al) projectile

Fig. 3

Velocity profiles of tests with a steel (C45) projectile

The tests with very high impact velocities exhibit a small velocity plateau at negative times, which lies in the range between 30 and 120 m/s. For test 0102 the plateau lies even higher at a velocity of 280 m/s. This rise of velocity is not induced by the impact of the projectile, but rather caused by the arrival of a preceding front of compressed residual gas (air shock). As the amplitude of the air shock is comparably small, it is neglected in the analysis.

The four tests with the lowest impact velocities (v_p ≤ 601 m/s) indicate an elastic behavior. After a steep rise, v_fs reaches a plateau of constant velocity, which equals roughly the impact velocity (since the acoustic impedances of SLG and aluminum are almost equal). 0.63 µs later, the release wave from the projectile back surface arrives at the free surface, dropping v_fs to a lower level of about 200 m/s.

In all other tests, the velocity curve exhibits a convex shape during the loading process. Therefore, SLG shows no clear two-wave structure when loaded above its elastic limit. This makes a classical “selective” analysis approach inappropriate (a detailed comparison of the analysis methods is outlined in the Appendix (Section “Details of the “Incremental Analysis” Applied for the Evaluation of Surface Velocity Measurements”)).

As observed in the elastic regime, unloading takes place when the release wave from the projectile back surface arrives at the free surface. At high loads (v_p > 1300 m/s) this happens even before a plateau of constant velocity can form. This can be explained with the assumption that the velocity of the unloading wave increases once a certain stress level is exceeded.

Looking only at the free surface measurements, it is not possible to determine if spallation is taking place. However, combining them with Lagrange diagrams derived from the high-speed videos enables a better understanding of the underlying processes. As will be shown in Section “New Insights Into the Failure Front Phenomenon”, no spallation is taking place. Instead, the reverberation signal is induced by the interaction of the release waves from the glass free surface with a failure front.

New Insights Into the Failure Front Phenomenon

The high-speed videos provide valuable information on the occurrence and velocities of damage and shock waves during the impact process of tests no. 4042 and 4143 to 4146. In particular, the simultaneous observation of the glass target from the lateral and rear side enables a more detailed localization of the damage sites. As the cameras are synchronized, it is possible to distinguish well between interior phenomena and phenomena on the lateral surface. No spallation plane can be witnessed in these tests.

In combination with the incremental analysis of the loading paths, it is possible to identify a minimum load limit for the onset of a failure front within the glass samples. For this purpose, Lagrange diagrams need to be carefully drawn and compared with the observations. The process is explained in detail in this section.

Figure 4 depicts a selection of nine pairs of high-speed images from test no. 4143. In this experiment, a 2 mm thick aluminum projectile impacted a 7.85 mm SLG target plate at a velocity of 893 m/s. The upper half of each image shows the side view and the lower half displays the back view observed by means of a mirror. The indicated times refer to the time of the impact.

Fig. 4

Selection of 9 pairs of high-speed images from test no. 4143 (2 mm Al vs. 7.85 SLG, v_P = 893 m/s). The upper half of each image shows the side view of the SLG target plate. The lower half displays the back view observed by means of a mirror

The impact caused the formation of an elastic wave, which can be identified in the side view as a grey area moving from left to right through the white glass. This is because the high compression of the SLG changes its optical properties resulting in a significantly different light transmission. The elastic wave is immediately followed by a darker failure front, which consists of a network of cracks at the lateral free surface. In the side view of the second picture (t = 0.4 µs) the position of the wave front and the surface failure front is indicated by a small arrow. The corresponding rear view shows the bright glow of an impact flash. This flash can be clearly identified by analyzing the videos; it clearly appears before failure in the glass starts. The thin layer of gold, which was vapor-deposited on each specimen, appears as a black square. In the center of the square is a white spot, which emerges from the VISAR laser.

The surface failure front following the shock wave is initially located only near the edges of the SLG specimen and therefore denoted as such. From there, it propagates inwards to the center of the target in the shape of a circular front. After 2 µs it enters the field of view of the rear camera (image at the left bottom of Fig. 4).

In both of the last images’ side views (t = 4 µs and t = 6 µs), an additional failure front can be seen. This second failure front moves planar inside the whole target, as opposed to the surface failure front. It directly influences the measured free surface velocities in the center of the target. This gets evident when examining the corresponding Lagrange diagrams.

In order to correlate the high-speed images with the free surface velocity measurements, Lagrange diagrams are particularly suitable. The input values for these diagrams are the positions of the different wave fronts as a function of time. To extract the values from the videos, the concept of a “streak analysis” is introduced.

The principle of the streak analysis is illustrated in Fig. 5. The intention is to discard redundant information in the pictures by focusing on the central part only. For each time step, a narrow strip is cut out of the corresponding camera image. The strips are then stacked to form a new image. This new image provides the wave positions in an Eulerian frame of reference. The temporal propagation of the waves and the development of the failure is displayed in the vertical direction, while the horizontal direction contains the spatial information.

Fig. 5

Principle of the streak analysis: For each time step, a narrow strip is cut out of the corresponding camera image. The strips are then stacked to form a new image. This new image provides the wave positions in an Eulerian frame of reference. The temporal propagation of the waves and the development of the failure is illustrated in the vertical direction, while the horizontal direction contains the spatial information. The white rectangle in the left pictures shows the cut out position of the strips for test no. 4144. The resulting final piled up image is shown on the right side

The next step is to extract the information from the Eulerian frame of reference and transfer it to the Lagrangian. In the Lagrangian diagram, the positions of the front and rear sides of the SLG target are fixed and the wave positions are provided relative to the material frame of reference. Therefore, only the corresponding starting and arrival times have to be determined from the Eulerian diagrams.

This is achieved by applying a linear best-fit line to every wave front. Figure 6 illustrates the result for test no. 4144 (2 mm aluminum impacting 7.85 mm SLG at 486 m/s). The left side shows the original stacked image. The impact time is labeled with 0 ns and the time interval between two stripes is 200 ns. In the middle picture, three fit lines are indicated for the positions of the shock wave, the surface failure front and the interface between the aluminum projectile and impact face of the SLG. The intersection of the interface line and the shock wave line determines the time of the impact. Furthermore, the starting point of the failure front can be obtained at the intersection point of the interface line and failure front line. The end points of the fit lines at the rear side of the SLG target analogously determine the arrival times. The resulting start and end times are then used to draw the corresponding lines in the Lagrangian diagram.

Fig. 6

Results of test no. 4144 (2 mm Al vs. 7.85 mm SLG, v_P = 486 m/s), left: Streak analysis; right: Lagrangian diagram

In Fig. 6, the initial shock wave arrives at the free surface about 1.4 µs after impact, indicating a wave velocity of 5760 m/s. Since the wave is moving through unloaded material, this velocity is the same for the Lagrangian and the Eulerian frame of reference. It is in good agreement with the literature sound velocity of 5740 m/s (Table 4). The failure front starts with a delay of 0.2 µs, but moves slightly faster with an Eulerian velocity of 5790 m/s or a Lagrangian velocity of 6000 m/s, respectively.

In addition, the impact also initiates a shock wave inside the aluminum projectile. This wave propagates leftwards in the Lagrange diagram, arriving at the back face of the projectile after 0.3 µs. Since it cannot be observed directly in the high-speed images, its position is inferred from the longitudinal sound velocity of aluminum (6300 m/s). When it arrives at the projectile’s back face, it partially transmits into the polycarbonate sabot. The majority of its amplitude however is reflected back into the aluminum as a release wave. Up to loading stresses of 6.7 GPa, all release waves are assumed to propagate with the sound velocity of the respective material. This assumption is validated by comparing the Lagrange diagram with measurements of the free surface velocity. The simplified Lagrange diagrams (with constant wave velocities and no wave interactions) are obviously sufficient to explain the crucial features of the velocity profiles. An in depth analysis of considering all wave interactions could be done but is beyond the scope of this paper.

The Lagrange diagram in Fig. 6 includes on the right side the free surface velocity of the central target area. The first rising edge of the velocity signal corresponds to the arrival of the elastic shock wave. In order to synchronize the time axis of the velocity measurement and the Lagrange diagram, the velocity signal is shifted in time, so that the arrival times match.

Upon the arrival of the shock wave, the free surface velocity rises to about 500 m/s. This value is in good agreement with the theoretical free surface velocity that can be calculated using the measured impact velocity together with the acoustic impedances of aluminum and SLG $\left({\rho }_{\mathrm{SLG}}\cdot {c}_{\mathrm{p},\mathrm{SLG}}\cdot \frac{{v}_{\mathrm{fs}}}{2}={\rho }_{\mathrm{Al}}\cdot {c}_{\mathrm{p},\mathrm{Al}}\cdot \left({v}_{\mathrm{P}}-\frac{{v}_{\mathrm{fs}}}{2}\right)\right)$.

2 µs after impact, the velocity drops to about 230 m/s. The Lagrange diagram reveals that this drop is caused by the arrival of the release wave from the back of the projectile. The velocity does not drop all the way down to 0 m/s since the release wave is partially reflected at the aluminum/polycarbonate interface.

This supports the observation that the fast surface failure front starts from the edge zone of the SLG target. If the damage were also in the central region, the release wave would be influenced by the failure front before it reaches the velocity measurement point. Furthermore, the initial shock wave in the SLG is reflected at the free surface and undisturbedly passes all the way back to the projectile/target interface as a release wave. There, it is subsequently reflected and moves through the SLG once more as a compression wave. After 4.1 µs it arrives at the free surface again, which is in good agreement with the experimentally observed velocity rise at 4.2 µs. The expected velocity drop after 4.7 µs does not occur. This can be attributed to the fact that the lateral release waves from the target edges arrive at the velocity measurement point after 4.55 µs, removing the one-dimensional strain condition (red dashed line in Lagrangian diagram of Fig. 6). In addition, it can be deduced, that spallation does not take place, since the velocity signal shows no signs of “ringing in spall”. As a consequence the spall strength of the SLG has to be greater than: ${\sigma }_{\mathrm{spall}}=\frac{1}{2}{\rho }_{0}{U}_{\mathrm{p}}{\Delta v}_{\mathrm{fs}}=\frac{1}{2}\cdot 2.5\frac{\mathrm{g}}{{\mathrm{cm}}^{3}} \cdot 5760\frac{\mathrm{m}}{\mathrm{s}}\cdot 270\frac{\mathrm{m}}{\mathrm{s}}=1.9\,\mathrm{GPa}$ [40].

In test no. 4042 the impact velocity was almost the same as in the aforementioned test no. 4144, however, the original thickness of the SLG target was only 4.85 mm. The resulting diagrams can be found in the Appendix (Fig. 21) and are in good accordance with the previous observations. The only differences are a slightly delayed initiation time of the surface failure front (0.5 µs after impact) moving at a little slower Lagrangian velocity of 5581 m/s.

Test no. 4146 used the same setup as test no. 4144, producing the same results. For the sake of completeness, the corresponding diagrams can also be found in the appendix (Fig. 22).

The three tests with impact velocities of about 500 m/s do not exhibit a planar failure front inside the whole SLG target, instead the observed damage is located only near the edge zones of the target plate. This changes fundamentally in the tests at higher impact velocities (test no. 4143 and 4146), which are analyzed in the following.

Figure 7 shows the results for test no. 4143 (3 mm aluminum impacting 7.85 mm SLG at 893 m/s). The initial shock wave propagates at 5710 m/s, which is in good agreement with the longitudinal sound velocity. The surface failure front directly follows the shock wave, making both fronts indistinguishable. A clear difference to the tests with lower impact velocities is the occurrence of a second failure front after 0.86 µs. It is most likely initiated by the release wave coming from the backside of the aluminum projectile. The analysis of the stacked high-speed image shows that this failure front moves significantly slower with an Eulerian velocity of 1660 m/s or a Lagrangian velocity of 1040 m/s respectively.

Fig. 7

Results of test no. 4143 (3 mm Al vs. 7.85 mm SLG, v_P = 893 m/s), left: Streak analysis; right: Lagrangian diagram

The free surface velocity exhibits a second rise 3.4 µs after impact, followed by a drop at 4.2 µs. This can be explained by a second reflection of the initial shock wave at the failure front after it has been reflected at the sample free surface as a release wave. This is reasonable since the glass exhibits a lower acoustic impedance after failure (see e.g. [41].). If the waves were passing undisturbedly through the whole SLG target after their reflection at the free surface, they would arrive more than 0.7 µs too late. Figure 7 illustrates that the interaction of the reflected initial shock wave with the failure front at 2.4 µs results in an arrival time at the target backside after 3.5 µs. This is in good agreement with the free surface velocity rise after 3.4 µs. Likewise, the second arrival of the release wave from the projectile precisely matches the velocity drop at 4.2 µs.

The reflection at the failure front at 2.4 µs is also evident in the high-speed images. During the process, the formation of an internal fracture plane is initiated. Its growth can be observed in the rear view of the high-speed images, since the additional surface reflects the light of the flash. In Fig. 4 it is tagged with an arrow at 4.0 µs.

After 4.6 µs the velocity signal collapses, which is in good agreement with the theoretically expected arrival time of the release waves from the target edges (red dashed line in the Lagrangian diagram of Fig. 7).

The fundamental effects observed in test no. 4143 are reproduced in test no. 4145 (see Fig. 23 in the Appendix). In this test, a 2 mm aluminum projectile impacts a 7.85 mm SLG target at 1049 m/s. The second front is again initiated at the arrival of the release wave from the back of the projectile, which is about 0.3 µs earlier than in test no. 4143 due to the thinner projectile.

In the previous section, only the results of the five planar plate tests, which were accompanied by high-speed video cameras, are discussed. The analysis reveals that a minimum load is required for the onset of a planar failure front within the whole glass target. This limit can be determined more accurately by analyzing the velocity signals of additional planar plate tests (without camera observation).

Figure 8 shows the measured free surface velocity (green curve) for test no. 3787 (2 mm aluminum impacting 4.85 mm SLG at 601 m/s) in combination with the corresponding Lagrange diagram (blue and red lines). Note that the positions of the waves and failure front are not based on optical measurements, since this test was not accompanied by video cameras. Instead, they are reconstructed based on the findings of the previously described tests. The velocity of the shock and release waves is set to 5740 m/s, resulting in a good match between the arrival of the release wave at the free surface at 1.48 µs and the first drop in the velocity curve.

Fig. 8

Lagrangian diagram for test no. 3787: 2 mm Al vs. 4.85 mm SLG, v_P = 601 m/s

If no failure front is generated within the central area of the target, the second rise of the free surface velocity would be expected at 2.53 µs similar to test no. 4042. However, the velocity rise is observed significantly earlier at about 2.23 µs. This can be explained with the presence of an internal failure front, reflecting the waves similar to test no. 4143 and 4145.

Accordingly, the timing for the onset of the failure front is set to the arrival of the first release wave at the projectile/target interface at 0.635 µs. The velocity of the failure front is subsequently adjusted to match the second arrival of the shock wave with the velocity rise at 2.53 µs. This gives a failure front velocity of 800 m/s, which is considerably slower than the failure fronts of test no. 4143 (1040 m/s) and 4145 (1140 m/s). It can therefore by suggested, that not only the presence of the failure front but also its velocity is dependent on the impact load (increasing with increasing impact velocity).

Analogously to test no. 3787, two high velocity tests (no. 0099 and 0114) are analyzed in order to estimate the failure front velocities (see Fig. 24). In these tests, the speed of the release wave has to be increased, in order to explain the earlier drop of the free surface velocity after the first rise.

Moreover, it can be inferred that no spallation takes place. Therefore, the spall strength, when shocked to a longitudinal stress of 10.6 GPa, has to be greater than [40]

$${\sigma }_{\mathrm{spall}}=\frac{1}{2}{\rho }_{0}{U}_{\mathrm{p}}{\Delta v}_{\mathrm{fs}}=\frac{1}{2}\cdot 2.5\frac{\mathrm{g}}{{\mathrm{cm}}^{3}} \cdot 5760\frac{\mathrm{m}}{\mathrm{s}}\cdot 936\frac{\mathrm{m}}{\mathrm{s}}=6.7\,\mathrm{GPa}$$

Table 7 contains a summary of all resulting failure front velocities and initial release wave speeds. They are dependent on the applied load, which is linked to the impact velocity and the material of the projectile. All listed tests used an aluminum projectile with impact velocities between 486 m/s and 2447 m/s as specified in the first column. The corresponding induced longitudinal stress results from the incremental analysis of the loading paths (Section “Incremental Analysis of the Loading Paths”) and is given in column two.

Table 7 Summary of resulting velocities of initial release wave (c_release) and planar failure front (c_fail)

Two important conclusions can be derived from Table 7:

• First, the properties of the failure front are highly dependent on the impact load. When shocked to a longitudinal stress of 3.8 GPa or less no failure front emerges inside the SLG. The damage, which can be observed in the high-speed videos, is limited solely on the lateral fringe area of the target. At a longitudinal stress of 3.9 GPa, a plane failure front arises inside the whole SLG plate, propagating at a velocity of 800 m/s. This front is induced by the arrival of the release wave from the back of the projectile. When the impact velocity, and therefore the longitudinal stress, is further increased, faster moving failure fronts are generated. The highest failure front velocity of 2100 m/s is inferred from tests with longitudinal stresses of 10.6 and 14.2 GPa. Since there is no further rise of the velocity, 2100 m/s could be an upper limit.

• Second, the velocity of the initial release wave is also dependent on the impact load. For all tests with a longitudinal stress of up to 6.7 GPa a constant velocity of 5740 m/s is inferred. Therefore, the velocity of the release wave equals the velocity of the preceding compression wave, within this loading range. A sharp increase is observed in the two tests with higher stresses. At a longitudinal stress of 10.6 GPa the release wave moves 30% faster, with a velocity of 7500 m/s. A further increase to a stress of 14.2 GPa results in an even higher release velocity of 9500 m/s. It can therefore be concluded, that the release wave velocity has an upper limit higher than 9500 m/s, which is much higher than the failure front velocity.

Incremental Analysis of the Loading Paths

In this section, the shock Hugoniot of SLG is determined. This is achieved through an incremental analysis of the free surface velocity measurements [42].

Figure 9 shows the free surface velocity of test no. 3787 in which a 2 mm aluminum projectile impacted a 4.85 mm thick SLG target with a velocity of 601 m/s. The blue line is the unsmoothed velocity signal derived from the interferometry measurement at the back face of the SLG. The smoothed red line results from a moving average over 35 data points.

Fig. 9

Original and smoothed velocity profile for test no. 3787

The ending point of the loading path, i.e. the final state, is obtained by analyzing the derivative of the velocity signal. Figure 10 illustrates the original velocity signal from test 3787 during the first 0.3 µs as a dark blue line. The light blue line depicts the derivative, i.e. the acceleration of the free surface. Since the absolute values of the acceleration are not of interest, a normalized representation is chosen. After a sharp increase, the acceleration rapidly decreases, reaching a value of almost zero at 0.06 µs. This inflection of the curve is marked by a red dashed line in the diagram and is set to be the ending point of the loading path.

Fig. 10

Determination of the time of the final state using the normalized acceleration for test 3787

The final state variables of the shocked SLG, like the longitudinal stress and the volumetric compression, are then calculated using Eqs. 27, 28, 29 and 32, as described in the Appendix. Hereby, an elastic wave speed of ${c}_{\mathrm{p}}=5740 \mathrm{m}/\mathrm{s}$ is chosen (Table 4).

An error estimation is needed in order to quantify the uncertainty associated with possible errors of the arrival time ${t}_{0}$ of the elastic wave and the velocity ${c}_{\mathrm{p}}$. This is realized by conducting two additional incremental analysis with shifts of ± 50 ns on ${t}_{0}$. Figure 11 illustrates the resulting input curves of test no. 3787. The green curves marks the velocity signal used for the standard analysis. By applying a shift of -50 ns (red graph) and + 50 ns (yellow graph) two additional velocity curves are created.

Fig. 11

Input data for the incremental analysis of test 3787; different ${t}_{0}$ offsets are indicated by different colors: original ${t}_{0}$ = green, ${t}_{0}$ − 50 ns = red, ${t}_{0}$ + 50 ns = yellow

The outlined analysis and error estimation concept is applied to all PPI tests. The result is depicted in the diagram in Fig. 12, where the longitudinal stress is plotted versus the volumetric compression. Each green point represents the final state of one PPI test, resulting from the standard incremental analysis. In addition, the results from the shifted analysis are marked as red and yellow circles. The diagram illustrates that a shift of − 50 ns yields a lower longitudinal stress but a higher volumetric compression than the corresponding standard value. For a shift of + 50 ns, the opposite applies. The size of the error bars (black markers) of the standard analysis is chosen to be the difference between the green and yellow data points. With this assumption, all shifted results lie within a range of one to two error bars.

Fig. 12

Resulting final states: the results of the standard incremental analysis are illustrated by the green circles. The yellow and red circles represent the results for the analysis in which ${t}_{0}$ was shifted by ± 50 ns

All values illustrated in Fig. 12 are listed in Table 8 together with some additional results. The first three columns provide information on the experimental setup and impact conditions. There, the thicknesses of the projectile and target are given together with the used material and the measured impact velocity v_p. Columns 4 and 5 show the resulting particle velocity u_p and shock wave velocity U_s of the final state. The next two columns contain the corresponding density and volumetric compression. In the last column, the induced longitudinal stress σ_x is given.

Table 8 Summary of all calculated values in the final states (standard incremental analysis without shift on t₀)

Figure 13 shows a graph of the U_s-u_p-relation of the final states. The results of the present work are illustrated by the green circles. For longitudinal stresses of 8.7 GPa and higher an almost linear correlation (${U}_{\mathrm{s}}=1.88 {u}_{\mathrm{p}}+2230\,\mathrm{m}/\mathrm{s}$) is observed, as indicated by the dashed line. For comparison, the literature data of Alexander et al. [43] is shown as grey triangles.

Fig. 13

U_s-u_p-relation for the final states: the results of the present work are illustrated by the green circles together with a dashed line indicating a linear correlation at higher stresses. The results of Alexander et al. [43] are indicated by the grey triangles

Derivation of an Equation of State for Soda-Lime Glass

In this section, it is outlined how an EOS for SLG can be derived from the shock Hugoniot deduced in the previous section (Fig. 12). The EOS of the Johnson-Holmquist-2 material model for glass [44] is taken as a representative example.

In this EOS, a polynomial formulation of the relation between the hydrostatic pressure and the volumetric compression is used. In order to determine the parameters, the hydrostatic pressure has to be derived from the longitudinal stress of the shock Hugoniot. The approach chosen here is to identify the Hugoniot elastic limit (HEL) and the yield strength by means of the von-Mises yield criterion, in order to subtract the shear-resisting term from the shock Hugoniot.

The underlying theoretical principles are shortly outlined below and are described in more detail by e.g. Hiermaier in [45] on pages 118 et seqq.

The hydrostatic pressure P can be expressed through the first invariant of the total stress tensor, which is one third of the sum of the principal stresses ${\sigma }_{x,y,z}$. In the following, stresses are taken to be positive in compression:

$$P = \frac{1}{3}\left( {\sigma_{x} + \sigma_{y} + \sigma_{z} } \right)$$

(1)

During the loading by a planar shock wave, the material is in a uniaxial strain state. Therefore, the stresses ${\sigma }_{y}$ and ${\sigma }_{y}$ which are perpendicular to the shock direction are equal:

$$\sigma_{y} = \sigma_{z}$$

(2)

Combining Eqs. 1 and 2 yields:

$$P = \frac{1}{3}\left( {\sigma_{x} + 2\sigma_{y} } \right)$$

(3)

With the von-Mises yield criterion the yield strength $Y$ can be written as:

$$\begin{aligned} Y & = \frac{1}{\sqrt 2 }\sqrt {\left( {\sigma_{x} - \sigma_{y} } \right)^{2} + \left( {\sigma_{y} - \sigma_{z} } \right)^{2} { + }\left( {\sigma_{z} - \sigma_{x} } \right)^{2} } \\ &{ \mathop {eq. 2}\limits_{ = } }\left| {\sigma_{x} - \sigma_{y} } \right| \\ \end{aligned}$$

(4)

which is identical to the Tresca yield condition in this case.

Combining Eqs. 3 and 4 yields:

$$P = \sigma_{x} - \frac{2}{3}Y$$

(5)

For uniaxial strain conditions, the HEL marks the longitudinal stress at which plastic deformations arise. In the elastic regime, below the HEL, Hooke’s law is applied:

$$\sigma_{y} = \frac{\nu }{1 - \nu }\sigma_{x}$$

(6)

where $\nu$ denotes the Poisson‘s ratio.

Since the transition from elastic to plastic behavior has to be continuous, Eqs. 4 and 6 have to be equal when ${\sigma }_{x}=\mathrm{HEL}$ which yields:

$$Y = {\text{HEL}}\frac{1 - 2\nu }{{1 - \nu }}$$

(7)

A possible approach to estimate $P$ from ${\sigma }_{x}$ is therefore to calculate $P$ with Eq. 5 within the plastic regime (${\sigma }_{x}\ge \mathrm{HEL}$). The elastic curve is then determined by a linear interpolation between ${\sigma }_{x}=0$ and ${\sigma }_{x}=\mathrm{HEL}$.

The required value for $Y$ can be determined using Eq. 7. Alternatively, $Y$ can be taken from experimental shear strength data in the literature, which varies typically between 0.3 GPa and 4.0 GPa (Table 2).

The literature values for the HEL vary quite considerably between 3.5 and 7.0 GPa as outlined in Table 1. In order to identify the HEL of the present data, a new approach has been developed, which is applied as described in the following.

Figure 14 displays the experimentally determined data points of the shock Hugoniot. The four data points at the lowest longitudinal stresses are in line with a linear fit through the origin. They are therefore identified as purely elastic states and represented as purple circles as opposed to the green circles of the plastic states. A polynomial fit of third degree through the plastic states results in the orange curve. Hereby, each data point is weighted with its corresponding measurement errors (black markers). The red lines represent the resulting confidence intervals of the fit. This means that with a probability of 68% the true shock Hugoniot is lying within the 1 standard deviation (SD) interval (area between the bright red lines) and with a probability of 95% within the 2 SD interval (area between the dark red lines).

Fig. 14

Final states resulting from the PPI tests. The purple points represent final states in the purely elastic range. The orange curve represents a polynomial fit of third degree through all other final states (green points). Hereby, the red lines indicate the corresponding 68% and 95% confidence intervals (1 and 2 standard deviations)

The HEL is subsequently defined to be the intersection point between the polynomial fit of the plastic regime and the linear fit of the elastic regime. This is illustrated in Fig. 15, where the linear fit is represented as a purple line. The intersection point yields a value for the HEL of (5.0 ± 0.2) GPa. Hereby, the standard deviation of the HEL is estimated from the intersections of the linear fit line with the 1 SD confidence interval of the polynomial fit.

Fig. 15

Determination of the HEL: The purple line represents a linear fit through the purely elastic final states. The orange curve represents a polynomial fit of third degree through all other final states. Hereby, the red lines indicate the corresponding 68% confidence interval (1 standard deviation). The intersection of both fits corresponds to the HEL. This can be seen in more detail in the bottom diagram, which shows an enlarged section of the low compression range. The standard deviation of the HEL is estimated from the intersections of the linear fit line with the 1 SD confidence interval of the polynomial fit

The HEL can be used to get an estimation for $Y$. Together with a Poisson’s ratio of $\nu =0.21$ (Table 4) Eq. 7 gives a yield strength of $Y=\left(3.65\pm 0.15\right) \mathrm{GPa}$.

Considering further literature results, a value of $Y=4\,\mathrm{GPa}$ has been selected for the calculation of $P$ with Eq. 5. On the one hand, this is in good agreement with Bourne’s measurements from 1995 and 1996 [28, 46]. Hereby, the strength curve of intact material is used since the failure front moves significantly slower than the shock waves (see Section "New insights into the failure front phenomenon"). On the other hand, this value is reasonably close to the estimation based on Hooke’s law and the von-Mises yield criterion of $Y=\left(3.65\pm 0.15\right) \mathrm{GPa}$. It is also in rough agreement with the measured static yield strength of $4.3\,\mathrm{GPa}$ [47].

On top of that, this approach results in an EOS with a very plausible bulk modulus of ${K}_{1}=42.5\,\mathrm{GPa}$ at low hydrostatic pressures (Fig. 17).

The resulting hydrostatic pressures are presented as blue squares in Fig. 16. Hereby, the illustrated error markers are adopted from the corresponding errors of the shock Hugoniot values (green circles). This is done since the errors on $Y$ are considered negligible compared to the errors of the shock Hugoniot states.

Fig. 16

Final states resulting from the PPI tests. The green points are the longitudinal stress values lying on the Shock-Hugoniot, represented by the orange polynomial fit curve. The blue points are the hydrostatic pressure states, calculated by subtracting two thirds of the yield stress

Applying a polynomial fit of third degree through the hydrostatic pressure points finally yields the EOS of the form

$$P = K_{1} \cdot \mu + K_{2} \cdot \mu^{2} + K_{3} \cdot \mu^{3}$$

(8)

with ${K}_{1}=\left(42.5\pm 1.5\right) \mathrm{GPa}$, ${K}_{2}=\left(-24.6\pm 16.9\right) \mathrm{GPa}$ and ${K}_{3}=\left(51.8\pm 40.5\right) \mathrm{GPa}$.

The result is plotted in the top diagram of Fig. 17 as a light blue line. The darker blue lines represent the corresponding 1 SD and 2 SD confidence intervals of the fit. For pressures and compressions greater than the highest measurement point at $\mu =0.43$ and $P=18.1\,\mathrm{GPa}$, the confidence intervals widen significantly. Therefore, an extrapolation to higher values has to be used with care. However, in case of a typical impact scenario on a glass laminate target this uncertainty has no relevance since the highest occurring pressures are expected to be well below $10\,\mathrm{GPa}$.

Fig. 17

Equation of state for soda-lime glass: Each blue square corresponds to the final state of one PPI test. The light blue curve is the related EOS resulting from a polynomial fit of third degree. The 68% and 95% confidence intervals (1 and 2 standard deviations) are shown as dark blue lines. The bottom diagram shows an enlarged section in the low compression range. Hereby, the red dashed line corresponds to the resulting bulk modulus at zero pressure

In the low-pressure range, the derivative of the EOS corresponds to the elastic bulk modulus. The bottom diagram of Fig. 17 depicts an enlarged section of this regime. The red dashed line represents the gradient at zero pressure, which equals ${K}_{1}$. The comparison of ${K}_{1}=\left(42.5\pm 1.5\right) \mathrm{GPa}$ with the literature value of $K=42.8\,\mathrm{GPa}$ (Table 4) yields a very good agreement. This is interesting as they could be different if the inelastic deformation was due to brittle failure and not due to plastic flow.

Discussion and Comparison with Literature Data

The first main results of this work are the new insights into the failure front phenomena, which were outlined in Section “New Insights Into the Failure Front Phenomenon”. They deliver arguments, which can support or refute some of the contradicting assumptions of previous studies, which are discussed in the following.

The determined onset of the failure front between 3.8 GPa and 3.9 GPa is in good agreement with the literature value of 4.0 GPa from Simha et al. [8] and Rosenberg et al. [41]. On the contrary, the observation of Dandekar and Beaulieu [48], that the failure front is initiated at stress levels between 4.7 and 5.2 GPa, is not supported. These stress levels correspond to the HEL, which was determined as $\left(5.0\pm 0.2\right) \mathrm{GPa}$ in this study. Therefore, it can be concluded that the HEL does not represent the threshold for the initiation of damage.

In all conducted experiments, the internal failure front was initialized by the release wave from the back of the projectile. This is concluded from the comparison of the high-speed observation with the corresponding Lagrange diagrams. In particular, the variation of the projectile thickness showed a clear correlation with the initiation time of the failure front (see Figs. 7 and 23).

This is in agreement with the observations of Bourne et al. [25]. Furthermore, the assumption of Kanel et al. [2, 3], Brar et al. [4] and Espinosa et al. [49] that the failure front originates at the sample surface at the start of compression, is not supported.

Horie [50] summarized that it is not established whether failure fronts occur above the HEL. The results of the present work however strongly support the hypothesis of their occurrence. At 6.7 GPa a failure front with a velocity of 1140 m/s was evidenced by means of high-speed videos as well as laser interferometry. For stress levels of 10.6 GPa and higher, the presence of a failure front with a velocity of 2100 m/s could be inferred from the interferometry data. Since the latter velocity surpasses the ultimate speed of growth of cracks of 1500 m/s in glasses [51], the failure front describes a different phenomenon and instead presumably consists of a propagating front of crack nucleation sites.

By means of high-speed imaging, Chocron et al. [30] could observe a failure front in borosilicate glass at very low stress levels of 0.8 GPa. Since they could not detect the recompression wave in the velocity profile, which originates from the reflection of the unloading wave from the surface at the failure front, they assumed that previous studies could maybe mistakenly have concluded the non-existence of the failure front at low velocities.

The results of the present work do not support this conclusion for SLG. At stress levels below 3.9 GPa, solely a surface failure front could be observed that originates at the specimen’s lateral free surface. This front exhibited failure nucleation sites trailing the shock wave, which were closer to the shock wave at higher impact velocities, similar to Chocron’s observations and the observations of Bourne et al. [25].

Only at higher stress levels, an internal failure front could be identified. The correlation with the corresponding velocity profiles revealed that this second front was located inside the whole glass specimen.

The differences to Chocron’s observation could be attributed to several reasons. First, it could be due to a different behavior of soda-lime and borosilicate glass. Second, it might have been difficult to separate the internal from the surface failure front. However, Chocron et al. used the intensity of the laser interferometer as an indication for the damage to be in the interior of the specimen.

Other main results of this work are the determined EOS as well as the HEL for soda-lime glass. The evaluated HEL of (5.0 ± 0.2) GPa lies well within the range of the reported literature values between 3.1 and 8.0 GPa (see Table 1). The discrepancies in the literature are mainly due to the fact that SLG exhibits no clear two-wave structure in its shock wave profiles making the common analysis methods of ductile materials hardly applicable. A major source of error was the lack of a clear-cut method for the evaluation of stress levels as pointed out by Grady et al. [1].

The elaborated incremental analysis approach of this work however provides a solution, which is less prone to errors. An incremental analysis of the differential form of the Rankine-Hugoniot equations is not completely new, as it was already used e.g. by Alexander et al. [43] or Reinhart et al. [52]. Information about the derivation of the concept and the corresponding formulas as well as an error estimation however, is sparse in the literature and not given in [43] and [52]. Furthermore, there has to be taken great caution when considering different frames of reference (Lagrangian vs. Eulerian) to avoid calculation errors on the wave speeds.

The determined shock Hugoniot and EOS significantly differ from the reported results of Grady et al. [1], Alexander et al. [43] and Holmquist et al. [44] as illustrated in Fig. 18 and 19. While there is a good agreement in the elastic range up to a volumetric compression of roughly µ = 0.1, the curves clearly diverge in the plastic regime. For equal levels of compression, the shock Hugoniot of the literature lies at stress values that are 3–5 GPa lower than that of the present work. Most notably, the shock Hugoniot of the present work does not exhibit the plateau of constant stress at ${\sigma }_{x}\approx 7\,\mathrm{GPa}$.

Fig. 18

Comparison of the present results (green circles and colored lines) with literature data (white symbols and dashed line). The present data matches the literature data for soda-lime glass within the low-pressure range (elastic behavior). For stresses higher than 7 GPa, the literature data is shifted towards higher compressions. Recalculation of some selected literature velocity curves from [1] and [43] yields a shift to lower compressions (blue symbols)

Fig. 19

Equation of state for soda-lime glass: Each blue square corresponds to the final state of one PPI test. The light blue curve is the related EOS resulting from a polynomial fit of third degree. The 95% and 68% confidence intervals (2 or 1 standard deviation) are shown as dark blue lines. The black spotted line is the EOS derived by Holmquist et al. [44]

The differences may most likely be attributed to the applied analysis methods. This finding is based on a recalculation of some selected velocity profiles from the aforementioned publications. The selected profiles (for details see Figs. 25 and 26 in the appendix) were digitized and the stress and compression of the final states were recalculated by means of the analysis method outlined in this work. The result is illustrated in Fig. 18 by blue squares. The final states are shifted to lower compressions as indicated by the blue arrows. The fact that the recalculated values are in good agreement with the shock Hugoniot of the present work suggests that the differences are due to the analysis methods and not due to the material properties.

In case of Grady’s data, the difference is most likely due to the lack of a clear-cut method as outlined above. In case of Alexander’s data, the analysis was also conducted by means of an incremental approach. Nevertheless, differences could arise from different estimations of the wave velocities and impact times or even the use of a different set of differential equations.

Further results of this work can be deduced from the observed release response:

• The spall strength of SLG has to be greater than 6.7 GPa, when shocked to a longitudinal stress of 10.6 GPa. This is inferred from test no. 0099, in which the SLG target was impacted with an aluminum plate at 1703 m/s and no spallation signal could be observed (Fig. 24). The result is in contrast to Rosenberg et al. [53] and Espinosa et al. [49] who determined a spall strength of 3.8 and 2.6 GPa, respectively. It supports however the observations of the other authors listed in Table 2.

• Determined release wave velocities of 5740 m/s and 9500 m/s are in good agreement with the data of Grady et al. [54] which lies in the range of 5300 m/s to 13,300 m/s. In contradiction, Bourne et al. [55] concluded that the earlier release is not caused by higher release velocities, but is rather an effect of the failure front reducing the shear strength. They base their conclusion on their observation that the distance between the failure front and the shock wave front reduces with rising loading stress. The present work however implies, that the failure front velocity does not rise with increasing stresses above 10.6 GPa. The presented results therefore support the argument of high release wave velocities as suggested by Grady et al. [54] and Kanel et al. [51].

Summary

A systematic study has been performed to gather more detailed experimental information on the equation of state and the HEL of soda-lime glass. Furthermore, new insights into the failure front phenomena could be gained by means of additional high-speed video observation.

The key innovations of this study comprise experimental as well as analytical aspects. On the one hand, an extensive PPI test series has been carried out over a wide range of shock loading stress levels instrumented with two high-speed cameras and laser interferometers (PDV and VISAR). On the other hand, a systematic analysis concept has been developed and adapted, including a combination of Lagrange diagrams with velocity profile data and a derivation of the EOS. A central part of the analysis concept is the derivation of an incremental analysis method together with an error estimation.

The described method is not restricted to SLG only. In principle, it can be universally used for the analysis of other materials that also exhibit a complex Shock Hugoniot behavior, like e.g. optical glass, ceramics or even high strength steels.

The resulting shock Hugoniot and equation of state for soda-lime glass show significant discrepancies at pressures above the HEL in comparison to available data from other authors.

Impact velocities ranged from 500 to 3000 m/s resulting in loadings of the soda-lime glass targets between 3.5 and 20.8 GPa. For stress levels between 3.5 and 6.7 GPa two high-speed cameras with 5 Mfps enabled the observation of shock waves and failure fronts from the side and rear view of the specimens. Therefore, visual information could be gathered not only in the purely elastic regime, but also in the transition region above 4 GPa and at stress levels beyond the HEL.

In all experiments with high-speed observation, a surface failure front could be observed. This front is initiated directly at the time of impact, originating only in the rear zones of the SLG targets. At stresses of 3.9 GPa and higher, the additional internal failure front was observed. This second front is clearly initialized by the release wave from the back of the projectile. This observation is deduced from evaluating the arrival times of recompression waves that originate from the reflection of release waves from the free surface at the failure front. This is in contrast to the assumption of several other authors that the internal failure front originates at the sample surface at the start of compression.

The evaluated internal failure front velocities range from 800 to 2100 m/s. In two tests an internal failure front was evidenced by means of high-speed videos as well as laser interferometry. The corresponding velocities were 1040 m/s and 1140 m/s at impact stresses of 5.8 and 6.7 GPa, respectively.

At 3.9 GPa and at stress levels of 10.6 GPa and higher, the presence of an internal failure front with velocities of 800 m/s, and 2100 m/s respectively, could be inferred from the interferometry data (Table 7).

As spallation could not be observed in the release response in any of the tests, the spall strength has to be higher than 6.7 GPa. Release wave velocities between 5740 and 9500 m/s are deduced.

The Hugoniot elastic limit of the soda lime glass is determined to $\left(5.0 \pm 0.2\right) \mathrm{GPa}$. For the onset of an internal failure front a minimum longitudinal stress between 3.8 and 3.9 GPa could be identified. Therefore, it can be concluded that the HEL does not represent the threshold for the initiation of damage.

Appendix

Transformation of Observed Shock Wave Data to the Lagrangian Frame of Reference

The Rankine-Hugoniot equations are usually derived in the laboratory coordinate system, also referred to as the Eulerian frame of reference. Especially for the evaluation of PPI test data it is, however, more convenient to use Lagrangian coordinates. Hereby, the coordinate system is tied to material instead of spatial points.

In this section, equations are derived, which can be used to transform the shock wave equations from one coordinate system to the other. More detailed information can be found in [56] (p. 329 et seq).

The starting point is the conservation of mass in a rectangular cuboid of area $A$, initial length $\Delta h=\Delta x={x}_{0}$ and initial density ${\rho }_{0}$ at time $t$. After a time interval $\Delta t$ the cuboid gets compressed lengthwise while keeping its cross-sectional area $A$. In the Lagrangian frame of reference, this compression has no influence on the density and length, since the coordinate system is deforming together with the mass points. Since the total mass has to be the same in both coordinate systems, this gives equation

$$A \cdot \rho_{0} \cdot {\Delta }h = A \cdot \rho \left( {t + {\Delta }t} \right) \cdot {\Delta }x\left( {t + {\Delta }t} \right)$$

(9)

which can be transcribed to

$$\frac{\partial x}{{\partial h}} = \frac{{\rho_{0} }}{\rho }$$

(10)

A relationship for steady shock waves can be obtained using the total time derivative of $x\left(h,t\right)$:

$$dx = \left. {\frac{\partial x}{{\partial t}}} \right)_{h} dt + \left. {\frac{\partial x}{{\partial h}}} \right)_{t} dh$$

(11)

Respectively:

$$\frac{dx}{{dt}} = \left. {\frac{\partial x}{{\partial t}}} \right)_{h} + \left. {\frac{\partial x}{{\partial h}}} \right)_{t} \frac{dh}{{dt}}$$

(12)

In this equation $\frac{dx}{dt}={\stackrel{\sim }{U}}_{\mathrm{s}}$ denotes the shock wave velocity in the Eulerian frame of reference, while $\frac{dh}{dt}={U}_{\mathrm{s}}$ and ${\left.\frac{\partial x}{\partial t}\right)}_{h}={u}_{\mathrm{p}}$ denote the shock wave velocity and particle velocity in the Lagrangian frame of reference.

Combining Eqs. 10 and 12 gives an equation that can be used to transform the shock wave velocity from one coordinate system to the other:

$$\tilde{U}_{{{\text{s}},i + 1}} = u_{{{\text{p}},i}} + \frac{{\rho_{0} }}{{\rho_{i} }}U_{{{\text{s}},i + 1}}$$

(13)

Here the states in front of the shock wave are denoted by the index $i$ and the states behind the shock wave by the index $\left(i+1\right)$.

Details of the “Incremental Analysis” Applied for the Evaluation of Surface Velocity Measurements

During experimental planar plate impact tests, usually a free surface velocity ${v}_{\mathrm{fs}}$ is measured at the back of the test sample as a function time. Using the free surface approximation [57,58,59] the particle velocity ${u}_{\mathrm{p}}$ can be inferred from ${v}_{\mathrm{fs}}$:

$$u_{{\text{p}}} \approx \frac{1}{2}v_{{{\text{fs}}}}$$

(14)

As long as the shock wave velocity ${U}_{\mathrm{s}}$ is slower than the elastic precursor, ${U}_{\mathrm{s}}$ can be calculated with the measured arrival time difference $\Delta {t}_{\mathrm{el}-\mathrm{pl}}$ between the elastic precursor wave and the shock wave [31]:

$$U_{{\text{s}}} = \frac{{c_{{\text{p}}} }}{{1 + \frac{{c_{{\text{p}}} {\Delta }t_{{{\text{el}} - {\text{pl}}}} }}{{d_{{\text{T}}} }}}}$$

(15)

Here ${d}_{\mathrm{T}}$ denotes the thickness of the test sample, ${c}_{\mathrm{p}}$ is the longitudinal elastic wave velocity and assumed constant.

With these quantities, the final stress ${\sigma }_{\mathrm{final}}$ and strain ${\varepsilon }_{\mathrm{final}}$ of the attained Hugoniot state of an elasto-plastic material are determined using the following standard equations [31] (in this work compression is defined by a positive sign):

$$\sigma_{{{\text{final}}}} = \sigma_{{{\text{el}}}} + \sigma_{{{\text{pl}}}} = \rho_{0} c_{{\text{p}}} u_{{{\text{HEL}}}} + U_{{\text{s}}} \rho_{0} \left( {u_{{{\text{final}}}} - u_{{{\text{HEL}}}} } \right)$$

(16)

$$\varepsilon_{{{\text{final}}}} = \varepsilon_{{{\text{el}}}} + \varepsilon_{{{\text{pl}}}} = \frac{{u_{{{\text{HEL}}}} }}{{c_{{\text{p}}} }} + \frac{{u_{{{\text{final}}}} - u_{{{\text{HEL}}}} }}{{U_{{\text{s}}} }}$$

(17)

This concept of a “selective analysis” works well as long as the examined material shows a clear two-wave structure under shock loading. Materials, which exhibit a convex shaped Hugoniot curve in the loading range of interest, however, do not show this behavior. The reason for this is that an increase of the stress within this loading range results in a decrease of the wave speeds, which in turn prevents the formation of a sharp wave front. Therefore, the application of the “selective analysis” on this kind of material, like it is done e.g. in [1], requires a different approach for the determination of precursor and shock front arrival times and particle velocities for Eqs. 15, 16 and 17, which may increase the measurement uncertainties.

For this reason, a different concept, the so-called “incremental analysis” has been used in this paper and is outlined in this section. The starting point is the passing of a shock wave increment with a constant shock velocity ${U}_{\mathrm{s}}$, which lifts the material almost instantaneously from one stress and compression level to a higher level, causing a discontinuous jump of stress and velocity as a function of time. Thereby, the material states on both sides of the shock front are related through mass, momentum and energy conservation laws.

The corresponding basic conservation equations can be investigated in the so-called shock tube problem or Riemann problem. Furthermore, they can be combined to derive the Rankine-Hugoniot equations, the most commonly used set of equations for evaluating shock wave experiments.

The derivation of the basic conservation equations based on the Riemann problem is done e.g. by Hiermaier [45] (p. 163) and results in:

Mass conservation:

$$\rho_{i} \left( {\tilde{U}_{{{\text{s}},i + 1}} - u_{{{\text{p}},i}} } \right)dt = \rho_{i + 1} \left( {\tilde{U}_{{{\text{s}},i + 1}} - u_{{{\text{p}},i + 1}} } \right)dt$$

(18)

Momentum balance:

$$\rho_{i + 1} \left( {\tilde{U}_{{{\text{s}},i + 1}} - u_{{{\text{p}},i + 1}} } \right)dt \cdot u_{{{\text{p}},i + 1}} - \rho_{i} \left( {\tilde{U}_{{{\text{s}},i + 1}} - u_{{{\text{p}},i}} } \right)dt \cdot u_{{{\text{p}},i}} = \left( {\sigma_{i + 1} - \sigma_{i} } \right)dt$$

(19)

Here, the states in front of the shock wave with wave velocity ${\stackrel{\sim }{U}}_{\mathrm{s},i+1}$ are denoted by the index $i$ and behind the shock wave by the index $\left(i+1\right)$. Furthermore, the material density, the particle velocity and the longitudinal stress are denoted by $\rho$, ${u}_{\mathrm{p}}$ and $\sigma$.

Combining Eqs. 18 and 19 yields the longitudinal stress state behind the shock front:

$$\sigma_{i + 1} = \sigma_{i} + \rho_{i} \left( {\tilde{U}_{{{\text{s}},i + 1}} - u_{{{\text{p}},i}} } \right)\left( {u_{{{\text{p}},i + 1}} - u_{{{\text{p}},i}} } \right)$$

(20)

For the concept of the “incremental analysis” it is postulated that the complete loading path of the material can be divided in a series of infinitesimal small step loadings. Each loading step $i$ is induced by the corresponding shock wave with wave velocity ${\stackrel{\sim }{U}}_{\mathrm{s},i+1}$.

Thus, the final stress state ${\sigma }_{\mathrm{final}}$ of a complete loading path of N small step loadings is given by the Riemann sum:

$$\sigma_{{{\text{final}}}} : = \sigma_{N} = \sigma_{0} + \mathop \sum \limits_{i = 0}^{N - 1} \left( {\sigma_{i + 1} - \sigma_{i} } \right)$$

(21)

With (20) follows

$$\sigma_{{{\text{final}}}} = \sigma_{0} + \mathop \sum \limits_{i = 0}^{N - 1} \left( {\rho_{i} \left( {\tilde{U}_{{{\text{s}},i + 1}} - u_{{{\text{p}},i}} } \right)\left( {u_{{{\text{p}},i + 1}} - u_{{{\text{p}},i}} } \right)} \right)$$

(22)

Analogously, rearranging Eqs. 17 and 18 leads to the density and strain:

$$\rho_{i + 1} = \rho_{i} \frac{{\tilde{U}_{{{\text{s}},i + 1}} - u_{{{\text{p}},i}} }}{{\tilde{U}_{{{\text{s}},i + 1}} - u_{{{\text{p}},i + 1}} }}$$

(23)

$$\varepsilon_{i + 1} : = 1 - \rho_{0} /\rho_{i + 1}$$

(24)

$$\varepsilon_{{\max}} : = \varepsilon_{N} = \varepsilon_{0} + \mathop \sum \limits_{i = 0}^{N - 1} \left( {\varepsilon_{i + 1} - \varepsilon_{i} } \right)$$

(25)

The conservation Eqs. 18 and 19 are formulated in the space-fixed laboratory coordinate system, i.e. the Eulerian frame of reference. Therefore, the shock wave velocity ${\stackrel{\sim }{U}}_{\mathrm{s},i+1}$ is referenced to the Eulerian frame of reference as well, which is denoted by the tilde. Since ${\stackrel{\sim }{U}}_{\mathrm{s},i+1}$ has to be calculated from time and distance measurements it is, however, more convenient to transform the velocity into the Lagrangian frame of reference. This is achieved by rearranging Eq. 13 to:

$$U_{{{\text{s}},i + 1}} = \frac{{\rho_{i} }}{{\rho_{0} }}\left( {\tilde{U}_{{{\text{s}},i + 1}} - u_{{{\text{p}},i}} } \right)$$

(26)

Substituting Eq. 26 in Eqs. 20, 23 and 24 yields the final set of equations for the “incremental analysis”:

$$\sigma_{i + 1} = \sigma_{i} + \rho_{0} U_{{{\text{s}},i + 1}} \left( {u_{{{\text{p}},i + 1}} - u_{{{\text{p}},i}} } \right)$$

(27)

$$\rho_{i + 1} = \rho_{i} \frac{{U_{{{\text{s}},i + 1}} }}{{U_{{{\text{s}},i + 1}} + \frac{{\rho_{i} }}{{\rho_{0} }}\left( {u_{{{\text{p}},i}} - u_{{{\text{p}},i + 1}} } \right)}}$$

(28)

$$\varepsilon_{i + 1} = \varepsilon_{i} + \frac{{u_{{{\text{p}},i + 1}} - u_{{{\text{p}},i}} }}{{U_{{{\text{s}},i + 1}} }}$$

(29)

Since the shock wave velocity ${U}_{\mathrm{s},i+1}$ is referenced to Lagrangian coordinates, it can be calculated directly from the experimentally measured quantities ${d}_{\mathrm{T}}$ and $\Delta {t}_{i+1}$. Hereby, ${d}_{\mathrm{T}}$ refers to the test sample thickness while $\Delta {t}_{i+1}=\left({t}_{i+1}-{t}_{0}\right)$ is the time difference between the arrival of the shock wave and the arrival of the elastic wave.

Figure 20 shows a schematic of the corresponding Lagrange diagram.

The elastic wave arrives at the time

$$t_{0} = \frac{{d_{{\text{T}}} }}{{c_{{\text{p}}} }}$$

(30)

Hereby, the longitudinal wave velocity ${c}_{\mathrm{p}}$ is derived from the elastic material properties (Table 4). Since the elastic wave travels through unstressed material, its Lagrangian and Eulerian wave speeds are identical. Furthermore, the point of the time measurement, that is the free surface of the test specimen, stays at a constant Lagrangian position $h={d}_{\mathrm{T}}=const$ for all times.

The shock wave increment arrives at the time

$$t_{i + 1} = \frac{{d_{{\text{T}}} }}{{U_{{{\text{s}},i + 1}} }}$$

(31)

Combining Eqs. 30 with 31 and rearranging yields the Lagrangian shock velocity as a function of the experimentally observed time difference $\Delta {t}_{i+1}$:

$$U_{{{\text{s}},i + 1}} \left( {{\Delta }t_{i + 1} } \right) = \frac{{c_{{\text{p}}} }}{{1 + \frac{{c_{{\text{p}}} \left( {t_{i + 1} - t_{0} } \right)}}{{d_{{\text{T}}} }}}} = \frac{{d_{{\text{T}}} }}{{\frac{{d_{{\text{T}}} }}{{c_{{\text{p}}} }} + {\Delta }t_{i + 1} }}$$

(32)

Fig. 20

Lagrange diagram illustrating the relation between shock wave velocity and time measurement

Additional Streak Analysis and Lagrangian Diagrams for PPI Tests

See Appendix Figs. 21, 22, 23, 24.

Fig. 21

Results of test no. 4042 (2 mm Al vs. 4.85 mm SLG, v_P = 497 m/s), left: Streak analysis; right: Lagrangian diagram

Fig. 22

Results of test no. 4146 (2 mm Al vs. 7.85 mm SLG, v_P = 493 m/s), left: Streak analysis; right: Lagrangian diagram

Fig. 23

Results of test no. 4145 (2 mm Al vs. 7.85 mm SLG, v_P = 1049 m/s), left: Streak analysis; right: Lagrangian diagram

Fig. 24

Left: Lagrangian diagram for test no. 0099 (2 mm Al vs. 4.85 mm SLG, v_P = 1703 m/s); right: Lagrangian diagram for test no. 0114 (2 mm Al vs. 4.85 mm SLG, v_P = 2447 m/s)

Incremental analysis of literature data

See Appendix Figs. 25, 26.

Fig. 25

Velocity profiles from other publications: To facilitate comparison a selection of different experimental curves were taken and analyzed with the incremental analysis method. From Grady [1] four measurements were chosen (AT-1, AT-4, AT-5 and AT-8). From Alexander [43] the curves SODA-7 and AT-3 were reanalyzed. The displayed velocity curves are digitized from the original graphs and shifted along the x-axis in such a way that they reach an interface velocity of 150 m/s at t₀

Fig. 26

Comparison of loading profiles taken from literature and a selection of the tests from the present work. The time axis was divided by the target thickness in order to make the velocity profiles directly comparable. The particle velocity of the literature data was approximated by the interface velocity (Fig. 25). Although some differences are visible in the velocity profiles, the Hugoniot states resulting from the incremental analysis are in good agreement (Fig. 18)