Introduction

Since being invented by DuPont scientists in the early 1930s [1], neoprene (or polychloroprene) has been widely used in many applications. Although this study focusses on its energy absorbing capability, it can also be found in applications as diverse as aquatics, consumer goods, sealants, coatings, and even fashion. The reason for its broad use is its favourable properties. It resists degradation more than natural or synthetic rubber, so is more durable and long-lasting. It also resists fire better than pure hydrocarbon rubbers. It is very pliable, highly insulating and can be made into foams, which, depending on whether closed-cell or open-cell, can be made to be either waterproof or breathable.

Many polymers, including rubbers, exhibit strong temperature and rate dependence in their mechanical responses, including modulus and yield strength [2, 3]. Inhibitions in various molecular motions increase this sensitivity with decreasing temperature and increasing rate [4]. However, experimental characterisation at high strain rates (c. \(>500~\mathrm{s}^{-1}\)) can be challenging. Since conventional techniques such as the split-Hopkinson pressure bar (SHPB) were developed for stiffer materials, they are not ideal for low modulus rubbers: the resulting low wavespeed of rubbers means the static equilibrium requirement for the analysis of the SHPB experiment takes longer to be reached. The time taken for this is similar to, or sometimes even greater than the experimental duration [5, 6]. Structural vibrations may also mask the material response as the natural frequency of the specimen is similar to the frequencies in the loading pulse. The low specimen strength can also lead to a poor signal to noise ratio in the measured transmitted force, used to calculate specimen stress, making measurements difficult [7, 8].

Some effort has been made to make the SHPB more appropriate for testing low-impedance materials. For example, by more closely matching the impedances of the bars and specimen, the signal induced by the transmitted force can be maximised. Furthermore, the bar cross-sectional area can be hollowed to increase the transmitted strain signal, and piezoelectric lead zirconium titanate (PZT) gauges used to increase sensitivity to the transmitted force signal [5, 9].

In the past, time–temperature superposition (TTS) has been used as an alternative method to validate high rate data [10]. Inhibitions to micromolecular movement at high rates were shown to be analogous to those at low temperature. Much of the constitutive modelling based on these observations has tended to focus on predicting single values such as the yield stress [11, 12] or made use of a large number of parameters [13, 14]. TTS was developed for thermo-rheologically simple materials, but the appropriateness of its application to complex, commercially-produced polymers at finite strains cannot always be assumed and needs to be experimentally established. Consequently, direct high rate measurement of mechanical properties serves as an experimental validation that TTS holds for this given material system.

This paper looks to provide the reader with a simple model, with minimal parameters, that can capture the full mechanical response of neoprene rubber at a variety of strain rates.

Experimental Characterisation

Material

The material used in this investigation was a commercial black neoprene rubber supplied by Brammer, UK in the form of a \(5~\mathrm{mm}\) thick sheet with a density of \(1300~\mathrm{kg}\,\mathrm{m}^{-3}\). The molecular structure of neoprene is depicted in Fig. 1.

Fig. 1
figure 1

Molecular structure of neoprene rubber

Full size image

Compression Experiments

The purpose of the compression experiments was to obtain the stress–strain relationship at various strain rates and temperatures.

For the series of compression experiments, right circular cylindrical samples with a diameter of \(5~\mathrm{mm}\) were carefully machined out from the sheet, ensuring there was not a substantial increase in temperature, which might change the polymer microstructure. A common alternative is to punch out samples using a suitable die; however, stresses during the punching process result in specimens resembling conical frustra, and as such, this method was avoided.

Petroleum jelly was used as a lubricant for all experiments to avoid frictional effects influencing the mechanical response.

Low Rate Experiments

For the low strain rate characterisation (\(10^{-3}~\mathrm{s}^{-1}\) to \(10^{-1}~\mathrm{s}^{-1}\)), experiments were performed on a commercially available Instron 5980 electromechanical static testing machine with a true strain rate feedback controller. This reduces the velocity of the crosshead as the specimen is compressed by using strain measured with a contacting extensometer attached to the loading platens.

When experimenting at sub-ambient temperatures, an environmental chamber with a liquid nitrogen feed was used. For supra-ambient temperatures, the chamber’s in-built heater was used. To measure the temperature close to the sample within a ±1 °C accuracy, a thermocouple integrated into the loading platen was used, as opposed to the chamber’s own feedback control thermocouple situated at the back. Each sample was held at temperature for a minimum of 30 min to ensure thermal stability. The holding time is significantly longer than the time scale for diffusion based on the thermal diffusivity of neoprene rubber at room temperature [15]. The experiment was started once the two thermocouple readings were within 0.5 °C of each other.

For low load cases (typically above the glass transition temperature, \(T_g\), of the rubber), a \(5~\mathrm{kN}\) load cell was sufficient to record the force imparted. For low temperature experiments below the \(T_g\) of the material, due to the higher loads experienced, a \(50~\mathrm{kN}\) load cell was used.

Although preliminary experiments showed fixture compliance to be negligible at temperatures above the \(T_g\), for consistency with the low temperature experiments, an extensometer with a \(12~\mathrm{mm}\) gauge length was mounted to the plattens close to the sample and used to measure the displacement and enable the calculation of strain.

Medium Rate Experiments

For compression experiments at intermediate strain rates (\(1\, \hbox {s}^{-1}\) to \(100\, \hbox {s}^{-1}\)), a custom-built hydraulic loading frame was used. The displacement of the moving anvil was measured using linear variable differential transformers (LVDTs). The force was measured using a load cell mounted on the static anvil.

High Rate Experiments

For compression experiments at strain rates of the order \(10^{3}\, \hbox {s}^{-1}\), an in-house split-Hopkinson pressure bar (SHPB) was used. Full details of the analysis procedure for the SHPB testing of soft materials can be found in Gray and Blumenthal [6].

Ti-6Al-4V alloy bars with a diameter of \(12.7\, \mathrm{mm}\) were used. Although the bar material could be changed to provide a lower impedance mismatch with neoprene, the data collected using titanium alloy bars were of sufficient quality for the study presented in this paper. The striker bar was able to reach speeds around 20 m s−1, corresponding to an average true strain rate of around \(4\times 10^{3}~\, \hbox {s}^{-1}\).

Dynamic Mechanical Analysis Experiments

Dynamic mechanical analysis (DMA) experiments were performed in order to quantify the response of the material in terms of its temperature and frequency dependent storage and loss moduli. The storage modulus relates the component of stress that is in phase with the applied strain; the loss modulus, that which is out of phase.

For these experiments, rectangular samples were cut from the rubber sheet with dimensions \(50\, \hbox {mm}~\times ~10\, \hbox {mm}~\times ~5\, \hbox {mm}\). These experiments were conducted on a TA Instruments Q800 apparatus, and all were in the dual cantilever configuration. Full calibration of the apparatus and clamp were performed in accordance with the manufacturer’s protocol prior to data acquisition. An oscillatory amplitude of \(0.1\%\) strain was implemented with an isothermal frequency sweep in 2 °C increments from − 50 to − 80 °C. The following frequencies were used with the intention they would be reasonably well spread out in the \(\log\) domain: 0.5, 2, 5 and \(10\, \hbox {Hz}\).

Results and Analysis

Varying Rate Experiments

Three experiments were performed at each strain rate for the Instron and hydraulic press apparatuses, and three experiments in total for the SHPB at impact speeds of approximately 10 m s−1. A summary of the compression experiments performed can be found in Table 1. The results of repeated experiments were averaged and all the data subsequently plotted as shown in Fig. 2a. Averaging was possible as the mean error between experiments was < 5%. Since true strain rate control was not possible on the hydraulic press, as it was on the Instron machine, it should be noted that the actual strain rates as documented in Fig. 2a varied from the intended ones. Also note, unless stated otherwise, true stresses and strains are plotted.

Table 1 Summary of compression experiments performed
Full size table
Fig. 2
figure 2

a Results from compression experiments for varying strain rates at a constant temperature (20 °C), and b results from varying temperature experiments conducted at a constant strain rate (\(10^{-2}~\, \hbox {s}^{-1}\)) (Color figure online)

Full size image

It is clear that as the strain rate increases, the stress at a given value of strain is higher. However, the variation in stress is less prominent at the lowest and highest strain rates, but more so at intermediate rates. In quantifying this, we consider the percentage difference in the characteristic stress (\(\sigma _c\), the value of stress where \(\varepsilon =0.1\)). At the lowest strain rates (\(10^{-3}~\, \hbox {s}^{-1}\) to \(10^{-1}~\, \hbox {s}^{-1}\)), \(\sigma _c\) increases from \(0.79\, \hbox {MPa}\) to \(1.00\, \hbox {MPa}\) representing a \(26.7\%\) rise. At intermediate strain rates (\(1.3~\, \hbox {s}^{-1}\) to \(80~\, \hbox {s}^{-1}\)), there is a \(123\%\) rise from \(1.54\, \hbox {MPa}\) to \(3.43\, \hbox {MPa}\). At strain rates of the order \(10^{3}~\, \hbox {s}^{-1}\), there is only a \(12.4\%\) increase in \(\sigma _c\).

An explanation of this can be provided if we consider a flexible molecular chain model for polymers [16]. The increase in stress with strain rate is due to the inability of sub-molecular chain motions, like rotations, to take place within the time-scale of the experiment. The low strain rate limit stress is that of viscous flow and the high strain rate limit stress arises from the maximum instantaneous stress, when there has been no time for any viscous effects.

Varying Temperature Experiments

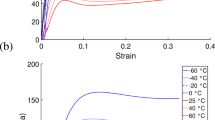
For the varying temperature experiments, the strain rate was kept constant at \(10^{-2}~\, \hbox {s}^{-1}\) and three runs were performed at each temperature and their results averaged. Up to strains of 0.5, the error was \(<5\%\). It only increased up to \(24\%\) at the largest strains. This is expected due the dominating hyperelastic behaviour (described further in “Hyperelasticity”) and the significant difference in large strain response that follows from any small difference in starting position of the loading anvils.

The mechanical response of the neoprene rubber down to temperatures of − 40 °C is largely similar to the supra-ambient cases, despite showing a small increase in stress with decreasing temperature. However, the response undergoes a drastic change as the temperature decreases below − 40 °C. The behaviour transitions from rubbery above this temperature to glassy below this temperature: the differing responses indicate the approximate value and effect of the \(T_g\) for neoprene rubber.

Considering the same flexible molecular chain model as in the previous section, the stress increase is due to the decreased temperature inhibiting cooperative segmental motion. This inhibition means a higher force is required for deformation. At higher temperatures, the material has considerable flexibility and can conform to many configurations minimising free energy and thus a lower deforming force is required.

Rate–Temperature Equivalence

It is clear to observe from Fig. 2, that stress increases with increasing strain rate and/or decreasing temperature. For the response at a particular high strain rate, it stands to reason that there is a corresponding temperature where the low strain rate response is the same. To investigate this, a graph plotting the characteristic stress, \(\sigma _c\), against the logarithm of the strain rate and the inverse of the temperature is shown in Fig. 3. By inverting the temperature axis, the similarities between the two dependences are clearer.

Fig. 3
figure 3

Equivalence between high strain rate and low temperature–low strain rate experiments (Color figure online)

Full size image

This figure allows the reader to qualitatively appreciate that there exists a certain temperature where the low strain rate compression response at that temperature corresponds to the high strain rate response at an ambient temperature. For example, if the characteristic stress, \(\sigma _c\), was desired at a strain rate of \(10^{3}~\, \hbox {s}^{-1}\), no further high rate experiments are required, as the value can simply be predicted by conducting a low strain rate (\(10^{-2}~\, \hbox {s}^{-1}\)) experiment at a temperature of around − 45 °C. This equivalence forms the basis of the TTS technique. Section 1 (see Supplementary information) contains supplementary data on the \(\varepsilon - t\) profiles for all experiments.

Time–Temperature Superposition

In order to better quantify the rate (or more accurately, frequency) and temperature dependences in the mechanical response of neoprene rubber, the results of the DMA experiments are used. At each temperature step from \(-50\) to 80 °C, the frequency dependence of the storage modulus was recorded and the results plotted in Fig. 4a.

The glassy nature of the material can be noted in the all-round stiffer response at the lowest temperatures. Likewise, the rubbery nature is clear from the low stiffness at the highest temperatures. The frequency dependence of the modulus is more noticeable as the temperature goes through the \(T_g\). This is evident from the increase in slope for the isotherms below the \(T_g\).

Fig. 4
figure 4

a Isotherms showing the frequency and temperature dependence of storage modulus, b shift factors required to move isotherms to construct a master curve and c master curve at a reference of 20 °C, and, inset, highlighting experimentally relevant frequencies (Color figure online)

Full size image

As the equivalence from the previous section showed, the modulus at a lower temperature is analogous to that of a higher frequency. Therefore, it is possible to construct a single graph at a reference temperature to show the full array of analogous responses using the well know TTS principle [17]. Here the reference temperature is selected to match that of the varying rate compression experiments, 20 °C. In order to construct this master curve, isotherms from Fig. 4a are shifted to the left if they are higher than the reference temperature (results analogous to lower frequencies) and shifted to the right is lower than the reference temperature (results analogous to higher frequencies). These shift factors (\(a_T\)) effectively allow isotherms to overlap with adjacent isotherms, thereby constructing the master curve of the response. In rubbers, an Arrhenius relationship is expected between the shift factors and temperature, i.e. \(\log a_T\) is linear in temperature. The shift factors allow experiments at different temperatures and strain rates to be compared, and therefore, their dependence on temperature is highlighted in Fig. 4b and used in comparisons with later experiments. The master curve that can be constructed using these shift factors is shown in Fig. 4c for a reference temperature of 20 °C.

Modelling

Hyperelasticity

One noticeable characteristic in the mechanical response of rubbers like the neoprene of this study is that they undergo large reversible deformation. Although the behaviour is Hookean initially, it soon changes to non-linear elasticity. This is due to the increasing amount of force required for each incremental deformation. In order to fully straighten the chain, entropy tends towards zero, and the force required tends to infinity. This type of behaviour is deemed hyperelastic. Models for this behaviour were initially developed by Mooney and Rivlin [18, 19], but for this study an Ogden model is used [20, 21].

Fig. 5
figure 5

a Ogden model fits to the full response of varying strain rate experiments conducted at 20 °C, and b to fit varying temperature experiments at \(10^{-2}~\, \hbox {s}^{-1}\) (Color figure online)

Full size image

Ogden proposed that the strain energy density function with respect to the principle stretches could be differentiated to obtain the nominal uniaxial stress response by making a few assumptions. Here, the strain energy density (Eq. 1) is expressed in true strain and the true stress response is obtained (Eq. 2). In this equation, \(\mu\) relates to the shear modulus and \(\alpha\), the strain hardening exponent, reflects the hyperelastic convexity. The initial Young’s modulus can then be found by Eq. 3. Incompressible, isothermal and isotropic material assumptions are made in order to fit the Ogden model to experimental results. Although more terms would improve the fit, in this study, only a one-term Ogden model was used due to its simplicity and its ability to capture the experimental data whilst easily relating the \(\mu\) parameter to the DMA experiments.

Adiabatic self-heating at high strain rates was neglected to comply with the isothermal assumption. This was appropriate since the results of a calculation (Eq. 4) in which all of the high strain rate mechanical work was transferred to heating the sample, only led to a 2 °C rise in temperature - a negligible amount. The heat capacity and density were 1.12 J g−1 °C−1 and \(1.5\, \hbox {g cm}^{-3}\) respectively [22].

$$\begin{aligned} \phi = \frac{2\mu }{\alpha ^2}(\mathrm {e}^{\alpha \varepsilon _1} + \mathrm {e}^{\alpha \varepsilon _2} + \mathrm {e}^{\alpha \varepsilon _3} - 3) \end{aligned}$$
(1)
$$\begin{aligned} \sigma _1 = \frac{\partial \phi }{\partial \varepsilon _1} = \frac{2\mu }{\alpha }\big (\mathrm {e}^{\alpha \varepsilon _1} - \mathrm {e}^{-\frac{1}{2}\alpha \varepsilon _1}\big ) \end{aligned}$$
(2)
$$\begin{aligned} E_0 = \lim _{\varepsilon \rightarrow 0} \frac{d\sigma }{d\varepsilon } = 3\mu \end{aligned}$$
(3)
$$\begin{aligned} \Delta T \approx \frac{1}{\rho C_p(T)}\int _{0}^{\varepsilon } \sigma (\varepsilon ) d\varepsilon \end{aligned}$$
(4)
Table 2 Ogden parameters required for fitting
Full size table

Viscoelasticity and Temperature Dependence

The results of the model are shown in Fig. 5. The one-term Ogden model shows a good ability to fit to experimental data for both varying strain rate, fixed temperature (a) and varying temperature, fixed strain rate (b) cases.

In this study, the Ogden parameters were allowed to vary to best fit the experimental data in a least squares sense (Table 2). Details on this are provided in Sect. 2 (see Supplementary information). From these data it is possible to infer a shift factor for \(\mu\) that can be used to take the varying temperature results at a fixed strain rate of \(10^{-2}~\, \hbox {s}^{-1}\) and map them to an effective strain rate as shown in Fig. 6a by noting that the shift factor is defined as \(\log a_T = -k(T-T_{ref})\). This is based on the observation from the DMA experiments that \(\log a_T\) was linear in temperature. The inferred shift factors gave a shifting gradient in decades per °C of \(k=0.07\). Note the similarity between this value, and that obtained for the modulus in DMA experiments (Fig. 4b), which gave \(k=0.101\). The rate–temperature dependence of the parameters is better observed in Fig. 6b.

Fig. 6
figure 6

a Implied shift factor relationship for \(\mu\), and b the rate and temperature dependence of Ogden parameters, with fits describing the dependences (Color figure online)

Full size image

It is possible to fit exponential graphs to describe the rate and temperature dependence for \(\mu\). Additionally, there is seemingly no rate dependent trend for \(\alpha\). Since \(\mu\) relates to the shear modulus of the material, it makes sense for it to depend on the strain rate. However, the strain hardening exponent refers to the large strain limiting response, which depend on the macromolecular geometry. As such, it makes sense physically, the \(\alpha\) parameter be considered as constant.

To investigate this further, the model was recalibrated using a constant value of \(\alpha =2.27\). This fixed average value can be used to obtain new fits to the experimental data as shown in Fig. 7a for the varying rate experiments and Fig. 7b for the varying temperature experiments. The parameters used in these updated fits are provided in Table 3 and fits to their dependence curves shown in Fig. 7c.

Table 3 Updated Ogden parameters
Full size table
Fig. 7
figure 7

a Updated Ogden model fits using a fixed \(\alpha\), b updated fits to the varying temperature experiments and c the fits to the updated parameter dependence curves (Color figure online)

Full size image

The fact that the rate and temperature dependences are so similar for the parameters gives confidence in the ability to use TTS for this material. In fact, by equating the \(\mu\) values for the rate and temperature dependences, it is possible to derive an expression for the shift factor. The process proceeds as follows.

By invoking the rate–temperature equivalence of \(\mu\) and using the model fits to the data in Fig. 7c, we can say that:

$$\begin{aligned} \begin{aligned} \mu _{{\dot{\varepsilon }}}&= \mu _{T} \\ 1.50 + 2.47{\dot{\varepsilon }}^{0.258}&= 1.54 + 1.11\mathrm {e}^{-0.0456T} \\ 2.47{\dot{\varepsilon }}^{0.258}&\approx 1.11\mathrm {e}^{-0.0456T} \\ \log {2.47} + 0.258\log {{\dot{\varepsilon }}}&\approx \log {1.11} -0.0456T\log {\mathrm {e}} \\ \end{aligned} \end{aligned}$$
(5)

The \(\mu\) values for the lowest strain rate and the highest temperature are deemed to be the same. This assumption is valid based on the closeness of the values in the obtained fits, and by consideration of the physical equivalence at those two extremes. Similarly:

$$\begin{aligned} \begin{aligned} \log {2.47} + 0.258\log {\dot{\varepsilon _0}}&\approx \log {1.11} -0.0456T_{ref}\log {\mathrm {e}} \\ \end{aligned} \end{aligned}$$
(6)

where \(\dot{\varepsilon _0}\) is the strain rate at which varying temperature experiments were conducted (\(10^{-2}~\, \hbox {s}^{-1}\)) and \(T_{ref}\) is the reference temperature (20 °C). By noting that the shift factor, \(\log a_T = \log {{\dot{\varepsilon }}} - \log {\dot{\varepsilon _0}}\), and subtracting Eq. 6 from Eq. 5:

$$\begin{aligned} \begin{aligned} \log a_T&= -\frac{0.0456\log {\mathrm {e}}}{0.258} \\&= -0.077(T-T_{ref}) \end{aligned} \end{aligned}$$
(7)

The shifting gradient of \(k=0.077\) obtained here using Eq. 7 is very close to that obtained through manual shifting as shown in Fig. 6a (\(k=0.070\)) and that of the storage modulus in the DMA experiments (\(k=0.11\)) as shown in Fig. 4b. A summary of the method employed to obtain the shift factors and the shifting gradient is shown in Table 4. Although the shift factors obtained using compression data and using models fit to their rate and temperature dependence are similar, those from the DMA experiments are slightly different.

Table 4 Summary of method used to obtain shift factors and the shifting gradient
Full size table

Based on this equivalence, a more accurate value for the equivalent temperature can be obtained than that estimated from the rate temperature equivalence in “Rate–Temperature Equivalence”. These equivalent temperature values are those that compression experiments at \(\dot{\varepsilon _0} = 10^{-2}~\, \hbox {s}^{-1}\) must be conducted at to obtain mechanical responses analogous to the desired strain rate. For reference, these are provided in Table 5.

Table 5 Equivalent temperatures and associated parameters for analogue fits as shown in Fig. 8
Full size table

Using the approach in Eq. 5:

$$\begin{aligned} \begin{aligned} \mu _{T_{eq}}&= \mu _{{\dot{\varepsilon }}} \\ 1.11\mathrm {e}^{-0.0456T_{eq}}&\approx 2.47{\dot{\varepsilon }}^{0.258} \\ T_{eq}&\approx -\frac{1}{0.0456\log {\mathrm {e}}}\log {\Bigg (\frac{2.47}{1.11}\Bigg )}+0.258\log {{\dot{\varepsilon }}} \\&\approx A+0.258\log {{\dot{\varepsilon }}} \end{aligned} \end{aligned}$$
(8)

By substituting these equivalent temperature values back into the \(\mu _T\) expression, the \(\mu\) values for the equivalent temperatures can be found.

$$\begin{aligned} \begin{aligned} \mu _{T_{eq}}&= 1.54 + 1.11\mathrm {e}^{-0.0456T_{eq}} \\&= 1.54 + 1.11\mathrm {exp}[-0.0456(A+0.258\log {{\dot{\varepsilon }}})] \end{aligned} \end{aligned}$$
(9)

By using this calculated value alongside the fixed \(\alpha\) value (average of the value for varying rate and varying temperature fits), the mechanical response at a variety of strain rates can be predicted by substituting these values into Eq. 2, thus producing the expression in Eq.  10.

$$\begin{aligned} \begin{aligned} \sigma _a&= \frac{2\mu _{T_{eq}}}{\alpha }\big (\mathrm {e}^{\alpha \varepsilon } - \mathrm {e}^{-\frac{1}{2}\alpha \varepsilon }\big ) \\&= \frac{2}{\alpha }\Big (1.54 + 1.11\mathrm {exp}[-0.0456(A+0.258\log {{\dot{\varepsilon }}})]\Big ) \\& \qquad\times\, \big (\mathrm {e}^{\alpha \varepsilon } - \mathrm {e}^{-\frac{1}{2}\alpha \varepsilon }\big ) \\&= \frac{1}{\alpha }\big (B+C\mathrm {exp}[D+E\log {{\dot{\varepsilon }}}]\big )\big (\mathrm {e}^{\alpha \varepsilon } - \mathrm {e}^{-\frac{1}{2}\alpha \varepsilon }\big ) \end{aligned} \end{aligned}$$
(10)

where \(\sigma _a\) is the analogue stress response, the fixed \(\alpha ~=~2.27\), \(B~=~3.08\), \(C~=~2.22\), \(D~=~0.800\) and \(E=-0.0118\), which are all constants.

These analogue stress responses are shown in Fig. 8 highlighting the value of using the TTS technique alongside a simple phenomenological model to enable the predictions of high strain rate responses.

Fig. 8
figure 8

Comparing Ogden fits as in Fig. 5a and their analogues obtained by considering the response at \(10^{-2}~\, \hbox {s}^{-1}\) and an equivalent lower temperature (Color figure online)

Full size image

Enhancing Predictability with DMA Results

It is evident that the form of graphs representing the rate and temperature dependence of the Ogden \(\mu\) parameter is very similar to that of the DMA master curve seen in Fig. 4c. To compare how similar, the rate dependent Ogden shear modulus, \(\mu _{{\dot{\varepsilon }}}\), obtained in Fig. 6 is expressed as an equivalent Young’s modulus using \(E~=~2\mu (1+\nu )\), where \(\nu = 0.5\), the Poisson’s ratio for an incompressible material. This comparison is shown in Fig. 9a.

If the rate dependent \(\mu\) can be related to the master curve to this extent, it should be possible to use the master curve to obtain the rate dependent \(\mu\). This is highly advantageous as it means that this relationship can be obtained without conducting any high strain rate experiments. Thereby, the predictability of this model can be enhanced.

Fig. 9
figure 9

a Highlighting the similarity between E′ and the equivalent Young’s modulus, E, b Comparison of \(\mu _{{\dot{\varepsilon }}}\) as obtained from the master curve with that from varying rate fits (Fig. 6), and c predictions of the response using these \(\mu\) values and the \(\alpha\) obtained in varying temperature fits (also Fig. 6) (Color figure online)

Full size image

In Fig. 9b it is clearly evident that the calculated \(\mu\) from the master curve is very similar to that obtained from fits to experiments. However, this likeness does not translate to accurate predictions of the high strain rate response as shown in Fig. 9c. Although the prediction of the response for a strain rate of \(2100~\, \hbox {s}^{-1}\) comes close to matching the experiment, the prediction for a strain rate of \(1.3~\, \hbox {s}^{-1}\) and \(10^{-3}~\, \hbox {s}^{-1}\) are overestimated considerably. This is likely due to the greater discrepancy between the two \(\mu\) values at the lower strain rates compared to that around \(1000~\, \hbox {s}^{-1}\) as can be seen in the inset in Fig. 9b. The \(\mu\) value is very sensitive to small errors in both DMA and compression experiments. To explore this further, a sensitivity analysis will be performed.

Sensitivity Analysis

The sensitivity of the model to changes in the two parameters that govern its response are investigated. For this analysis, the model is applied to three strain rate experiments (2100, 1.3 and \(10^{-3}~\, \hbox {s}^{-1}\)) as before to cover the broad spectrum of responses. The fits to the experiments are those from “Viscoelasticity and Temperature Dependence” and in Fig. 8. Perturbation of the \(\mu\) and \(\alpha\) values were made and the effects plotted in Fig. 10. Although the sensitivity would depend on the relative magnitude of the values, this analysis based on perturbations helps to provide a visual impression of the effect of errors on these specific parameter values.

Fig. 10
figure 10

a \(\mu ~\pm ~25\%\) and b \(\alpha ~\pm ~25\%\). Solid blue lines are experimental, solid black are the analogue fits using \(\mu\) values based on \(T_{eq}\), red dashed lines are the simulations with + 25% values and red dotted lines are simulations with − 25% values (Color figure online)

Full size image

For this sensitivity analysis, it is clear that overall there is much greater sensitivity to variation in \(\mu\) rather than \(\alpha\). One reason for this is that since the \(\mu\) parameter relates to the shear modulus, its effect dominates the overall mechanical response. On the other hand, since the \(\alpha\) parameter only corresponds to large strain convexity in the response, its effect is insignificant at low strains. It does however become increasingly important at larger strains as can be seen in Fig. 10b for the lowest strain rate case at the highest strains. This sensitivity analysis can help us understand the discrepancies in the DMA based predictions in Fig. 9c.

In these predictions, the \(\alpha\) value was kept constant as the averaged value found from fits to varying temperature experiments as in Fig. 6, and the \(\mu\) value was obtained based on the results of the DMA experiment. In this case the \(\alpha\) value was only \(8.61\%\) lower than the ideal value and since its impact is mostly at higher strains, it did not cause the discrepancies in the predictions. Qualitatively, this is supported by the observation that at the larger strains, the predicted responses show similar convexity to both experimental and optimised fits.

However, the \(\mu\) value varied considerably from the ideal case for each of the predictions. It was \(25.4\%\) lower for the \(2100~\, \hbox {s}^{-1}\) case, \(75.4\%\) higher for the \(1.3~\, \hbox {s}^{-1}\) case and \(109\%\) higher for the \(10^{-3}~\, \hbox {s}^{-1}\) case. This explains why the prediction for the \(2100~\, \hbox {s}^{-1}\) response looked better as it was almost in line with the discrepancies noticed in this sensitivity analysis. However, the significant difference in \(\mu\) value for the \(1.3~\, \hbox {s}^{-1}\) and \(10^{-3}~\, \hbox {s}^{-1}\) cases led to their poor prediction.

Conclusions

In this study, a simple rate and temperature dependent two parameter hyperelastic model was developed and shown to accurately represent high strain rate experimental results for neoprene rubber. The low strain viscoelastic modulus was captured well by relation to a rate dependent \(\mu\) parameter and the large strain non-linear rubber elasticity was captured by a fixed \(\alpha\) parameter.

The model has its foundations on the one-term, two-parameter Ogden model, chosen for its simplicity and capability to capture the experimental data. The existing model was subsequently adapted to take rate and temperature dependence into account. This was possible due to the TTS technique verified by DMA experiments, observing the similarity in the dependence of \(\mu\) fitting parameter to both rate and temperature, manually shifting fixed strain rate, varying temperature \(\mu\) values to those at equivalent strain rates at the reference temperature and by obtaining a more quantitative relation for this shift factor.

There are some limitations with this modelling strategy. As it stands, the rate and temperature dependence of the model parameters need to be characterised with a multitude of experiments. This is not as challenging for the varying temperature experiments, which are conducted on one instrument. For the varying rate experiments, three different instruments are required adding time, cost and potential errors and artefacts associated with making comparisons between very different types of apparatus.

Moreover, the fact that high rate experiments must be performed prior to the modelling means the predictive capability of this model is lacking. Although this was attempted to be mitigated by using the results of the DMA to provide the rate dependence, the relative small differences in modulus values from the DMA experiments for the neoprene in its rubbery state translates to a large difference in the predicted mechanical response. The \(\mu\) parameter is very sensitive to small errors in both DMA and compression experiments. There also was a slight discrepancy in the shifting gradient obtained from DMA experiments compared to that as inferred from the compression experiments or calculated by invoking the rate–temperature equivalence. This variation needs to be investigated further. In the future, predictions from this model could be validated against experiments conducted at higher strain rates and lower temperatures. This would promote a glassy response and variation in modulus values as obtained from the DMA would be less significant to the overall prediction.

In future iterations, this model will have to incorporate plasticity. This would also extend its range to cover the lower temperature quasi-static experiments. There were also assumptions made invoking the materials’ isotropy and incompressibility, along with the requirement for the experiment to be performed isothermally. A time domain model such as the Prony series could also be fitted to the DMA experimental data to improve the accuracy in determining the modulus. Therefore, there are many opportunities to extend this model to include heterogeneity, compressibility, effects from adiabatic self-heating, (rate dependent) plasticity and even evolving damage for materials where this is relevant.

Overall, this model provides the user with a simple method to represent the high strain rate behaviour of neoprene rubber. By characterising only two parameters with varying temperature and varying strain rate experiments, it is possible to interpolate the mechanical response at any temperature or strain rate within the range used in the characterisation process. In future, developments to this model will be used to make predictions of the high strain rate mechanical response for other soft polymers and even their particulate composites.