1 Introduction

Over the past decade, China's high-speed rail (HSR) industry has grown rapidly [1]. Dual traction power supply system (DTPSS) technology is already being implemented in Chongqing City, China. Based on the current transportation system, HSR plays a vital role in social, communication, and economic development [2]. HSR construction requires AC electrification because a massive power transfer capacity accumulates low currents from the catenary. The DC system for electricity must be compact with the connection between AC and DC systems operating in nearby cities [3]. The moving trains are utilized as the current return conductor in DC traction power systems (DCTPS), primarily employed in multi-train systems. Many traction substations (TSSs) and rails operate simultaneously while using various systems to maintain the conductivity of the catenaries across the entire route [4].

The urban rail transit system (URTS) frequently uses a DCTPS, which typically includes rail potential and stray current [5]. When the traction current returns to the TSSs, there will be an increase in potential between the running rail (RR) and the ground due to the horizontal resistance of the RR. This rise in potential in RR is known as rail potential. A certain amount of the rail current leaks into the ground and flows into the buried metal due to improper insulation between the RR and the earth. This leakage of current is referred to as stray current [6]. The stray current creates serious problems with metallic corrosion on RR and buried metallic pipelines. However, high rail potential can be caused by electric shocks, which affect personal safety [7]. For safety purposes, the highest rail voltage must be below 90 V [8].

Many researchers have studied the causes and control strategies related to rail potential and stray current. A novel bidirectional variable resistance module (BVRM) was employed to simulate train movement under the multiple operational scenarios. A simulation model was proposed to simulate and analyze the dynamic distribution of stray current and rail potential [9]. Another study proposed new techniques for utilizing a negative resistance converter (NEG-TPS) which provides zero resistance in a loop to decrease the rail potential and stray current. The NEG-TPS is constructed by adding power electronic devices in a traditional TPS [10]. To examine the rail potential and stray current at a particular point between the two TSSs, a two-layer transmission model is recommended [11]. The selection of grounding techniques for the transit system has a major impact on both. These techniques are categorized as underground, diode grounded, solidly grounded, and underground with an overvoltage protection device (OVPD). The amplitude of rail potential and stray current depends upon the mode of RR, including acceleration, coasting, uniform speed, or braking [12]. The power distribution of multi-train and TSSs is complicated, which has a significant effect on the rail potential. A parallel multiconductor model of TPS under multi-train parallel operation was proposed [13]. To evaluate the effect of traction system resistance, capacitance, inductance, and rail-to-ground resistance, a state space average (SSA) model of the TPS was utilized. The SSA model demonstrated that the inductance and capacitance of the TPS has a significant influence on rail potential [14].

Multiple features and characteristics can affect the rail potential and stray current during the operation of TPS. The magnitude of rail potential can be decreased by increasing the power supply voltage in the traction system to decrease the traction current, increasing the quantity of connecting cables between the rails to decrease the longitudinal resistance of the rail, and decreasing the spacing of the TSSs [15]. To consider the dynamic variation in the stray current, a diffusion model of the dynamic stray current of the DCTPS in a multi-layer soil medium and a large-texture soil medium is constructed [16]. The distribution of the rail potential can be modified by the DCTPS grounding mode. The drainage process of stray current can increase the rail potential of the entire system [17]. The corrosion appears in the anode section of buried pipelines, the area from which current exits the buried metallic and again enters the earth. To prevent corrosion, the average stray current must be less than 2.5 mA/m [18]. An equivalent circuit of rail skin effect is established, based on new techniques with a dynamic DCTPS considering the control features of the OVPD and unidirectional connection device to analyze the rail potential in multi-train and multi-station working situations [19].

Currently, research is being conducted regarding TPS based on power electronics technology. To minimize the stray current and rail potential, DC auto-transformer (DCAT) TPS has been implemented. As compared with traditional TPS, DCAT can add a negative feeder and may solve stray current and rail potential problems efficiently by transferring the rail current to the catenary and negative feeders [20]. A multiconductor model of DCTPS was developed based on real characteristics of the system. To simplify the complex operating mode of TSSs and train, a chain model of the DCTPS was established. The simulation model was employed to examine the effect of over-zone feeding on rail potential and stray current [21]. In an extensive analysis including medium-voltage DC-railway electrification along with multiple lengths across the lines of traction and load schemes, various grounding arrangements were proposed, including single train, two TSSs, and multi-train multi-TSS methods [22]. A stray current limitation technique that includes cross-bonding of the RR and stray current collector cables is typically needed to equalize the negative traction return current, lower the resistance of the negative return circuit, and reduce the rail potential in order to decrease the influence of stray current [23]. The impedance of the rail, the rail to ground, the stray current collector system, and other metal structures, as well as different soil resistivity, all have an impact on the rail potential and stray current. A variable impedance model has been proposed to demonstrate the variations in rail potential and stray current under various operational scenarios [24].

The main research innovation and contribution of this paper are as follows:

  1. (1)

    An integrated model of AC and DC TPS is constructed, along with a unified chain equivalent circuit model, the ground wire through the AC section, and the insulation joints set in the AC–DC neutral section under different operating positions.

  2. (2)

    A unified impedance and admittance matrix is created by adding a virtual conductor wire in the DC section to make the balance order of the TPS.

  3. (3)

    A calculation technique for rail potential and stray current is applied to DTPSS using various feedback current configurations by considering four cases. The influence of reflex system configuration on rail potential, stray current, and distribution of rail potential at AC and DC stations has also been calculated.

The rest of the paper is organized as follows: The DTPSS design circuit is established in Sect. 2. Section 3 presents the calculation of rail potential and stray current. Simulation case studies with different conditions are explained in Sect. 4. Section 5 contains the conclusions.

2 Design and Distributed Parameter Model of Dual Traction Power System

2.1 Formation of the Dual Traction Power Supply System

The distribution of DTPSS is a primary representation of the circumstances and fluctuating line operation caused by multiple power supply networks utilized by urban and municipal railway systems. The AC–DC section divides the neutral part of the track, and the locomotive moves through each section. It isolates the OCS and the rail, which meets the parallel multi-conductor structure process. The DTPSS is equipped with traction transformers, traction converters, and traction inverters.

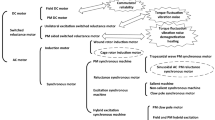
For the grounding return system, it is necessary to meet the proper return flow requirements under AC and DC working conditions, and improper design of the grounding system of the train will cause problems such as vehicle body rail circulation, vehicle body potential, and bearing electric corrosion. High current and potential flow through the vehicle body will affect the on-board weak current equipment and deteriorate the electromagnetic environment of train operation, and the damage to the bearing will directly affect the safety of the train driving process. The AC to DC switching divides the AC and DC portions, and the architectural diagram of the DTPSS is represented in Fig. 1.

Fig. 1
figure 1

Dual traction power supply system

Full size image

To establish a unified integrated chain network system, the entire traction network (TN), including the multi-conductor transmission line distribution parameters, reflex system, terminal truncation, and others, is considered in a unified chain circuit network. The series or shunt components typically split the multi-conductor transmission line into numerous sections. The TN can be described as a chain circuit model. It consists of parallel multi-conductor transmission lines connecting the two portions and has similar characteristics to a π-type design model, as shown in Fig. 2.

Fig. 2
figure 2

Chain circuit model of TN with multi-branch

Full size image

In Fig. 2, L represents the section length, ZL is the impedance matrix, and YL is the admittance matrix of the TN of the AC section. The RL is the resistance matrix, and the GL is the conductance matrix in the DC section. The chain circuit is divided into n and m sections according to the location of the traction station and the train. The node admittance matrix Y in the AC source having a \({R}_{m}\) section and the conductance matrix G in the DC source having a section of the TN with a neutral section matrix can be written as expressed in Eqs. (1), (2), and (3).

$$Y = \left( {\begin{array}{*{20}c} {Z_{L1}^{ - 1} + Y_{L1} } & { - Z_{L1}^{ - 1} } & {} & {} & {} & {} \\ { - Z_{L1}^{ - 1} } & {Z_{L1}^{ - 1} + Y_{L2} + Z_{L2}^{ - 1} } & { - Z_{L2}^{ - 1} } & {} & {} & {} \\ {} & { - Z_{L2}^{ - 1} } & {Z_{L2}^{ - 1} + Y_{L3} + Z_{L3}^{ - 1} } & { - Z_{L3}^{ - 1} } & {} & {} \\ {} & {} & \ddots & \ddots & \ddots & {} \\ {} & {} & {} & { - Z_{R(m - 2)}^{ - 1} } & {Z_{R(m - 2)}^{ - 1} + Y_{R(m - 1)} + Z_{R(m - 1)}^{ - 1} } & { - Z_{R(m - 1)}^{ - 1} } \\ {} & {} & {} & {} & { - Z_{R(m - 1)}^{ - 1} } & {Y_{Rm} + Z_{R(m - 1)}^{ - 1} } \\ \end{array} } \right)$$
(1)
$$G = \left( {\begin{array}{*{20}c} {R_{L1}^{ - 1} + G_{L1} } & { - R_{L1}^{ - 1} } & {} & {} & {} & {} \\ { - R_{L1}^{ - 1} } & {R_{L1}^{ - 1} + G_{L2} + R_{L2}^{ - 1} } & { - R_{L2}^{ - 1} } & {} & {} & {} \\ {} & { - R_{L2}^{ - 1} } & {R_{L2}^{ - 1} + G_{L3} + R_{L3}^{ - 1} } & { - R_{L3}^{ - 1} } & {} & {} \\ {} & {} & \ddots & \ddots & \ddots & {} \\ {} & {} & {} & { - R_{L(n - 2)}^{ - 1} } & {R_{L(n - 2)}^{ - 1} + G_{L(n - 1)} + R_{L(n - 1)}^{ - 1} } & { - R_{L(n - 1)}^{ - 1} } \\ {} & {} & {} & {} & { - R_{L(n - 1)}^{ - 1} } & {G_{Ln} + R_{L(n - 1)}^{ - 1} } \\ \end{array} } \right)$$
(2)
$$\left[ {\begin{array}{*{20}c} {L_{L1} } \\ \vdots \\ {I_{Ln} } \\ {I_{N} } \\ {I_{R1} } \\ \vdots \\ {I_{Rm} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {R_{L1}^{ - 1} + G_{L1} } & { - R_{L1}^{ - 1} } & {} & {} & {} & {} & {} \\ { - R_{L1}^{ - 1} } & {R_{L1}^{ - 1} + G_{L2} + R_{L2}^{ - 1} } & { - R_{L2}^{ - 1} } & {} & {} & {} & {} \\ {} & \ddots & \ddots & {} & {} & {} & {} \\ {} & {} & { - Z_{N - 1}^{ - 1} } & {Z_{N - 1}^{ - 1} + Y_{L1} + Z_{L1} } & { - Z_{N - 1}^{ - 1} } & {} & {} \\ {} & {} & {} & \ddots & \ddots & {} & {} \\ {} & {} & {} & {} & { - Z_{R(m - 2)}^{ - 1} } & {Z_{R(m - 2)}^{ - 1} + Y_{R(m - 1)} + Z_{R(m - 1)}^{ - 1} } & { - Z_{R(m - 1)}^{ - 1} } \\ {} & {} & {} & {} & {} & { - Z_{R(m - 1)}^{ - 1} } & {Y_{Rm} + Z_{R(m - 1)}^{ - 1} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {U_{L1} } \\ \vdots \\ {U_{Ln} } \\ {U_{N} } \\ {U_{R1} } \\ \vdots \\ {U_{Rm} } \\ \end{array} } \right]$$
(3)

The impedance admittance matrix of a TN with length l of AC and DC sections can be represented by the following equation (4):

$$\left\{ {\begin{array}{*{20}c} {{\varvec{Z}}_{l} \user2{ = }\sinh (\sqrt {{\varvec{ZY}}} l)({\varvec{ZY}})^{{ - \frac{1}{2}}} \user2{Z = }\left[ {\sum\limits_{n = 0}^{\infty } {\frac{{l^{2n + 1} }}{(2n + 1)!}({\varvec{ZY}})^{n} } } \right]{\varvec{Z}}} \\ {{\varvec{Y}}_{l} /2 = {\varvec{Z}}({\varvec{ZY}})^{{ - \frac{1}{2}}} \tanh (\sqrt {{\varvec{ZY}}} l/2) = {\varvec{Z}}_{L}^{ - 1} \sum\limits_{n = 1}^{\infty } {\frac{{l^{2n} }}{(2n)!}({\varvec{ZY}})^{n} } } \\ \end{array} } \right.$$
(4)

As explained by the superposition principle, the node voltage equations in the TPS calculation model of AC and DC sections are expressed as shown in Eq. (5)

$$\left\{ {\begin{array}{*{20}l} {{\varvec{U}}_{{{\text{Sdc}}}} = {\varvec{G}}_{j(a + b) \times j(a + b)}^{ - 1} {\varvec{I}}_{{{\text{dcs}}}} } \hfill \\ {{\varvec{U}}_{{{\text{Sac}}}} = {\varvec{Y}}_{j(a + b) \times j(a + b)}^{ - 1} {\varvec{I}}_{{{\text{acs}}}} } \hfill \\ \end{array} } \right.$$
(5)

where \({U}_{{\text{Sdc}}}\) is the DC component of the system voltage matrix. \({U}_{{\text{Sac}}}\) is the AC component of the system voltage matrix. \({I}_{{\text{dcs}}}\) is the DC current matrix, \({I}_{{\text{acs}}}\) is the AC current matrix. j is the matrix order, a is the number of DC sections, and b is the number of AC sections.

2.2 Effect of Insulation Joint, Ground Wire, and Neutral Section

The insulation rail joint (IRJ) is commonly used for the connection of two tracks. The electrical signaling systems are used to identify trains and enable the detection of a broken rail. Electrical insulation of the rails in an insulation joint configuration is carried out by breaking the continuity of the steel [25]. It is a safety-sensitive feature and an essential component of the railway track system. Injecting a DC current source at both ends of the insulation joint can cause the current path to form a closed circuit during the process of the train wheels crossing the insulation joint. The return path will repeatedly close and open due to the movement of the train wheelset. The contact area between the train wheelset and the steel rail is greater than the area of the insulation joint, which will cause the wheelset to conduct the insulation joint at both ends when crossing the insulation joint. The insulation joint along the track of AC–DC sections is represented in Fig. 3.

Fig. 3
figure 3

Insulation joint of railway track

Full size image

The neutral section is arranged between the DC and AC sections, and insulated joints are installed at the rail of the AC–DC neutral section, depending on whether the on-board switching scheme or the ground switching scheme is employed. The neutral section causes traction loss, speed loss, and mechanical breakdown, which is dangerous for the train and the network’s ability to operate in a fast and reliable way. The continuous power flow through the neutral section has gained great importance, and has led to the development of certain techniques, such as the flexible ground-auto-passing neutral section mechanism and ground-auto-passing neutral region patterns for mechanical switches and electronic switches. To meet the safety requirements, the distance between each of the insulated joints must not be longer than the length of the train grounding return current system. The TPS and stray current are both affected by the grounding system, which is used in railway tracks. When choosing the grounding system, many factors need to be taken into consideration, specifically electrical safety for touch voltage and minimization of stray current. The DC and AC sections of steel rails are all grounded. The grounding must be maintained to keep the track under control as well as to avoid electric potential that might cause a public safety hazard [26].

The AC TN consists of a return line, catenary, rail, integrated ground wire, and network admittance and impedance matrix of order 4. The TN in the DC section is composed of a catenary, rail, and drainage network, with an impedance admittance matrix order of 3. The total number of conductors in the DC section Ndc is different from the conductors in the AC sections Nac and Ndc<Nac.

To form a unified impedance and admittance matrix of the TPS, a virtual conductor Nxn has been added in the DC section to make the balance order 4×4 matrix of the TN, and it becomes equivalent to Ndc=Nac. A significant resistance transverse connection can be fixed between the virtual conductor and the rail to create the node admittance matrix of the non-singular system. The unified equivalent distribution model of the TN with conductors in different sections using a common power supply method in AC and DC sections is presented in Fig. 4.

Fig. 4
figure 4

Unified chain and equivalent circuit of AC–DC section model

Full size image

2.3 Computation of Combined AC and DC Power Supply

The combined power supply method is not only suitable for the research of dual-flow train grounding systems but can also be used for the analysis of single-power supply systems or other multi-power supply train grounding systems. The flowchart demonstrated in Fig. 5 illustrates the specific procedure and stages for calculating the combined TPS of the AC and DC sections, which are described below.

Fig. 5
figure 5

Flow chart of DTPSS.

Full size image

Step 1. Read the train information of the up and down train, such as the position, speed, power, and current of the entire train under the time t. Generate the train running chart diagram as per the data acquired.

Step 2. Arrange the parameters of each wire according to the suspension mode of the TN in the DC and AC sections. Build the node admittance matrix Y of the whole line under the action of the AC source only and the node admittance matrix G of the whole line under the action of the DC source only through the superposition theorem. Set the iterative calculation convergence accuracy of the voltage in the power supply calculation and establish a full-line node admittance matrix.

Step 3. Build the AC–DC neutral segment configuration information. Check whether the rail insulation joint is fixed in the AC–DC neutral section. If fixed, update the node admittance matrix Y and G of the whole line.

Step 4. Update the admittance matrices Y and G of the whole line according to the status of each part of the system at time t.

Step 5. Generate an initial current vector Iacs of the whole line at time t under the action of the AC source only and the initial current vector Idcs of the whole line at time t under the action of the DC source only.

Step 6. Establish the node voltage equation of the DTPSS and solve it to calculate the node voltage vectors Usac and Usdc.

Step 7. Determine whether the voltage vectors Usac and Usdc of the whole node meet the convergence conditions. If not satisfied, update the current vectors Iacs and Idcs, and return to step 5; otherwise, continue.

Step 8. According to the time t calculated by the power supply, the Usac and Usdc, Iacs and Idcs are calculated to find the current information of each train on the line and the rail current information of the adjacent facet of the train.

Step 9. Determine if the end of the simulation has been reached. If so, the simulation ends; otherwise, t=t+Δt, return to step 4.

3 Calculation of Rail Potential and Stray Current

3.1 Limitation of Rail Potential

The size of the contact voltage is related to the position of the contact point. The closer the contact point to the rail, the greater the contact voltage is almost equal to the rail potential. On the contrary, the contact voltage is approximately 0V. There is no relevant standard for the ACTPS to limit the value of rail potential. Once the AC and DC sections are connected through the neutral section, it is very difficult for the AC and DC sections to interfere with each other. The improper design of the returning power supply system may further cause problems with rail potential and stray current. For the DCTPS under normal operation, the ground potential of the RR at the platform should not be greater than 90 V. The limit range of rail potential at DC and AC components is presented in Fig. 6.

Fig. 6
figure 6

Limit range of combined rail potential at stations of double-current line.

Full size image

3.2 Analysis and Calculation of Stray Current

For the returning system in DTPSS, the rail is generally used as the return path in the DC section, and insulation is required between the rail and the ground. In the AC section, the rails and return lines are generally used as the return flow path, but no insulation is required between the rail and the ground. The leakage current is generated in the DC section while returning back to the DC traction substation and it forms a stray current \(I_{{{\text{sc}}}}\) in the DC section. There will also be some leaks through the AC section of the rails and the formation of the AC–DC section transition current \(I_{gd}\), causing stray current problems. When the AC–DC section is not provided with the rail insulation section, the transition current flows into the AC section through the rail, and when the AC and DC sections are set up with the rail insulation section, the transition current flows into the AC section through the train body that spans the rail insulation section. The schematic diagram of the transition current return path is shown in Fig. 7.

Fig. 7
figure 7

Schematic diagram of transition current return path

Full size image

The leakage current generated at the rail of the DC section and the rail of transition to the AC section should be summed up. The stray current \(I_{DSsc}\) of the dual-current system can be expressed using the equation shown in (6).

$$\begin{array}{*{20}c} {I_{{{\text{DSsc}}}} = I_{{{\text{sc}}}} + I_{{{\text{gd}}}} ,} & {I_{{{\text{gd}}}} > 0} \\ \end{array}$$
(6)

3.3 Limitation of Stray Current in Dual System

To determine the limitation value of stray current in a DTPSS, the relevant standards of stray current limitation values can be referred to in IEC 62128-2 [27], which stipulates that the average stray current limit of single-track rail is 2.5 mA/m. The typical range of the stray current limit of DTPSS is expressed in (7).

$$\frac{{\int {I_{{{\text{DSsc}}}} (t)dt} }}{T} \le I_{{{\text{sclim}}}} L_{{{\text{qd}}}}$$
(7)

in which Isclim is the average time limit of the stray current of the double line, taking 5 A/km; Lqd is the length of the DC section of the line, in km; T is the time, in seconds (s).

4 Case Studies

The total distance between the new AC municipal railway and the DC railway is 51.7 km. The DC section length is 27.76 km, and the AC section is 23.83 km long. There are 22 DC stations, 5 AC stations, and 11 DC traction stations marked with bold dotted circles as TS1, TS2, and so on. T1 and T2 are AC traction stations which are presented as small boxes and the AC and DC stations along their locations with distance values are explained in Tables 1 and 2. The red box represents the section post. The circle symbol depicts the other stations, as shown in Fig. 8 of the line diagram. The neutral section is located between stations S22 and S23, with a length of 0.15 km. All DC sections are underground. The 1500 V DC voltage rigid catenary is used for current collection and rail return, and OVPD is installed in all DC stations. The value of OVPD is synchronized to 120 V, and without any load voltage, the rectifier unit voltage in the DC traction station is 1668 V.

Table 1 Location information of DC substation
Full size table
Table 2 Location information of AC substation
Full size table
Fig. 8
figure 8

Line operation diagram

Full size image

The AC section is an elevated section, and a 25 kV AC flexible catenary is used for the current collection return line and rail return. The train selects a type of double-flow system without on-board braking resistance. When the urban rail system regeneratively breaks, an excess of energy is generated, which will cause the TN to increase rapidly. It can cause a reduction in the train's regenerative braking ability, or it can cause failure in regenerative braking. The energy feedback system (EFS) device absorbs the energy of regenerative braking of the rail in the DC section, and the starting voltage of the EFS is adjusted to 1750 V. From the first to the last station, a single operation route is adopted for the whole day, and the departure interval is 600 s.

The simulation running time is set to 300 s, and the operation and schematic train running chart diagram is represented in Fig. 9.

Fig. 9
figure 9

Train running chart diagram

Full size image

The train location of the DC stations and traction substation details are provided in Table 1.

The train location of the AC stations is provided in Table 2.

4.1 Back Flow System Configuration

The AC urban rail system (ACURS) should adopt the power supply mode of direct supply with return current and set an independent return line as the parallel return channel of RR. The ACURS can also be set up through the grounding system. Connecting the insulation joint with the unique feeder and switchgear is suitable to limit the traction return current exchange between different power supply systems.

The simulation settings are adjusted to determine the rail potential distribution and transition current of DTPSS lines depending on various reflux system conditions, which are provided in Table 3.

Table 3 Condition of different reflux systems
Full size table

The AC section in cases 3 and 4 are arranged with through-ground wires. The AC sections are elevated in both cases, and the through-ground cables cannot be buried. The overhead method is adopted, and the ground wires are grounded through the catenary pillar structure. While considering cases 2 and 4, which are erected with rail insulation joint segments, the length between the rail insulation joints is considered to be 8 m. The value of the AC inductor is set to 0.43 mH/km. The TN parameter details are provided in Table 4.

Table 4 Traction network parameters details
Full size table

4.2 Influence of Reflex System Configuration on Rail Potential and Stray Current

The simulation time of the rail potential distribution of the whole network is considered to be 600 s, and it is calculated for cases 1 to 4. Considering all four cases, it can be observed that the value of rail potential will increase when the insulation joint is set at the rail of the AC–DC neutral section. Referring to Figs. 10a and 11a, when the AC section is not equipped with a through-ground wire, the value of DC rail potential in the DC section will increase from 134.08 to 157.17 V; however, the maximal value of AC rail potential in the AC part will increase from 83.96 to 105.88 V, as presented in Figs. 10b and 11b. As observed from Figs. 12a and 13a, as the ground wire is fixed in the AC section, the maximum DC rail potential in the DC section will increase from 125.08 V to 157.17V, whereas the largest rail potential in the AC section will increase from 36.30 V to 37.18 V, as shown in Figs. 12b and 13b.

Fig. 10
figure 10

Case 1: Rail potential distribution along the entire line. a DC rail potential distribution along the whole line, b AC rail potential distribution

Full size image
Fig. 11
figure 11

Case 2: Rail potential distribution along the whole line. a DC rail potential distribution, b AC rail potential distribution

Full size image
Fig. 12
figure 12

Case 3: Rail potential distribution along the whole line. a DC rail potential distribution, b AC rail potential distribution

Full size image
Fig. 13
figure 13

Case 4: Distribution of rail potential along the entire system. a DC rail potential distribution, b AC rail potential distribution

Full size image

By comparing cases 1 and 3, it can be concluded that when there is no insulating joint connected at the rails in the AC–DC neutral part, setting a through-ground wire in the AC section can reduce the value of rail potential. Among them, the maximal value of rail potential in the DC section will decrease from 134.08 to 125.08 V, while the high rail potential in the AC section will decrease from 83.96 to 36.30 V. In contrast with case 2 and case 4, when insulating joints are installed at the rails in the AC–DC neutral section, adjusting through-ground wires in the AC section can only reduce rail potential in the AC section.

4.3 Distribution of Rail Potential at AC and DC Stations

We can select the DC station at S22 and the AC station at S23 nearest to the AC–DC neutral part and check whether the train’s rail potential exceeds the predetermined value within the simulation duration. The rail potential distribution at the AC and DC stations under cases 1 and 2 is presented in Figs. 14 and 15.

Fig. 14
figure 14

Case 1: Potential distribution of rails in AC and DC stations. a The rail potential distribution at station S22, b the rail potential distribution at station S23

Full size image
Fig. 15
figure 15

Case 2: Potential distribution of rails in AC and DC stations. a The rail potential distribution at station S22, b the rail potential distribution at station S23

Full size image

The DC station is equipped with OVPD, and when the rail potential of the DC component at the station is greater than 120 V, the OVPD will close to ground the rail at the station. Therefore, the DC component rail potential is always under the specified value of the combined rail voltage in the DC section.

Compared with cases 1 and 2, when the AC–DC neutral sections are equipped with insulated sections to block the traction reflux systems, the content of various components in the rail potential effectively decreased, but the content of the same components in the combined rail potential increased. The rail potential value of the DC station at S22 meets the limitation requirements in both conditions of cases 1 and 2. However, the effective value of the AC component of the rail potential of the AC station at station S23 does not meet the limitation requirements. In the simulation time, under case 1, there are five intervals of time in which the effective limit value of the AC component is exceeded by 65 V, and the most prolonged duration is 18 s. In case 1, the maximum time is 39 s, and there are 13 times when the RMS value of the AC component is exceeded by 65 V. The highest values of DC and AC components at stations S22 and S23, as well as rail potential values under the case 1 and case 2 conditions, are provided in Table 5.

Table 5. Comparison of max rail potential value
Full size table

The rail potential distribution at the AC and DC stations under cases 3 and 4 is displayed in Figs. 16 and 17.

Fig. 16
figure 16

Case 3: Potential distribution of rails in AC and DC stations. a The rail potential distribution at station S22, b the rail potential distribution at station S23

Full size image
Fig. 17
figure 17

Case 4: Potential distribution of the rails in AC and DC stations. a The rail potential distribution at station S22, b the rail potential distribution at station S23

Full size image

By differentiating between cases 1 and 3, when no insulation section is set at the rail of the AC–DC neutral section, and when the grounding wire is set at the AC section, the AC component of the rail potential might be significantly lower. The maximum value of the AC component of the compound rail potential at the S23 station can be reduced from 78.05 to 27.91 V.

As compared to cases 3 and 4, when the ground wire is installed in both AC sections and the insulation joint is installed at the rail of the AC–DC neutral region, the AC component of the rail potential in the AC section will not change. In the situations of cases 3 and 4, the rail potential values at both AC and DC stations are within the requirements of the range. The maximum DC and AC component values for the rail potential of stations S22 and S23 for conditions in case 1, case 3, and case 4 are provided in Table 6.

Table 6 Comparison of max DC and AC rail potential values
Full size table

4.4 Reflex System Distribution of Stray Current

When the AC–DC neutral section rail is not equipped with an insulation joint, a transition current always exists. After, that when the AC–DC neutral section rail is set with an insulation joint, the AC–DC traction return exchange path is cut off. However, when the train crosses at both ends of the AC–DC neutral insulation section of the rail, only the transition current will be present. The ground wire is set in the AC section to improve the grounding effect of the rail in the AC section, which will increase the transition current.

For all four scenarios, the calculated average stray current is below the average standard limitation value. Adjusting the rail insulation joints at the AC–DC neutral section can reduce the average stray current value. As the AC section is not fixed across the ground wire, the average stray current value is decreased by 19.67% lower than that of the section without rail insulation joints. However, when the AC section is set through the ground wire, the average stray current value is reduced by 36.27% compared with the rail insulation without the rail insulation section.

In case 1 and case 2 scenarios, the composite rail at the station in the AC section exceeds the limit range, and case 4 improves the stray current problem as compared with case 3; therefore, improving the effect of rail potential and stray current problem, the effect of case 4 is the best under these four scenarios. The distribution of rail to ground leakage current in the DC area under case 1 to case 4, as shown in Fig. 18.

Fig. 18
figure 18

Distribution of rail-to-ground leakage current in the DC section under different cases.

Full size image

The maximum transition current values and the average stray current values under the four scenarios are shown in Table 7.

Table 7 Max transient and stray current values
Full size table

The distribution of transition current under the different cases 1 to case 4 is shown in Fig.19

Fig. 19
figure 19

Transition current distribution under different scenarios

Full size image

5 Conclusions

This paper proposed a unified chain model of DTPSS, including the neutral section, rail insulation joint, ground wire, and virtual conductor wire, which has been added to the DC section to make the balanced matrix of the TN. The calculation method for limiting rail potential and stray current is presented. By considering the different cases of rail insulation joints of AC–DC neutral and ground wire through the AC section, the reflux system configuration of rail potential and rail current condition under the four cases is discussed and analyzed. Here are the major conclusions, as follows:

  1. 1.

    It is concluded from observing case 1 and case 3 that the value of rail potential in the DC section will decrease from 134.08 to 125.08 V when the AC section is equipped with a through-ground wire and the insulation joint is not set at the rail of the AC–DC neutral section in case 3. On the contrary, the value of rail potential in the AC section decreases from 83.96 to 36.30 V. Case 3 describes the minimal value of DC and AC rail potential.

  2. 2.

    In case 2, when the insulation joint is set at the rail of the AC–DC neutral section and the AC section is not equipped with a through-ground wire, and in case 4, when the insulation joint is set at the rail of the AC–DC neutral section and the AC section is equipped with a through-ground wire, the value of DC rail potential remains the same in both cases, which is 157.17 V. However, the value of AC rail potential is 105.88 V in case 2, while in case 4, the value of AC rail potential is 37.18 V. Case 4 describes the minimal value of AC rail potential.

  3. 3.

    The average stray current value falls by 19.67%, while the AC section is not equipped with a through-ground wire as compared to the section without a rail insulation joint. The average stray current value in the AC section decreased by 36.27% when a through-ground wire was installed as compared to the section without rail insulation joints.

  4. 4.

    The rail potential value of the DC component at the DC station meets the limitation requirements in both case 1 and case 2. However, the effective rail potential value of the AC component at AC station does not meet the limit requirements.

For future research work, the train grounding system can be analyzed and observed to optimize the value of the grounding protection resistance of the train body. To improve the performance of the train grounding system, an optimized algorithm can be implemented to construct an integrated model of the train grounding system to optimize the value of grounding protection resistance.