Skip to main content
SpringerLink
Log in

Dynamics of multicritical circle maps

  • Special issue commemorating the Golden Jubilee of the Institute of Mathematics and Statistics of the University of São Paulo
  • Published:
São Paulo Journal of Mathematical Sciences Aims and scope Submit manuscript

Abstract

This paper presents a survey of recent and not so recent results concerning the study of smooth homeomorphisms of the circle with a finite number of non-flat critical points, an important topic in the area of One-dimensional Dynamics. We focus on the analysis of the fine geometric structure of orbits of such dynamical systems, as well as on certain ergodic-theoretic and complex-analytic aspects of the subject. Finally, we review some conjectures and open questions in this field.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Notes

  1. The fact that the Schwarzian derivative vanishes at Möbius transformations is a straightforward computation. On the other hand, given an increasing \(C^3\) diffeomorphism f, consider \(g=(Df)^{-1/2}\) and note that \(Sf=-2\,D^2g/g\). If f has zero Schwarzian derivative then g is affine, which implies at once that f is a Möbius transformation.

  2. Here, as usual, the mesh of a partition is the maximum length of its atoms.

  3. The set \({\mathscr {D}}_0\) is precisely the set of numbers of bounded type, as previously defined.

  4. As a first step, the real bounds (Theorem 5.2) can be used to establish \(C^r\) bounds for return maps, see for instance [35, Appendix A]. A standard Arzelà-Ascoli argument gives then pre-compactness of renormalization orbits.

  5. Let \(\Omega \subset {\mathbb {C}}\) be a domain and let \(K \ge 1\). An orientation-preserving homeomorphism \(f:\Omega \rightarrow f(\Omega )\) is K-quasiconformal if it is absolutely continuous on lines and satisfies

    $$\begin{aligned} \left| {\overline{\partial }}f(z)\right| \le \left( \frac{K-1}{K+1}\right) \big |\partial f(z)\big |\quad \text{ for } \text{ Lebesgue } \text{ a.e. } z\in \Omega \,. \end{aligned}$$

    The Beltrami coefficient of such homeomorphism f is the measurable function \(\mu _f:\Omega \rightarrow {\mathbb {D}}\) given by

    $$\begin{aligned} \mu _f(z)=\frac{{\overline{\partial }}f(z)}{\partial f(z)}\quad \text{ for } \text{ Lebesgue } \text{ a.e. } z\in \Omega \,. \end{aligned}$$

  6. However, we warn the reader that the renormalization “operator” is not a complex-analytic operator.

  7. A quasi-circle, we recall, is the image of a round disk under a quasiconformal homeomorphism of the plane.

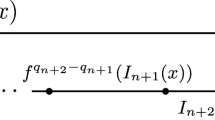
  8. It is easy to see that \([f^{q_{m+1}}(c), f^{q_m-q_{m+1}}(c)]\supset I_m\cup I_{m+1}\).

References

  1. Ahlfors, L.V.: Lectures on quasi-conformal mappings. In: University Lecture Series, vol. 30, 2nd edn. American Mathematical Society (2006)

  2. Arnol’d, V.I.: Small denominators I. Mappings of the circle onto itself. Izv. Akad. Nauk. Math. Ser. 25, 21–86 (1961) (Translations of the Amer. Math. Soc. (series 2) 46 (1965), 213–284)

  3. Avila, A.: Dynamics of renormalization operators. In: Proceedings of the International Congress of Mathematicians. Hyderabad, India (2010)

  4. Avila, A.: On rigidity of critical circle maps. Bull. Braz. Math. Soc. 44, 611–619 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  5. Avila, A., Kocsard, A.: Cohomological equations and invariant distributions for minimal circle diffeomorphisms. Duke Math. J. 158, 501–536 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  6. Avila, A., Lyubich, M.: The full renormalization horseshoe for unimodal maps of higher degree: exponential contraction along hybrid classes. Publ. Math. IHES 114, 171–223 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  7. Bohl, P.: Uber die hinsichtlich der unabhängigen variabeln periodische. Acta Math. 40, 321–336 (1916)

    Article  MathSciNet  MATH  Google Scholar 

  8. Bordignon, L., Iglesias, J., Portela, A.: About \(C^1\)-minimality of the hyperbolic Cantor sets. Bull. Braz. Math. Soc. 45, 525–542 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  9. Boyland, P.: Bifurcations of circle maps: Arnol’d tongues, bistability and rotation intervals. Commun. Math. Phys. 106, 353–381 (1986)

    Article  MATH  Google Scholar 

  10. Carleson, L., Gamelin, T.W.: Complex Dynamics. Springer-Verlag, New York (1993)

    Book  MATH  Google Scholar 

  11. Chenciner, A., Gambaudo, J.-M., Tresser, C.: Une remarque sur la structure des endomorphismes de degré \(1\) du cercle. C. R. Acad. Sci. Paris. Série I 299, 145–148 (1984)

    MathSciNet  MATH  Google Scholar 

  12. Clark, T., Trejo, S.: The boundary of chaos for interval mappings. Proc. London Math. Soc. 121, 1427–1467 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  13. Clark, T., van Strien, S., Trejo, S.: Complex bounds for real maps. Comm. Math. Phys. 355, 1001–1119 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  14. Crovisier, S., Guarino, P., Palmisano, L.: Ergodic properties of bimodal circle maps. Ergod. Theory Dyn. Syst. 39, 1462–1500 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  15. Cvitanović, P., Gunaratne, G.H., Vinson, M.J.: On the mode-locking universality for critical circle maps. Nonlinearity 3, 873–885 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  16. Cvitanović, P., Shraiman, B., Söderberg, B.: Scaling laws for mode locking in circle maps. Physica Scrypta 32, 263–270 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  17. Davie, A.: Period doubling for \(C^{2+\varepsilon }\) mappings. Commun. Math. Phys. 176, 261–272 (1996)

    Article  MATH  Google Scholar 

  18. Denjoy, A.: Sur les courbes définies par les équations différentielles à la surface du tore. J. Math. Pure Appl. 11, 333–375 (1932)

    MATH  Google Scholar 

  19. Dixon, T.W., Gherghetta, T., Kenny, B.G.: Universality in the quasiperiodic route to chaos. Chaos 6, 32–42 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  20. Douady, A.: Disques de Siegel et anneaux de Herman. In: Sém. Bourbaki 1986/87, Astérisque, 1986/87, pp. 151–172 (1987)

  21. Douady, A.: Does a Julia set depend continuously on the polynomial? Complex dynamical systems. Proc. Symp. Appl. Math. 49, 91–138 (1994)

    Article  MATH  Google Scholar 

  22. Douady, A., Hubbard, J.: On the dynamics of polynomial-like mappings. Ann. Sci. Ec. Norm. Sup. 18, 287–343 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  23. Eliasson, H., Fayad, B., Krikorian, R.: Jean-Christophe Yoccoz and the theory of circle diffeomorphisms. Available at arXiv:1810.07107

  24. Epstein, A., Keen, L., Tresser, C.: The set of maps \(F_{a, b}:x \mapsto x+a+\frac{b}{2\pi }\sin (2\pi x)\) with any given rotation interval is contractible. Commun. Math. Phys. 173, 313–333 (1995)

    Article  MATH  Google Scholar 

  25. Estevez, G., de Faria, E.: Real bounds and quasisymmetric rigidity of multicritical circle maps. Trans. Amer. Math. Soc. 370, 5583–5616 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  26. Estevez, G., de Faria, E., Guarino, P.: Beau bounds for multicritical circle maps. Indagationes Mathematicæ 29, 842–859 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  27. Estevez, G., Guarino, P.: Renormalization of multicritical circle maps (submitted)

  28. Estevez, G., Smania, D., Yampolsky, M.: Complex bounds for multicritical circle maps with bounded type rotation number. Available at arXiv:2005.02377

  29. de Faria, E.: Proof of universality for critical circle mappings, Ph.D. Thesis, CUNY (1992)

  30. de Faria, E.: On conformal distortion and Sullivan’s sector theorem. Proc. Am. Math. Soc. 126, 67–74 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  31. de Faria, E.: Asymptotic rigidity of scaling ratios for critical circle mappings. Ergod. Theory Dyn. Syst. 19, 995–1035 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  32. de Faria, E., Guarino, P.: Real bounds and Lyapunov exponents. Disc. Cont. Dyn. Syst. A 36, 1957–1982 (2016)

    MathSciNet  MATH  Google Scholar 

  33. de Faria, E., Guarino, P.: Quasisymmetric orbit-flexibility of multicritical circle maps. Available at arXiv:1911.04375 (submitted)

  34. de Faria, E., Guarino, P.: There are no \(\sigma\)-finite absolutely continuous invariant measures for multicritical circle maps. Available at arXiv:2007.10444 (submitted)

  35. de Faria, E., de Melo, W.: Rigidity of critical circle mappings I. J. Eur. Math. Soc. 1, 339–392 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  36. de Faria, E., de Melo, W.: Rigidity of critical circle mappings II. J. Am. Math. Soc. 13, 343–370 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  37. de Faria, E., de Melo, W.: Mathematical Tools for One-Dimensional Dynamics. Cambridge University Press, Cambridge (2008)

    Book  MATH  Google Scholar 

  38. de Faria, E., de Melo, W., Pinto, A.: Global hyperbolicity of renormalization for \(C^r\) unimodal mappings. Ann. Math. 164, 731–824 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  39. Feigenbaum, M., Kadanoff, L., Shenker, S.: Quasi-periodicity in dissipative systems. A renormalization group analysis. Physica 5D, 370–386 (1982)

    Google Scholar 

  40. Ghys, E.: Laminations par surfaces de Riemann, Dynamique et géométrie complexes (Lyon, 1997), ix, xi, 49-95, Panor. Synthèses, 8, Soc. Math. France, Paris (1999)

  41. Gorbovickis, I., Yampolsky, M.: Rigidity, universality, and hyperbolicity of renormalization for critical circle maps with non-integer exponents. Ergod. Theory Dyn. Syst. 40, 1282–1334 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  42. Graczyk, J., Sands, D., Świątek, G.: Decay of geometry for unimodal maps: negative Schwarzian case. Ann. Math. 161, 613–677 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  43. Graczyk, J., Świątek, G.: Singular measures in circle dynamics. Commun. Math. Phys. 157, 213–230 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  44. Graczyk, J., Świątek, G.: Critical circle maps near bifurcation. Commun. Math. Phys. 176, 227–260 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  45. Guarino, P.: Rigidity conjecture for \(C^3\) critical circle maps. Ph.D. Thesis. IMPA (2012)

  46. Guarino, P., Martens, M., de Melo, W.: Rigidity of critical circle maps. Duke Math. J. 167, 2125–2188 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  47. Guarino, P., de Melo, W.: Rigidity of smooth critical circle maps. J. Eur. Math. Soc. 19, 1729–1783 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  48. Hall, G.R.: A \(C^\infty \) Denjoy counterexample. Ergod. Theory Dyn. Syst. 1, 261–272 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  49. Herman, M.: Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations. Publ. Math. IHES 49, 5–234 (1979)

    Article  MATH  Google Scholar 

  50. Herman, M.: Résultats récents sur la conjugaison différentiable. In: Proceedings of the International Congress of Mathematicians (Helsinki, 1978), pp. 811–820 (1978)

  51. Herman, M.: Conjugaison quasi-simétrique des homéomorphismes du cercle à des rotations (manuscript) (1988). (see also the translation by A. Chéritat, Quasisymmetric conjugacy of analytic circle homeomorphisms to rotations. www.math.univ-toulouse.fr/~cheritat/Herman/e_,herman.html)

  52. Hu, J., Sullivan, D.: Topological conjugacy of circle diffeomorphisms. Ergod. Theory Dyn. Syst. 17, 173–186 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  53. Kadanoff, L., Shenker, S.: Critical behavior of a KAM surface. I. Empirical results. J. Stat. Phys. 27, 631–656 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  54. Katznelson, Y.: Sigma-finite invariant measures for smooth mappings of the circle. J. d’Analyse Math. 31, 1–18 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  55. Katznelson, Y., Ornstein, D.: The differentiability of the conjugation of certain diffeomorphisms of the circle. Ergod. Theory Dyn. Syst. 9, 643–680 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  56. Katznelson, Y., Ornstein, D.: The absolute continuity of the conjugation of certain diffeomorphisms of the circle. Ergod. Theory Dyn. Syst. 9, 681–690 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  57. Khanin, K.: Universal estimates for critical circle mappings. Chaos 1, 181–186 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  58. Khanin, K.: Renormalization and rigidity. In: Proceedings of the International Congress of Mathematicians. Rio de Janeiro, Brazil (2018)

  59. Khanin, K., Teplinsky, A.: Robust rigidity for circle diffeomorphisms with singularities. Invent. Math. 169, 193–218 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  60. Khanin, K., Teplinsky, A.: Herman’s theory revisited. Invent. Math. 178, 333–344 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  61. Khinchin, A. Ya.: Continued fractions, (reprint of the 1964 translation), Dover Publications, Inc. (1997)

  62. Khmelev, D., Yampolsky, M.: The rigidity problem for analytic critical circle maps. Mosc. Math. J. 6, 317–351 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  63. Klein, S., Liu, X.-C., Melo, A.: Uniform convergence rate for Birkhoff means of certain uniquely ergodic toral maps. Ergodic Theory Dyn. Syst. (to appear)

  64. Lanford, O.E.: Renormalization group methods for critical circle mappings with general rotation number. In: VIIIth International Congress on Mathematical Physics (Marseille, 1986), pp. 532–536. World Scientific. Singapore (1987)

  65. Lanford, O.E.: Renormalization group methods for circle mappings. In: Nonlinear Evolution and Chaotic Phenomena (NATO Adv. Sci. Inst. Ser. B: Phys., 176), pp. 25–36. Plenum, New York (1988)

  66. Lyubich, M.: Feigenbaum-Coullet-Tresser universality and Milnor’s hairiness conjecture. Ann. Math. 149, 319–420 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  67. Lyubich, M.: Teichmüller space of Fibonacci maps. In: Pacifico, M., Guarino, P. (eds.) New Trends in One-Dimensional Dynamics, vol. 285, pp. 221–237. Springer Proceedings in Mathematics & Statistics (2019)

  68. MacKay, R.S.: A renormalisation approach to invariant circles in area-preserving maps. Physica 7D, 283–300 (1983)

    MathSciNet  MATH  Google Scholar 

  69. MacKay, R.S.: Renormalisation in Area-Preserving Maps. In: Advanced Series in Nonlinear Dynamics vol. 6, World-Scientific, Singapore (1993)

  70. Martens, M.: The periodic points of renormalization. Ann. Math. 147, 543–584 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  71. Martens, M., de Melo, W., van Strien, S.: Julia-Fatou-Sullivan theory for real one-dimensional dynamics. Acta Math. 168, 273–318 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  72. Duff, D. M.c.: \(C^{1}\)-minimal subsets of the circle. Ann. de l’Institut Fouri. 31, 177–193 (1981)

  73. McMullen, C.T.: Complex dynamics and renormalization, Ann. Math. Stud. 135 (1994)

  74. McMullen, C.T.: Renormalization and 3-manifolds which fiber over the circle, Ann. Math. Stud. 142 (1996)

  75. McMullen, C.T.: Rigidity and inflexibility in conformal dynamics. In: Proceedings of the International Congress of Mathematicians, vol. II, pp. 841–855. Doc. Math., Berlin (1998)

  76. de Melo, W.: Rigidity and renormalization in one-dimensional dynamics, In: Proceedings of the International Congress of Mathematicians, vol. II, pp. 765–778. Doc. Math., Berlin (1998)

  77. de Melo, W., van Strien, S.: A structure theorem in one-dimensional dynamics. Ann. Math. 129, 519–546 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  78. de Melo, W., van Strien, S.: One-Dimensional Dynamics. Springer-Verlag Berlin Heidelberg (1993)

    Book  MATH  Google Scholar 

  79. Milnor, J.: Dynamics in one complex variable. In: Annals of Mathematics Studies vol. 160, Princeton University Press, Princeton and Oxford (2006)

  80. Misiurewicz, M.: Rotation intervals for a class of maps of the real line into itself. Ergod. Theory Dyn. Syst. 6, 117–132 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  81. Ostlund, S., Rand, D., Sethna, J., Siggia, E.: Universal properties of the transition from quasi-periodicity to chaos in dissipative systems. Physica 8D, 303–342 (1983)

    MATH  Google Scholar 

  82. Palmisano, L.: A Denjoy counterexample for circle maps with an half-critical point. Math. Z. 280, 749–758 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  83. Petersen, C., Zakeri, S.: On the Julia set of a typical quadratic polynomial with a Siegel disk. Ann. Math. 159(2), 1–52 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  84. Rand, D.: Universality and renormalisation in dynamical systems, In: Bedford, T., Swift, J.W. (eds.) New Directions in Dynamical Systems. Cambridge University Press, Cambridge (1987)

  85. Rand, D.: Global phase space universality, smooth conjugacies and renormalisation: I. The \(C^{1+\alpha }\) case. Nonlinearity 1, 181–202 (1988)

  86. Rand, D.: Existence, non-existence and universal breakdown of dissipative golden invariant tori: I. Golden critical circle maps. Nonlinearity 5, 639–662 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  87. Shenker, S.: Scaling behaviour in a map of a circle onto itself: empirical results. Physica 5D, 405–411 (1982)

    Google Scholar 

  88. Shishikura, M.: The Hausdorff dimension of the boundary of the Mandelbrot set and Julia sets. Ann. Math. 147, 225–267 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  89. Shishikura, M.: Bifurcation of parabolic fixed points. In: Lei, T. (ed.) The Mandelbrot Set, Theme and Variations (London Mathematical Society Lecture Note Series, pp. 325–364). Cambridge University Press (2000)

  90. Stark, J.: Smooth conjugacy and renormalisation for diffeomorphisms of the circle. Nonlinearity 1, 541–575 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  91. Sullivan, D.: Quasiconformal homeomorphisms and Dynamics I. Fatou-Julia Problem on Wandering Domains. Ann. Math. 122, 401–418 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  92. Sullivan, D.: Quasiconformal homeomorphisms in dynamics, topology, and geometry. In: Proceedings of the International Congress of Mathematicians, pp. 1216–1228. Berkeley (1986)

  93. Sullivan, D.: Bounds, quadratic differentials, and renormalization conjectures. AMS Centen. Pub. II, 417–466 (1992)

    MathSciNet  MATH  Google Scholar 

  94. Świątek, G.: Rational rotation numbers for maps of the circle. Commun. Math. Phys. 119, 109–128 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  95. Trujillo, F.: Hausdorff dimension of invariant measures of multicritical circle maps. Ann. Henri Poincaré 21, 2861–2875 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  96. Vieira, A.M.S.: Pares holomorfos e a família de Arnol’d generalizada. Ph.D. Thesis, IME-USP (2015)

  97. Voutaz, E.: Hyperbolicity of the renormalization operator for critical \(C^r\) circle mappings. Ergod. Theory Dyn. Syst. 26, 585–618 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  98. Yampolsky, M.: Complex bounds for renormalization of critical circle maps. Ergod. Theory Dyn. Syst. 19, 227–257 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  99. Yampolsky, M.: The attractor of renormalization and rigidity of towers of critical circle maps. Commun. Math. Phys. 218, 537–568 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  100. Yampolsky, M.: Hyperbolicity of renormalization of critical circle maps. Publ. Math. IHES 96, 1–41 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  101. Yampolsky, M.: Renormalization horseshoe for critical circle maps. Commun. Math. Phys. 240, 75–96 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  102. Yampolsky, M.: Renormalization of unicritical analytic circle maps. C.R. Math. Rep. Acad. Sci. Canada 39, 77–89 (2017)

    MathSciNet  MATH  Google Scholar 

  103. Yampolsky, M.: Renormalization of bi-cubic circle maps. C. R. Math. Rep. Acad. Sci. Canada 41, 57–83 (2019)

    MathSciNet  Google Scholar 

  104. Yoccoz, J.-C.: Il n’y a pas de contre-exemple de Denjoy analytique. C. R. Acad. Sci. Paris 298, 141–144 (1984)

    MathSciNet  MATH  Google Scholar 

  105. Yoccoz, J.-C.: Conjugaison différentiable des difféomorphismes du cercle dont le nombre de rotation vérifie une condition diophantienne. Ann. Sci. Éc. Norm. Sup. 17, 333–359 (1984)

    Article  MATH  Google Scholar 

  106. Yoccoz, J.-C.: Continued fraction algorithms for interval exchange maps: an introduction. In: Frontiers in Number Theory, Physics and Geometry, vol 1. On Random Matrices, Zeta Functions and Dynamical Systems. Springer-Verlag (2006)

  107. Zakeri, S.: Dynamics of cubic Siegel polynomials. Commun. Math. Phys. 206, 185–233 (1999)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Instituto de Matemática e Estatística, Universidade de São Paulo, Rua do Matão 1010, 05508-090, São Paulo, SP, Brasil

    Edson de Faria

  2. Instituto de Matemática e Estatística, Universidade Federal Fluminense, Rua Prof. Marcos Waldemar de Freitas Reis, S/N, 24.210-201, Bloco H, Campus do Gragoatá, Niterói, Rio de Janeiro, RJ, Brasil

    Pablo Guarino

Authors
  1. Edson de Faria
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pablo Guarino
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Edson de Faria.

Additional information

Communicated by Philip Boyland.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Edson de Faria has been supported by “Projeto Temático Dinâmica em Baixas Dimensões” FAPESP Grant 2016/25053-8, while the second author has been supported by Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES) grant 23038.009189/2013-05.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

de Faria, E., Guarino, P. Dynamics of multicritical circle maps. São Paulo J. Math. Sci. 16, 340–395 (2022). https://doi.org/10.1007/s40863-021-00236-1

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40863-021-00236-1

Keywords

Mathematics Subject Classification

Search

Navigation