Production economy and industry studies

Abstract

This paper explores the concept of production economy, or the contemporary version of plutology, the study of production and distribution of wealth originally found in classical economics, for the empirical analysis of industries as flows of specific value-carrying design information to the market. The concepts and logic discussed in this article include the following: industrial/manufacturing sites as basic economic agents; design information as the source of value-added; the combination of downward-sloping market demand curves and flat individual supply curves generated by design-based product differentiation; design as an additional variable to make profit and employment goals compatible; manufacturing capabilities and their evolutions; a substantial, flow-oriented view of industries; Sraffian steady-state price systems at the national level; the concept of industrial competitiveness; the Ricardian theory of international production cost comparison; design-based comparative advantage; the CAP (capability-architecture-performance) approach to industrial evolutionary analysis. The present framework of production economy is also applied to the case of global competition during the post-Cold-War era (1990s–2010s).

1 Production economy as analysis of industrial sites

1.1 Economics of exchange and production

1.1.1 Motivation and purpose

This article attempts to explore the concept of production economy, or plutology, for the analysis of industries, where production occurs. The models used here are mostly those of classical economics, in which prices are determined by production costs, rather than of the mainstream neoclassical economics, where prices and quantities are simultaneously determined by demand and supply equilibrium. This choice is not because of theoretical preference, but because of the author’s judgment as an empirical social scientist who visited over one thousand manufacturing sites in the late twentieth century and early twenty-first century, when both the wages and productivities of factories changed rapidly worldwide. The author’s conclusion, after analyzing the evolutions of industrial performances and capabilities for about 40 years (Fujimoto 1989; Clark and Fujimoto 1991; Fujimoto 1999; Fujimoto and Ikuine 2018, etc.), is that we need a revival of production economy, in its twenty-first century version, at least for empirical reasons. In other words, the analytical framework of production economy proposed in this article does not arise from a theoretical thrust but from the needs of an empirical researcher of technology and operations management (TOM) as a user of economic theories. Just like craftspeople make or modify their own tools when there are no appropriate ones, we empirical researchers sometimes build our own analytical tools for better interpretations of what we observe.

Moving from this motivation, the present article examines a possible modern version of production economy that can be used for analyzing changes in industrial performances in the late twentieth century and early twenty-first century. Although the roots of production economy (i.e., plutology) are found in the theories of nineteenth-century classical economists, including David Ricardo, we need newer concepts, such as design information, product architectures, organizational capability, evolution and innovation, for analyzing modern industrial phenomena, particularly in the post-Cold-War era (1990s–2010s).

This article is thus related to the basic logic and theories of production economy in their twenty-first century version and discusses such key concepts as industrial sites (genba), flow-based-manufacturing, design information as source of value-added, industrial competitiveness, Ricardian comparative production cost, Sraffian price system, full/direct costing, manufacturing/improvement/evolutionary capabilities, product-process architectures of integral/modular types, design-based comparative advantage, site-oriented firms, grassroots innovations and fractal system of employment creation. Because of the empirical motivation of this article, the only concepts that can be used persuasively for the empirical analysis of actual industrial phenomena are chosen as components of production economy.

1.1.2 Sir Hicks and plutology

In 1976, when there were active academic discussions on Thomas Kuhn’s paradigm or Imre Lakatos’s research program, Sir John Hicks, the prominent economist of the twentieth century, presented an article on revolutions in economics (Hicks 1976), in which he distinguished between two major economics paradigms, i.e., plutology and catallactics. Plutology, which stems from the work of classical economists, such as Adam Smith and David Ricardo, focuses on production (i.e., flow) and distribution of wealth and is nowadays often called “political economy”. Prices (i.e., natural or normal prices) are determined by unit production costs and profits.¹Catallactics, on the other hand, which stems from the “marginal revolution” of the nineteenth century, focuses on the exchange of goods and services and is now recognized as the neoclassical school, its microeconomics in particular. Prices (i.e., market prices) are determined by demand–supply equilibrium. Hicks then argued that the “triumph of catallactics” in the twentieth century was mainly based on its intellectual quality, including its mathematical sophistication, rather than ideology (e.g., socialism versus free economy).

As of 1976, Hicks did not make any predictions on the economics of the twenty-first century, but he does not seem to have assumed unilateral convergence to catallactics. First, in the last part of his article, he said that “what we want, in economics, are theories which will be useful, practically useful,” indicating the pragmatic criterion that any theories that are useful should survive. Second, he hinted at the possibility of a “revival of the classical political economy” when he referred to Pigou’s welfare economics in the same article. Third, Hicks is known to have classified the economy into fix-price sectors (e.g., manufacturing goods) and flex-price sectors (e.g., agricultural goods), in which the former notion is closer to the classical price model, based on unit production costs rather than demand–supply equilibrium (Hicks 1965).

1.1.3 Why production economy?

The idea of production economy presented here follows Sir Hicks’s abovementioned stance. That is, in this article, the author selects the concepts and logic that seem “practically useful” for the analysis of actual industrial competition, firms’ production activities and manufacturing processes. The author’s conclusion, according to this criterion, is that the classical assumption that normal prices are determined by unit production costs is more realistic as far as today’s manufactured goods are concerned.

My belief that the analysis of industrial production should be based primarily on the classical production cost principle does not imply that it is theoretically superior to the neoclassical assumption of equilibrium, but simply that it tends to be more “practically useful” for empirical analyses of industries as systems of value flows. Again, as an empirical researcher, the author is a user of theories, and users normally prefer variety in what they use. For this reason, the author favors the coexistence of classical plutology and neoclassical catallactics, as long as they are both useful for analyzing different industrial phenomena.

Therefore, the present paper attempts to propose a contemporary plutology, as it were, for the empirical analysis of industrial competition and capability-building. As such, production economy shares its basic theoretical stance with contemporary classical economics, but note that the focus of this article is on production rather than distribution, which is emerging as another critical topic in the twenty-first century. Classical economics, including that of Marxists, is often called “political economy,” but its theoretical focus leans toward distribution and government policies rather than actual production by factories, firms and industries. Thus, the author has chosen a straightforward name, “production economy.” It implies a social scientific framework for empirically analyzing production, or manufacturing, in industries by applying the concepts of classical economics and other related academic fields, including technology and operations management, industrial engineering, design theories, evolutionary economics and even neoclassical economics, wherever appropriate.

Production economy is, in a sense, an interdisciplinary field, partly because its most basic unit of analysis is a wealth-creating industrial site (e.g., a factory), rather than a profit-maximizing firm, and because an industrial site possesses a multifaceted nature—it belongs to a firm, an industry and a region at the same time.

1.2 The nature of an industrial site

1.2.1 Genba as industrial site

Let us first discuss the nature of industrial/manufacturing sites, called genba (actual place) in Japanese, as a socioeconomic entity. An industrial site refers to the place in which wealth (i.e., value-added) flows to the market, as well as the people operating/managing/improving such flows. As Sir Hicks pointed out, production is “the flow of wealth” in Adam Smith’s sense and the “wealth of a nation is what we now call the national product” (Hicks 1976; Smith 1776).

Then, it follows from this insight that the very basic unit of analysis in production economy is a place or a space where the flows of wealth or value-added are created by the people working there, which we call an industrial site (or, from now on, simply a site) and which may include a workstation, a production line, a factory, as well as a product development project. To rephrase the idea, an industrial/manufacturing site is a place in which value-added flows to the customers in the market; thus, it is the most fundamental unit of the national economy on the supply side.

In production economy, value flow is a very important concept. For example, whereas equilibrium is the core concept in neoclassical economics, as the theory of exchange/matching, steady state of the flows, or reproduction, has been central to classical economics in a broad sense, from François Quesnay to Adam Smith, David Ricardo, Karl Marx, as well as Piero Sraffa, as a modern classical economist. A general equilibrium creates an order by essentially stopping the flow, just like thermal equilibrium, whereas a steady state is a self-organizing situation in which an order is created by the flow itself, just like a river in normal times or the flame of a candle. Thus, in production economy, flow and steady state, rather than equilibrium, are the key analytical concepts.

Besides, in production economy, we regard a site (or its people), having a collective will to survive, as an agent of a regional economy. In catallactics, which primarily analyzes economic exchanges, the basic economic agent is a firm, because an exchange means a change of ownership and because it is the firm as a corporate body, not the site, that owns goods, materials and capital.

In production economy (plutology), by contrast, the main research theme is the generation of wealth, rather than its ownership and exchange, so an organization that has the will and capability to control and improve the flows of value-added is regarded as an economic agent and it is usually referred to as an industrial site (genba). Hence, production economy treats both sites and firms as economic agents despite the fact that the former are owned by the latter. In fact, knowledge sharing and trust relationships between an industrial site and a corporation (e.g., headquarters, top management teams) are crucial topics in production economy.

1.2.2 The standard three-layer model of national/global economy

If we put an industrial site instead of a firm at the bottom of the supply side of an economic system, we have to modify the conventional three-layer view of firms, industries (markets) and national economy from the bottom up (Fig. 1(1)). Indeed, the alternative view used in this article is also three-layered, but the industrial sites are at the bottom, and the firms are moved up to the second layer together with the industries and regions, with the national economy at the top, as before (Fig. 1(2)).

Fig. 1

Economy, industry, firm and site

In today’s standard (i.e., neoclassical or catallactics) economic textbooks, a firm that makes one kind of product appears at the first level as a price-taker and determines its individual upward-sloping supply curve, which shows its profit-maximizing supply quantity as a function of a given price.

At the second level, the individual supply curves of all the firms making the same product are aggregated into a market-level (or industry-level) supply curve, which meets the market-level demand curve, that is, the aggregation of the consumers’ utility-maximizing individual demand curves. The price and quantity of this particular product are determined simultaneously at the intersection of the two market-level curves—the partial (i.e., industrial) equilibrium in a perfectly competitive market, assuming that this market is independent from other markets.

At the top level, all the markets of a national economy, as well as their interdependence, are taken into account and it is shown that, in all the markets, prices and quantities can be optimally determined at the same time as a general equilibrium. In this standard-textbook-type three-layer model, a firm is a single-product firm and an industry is illustrated by a market (or industry) supply curve, which is a simple summation of the firms’ individual supply curves. The word “industry” is often replaced by a more popular notion, i.e., “market.” Thus, in this standard model, “industry” has been a less important concept, in that it is merely an interim layer for explaining partial equilibrium and ultimately general equilibrium. Indeed, in the mathematically sophisticated model of today’s neoclassical microeconomics, the only operation that is needed to explain an industry is a simple summation.

1.2.3 An alternative three-layer model of production economy

Production economy, on the other hand, starts from the sheer empirical fact that production of a product, or generation of value-added, occurs at industrial sites, including factories, production processes and workstations. This is why we put the industrial site at the first level of our alternative three-layer model (Fig. 1(2)).

The second level has at least three components: industry, firm and region. An industry is a collection of sites that make the same or similar products and their parts. These industrial sites are interconnected by transaction, competition and complementation. A firm may produce multiple products, which is closer to today’s reality, so it consists of multiple sites, often across different industries and countries. It pursues profit, cash flow and revenue. Yet, it may not determine production quantities based on the profit-maximizing principle but uses the firm-level principle of effective demand, as explained later. A region is usually a part of a nation (possibly also across borders), where people live their lives as residents, consumers, employees and so on, and it includes communities, municipalities and districts. On its supply side, a region may be described as an area with a boundary, or as a network of inter-related sites (e.g., industrial agglomeration).

As also indicated in Fig. 1(2), when a firm intersects an industry, this intersection is called a business. Today’s firms are mostly multi-business or at least multi-product firms (Chandler 1962), in which a single-product manufacturing site may belong to one of such business units. When an industry and its supporting industries take root in a region, this is called an industrial agglomeration, or cluster (Marshall 1890; Porter 1990). When a particular firm and its supporting firms are concentrated in one region, the area is often referred to as a company town.

In this way, the supply side of the national and/or world economy may be decomposed into industries, firms and regions, but these three entities at the second level can all be regarded as certain collections of industrial sites. In other words, a site belongs to an industry, a firm and a region at the same time.

1.2.4 Three-way contributions of sites

Thus, the alternative three-layer model is shaped like a trident when looking up from the sites in the bottom layer, which accounts for its multifaceted nature (Fig. 1(2)). That is, for the sake of its social legitimacy and survival, an industrial site needs to contribute to each of the three entities to which it belongs, i.e., to the industry through value-added, to the firm through profit and to the region through employment.

First, value-added is preceded by revenue, and revenue requires corresponding customer expectations and effective demand for a particular product. Second, its profit contribution, following the markup or full-cost principle of the so-called Oxford Study (Hall and Hitch 1939), serves to achieve a certain target markup ratio rather than profit maximization. Third, employment at a site generates corresponding income for its employees in the region.

We may, therefore, rephrase the industrial site’s abovementioned contributions as (i) creating effective demand for the product, (ii) achieving target markup (profit-added) ratios that satisfy the firm to which it belongs, (iii) securing employment levels that satisfy the regions in which the employees live. The weight given to these three elements may be different case by case, but some empirical studies indicate that there are certainly many industrial sites or site-oriented firms that have pursued the three goals at the same time.²

To sum up, an industrial site is described as an economic agent that aims to reach certain satisfactory levels of profit rates and employment levels at the same time, by simultaneously generating effective demand and achieving efficient production.

2 Industry as a system of design, capability and performance

2.1 The economic function of design information

2.1.1 Design as a source of value-added

We have so far argued that plutology, the study of the flows of wealth, or production economy, can be an alternative research framework, at least from the point of view of empirical industrial research, and that a value-generating industrial site, rather than a profit-maximizing firm, is the most basic unit of analysis for production economy. A site’s multifaceted contribution to industries, firms and regions by generating effective demand, achieving profit targets and securing employment has also been discussed.

Our next question regarding production economy is what the source of wealth, or value-added, is in the first place. In modern production economy, it is design, as information/knowledge about the relations between an artifact’s functional and structural elements, defined in design theories (Simon 1969; Suh 1990; Ulrich 1995). In other words, this article argues that value-added dwells in design information (Fujimoto 2007). Design is a relatively new concept emerged in the twentieth century, which did not exist in the heyday of classical economics, so this may be one of the main additional factors in modern production economy vis-à-vis its classical version, plutology.

But how can we say that design information is the source of value-added? Let us regard a product as a tradable artifact and an artifact as a “designed thing”, a combination of design information and its media (material and/or energy). This may be seen as a modern application to the case of artifacts of Aristotle’s idea of a “being as a combination of form and matter”.

Suppose that the price of a paper cup is 1 dollar and that the cost of the paper that the manufacturing firm bought from a supplier (i.e., direct material) is 30 cents per cup. Then, the value-added is 70 cents per cup. Where did it come from? There are no other inputs except the structural/functional design information that the firm’s planners, designer and engineers created regarding the cup’s shape, style, durability, ease of use, stability and so on—its functions and structures. That is, the firm has generated 70 cents of value-added by creating and transferring certain design information to the material.

Incidentally, “cup” is the name of the design information, because a cup made of any material (e.g., paper, metal, ceramic, glass) is called a “cup.” A natural stone which may be used as a cup, on the other hand, may simply be called a “stone” because the users do not recognize the designer’s intention in it. Thus, design information as the source of value-added is a more essential part of products than their materials, as stated by Aristotle, who said form is more essential than matter.

It follows from this design view of value-added that production should be looked upon as “transfer/transmission of value-carrying design information to the materials-as-media” rather than “transformation of the materials,” which is a standard definition of production. We use this design-information view of production and manufacturing consistently throughout this article.

It is important here to also note that design information, including design knowledge, has two aspects: that of concrete causal relations between a given artifact’s structures and functions is called technology and that of abstract correspondences between functional and structural elements, often expressed by a bipartite graph, is called architecture. We rely heavily on this concept of product–process architecture in our production-economy-based industrial analyses.

2.1.2 Design and downward-sloping demand curve

Since products that are designed differently are mutually differentiated in the market, the situation for each firm or site is akin to that of monopolistic competition, in which competing products are similar but heterogeneous, and each product faces a downward-sloping demand curve (Chamberlin 1933).

What is different from the conventional monopolistic competition model, however, is that a firm with a new product is neither a simple price-taker nor a simple price setter. The process in this model of design-based production economy is more like a dialog between the firm and the future market through design. That is, the firm provides a new design to the market, forecasts market responses in the form of predicted demand curves and determines a new product’ price and quantity plan. In other words, in our model of production economy, design is an additional independent variable that the firm can manipulate.

To explain the downward-sloping demand curve more precisely, let us assume here that a customer’s reservation price (willingness to pay) for a product with given design information is determined by the product’s functions and the customer’s tastes and, in addition, that the product functions are realized when the customer-user uses/operates the product’s structures under certain use environments. That is, when consumer i chooses to buy or not to buy product j at a certain time (e.g., a passenger car), the reservation price (p^r_ij) of consumer i for product j can be expressed as shown below, where the product’s structure is S_i, the user’s predicted pattern of product operation/usage is $\tilde{O}_{ij}$, the predicted use environment is $\tilde{E}_{ij}$, the product’s expected function is $\tilde{F}_{ij}$ and the customer’s taste converting the product functions into the reservation price is f_ij:

$$ p^{r}_{ij} \, = \,f_{ij} \left( {\tilde{F}_{ij} } \right)\, = \,f_{ij} (S_{j} ,\,\,\,\tilde{O}_{ij} ,\,\,\tilde{E}_{ij} ). $$

It is obvious that the reservation price (p^r_ij) of the same product structure (Sj) will be different from customer to customer because of the distribution of their tastes (f_ij), predicted operation patterns ($\tilde{O}_{ij}$) and predicted use environments ($\tilde{E}_{ij}$). If we aggregate all potential customers’ individual demand functions that connect selling price p^s_j and demand quantity 1 or 0 (1 if p^r_ij ≥ p^s_j; 0 if p^r_ij < p^s_j), we can obtain a market demand function for product j that is downward sloping (Fig. 2).

Fig. 2

Product j with its flat supply curve facing a down-sloping market demand curve

On the supply curve side, if we adopt the classical assumption that a product’s price is determined not by demand–supply equilibrium but by unit production cost plus markup regardless of quantity (p^s_j = (1 + r)C_j), the individual supply curve for product j can be drawn as a flat curve. The quantity at the intersection of a product’s individual flat supply curve and downward-sloping market demand curve can be interpreted as the effective demand quantity for product j.

In this way, our production economy framework starts from the classical assumption of normal price as production cost plus normal profit but adds an additional factor called “design.” As a result, the product in question is now differentiated by design, so each product design faces a downward-sloping demand curve as a summary of the market’s evaluation of that particular product. Since effective demand quantity is determined at the intersection of the supply and demand curves, design quality will influence the effective demand quantity through shifts in the demand curves.

In any case, unlike in the standard neoclassical model, in which prices and quantities are simultaneously determined by demand–supply equilibrium, in the present model of production economy, prices and quantities are not determined simultaneously, partly because the supply curve is flat and partly because the product design affects the demand curve and the effective demand quantity.

2.1.3 Demand creation and innovation-as-new-design

In this context, design information concerns the predicted causal relations between product j’s structures and predicted functions when customer i uses it, or (S_j,$\tilde{F}_{ij}$). Hence, if a firm can successfully improve the quality of its product design, potential customers are likely to revise their reservation prices, p^r_ij, so that the market demand curve is likely to be shifted upward.

As shown in Fig. 2, given the supply curve, or the planned unit production cost (C_j^*), markup ratio (r^*) and supply price (p^s_j^* = (1 + r^*)C_j^*) of product j, the upward shift of the demand curve through effective design will expand the effective demand quantity (x^s_j), thereby increasing the employment level at the site manufacturing the product. Conversely, given the target production quantity of the product (x^s_j^*) required for the site to retain employment, higher design quality, through the shift of the demand curve, will bring about higher supply price (p^s_j) and, consequently, higher site-specific wage rate and/or profit rate, at least temporarily.

This is the power of effective design, which should be incorporated into the analysis of modern production economy. With design as an independent variable that can shift the market demand curve, a firm’s product and site may be able to achieve target employment level, corresponding target sales quantity (x^s_j^*), target selling price (p^s_j^*), markup ratio (r^*) and target unit cost (C_j^*) at the same time as a steady state. The author calls this framework the PXNW model (Fujimoto and Ikuine 2018, 123‒154), which simultaneously describes and analyzes P (price–cost), X (production quantity), N (required employment in person-hours) and W (hourly wage rate) within a four-quadrant diagram.

In this context, we can also reinterpret Joseph Schumpeter’s concept of innovation, which is a new combination of materials and forces that generates economic development (Schumpeter 1934). Production economy reinterprets innovation as new combination of an artifact’s functions and structures creating economic value, which is nothing but “new design” according to our definition of design. The concept of design was not known to economists when Schumpeter published his first version of The Theory of Economic Development, but it seems obvious that his famous five examples of new combinations (e.g., new good, new production method) involve new designs and artifacts.

We can thus regard the abovementioned upward shift of the demand curve in Fig. 2 as “innovation-as-new-design” for generating additional effective demand at the firm level. While Schumpeter focused on discontinuous innovations for major economic development at the level of the national economy, we also recognize that rather incremental innovations, leading to small shifts of the demand curves for individual products, can have significant economic impacts when many products and sites implement them at the same time.

Furthermore, if the target sales quantity (x^s_j^*) mentioned above is set so as to secure employment at the site producing a product and effective “new design” is used for achieving it, we may regard this as “innovation for employment.” Many such grassroots innovations are observed in small community-based and site-oriented firms in Japan, for instance.

2.1.4 Industry as flows of design information

We have just discussed the concept of design information as a source of value-added and stated that production can be seen as transfer of value-carrying design information to the customers, which is consistent with Hicks’ aforementioned concept of production as flow of wealth. We have also pointed out that, by adding the design factor to the price-quantity model of production economy, products become differentiated and each of them faces a flat supply curve and a downward-sloping market demand curve.

Now, let us turn to the supply curve side. Here our production economy argues that the patterns of the flow of value-carrying design information significantly affect the level of unit production cost (C_j) and the corresponding supply price (p^s_j), and that the manufacturing capabilities of each industrial site, or of the whole industry, have major impacts on such flow patterns, given its productive resources.

As defined earlier, an industrial site is a place where value-carrying design information flows to the customers, as well as the people controlling and improving it. An industry is a collection of sites that develop and produce functionally similar products. The sites and products in an industry are interconnected by transaction, competition and complementation. We can, therefore, define an industry as a network of flows of design information of a similar kind.

Such a substantial view of an industry is very different from the abstract view of an industry as a market supply curve in the model of neoclassical microeconomics. This view of industries and sites is also akin to Edith Penrose’s substantial model of a firm as a collection of productive resources, including production equipment and tools, human resources, materials, work-in-process, product inventories and so on (Penrose 1959). That is, from the standpoint of our design-flow view of manufacturing, we can regard a firm as a collection of sites in which value-carrying design information flows among Penrose’s productive resources deployed on the shop floor, each of which can be seen as a stock of design information embedded in various tangible/intangible media.

As Penrose pointed out, a firm’s productive resources are significantly underutilized, which implies that there is significant room for making the flows more efficient, given the productive resources. For example, the ratios of the time when value-carrying design information actually flows among the productive resources on the shop floor (i.e., value-adding time ratios) are surprisingly low in most fabrication-assembly factories worldwide—less than 10% on the design-information-sending side and less than 1% on the design-information-receiving side. If these numbers increase by N times, other things being equal, physical productivities will increase by N times in the former case and production lead times will become 1/N in the latter case.

Thus, although capital investment and human training are important for productivity enhancement, physical productivities and other industrial competitiveness factors may be improved by enhancing efficiency and accuracy of the flows of design information among productive resources. The product’s unit production cost (C_j↓) will be reduced accordingly, which may lead to a downward shift of the supply curve (p^s_j↓), an increase in markup ratio (r*↑) or an increase in wage rate (w_j).

To sum up, a modern version of production economy needs to incorporate the flow analysis of value-carrying design information to the market, which also implies that, in addition to classical unit production cost, unit design cost should be taken into account when analyzing price and cost. This is an important assumption for establishing the hypothesis of design-based comparative advantage (Fujimoto 2007; Fujimoto and Ikuine 2018).

2.2 Capability, productivity, cost and price

2.2.1 Manufacturing capability and its evolution

Wherever there are stable and repetitive flows at industrial sites, which is mostly the case in modern manufacturing, better managed factories utilize a certain set of organizational routines that control and improve the flows among productive resources, which we may call manufacturing routines. Then we may call a system of interconnected routines that governs the total flow of value-carrying design information “organizational capability for manufacturing,” or simply manufacturing capability. For example, the Toyota Production System is one of such examples of manufacturing capability, and its expert practitioners tell us that it consists of about two hundred routines.

Better manufacturing capabilities not only help sites, firms and industries improve their flow of value-added but also evolve over time themselves. We can thus conceive of three types of capabilities: (i) static manufacturing capability for sustaining effective flows; (ii) improvement capability for continuously improving the flows on a routine basis; (iii) evolutionary capability for making the emergence of new routines happen (Fujimoto 1999).

In actual industrial practices, the flow of value-added and materials has been an important concept in the Ford System, Toyota System. Lean System, Theory of Constraints and so on. Continuous flow improvements have been quite common industrial practices for many years in the late twentieth and early twenty-first century. The author has also seen a number of actual cases where improvement of the value-added flows at better managed factories resulted in the enhancement of physical productivities of their production lines by several times in several years, without much capital investments.

To sum up, in order to follow the rapid changes of the flows constantly happening at actual manufacturing sites, firms and industries, the modern version of plutology, or production economy, needs to incorporate an evolutionary perspective when describing and analyzing the dynamics of design information flows and the manufacturing capabilities behind them.

2.2.2 Steady-state prices

Let us now move up to the third level of Fig. 1, the national economy. At this level, the value-added of domestic sites, firms and industries is aggregated into national products (e.g., GNP, GDP) in standard macroeconomics. As for the prices of all the products in the national economy, the general equilibrium theory in microeconomics mathematically proves (by solving simultaneous price-quantity equations) that a set of prices that achieve demand–supply equilibriums in all markets exists under perfect competition (e.g., Arrow and Debreu 1954). This is the consensus on the side of Hicks’ catallactics.

On the side of plutology, on the other hand, there is no clear consensus but, from the production economy’s point of view, the most complete theory of prices regarding multiple products and markets at the level of the national economy has so far been provided by Piero Sraffa’s Production of Commodities by Means of Commodities (Sraffa 1960).

This concise but mathematically precise book follows the aforementioned Ricardian (or classical) view that price is determined by unit production cost and markup ratio (p = (1 + r)C). However, unlike Ricardo, who reduced unit production cost to direct labor cost (C = aw, where a is the labor input coefficient and w is the average hourly wage), Sraffa included not only labor cost but also what today’s cost accounting calls direct material costs and factory overhead (e.g., production tools and equipment), each of which can also be calculated as input coefficient times input price. That is, C = (a₀w + ∑a_jp_j). So the corresponding selling price is p_j = (1 + r)(a₀w + ∑a_jp_j), where a₀ is the labor input coefficient and a_j is equal to the input coefficients of product j. Note here that there is a circular relation whereby inputs become outputs and outputs become inputs (p_j shows up twice in this equation).

Sraffa (1960) proved that we can solve these simultaneous equations in the cases of non-growth economies and growing economies, as discussed later. It is important to note that, in Sraffa’s price system, the prices, including the wage rate (w, p_j), are determined by input coefficients (a₀, a_j), which are nothing but the inverse of physical factor productivities, and markup ratio (r), which is related to the distribution of income between capital and workers. That is, in Sraffa’s system, prices and wages, given the markup ratio, are determined by the productive performance of manufacturing sites. Thus, we adopt this Sraffian model of prices as a basis for the production economy concept.

We should also note that this pricing system of modern production economy is not dependent on the classical labor theory of value, or the subsistence theory of wages, which is not realistic in most of the industrialized nations today. Sraffa’s prices are based only on productivities (input coefficients) and profit (markup) ratios, regardless of any definition of substance wages. These prices of modern plutology are not equilibrium prices either, unlike in catallactics (e.g., general equilibrium theory). They are, as it were, steady-state prices, or the prices that sustain a stable pattern of flows or circulation of merchandise and value-added.

To sum up, instead of using the neoclassical general equilibrium model, modern production economy adopts the steady-state price model, in which all the prices in the national economy are compatible with stable flows/circulation of materials, goods and value-added, given the sites’ productivity and profit requirements. We may regard this as a flow-sustaining system of prices. As such, the model adheres to the classical assumption of the “production cost plus markup” theory of value, but it departs from the seemingly now-obsolete labor theory of value of the nineteenth century. In any case, the price (value) model that production economy adopts is a flow-oriented one.

2.2.3 Summary: price-quantity model of production economy

Let us review the discussion up to this point. This article has argued that today’s empirical economic analyses call for not only economics of exchange (catallactics), represented by the neoclassical school, but economics of production (flow of wealth in Hicks’ terminology), or plutology in a modern version. Various potential components of twenty-first-century production economy have also been discussed. Going back to Fig. 2, the basic price-quantity system of production economy, as presented in this article, may be summarized as follows:

• 1. Production economy regards a value-generating industrial site, rather than a profit-maximizing firm, as the most fundamental economic agent on the supply side of the national/world economy. It recognizes both sites and firms as economic agents. An industrial/manufacturing site belongs to, and contributes to, an industry, a firm and a region at the same time by pursuing goals related to value-added, profit rates and employment size (Fujimoto and Ikuine 2018, 123‒154).

• 2. It adopts the classical assumption of value, in which normal price equals unit production cost plus normal profit, but abandons the labor theory of value, in the form of the subsistence theory of wages. This results in a flat market supply curve for a given product, unlike the neoclassical upward-sloping curve.

• 3. It adopts a non-classical concept of design, which is information on the structure–function relations of products and other artifacts. Design information is the source of value-added (wealth), in that buyers’ reservation prices (willingness to pay) are determined by the product’s functions expected by the buyers-users.

• 4. Design is an additional independent variable that firms can manipulate, so most of today’s manufactured goods competing in the market are functionally similar but differentiated from each other by design differences. Consequently, each product of identical design faces a downward-sloping market demand curve, which reflects variances in product functions and users’ tastes. Effectiveness, or quality, of product design affects the shape of product-specific market demand curves.

• 5. Production economy also adopts the concept of flow, or value-added and materials, which some classical economics also emphasized, but it elaborates it by reinterpreting the flows of value-added as flows of value-carrying design information and applies it to the details of the manufacturing process in sites, industries and firms. Such key concepts as manufacturing, production, development, sales, productivity, quality, lead time, as well as manufacturing routine and capability, are all defined consistently in relation to the concept of flow of value-carrying design information among productive resources and eventually to the customers in the market.

• 6. It assumes that this flow determines the supply prices of the products and, consequently, the height of the flat supply curve for each differentiated product. First, the unit production cost of each individual product is the sum of the physical productivities (inverse of) times the unit prices of all the productive resources whose design information is transferred to that product. Second, the productivities of all the productive resources are determined by the patterns of this flow. Third, the unit prices of all the productive resources (i.e., commodities in the production process) are determined by a Sraffian steady-state (flow-sustaining) price system, in which the productivities and profit (markup) ratios of all the products and labor determine all the prices and a wage rate. As a result, in our production economy model, the price of a given product is determined by the productivities of all the productive resources and the markup ratio.

• 7. The system of organizational routines that controls and improves the flow, thereby achieving high and increasing productivities and other productive performances, is called manufacturing capability in production economy. It is essentially a capability for attaining high and better flows, so manufacturing capability-building has a significant impact on the height of a product’s supply curve. We may also conceive of design capability, or a system of routines that brings more effective design to the market. Design capability, therefore, primarily affects a product’s market demand curve. Capability is defined for each individual site but, when capabilities are similar across sites within a firm or an industry, we may be able to say that there are firm-level or industry-level capabilities (Fujimoto 1999).

• 8. To sum up, the major conceptual additions of twenty-first-century production economy to classical plutology are design and flow, as well as capabilities related to them. Building design capability primarily shifts a product’s market demand curve upward, whereas building manufacturing (flow) capability shifts its supply curve downward.

2.3 Competitive performance and comparative advantage

2.3.1 Industrial competitiveness

Having outlined the model of production economy, let us now turn to its international aspects, since our discussion has so far been essentially domestic. For the empirical analysis of today’s global competition, we need to introduce an analytical framework of the international competitiveness of industries.

Again, we define an industry as a collection of sites within a country that make similar but differentiated products competing with each other. To the extent that the sites within an industry face similar competitive environments and build similar capabilities and productivities for their survival, we may view an industry as an economic quasi-agent with similar competitive behaviors observed inside it. Although, strictly speaking, an industry is not an economic agent, unlike a firm, it is common for industrial observers to say “country A’s auto-industry is competing against country J’s auto-industry.”

Thus, when large international differences in average productivities are observed among industries making similar products compared with those among sites within a domestic industry, we regard this situation as international industrial competition. Such a situation has commonly been observed, for instance, in the world automobile industry in both assembly and product development productivities since the 1980s (Womack et al. 1990; Clark and Fujimoto 1991; Holweg and Pil 2005).

Then, generally speaking, what is competitiveness, or competitive performance? Although perfect and imperfect competitions are clearly defined in neoclassical microeconomics, competitiveness is not. Therefore, it is up to production economy to define it.

Based on numerous observations of actual competitive behaviors, we define competitiveness as the ability of a subject (i.e., selectee) to be selected by another subject (i.e., selector) according to certain criteria under the condition of free choice. If the selectee is the firm as a whole and the selector is the capital market, the former’s competitiveness is profit performance. If the selectee is a product and the selector is the product market, it is market performance, and its criteria include price. If the selectee is a site striving for survival and the selector is the firm that can close it down, it is productive performance and its criteria include physical productivity.

2.3.2 Reinterpreting Ricardo’s example

The starting point for analyzing international industrial competition is, again, David Ricardo’s theory of comparative advantage (Ricardo 1817, Chapter 7), because it can easily take into account changes and international differences in productivities (i.e., input coefficients).

Ricardo’s original trade theory deals with a simple situation in which industries producing two products (e.g., cloth and wine) in two countries (e.g., England and Portugal) compete internationally based on the same physical productivity within each industry. Hence, there are four so-called “magic numbers” of physical productivities (productive performances) in the four industries (2 products × 2 countries). Let us call them labor input coefficients a_ij (inverse of physical labor productivities). Ricardo’s famous example is as follows: a_Ec = 100 (cloth industry in England); a_Pc = 90 (cloth industry in Portugal); a_Ew = 120 (wine industry in England); a_Pw = 80 (wine industry in Portugal). Let us assume that the unit of measurement here is person-hours per unit.

Then, it is obvious that the Portuguese industrial sites enjoy higher physical productivities (smaller coefficients) than their English rivals in both industries, i.e., wine and cloth. Yet, two-way international trade, in which Portugal exports its wine and England exports its cloth, can happen and both countries gain from this trade. This is called Ricardo’s theory of comparative advantage.

There are at least three ways to explain these directions of trade that are mathematically equivalent, and there are still controversies about how to explain Ricardo’s example. Production economy, as proposed in this article, takes the viewpoint of each individual industrial site competing daily rather than national decision makers pursuing the benefits of international trade.³ Then, what the managers of these industrial sites watch daily are their own international prices versus those of their rivals (p_Ec vs. p_Pc and p_Ew vs. p_Pw). Ignoring transportation costs and tariffs for simplicity and assuming that the same rates of profit (r) are needed to satisfy international traders, we come to the principle of comparing unit production costs for determining the directions of exports and imports: England exports cloth if C_Ec < C_Pc, and Portugal exports wine if C_Ew > C_Pw. We also assume the case of complete specialization between the two countries to make the discussion simpler.

We already know that Ricardo’s unit production cost for product j in country i is C_ij = a_ijw_i, where wi is the hourly wage rate that is common in each country but may be different across countries. Thus, when we observe the abovementioned trade pattern, this means that a_Ecw_E < a_Pcw_P, and a_Eww_E > a_Pww_P.

We can rewrite these inequalities as follows: a_Ec/a_Pc < w_P /w_E < a_Ew/a_Pw. This is a realistic inequality for local factory owners of trading goods—if an emerging country’s hourly wage rate is one-fifth that of an advanced country, the productivity of the latter’s factories must be at least five times as high as that of the former’s factories to survive this international cost/price competition.

Now, if we remove the international wage ratio (w_P/w_E) from the middle of this equation, we obtain a_Ec/a_Pc < a_Ew/a_Pw, comparing “same-industry-different-country” ratios of productivities. This is a microscopic interpretation of Ricardo’s comparative advantage, which is meaningful to individual industrial sites involved in daily international competition.

We can further rewrite the above inequality as the following mathematically equivalent one: a_Pw/a_Pc < a_Ew/a_Ec, comparing “same-country-different-industry” ratios of productivities. Note that this is an inequality that national leaders or general trading firms may comprehend, but individual shop owners will not, because they do not know anything about other industries’ productivities. We may, therefore, call this a macroscopic interpretation of Ricardo’s comparative advantage.

What most standard textbooks of international economics explain as the “theory of comparative advantage” is the latter macroscopic inequality. The way in which Ricardo explains the above cloth and wine example also refers to the latter inequality.⁴

In summary, regarding Ricardian comparative advantage, the three inequalities are mathematically equivalent: (i) international comparison of unit production cost, a_Ecw_E < a_Pcw_P, and a_Eww_E > a_Pww_P; (ii) inter-industrial comparison of nation-to-nation relative productivities, a_Ec/a_Pc < w_P/w_E < a_Ew/a_Pw or a_Ec/a_Pc < a_Ew/a_Pw; (iii) international comparison of industry-to-industry relative productivities, a_Pw/a_Pc < a_Ew/a_Ec.⁵ Standard textbooks tend to explain Ricardian/classical comparative advantage according to logic (iii) to account for gains from trade at the national level, but our production economy, starting from the reality of manufacturing sites, explains the same phenomenon from the bottom up, or in the order of (i), (ii), and (iii).

To sum up, our analysis of international industrial competition in this article starts from Ricardo’s classical international trade theory, or the principle of comparative advantage, but our interpretation is somewhat different from the standard one—production economy emphasizes the reality of international price competition among products, as well as productivity competition among industrial sites.

That is, in Ricardian price competition, industrial site A, which aims to survive, will start from the comparison of market performance regarding its international prices vis-à-vis rival site B, i.e., comparing p_Aj = (1 + r) C_Aj = (1 + r) a_Aj w_A and p_Bj = (1 + r) C_Bj = (1 + r) a_Bj w_B. This means that, in terms of productive performance, in order to withstand global competition, site A has to achieve a productivity of more than N times that of its international rival site B, when B’s wage is as low as 1/N. That is, for a_Aj w_A < a_Bji w_B, to happen, the productivity advantage of A has to be a_Aj/a_Bj < w_B/w_A = 1/N. Note again that physical productivity is the inverse of a_ij.

Thus, all industrial sites of tradable goods in higher wage countries have to survive productivity competition with the “handicap” of international wage differences. In addition, this was the reality of many of the higher wage industrial sites during the post-Cold-War global competition (i.e., 1990s–2010s), when unusual wage gaps between advanced and some emerging nations (e.g., China) were revealed and persisted.

2.3.3 Design-based comparative advantage

As explained above, in order to analyze the international industrial competition of the twenty-first century, modern production economy, while starting from the classical theory of comparative advantage and international production cost comparison, needs to modify the Ricardian model in at least four ways.

First, as explained with regard to the abovementioned inequalities, modern production economy should reinterpret the logic of comparative advantages from the bottom up: (i) comparative cost, (ii) microscopic view, and (iii) macroscopic view. Second, it must no longer interpret labor input coefficient a_ij as a static coefficient, but as productivity-as-a-variable, which competing industrial sites continuously try to enhance to secure their own survival. This means making the Ricardian model more dynamic (Fujimoto and Shiozawa 2011–12). Third, the model of unit production cost may need to be brought closer to a more realistic one, including not only direct labor cost but also direct material cost and factory overhead, just like a modern full-costing system. In a sense, this is a Sraffian modification of the Ricardian trade theory, which was made by Yoshinori Shiozawa (Shiozawa 2007).

Fourth, twenty-first-century production economy needs to take the design factor into account. That is, while keeping the classical price setting principle of unit cost plus markup, production economy, as proposed in this article, incorporates not only unit production cost but also unit design cost. More specifically, we explore the relations between the design characteristics of a product and its unit design cost, which we call the theory of design-based comparative advantage, or international design cost comparison (Fujimoto 2007; Fujimoto and Ikuine 2018).

Such design perspectives of comparative advantage are important, first, because the design and development facilities of multinational and local firms are rapidly proliferating in many nations, including emerging countries, in this century, so that today’s trade theories have to ask not only “where to produce a certain product” but also “where to design a certain new product.” Second, they are important because the design location of a particular new product tends to become the location of its initial production, which in turn tends to become the place of volume production when scale economies exist (Helpman and Krugman 1985; Melitz 2003). The third reason for their importance is that, due to the proliferation of new product development facilities worldwide, we frequently observe minute intra-industrial trade, in which apparently similar products (e.g., cold-rolled steel sheets for a car’s inner panels and zinc-coated steel sheets for its outer panels) are imported and exported simultaneously between two countries, so we need a certain design-based trade theory to interpret such phenomena.

Thus, the addition of design factors to the analysis of international industrial competition and trade is one of the major modifications to the classical trade theory for explaining the newer competitive phenomena of this century.

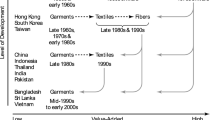
The framework of deign-based comparative advantage incorporated into production economy may be graphically summarized as follows (Fig. 3; Fujimoto 2007, 2012; Fujimoto and Ikuine 2018). The diagram also indicates the main additional components of production economy explored in this article, including capability (flow), architecture (design) and competitive performance, on top of those existing in classical plutology. As such, we may call this framework the CAP approach for analyzing industrial evolutions.

Fig. 3

A framework of design-based comparative advantage

The framework shown in Fig. 3 can also be seen as a framework for design-based comparative advantage, centered around the dynamic fit between an industrial site’s manufacturing/design capabilities and the architecture of its products and its processes. Whereas this framework may be applied to individual industrial sites (e.g., factories), it may also be used to analyze international inter-industrial competition of the aforementioned Ricardian type wherever intra-indusial similarities across sites and international differences among competing industries are both observed.

Both capabilities and architectures evolve over time as a result of certain changes in market requirements, socio-technical constraints, the firms’ capability-building capability, the industries’ capability-building competition and so on, as well as specific decisions made by firms and sites. The changes may occur as a result of deliberate choices of the economic agents or emergent processes, or chance events, which makes the changes evolutionary (Nelson and Winter 1982; Mintzberg and Waters 1985; Fujimoto 1999).

3 Conclusion: back to Alfred Marshall

In this article, we outlined the basic framework of production economy and explained its main components and concepts, among which industrial/manufacturing sites as multifaceted basic economic agents, design information as the source of value-added, the combination of downward-sloping market demand curves and flat individual supply curves generated by design-based product differentiation, design as an additional variable to make profit and employment goals compatible, manufacturing capabilities and their evolutions, the substantial flow-oriented view of industries, a Sraffian steady-state price system at the national level, as well as the concept of industrial competitiveness, Ricardian comparative cost theory and design-based comparative advantage. While this contribution sketched out the overall skeleton of production economy, its details are partially discussed in other books and articles (Fujimoto 2007, 2012; Fujimoto and Shiozawa 2011–2012; Fujimoto and Ikuine 2018, etc.).

In empirical terms, to reflect the intensifying international inter-industrial competition in the post-Cold-War era (1990s–2010s), the present framework of production economy was applied primarily to the design-based comparative advantages of differentiated products, often resulting in minute intra-industrial trade.

Our focus on international industrial competition in the early twenty-first century may remind us of Alfred Marshall’s studies of industries, as well as those of industrial leadership in the early twentieth century. In the former book, Marshal took what may be called a substantial approach to the industry in the entire volume IV of Principles of Economics (Marshall 1890), including his famous discussions on industrial agglomeration.

Marshall is often remembered as the founder of the neoclassical partial equilibrium theory, including the so-called “Marshallian cross”, with upward-sloping industrial supply curve and downward-sloping market demand curve; yet, what he wrote about industries was much more than that. That is, Marshall himself regarded this mechanical theory merely as the beginning of the industry-level analysis and said that the ultimate goal (“Mecca”) is to establish economic biology, in order to study organic growth and thereby solve the problem of poverty. In addition, this is why Marshall is often recognized as one of the early founders of evolutionary economics (Hodgson 1993).

In his Industry and Trade (Marshall 1919), Marshall spent most of the volume I analyzing the “industrial leadership” of some major economic powers at the time, such as England, the USA and Germany. He argued that international trade is caused by “industrial leadership,” or a specific national industry’s advantages in technology or organization over competing industries in other nations, and that such leadership evolves over time when a particular industry embodies a nation’s unique strength (e.g., standardization in the USA, scientific application to industries in Germany).

We may notice that the basic logic of Marshall’s concept of industrial leadership is somewhat akin to the hypothesis of design-based comparative advantage. Assuming that there is a nationwide tendency toward a specific type of capability that evolves over time, an industry whose product/process architecture fits with this national pattern of capability is likely to enjoy comparative advantages in design or design costs.

We should also note that Alfred Marshall was arguably the last truly mainstream economist who took a substantial approach to industries. After him, in the thrust of neoclassical microeconomics to perfect its general equilibrium theory, industry as a substantial economic entity was almost regarded as some sort of impurity and carefully taken out of the main discussion of catallactics. Ironically, Marshall’s partial equilibrium theory, in which an industry is abstracted to market demand–supply curves, remained in the mainstream framework as a rather interim step toward general equilibrium. There is an important branch of mainstream economics that contains the word “industry,” namely industrial organization, but it is seen as applied microeconomics, rather than as a substantial study of industries per se.

Thus, although there have been a variety of empirical contributions on international industrial competitiveness in the past decades (Dertouzos et al. 1989; Womack et al. 1990; Clark and Fujimoto 1991), mainstream economists have seldom been involved in such studies.

In this sense, the idea of this article to propose production economy to analyze international industrial competitiveness may be seen as a small attempt to re-establish the link between studies of international industrial performances and economics, if not mainstream economics, about one hundred years after Marshall’s work on industry leadership.